circRNA是具有共价闭环结构的内源性非编码RNA，最初被认为是RNA错误剪接的副产物^[1]. 随着高通量测序方法和生物信息学的飞速发展，多项研究已证明circRNA与其他分子存在相互作用，参与生物体内各项生命活动的调控，例如靶基因表达、细胞增殖、免疫应答、遗传印迹、肿瘤侵袭等^[2-5]. 与circRNA 相关的各种生物学数据存储在公共数据库中，如circBase^[6]、CircR2Disease^[7]、circRNADisease^[8]和circ2Traits^[9]等.

在“相似的circRNA可能与相同的疾病有相似的关联”假设下，许多计算模型被用于挖掘潜在的circRNA-疾病关联，解决了传统生物实验耗时长且高成本的问题^[10]. 这些模型可以大致分为3类：基于信息在网络中的传播、基于机器学习和基于深度学习. Fan等^[11]提出使用异构网络的路径信息进行circRNA-疾病关联预测的KATZ度量计算模型（KATZHCDA）. Li等^[12]提出基于网络一致性投影的计算方模型（NCPCDA），利用多源相似性和一致性投影得到预测得分矩阵. Ding等^[13]结合随机游走算法和逻辑回归方法开发了名为RWLR的计算模型. Lei等^[14]提出名为ICFCDA的基于协作过滤推荐系统的计算模型. Deepthi等^[15]提出计算模型AE-DNN，它依赖自动编码器和深度神经网络来预测新的circRNA-疾病关联. Xiao等^[16]提出基于网络嵌入的自适应子空间学习方法（NSL2CD），同时在模型中加入综合加权图正则化项和L1范数约束来实现投影矩阵的平滑性和稀疏性. 不难看出，已有的计算模型还存在一些缺陷：1）模型使用的训练数据有限，这对模型的鲁棒性和覆盖范围有影响；2）模型主要基于单一的数据描述方法，没有将circRNA与疾病行为信息和属性信息结合起来，全面定义circRNA与疾病的特征，导致预测性能有限；3）研究者没有考虑编码-非编码基因-疾病关联的异质性，无法准确测量circRNA-disease关联信息.

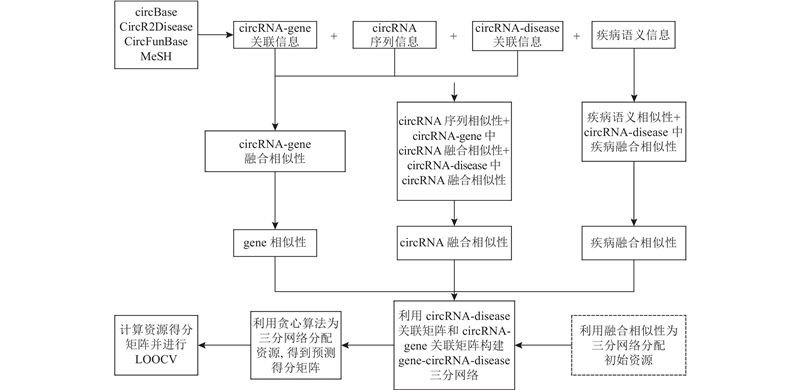
为了改善现有计算模型不足，本研究提出基于融合相似性和三部图的circRNA与疾病关联预测模型（prediction of circRNA and disease association based on fusion similarity and tripartite graph, FSTPGCDA）. 研究工作包括1）利用数据库得到circRNA序列信息、 circRNA-gene关联信息、circRNA-disease关联信息和疾病语义信息，把数据处理成circRNA-disease关联矩阵和circRNA-gene关联矩阵. 2）利用混沌博弈表示（chaotic game representation，CGR）^[17]、语义相似性、Jaccard系数^[18]与拉普拉斯特征映射^[19]融合相似性计算相似性. 3）加权相似性得到融合相似性. 4）利用circRNA-disease关联信息和circRNA-gene关联信息构建gene-circRNA-disease三部图^[20]. 5）通过融合相似性方法为三部图分配初始资源，使用贪心算法进行资源分配，得出最终circRNA-disease资源得分矩阵. 6）计算预测得分并排序，进行留一交叉验证（leave-one-out cross-validation, LOOCV）^[21].

通过整合不同种类的生物关联信息，构建数据集D1、D2. 在D1中，circRNA-diseas关联从CircFunBase数据库^[22]中下载；分别从circBase、circR2Disease和MeSH^[23]中收集circRNA序列信息、circRNA-gene关联信息和疾病语义信息；剔除重复后，共收集2983个circRNA-diseas关联和2318个circRNA-gene关联信息. 在D2中，circRNA-diseas关联信息从circR2Cancer^[24]数据库中下载；分别从circBase、miR2Disease^[25]和MeSH中收集circRNA序列信息、circRNA-miRNA关联信息和疾病语义信；剔除重复后，共收集到647个circRNA-diseas关联信息和756个circRNA-miRNA关联信息. 数据集的关联信息及数据个数n如表1所示.

本研究的数据集存在稀疏问题，使得计算的过程时间长，算法时间复杂度高. 与传统相似性度量方法相比，Jaccard相似性能够改善余弦相似性^[26]只考虑单一变量而忽略其他信息量的弊端，适合在稀疏度过高的数据中使用. 拉普拉斯特征映射是基于图的降维算法，在降维后仍能保持原有的数据结构. 本研究将拉普拉斯特征映射和Jaccard结合进行相似性计算. 基本思路如下.

1）以计算样本关联矩阵相似性为例，a、b关联矩阵记为 ${\boldsymbol{M}}$，元素 $ {M_{i,j}} = 1 $为第 $ i $个a样本和第 $ j $个b样本存在关联. 将 ${\boldsymbol{M}}$拆分成2个矩阵 ${\boldsymbol{A}}$和 ${\boldsymbol{B}}$，操作方式如下：将 ${\boldsymbol{M}}$每行中值为1的列下标分别作为对应的b样本的属性，构成行向量，该行向量的元素数量 ${{{n}}_{{B}}}$表示b样本的数量. 例如，如果第 $ i $行中值为1的列下标为 $ \{ {j_1},{j_2},{j_3}\} $，那么 ${{\boldsymbol{A}}_{{i}}} = [0,0,0,\cdots, 0,1,0,\cdots,0,1,0,\cdots,0,0,0]$中1的位置分别对应第 $ {j_1},{j_2},{j_3} $个b样本的属性，其余位置为0. 将所有 ${{{n}}_{{A}}}$个向量按行堆叠，得到 $ {n_A} \times {n_B} $的矩阵，其中 ${{{n}}_{{A}}}$为a样本的数量. 矩阵 ${\boldsymbol{B}}$同理可得. 其中 $ {A_{i,j}} = 1 $为第 $ i $个a样本具有第 $ j $个属性， $ {B_{i,j}} = 1 $为第 $ i $个b样本具有第 $ j $个属性.

2）使用拉普拉斯特征映射将 ${\boldsymbol{A}}$和 ${\boldsymbol{B}}$映射到特征空间中，得到 ${k_{{A}}}$个a样本的特征向量和 ${k_{{B}}}$个b样本的特征向量. 使用Jaccard系数计算这些特征向量之间的相似性，即计算所有非零元素的索引集合的Jaccard系数的平均值，即

(1) $ {L_{\rm{s}}}({{A}},{{B}}) = \frac{1}{{{k_{{A}}}{k_{{B}}}}}\sum\limits_{i = 1}^{{k_{{A}}}} {\sum\limits_{j = 1}^{{k_{{B}}}} {J(\{ p|{\varphi _{{A}}}{{({a_i})}_p} \ne 0\} ,} } \{ q|{\varphi _{{B}}}{({b_j})_q} \ne 0\} )\;. $

(2) $ J({\boldsymbol{A}},{\boldsymbol{B}}) = \frac{{|{\boldsymbol{A}} \cap {\boldsymbol{B}}|}}{{|{\boldsymbol{A}} \cup {\boldsymbol{B}}|}}\;. $

式中： $J({\boldsymbol{A}},{\boldsymbol{B}})$为矩阵 ${\boldsymbol{A}}$和 ${\boldsymbol{B}}$的Jaccard系数， ${{\bf\textit{φ}}_{{A}}}({{{a}}_{{i}}})$为将a样本 $ i $映射到特征空间中得到的特征向量， ${{\bf\textit{φ}}_{{B}}}({{{a}}_{{j}}})$为将b样本 $ j $映射到特征空间中得到的特征向量.

现有序列比对算法只能量化位置信息或非线性信息，能够将这2类信息结合的算法鲜少. 为此基于CGR的方法利用Pearson相关系数^[27]来量化位置与非线性信息之间的相似性和差异性. 1）将CGR空间划分为 $ {N_{\rm{g}}} $网格( $ {N_{\rm{g}}} = {2^s} \times {2^s};在本研究中s = 3 $)，网格表示为

(3) $ {G_i} = ({X_i},{Y_i},{Z_i})\;. $

2）分别对每个网格中横坐标x和纵坐标y进行累加，若点在网格内，量化位置信息为

(4) $ {X}_{i}={\displaystyle \sum x}, $

(5) $ {Y}_{i}={\displaystyle \sum y}. $

3）计算每个网格 $ {Z_i} $的评分量化非线性信息，其中N_i为第i个网络的评分，

(6) $ {Z_i} = \frac{{{N_i} - \dfrac{{\displaystyle\displaystyle\sum\nolimits_{i = 1}^{{N_{\rm{g}}}} {{N_{i}}} }}{{{N_{\rm{g}}}}}}}{{\sqrt {\dfrac{1}{{{N_{\rm{g}}}}}\displaystyle\sum\nolimits_{i = 1}^{{N_{\rm{g}}}} {{{\left({N_{i}} - \dfrac{{\displaystyle\sum\nolimits_{i = 1}^{{N_{\rm{g}}}} {{N_{i}}} }}{{{N_{\rm{g}}}}}\right)}^2}} } }}\;. $

4）每个网格被描述为3个属性, 并融合属性构造描述第 $ i $个circRNA c (i). 通过Pearson相关系数确定序列相似度 $S_{{\rm{seq}}}^{{{\rm{C}}}}(c(i),c(j))$.

(7) $ S_{{\text{seq}}}^{\rm{C}}(c(i),c(j)) = \frac{{{\rm{Cov}}(c(i)) \cdot {\rm{Cov}}(c(j))}}{{D(c(i)) \cdot D(c(j))}}\;. $

式中： ${\rm{Cov}}$为协方差， $D$为方差. circRNA序列相似度矩阵 ${\boldsymbol{S}}_{{\rm{seq}}}^{\rm{C}}$大小为 $ n \times n $.

如果RNA影响同一种人类疾病，它们的功能往往是相似的^[28]. 从circRNA-gene关联矩阵中利用融合相似性计算得出circRNA-gene之间circRNA的相似性 ${\boldsymbol{S}}_{{\rm{C}} - {\rm{G}}}^{\rm{C}}$. 从circRNA-disease关联矩阵中利用上述的融合相似性计算得出circRNA-disease之间circRNA的相似性 ${\boldsymbol{S}}_{{\rm{C}} {\text{-}} {\rm{D}}}^{\rm{C}}$.

通过从不同角度分析circRNA的特征，可以得到3个相似矩阵，包括 ${\boldsymbol{S}}_{{\text{seq}}}^{\rm{C}}$、 ${\boldsymbol{S}}_{{\rm{C - G}}}^{\rm{C}}$和 ${\boldsymbol{S}}_{{\rm{C}} {\text{-}} {\rm{D}}}^{\rm{C}}$. 为了解决由于数据和可用性不足导致的circRNA之间差异较小的问题，引入序列相似度和circRNA-gene从不同的角度来描述circRNA，使模型更具信息量. 相似性信息的完成是通过组合3个矩阵来完成的. 融合相似度定义如下：

(8) $ {S}^{\rm{C}} = \left\{ \begin{array}{l} \dfrac{{S}_{\text{seq}}^{\rm{C}}(c(i), c(j)) + {S}_{{\rm{C}} {\text{-}} {\rm{G}}}^{\rm{C}}(c(i), c(j)) + {S}_{{\rm{C}} {\text{-}} {\rm{D}}}^{\rm{C}}(c(i), c(j))}{3}, \\ S_{{\rm{seq}}}^{\rm{C}} \left( {c\left( i \right),c\left( j \right)} \right) \ne 0;\\ \dfrac{{S}_{\text{seq}}^{\rm{C}}(c(i),c(j))+{S}_{{\rm{C}}{\text{-}}{\rm{D}}}^{\rm{C}}(c(i),c(j))}{2},其他. \end{array}\right. $

疾病语义相似. 根据MeSH数据库的语义信息将疾病表示为有向无环图（directed acyclic graph，DAG）. DAG中的节点代表疾病，边代表疾病之间的关系. 如果疾病在病理上相似，则DAG的更多部分将被共享^[29]. 计算疾病贡献值的模型为

(9) $ {S_{d(i)}}(q) = {{\rm{lb}} }\left(1+\frac{{n({\text{DA}}{{\text{G}}_s}(q))}}{{n_{\rm{d}}}}\right)\;. $

式中： $n({\text{DA}}{{\text{G}}_s}(q))$为疾病q的 ${\text{DA}}{{\text{G}}_s}$的数量定义，并将所有疾病的数量定义为 $n_{\rm{d}}$. 疾病d(i)与疾病d(j)的语义相似度评分 $S_{{\text{sem}}}^{\rm{D}}$描述为

(10) $ S_{{\text{sem}}}^{\rm{D}}(d(i),d(j)) = \frac{{\displaystyle\sum\nolimits_{q \in {N_{d(i)}} \cap {N_{d(j)}}} {({S_{d(i)}}(q)+{S_{d(j)}}(q))} }}{{\displaystyle\sum\nolimits_{q \in {N_{d(i)}}} {{S_{d(i)}}(q)+\displaystyle\sum\nolimits_{q \in {N_{d(j)}}} {{S_{d(j)}}(q)} } }}\;. $

式中： $ {N_{d(i)}} $为疾病 $ d(i) $的DAG出现的所有疾病. 病理相似的疾病往往与功能相似的circRNAs相关. 从circRNA-disease关联矩阵中利用融合相似性计算得出circRNA-disease之间的disease相似性 ${\boldsymbol{S}}_{{\rm{C}} {\text{-}} {\rm{D}}}^{\rm{D}}$. 通过多角度分析疾病相似度度量，得到相似度矩阵，包括 ${{S}}_{{\text{sem}}}^{\rm{D}}$和 ${{S}}_{{\rm{C}} {\text{-}} {\rm{D}}}^{\rm{D}}$. 如果疾病没有DAG，语义相似性无法计算. 为了弥补这一不足，将 ${{S}}_{{\text{sem}}}^{\rm{D}}$和 ${{S}}_{{\rm{C}} {\text{-}} {\rm{D}}}^{\rm{D}}$融合在一起. 疾病d(i)与d(j)之间的疾病融合相似度 ${S^{\rm{D}}}$定义为

(11) $ {S}^{\rm{D}}(d(i),d(j))=\left\{\begin{array}{l}\dfrac{{S}_{\text{sem}}^{\rm{D}}(d(i),d(j))+{S}_{{\rm{C}}{\text{-}}{\rm{D}}}^{\rm{D}}(d(i),d(j))}{2}, \\ d(i)、d(j)\in {\rm{DAG}};\\ {S}_{{\rm{C}}{\text{-}}{\rm{D}}}^{\rm{D}}(d(i),d(j)),\;其他.\end{array}\right. $

从circRNA-gene关联矩阵中利用融合相似性计算得出circRNA-gene之间gene的相似性 ${\boldsymbol{S}}_{{\rm{C}} {\text{-}} {\rm{G}}}^{\rm{G}}$.

由circRNA-disease和circRNA-gene构建三部图，加入circRNA相似性和disease相似性来对节点进行资源分配.

受使用用户、商品和标签三部图进行推荐的启发，构建gene-circRNA-disease三方图T（C，D，G，E）， ${{C}} = ({c_1},{c_2},{c_3},\cdots,{c_m})$、 ${{D}} = ({d_1},{d_2},{d_3},\cdots,{d_n})$和 ${{G}} = ({g_1},{g_2},{g_3},\cdots,{g_r})$分别为m个circRNA的节点集，n个疾病的节点集，r个gene的节点集. E为节点C与节点D、C与节点G之间的相互作用(边)集合. 三部图也可以表示为2个邻接矩阵 ${{\boldsymbol{A}}^{{\rm{CD}}}} = {[ a_{ij}^{{\rm{CD}}}] _{m \times n}}$和 ${{\boldsymbol{A}}^{{\rm{CG}}}} = {[ a_{ij}^{{\rm{CG}}}] _{m \times r}}$. 如果 $ {c_i} $与疾病相关，则 $ a_{ij}^{{\rm{CD}}} = 1 $，否则 ，表示circRNA与疾病对为未知关联. 类似地，如果 $ {c_j} $与基因 $ {g_i} $相关，则设 $ a_{ij}^{{\rm{CG}}} = 1 $，否则设为0. FSTPGCDA流程图如图1所示.

三分网络资源分配的贪心算法^[30]流程如下. 1）对每个节点初始化资源. 根据相似性矩阵 ${{\boldsymbol{S}}^{\rm{C}}}$、 ${{\boldsymbol{S}}^{\rm{D}}}$、 ${{\boldsymbol{S}}^{\rm{G}}}$，为gene-circRNA-disease中每个节点分配资源，分别为节点C、D、G，分配初始资源 $R_C$、 $R_D$、 $R_G$. 例如，对于特定的 $ {c_i} $，位于疾病 $ {d_j} $上的初始资源定义为

(12) $ f({c_i}) = a_{ij}^{{\rm{CD}}};\;j = 1,2,\cdots,n\;. $

2）对于每个节点，计算与其相邻的节点之间的收益值：

(13) $\begin{split} \\ {\text{Gai}}{{\text{n}}_{i,j}} = {w_{i,j}} \times \frac{{{R_i}+{R_j}}}{2}\;. \end{split} $

式中： ${\text{Gai}}{{\text{n}}_{i,j}}$ 为节点 $ i $和节点 $ j $之间的收益值， $ {w_{i,j}} $为节点 $ i $和节点 $ j $之间的相似性， $ {R_i} $、 $ {R_j} $分别为节点 $ i $和节点 $ j $目前拥有的资源数量. 3）选择最优节点，即从未被选择的节点中, 选择与已选择节点之间的收益值最大的节点加入已选择节点集合中. 4）更新资源，根据新加入的节点，更新其相邻节点的资源数量：

(14) $ R_i' = {R_i} - \alpha \times {\text{Gai}}{{\text{n}}_{i,j}}\;. $

式中： $R_i'$为节点 $ i $更新后的资源数量； $ \alpha $为分配给相邻节点的收益值的比例，初始值为0.4. 重复步骤3）、4），直到所有节点都被分配资源为止.

构建三部图时存在的孤立节点的处理过程：在贪心算法的过程中，比较孤立节点与已有资源的节点，并将资源分配给孤立节点的邻居节点，以提高整个网络的连通性. 计算每个节点的收益值：

(15) $ {\text{Gai}}{{\text{n}}_v} = \sum\nolimits_{u \in {N_v}} {{\rm{sim}}(v,u)} \cdot {r_u}\;. $

式中： $ v $为当前节点， $ {N_v} $为 $ v $的邻居节点集合， $ {\rm{sim}} (v,u) $为节点 $ v $和 $ u $之间的相似度， $ {r_u} $为节点 $ u $已经分配的资源值. ${\text{Gai}}{{\text{n}}_v}$的计算结果代表如果将资源分配给节点 $ v $整个网络的收益会增加多少.

FSTPGCDA推断circRNA-disease之间潜在关联的性能使用LOOCV进行评估. 在每个LOOCV实验的步骤中，将每个已知的circRNA-disease关联从训练样本中依次移除，作为测试样本，其他已知关联作为模型学习的训练样本. 定义TP为被预测为正类的样本，TN为被预测为负类的负样本，FP为被预测为正类的负样本，FN为被预测为负类的正样本. 根据ROC曲线下的相应面积计算AUC（area under curve）^[31]. 根据PR曲线计算曲线下面积AUPR（area under precision-recall curve）^[32].

(16) $ {\text{TPR}} = \frac{{{\text{TP}}}}{{{\text{TP+FN}}}}\;, $

(17) $ {\text{FPR = }}\frac{{{\text{FP}}}}{{{\text{FP+TN}}}}\;, $

(18) $ {{p = }}\frac{{{\text{TP}}}}{{{\text{TP+FP}}}}\;, $

(19) $ {\text{F1 = }}\frac{{{\text{2}} \cdot {{(p}} \cdot {\text{TPR)}}}}{{{{(p}} + {\text{TPR)}}}}\;, $

(20) $ {\text{MCC = }}\frac{{{\text{TP}} \cdot {{\rm{TN}} - {\rm{FP}}} \cdot {\text{FN}}}}{{\sqrt {{\text{(TP+FP)}} \cdot {\text{(TP+FN)}} \cdot {\text{(TN+FP)}} \cdot {\text{(TN+FN)}}} }}\;, $

(21) $ {\rm{AUC}}=(1+{\rm{TP}}/({\rm{TP}}+{\rm{FN}})-{\rm{TN}}/({\rm{TN}}+{\rm{FP}}))/2, $

(22) $ {\text{AUPR}} = \sum\nolimits_{i = 1}^{n - 1} {\left( {{\text{TP}}{{\text{R}}_{i+1}} - {\text{TP}}{{\text{R}}_i}} \right) \cdot {p_i}} \;. $

式中： $ n $为正负样本总数，p为精密度.

自身效果对比采用AUC、AUPR、TPR、精密度、F1评分和MCC评估指标，分别用LOOCV和5、10折对比. 对比结果如表2所示. 可以看出，各评估指标在交叉验证中差异不超0.1%，该模式具有较好的鲁棒性.

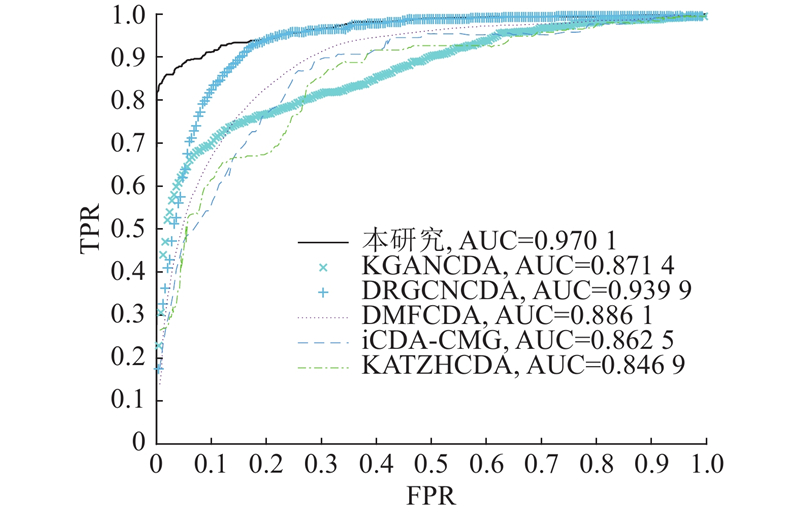
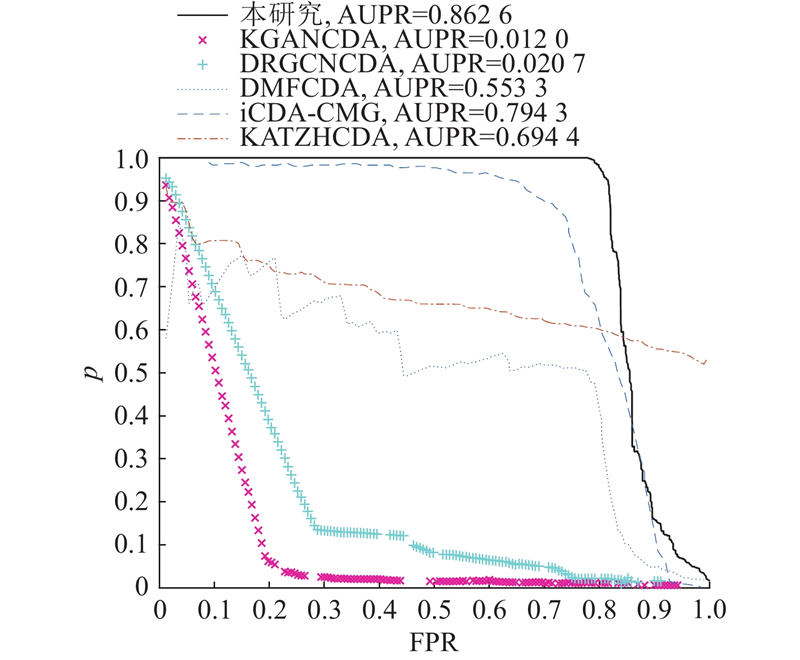
进行FSTPGCDA与KATZHCDA、iCDA-CMG^[33]、DMFCDA^[34]、KGANCDA^[35]和DRGCNCDA^[36]的模型性能对比实验. 不同模型的ROC曲线如图2所示. KATZHCDA、iCDA-CMG、DMFCDA、KGANCDA和DRGCNCDA的AUC分别为84.69%、86.25%、88.61%、87.14%和93.99%，FSTPGCDA的AUC为97.01%，优于其他5种方法. 不同方法的PR曲线如图3所示. KATZHCDA、iCDA-CMG、DMFCDA、KGANCDA和DRGCNCDA的AUPR分别为69.44%、79.43%、55.33%、1.20%和2.07%，FSTPGCDA的AUPR为86.26%，优于其他5种方法.

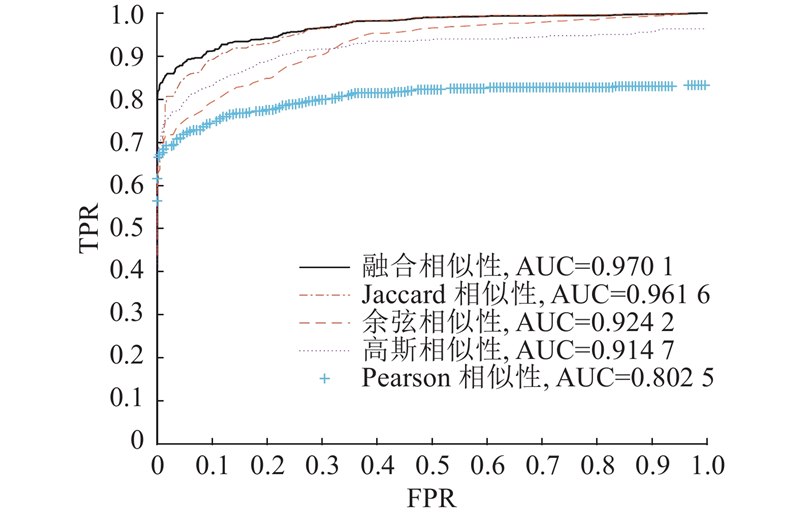
为了验证不同相似性在FSTPGCDA的效果，将融合相似性与Jaccard相似性、余弦相似性、高斯核相似性和Pearson相似性对比，不同相似性在dataset1的相应ROC曲线如图4所示. Jaccard相似性、余弦相似性、高斯核相似性和Pearson相似性的AUC分别为96.16%、92. 42%、91.47%和80.25%，融合相似性的AUC为97.01%，优于其他相似性计算.

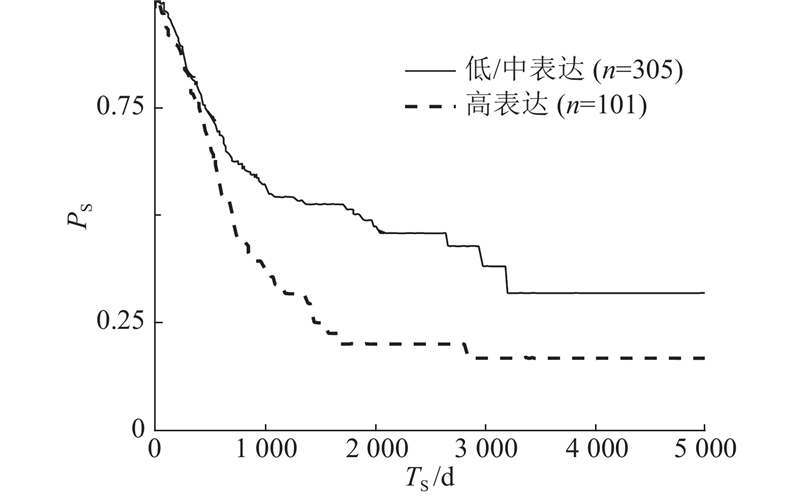
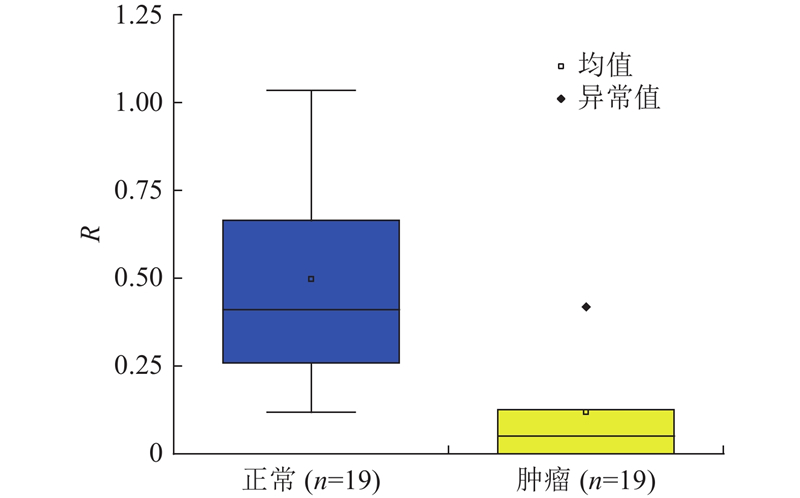
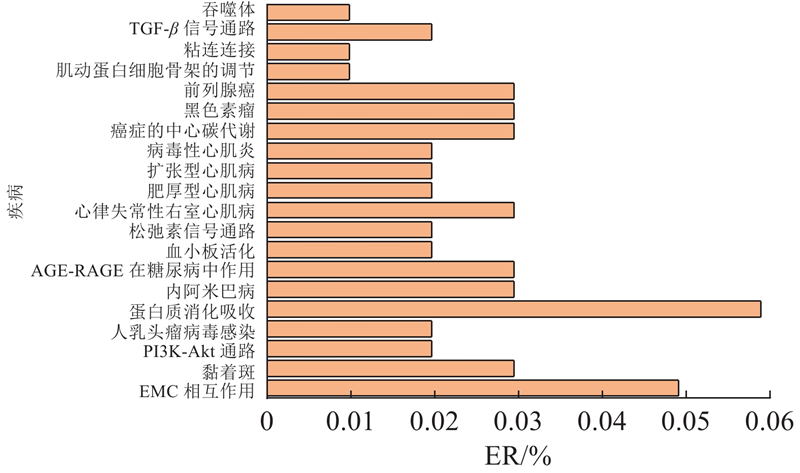
为了评估FSTPGCDA的实用价值，进行膀胱癌案例研究，膀胱癌在circFunBase和circR2Disease数据集中有足够的数据，能够避免模型缺陷导致的偏差. 根据相应的预测得分，通过按降序排列选择前15个分数，并通过PubMed进行验证，验证结果为PMID号. 膀胱癌是发生在膀胱黏膜上的恶性肿瘤，是泌尿系统最常见的恶性肿瘤，占中国泌尿生殖系肿瘤发病率的第一位^[37]. 膀胱癌筛查模型的研究，对膀胱癌早期发现和高危人群预警具有重要意义. 在癌前病变阶段进行筛检，早诊早治，可降低膀胱癌发病率和病死率. 进一步研究膀胱癌与circRNA之间关联有助于提高膀胱癌的诊断和治疗水平. 选择预测分数前15名的CircRNA进行验证，有14个得到验证. 如表3所示，hsa_circ_0001946（排名第1）对应的CDR1基因，与Purkinje细胞质抗原34和62 kd反应的抗Yo (I型)自身抗体在一例膀胱移行细胞癌并发副肿瘤性小脑变性和抗Yo抗体反应的患者的血清和脑脊液中被发现. 肿瘤切除后抗体滴度下降^[38]. hsa_circ_0028173（排名第8）在膀胱癌细胞中，这些 DEmRNA 在甘油酯代谢、p53 信号通路和卵母细胞减数分裂中显着富集. circRNA相互作用对可能在BC中发挥重要作用^[39]. hsa_circ_0000144（排名第9）下调环状RNA hsa_circ_0000144通过刺激miR-217和抑制RUNX2表达抑制膀胱癌进展^[40]. 以CDR1基因为例进行进一步分析，验证该基因是否与膀胱癌相关. 如图5所示，在研究中，将所有膀胱癌患者样本分为高表达组和低表达组，通过生存分析看到CDR1基因高表达组膀胱癌患者的生存天数相对较短. 图中，T_S为生存时间，P_S为生存概率. 如图6所示，进一步的结果表明，这些基因在癌症样本中的表达明显低于正常样本. 图中，R为每百万份转录数. 基于以上结果，最终得出这些基因的表达与膀胱癌患者的生存时间和临床病理特征显著负相关. 此外，BLCA富集分析也显示，CDR1基因低表达组对人类来说主要在蛋白质消化吸收、EMC受体相互作用、心肌病、癌症中枢碳代谢、黑色素瘤等疾病过程中富集，如图7所示. 图中，ER为富集率.

在生物医学研究中，预测circRNA与疾病关联有利于理解疾病的发病机制，进一步提高疾病诊断、治疗、预后和预防的质量. 本研究提出新的计算模型FSTPGCDA，通过整合实验验证的circRNA序列信息、circRNA-disease关联信息、circRNA-gene关联信息和疾病语义信息来识别潜在的circRNA-disease关联. 基于gene-circRNA-disease三部图的资源分配模型，能够更好地描述编码非编码基因疾病关联的异质性，丰富资源分配过程中的生物信息. 先用各种相似性和融合相似性计算得到各自相似性，通过加权融合相似性得到融合相似性矩阵，解决了数据高度稀疏性，以便更好地预测得分. 利用融合相似性矩阵为三部图分配初始资源，利用贪心算法为三部图进行资源分配，产生推荐该算法有效地减少了资源分配过程中的不可知偏差. 在LOOCV、5折和10折对比实验中，不同评估指标的评估结果表明，相比其他参与对比的模型，FSTPGCDA具有较好的预测能力和鲁棒性. 案例研究的分析进一步证明，FSTGPCDA有助于在实践中识别潜在的circRNA疾病关联. 下一步计划整合gene-disease关联或采用的其他生物信息，增加更多的经过实验验证的circRNA-disease关联，从资源分配方面进行致病机制的具体分析.