气动性能评估是空天飞行器[1-6]设计阶段的重要环节,其中气动力数据的获取是空天飞行器气动布局、结构设计、轨迹仿真等相关工作的基础. 传统上,空天飞行器气动力数据可以通过地面风洞实验、飞行实验、计算流体动力学(computational fluid dynamics,CFD)数值模拟、工程估算等多种途径获得. 其中,工程估算计算结果置信度不高,依赖于风洞试验结果修正,对不同外形的适应性差,一般只用于简单外形或飞行器概念设计的气动估算. 地面试验存在静温低、雷诺数低、有洞壁干扰、支架干扰等问题. 飞行试验产生的数据是客观的,但数据量通常偏少,且来流条件存在扰动以及传感器精度问题也会导致辨识的数据存在偏差. 虽然准确可靠的气动力数据可以通过建造更先进的风洞、采用更高性能的数值模拟系统以及进行更多更精细的飞行试验来获取,但在短时间内采用单一方式提高气动力数据精准度的程度有限,不能完全满足未来飞行器研制的需要,而且将付出高昂的成本[7]. 研究者希望可以将这些复杂来源的气动力数据进行融合、建模,降低气动数据获取成本,最大限度的提升气动模型建模精度.
对于气动力多源数据融合方法的研究,目前主要围绕以下2类问题展开:1)气动力数据源之间存在明显精度差异的数据融合问题(有相对真解的数据融合问题). 受到计算成本、变量多样、鲁棒性等条件限制,高精度的气动数据(比如飞行试验)难以充分获得,而低精度气动数据的获取较便利. 考虑到低精度气动数据与高精度气动数据的匹配特性,低精度和高精度模型具有相近的或者有关联的内在特征,因此可以通过混合高精度与低精度数据(或模型)建立数据融合模型以逼近更高的数据精度[8-13]. 2)气动数据精度区分不明确、状态不匹配的数据融合问题. 在采用数值计算气动数据、风洞试验数据与飞行试验数据对飞行器气动力或模型进行确定时,须考虑不同状态、不同数据来源的影响. 不同气动数据间的状态与参数很难达到统一,这时就须针对不同状态、不同来源的数据进行融合,提升多源气动力数据库的一致性和精度. 近年来,机器学习在多源数据融合工作中逐步得到了尝试和应用[14-18]. 它不仅能通过融合不同精度的数据实现高精确度预测,而且可以对模型的不确定性进行量化估计. 因此,将传统方法与机器学习技术紧密结合,为空天飞行器气动问题求解,甚至流体力学的发展都提供了崭新的思路.
传统的工程估算方法计算速度快,但是无法考虑飞行中的诸多特殊复杂的物理现象,预测精度低;CFD数值模拟可以高分辨率解析飞行中的物理现象,但是计算成本大、周期长. 本研究基于工程估算和CFD数值模拟方法,引入高斯过程回归理论,提出面向空天飞行器的多精度气动建模方法,以求在较低计算成本下实现高精度气动特性预测. 随后,将该方法应用于FTB空天飞行器的气动建模问题中,构建了该飞行器的多精度气动模型,并将气动模型与再入轨迹仿真模型相耦合. 通过对比分析仿真结果,凸显多精度气动建模方法的工程价值.
1. 空天飞行器气动分析方法
1.1. CFD数值模拟
基于物理学三大守恒定律可以对流体运动进行严格的数学描述,从而推及由质量守恒方程、动量守恒方程、能量守恒方程构成的流体力学基本方程形式即N-S方程组. 由于空天飞行器的高速运动特性,忽略其中黏性项,进而得到三维非定常可压缩流体的Euler方程组,其微分形式如下:
式中:
采用由美国斯坦福大学开发的开源CFD求解器SU2,它是一款基于C++编程语言和非结构网格的高精度偏微分方程求解器,能够解决非结构网格拓扑下的多物理场分析和优化问题. SU2求解器的流动分析能力在RAM-C II高超音速飞行器的试验案例中[19]已经过严格验证和确认,可确保对复杂外型的气动特性实现准确评估.
1.2. 基于工程估算的快速预测方法
针对空天飞行器的复杂外形,在应用物面压力估算方法进行气动力计算前,须将其表面划分为很多小的网格面元. 一般划分为三角形或四边形网格面元,本研究采用典型的三角形非结构网格面元.
在高超声速条件下,基于工程估算理论求解飞行器的气动力系数的基本流程如图1所示. 该流程主要包括4个部分,通过几何生成软件定义气动外形,再利用网格生成软件作非结构网格面元的划分. 将飞行器分解为机身、机翼区域,再结合迎风/背风情况,在不同区域的网格面元上采用适合的方法计算压力系数并求和,最后进行数据转化,将气动力系数由机体系映射为惯性系,转换完毕后存储或输出. 其中,机身迎风面采用修正牛顿法:
图 1
式中:
式中:
机翼背风面采用激波膨胀波法,迎风面采用切楔/切锥法. 在存在攻角
式中:
采用自主开发的高超声速飞行器气动力快速预测平台,它遵循工程估算中气动力的一般求解流程. 该平台是基于非结构网格文件进行计算求解的,它主要由输入模块、几何处理模块、求解模块、数据转换模块、输出模块等模块构成.
2. 多精度高斯过程回归
2.1. 高斯过程回归
高斯过程回归(Gaussian process regression,GPR)是通过对样本数据构建高斯过程,再基于贝叶斯理论求解后验概率分布实现的,本质上是利用高斯过程先验知识对样本数据进行回归分析的非参数回归模型[20]. 训练集为
假设该映射关系服从均值为0的高斯分布,则
式中:x'为核函数中心,k为由超参数
由核函数k确定其协方差矩阵:
式中:k (xi, xj)为样本xi、xj之间的协方差.
协方差矩阵由核函数k确定,一般选用径向基函数作为高斯过程的核函数,定义如下:
式中:
式中:
本研究采用L-BFGS算法来求解该优化问题的最优参数.
2.2. 基于高斯过程的多精度回归实现
针对不同信息源或不同模型提供的数据,根据模型本身在计算精度和计算成本方面的特征,可以将数据划分为多个精度的数据集. 其中,多精度高斯过程回归方法最适合处理由具备如图2所示特征的模型生成的数据,它能够利用不同精度数据实现多精度建模,获得的代理模型精度不仅高于低精度模型,而且求解速度远快于高精度计算模型,这是多精度高斯过程回归模型的优势所在.
图 2
图 2 高低精度模型的计算精度与成本分布
Fig.2 Calculation fidelity versus cost distribution for high fidelity and low fidelity model
多精度高斯过程回归是在高斯过程回归的基础上,基于不同精度的数据集实现的. 假设不同精度数据集为
式中:
式中:
式中:X为观测值输入集合.
根据贝叶斯定理,该后验分布在精度t中的均值和方差表达式如下:
式中:
3. 空天飞行器再入段运动模型
3.1. 运动模型
在再入飞行过程中,飞行器可以视作质量不变的刚体,对其运动模型作简化处理,仅考虑它的平移运动. 所采用的算例初始再入高度为70 km,飞行器发动机推力降低为0,由于科氏加速度较小忽略不计,此时地球自转影响可忽略不计,飞行器受到的外力仅为气动力和重力. 在再入过程中假设侧滑角为0°,速度矢量始终保持在飞行器的纵向平面内. 因此,可以建立飞行器在航迹坐标系下的三自由度运动模型如下:
式中:
式中:
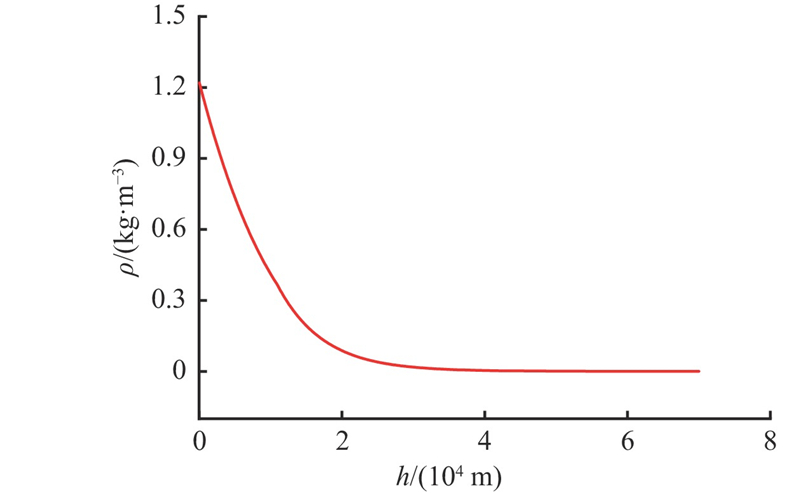
3.2. 大气模型
图 3
4. 仿真分析
4.1. FTB模型描述
图 4
4.2. 气动分析方法比较
4.2.1. 计算精度
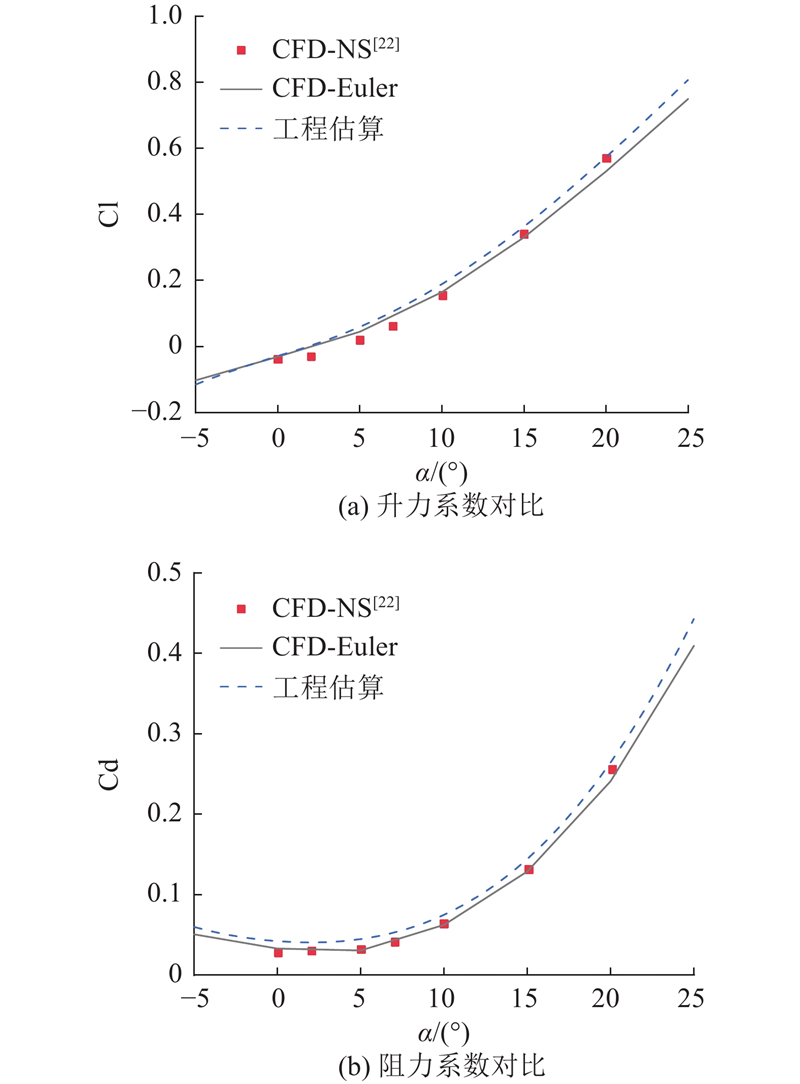
图 5
图 5 升、阻力系数的计算结果对比
Fig.5 Comparison of calculation results of lift and drag coefficients
定义计算方法的平均误差
式中:
表 1 2种方法求解气动系数的平均误差对比
Tab.1
| 气动系数 | | | |
| Cl | 0.02763 | 0.02222 | 3.53 |
| Cd | 0.01203 | 0.00411 | 9.56 |
4.2.2. 计算成本
2种方法对于计算成本的要求如表2所示. 表中,Ns为网格数量,NC为CPU使用数,t为计算时间. CFD数值模拟中的网格数量更多,且在时间、空间维度上迭代求解,故在计算设备配置和计算时间方面的要求均远高于工程估算的,尤其在计算时间方面,CFD数值模拟所需时间是工程估算的104数量级倍. 综合计算方法的平均误差和计算成本的对比结果,CFD数值模拟方法相较于基于工程估算的快速预测方法可以作为高精度计算方法使用.
表 2 2种方法求解气动系数的计算成本对比
Tab.2
| 方法 | Ns | CPU配置 | NC | t |
| CFD数值模拟 | 1997434 | Intel(R) Xeon(R) Platinum 8175M CPU @ 2.50 GHz | 45 | 1.79 h |
| 基于工程估算的 快速预测方法 | 5912 | Intel(R) Core(TM) i5-8400 CPU @ 2.80 GHz | 1 | 0.58 s |
4.3. 多精度气动建模
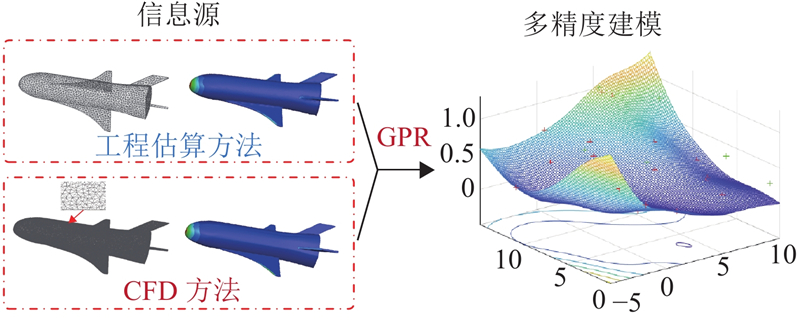
根据前面的结论,将通过CFD数值模拟和基于工程估算的快速预测方法获得的数据分别用作高精度数据和低精度数据. 多精度气动建模如图6所示,将2种信息源数据通过GPR完成多精度建模. 由496个低精度样本点和42个高精度样本点共同组成多精度气动建模的数据集,从数据集中随机选取42个高精度样本构建高精度训练集,选取256个低精度样本构建低精度训练集. 在
图 6
4.3.1. 拟合效果
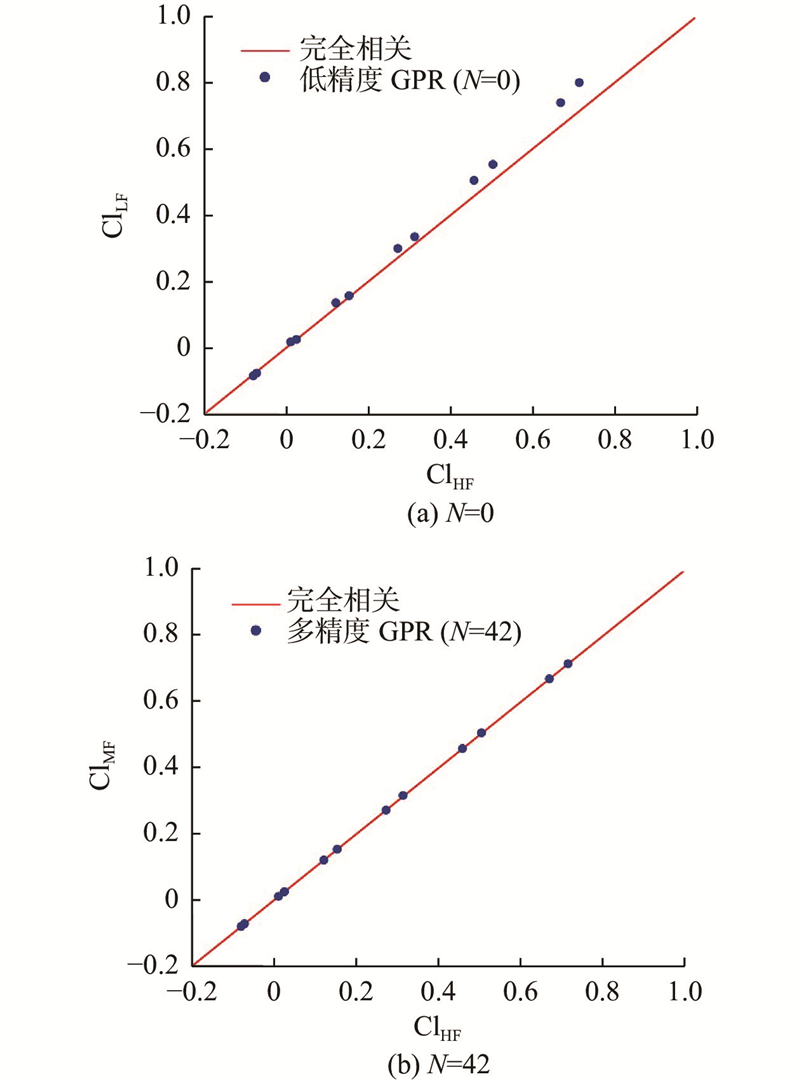
选取高精度训练集中的数据为参考值,通过绘制高精度样本与多精度预测值间的相关性图展现多精度高斯过程回归对数据的拟合效果,如图7所示. 图中,
图 7
图 7 不同高精度样本数量下升力系数的高精度样本与多精度预测值间的相关性
Fig.7 Correlation between high-fidelity samples and multi-fidelity predicted values for lift coefficient under different numbers of high-fidelity samples
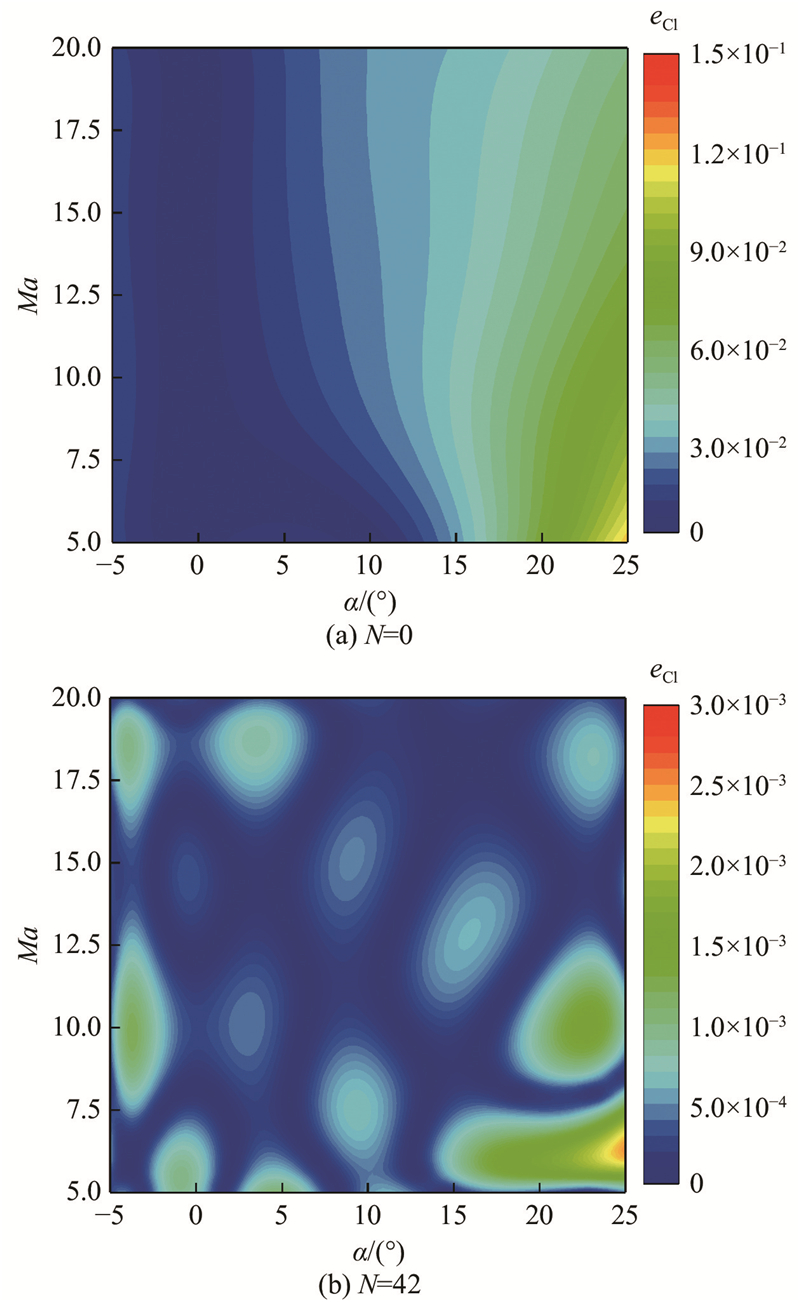
将预测结果与训练集中高精度样本作差得到升力系数的拟合误差eCl,并以云图形式呈现. 如图8所示为2种高精度样本数下,预测模型给出的升力系数拟合误差. 当N=0时,低精度代理模型在参数空间内的最大拟合误差稳定在约0.12;当N=42时,多精度代理模型在参数空间内的最大误差仅为0.0025. 多精度升力系数模型的拟合精度得到了极大的提升,将升力系数的拟合误差降低至原来的1/48,相对误差小于1%.
图 8
图 8 多精度升力系数模型的误差云图
Fig.8 Error cloud figure of multi-fidelity model for lift coefficient
4.3.2. 预测效果
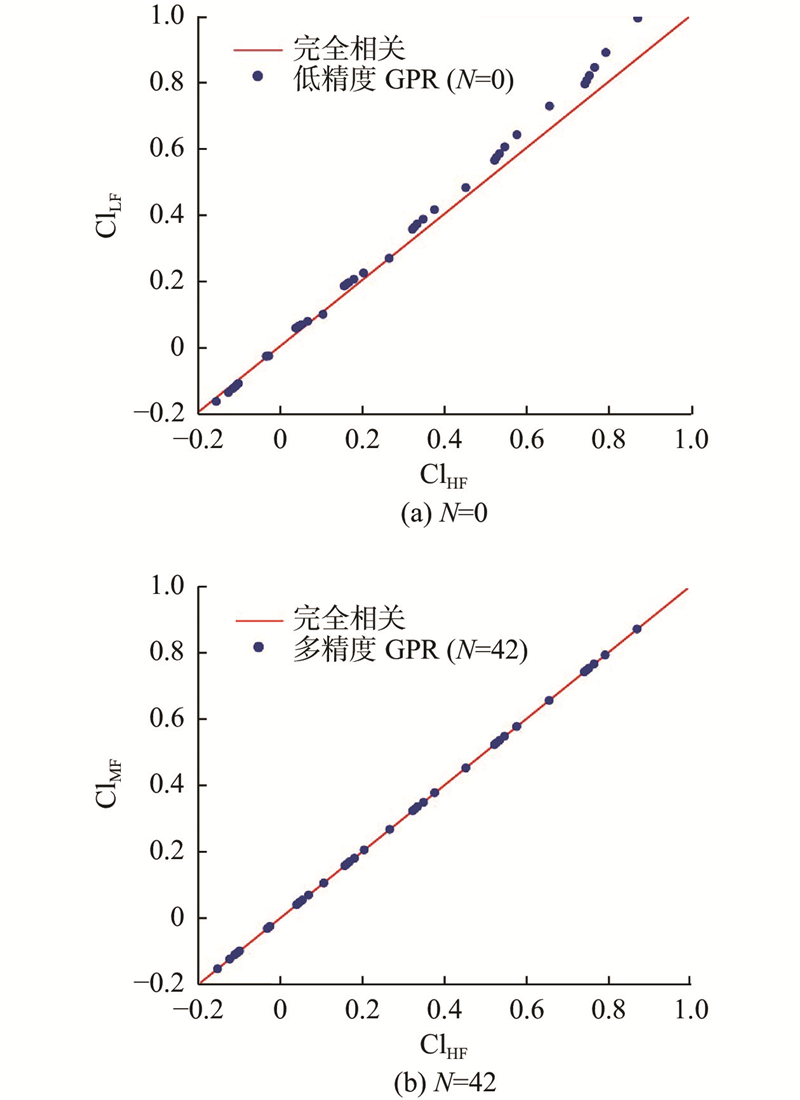
在参数空间内随机选取12个有别于训练集的位置点,基于CFD数值模拟构建升力系数多精度预测模型的测试集,将该测试集作为参照用以说明多精度高斯过程回归对参数空间的预测能力. 如图9所示为N=0,42时升力系数测试集数据与多精度预测值之间的相关性结果. 当N=42时升力系数预测结果几乎与完全相关曲线重合,多精度代理模型对升力系数表现出良好的预测能力.
图 9
图 9 不同数量高精度样本下升力系数的测试集数据与多精度预测值的相关性
Fig.9 Correlation between data of test set and multi-fidelity predicted values for lift coefficient under different numbers of high-fidelity samples
进一步地,以测试集中高精度样本数据为参照,对多精度气动模型的误差进行定量的分析. 其中,多精度气动模型的误差(平方误差的平均值)
式中:
基于测试集数据计算得到的多精度气动模型的平方误差的平均值及平方误差的方差
表 3 多精度升力系数模型的平方误差的平均值
Tab.3
| N | | |
| 单精度GPR | 多精度GPR | |
| 4 | −1.286 | −3.097 |
| 9 | −2.325 | −4.281 |
| 18 | −2.149 | −4.245 |
| 35 | −5.623 | −6.082 |
| 42 | −5.733 | −6.083 |
表 4 多精度升力系数模型的平方误差的方差
Tab.4
| N | | |
| 单精度GPR | 多精度GPR | |
| 4 | −2.337 | −6.225 |
| 9 | −4.407 | −8.059 |
| 18 | −4.011 | −7.966 |
| 35 | −10.956 | −11.515 |
| 42 | −11.146 | −11.367 |
4.3.3. 气动建模结果
类似地,对FTB模型的阻力系数也进行多精度建模,当训练集高精度样本数为42、低精度样本数为256时,升、阻力系数的多精度建模结果如图10所示. 此时阻力系数与升力系数模型预测效果相仿,在高精度样本数小于等于42范围内达到最优.
图 10
图 10 升、阻力系数的多精度建模结果云图
Fig.10 Cloud figure of multi-fidelity modeling results for lift and drag coefficients
4.4. 基于多精度气动模型的轨迹仿真
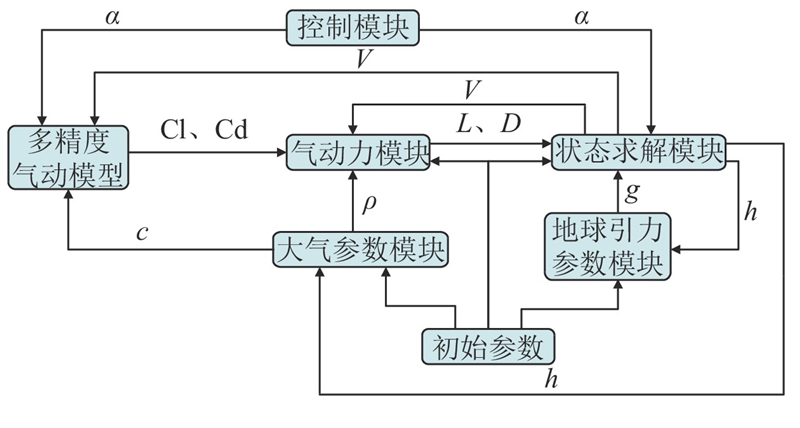
针对空天飞行器的再入问题,将已经构建的多精度气动模型应用在轨迹仿真中,模拟出FTB模型在控制攻角条件下的飞行状态变化. 根据飞行动力学方程求解流程,构建轨迹仿真模型,再入轨迹仿真流程如图11所示. 其中,初始参数包括飞行器质量m、初始高度h、飞行速度V、参考面积S、航迹角γ、航向角ψ、经度λ、纬度Φ、倾斜角σ等.
图 11
在再入过程中,存在严重的气动加热现象、巨大的动压以及过载情况,超过一定限制会对机体本身产生破坏,一般气动加热取驻点处热流率密度作为参考,热流率密度
式中:
4.4.1. 问题描述
在再入过程中,通常会预先定义飞行器制导策略,而定义制导策略常见的方式就是使用预先定义的攻角曲线. 这里给出攻角控制方案,假设它是随速度变化的函数,表达式如下:
在再入过程初期飞行速度和初始高度都较大,初始仿真条件如下:机体驻点曲率半径为0.12 m,质量为2000 kg,参考面积为5.18 m2,初始高度为70 km,速度为6 km/s,航迹角为−2°,航向角为0°,起始经纬度均为0°,倾斜角σ为0°. 根据Detra-Hidalgo模型[21],计算驻点热流率密度的常数取K=5.16×10−5. 由于多精度气动模型基于参数空间
4.4.2. 轨迹仿真结果
将仅用42个高精度样本、仅用256个低精度样本以及使用256个低精度样本和42个高精度样本构建的3种气动模型分别作为再入轨迹仿真的气动数据输入,并根据仿真条件和初始参数设置再入轨迹模型. 在多精度气动建模中,本研究已经从定性和定量的角度证明了多精度相对于单精度模型具有更好的预测效果,因此这里以基于多精度模型的轨迹仿真结果为参照,将单精度的仿真结果分别与多精度的仿真结果作差获得再入特征变量的偏差,仿真结果及偏差对比如图12所示.
图 12
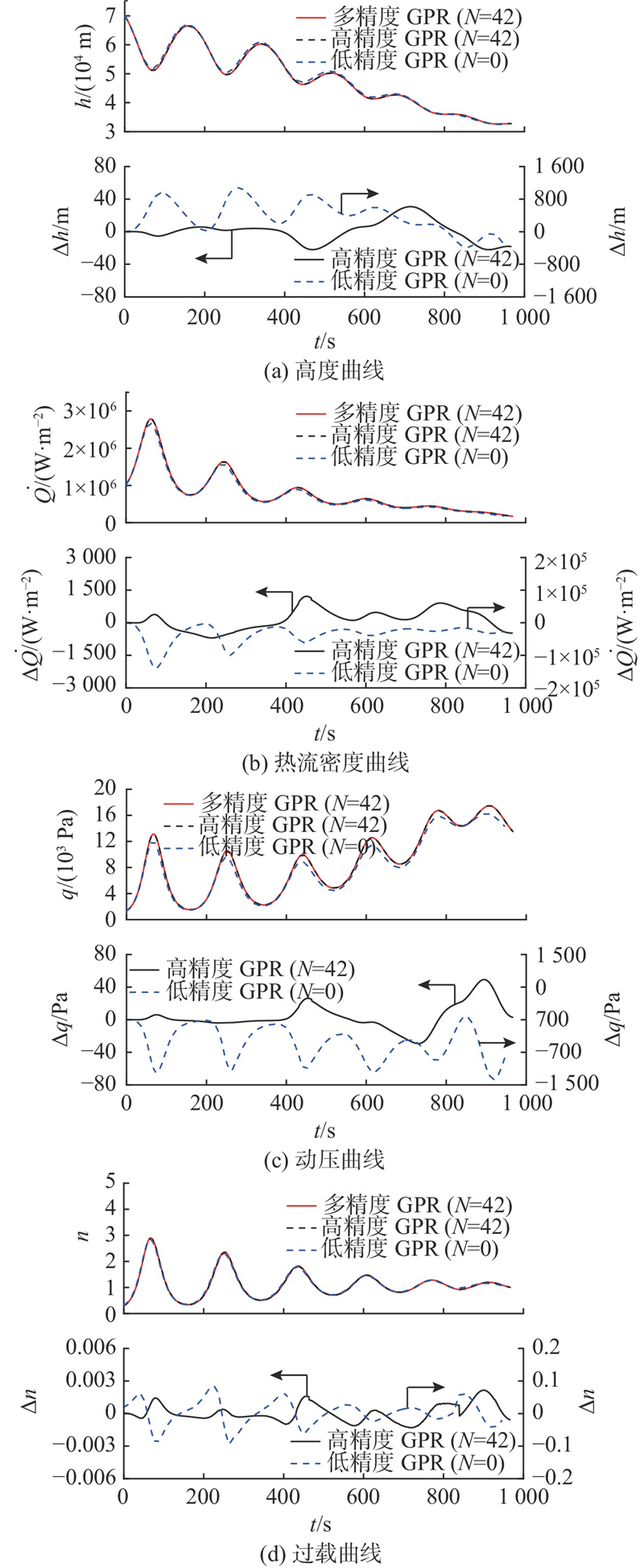
图 12 基于单、多精度气动模型的再入特征曲线及偏差比较
Fig.12 Curve of reentry characteristic and comparison of errors based on single-fidelity and multi-fidelity aerodynamic models
根据仿真结果,高度随时间的变化呈震荡曲线下降,这是空天飞行器再入过程中的典型路径特征,它是下降过程中升阻力系数、速度、空气密度等综合影响的结果. 根据热流率密度曲线、过载曲线、动压曲线,热流率密度和过载为再入初期影响飞行的主要因素,随着飞行速度下降和高度下降,空气密度急速上升,动压对飞行器状态影响逐渐显著. 偏差对比结果显示,通过多精度GPR、高精度GPR构建的气动模型分别作为输入获得的再入曲线相差较小,通过低精度GPR构建的气动模型作为输入获得的再入曲线与前面两者相差较大,采用低精度GPR的最大仿真偏差约为采用高精度GPR的10~100倍. 具体地,初始高度、速度较大,热流率密度、动压为速度的函数,因此低精度GPR构建的气动模型对再入高度、速度以及热流率密度、动压偏差均带来显著影响. 其中,热流率密度偏差绝对值最大至105数量级,多精度气动建模的工程意义也因此得到体现. 由于不能获取轨迹仿真所需要的全部高精度气动数据,无法对多精度气动模型获得的再入仿真结果给出定量的误差分析.
5. 结 论
(1)以FTB气动外形为研究对象,分析得出相较于工程估算,CFD数值模拟方法求解阻力系数的精度提升9.56%,而升力系数的结果差距略小. 但是,CFD数值模拟计算成本要远高于工程估算的.
(2)采用多精度高斯过程回归方法,能以低计算成本完成该空天飞行器的多精度气动建模,且模型精度较高. 当训练集使用42个高精度样本、256个低精度样本时,所提出的多精度气动模型均方误差低至10−5数量级,且比仅用相同数量高精度数据构建的单精度模型精确度和稳定性更高.
(3)将多精度气动模型与再入轨迹仿真耦合,模拟再入过程中的重要状态参数变化,对比分析单、多精度气动模型的仿真结果,发现气动模型的微小差异对再入高度、速度、热流密度、动压影响显著,进一步验证了所提出的多精度气动建模方法对于空天飞行器再入过程轨迹高精度仿真的工程意义.
(4)本研究在多精度气动建模中,并未对训练集和测试集的选用策略作深入考量,最终采用模型是否为全局最优模型也未分析论证. 在未来研究中可将优化过程和多精度气动建模方法相结合,选用不同采样策略,通过迭代寻优给出目标误差下的最优气动模型.
参考文献
从SR-72项目看美国高超声速平台研究现状
[J].DOI:10.16338/j.issn.1009-1319.2013.12.010 [本文引用: 1]
The research status of American hypersonic platform from the perspective of SR-72 project
[J].DOI:10.16338/j.issn.1009-1319.2013.12.010 [本文引用: 1]
X-51A超燃冲压发动机及飞行验证计划
[J].
X-51A scramjet engine flight and demonstration program
[J].
A preliminary investigation on aerodynamic characteristics of an X-51A-like aircraft model
[J].
从"银乌"到航天飞机: 20世纪50年代到80年代的美国助推-滑翔技术发展
[J].
From "silver crow" to the space shuttle: the development of American boost-gliding technology from the 1950s to the 1980s
[J].
更准确、更精确、更高效—高超声速流动数值模拟研究进展
[J].
More accurate, more precise, more efficient-research progress in numerical simulation of hypersonic flow
[J].
类X-37B航天器气动力天地相关性数值模拟
[J].
Numerical simulation of aerodynamic space-earth correlation of X-37B-like spacecraft
[J].
A variable fidelity information fusion method based on radial basis function
[J].
Neural-net-induced Gaussian process regression for function approximation and PDE solution
[J].
Predicting the output from a complex computer code when fast approximations are available
[J].
Multi-fidelity Gaussian process regression for prediction of random fields
[J].DOI:10.1016/j.jcp.2017.01.047 [本文引用: 1]
Nonlinear information fusion algorithms for data-efficient multi-fidelity modelling
[J].DOI:10.1098/rspa.2016.0751 [本文引用: 1]
标准大气参数的公式表示
[J].
Formula representation of standard atmospheric parameters
[J].
Aerodynamic performance analysis of a winged re-entry vehicle from hypersonic down to subsonic speed
[J].
Aerodynamic and aerothermodynamic trade-off analysis of a small hypersonic flying test bed
[J].DOI:10.1016/j.actaastro.2011.03.004