[1]
EKANAYAKE J, SHRIDEEP P, GEOFFREY F. Mapreduce for data intensive scientific analyses [C]// 2008 IEEE 4th International Conference on eScience . Washington: IEEE Computer Society, 2008: 277-284.
[本文引用: 1]
[2]
ZAïANE O R, FOSS A, LEE C H, et al. On data clustering analysis: scalability, constraints, and validation[C]// Pacific-Asia Conference on Knowledge Discovery and Data Mining . [s.l.]: PAKDD , 2002: 28-39.
[本文引用: 1]
[3]
STOJADINOVIĆ Z, KOVAČEVIĆ M, MARINKOVIĆ D, et al Rapid earthquake loss assessment based on machine learning and representative sampling
[J]. Earthquake Spectra , 2022 , 38 (1 ): 152 - 177
DOI:10.1177/87552930211042393
[本文引用: 1]
[4]
MARINIELLO G, PASTORE T, BILOTTA A, et al Seismic pre-dimensioning of irregular concrete frame structures: mathematical formulation and implementation of a learn-heuristic algorithm
[J]. Journal of Building Engineering , 2022 , 46 : 103733
DOI:10.1016/j.jobe.2021.103733
[本文引用: 1]
[5]
JALAYER F. Direct probabilistic seismic analysis: implementing non-linear dynamic assessments [M]. Palo Alto: Stanford University, 2003.
[本文引用: 1]
[6]
NAZRI F M. Seismic fragility assessment for buildings due to earthquake excitation [M]. Penang Malaysia: School of Civil Engineering Universiti Sains Malaysia, 2018
[本文引用: 1]
[7]
HARIRI-ARDEBILI M A, SAOUMA V E, PORTER K A Quantification of seismic potential failure modes in concrete dams
[J]. Earthquake Engineering and Structural Dynamics , 2016 , 45 (6 ): 979 - 997
DOI:10.1002/eqe.2697
[本文引用: 1]
[8]
中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011-2010 [S]. 北京: 中国建筑工业出版社, 2010.
[本文引用: 3]
[9]
COUNCIL A T. Quantification of building seismic performance factors [M]. Washington: US Department of Homeland Security, FEMA, 2009.
[本文引用: 1]
[10]
JAYARAM N, LIN T, BAKER J W A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance
[J]. Earthquake Spectra , 2011 , 27 (3 ): 797 - 815
DOI:10.1193/1.3608002
[本文引用: 1]
[11]
BAKER J W, LEE C An improved algorithm for selecting ground motions to match a conditional spectrum
[J]. Journal of Earthquake Engineering , 2018 , 22 (4 ): 708 - 723
DOI:10.1080/13632469.2016.1264334
[本文引用: 1]
[12]
BIAN X, XIE Q Fragility analysis of substation equipment based on ground motion clustering
[J]. Proceedings of the CSEE , 2021 , 41 (8 ): 2671 - 2682
[本文引用: 1]
[14]
DING C, HE X, SIMON H D. On the equivalence of nonnegative matrix factorization and spectral clustering [C]// Proceedings of the 2005 SIAM International Conference on Data Mining , 2005.
[本文引用: 1]
[15]
WEN Z, YANG C, LIU X, et al Trace-penalty minimization for large-scale eigenspace computation
[J]. Journal of Scientific Computing , 2016 , 66 (3 ): 1175 - 1203
DOI:10.1007/s10915-015-0061-0
[本文引用: 2]
[16]
WEDDERBURN R W Quasi-likelihood functions, generalized linear models, and the Gauss-Newton method
[J]. Biometrika , 1974 , 61 (3 ): 439 - 447
[本文引用: 1]
[17]
范书立, 田硕, 陈健云 基于向量地震动强度指标的拱坝地震易损性分析
[J]. 水利学报 , 2019 , 50 (3 ): 335 - 345
[本文引用: 4]
FAN Shu-li, TIAN Shuo, CHEN Jian-yun Seismic fragility analysis of arch dam based on vector-valued intensity measure
[J]. Journal of Hydraulic Engineering , 2019 , 50 (3 ): 335 - 345
[本文引用: 4]
[18]
于晓辉. 钢筋混凝土框架结构的概率地震易损性与风险分析[D]. 哈尔滨: 哈尔滨工业大学, 2012.
[本文引用: 1]
YU Xiao-hui. Probabilistic seimic fragility and risk analysis of reinforced concrete frame structures[D]. Harbin: Harbin Institute of Technology, 2012.
[本文引用: 1]
[19]
KODINARIYA T M, MAKWANA P R Review on determining number of Cluster in K-Means Clustering
[J]. International Journal of Advance Research in Computer Science and Management Studies , 2013 , 1 (6 ): 90 - 95
[本文引用: 1]
[21]
PANG R, XU B, KONG X, et al Seismic fragility for high CFRDs based on deformation and damage index through incremental dynamic analysis
[J]. Soil Dynamics and Earthquake Engineering , 2018 , 104 : 432 - 436
DOI:10.1016/j.soildyn.2017.11.017
[本文引用: 1]
[22]
李琳. 强震动记录选取中目标谱的研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所, 2015.
[本文引用: 1]
LI Lin. Research and application of the target spectrum in strong motion records selection[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2015.
[本文引用: 1]
[23]
靳聪聪, 迟世春 高心墙堆石坝弹塑性动力反应分析及地震易损性研究
[J]. 浙江大学学报: 工学版 , 2020 , 54 (7 ): 1390 - 1400
[本文引用: 1]
JIN Cong-cong, CHI Shi-chun Elasto-plastic dynamic response analysis and seismic fragility research of high core earth-rockfill dam
[J]. Journal of Zhejiang University: Engineering Science , 2020 , 54 (7 ): 1390 - 1400
[本文引用: 1]
[24]
孙宝成. 基于 ABAQUS 的混凝土高拱坝三维有限元静动力分析[D]. 郑州: 郑州大学, 2016.
[本文引用: 1]
SUN Bao-cheng. Static and dynamic analysis of high concrete arch dam was studied using the 3D finite element method on ABAQUS[D]. Zhengzhou: Zhengzhou University, 2016.
[本文引用: 1]
[25]
田硕. 混凝土高拱坝地震易损性分析[D]. 大连: 大连理工大学, 2019.
[本文引用: 1]
TIAN Shuo. Seismic fragility analysis of high concrete arch dam [D]. Dalian: Dalian University of Technology, 2019.
[本文引用: 1]
[26]
QIU Y X, WANG J T, JIN A Y, et al Simple models for simulating shear key arrangement in nonlinear seismic analysis of arch dams
[J]. Soil Dynamics and Earthquake Engineering , 2021 , 151 : 107006
DOI:10.1016/j.soildyn.2021.107006
[本文引用: 2]
[27]
WANG J T, JIN A Y, DU X L, et al Scatter of dynamic response and damage of an arch dam subjected to artificial earthquake accelerograms
[J]. Soil Dynamics and Earthquake Engineering , 2016 , 87 : 93 - 100
DOI:10.1016/j.soildyn.2016.05.003
[本文引用: 2]
[29]
张建伟, 刘鹏飞, 王涛, 等 基于混凝土塑性损伤本构的高拱坝损伤开裂分析
[J]. 中国农村水利水电 , 2020 , (4 ): 158 - 165
DOI:10.3969/j.issn.1007-2284.2020.04.029
[本文引用: 1]
ZHANG Jian-wei, LIU Peng-fei, WANG Tao, et al Damage cracking analysis of high arch dam based on plastic damage constitutive model of concrete
[J]. China Rural Water and Hydropower , 2020 , (4 ): 158 - 165
DOI:10.3969/j.issn.1007-2284.2020.04.029
[本文引用: 1]
[30]
徐强, 张天然, 陈健云, 等 基于ETA模型的配筋措施对于高拱坝变形损伤指标的影响
[J]. 工程科学与技术 , 2021 , 53 (3 ): 77 - 88
[本文引用: 1]
XU Qiang, ZHANG Tian-ran, CHEN Jian-yun, et al Influence of reinforcement measures on deformation damage index of high-arch dam based on endurance time analysis model
[J]. Advanced Engineering Sciences , 2021 , 53 (3 ): 77 - 88
[本文引用: 1]
[32]
曹翔宇. 高拱坝动力监测的传感器优化布置与基于深度学习的地震损伤识别方法研究[D]. 大连: 大连理工大学, 2021.
[本文引用: 1]
CAO Xiang-yu. Study on optimal sensor placement for dynamic monitoring and seismic damage identification method based on deep learning for high arch dams [D]. Dalian: Dalian University of Technology, 2021.
[本文引用: 1]
[33]
姚霄雯. 基于性能的高拱坝地震易损性分析与抗震安全评估[D]. 杭州: 浙江大学, 2013.
[本文引用: 1]
YAO Xiao-wen. Performance-based seismic fragility analysis and safety assessment of high arch dams[D]. Hangzhou: Zhejiang University, 2013.
[本文引用: 1]
[34]
WANG J, ZHANG M, JIN A, et al Seismic fragility of arch dams based on damage analysis
[J]. Soil Dynamics and Earthquake Engineering , 2018 , 109 : 58 - 68
DOI:10.1016/j.soildyn.2018.01.018
[本文引用: 1]
[35]
李静, 陈健云, 徐强, 等 高拱坝抗震性能评价指标研究
[J]. 水利学报 , 2015 , 46 (1 ): 118 - 124
DOI:10.13243/j.cnki.slxb.2015.01.016
[本文引用: 1]
LI Jing, CHEN Jian-yun, XU Qiang, et al Study on index of seismic performance evaluation of arch dam
[J]. Journal of Hydraulic Engineering , 2015 , 46 (1 ): 118 - 124
DOI:10.13243/j.cnki.slxb.2015.01.016
[本文引用: 1]
[36]
XU Q, ZHANG T, CHEN J, et al The influence of reinforcement strengthening on seismic response and index correlation for high arch dams by endurance time analysis method
[J]. Structures , 2021 , 32 : 355 - 379
DOI:10.1016/j.istruc.2021.03.007
[本文引用: 1]
[37]
SONG Z, LIU Y, YANG Q Experimental and numerical investigation on the stability of a high arch dam with typical problems of nonsymmetry: Baihetan Dam, China
[J]. Bulletin of Engineering Geology and the Environment , 2016 , 75 (4 ): 1555 - 1570
DOI:10.1007/s10064-015-0819-5
[本文引用: 1]
1
... 聚类算法是发掘数据的类别标记、揭示数据内在结构及规律的无监督学习算法. 传统的聚类算法主要包括K-means法[1 ] 、层次聚类法[2 ] ,皆具备较好的数据处理效果. 近年来,在识别数据典型特征时,一些学者将聚类算法引入到了地震工程研究领域中. Stojadinović等[3 ] 基于K-means法改进结构震后损伤评估的计算效率. Mariniello等[4 ] 将遗传算法与K-means法相结合,证实在对结构开展抗震安全评估时,聚类算法可以优化解决方案的可行性. 在以往的抗震研究中,研究人员经常优先研究结构自身优化、震后评估问题,再对结构的抗震安全性能做出合理评价. 鉴于实际震害资料的匮乏,如果得到的震害数据有限,也将很难全面评估结构的抗震效果. 为此,地震易损性的研究受到了学者们的广泛关注. ...
1
... 聚类算法是发掘数据的类别标记、揭示数据内在结构及规律的无监督学习算法. 传统的聚类算法主要包括K-means法[1 ] 、层次聚类法[2 ] ,皆具备较好的数据处理效果. 近年来,在识别数据典型特征时,一些学者将聚类算法引入到了地震工程研究领域中. Stojadinović等[3 ] 基于K-means法改进结构震后损伤评估的计算效率. Mariniello等[4 ] 将遗传算法与K-means法相结合,证实在对结构开展抗震安全评估时,聚类算法可以优化解决方案的可行性. 在以往的抗震研究中,研究人员经常优先研究结构自身优化、震后评估问题,再对结构的抗震安全性能做出合理评价. 鉴于实际震害资料的匮乏,如果得到的震害数据有限,也将很难全面评估结构的抗震效果. 为此,地震易损性的研究受到了学者们的广泛关注. ...
Rapid earthquake loss assessment based on machine learning and representative sampling
1
2022
... 聚类算法是发掘数据的类别标记、揭示数据内在结构及规律的无监督学习算法. 传统的聚类算法主要包括K-means法[1 ] 、层次聚类法[2 ] ,皆具备较好的数据处理效果. 近年来,在识别数据典型特征时,一些学者将聚类算法引入到了地震工程研究领域中. Stojadinović等[3 ] 基于K-means法改进结构震后损伤评估的计算效率. Mariniello等[4 ] 将遗传算法与K-means法相结合,证实在对结构开展抗震安全评估时,聚类算法可以优化解决方案的可行性. 在以往的抗震研究中,研究人员经常优先研究结构自身优化、震后评估问题,再对结构的抗震安全性能做出合理评价. 鉴于实际震害资料的匮乏,如果得到的震害数据有限,也将很难全面评估结构的抗震效果. 为此,地震易损性的研究受到了学者们的广泛关注. ...
Seismic pre-dimensioning of irregular concrete frame structures: mathematical formulation and implementation of a learn-heuristic algorithm
1
2022
... 聚类算法是发掘数据的类别标记、揭示数据内在结构及规律的无监督学习算法. 传统的聚类算法主要包括K-means法[1 ] 、层次聚类法[2 ] ,皆具备较好的数据处理效果. 近年来,在识别数据典型特征时,一些学者将聚类算法引入到了地震工程研究领域中. Stojadinović等[3 ] 基于K-means法改进结构震后损伤评估的计算效率. Mariniello等[4 ] 将遗传算法与K-means法相结合,证实在对结构开展抗震安全评估时,聚类算法可以优化解决方案的可行性. 在以往的抗震研究中,研究人员经常优先研究结构自身优化、震后评估问题,再对结构的抗震安全性能做出合理评价. 鉴于实际震害资料的匮乏,如果得到的震害数据有限,也将很难全面评估结构的抗震效果. 为此,地震易损性的研究受到了学者们的广泛关注. ...
1
... 地震易损性是指在不同地震动激励下,结构可能发生的破坏状态[5 ] ,研究方法通常分为专家法、经验法及解析型研究法等[6 ] .目前,在解析型地震易损性的研究中,通常需要增量动力分析法(incremental dynamic analysis,IDA)、多样条带分析法(multiple stripe analysis,MSA)和耐震时程分析法(endurance time analysis,ETA)等[7 ] 执行大规模的非线性计算. 虽然这些方法简便、稳定且发展成熟,能得到较精确的结构性能评估效果,但是计算成本较高. ...
1
... 地震易损性是指在不同地震动激励下,结构可能发生的破坏状态[5 ] ,研究方法通常分为专家法、经验法及解析型研究法等[6 ] .目前,在解析型地震易损性的研究中,通常需要增量动力分析法(incremental dynamic analysis,IDA)、多样条带分析法(multiple stripe analysis,MSA)和耐震时程分析法(endurance time analysis,ETA)等[7 ] 执行大规模的非线性计算. 虽然这些方法简便、稳定且发展成熟,能得到较精确的结构性能评估效果,但是计算成本较高. ...
Quantification of seismic potential failure modes in concrete dams
1
2016
... 地震易损性是指在不同地震动激励下,结构可能发生的破坏状态[5 ] ,研究方法通常分为专家法、经验法及解析型研究法等[6 ] .目前,在解析型地震易损性的研究中,通常需要增量动力分析法(incremental dynamic analysis,IDA)、多样条带分析法(multiple stripe analysis,MSA)和耐震时程分析法(endurance time analysis,ETA)等[7 ] 执行大规模的非线性计算. 虽然这些方法简便、稳定且发展成熟,能得到较精确的结构性能评估效果,但是计算成本较高. ...
3
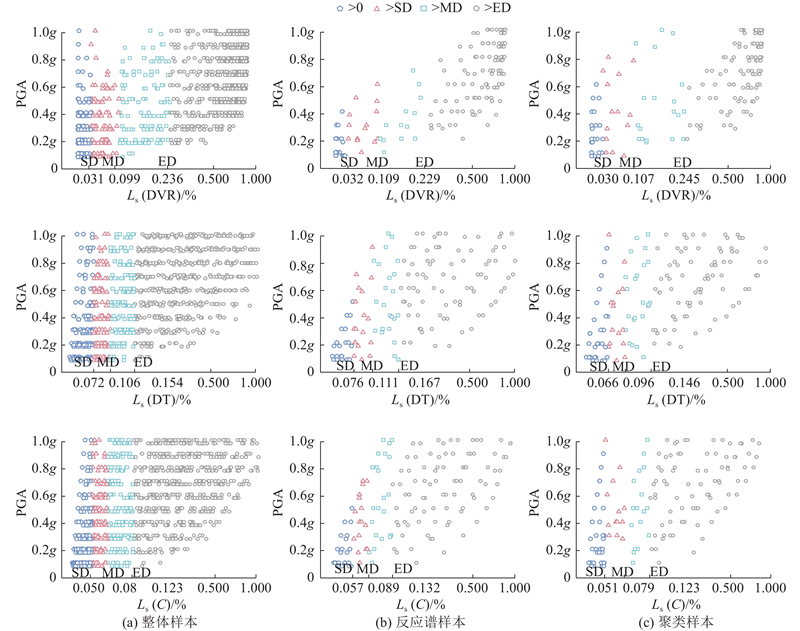
... 为了解决这个问题,一些学者提出以规范标准反应谱法[8 ] 、应用技术委员会法(applied technology council,ATC)[9 ] 、改进程序法[10 -11 ] 等筛选地震波子集以降低地震易损性计算成本. 这些方法能大幅度降低计算量,但研究人员仍然面临着所选地震波过多及无法合理选择具有代表性的地震波问题. 此外,传统的地震波筛选方式较难涉及复杂的地震动强度指标(intensity measures,IM),在地震波随机性的问题上也较难考虑全面,从而使得地震易损性的结果可能不够准确. ...
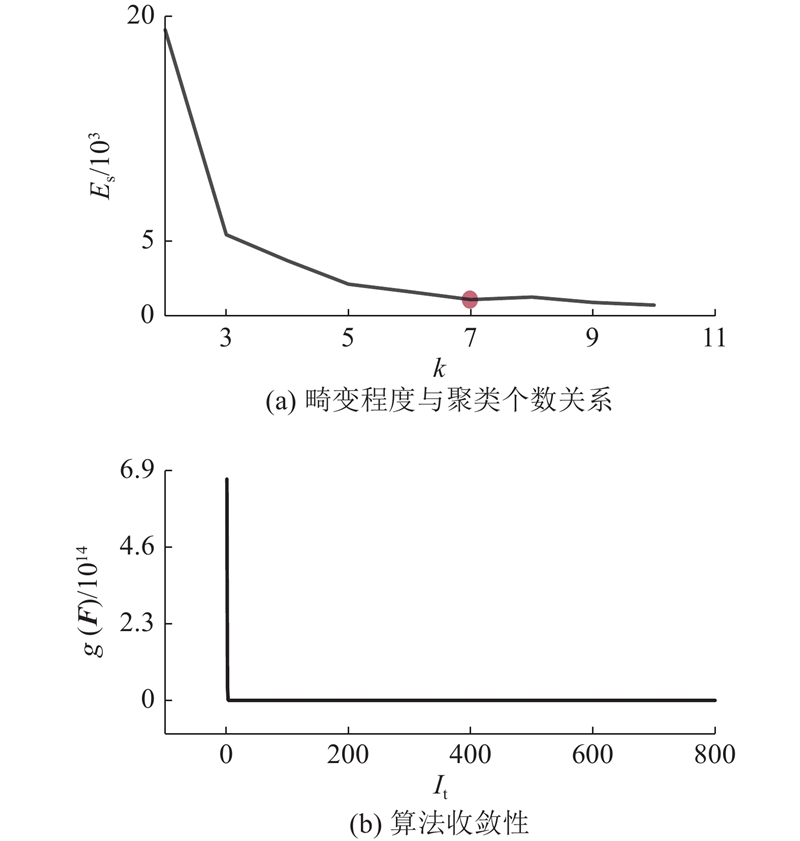
... 考虑《建筑设计抗震规范》[8 ] 以峰值加速度(peak ground acceleration,PGA)为设防标准,本研究以拱坝100 a基准期超越概率2%的工程场地基岩地震峰值加速度0.325g 作为标准化指标. 在聚类时设置最大迭代次数 $ T{\text{ = }}1 \times {10^5} $ $ \varepsilon {\text{ = }}1 \times {10^{{{ - }}6}} $ . 采用肘部判别法[19 ] 确定109条地震波的聚类类别数,如图2 (a)所示. 图中,k 为聚类数;E s 为反映聚类算法畸变程度的簇内误差平方和,该值越小,聚类效果越显著. 可知,随着k 逐渐增大,E s 逐渐降低,当k =7时,E s 接近最低水平,斜率近似为0,表明选择聚类数k =7,聚类效果较好. 如图2 (b)所示为聚类算法收敛性效果图. 图中,I t 为迭代次数,g (F
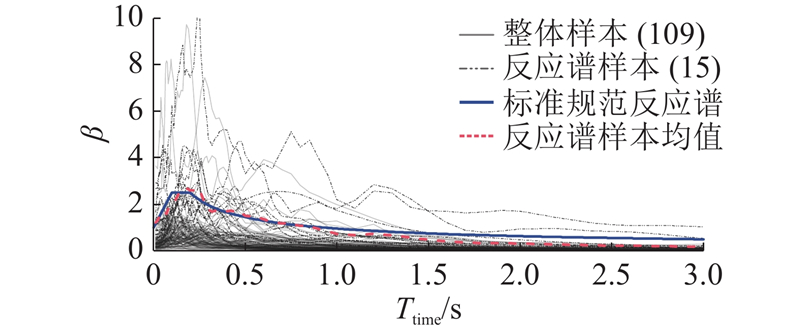
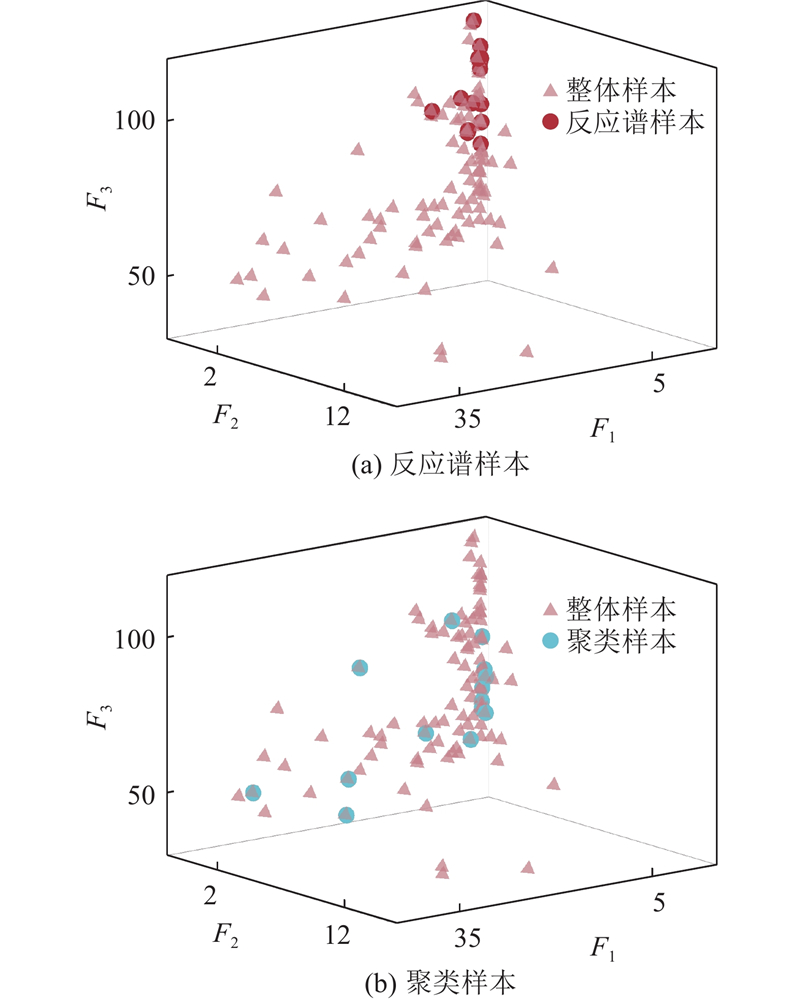
... 另一个对比案例仍以1.3节筛选标准作为基本条件,参考《建筑设计抗震规范》[8 ] 中多组地震动时程分析的标准规定,并结合学者在大坝[21 ] 结构地震易损性分析时应用的规范反应谱法,同样在109条地震波中选择15条作为反应谱样本. 考虑到本研究所选的109条地震波反应谱的离散性较大,很可能导致反应谱样本计算的反应谱均值与标准规范反应谱出现较大误差,因此,参考文献[22 ]的选波方式,以反应谱在[0.1,T g
1
... 为了解决这个问题,一些学者提出以规范标准反应谱法[8 ] 、应用技术委员会法(applied technology council,ATC)[9 ] 、改进程序法[10 -11 ] 等筛选地震波子集以降低地震易损性计算成本. 这些方法能大幅度降低计算量,但研究人员仍然面临着所选地震波过多及无法合理选择具有代表性的地震波问题. 此外,传统的地震波筛选方式较难涉及复杂的地震动强度指标(intensity measures,IM),在地震波随机性的问题上也较难考虑全面,从而使得地震易损性的结果可能不够准确. ...
A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance
1
2011
... 为了解决这个问题,一些学者提出以规范标准反应谱法[8 ] 、应用技术委员会法(applied technology council,ATC)[9 ] 、改进程序法[10 -11 ] 等筛选地震波子集以降低地震易损性计算成本. 这些方法能大幅度降低计算量,但研究人员仍然面临着所选地震波过多及无法合理选择具有代表性的地震波问题. 此外,传统的地震波筛选方式较难涉及复杂的地震动强度指标(intensity measures,IM),在地震波随机性的问题上也较难考虑全面,从而使得地震易损性的结果可能不够准确. ...
An improved algorithm for selecting ground motions to match a conditional spectrum
1
2018
... 为了解决这个问题,一些学者提出以规范标准反应谱法[8 ] 、应用技术委员会法(applied technology council,ATC)[9 ] 、改进程序法[10 -11 ] 等筛选地震波子集以降低地震易损性计算成本. 这些方法能大幅度降低计算量,但研究人员仍然面临着所选地震波过多及无法合理选择具有代表性的地震波问题. 此外,传统的地震波筛选方式较难涉及复杂的地震动强度指标(intensity measures,IM),在地震波随机性的问题上也较难考虑全面,从而使得地震易损性的结果可能不够准确. ...
Fragility analysis of substation equipment based on ground motion clustering
1
2021
... 学者们采用聚类算法来解决上述问题. 例如,K-means、层次聚类法皆可以用于筛选地震波子集以降低易损性计算成本[12 ] . 然而,K-means法仅适用于样本分布为近似“超球”状的数值型数据,层次聚类法不能回溯调整已构成的簇结构,具有不可逆性. 并且,两者在直接面对高维数据时也容易陷入“维数灾难”的问题. ...
A tutorial on spectral clustering
3
2007
... 谱聚类(spectral clustering,SPC)是基于谱图划分的聚类算法[13 ] . 该算法适合对任意呈流行状分布的数据进行聚类,适用于高维数据且具备收敛到全局最优解的特点. 不过,要解决各种情形下的数据聚类问题,已有算法都是不完美的,SPC法也不例外. 传统的SPC算法仅适用于原始各簇数据分布较均衡的情形. 当面对各簇样本数相差悬殊的类不平衡问题时,SPC算法将不再适用. ...
... SPC算法通过无向带权图 ${\boldsymbol{G}}{\text{ = }}\left( {V{\text{,}}E{\text{,}}{\boldsymbol{W}}} \right)$ $X = \left\{ {{x_i}} \right\}_{i = 1}^n$ [13 ] . 其中,V 为顶点集, $V = \left\{ {{v_i}} \right\}_{i = 1}^n$ E 为连接顶点 ${v_i}$ ${v_j}$ $E = \left\{ {{e_{ij}}} \right\}$ W ${\boldsymbol{G}}$ ${\boldsymbol{W}} = {\left[ {{w_{ij}}} \right]_{n \times n}}$ . 该算法要求图的顶点集V 与样本点集X 一一对应. 同时,采用一种保留数据局部特征的流行降维方法,即转换图Laplacian矩阵,达到降维效果. 定义图Laplacian矩阵为 $ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{W}} $ . 其中,D ${\boldsymbol{D}} = {\rm{diag}}\;\left( {{{\left[ {{d_{ii}}} \right]}_{n \times n}}} \right)$ d ii ${v_i}$ ${d_{ii}} = \displaystyle \sum\nolimits_j {{w_{ij}}} $ . 传统SPC算法具体可参考文献[13 ].SPC的优化问题表达式如下: ...
... .传统SPC算法具体可参考文献[13 ].SPC的优化问题表达式如下: ...
1
... 2)约束“ ${\kern 1pt} {{\boldsymbol{F}}^{\text{T}}}{\boldsymbol{F}} = {\boldsymbol{I}}$ [14 ] .若约束隶属度矩阵 $ {\boldsymbol{F}} $ $ {{\boldsymbol{F}}^{\text{T}}}{\boldsymbol{F}} \approx {\boldsymbol{I}} $ $ {{\boldsymbol{F}}_{ \cdot p}} $ $ {\boldsymbol{F}} $ $ p $
Trace-penalty minimization for large-scale eigenspace computation
2
2016
... 利用文献[15 ]中的迹惩罚函数求解式(2),则问题(2)转化为如下罚函数模型: ...
... 根据文献[15 ],应用GN方向的解析表达式求解式(7),其中,GN方向的解析表达式为 ...
Quasi-likelihood functions, generalized linear models, and the Gauss-Newton method
1
1974
... 由于式(7)的目标函数是二次函数,考虑应用Gauss-Newton(GN)法[16 ] 对其求解. 记 $ S({{\boldsymbol{F}}^t}) $ $ {g} ({\boldsymbol{F}}) $ $ {{\boldsymbol{F}}^t} $
基于向量地震动强度指标的拱坝地震易损性分析
4
2019
... 为了准确反映拱坝结构真实性态,考虑震级、频谱特性及持时的影响,从美国太平洋地震研究中心地震动数据库中,根据水工抗震规范反应谱共选择了109条地震波(每条地震波有3个方向),如图1 所示. 图中,β 为谱加速度放大系数,T time 为时间. 具体筛选准则如下:1)参照文献[17 ]的选波标准,以震级5~8级,震中距0~100 km,剪切波速 $ {V_{\rm{s}}} $ g 为间隔,调幅10次至1.0g ;3)地震波归一化处理,在非线性分析时考虑3个方向的地震动作用. ...
... 以双曲型白鹤滩拱坝为例构建模型. 该拱坝工程场地类别为Ⅰ类,场地基本地震烈度为Ⅷ度,100 a基准期超越概率2%的工程场地基岩地震PGA为 0.325g [17 ] .拱坝坝顶高程834 m,坝高289 m,坝体上游正常蓄水位825 m,下游水位604 m,更多模型参数可参考文献[24 ]、[25 ],如表2 所示. 图中,E 为弹性模量,ρ 为密度,ν 为泊松比. 考虑到工程实际,对现有数值模型进行适当简化,地基部分延伸为约2倍的拱坝坝体结构高度及宽度. 该有限元模型共36178个单元、40286个节点,坐标y 轴负向为顺水流向,z 轴正向向上. 坝体及地基均为Solid 65单元,少部分坝肩衔接处采用六节点棱柱体单元. ...
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
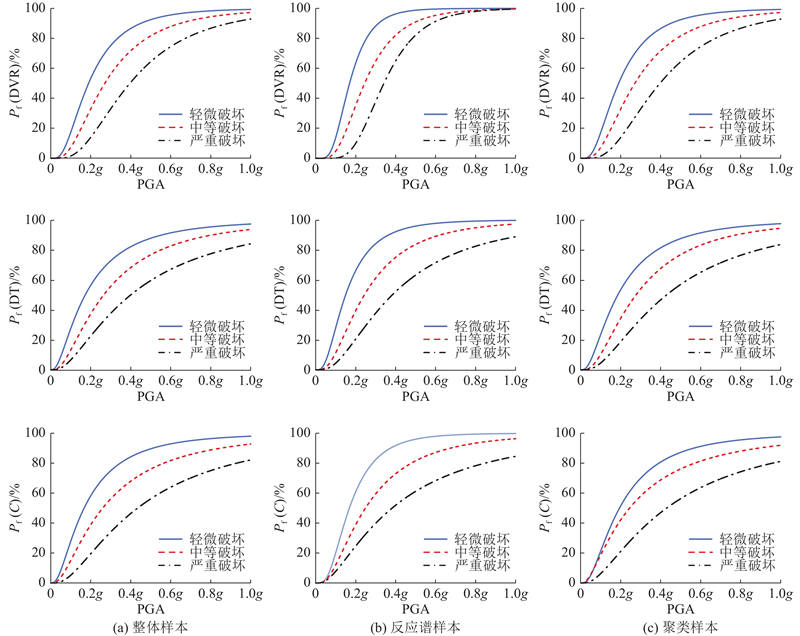
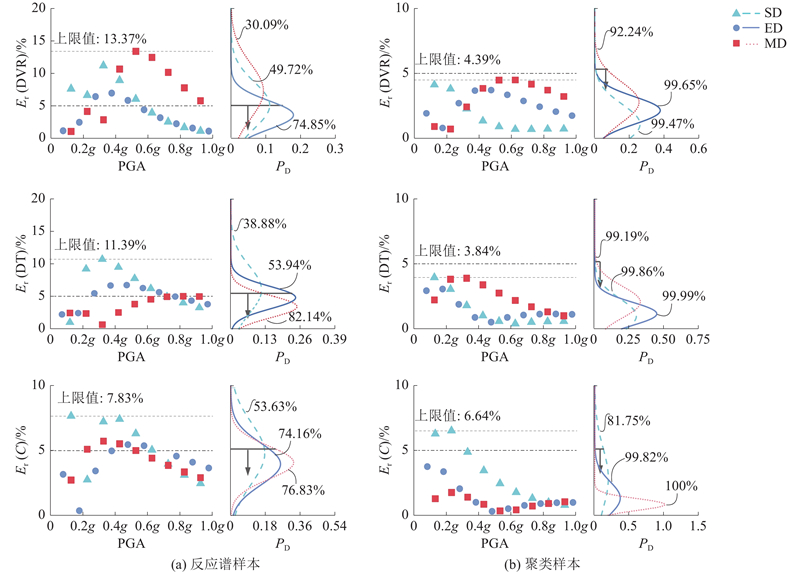
... 结合文献[17 ]对白鹤滩拱坝性能指标的定义标准,将拱坝损伤发展历程的4个阶段作为极限状态划分的典型标志,分为基本完好、轻微破坏、中等破坏、严重破坏4类,并以每条地震波达到上述4种极限状态时的均值量化结构性能指标限值. 拱坝各类样本的性能水平划分取值如表3 所示. ...
基于向量地震动强度指标的拱坝地震易损性分析
4
2019
... 为了准确反映拱坝结构真实性态,考虑震级、频谱特性及持时的影响,从美国太平洋地震研究中心地震动数据库中,根据水工抗震规范反应谱共选择了109条地震波(每条地震波有3个方向),如图1 所示. 图中,β 为谱加速度放大系数,T time 为时间. 具体筛选准则如下:1)参照文献[17 ]的选波标准,以震级5~8级,震中距0~100 km,剪切波速 $ {V_{\rm{s}}} $ g 为间隔,调幅10次至1.0g ;3)地震波归一化处理,在非线性分析时考虑3个方向的地震动作用. ...
... 以双曲型白鹤滩拱坝为例构建模型. 该拱坝工程场地类别为Ⅰ类,场地基本地震烈度为Ⅷ度,100 a基准期超越概率2%的工程场地基岩地震PGA为 0.325g [17 ] .拱坝坝顶高程834 m,坝高289 m,坝体上游正常蓄水位825 m,下游水位604 m,更多模型参数可参考文献[24 ]、[25 ],如表2 所示. 图中,E 为弹性模量,ρ 为密度,ν 为泊松比. 考虑到工程实际,对现有数值模型进行适当简化,地基部分延伸为约2倍的拱坝坝体结构高度及宽度. 该有限元模型共36178个单元、40286个节点,坐标y 轴负向为顺水流向,z 轴正向向上. 坝体及地基均为Solid 65单元,少部分坝肩衔接处采用六节点棱柱体单元. ...
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
... 结合文献[17 ]对白鹤滩拱坝性能指标的定义标准,将拱坝损伤发展历程的4个阶段作为极限状态划分的典型标志,分为基本完好、轻微破坏、中等破坏、严重破坏4类,并以每条地震波达到上述4种极限状态时的均值量化结构性能指标限值. 拱坝各类样本的性能水平划分取值如表3 所示. ...
1
... 目前,研究人员已提出了大量的IM用于实现结构地震易损性研究[18 ] .本研究参考上述文献共选择了50个具有代表性的IM,详细定义如表1 所示. ...
1
... 目前,研究人员已提出了大量的IM用于实现结构地震易损性研究[18 ] .本研究参考上述文献共选择了50个具有代表性的IM,详细定义如表1 所示. ...
Review on determining number of Cluster in K-Means Clustering
1
2013
... 考虑《建筑设计抗震规范》[8 ] 以峰值加速度(peak ground acceleration,PGA)为设防标准,本研究以拱坝100 a基准期超越概率2%的工程场地基岩地震峰值加速度0.325g 作为标准化指标. 在聚类时设置最大迭代次数 $ T{\text{ = }}1 \times {10^5} $ $ \varepsilon {\text{ = }}1 \times {10^{{{ - }}6}} $ . 采用肘部判别法[19 ] 确定109条地震波的聚类类别数,如图2 (a)所示. 图中,k 为聚类数;E s 为反映聚类算法畸变程度的簇内误差平方和,该值越小,聚类效果越显著. 可知,随着k 逐渐增大,E s 逐渐降低,当k =7时,E s 接近最低水平,斜率近似为0,表明选择聚类数k =7,聚类效果较好. 如图2 (b)所示为聚类算法收敛性效果图. 图中,I t 为迭代次数,g (F
Effects of connection fractures on SMRF seismic drift demands
1
2000
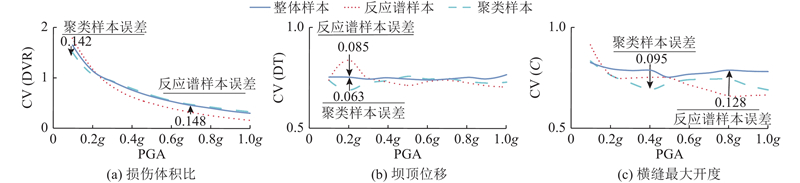
... 理论上,计算的地震波数量越多,性能评估结果越可靠. Luco等[20 ] 研究发现,选取10~20条地震波可以精确评估结构的抗震能力. 因此,本研究将109条地震波调幅10次后的有限元结果(1090次)作为参照基准(整体样本). 根据BSPC算法的思想,将109条地震波聚类后(共7簇)按照各簇隶属度值降序排列,在每簇样本中均匀选取15条地震波作为聚类样本. 其中,均匀选取规则由各簇样本数与整体样本数(109条)的比例决定,如 ...
Seismic fragility for high CFRDs based on deformation and damage index through incremental dynamic analysis
1
2018
... 另一个对比案例仍以1.3节筛选标准作为基本条件,参考《建筑设计抗震规范》[8 ] 中多组地震动时程分析的标准规定,并结合学者在大坝[21 ] 结构地震易损性分析时应用的规范反应谱法,同样在109条地震波中选择15条作为反应谱样本. 考虑到本研究所选的109条地震波反应谱的离散性较大,很可能导致反应谱样本计算的反应谱均值与标准规范反应谱出现较大误差,因此,参考文献[22 ]的选波方式,以反应谱在[0.1,T g
1
... 另一个对比案例仍以1.3节筛选标准作为基本条件,参考《建筑设计抗震规范》[8 ] 中多组地震动时程分析的标准规定,并结合学者在大坝[21 ] 结构地震易损性分析时应用的规范反应谱法,同样在109条地震波中选择15条作为反应谱样本. 考虑到本研究所选的109条地震波反应谱的离散性较大,很可能导致反应谱样本计算的反应谱均值与标准规范反应谱出现较大误差,因此,参考文献[22 ]的选波方式,以反应谱在[0.1,T g
1
... 另一个对比案例仍以1.3节筛选标准作为基本条件,参考《建筑设计抗震规范》[8 ] 中多组地震动时程分析的标准规定,并结合学者在大坝[21 ] 结构地震易损性分析时应用的规范反应谱法,同样在109条地震波中选择15条作为反应谱样本. 考虑到本研究所选的109条地震波反应谱的离散性较大,很可能导致反应谱样本计算的反应谱均值与标准规范反应谱出现较大误差,因此,参考文献[22 ]的选波方式,以反应谱在[0.1,T g
高心墙堆石坝弹塑性动力反应分析及地震易损性研究
1
2020
... 多样条带分析法是根据最大似然估计原理得到结构的地震易损性概率. 靳聪聪等[23 ] 的研究表明,MSA法在一定结构分析数量下比IDA法能够更有效地估计易损性方程参数. 易损性函数描述结构在对应地震动强度下达到或超过规定损伤极限状态的概率,表达式为 ...
高心墙堆石坝弹塑性动力反应分析及地震易损性研究
1
2020
... 多样条带分析法是根据最大似然估计原理得到结构的地震易损性概率. 靳聪聪等[23 ] 的研究表明,MSA法在一定结构分析数量下比IDA法能够更有效地估计易损性方程参数. 易损性函数描述结构在对应地震动强度下达到或超过规定损伤极限状态的概率,表达式为 ...
1
... 以双曲型白鹤滩拱坝为例构建模型. 该拱坝工程场地类别为Ⅰ类,场地基本地震烈度为Ⅷ度,100 a基准期超越概率2%的工程场地基岩地震PGA为 0.325g [17 ] .拱坝坝顶高程834 m,坝高289 m,坝体上游正常蓄水位825 m,下游水位604 m,更多模型参数可参考文献[24 ]、[25 ],如表2 所示. 图中,E 为弹性模量,ρ 为密度,ν 为泊松比. 考虑到工程实际,对现有数值模型进行适当简化,地基部分延伸为约2倍的拱坝坝体结构高度及宽度. 该有限元模型共36178个单元、40286个节点,坐标y 轴负向为顺水流向,z 轴正向向上. 坝体及地基均为Solid 65单元,少部分坝肩衔接处采用六节点棱柱体单元. ...
1
... 以双曲型白鹤滩拱坝为例构建模型. 该拱坝工程场地类别为Ⅰ类,场地基本地震烈度为Ⅷ度,100 a基准期超越概率2%的工程场地基岩地震PGA为 0.325g [17 ] .拱坝坝顶高程834 m,坝高289 m,坝体上游正常蓄水位825 m,下游水位604 m,更多模型参数可参考文献[24 ]、[25 ],如表2 所示. 图中,E 为弹性模量,ρ 为密度,ν 为泊松比. 考虑到工程实际,对现有数值模型进行适当简化,地基部分延伸为约2倍的拱坝坝体结构高度及宽度. 该有限元模型共36178个单元、40286个节点,坐标y 轴负向为顺水流向,z 轴正向向上. 坝体及地基均为Solid 65单元,少部分坝肩衔接处采用六节点棱柱体单元. ...
1
... 以双曲型白鹤滩拱坝为例构建模型. 该拱坝工程场地类别为Ⅰ类,场地基本地震烈度为Ⅷ度,100 a基准期超越概率2%的工程场地基岩地震PGA为 0.325g [17 ] .拱坝坝顶高程834 m,坝高289 m,坝体上游正常蓄水位825 m,下游水位604 m,更多模型参数可参考文献[24 ]、[25 ],如表2 所示. 图中,E 为弹性模量,ρ 为密度,ν 为泊松比. 考虑到工程实际,对现有数值模型进行适当简化,地基部分延伸为约2倍的拱坝坝体结构高度及宽度. 该有限元模型共36178个单元、40286个节点,坐标y 轴负向为顺水流向,z 轴正向向上. 坝体及地基均为Solid 65单元,少部分坝肩衔接处采用六节点棱柱体单元. ...
1
... 以双曲型白鹤滩拱坝为例构建模型. 该拱坝工程场地类别为Ⅰ类,场地基本地震烈度为Ⅷ度,100 a基准期超越概率2%的工程场地基岩地震PGA为 0.325g [17 ] .拱坝坝顶高程834 m,坝高289 m,坝体上游正常蓄水位825 m,下游水位604 m,更多模型参数可参考文献[24 ]、[25 ],如表2 所示. 图中,E 为弹性模量,ρ 为密度,ν 为泊松比. 考虑到工程实际,对现有数值模型进行适当简化,地基部分延伸为约2倍的拱坝坝体结构高度及宽度. 该有限元模型共36178个单元、40286个节点,坐标y 轴负向为顺水流向,z 轴正向向上. 坝体及地基均为Solid 65单元,少部分坝肩衔接处采用六节点棱柱体单元. ...
Simple models for simulating shear key arrangement in nonlinear seismic analysis of arch dams
2
2021
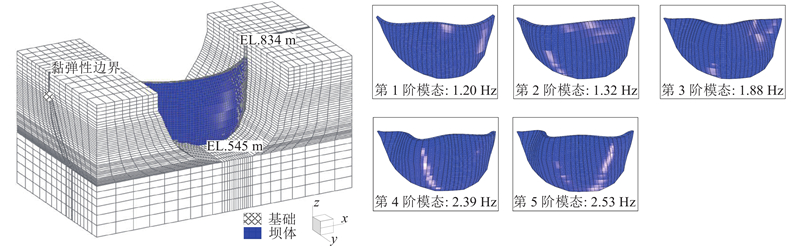
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
... [26 -27 ],在地震分析时选用瑞利阻尼,阻尼比为5%. ...
Scatter of dynamic response and damage of an arch dam subjected to artificial earthquake accelerograms
2
2016
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
... -27 ],在地震分析时选用瑞利阻尼,阻尼比为5%. ...
A plastic-damage concrete model for earthquake analysis of dams
1
1998
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
基于混凝土塑性损伤本构的高拱坝损伤开裂分析
1
2020
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
基于混凝土塑性损伤本构的高拱坝损伤开裂分析
1
2020
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
基于ETA模型的配筋措施对于高拱坝变形损伤指标的影响
1
2021
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
基于ETA模型的配筋措施对于高拱坝变形损伤指标的影响
1
2021
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
Seismic safety of high concrete dams
1
2014
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
1
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
1
... 在进行非线性分析时在地基边界截断处设置弹簧-阻尼器实现黏弹性边界的施加[26 ] .坝体共计30条横缝,考虑到计算时拱坝收缩缝产生的开合-接触-滑移现象,选用商业软件ABAQUS提供的动态接触模型. 在接触设置时仅考虑横缝的张开与闭合,接触面之间的相互作用遵循接触-嵌入原则[27 ] .同时,引入Lee等[28 ] 提出的混凝土塑性损伤本构研究坝体损伤特性,本构设置参数可以参考文献[29 ]. 此外,由于本研究拱坝模型仅在坝面上下游铺设钢筋,坝面位置仍采用混凝土的弹性模量代替钢筋混凝土的弹性模量,并忽略钢筋的强化阶段,选择理想本构模型代替[30 ] . 针对白鹤滩拱坝进行模态计算,选择Chen[31 ] 修正的动水压力模型实现正常蓄水位的模拟,获取的前5阶模态振型图如图4 所示. 该模态结果与文献[32 ]中白鹤滩拱坝提取正常蓄水位下的振动数据响应模态较吻合,最大模态差异值仅6%.参考关于拱坝抗震的类似文献成果[26 -27 ] ,在地震分析时选用瑞利阻尼,阻尼比为5%. ...
1
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
1
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
Seismic fragility of arch dams based on damage analysis
1
2018
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
高拱坝抗震性能评价指标研究
1
2015
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
高拱坝抗震性能评价指标研究
1
2015
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
The influence of reinforcement strengthening on seismic response and index correlation for high arch dams by endurance time analysis method
1
2021
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...
Experimental and numerical investigation on the stability of a high arch dam with typical problems of nonsymmetry: Baihetan Dam, China
1
2016
... 目前,学者们将峰值位移、应力分布、损伤等性能指标作为拱坝性能分析时的常用指标. 姚霄雯[33 ] 根据拱坝概率需求曲线的斜率突变特性,分别选择拱冠梁顶部位移、横缝开度及切向滑移指标评估拱坝抗震性能. Wang等[34 ] 结合大岗山拱坝的损伤分布及横缝开度,量化了性能指标的极限状态. 李静等[35 ] 认为坝面损伤面积比及坝体损伤体积比可以清晰地反映拱坝结构损伤规律. 范书立等[17 ] 建立以拱冠梁顶部位移、横缝开度、损伤体积比3项性能指标为基准的白鹤滩拱坝易损性曲面,Xu等[36 ] 证实上述3项指标具备评估拱坝抗震性能的能力. Song等[37 ] 针对白鹤滩拱坝开展了稳定性实验研究,表明拱坝坝顶位移值得关注. ...