工程流体静态混合是高压、高速势场驱动下的流体介质流经固定机械构件而产生相互交融的过程. 静态混合过程伴随强剪切、回流反冲、壁面冲击等物理现象, 由流固耦合产生的流致振动较显著. 因此, 研究静态混合过程所涉及的流固耦合振动特性对于航空航天、绿色石化、核电、新能源等工业领域具有重要意义^[1-3]. 在化工强化过程中需要多种高效混合设备, 静态混合器作为其中一种, 其共性特征如下：流体介质为工程多相流, 固体边界为薄壁圆柱壳结构；应用过程中流体经过内部混合叶片或孔板后不断分流、拉伸、碰撞, 具有高度非线性动力学特征；流体冲击壁面, 迫使管壳产生振动及噪声. 在绝大多数情况下, 这种振动和噪声是有害的^[4]. 因此, 开展流体激励下静态混合器流固耦合振动响应特性, 探究其流场演化及振动传播机理, 总结其振动响应规律, 降低静态混合过程壁面振动和保证混合安全, 在理论和实践上有着重大研究意义.

在内部流体冲击作用下静态混合器中会形成复杂的流致振动, 其特征参数与静态混合管道几何尺寸、内置元件、流场分布等因素有关^[5-6]. 目前尚未有成熟的理论模型对静态混合过程流致振动规律进行定量分析, 只能在某种假设下或结合实验研究, 得到有限的流场特性^[7-9]. Haddadi等^[10]采用雷诺平均方程( $k \text{-} \omega $)湍流模型对静态混合器中流场进行研究, 最终得出的结果与实验数据较一致. Murasiewicz等^[11]采用大涡模拟方法得到Kenics混合器3个分量(轴向、切向和径向)上速度波动的时间演变, 得到静态混合器内部的稳定速度. 孟辉波等^[12]通过实验研究静态混合器内瞬态壁压波动特性, 发现管壁各点均存在一定程度的压力波动. Nikolic等^[13]对管道的动力特性和稳定性问题进行研究, 得出当内部流体为恒定流时, 在较高流速下管道不仅会发生弯曲而且还会发生颤振现象的结论. Leclaire等^[14]采用格子Boltzmann方法（lattice Boltzmann method，LBM）模拟层流和过渡流中液-液系统的压降和流速之间的关系, 最终仿真结果与实验结果较吻合. 此外权登辉等^[15-16]对Kensic静态混合器和LSM静态混合器进行内部流场的研究, 得到混合流场的传热和混合性能演变规律.

从上述文献可以推断, 当前对静态混合的研究主要集中在两相动态建模、稳定流场、壁面压力波动等方面. 针对流固耦合界面求解、流致振动特性问题的研究较少. 静态混合内部可以认为是柔性体多个速度分量与刚体产生强烈流固耦合的过程, 导致流致振动具有高度非线性特征, 这无疑增加了流固耦合求解精度及稳定性. 因此需要静态混合过程流固耦合建模与求解方法, 以开展静态混合器内部流固耦合振动现象的研究.

针对以上问题, 本研究提出基于LBM的多速度分量流固耦合模型, 结合大涡模拟（large eddy simulation, LES）湍流模型和流固弱耦合求解方法. 基于上述模型, 建立静态混合过程流固耦合动力学模型, 并讨论内流冲击与壁面振型的关联性, 揭示静态混合过程中流体与壁面的相互作用机理.

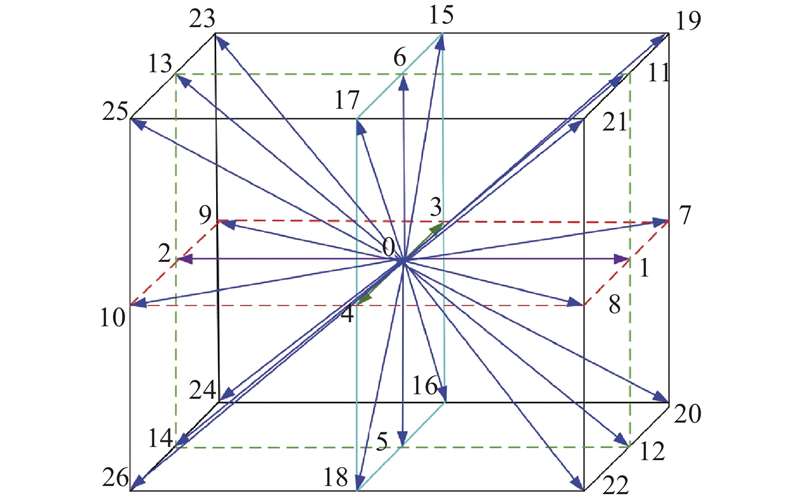
为了描述高度非线性特征下的静态混合刚柔接触过程，须详细考虑各种速度分量. 因此, 对于LBM的流固耦合模型, 采用多速度分量的格子模型, 并通过完全离散的玻尔兹曼输运方程进行求解. 对于流固耦合振动过程的求解，随着速度分量的增加, 会面临求解精度及稳定性的挑战. 针对此问题, 给出流场-结构场弱耦合求解策略.

静态混合过程具有复杂边界条件, 在工作过程中具有强剪切、回流反冲以及强烈的壁面碰撞效应, 这种现象可以视为多个柔性体与刚体碰撞进而产生强湍流促进混合.

基于介观的格子-玻尔兹曼方法(LBM)是把时间和空间完全离散, 然后将流体离散为若干粒子, 将流场划分为格子, 让这些粒子的分布函数沿网格线运动, 并在网格点上根据一定的规则相互碰撞. 分布函数的演化在宏观上反映了流体的运动规律, 流场的密度、速度、压力等力学参数都可以由分布函数的计算得到^[17]. 本研究提出的基于LBM的静态混合流固耦合动力学模型, 采用的格子模型为D3Q27速度模型(D表示维数, Q表示粒子运动方向的总数), 如图1所示. 该格子模型每个离散节点比其他格子模型具有更高的自由度, 更加适用于流体与壁面碰撞过程, 能获得更加精确的壁面振动特性.

速度离散后的玻尔兹曼输运方程如下：

(1) $ \frac{\partial f_\alpha }{\partial {t}}+{{\boldsymbol{e}}}_{\alpha }·\nabla {f}_{\alpha }={{{\varOmega}} }_{\alpha }+{{{F}}}_{\alpha },\;\; \alpha =0,1,\cdots ,{n}. $

式中： ${f_\alpha } = {f_\alpha }\left( {{\boldsymbol{r}},t} \right)$表示t时刻r点处α方向上的粒子分布函数, e_α为相应的离散速度, ${{{\varOmega}} _\alpha }$为碰撞算子, ${{{F}}_\alpha }$为外力F在α方向的投影.

为了求解式(1), 须对其时间及空间离散, 得到完全离散化的玻尔兹曼方程, 并对其滤波得到如下公式：

(2) $ {\bar f_\alpha }\left( {{{{\boldsymbol{r}}}}+{{\boldsymbol{e}}_\alpha }{{\delta}} t, t+{{\delta}} t} \right) - {\bar f_\alpha }\left( {{\boldsymbol{r}},t} \right) = {{{\varOmega}} _\alpha }+\delta t{\bar {{F}}_\alpha }. $

式中：“－”表示滤波. $\bar f$与 $f$的关系为

(3) $ \bar f\left( {{\boldsymbol{r}},t} \right) = \int {G\left( {{\boldsymbol{r}},{\boldsymbol{r}}'} \right)} f\left( {{\boldsymbol{r}},{\boldsymbol{r}}'} \right){\rm{d}}{\boldsymbol{r}}'. $

式中： $ G\left( {{\boldsymbol{r}},{\boldsymbol{r}}'} \right) $为滤波函数.

采用多松弛时间算法^[18], 则碰撞因子 ${\varOmega _\alpha }$可以写为

(4) $ {\varOmega _\alpha } = - {{{M}}_{ij}}{\hat {{s}}_{ij}}\left( {\bar f_\alpha ^{{\rm{eq}}} - {{\bar f}_\alpha }} \right). $

式中： ${{{\hat s}}_{ij}}$为对角松弛矩阵第i行、第j列的元素^[19], ${{{M}}_{ij}}$为转换矩阵第i行、第j列的元素, $\bar f_\alpha ^{{\rm{eq}}}$为 ${\bar f_\alpha }$的平衡态分布函数.

(5) $ {f}_{\alpha }^{{\rm{eq}}}\left({\boldsymbol{r}},t\right)={\omega }_{\alpha }\rho_{\rm{w}} \left[1+\frac{{{\boldsymbol{e}}}_{\alpha }\cdot \overline{{\boldsymbol{u}}}}{{c}_{{\rm{s}}}^{2}}+\frac{{\left({{\boldsymbol{e}}}_{\alpha }\cdot \overline{{\boldsymbol{u}}}\right)}^{2}}{2{c}_{{\rm{s}}}^{4}}-\frac{{\overline{{\boldsymbol{u}}}}^{2}}{2{c}_{{\rm{s}}}^{2}}\right]. $

式中： ${c_{\rm{s}}} = {c}/{{\sqrt 3 }}$,c为网格步长与时间步长之比,一般取值为1； $ \rho_{\rm{w}} $为流体密度；u 为宏观速度； ${\omega _\alpha }$为权系数.

(6) $ {\omega _\alpha } = \left\{ \begin{gathered} 8/27,\; \alpha = 0; \\ 2/27,\; \alpha = 1, \cdots ,6; \\ 1/54,\; \alpha = 7, \cdots ,18; \\ 1/216,\; \alpha = 19 ,\cdots ,26 . \\ \end{gathered} \right. $

(7) $ \begin{array}{c}\dfrac{{{\boldsymbol{e}}}_{\alpha }}{c}=\left\{ \begin{array}{ll}\left[0\text{，}0\text{，}0\right],\; \alpha=0; & \\ \left(\pm 1,\;0,\;0\right),\left(0,\;\pm 1,\;0\right),\left(0,\;0,\;\pm 1\right),\;\alpha=1,\cdots ,6;& \\ \left(\pm 1,\pm 1,0\right),\left(\pm 1,0,\pm 1\right),\left(0,\pm 1,\pm 1\right),\; \alpha=7 ,\cdots,18;& \\ \left(\pm 1,\pm 1,\pm 1\right),\; \alpha=19 ,\cdots,26. \end{array}\right. \end{array} $

相关研究表明, LES湍流模型能比其他模型更好地描述静态混合器内部流场^[7]. 根据LES方法, 引入附加黏性系数, 即亚格子尺度涡黏系数 ${\upsilon _{\rm{T}}}$. 为了模拟亚格子湍流, 选用wall-adapting local-eddy（WALE）涡黏模型, 可以更好地反映近壁面区域涡黏系数变化规律, 并适合复杂湍流模拟, 求解形式如下：

(8) $ {v_{\rm{T}}} = \frac{{\rho_{\rm{w}} \varDelta _{\rm{f}}^2{{\left( {s_{ij}^{\rm{d}}s_{ij}^{\rm{d}}} \right)}^{{3}/{2}}}}}{{{{\left( {{{\bar s}_{ij}}{{\bar s}_{ij}}} \right)}^{{5}/{2}}}+{{\left( {s_{ij}^{\rm{d}}s_{ij}^{\rm{d}}} \right)}^{{5}/{4}}}}}. $

式中： ${\bar {{s}}_{ij}} =\left( {{{\partial {{\bar u}_i}}}/{{\partial {x_j}}}+{{\partial {{\bar u}_j}}}/{{\partial {x_i}}}} \right)/2$为可解尺度应变率张量第i行、第j列的元素； ${\varDelta _{\rm{f}}} = {C_{\rm{W}}}\varDelta$为滤波尺度, ${C_{\rm{W}}}$为常数, $\varDelta$为单位网格尺度.

(9) $ s_{ij}^{\rm{d}} = {\bar s_{ij}}{\bar s_{kj}}+{\bar \varOmega _{ik}}{\bar \varOmega _{kj}} - {\delta _{ij}}\left( {{{\bar s}_{mn}}{{\bar s}_{mn}} - {{\bar \varOmega }_{mn}}{{\bar \varOmega }_{mn}}} \right)/3. $

式中： ${\bar \varOmega _{ik}} = \left( {{{\partial {{\bar u}_i}}}/{{\partial {x_j}}} - {{\partial {{\bar u}_j}}}/{{\partial {x_i}}}} \right)/2$, ${\delta _{ij}}$为克罗内克尔符号, i、j、k、m、n 均为张量下标.

由于静态混合器的复杂边界条件, 所采用的多松弛时间计算方法的散射算子在中心动量空间实现并独立松弛, 然后执行逆变换以恢复概率分布函数. 通过局部宏观速度离散粒子速度, 提高给定速度集的伽利略不变性和数值稳定性. WALE涡黏模型提供了在叶片边界处局部涡流黏度, 可提高近壁面碰撞效应从而促进流固耦合求解精度.

LBM方法中空间是格子化的, 时间也是离散化的, 因此, 为了模拟真实的物理过程, 须考虑量纲的变化问题^[20]. 假设格子上长度的量纲为L, 时间量纲为T, 质量量纲为G, 加上“´”表示对应格子参数, 不加则表示对应的宏观参数. 以粒子直径、流体的运动学黏滞系数以及流体的密度作为基准量. 设粒子直径为D, 流体的运动学黏滞系数为ν, 流体密度为 $\rho $, 则 $L = \dfrac{D}{{D'}}$, $T = \dfrac{{\nu '}}{\nu}{\left( {\dfrac{D}{{D'}}} \right)^2}$, $G = \dfrac{\rho }{{\rho '}}{\left( {\dfrac{D}{{D'}}} \right)^3}$, 则宏观参数到格子参数的变换关系如下：时间 $t = t'T$, 长度 $l = l'L$, 速度 $v = v '\dfrac{L}{T}$, 压强 $P = P'G\dfrac{1}{{L{T^2}}}$.

采用粒子法与网格法相结合的流固耦合方法, 耦合策略采用分区耦合即流体域与结构域采用不同的控制方程. 控制结构单元运动变形的动力学方程如下：

(10) $ {\boldsymbol{M}}\ddot {\boldsymbol{y}}+{\boldsymbol{C}}\dot {\boldsymbol{y}}+{\boldsymbol{Ky}} = {\boldsymbol{F}}\left( t \right), $

(11) $ {\boldsymbol{C}} = {\alpha _1}{\boldsymbol{M}}+{\alpha _2}{\boldsymbol{K}}. $

式中：M、C、K分别为结构的质量矩阵、瑞利阻尼矩阵和结构刚度矩阵；F(t)为施加在结构上的时域变化外力；y为结构单元节点的位移矢量； ${\alpha _1}$和 ${\alpha _2}$为系数, 与结构的固有频率及阻尼比相关.

为了得到结构单元节点的位移信息, Newmark-β方法^[21]被广泛应用于式(10)的求解. 在 ${{t = t+}}\Delta t$时刻, 由于式(10)同时包含未知矢量 ${\boldsymbol{y}}$、 $\dot {\boldsymbol{y}}$和 $\ddot {\boldsymbol{y}}$, 尚须补充2组方程才能使式(10)封闭. 对结构单元节点的速度和位移进行泰勒展开, 以实现对式(10)的求解：

(12) $ {{{\dot {\boldsymbol{y}}}_{t+\Delta t}} = {{\dot {\boldsymbol{y}}}_t}+\left( {1 - \gamma } \right)\ddot {\boldsymbol{y}}\Delta t+\gamma {{\ddot {\boldsymbol{y}}}_{t+\Delta t}}\Delta t} ,\; { {0 < \gamma < 1.0} } . $

(13) $ {{{\boldsymbol{y}}_{t+\Delta t}} = {{\boldsymbol{y}}_t}+\dot {\boldsymbol{y}}\Delta t+\frac{{1 - 2\beta }}{2}{{\ddot {\boldsymbol{y}}}_t}\Delta {t^2}+\beta {{\ddot {\boldsymbol{y}}}_{t+\Delta t}}\Delta {t^2}},\; { {0 < \beta < 1.0} } . $

式中：β和γ为权重参数, 与计算静态混合器模型稳定性相关, 本研究分别取β＝0.25, γ＝0.5.

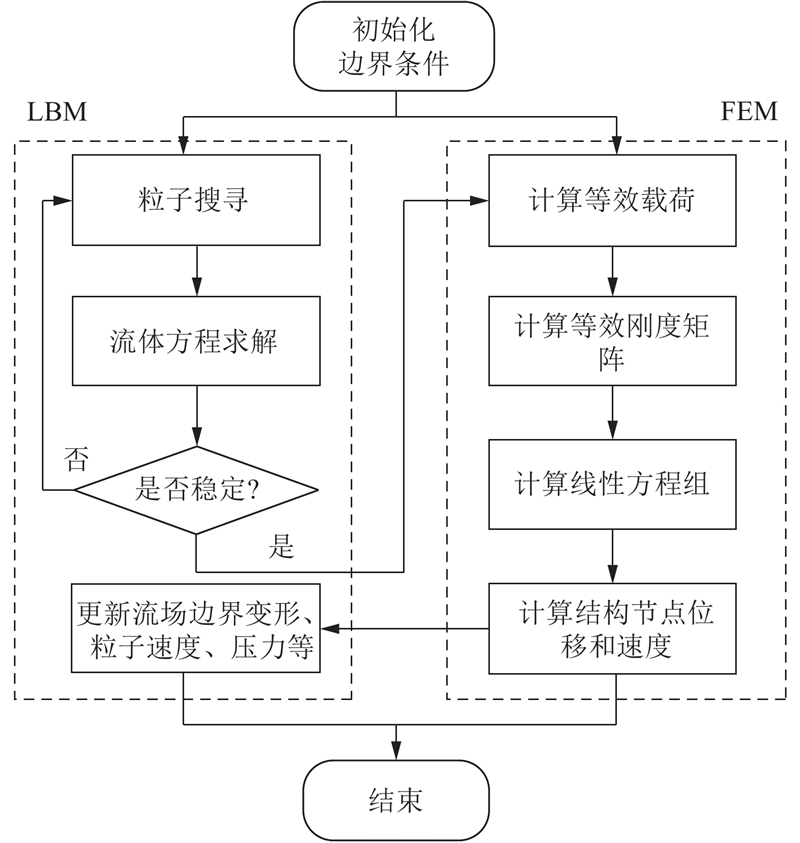
基于上述数学模型, 提出流固耦合弱耦合求解方法, 如图2所示. 该方法计算流程主要包括初始化边界条件、LBM控制方程和LES方程求解、结构场控制方程求解、流固耦合面分布函数重构等. 在分区求解过程中选择大小合适的计算域, 划分流场网格, 进行流固耦合计算初始化, 对流场和结构赋初值；求解LBM流场控制方程和LES湍流模型, 得到流体的压力和速度.采集流固耦合面上流体作用力, 将流体作用力施加在结构上, 求解式(10)并提取结构运动的位移、速度数据；根据结构位移更新结构在流场中的位置, 根据Yu等^[22]提出的插值反弹格式方法, 通过邻近点的流体粒子分布函数进行插值计算, 最终保证流固耦合面上速度、压力、变形等物理量的守恒. 上述求解过程不断重复, 最终输出结构变形结果和流场计算结果.

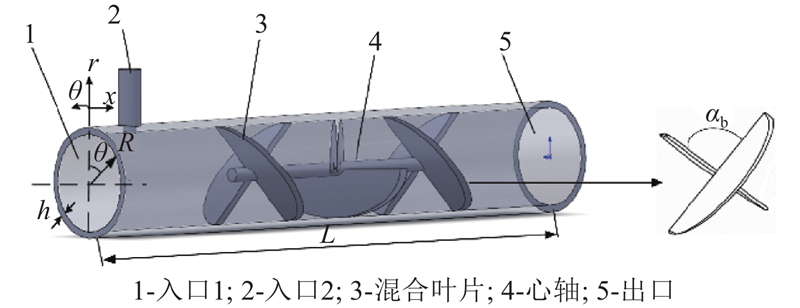
以Ross LPD型号静态混合器为对象实例进行研究. 为了简化建模过程及降低对计算机硬件的要求, 将几何模型进行合理的简化, 简化后的几何模型如图3所示. 该几何模型只保留了静态混合器自身主要构件, 包含2个入口和1个出口与大气相通, 以及心轴与混合叶片. 以入口处为原点, 建立柱坐标系, 分别用x轴表示轴向, r轴表示径向, θ轴表示周向描述整个模型. 根据相同比例对数值计算进行建模, 静态混合器和流体的几何参数如表1所示. 表中，L₀为长度, R为内径, h为壁厚, d为心轴直径, ρ为静态混合器密度, E为弹性模量, μ为泊松比, ρ_w为水的密度, μ_w为黏度. 内部一系列交错的半椭圆板周期交叉焊接在圆柱心轴上^[23], 3种螺旋叶片夹角 $\alpha_{\rm{b}} $分别取80°、90°、100°, 3组叶片左旋右旋交错排布.

在流固耦合求解中, 流体通道的主入口（入口1）直径为70 mm, 侧入口（入口2）直径为10 mm. 流体入口设置为速度入口, 出口均为自由出口, 入口2速度恒定为4 m/s, 由于主次入口直径比为7∶1, 相同入口速度情况下的体积流量比为49∶1, 因此主要考虑入口1的速度变化对静态混合器壁面的振动影响. 侧面采用零摩擦的自由滑移墙面边界, 静态混合器的边界条件设置为两端固支, 流固耦合面选取为静态混合器内壁面以及叶片表面. 为了观察静态混合器变形随时间变化的过程, 采用非定常求解方法进行计算. 计算时间步长为0.00 002 s, 时间步为10 000步, 总时间为0.2 s. 由于总仿真时间较长, 在0.2 s后, 静态混合器内部流体已达到稳定状态.

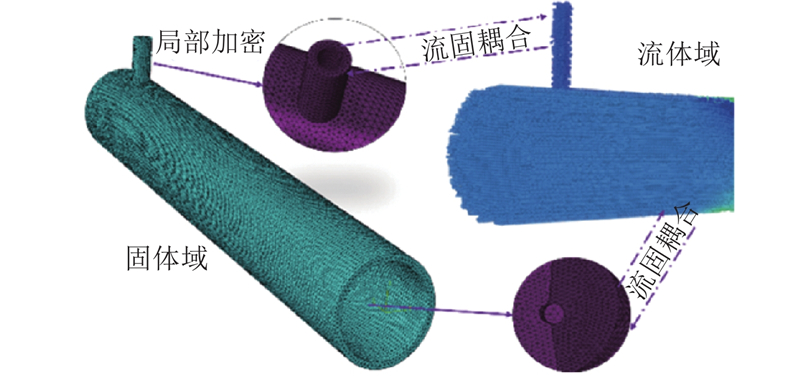
基于上述几何尺寸模型, 建立静态混合过程流固耦合动力学模型, 如图4所示. 格子玻尔兹曼模型使用的格子划分策略采用八叉树晶格结构划分流场格子, 然后生成粒子, 固体域采用非结构化网格, 在流固耦合面处进行节点与格子匹配, 保证固体域网格和流体域最大格子尺寸相同, 目的是使流体域粒子各速度分量与固体域网格节点之间准确地相互传递数据, 保证数值模拟的准确性.

考虑到格子大小和网格尺寸会直接影响结果的精度, 使用不同的格子和网格密度进行无关性验证. 模拟p_out=0 Pa, 入口速度v_in=4 m/s的工况下静态混合过程流固耦合, 使用5种网格尺寸(编号1~5), 考察格子尺寸对数值结果的影响. 对0.2 s时x=0.275 m, θ=0°处外壁面振幅以及总仿真时间进行对比, 综合考虑流体域粒子数量和固体域网格数量与振幅和仿真时间的变化趋势, 如表2所示. 表中, M为流体粒子数, N为固体域网格数, A_r为混合器壁面径向振幅. 随着粒子数量与网格密度增加, 幅值逐渐相差较小. 编号3、4、5这3种网格尺寸, 振幅呈现基本一致, 表示已经满足了网格无关性要求, 保证了数值计算的准确性和可重复性. 本研究最终采用方案4进行流体域与结构域离散化处理.

为了验证该方法的正确性, 利用Ansys-Fluent软件计算相同物理参数下的算例, 并将轴向位移时间曲线与LBM方法计算得到的结果对比. 在Fluent中流体同样采用LES模型, 在流固耦合的每一步内, 先求解流体控制方程, 得到速度场、压力场以及作用在壁面的作用力, 然后求解固体域方程, 将静态混合器流固耦合面变形通过Fluent动网格宏进行处理, 实现动边界对流场的反馈作用, 从而进行双向流固耦合.

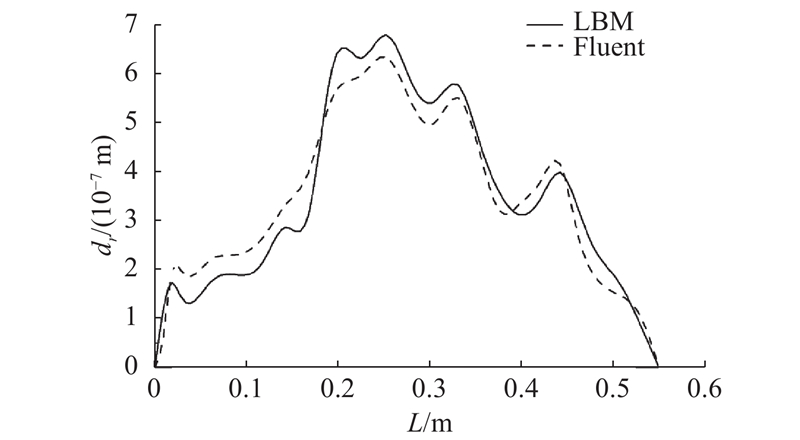
LBM方法和Fluent流固耦合分析后的变形对比，如图5所示. 图中, L为轴向距离, d_r为混合器壁面径向位移. 通过2种模拟方法得到0.2 s时刻在θ=0°沿x轴方向上的位移响应曲线, 2种计算得到的结果大致吻合. 由于2种方法是截然不同的理论公式, 在网格划分过程中，传统方法是流体网格与固体网格间相互传递数据, LBM方法采用的则是粒子与固体网格之间相互传递数据, 本研究通过LBM方法采用27个速度分量在流固耦合面处传递更多方向上的速度、压力数据. 因此采用LBM流固耦合建模方法, 可以更加真实精确地模拟静态混合器内部的流体冲击.

静态混合器物理空间内部叶片的存在增加了湍流场的无序性和非线性, 为了获得其中流固耦合特性, 须研究静态混合器整体外壁面位移响应和不同流速、不同叶片夹角条件下的静态混合器局部外壁面位移响应和幅频响应.

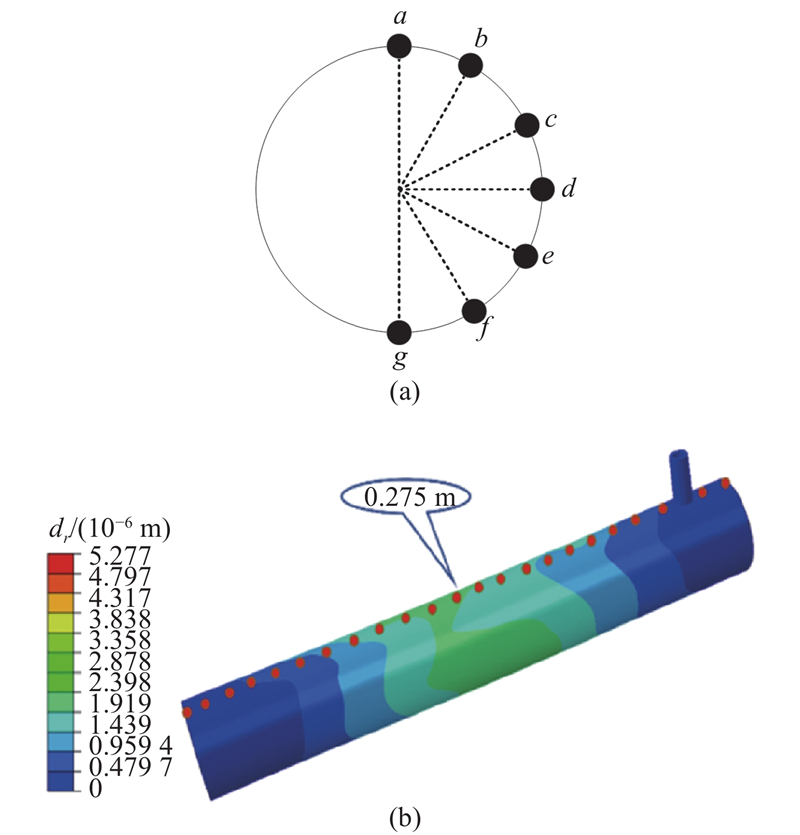
在静态混合过程中, 由于内部流体瞬态冲击, 流致振动规律具有高度非线性特征.为了更好地观察管道内流体对管道振动的影响, 在静态混合器模型壁面上添加监测点, 沿管体x轴方向, 平均每隔0.025 m设置1个监测点, 共设置23个监测点. 由于模型具有对称性, 在半周向进行监测点的选取, 周向选取相位角分别为θ=0°, 30°, 60°, ···, 180°的a~g共7个监测点. 如图6所示为静态混合器在内部流体激励作用下的形变云图. 可以看出，中间部位变形最大.

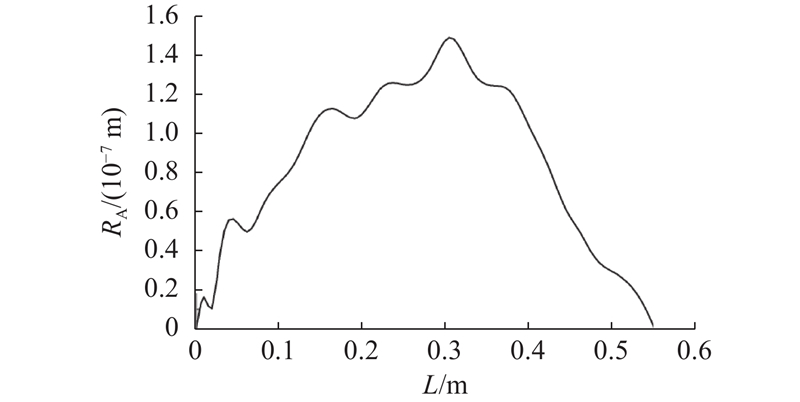
如图7所示为静态混合器沿x轴方向的振幅均方根. 图中, R_A为振幅均方根. 可以看出，静态混合器呈现五阶振型模态, 中部振幅均方根最大. 由于静态混合器和管道类似属于细长结构, 会在重力作用下发生较为明显的形变. 静态混合器内介质流经叶片的管道时, 由于叶片的阻碍, 流体速度发生改变，轴向速度转变为径向速度和切向速度, 这些加速的力反过来作用在管道上, 引起管道的附加振动.

在数值仿真结果的处理中, 为了便于系统比较, 选取混合器振幅最大位置(即x=0.275 m)处的振动情况进行研究. 对圆周方向上的7个监测点提取径向、周向和轴向位移响应, 如图8所示. 图中，d_θ、d_x分别为周向、轴向位移. 可以看出, 在初始阶段, 位移响应趋势不太稳定, 表明流体在刚冲入时对壁面产生压力, 壁面也会施加给流体一个回弹力, 短时间内这种反复的耦合响应导致初始位移失稳, 在一定时间后达到稳定的力场, 进而形成一个稳定的振动响应.

由图8(b)、(c)可知, 当振动响应稳定后, 周向和轴向位移响应曲线几乎完全重合. 由图8(a)的径向位移响应对比可以看出, a比g的变形大, b比f的变形大, c比e的变形大, 表示对称的两侧所受的力大小不等, 主要原因是流体受到重力的影响, 混合器壁面上侧的流体冲击力与流体重力相互抵消, 混合器壁面下侧流体冲击力与流体重力叠加. 同样，g、a变形相差值大于b、f和c、e两组. 另外, 对比3个方向上的振动位移响应曲线可知, 静态混合器的径向位移响应最大, 其次是周向, 轴向的位移响应最小, 而且径向位移的峰值更为密集. 这表示静态混合器内部流体冲击导致的附加振动对径向位移响应的影响最大, 同时验证了静态混合器内部流体速度转化会导致附加振动且使得静态混合器壁面振动现象更加复杂.

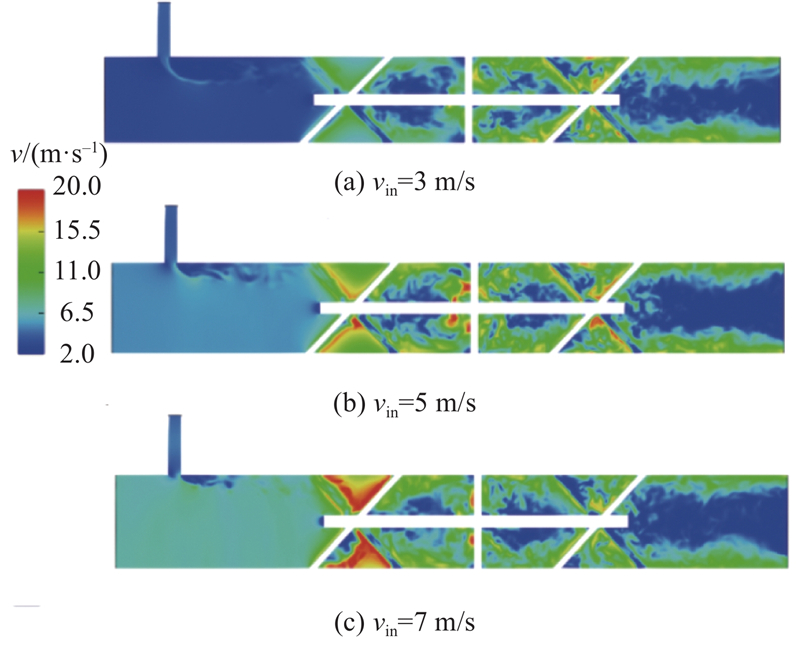
在静态混合器实际应用过程中, 常采用不同的入口速度提高混合器的混合效率, 而不同流速变化将产生不同的振动响应. 为了研究不同流速对静态混合器壁面冲击的影响，选取t=0.2 s的内部流场速度分布以及x=0.275 m, θ=0°处静态混合器外壁面监测点的壁面位移响应变化情况. 如图9(a)~(c)所示为3种v_in下流场速度分布云图. 图中, v为流场速度. 可以看出, 流体与第1组叶片接触, 流动方向突然改变, 形成高速旋转的流体；之后继续与第2组和第3组快速接触, 必然引起局部湍流涡团的耗散, 增加湍流状态的非线性, 这也是引起静态混合器壁面附加振动的主要原因. 同时, 对比3种工况下云图.可以发现，速度越大, 在叶片表面附近速度突变程度越大, 且主要发生在第1组叶片处, 表明第1组叶片比其他2组更容易受磨损, 损坏概率更高.

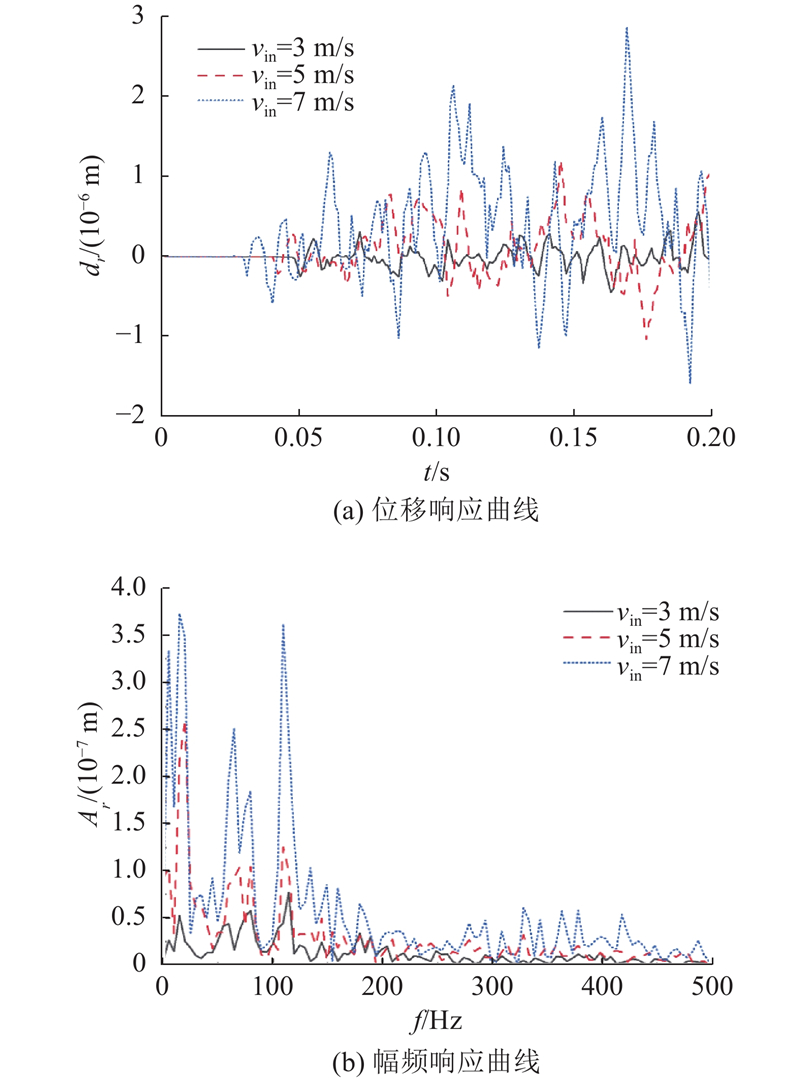
如图10所示为不同流速流体激励下静态混合器壁面振动响应曲线. 图中, A_r为径向振幅, f为频率. 由图10(a)可以看出，入口流速对混合器的位移响应和振动频率有较大影响, 三者振型都不太规则, 平均振幅差别显著, 随着流体速度增大, 流体对静态混合器冲击振动的影响愈发显著, 流体速度越大, 平均振幅越大.

由图10(b)可以看出流体入口速度为3、5、7 m/s的工况, 三者振动情况较为相似, 静态混合器的振动普遍存在多模态共存的现象, 振动情况较分散, 这是因为静态混合器内部不规则漩涡会诱发随机振动. 三者工况的主振动频率分别为114.4、19.9、14.9 Hz, 可见随着内部流体速度的变化, 流速较大的工况使振动更加趋于低频化, 促使静态混合器在低频段更容易发生共振现象. 对比不同速度下的振幅可知, 随着速度增加, 最大振幅差距显著, 7 m/s时最大振幅为3 m/s时最大振幅的4.86倍, 5 m/s时最大振幅为3 m/s时最大振幅的3.38倍, 表明速度越大, 最大振幅越大, 随着速度增大, 最大振幅增加的比值有减小的趋势. 静态混合器的振动过程通常会由多个频率共同影响, 但其振动主要受某一阶模态控制, 其他模态对静态混合器的振动影响较小.

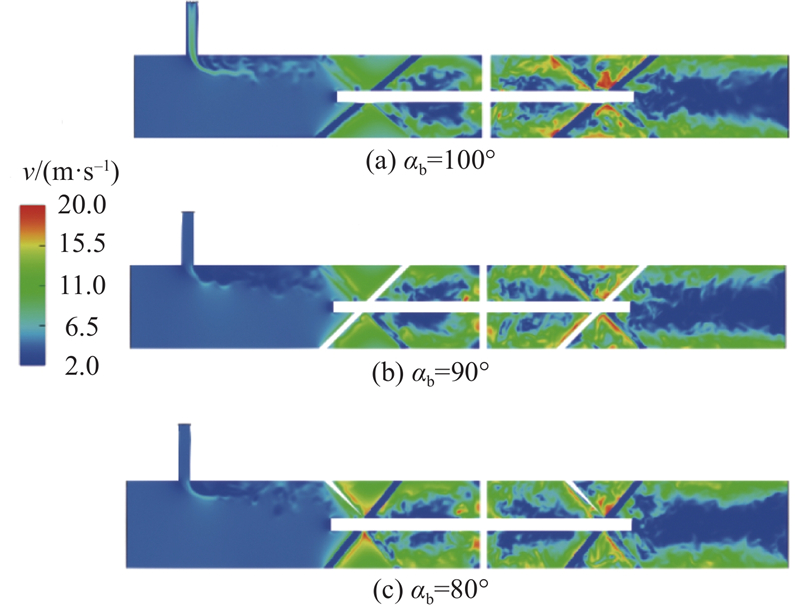
在静态混合器设计过程中, 混合原件扮演着重要的角色, 不同的混合原件对流场的剪切作用不同从而产生不同的振动诱导因素, 造成不同程度的疲劳损伤. 在实际情况中, 主入口速度越大, 压力降越大, 能量损失越多. 考虑到静态混合器实际情况,采用偏小的主入口速度, 主要研究叶片对振动特性的影响. 选取t=0.2 s时刻入口1速度4 m/s内流场速度分布以及x=0.275 m, θ=0°处静态混合器外壁面监测点的壁面位移响应的变化情况. 不同叶片夹角下流场速度分布如图11所示. 可以发现, 随着叶片夹角的减小, 第1组叶片表面处流速突变越来越明显, 而第3组叶片处流速突变减弱. 这是因为第1组叶片夹角最先改变流场的径向剪切流动能量, 诱导轴向速度转化为径向速度, 而轴向速度的减小势必导致第3组叶片处轴向速度向径向速度的转化减少. 管壁附近速度远远大于中心部位; 叶片夹角越小, 混合前、后叶片流速相差越大，叶片夹角较小时混合后的速度波动比混合前起伏更大且稳定时流速相对较高, 表明叶片夹角越小, 对流体的引流剪切作用越强, 可能导致混合器的稳定性下降.

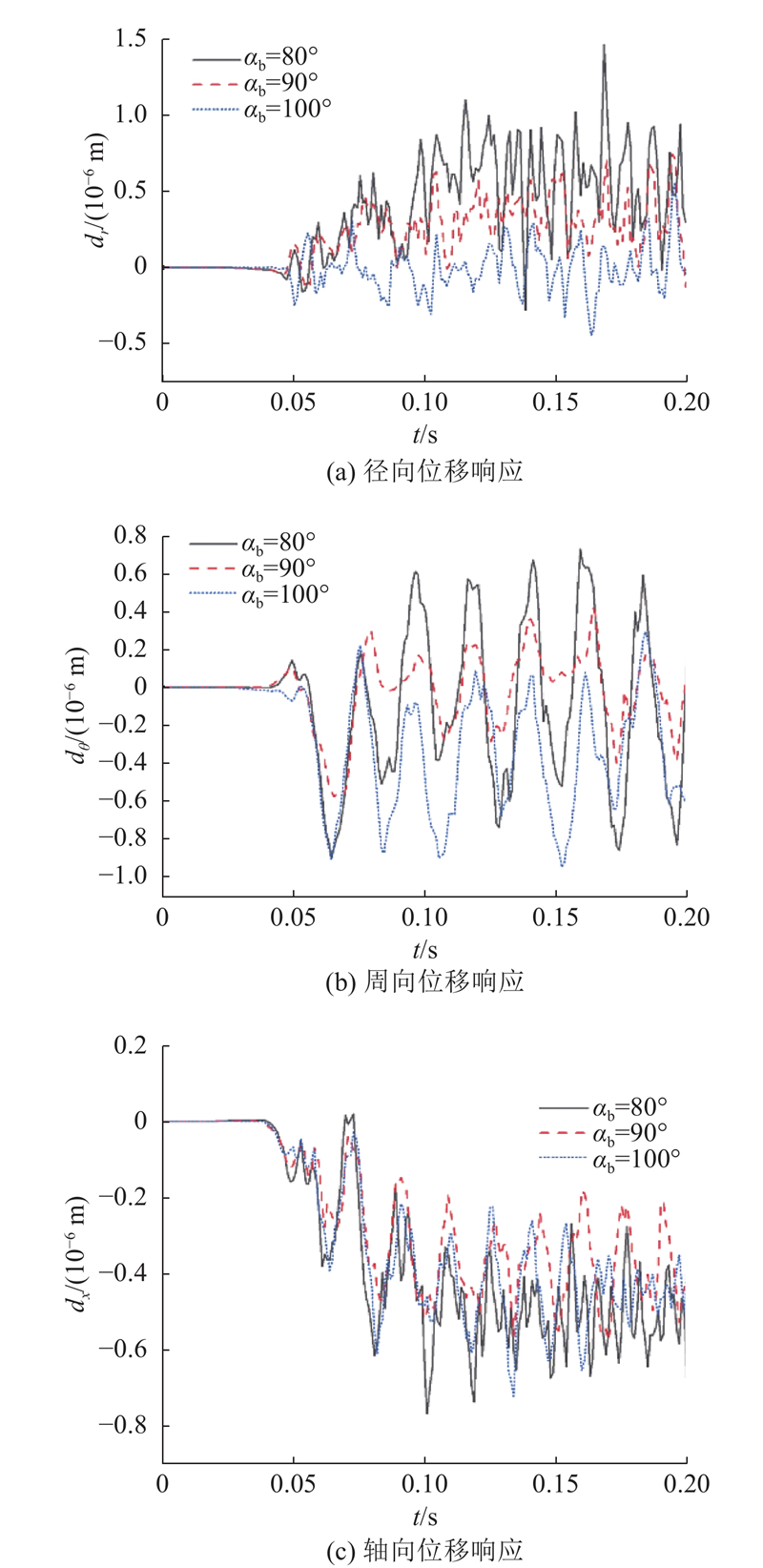
如图12所示为不同叶片夹角对混合器壁面位移响应的影响. 可以看出，静态混合器中的位移响应有延迟, 初始阶段周向位移反应较迅速, 径向和轴向则需要一定时间达到稳态; 在达到稳态时, 角度越小, 径向位移响应越大；对于周向位移, 90°时周向位移最小, 100°周向位移最大；轴向位移随着角度变化，夹角越小，位移响应越大. 对比3个方向的位移响应, 径向位移响应最大, 其次是周向, 轴向位移响应最小.

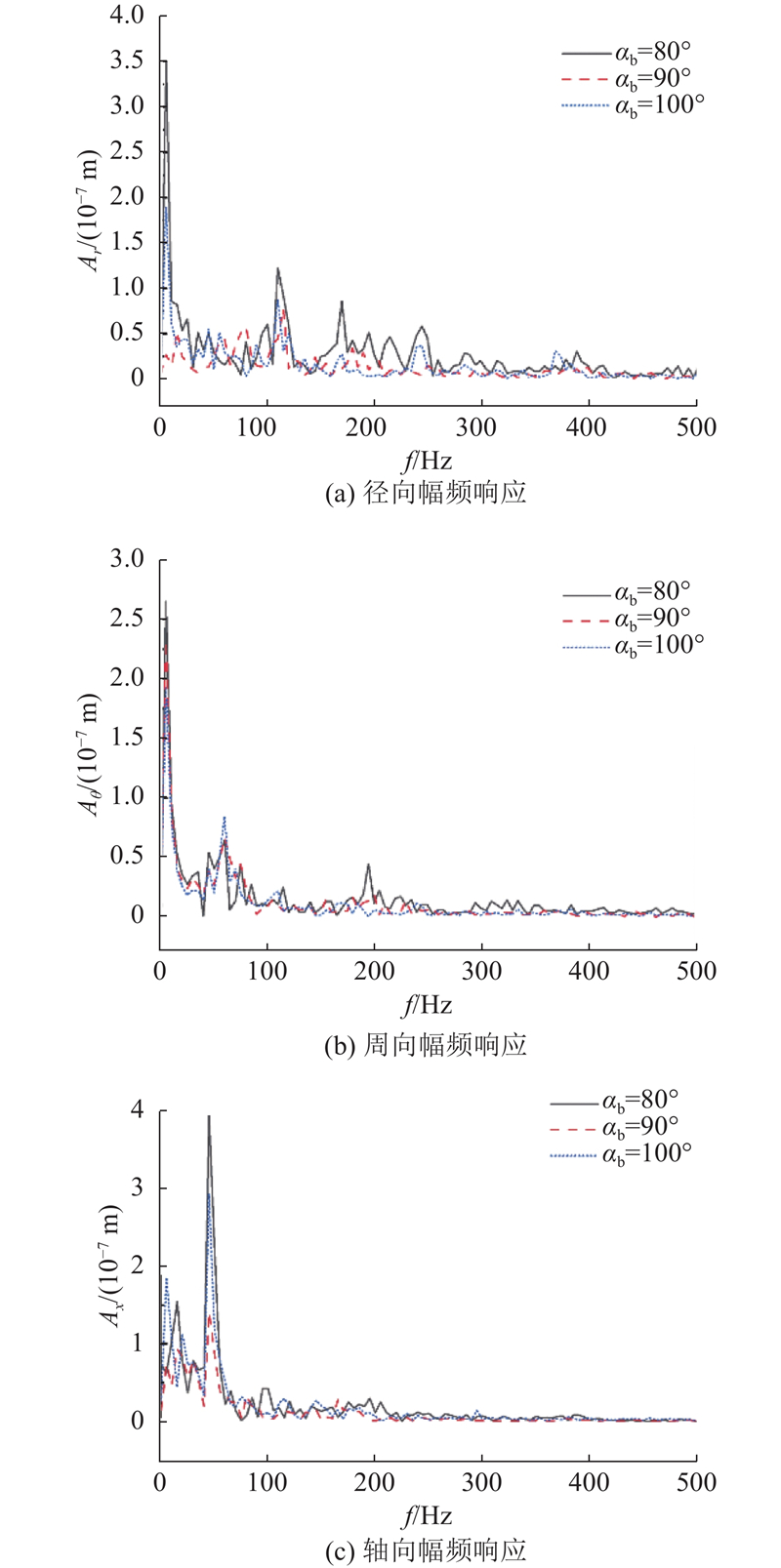
如图13所示为不同叶片对混合器壁面幅频响应的影响. 图中，A_θ、A_x分别为周向、轴向振幅. 可以看出，当改变叶片的夹角时, 幅频响应的低频段出现幅值较大的峰值, 周向方向叶片夹角越小峰值越大, 而径向方向和轴向方向, 在叶片夹角为90°时峰值偏小, 增大或减小夹角低频段峰值都会增大, 这种现象是由于结构改变造成刚度变化, 造成的影响主要表现在幅频曲线的低频段. 不同叶片夹角其主振动频率未发生改变, 径向、周向、轴向主振动频率分别为4.97 、4.97 、44.77 Hz. 原因是径向主频率与轴向主频率频率受叶片的影响, 流体速度经叶片引导, 轴向速度转变为径向速度和周向速度, 从而引发周向和径向附加振动, 振动频率偏小, 整体未出现低频化现象, 表明改变叶片夹角不会促使静态混合器在低频段发生共振现象.

(1) 对壁面的位移响应分析表明, 在混合过程中静态混合器会在流体重力的作用下呈现五阶振型, 内部叶片的存在将流场轴向速度转化为切向速度引发附加振动, 使得径向位移响应最大, 而且径向位移峰值更为密集.

(2) 在叶片相同的工况, 增加入口流体速度, 叶片附近流场速度突变会越明显, 且主要发生在第1组叶片处；当入口流速较大时, 静态混合器振动频率趋向于低频化, 振幅会增大, 即加剧了振动响应.

(3) 在流速相同的工况下, 叶片夹角越小, 对流体的引流剪切作用越强, 管壁处速度显著增大, 振动幅值增大. 周向位移在叶片夹角为90°时位移响应最小. 不管混合叶片怎么改变, 频率都不发生改变, 叶片夹角对振动频率无影响.

基于LBM流固耦合模型的静态混合系统具有高度的复杂性, 本研究在此方面进行了有益的尝试. 在理论方面可以为基于LBM的流体-结构耦合求解方法和多速度分量描述系统的建模提供参考；在技术方面, 可以为工业过程监测提供更多的技术解决方案, 具有较好的工程应用前景.

本研究仅通过数值计算模拟单向流条件下静态混合器壁面振动响应特点, 今后工作重点将放在LBM多相流流固耦合动力学模型建立上, 以实现多种流体的混合计算. 除此之外, 本研究偏向于理论计算, 后续将建立静态混合实验平台对数值计算模型进行验证.