浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(10): 2126-2132 doi: 10.3785/j.issn.1008-973X.2023.10.021

土木工程

微生物作用下含有机质沉积物起动的定量研究

占斯宁,, 袁栋栋, 林永钢, 张仪萍, 周永潮,, 张土乔

1. 浙江大学 建筑工程学院，浙江 杭州 310058

2. 中国电建集团环境工程有限公司，浙江 杭州 310058

3. 中电建路桥集团有限公司，浙江 杭州 310058

Quantitative study on incipient motion of organic sediments with bio-adhesive effect

ZHAN Si-ning,, YUAN Dong-dong, LIN Yong-gang, ZHANG Yi-ping, ZHOU Yong-chao,, ZHANG Tu-qiao

1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou, 310058, China

2. Powerchina Environmental Epaperngineering Co Ltd., Hangzhou, 310058, China

3. Powerchina Roadbridge Group Co Ltd., Hangzhou, 310058, China

通讯作者: 周永潮，男，教授，博士. orcid.org/0000-0002-5524-4016. E-mail： zhoutang@zju.edu.cn

收稿日期: 2022-12-1  

基金资助: 国家自然科学基金资助项目（51878597）

Received: 2022-12-1  

Fund supported: 国家自然科学基金资助项目（51878597）

作者简介 About authors

占斯宁（1998—），女，硕士生，从事城市排水管道沉积物管理研究.orcid.org/0000-0003-3567-1384.E-mail：22012243@zju.edu.cn , E-mail：22012243@zju.edu.cn

摘要

为了探究微生物作用对沉积物起动规律的影响，提出考虑微生物培养时间和有机质含量的沉积物临界起动剪切应力计算方法. 通过明渠冲刷试验分析了微生物培养时间及有机质含量对沉积物临界起动剪切应力的影响规律；引入絮体强度常数γ值对微生物黏性作用进行定量表征；基于沉积物起动理论，提出在微生物作用下沉积物的临界起动剪切应力经验公式. 结果表明，随着微生物作用时间的增加，临界起动剪切应力先增大后减小，并在10或15 d左右达到峰值，最终达到0.072~0.117 N/m2. 临界起动剪切应力随着有机质含量的增大而减小. 微生物黏性作用与γ值呈现显著的负相关，皮尔逊相关系数为−0.767，临界起动剪切应力公式计算值与实验值较为吻合.

关键词： 沉积物 ; 微生物活动 ; 有机质含量 ; 临界起动剪切应力 ; 絮体强度

Abstract

A calculation method of the critical shear stress considering the microbial incubation time and organic matter content was proposed to study the influence of microbial biofilm on the erosion behavior of sediment. An open channel flume experiment was conducted to analyze the effects of microbial incubation time and organic matter content on the critical shear stress. The stable floc size constant γ was introduced to quantify the bio-adhesive effect. An empirical formula for the critical shear stress of sediment initiation with organic matter under microbial activity was proposed based on the theory of sediment initiation. Results showed that the critical shear stress increased first and then decreased over time. The peak value was reached around 10 or 15 days, and the critical shear stress reached 0.072~0.117 N/m2. The critical starting shear stress decreased with the increase of organic matter content. The correlation between the bio-adhesive effect and γ was calculated and a significant negative correlation was found. Pearson correlation coefficient was −0.767. The calculated value of the critical starting shear stress formula was in good agreement with the experimental value.

Keywords： sewer sediment ; biological activities ; organic matter content ; critical shear stress ; floc strength

PDF (972KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

占斯宁, 袁栋栋, 林永钢, 张仪萍, 周永潮, 张土乔. 微生物作用下含有机质沉积物起动的定量研究. 浙江大学学报(工学版)[J], 2023, 57(10): 2126-2132 doi:10.3785/j.issn.1008-973X.2023.10.021

ZHAN Si-ning, YUAN Dong-dong, LIN Yong-gang, ZHANG Yi-ping, ZHOU Yong-chao, ZHANG Tu-qiao. Quantitative study on incipient motion of organic sediments with bio-adhesive effect. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(10): 2126-2132 doi:10.3785/j.issn.1008-973X.2023.10.021

排水管道的沉积现象是管道主要功能性病害之一. 管道淤积可能导致管道过流断面减小，降低管道过流能力[1-2]，甚至可能造成上游窨井漫溢，进而引发城市内涝，影响城市的正常生产、生活. 目前控制管道沉积物淤积的方法主要包括离线和在线的水力冲刷、机械清淤以及管道自清淤设计等[3-5]. 为了更好地控制管道沉积物淤积，以及给清淤技术设计提供理论性支持，因此开展管道沉积物的起动冲蚀特性研究具有十分重要的意义.

沉积物起动研究是学者关注的热点. 早期的研究主要针对无黏性沙或黏性细颗粒沙. Shields等[6]对无黏性沙展开研究，得到临界起动剪切应力与沙颗粒粒径的关系，发现粗颗粒临界起动剪切应力和平均粒径在双对数坐标下呈线性关系. Tait等[7]通过研究下水道沉积物的特征，发现沉积物表现出明显的内聚力，揭示沉积物起动过程中黏性作用的存在. Banasiak等[2]通过试验发现沉积物的起动还受到微生物的影响，管道沉积物在沉积过程中发生生化反应，这种生物黏性作用会对沉积物堆积密度、含水率、沉积结构产生影响. 方红卫等[8-9]通过水槽试验研究微生物作用下无机质沉积物的起动规律，发现生物黏性作用可以增强沉积物的抗侵蚀性能，在此基础上将微生物作用模化为生物膜产生的表面黏力，推导出沉积物在微生物作用下的起动公式.

排水管道内沉积物还有较多有机质，研究发现，含有机质沉积物在微生物作用下的起动规律表现出了与无机沉积物不同的特征[10]. 沉积物中的有机质会对微生物作用产生影响，导致沉积物的内部结构发生变化，进而影响抗侵蚀能力[11]. 马妍等[12]对不同有机物含量的管道沉积物在微生物作用下的起动规律进行研究，发现有机质含量对沉积物的抗侵蚀性能影响重大。目前针对含有机质沉积物在微生物作用下的起动规律和生物黏性作用仍缺乏定量的研究.

本研究拟开展在不同有机质含量和不同微生物作用时间下沉积物的起动规律试验，研究有机质含量与微生物作用时间对沉积物起动的影响. 引入絮体强度常数γ，对含有机质沉积物在起动过程中受到的生物黏性作用进行定量分析和表征，在此基础上建立生物作用下沉积物临界起动剪切应力的经验公式，为排水管道沉积物管理提供一定的理论支撑.

1. 试验装置及试验方案

1.1. 小型明渠冲刷试验装置与方法

本研究试验装置包括小型明渠装置与圆桶搅拌装置. 小型明渠试验装置由水箱、水泵、阀门、电磁流量计、明渠、整流板、采样盒等部分组成，如图1所示. 明渠尺寸为70 cm×5 cm×16 cm，水流由水泵注入明渠，通过阀门和电磁流量计对流量进行调整和检测，前端设置的整流板用以稳定明渠流. 在明渠中段放置不同培养时间后的沉积物（与培养盒同步放置），在沉积物下游段设置3层采沙盒，尺寸为30.0 cm×5.0 cm×0.6 cm，用于收集不同冲刷工况下的推移质.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   小型明渠冲刷试验的装置图

1-上游水箱；2-进水水泵；3-旁通闸阀；4-主阀门；5-电磁流量计；6-穿孔板；7-斜板；8-沉积物试样；9-培养盒；10-采沙盒；11-溢流堰   Scheme of experimental open channel flume


试验开始前先将培养好的沉积物试样与培养盒整体放入水槽，开启阀门逐级提高流速. 待每级流速稳定后，每隔30 s放置1块采沙盒以采集不同时间段内的推移质，同步在明渠末端采集水样以测定悬移质. 每级冲刷结束后依次收集推移质和悬移质，将收集到的悬移质和推移质依次进行抽滤、烘干和称重. 根据沉积物冲蚀重量计算沉积物冲蚀率（E），沉积物冲蚀率计算为

$ \begin{array}{*{20}{c}} {E = \dfrac{M}{t}} , \end{array} $

$ \begin{array}{*{20}{c}} {M = {m_1}+{m_2} \times Q \times t} \end{array}. $

式中：M为冲蚀量，m1为推移质重量，m2为明渠出水中悬移质的浓度，Q为流量，t为冲刷的时间.

水流剪切应力计算式为

$ \begin{array}{*{20}{c}} {\tau = \rho u^{*2}} \end{array}. $

式中： $\tau $为水流剪切应力， $\;\rho $为水的密度， ${u^*}$为摩阻流速. 摩阻流速计算式[13]为

$ \begin{array}{*{20}{c}} {\dfrac{{\bar u}}{{{u^*}}} = 5.75\lg \left( {12.27\dfrac{{Rh }}{{{k_{\rm{s}}}}}} \right).} \end{array} $

式中： $ \overline{u} $为渠道断面的平均流速， $\bar u = Q/A$；A为渠道断面面积；ks为床面粗糙度；R为渠道断面的湿周；h为校正系数.

实验以沉积物试样的冲蚀率作为起动的判断标准[14]，当冲蚀率达到0.0078 g/s时，沉积物受到的水流剪切应力为该沉积物试样的临界起动剪切应力。

1.2. 圆筒搅拌试验装置与方法

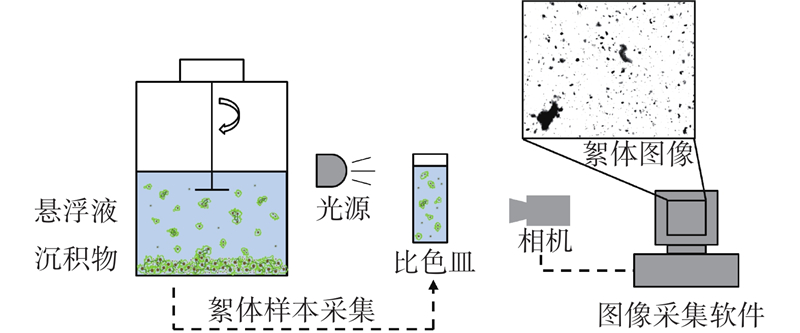
圆筒搅拌试验装置示意图如图2所示. 试验开始前，将培养结束的含有机质沉积物转移至1 L烧杯中. 选用搅拌机（RWD50）对沉积物试样进行搅拌，使得在微生物作用下含有机质沉积物试样以絮体形式悬浮在溶液中. 待絮体尺寸稳定后，采集悬浮液放入比色皿，用相机（Baumer VCXG–13M）对沉积物絮体样本进行图像采集，利用Image Pro Plus软件对絮体的直径进行计算和分析.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   圆筒搅拌试验装置的示意图

Fig.2   Scheme of cylinder stirring experiment


圆筒搅拌试验选取5级搅拌转速，分别为160、175、190、205及220 r/min. 本试验选用速度梯度（G）表征不同转速下的水流剪切力，计算式[15]为

$ \begin{array}{c}G=\sqrt{\epsilon /v}\end{array}. $

式中： $v$为水的动力黏度； $ \epsilon $为平均湍流能量耗散率. 平均湍流能量耗散率的表达式为

$ \begin{array}{c}\epsilon =\dfrac{{N}_{{\rm{p}}}{N}^{3}{D}^{5}}{V}\end{array}. $

式中：Np为功率准数，N为搅拌桨转速，D为搅拌桨直径，V为水体的体积. 不同转速下的G值如表1所示.

表 1   圆筒搅拌试验的搅拌转速及速度梯度

Tab.1  Stirring speed and velocity gradient of cylinder stirring experiment

N/(r·min−1) G/s−1
160 78.93
175 90.29
190 102.15
205 114.48
220 127.27

新窗口打开| 下载CSV


1.3. 试验材料及工况

为了研究微生物作用下不同有机质含量（organic matter content, OMC）沉积物的抗冲蚀性能，本试验选用与部分雨污混接的分流制雨水管道沉积物相近的塑料沙作为沉积物主体. 选用成分与分流制雨水管道沉积物所含有机物相近的面粉作为有机质，将两者以一定比例混合后得到不同有机质含量的沉积物试样. 使用马尔文激光粒度仪（Malvern-MS2000）和真密度仪（TD-1200）对模型沙粒径和密度进行分析，其物理参数如表2所示. 表中ρ为真密度，d50为中值粒径，Cu为不均匀系数. 为了研究不同有机质含量和微生物作用时间对沉积物抗侵蚀性能的影响，配置了有机质含量为2%、3.5%、5%、6.5%、8%的含有机质沉积物. 每种有机质含量沉积物设置7组不同的培养时间，每种工况设置3个平行样. 具体工况如表3所示，表中T为培养时间.

表 2   塑料沙的物理参数

Tab.2  Physical parameters of plastic sand

目数 ρ/(g·cm−3) d50/mm Cu
60 1.409 0.427 1.51

新窗口打开| 下载CSV


表 3   沉积物试样的培养时间及有机质含量

Tab.3  Incubation time and organic matter content of sediments

序号 T/d OMC/% 序号 T/d OMC/% 序号 T/d OMC/%
1 0 2.0 13 10 5.0 25 20 8.0
2 0 3.5 14 10 6.5 26 25 2.0
3 0 5.0 15 10 8.0 27 25 3.5
4 0 6.5 16 15 2.0 28 25 5.0
5 0 8.0 17 15 3.5 29 25 6.5
6 5 2.0 18 15 5.0 30 25 8.0
7 5 3.5 19 15 6.5 31 30 2.0
8 5 5.0 20 15 8.0 32 30 3.5
9 5 6.5 21 20 2.0 33 30 5.0
10 5 8.0 22 20 3.5 34 30 6.5
11 10 2.0 23 20 5.0 35 30 8.0
12 10 3.5 24 20 6.5 — — —

新窗口打开| 下载CSV


沉积物试样在相同环境下进行微生物培养，在培养箱中注入污水进行微生物接种与培养. 箱内水位保持恒定，水力停留时间为48 h，并进行曝气以形成适宜的微生物生长条件. 将含有机质沉积物装填入内径尺寸为10 cm×5 cm×2 cm的培养盒中，铺设高度为2 cm，浸没于培养箱中进行微生物培养.

2. 结果与讨论

2.1. 微生物作用对沉积物临界起动剪切应力的影响规律

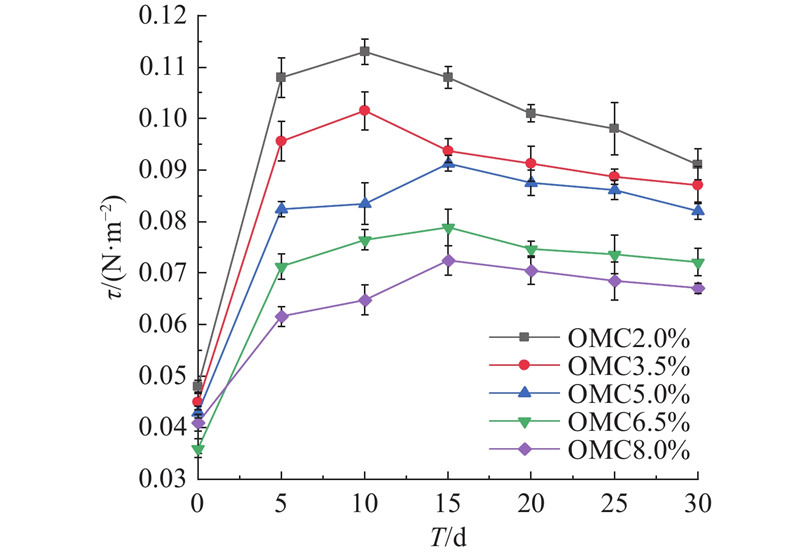
不同微生物作用时间、有机质含量沉积物的临界起动剪切应力的变化情况如图3所示. 由图3可知，含有机质沉积物起动规律与微生物作用时间、沉积物有机质含量有关. 当有机质含量一定时，沉积物试样的临界起动剪切应力随着微生物作用时间的增长呈现先增大后减小的变化规律. 当初始时刻沉积物起动并未受到微生物作用的影响时，其临界起动剪切应力在0.036~0.048 N/m2内. 当沉积物试样培养5 d后，沉积物的临界起动剪切应力出现大幅上升，几乎达到初始时刻的两倍. 临界起动剪切应力峰值分别出现在第10或15 d. Fang[9]等在研究微生物作用下无机沉积物的抗侵蚀性能变化规律时也得到了相同的变化趋势. 这种先增后减的现象产生原因主要是在培养前期，沉积物试样中有机质含量充足，微生物活动剧烈，分泌出大量胞外聚合物（extracellular polymeric substances, EPS）. EPS将沉积物颗粒紧密黏结，形成稳定的三维网状结构[16]，使得沉积物颗粒的结合力逐渐增强，临界起动剪切应力随之增大. 当培养进行至中后期时，微生物活动进入主动分散阶段，这个阶段中微生物将产生特定酶对部分生物膜进行降解和重构[16]，因此生物膜强度降低，临界起动剪切应力随之减小.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   不同工况下的临界起动剪切应力图

Fig.3   Change of critical shear stress at different experiment conditions


相同微生物作用时间下沉积物试样的临界起动剪切应力还与其有机质含量呈负相关（R=−0.939，p<0.01）. 在OMC为2%时，临界起动剪切应力在0.10 N/m2 左右. 而随着OMC逐渐提高，临界起动剪切应力不断下降. 当OMC提高到8%时，临界起动剪切应力下降到0.065 N/m2左右. 这种现象与文献[12]的研究结论一致. 过量的有机质含量使得微生物活动更加剧烈，这些微生物会产生大量的EPS并在沉积物内部形成气泡，气泡的逸出和过量的EPS导致沉积物试样发生膨胀，从而造成沉积物试样堆积变得松散，堆积密度减小[11,17]. 过量的EPS还会降低无机颗粒黏结力，阻碍沉积物絮体的形成[18-19].

2.2. 微生物作用对沉积物起动影响的定量表征

为了表征微生物作用对沉积物起动的影响，将进一步对生物黏性作用进行分析. 研究表明生物黏性作用会使沉积物颗粒聚集形成生物絮体颗粒，从而导致沉积物絮体的粒径发生变化[20]，而絮体粒径大小与生物黏性作用大小有关[20-21]. 本研究引入絮体强度试验方法，通过探究不同速度梯度下沉积物产生的絮体粒径大小对生物黏性作用强度进行分析. 不同G值下沉积物试样悬浮后的絮体平均直径如图4所示. 图中d为絮体的平均直径.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   不同G值下沉积物试样的絮体平均直径

Fig.4   Average floc diameter of sediments at different G


由图4可知，沉积物絮体的平均直径受速度梯度、有机质含量的影响显著. 由于G值越高，水流剪切力越大，对沉积物絮体造成的剪切破坏作用越强，相同有机质含量下沉积物絮体平均直径随着G值的增加而减小；相同G值下沉积物试样的絮体平均直径随着有机质含量的增高而降低. 在相同的工况下，沉积物试样的有机质含量越高，其形成的絮体结合强度越弱，这与临界起动剪切应力随有机质含量增高而下降的变化规律一致. Leentvaar等[22-23]提出絮体结合强度可以用絮体强度常数γ进行表征，因此进一步引入絮体强度常数γ对生物黏性作用进行定量表征，絮体强度常数计算式[23] 为

$ \begin{array}{*{20}{c}} {\gamma = \dfrac{{{\rm{ln}}\; C - {\rm{ln}}\; d}}{{{\rm{ln}}\; G}}} \end{array}. $

式中：C为絮体强度系数.

由式（7）计算得到絮体强度常数结果如图5所示. 由图5可知，对于OMC为2.0%、3.5%的沉积物试样，在沉积物培养前10 d时，γ值随微生物作用时间的增加而减小；在第10 d达到最小值，随后逐渐增大. 这表明沉积物试样的絮体结合强度随着微生物作用时间先增后减，并在第10 d时达到峰值. 对于OMC为5.0%、6.5%、8.0%的沉积物，γ值也呈现出类似变化规律，不同的是最低值出现在第15 d.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

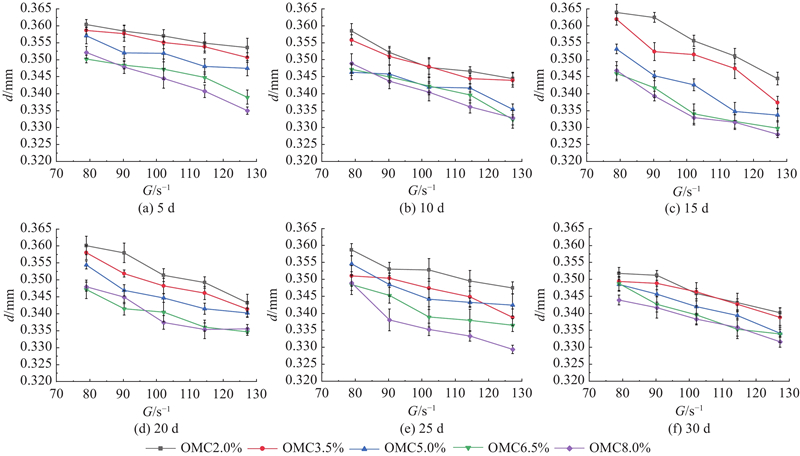
图 5   沉积物试样絮体强度常数随时间变化的示意图

Fig.5   Change of stable floc size constant with microbial activity time for different sediments


由图5还可知絮体强度常数随着有机质含量的增大而增大（R=0.709，p<0.01），即高有机质含量沉积物形成的絮体在受到水流剪切应力时更容易发生破碎，这表明沉积物絮体的抗侵蚀能力与沉积物的有机质含量呈负相关，与临界起动剪切应力随有机质含量增高而减小的变化规律相同（图3）. γ值是有机质含量与微生物作用时间的函数，通过拟合可得γ值计算式，拟合结果见图6. 图中γc为γ值的计算值，γe为γ值的实验所得值. 由图6所示，式（8）的拟合效果较好， R2=0.91.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

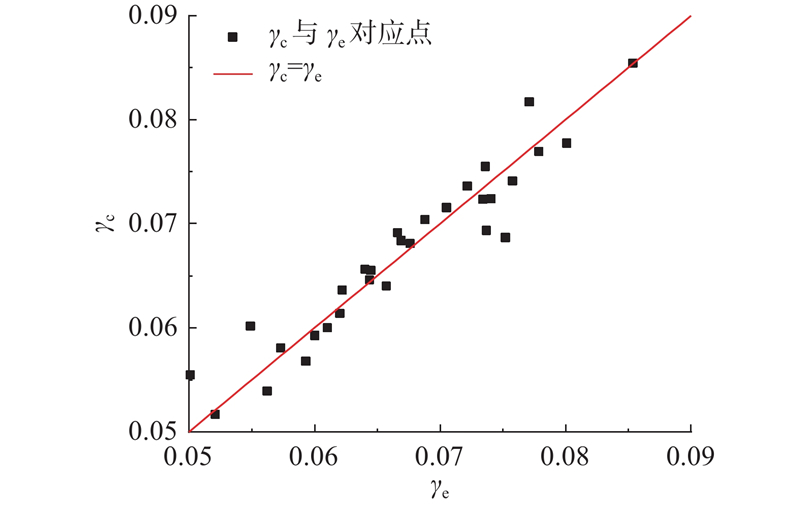
图 6   絮体强度常数计算值与实验值的对比结果

Fig.6   Comparison of calculated and experimental values of stable floc size constant


$ \begin{split} \gamma = & 0.090\; 676 - 0.007 \; 159T+0.284\; 889{\text{OMC}}+ \\ & 0.000\; 363{T^2} - 0.000 \;005\; 48{T^3}. \end{split} $

2.3. 微生物作用下含有机质沉积物起动经验公式推求

微生物作用下的临界起动剪切应力可以分成无黏性项、黏性项以及生物黏性作用项3个部分组成[9, 24]. 本试验研究的模型沙粒径为0.183 mm，黏性特征并不显著，黏性项在泥沙起动过程中的作用可以忽略不计[13]. 因此，微生物作用下的沉积物临界起动剪切应力为

$ \begin{array}{*{20}{c}} {\tau = {\tau _0}+{\tau _a}}. \end{array} $

式中： ${\tau _{\text{a}}}$为生物的黏性作用， ${\tau _0}$为无黏性沙的临界起动剪切应力. 当沙粒以滚动作为起动的模式时， ${\tau _0}$可以通过受力平衡计算[24]得

$ \begin{array}{*{20}{c}} {{\tau _0} = \dfrac{{a\alpha \left( {{\rho _{\rm{s}}} - \rho } \right)g{d_{50}}}}{{{\alpha _{\rm{d}}}\left( {b+a\eta } \right)}}} \end{array}. $

式中：ρs和ρ分别为沙颗粒和水的真密度；g为重力加速度，g=9.8 N/kg； $\alpha$为形状系数；αd为拖曳力系数；η为拖曳力和上举力的联系系数，拖曳力系数、拖曳力和上举力的联系系数均是粒子雷诺数Re*的函数； $a$为颗粒水下重力和上举力的力臂； $b$为拖曳力的力臂.

对比图3、5发现，γ值变化规律与临界起动剪切应力变化较为一致. 通过对比生物黏性作用与絮体强度常数的变化规律发现二者具有很好的相关性（R=−0.767，p<0.01），如图7所示. 由此可知，生物黏性作用可以用γ值进行表征.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   生物黏性作用与絮体强度常数的关系

Fig.7   Relationship between bio-adhesive effect and stable floc size constant


生物黏性作用的计算式如下，此时公式的拟合效果最佳，R2=0.9.

$ \begin{array}{*{20}{c}} {{\tau _a} = 0.089{\kern 1pt} {\kern 1pt} 169 - 0.506{\kern 1pt} {\kern 1pt} 986{\rm{OMC}} - 0.323{\kern 1pt} {\kern 1pt} 215\gamma } \end{array}. $

微生物作用下的含有机质沉积物临界起动剪切应力为

$ \begin{split} \tau =& {\tau _0}+{\tau _a} = \frac{{a\alpha \left( {{\rho _{\rm{s}}} - \rho } \right)g{d_{50}}}}{{{\alpha _{\rm{d}}}\left( {b+a\eta } \right)}}+0.089\; 169 - \\ & 0.506\; 986{\rm{OMC}} - 0.323\; 215\gamma . \end{split} $

通过式（12）计算的临界起动剪切应力与实际剪切应力的效果如图8所示. 图中 $ {\tau _{\rm{c}}} $为临界起动剪切应力计算值， $ {\tau _{\text{e}}} $为临界起动剪切应力实验值. 由图8可知，式（12）可以较为准确地计算在微生物作用下含有机质沉积物的临界起动剪切应力。

图 8

新窗口打开| 下载原图ZIP| 生成PPT

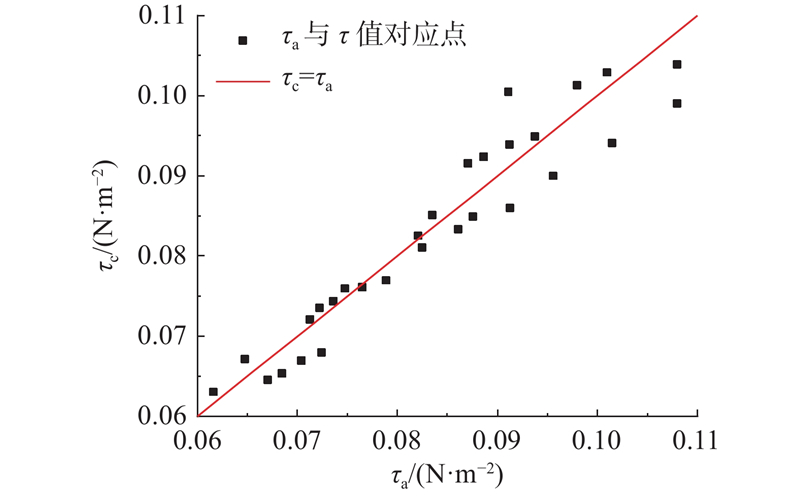
图 8   临界剪切应力计算值与实验值的对比结果

Fig.8   Comparison of calculated and experimental values of critical shear stress


3. 结　论

在微生物作用下，针对不同微生物的作用时间、有机质含量沉积物的临界起动剪切应力，展开试验研究. 结合在微生物作用下絮体强度常数的变化规律，对起动过程中的生物黏性作用进行量化与表征，主要研究结论如下.

（1）在微生物的作用下，含有机质沉积物的临界起动剪切应力显著增大. 微生物作用下含有机质沉积物的临界起动剪切应力变化情况与微生物的作用时间、沉积物的有机质含量有关，沉积物的临界起动剪切应力随着微生物作用时间的增大呈现出先增大后减小的趋势，与有机质含量呈现显著的负相关关系.

（2）在沉积物起动过程中，生物黏性作用可以用絮体强度常数进行表征. 絮体强度常数的大小受到微生物的作用时间以及有机质含量的影响. 絮体强度常数与沉积物的临界起动剪切应力呈现类似变化规律，与生物黏性作用呈现较强的负相关.

（3）通过引入生物黏性作用项，可得到在微生物作用下含有机质沉积物的临界起动公式. 公式计算值与实验值的对照结果表明，该公式可以较准确地计算微生物作用下含有机质沉积物的临界起动剪切应力大小。

参考文献

朱永明. 合流制排水管道沉积物调查研究[D]. 武汉: 武汉理工大学, 2011: 9-11.

[本文引用: 1]

ZHU Yong-ming. Research on sediment in combined sewer [D]. Wuhan: Wuhan University of Technology, 2011: 9-11.

[本文引用: 1]

BANASIAK R

Hydraulic performance of sewer pipes with deposited sediments

[J]. Water Science and Technology, 2008, 57 (11): 1743- 1748

DOI:10.2166/wst.2008.287      [本文引用: 2]

MONTES C, BERARDI L, KAPELAN Z, et al

Predicting bedload sediment transport of non-cohesive material in sewer pipes using evolutionary polynomial regression–multi-objective genetic algorithm strategy

[J]. Urban Water Journal, 2020, 17 (2): 154- 162

DOI:10.1080/1573062X.2020.1748210      [本文引用: 1]

MONTES C, KAPELAN Z, SALDARRIAGA J

Predicting non-deposition sediment transport in sewer pipes using random forest

[J]. Water Research, 2021, 189: 116639

DOI:10.1016/j.watres.2020.116639     

黄乃先, 齐一凡, 金伟

排水管道沉积物控制的研究进展

[J]. 环境工程技术学报, 2021, 11 (3): 507- 513

[本文引用: 1]

HUANG Nai-xian, QI Yi-fan, JIN Wei

Research progress on the control of sediments in the drainage pipe

[J]. Journal of Environmental Engineering Technology, 2021, 11 (3): 507- 513

[本文引用: 1]

SHIELDS A. Application of similarity principles and turbulence research to bed-load movement [D]. California: California Institute of Technology, 1936: 9-20.

[本文引用: 1]

TAIT S J, RUSHFORTH P J, SAULA J

A laboratory study of the erosion and transport of cohesive-like sediment mixtures in sewers

[J]. Water Science and Technology, 1998, 37 (1): 163- 170

DOI:10.2166/wst.1998.0040      [本文引用: 1]

方红卫, 尚倩倩, 府仁寿, 等

泥沙颗粒生长生物膜后起动的实验研究——Ⅱ: 起动流速计算

[J]. 水科学进展, 2011, 22 (3): 301- 306

[本文引用: 1]

FANG Hong-wei, SHANG Qian-qian, FU Ren-shou, et al

Experimental study of the effect of biofilm formation on sediment incipient motion Ⅱ: incipient velocity calculation

[J]. Advances in Water Science, 2011, 22 (3): 301- 306

[本文引用: 1]

FANG H, SHANG Q, CHEN M, et al

Changes in the critical erosion velocity for sediment colonized by biofilm

[J]. Sedimentology, 2014, 61 (3): 648- 659

DOI:10.1111/sed.12065      [本文引用: 3]

SECO I, GOMEZ VALENTIN M, SCHELLART A, et al

Erosion resistance and behavior of highly organic in-sewer sediment

[J]. Water Science and Technology, 2014, 69 (3): 672- 679

DOI:10.2166/wst.2013.761      [本文引用: 1]

ZHOU Y, YAO X, GU Y, et al

Biological effects on incipient motion behavior of sediments with different organic matter content

[J]. Journal of Soils and Sediments, 2021, 21 (1): 627- 640

DOI:10.1007/s11368-020-02807-9      [本文引用: 2]

马妍. 排水系统管内沉积物的冲蚀输移特性与规律研究[D]. 杭州: 浙江大学, 2014: 35-36.

[本文引用: 2]

MA Yan. Study on erosion characteristics and transport principles of sewer sediment in sewerage system [D]. Hangzhou: Zhejiang University, 2014: 35-36.

[本文引用: 2]

钱宁, 万兆惠. 泥沙运动力学[M]. 北京: 科学出版社, 1983: 85-105.

[本文引用: 2]

LICK W, JIN L, GAILANI J

Initiation of movement of quartz particles

[J]. Journal of Hydraulic Engineering, 2004, 130 (8): 755- 761

DOI:10.1061/(ASCE)0733-9429(2004)130:8(755)      [本文引用: 1]

CAMP T R

Velocity gradients and internal work in fluid motion

[J]. Journal of the Boston Society of Civil Engineers, 1943, 30: 219- 230

[本文引用: 1]

YIN W, WANG Y, LIU L, et al

Biofilms: the microbial “protective clothing” in extreme environments

[J]. International Journal of Molecular Sciences, 2019, 20 (14): 3423

DOI:10.3390/ijms20143423      [本文引用: 2]

AMOS C L, DROPPO I G, GOMEZ E A, et al

The stability of a remediated bed in Hamilton Harbour, Lake Ontario, Canada

[J]. Sedimentology, 2003, 50 (1): 149- 168

DOI:10.1046/j.1365-3091.2003.00542.x      [本文引用: 1]

WILEN B M, JIN B, LANT P

The influence of key chemical constituents in activated sludge on surface and flocculating properties

[J]. Water Research, 2003, 37 (9): 2127- 2139

DOI:10.1016/S0043-1354(02)00629-2      [本文引用: 1]

LI X Y, YANG S F

Influence of loosely bound extracellular polymeric substances (EPS) on the flocculation, sedimentation and dewaterability of activated sludge

[J]. Water Research, 2007, 41 (5): 1022- 1030

DOI:10.1016/j.watres.2006.06.037      [本文引用: 1]

尚倩倩, 方红卫, 赵慧明, 等

泥沙颗粒生长生物膜后沉降的实验研究Ⅰ: 实验设计及粒径变化

[J]. 水利学报, 2012, 43 (3): 275- 281

[本文引用: 2]

SHANG Qian-qian, FANG Hong-wei, ZHAO Hui-ming, et al

Experiment on the biofilm effects on sediment setting Ⅰ: experimental design and grading variation

[J]. Journal of Hydraulic Engineering, 2012, 43 (3): 275- 281

[本文引用: 2]

RIGHETTI M, LUCARELLI C

May the Shields theory be extended to cohesive and adhesive benthic sediments?

[J]. Journal of Geophysical Research: Oceans, 2007, 112 (5): 1- 14

[本文引用: 1]

LEENTVAAR J, REBHUN M

Strength of ferric hydroxide flocs

[J]. Water Research, 1983, 17 (8): 895- 902

DOI:10.1016/0043-1354(83)90163-X      [本文引用: 1]

PARKER D S, KAUFMAN W J, JENKINS D

Floc breakup in turbulent flocculation processes

[J]. Journal of the Sanitary Engineering Division, 1972, 98 (1): 79- 99

DOI:10.1061/JSEDAI.0001389      [本文引用: 2]

钱栋. 生物作用下排水管道沉积物起动规律研究[D]. 杭州: 浙江大学, 2017: 42-45.

[本文引用: 2]

QIAN Dong. Study on laws for the incipient motion of sewer sediments with biological activities [D]. Hangzhou: Zhejiang University, 2017: 42-45.

[本文引用: 2]

/

〈 〉