[58]
FATHI S, DICKENS P, FOUCHAL F Regimes of droplet train impact on a moving surface in an additive manufacturing process
[J]. Journal of Materials Processing Technology , 2010 , 210 (3 ): 550 - 559
DOI:10.1016/j.jmatprotec.2009.10.018
[本文引用: 1]
[59]
FATHI S, DICKENS P, HAGUE R J M, et al, Analysis of droplet train/moving substrate interactions in ink-jetting processes [C]// 2008 International Solid Freeform Fabrication Symposium , Texas: [s. n.], 2008: 230-237.
[本文引用: 1]
[60]
LI H, WANG P, QI L, et al 3D numerical simulation of successive deposition of uniform molten Al droplets on a moving substrate and experimental validation
[J]. Computational Materials Science , 2012 , 65 : 291 - 301
DOI:10.1016/j.commatsci.2012.07.034
[本文引用: 1]
[61]
屈冲. 液滴与旋转壁面的冲击动力学研究[D]. 哈尔滨: 哈尔滨工业大学, 2020: 24-42.
[本文引用: 3]
QU Chong. A study of impact dynamics of droplet on the rotating substrate [D]. Harbin: Harbin Institute of Technology, 2020: 24-42.
[本文引用: 3]
[62]
SAHOO S, ORPE A V, DOSHIB P Spreading dynamics of superposed liquid drops on a spinning disk
[J]. Physics of Fluids , 2018 , 30 (1 ): 012110
DOI:10.1063/1.5002601
[本文引用: 2]
[63]
CHOU F C, ZEN T S, LEE K W An experimental study of a water droplet impacting on a rotating wafer
[J]. Atomization and Sprays , 2009 , 19 (10 ): 905 - 916
DOI:10.1615/AtomizSpr.v19.i10.10
[本文引用: 1]
[64]
MANZELLO S L, YANG J C An experimental study of a water droplet impinging on a liquid surface
[J]. Experiments in Fluids , 2002 , 32 (5 ): 580 - 589
DOI:10.1007/s00348-001-0401-8
[本文引用: 2]
[65]
REIN M Phenomena of liquid drop impact on solid and liquid surfaces
[J]. Fluid Dynamics Research , 1993 , 12 (2 ): 61 - 93
DOI:10.1016/0169-5983(93)90106-K
[66]
REIN M. Wave phenomena during droplet impact [C]// IUTAM Symposium on Waves in Liquid/Gas and Liquid/Vapour Two-Phase Systems . Kyoto: Springer, 1995: 171-190
[本文引用: 1]
[67]
ZHAO K, WANG Y, DING Y, et al Numerical and theoretical study on the spreading characteristics of droplet impact on a horizontal flowing liquid film
[J]. Colloids and Surfaces a Physicochemical and Engineering Aspects , 2021 , 616 (1 ): 126338
[本文引用: 3]
[68]
HE J, YUAN H, HE X, et al Droplet impact on a moving thin film with pseudo potential lattice Boltzmann method
[J]. Mathematical Problems in Engineering , 2020 , 2020 (3 ): 1 - 15
[本文引用: 3]
[1]
王亚青, 刘明侯, 刘东 喷雾冷却换热机理和影响换热性能的因素
[J]. 强光与粒子束 , 2011 , 23 (9 ): 2277 - 2281
[本文引用: 1]
WANG Ya-qing, LIU Ming-hou, LIU Dong Heat Transfer mechanism and influence factors in spray cooling
[J]. High Power Laser and Particle Beams , 2011 , 23 (9 ): 2277 - 2281
[本文引用: 1]
[69]
CASTREJÓN-PITA J R, MUÑOZ-SÁNCHEZ B N, HUTCHINGS I M, et al Droplet impact onto moving liquids
[J]. Journal of Fluid Mechanics , 2016 , 809 : 716 - 725
DOI:10.1017/jfm.2016.672
[本文引用: 1]
[70]
范国军. 液滴碰撞流动液膜的特性及影响因素研究[D]. 北京: 北京工业大学, 2014: 2-8.
[本文引用: 1]
FAN Guo-jun. Study on the characteristics and influencing factors of the droplets impacting onto the moving liquid film [D]. Beijing: Beijing University of Technology, 2014: 2-8.
[本文引用: 1]
[72]
LIU J, GOLLUB J P Solitary wave dynamics of film flows
[J]. Physics of Fluids , 1994 , 6 (5 ): 1702
DOI:10.1063/1.868232
[73]
KALLIADASIS S, RUYER-QUIL C, SCHEID B, et al. Falling liquid films [C]// Applid Mathmatical Sciences . London: Springer, 2011: 1-440.
[本文引用: 1]
[75]
CHENG M, LOU J Lattice Boltzmann simulation of a drop impact on a moving wall with a liquid film
[J]. Computers and Mathematics with Applications , 2014 , 67 (2 ): 307 - 317
DOI:10.1016/j.camwa.2013.07.003
[本文引用: 1]
[77]
陈烽, 王登飞, 蔡子琦, 等 液滴撞击固体表面过程的实验研究
[J]. 北京化工大学学报: 自然科学版 , 2019 , 46 (4 ): 15 - 22
[本文引用: 1]
CHEN Feng, WANG Deng-fei, CAI Zi-qi, et al Experimental study on the process of droplet impacting solid surface
[J]. Journal of Beijing University of Chemical Technology: Natural Science , 2019 , 46 (4 ): 15 - 22
[本文引用: 1]
[78]
CHANDRA S, AVEDISIAN C T On the collision of a droplet with a solid surface
[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences , 1991 , 432 : 13 - 41
[本文引用: 2]
[79]
PASANDIDEH M, QIAO Y M, CHANDRA S, et al Capillary effects during droplet impact on a solid surface
[J]. Physics of Fluids , 1996 , 8 (3 ): 650 - 658
DOI:10.1063/1.868850
[80]
UKIWE C, KWOK D Y On the maximum spreading diameter of impacting droplets on well-prepared solid surfaces
[J]. Langmuir , 2005 , 21 (2 ): 666 - 673
DOI:10.1021/la0481288
[81]
WANG F, YANG L, WANG L, et al. Maximum spread of droplet impacting onto solid surfaces with different wettabilities: adopting a rim lamella shape [J]. Langmuir 2019, 35(8): 3204-3214.
[本文引用: 1]
[82]
ATTANE P, GIRARD F, MORIN V An energy balance approach of ́ the dynamics of drop impact on a solid surface
[J]. Physics of Fluids , 2007 , 19 (1 ): 012101
DOI:10.1063/1.2408495
[83]
KIM H Y, CHUN J H The recoiling of liquid droplets upon collision with solid surfaces
[J]. Physics of Fluids , 2001 , 13 (3 ): 643 - 659
DOI:10.1063/1.1344183
[84]
BECHTEL S E, BOGY D, TALKE F E Impact of a liquid drop against a flat surface
[J]. IBM Journal of Resaerch and Development , 1981 , 25 (6 ): 963 - 971
DOI:10.1147/rd.256.0963
[85]
DELPLANQUE J P, RANGEL R H An improved model for droplet solidification on a flat surface
[J]. Journal of Materials Science , 1997 , 32 (6 ): 1519 - 1530
DOI:10.1023/A:1018522521531
[86]
CLANET C, BÉGUIN C, RICHARD D, et al Maximal deformation of an impacting drop
[J]. Journal of Fluid Mechanics , 2004 , 517 : 199 - 208
DOI:10.1017/S0022112004000904
[本文引用: 1]
[87]
STOW C D, HADFIELD M G An experimental investigation of fluid-flow resulting from the impact of a water drop with an unyielding dry surface
[J]. Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences , 1981 , 373 (1755 ): 419 - 441
[本文引用: 1]
[88]
RIBOUX G, GORDILLO J M Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing
[J]. Physical Review Letters , 2014 , 113 (2 ): 024507
DOI:10.1103/PhysRevLett.113.024507
[本文引用: 1]
[89]
MOULSON J B T, GREEN S I Effect of ambient air on liquid jet impingement on a moving substrate
[J]. Physics of Fluids , 2013 , 25 (10 ): 102106
DOI:10.1063/1.4823726
[本文引用: 1]
[90]
詹海洋. 液滴撞击超疏水表面的非对称动力学特性研究[D]. 大连: 大连理工大学, 2019: 19-22.
[本文引用: 1]
ZHAN Hai-yang. Study on asymmetric dynamics of droplets impacting on superhydrophobic surfaces [D]. Dalian: Dalian University of Technology, 2019: 19-22.
[本文引用: 1]
[91]
LIU X, ZHANG X, MIN J Maximum spreading of droplets impacting spherical surfaces
[J]. Physics of Fluids , 2019 , 31 (9 ): 092102
DOI:10.1063/1.5117278
[本文引用: 1]
[92]
BARTOLO D, JOSSERAND C, BONN D Retraction dynamics of aqueous drops upon impact on non-wetting surfaces
[J]. Journal of Fluid Mechanics , 2005 , 545 (1 ): 329 - 338
[本文引用: 1]
[93]
ROISMA I V, TROPEA C Impact of a drop onto a wetted wall: description of crown formation and propagation
[J]. Journal of Fluid Mechanics , 2002 , 472 : 373 - 397
DOI:10.1017/S0022112002002434
[本文引用: 1]
[94]
YARIN A L, WESS D A Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity
[J]. Journal of Fluid Mechanics , 1995 , 283 (1 ): 141 - 173
[本文引用: 1]
[95]
崔守鑫, 胡海泉, 肖效光, 等 分子动力学模拟基本原理和主要技术
[J]. 聊城大学学报: 自然科学版 , 2005 , 18 (1 ): 31 - 34
[本文引用: 2]
CUI Shou-xin, HU Hai-quan, XIAO Xiao-guang, et al The basic principles and methods of mplecuar dynamics simulation
[J]. Journal of Liaocheng University: Natural Science , 2005 , 18 (1 ): 31 - 34
[本文引用: 2]
[96]
张嫚嫚. 气液两相流界面追踪方法的数值研究[D]. 天津: 河北工业大学, 2019: 4-11.
[本文引用: 2]
Zhang Man-man. Numerical study on the interface tracking method of gas-liquid two-phase flow [D]. Tianjin: Hebei University of Technology, 2019: 4-11.
[本文引用: 2]
[97]
LIANG G, GUO Y, SHEN S Analysis of liquid sheet and jet flow mechanism after droplet impinging onto liquid film
[J]. Acta Physica Sinica Chinese Edition , 2013 , 62 (2 ): 024705
DOI:10.7498/aps.62.024705
[本文引用: 1]
[98]
赵可, 佘阳梓, 蒋彦龙, 等 液氮滴撞击壁面相变行为的数值研究
[J]. 物理学报 , 2019 , 68 (24 ): 244401
DOI:10.7498/aps.68.20190945
[本文引用: 1]
ZHAO Ke, SHE Yang-zi, JIANG Yan-long, et al Numerical study on phase change behavior of liquid nitrogen droplets impinging on solid surface
[J]. Acta Physica Sinica Chinese Edition , 2019 , 68 (24 ): 244401
DOI:10.7498/aps.68.20190945
[本文引用: 1]
[99]
FANG T H, CHANG W J, LIN S H Effects of temperature and velocity of droplet ejection process of simulated nanojets onto a moving plate’s surface
[J]. Applied Surface Science , 2006 , 253 (3 ): 1649 - 1654
DOI:10.1016/j.apsusc.2006.02.062
[本文引用: 1]
[100]
ABASCALA J L F, VEGA C A general purpose model for the condensed phases of water: TIP4P/2005
[J]. The Journal of Chemical Physics , 2005 , 123 (23 ): 234505
DOI:10.1063/1.2121687
[本文引用: 1]
[101]
RITOS K, DONGARI N, BORG M K, et al Dynamics of nanoscale droplets on moving surfaces
[J]. Langmuir , 2013 , 29 (23 ): 6936 - 6943
DOI:10.1021/la401131x
[本文引用: 1]
[102]
RITOS K, DONGARI N, ZHANG Y, et al. Dynamic wetting on moving surfaces: a molecular dynamics study [C]// Proceedings of the ASME 2012 10th International Conference on Nanochannels Microchannels and Minichannels . Puerto Rico: [s. n.], 2012: 73179.
[本文引用: 1]
[103]
HEINZ H, VAIA R A , FARMER B L, et al. Accurate simulation of surfaces and interfaces of face-centered cubic metals using 12-6 and 9-6 Lennard-Jones potentials
[J]. The Journal of Physical Chemistry C , 2008 , 112 (44 ): 17281 - 17290
DOI:10.1021/jp801931d
[本文引用: 1]
[104]
ZHANG H, LING P, XIE X Molecular dynamics simulation on behaviors of water nanodroplets impinging on moving surfaces
[J]. Nanomaterials , 2022 , 12 (2 ): 247
DOI:10.3390/nano12020247
[本文引用: 3]
[105]
HOU J, GONG J, WU X, et al Numerical study on impacting-freezing process of the droplet on a lateral moving cold super hydrophobic surface
[J]. International Journal of Heat and Mass Transfer , 2022 , 183 : 122044
DOI:10.1016/j.ijheatmasstransfer.2021.122044
[本文引用: 3]
[106]
YAO Y, LI C, ZHANG H, et al Modelling the impact, spreading and freezing of a water droplet on horizontal and inclined super hydrophobic cooled surfaces
[J]. Applied Surface Science , 2017 , 419 : 52 - 62
DOI:10.1016/j.apsusc.2017.04.085
[本文引用: 1]
[107]
ZHANG X, LIU X, WU X, et al Impacting-freezing dynamics of a supercooled water droplet on a cold surface: rebound and adhesion
[J]. International Journal of Heat and Mass Transfer , 2020 , 158 : 119997
DOI:10.1016/j.ijheatmasstransfer.2020.119997
[本文引用: 1]
[108]
RAMAN K A Normal and oblique droplet impingement dynamics on moving dry walls
[J]. Physical Review , 2019 , 99 (5 ): 053108
[本文引用: 2]
[109]
ZHAN H, LU C, LIU C, et al Horizontal motion of a super hydrophobic substrate affects the drop bouncing dynamics
[J]. Physical Review Letters , 2021 , 126 : 234503
DOI:10.1103/PhysRevLett.126.234503
[本文引用: 1]
[110]
LIANG G, CHEN L, WANG T, et al Parametric Effects on interface evolution and heat transfer in droplet impact on flowing liquid film
[J]. Industrial and Engineering Chemistry Research , 2020 , 59 : 379 - 388
DOI:10.1021/acs.iecr.9b04717
[本文引用: 1]
[111]
LIANG G, CHEN L, CHEN Y, et al Interfacial phenomena and heat transfer associated with multi-droplet impact on flowing liquid film
[J]. Numerical Heat and Transfer Applications , 2020 , 77 (1 ): 80 - 89
DOI:10.1080/10407782.2019.1678325
[本文引用: 1]
[112]
LI J, ZHANG H, LIU Q Characteristics of secondary droplets produced by a single drop impacting on a static liquid film
[J]. International Journal of Multiphase Flow , 2019 , 119 : 42 - 55
DOI:10.1016/j.ijmultiphaseflow.2019.06.015
[本文引用: 1]
[113]
WANG Y, WANG X, WANG T, et al Asymmetric heat transfer characteristics of a double droplet impact on a moving liquid film
[J]. International Journal of Heat and Mass Transfer , 2018 , 126 : 649 - 659
DOI:10.1016/j.ijheatmasstransfer.2018.05.161
[本文引用: 1]
[114]
XIE Z, HEWITT G F, PAVLIDIS D, et al Numerical study of three-dimensional droplet impact on a flowing liquid film in annular two-phase flow
[J]. Chemical Engineering Science , 2017 , 166 : 303 - 312
DOI:10.1016/j.ces.2017.04.015
[本文引用: 1]
[115]
HE X, CHEN S, ZHANG R A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh Taylor instability
[J]. Journal of Computational Physics , 1999 , 152 (2 ): 642 - 663
DOI:10.1006/jcph.1999.6257
[本文引用: 1]
[116]
LEE T, LIN C L A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ratio
[J]. Journal of Computational Physics , 2005 , 206 (1 ): 16 - 47
DOI:10.1016/j.jcp.2004.12.001
[本文引用: 1]
[117]
RAMAN K A, JAIMAN R K, LEE T S, et al On the dynamics of crown structure in simultaneous two droplets impact onto stationary and moving liquid film
[J]. Computers and Fluids , 2015 , 107 : 285 - 300
DOI:10.1016/j.compfluid.2014.11.007
[本文引用: 1]
[118]
LIU C, SHEN M, WU J Investigation of a single droplet impact onto a liquid film with given horizontal velocity
[J]. European Journal of Mechanics/B Fluids , 2018 , 67 : 269 - 279
DOI:10.1016/j.euromechflu.2017.09.012
[本文引用: 1]
[119]
DING H, SPELT P D M, SHU C Diffuse Interface model for incompressible two phase flows with large density ratios
[J]. Journal of Computational Physics , 2007 , 226 : 2078 - 2095
DOI:10.1016/j.jcp.2007.06.028
[本文引用: 1]
[2]
HOPKINSON N, HAGUE R J M, DICKENS P M. Rapid manufacturing: an industrial revolution for the digital age [M]. UK: John Wiley and Sons, 2006: 58-63.
[本文引用: 1]
[4]
MOHLER S H Predicting droplet impingement on yawed wings
[J]. Journal of Aircraft , 2015 , 29 (5 ): 964 - 966
[本文引用: 1]
[5]
FORNEY L J Droplet impaction on a supersonic wedge- consideration of similitude
[J]. AIAA Journal , 1990 , 28 (4 ): 650 - 654
DOI:10.2514/3.10442
[本文引用: 1]
[6]
张丽芬, 张美华, 吴丁毅, 等 旋转帽罩结冰相似准则的研究
[J]. 推进技术 , 2015 , 36 (8 ): 1164 - 1169
DOI:10.13675/j.cnki.tjjs.2015.08.007
[本文引用: 1]
ZHANG Li-fen, ZHANG Mei-hua, WU Ding-yi, et al Research on icing scaling law for rotating cone
[J]. Journal of Propulsion Technology , 2015 , 36 (8 ): 1164 - 1169
DOI:10.13675/j.cnki.tjjs.2015.08.007
[本文引用: 1]
[7]
李岩, 王绍龙, 易贤, 等 绕轴旋转圆柱结冰特性结冰风洞试验
[J]. 航空学报 , 2017 , 38 (2 ): 1 - 11
[本文引用: 1]
LI Yan, WANG Shao-long, YI Xian, et al An icing wind tunnel test on icing characteristics of cylinder rotating around a shaft
[J]. Acta Aeronautica Et Astronautica Sinica , 2017 , 38 (2 ): 1 - 11
[本文引用: 1]
[8]
李岩, 孙策, 郭文峰, 等 利用自然低温的旋转叶片结冰风洞试验系统设计
[J]. 实验流体力学 , 2018 , 32 (2 ): 40 - 47
DOI:10.11729/syltlx20170073
LI Yan, SUN Ce, GUO Wen-feng, et al Design of icing wind tunnel experiment system for rotating blades by using natural low temperature
[J]. Journal of Experiments in Fluid Mechanics , 2018 , 32 (2 ): 40 - 47
DOI:10.11729/syltlx20170073
[9]
李岩, 王绍龙, 冯放, 等 绕轴旋转翼型结冰分布的结冰风洞试验研究
[J]. 哈尔滨工程大学学报 , 2017 , 38 (4 ): 545 - 553
DOI:10.11990/jheu.201610051
[本文引用: 1]
LI Yan, WANG Shao-long, FENG Fang, et al An icing wind tunnel experiment on the icing distribution of a blade airfoil rotating around a shaft
[J]. Journal of Harbin Engineering University , 2017 , 38 (4 ): 545 - 553
DOI:10.11990/jheu.201610051
[本文引用: 1]
[10]
WORTHINGTON A M On the forms assumed by drops of liquids falling vertically on a horizontal plate
[J]. Proceedings of the Royal Society of London , 1876 , 25 : 261 - 271
[本文引用: 1]
[11]
WORTHINGTON A M A second paper on the forms assumed by drops of liquids falling vertically on a horizontal plate
[J]. Proceedings of the Royal Society of London B , 1877 , 25 : 498 - 503
DOI:10.1098/rspl.1876.0073
[本文引用: 1]
[12]
权生林, 李维仲, 朱卫英 水滴撞击固体表面实验研究
[J]. 大连理工大学学报 , 2009 , 49 (6 ): 833 - 836
DOI:10.7511/dllgxb200906010
[本文引用: 1]
QUAN Sheng-lin, LI Wei-zhong, ZHU Wei-ying Experimental study of water droplet impacted onto solid surfaces
[J]. Journal of Dalian University of Technology , 2009 , 49 (6 ): 833 - 836
DOI:10.7511/dllgxb200906010
[本文引用: 1]
[13]
ENGEL O G Waterdrop collisions with solid surfaces
[J]. Journal of Research of the National Bureau of Standards , 1955 , 54 (5 ): 281 - 298
DOI:10.6028/jres.054.033
[本文引用: 2]
[14]
施明恒 单个液滴碰击表面时的流体动力学特性
[J]. 力学学报 , 1985 , 17 (5 ): 419 - 425
[本文引用: 1]
SHI Ming-heng Behavior of a liquid droplet impacting on a solid surface
[J]. Chinese Journal of Theoretical and Applied Mechanics , 1985 , 17 (5 ): 419 - 425
[本文引用: 1]
[15]
SIKALO S, MARENGO M, TROPEA C, et al Analysis of impact of droplets on horizontal surfaces
[J]. Experimental Thermal and Fluid Science , 2002 , 25 (7 ): 503 - 510
DOI:10.1016/S0894-1777(01)00109-1
[本文引用: 1]
[17]
SIKALO S, TROPEA C, GANIC E N Impact of droplet onto inclined surface
[J]. Journal of Colloid and Interface Science , 2005 , 286 (2 ): 661 - 669
DOI:10.1016/j.jcis.2005.01.050
[19]
ALMOHAMMADI H, AMIRFAZLI A Understanding the drop impact on moving hydrophilic and hydrophobic surfaces
[J]. Soft Matter , 2017 , 13 (10 ): 2040
DOI:10.1039/C6SM02514E
[本文引用: 5]
[20]
BUKSH S, ALMOHAMMADI H, MARENGO M, et al Spreading of low-viscous liquids on a stationary and a moving surface
[J]. Experiments in Fluids , 2019 , 60 (4 ): 60 - 76
DOI:10.1007/s00348-019-2709-2
[本文引用: 4]
[21]
HAO J, GREEN S Splash threshold of a droplet impacting a moving substrate
[J]. Physics of Fluids , 2017 , 29 (1 ): 012103
DOI:10.1063/1.4972976
[本文引用: 3]
[24]
ZHANG X, ZHU Z, ZHANG C, et al Reduced contact time of a droplet impacting on a moving superhydrophobic surface
[J]. Applid Physics Letters , 2020 , 117 (15 ): 151602
DOI:10.1063/5.0023896
[本文引用: 6]
[25]
MUNDO C, SOMMERFELD M, TROPEA C Droplet-wall collisions: experimental studies of the deformation and breakup process
[J]. International Journal of Multiphase Flow , 1995 , 21 (2 ): 151 - 173
DOI:10.1016/0301-9322(94)00069-V
[本文引用: 2]
[26]
CHEN R H, WANG H W Effects of tangential speed on low-normal-speed liquid drop impact on a non-wettable solid surface
[J]. Experiments in Fluids , 2005 , 39 (4 ): 754 - 760
DOI:10.1007/s00348-005-0008-6
[本文引用: 2]
[27]
BIRD J C, TSAI S S H, STONE H A Inclined to splash: triggering and inhibiting a splash with tangential velocity
[J]. New Journal of Physics , 2009 , 11 : 063017
DOI:10.1088/1367-2630/11/6/063017
[本文引用: 4]
[28]
BUKSH S, MARENGO M, AMIRFAZLI A Impacting of droplets on moving surface and inclined surfaces
[J]. Atomization and Sprays , 2021 , 30 (8 ): 557 - 574
[本文引用: 4]
[29]
LI J, YUAN X, HAN Q Time evolutions of water drops impacting on a rotating disk
[J]. Advanced Materials Research , 2012 , 354-355 : 609 - 614
[本文引用: 2]
[30]
LI J, YUAN X, HAN Q, et al Impact patterns and temporal evolutions of water drops impinging on a rotating disc
[J]. Journal of Mechanical Engineering Science , 2012 , 226 (4 ): 956 - 967
DOI:10.1177/0954406211419604
[本文引用: 1]
[31]
YUAN X, LI J, ZHANG B Effects of surface tension on drop impact on a horizontal rotating disk
[J]. Applied Mechanics and Materials , 2013 , 268-270 : 1084 - 1093
[本文引用: 1]
[32]
MOGHTADERNEJAD S, JADIDI M, JOHNSON Z, et al Droplet impact dynamics on an aluminum spinning disk
[J]. Physics of Fluids , 2021 , 33 (7 ): 072103
DOI:10.1063/5.0050997
[本文引用: 9]
[33]
ALGHOUL S K, EASTWICK C N, HANN D B Normal droplet impact on horizontal moving films: an investigation of impact behaviour and regimes
[J]. Experiments in Fluids , 2011 , 50 (5 ): 1305 - 1316
DOI:10.1007/s00348-010-0991-0
[本文引用: 6]
[34]
GUPTA G, KUMAR P Splashing dynamics of a drop impact onto a deep liquid pool with moving film interface
[J]. Physics of Fluids , 2020 , 32 (1 ): 012102
DOI:10.1063/1.5131637
[本文引用: 3]
[35]
GAO X, LI R Impact of a single drop on a flowing liquid film
[J]. Physical Review , 2015 , 92 (5 ): 053005
[本文引用: 5]
[36]
CHE Z, DEYGAS A, MATAR O K Impact of droplets on inclined flowing liquid films
[J]. Physical Review , 2015 , 92 (2 ): 023032
[本文引用: 7]
[38]
ADEBAYO I T, MATAR O K Droplet impact on flowing liquid films with inlet forcing: the splashing regime
[J]. Soft Matter , 2017 , 13 (41 ): 7473
DOI:10.1039/C7SM01468F
[本文引用: 7]
[41]
RIOBOO R, TROPEA C, MARENGO M Outcomes from a drop impact on solid surfaces
[J]. Atomization and Sprays , 2001 , 11 (2 ): 155 - 165
[本文引用: 3]
[42]
MEHDIZADEH N Z, CHANDRA S, MOSTAGHIMI J Formation of fingers around the edges of a drop hitting a metal plate with high velocity
[J]. Journal of Fluid Mechanics , 2004 , 510 : 353 - 373
DOI:10.1017/S0022112004009310
[本文引用: 1]
[43]
MAO T, KUHND D C S, TRAN H Spread and rebound of liquid droplets upon impact on flat surfaces
[J]. American Institute of Chemical Engineers Journal , 1997 , 43 (9 ): 2169 - 2179
DOI:10.1002/aic.690430903
[本文引用: 1]
[46]
陆军军, 陈雪莉, 曹显奎, 等 液滴撞击平板的铺展特征
[J]. 化学反应工程与工艺 , 2007 , 23 (6 ): 506 - 511
DOI:10.3969/j.issn.1001-7631.2007.06.005
[本文引用: 1]
LU Jun-jun, CHEN Xue-li, CAO Xian-kui, et al Characteristic phenomenon and analysis of a single liquid droplet impacting on dry surfaces
[J]. Chemical Reaction Engineering and Technology , 2007 , 23 (6 ): 506 - 511
DOI:10.3969/j.issn.1001-7631.2007.06.005
[本文引用: 1]
[47]
春江, 王瑾萱, 徐晨, 等 液滴撞击超亲水表面的最大铺展直径预测模型
[J]. 物理学报 , 2021 , 70 (10 ): 106801
DOI:10.7498/aps.70.20201918
[本文引用: 3]
CHUN Jiang, WANG Jin-Xuan, XU Chen, et al Theoretical model of maximum spreading diameter on super hydrophilic surfaces
[J]. Acta Physica Sinica , 2021 , 70 (10 ): 106801
DOI:10.7498/aps.70.20201918
[本文引用: 3]
[48]
WAL R L V, BERGER G M, MOZES S D The splash/non-splash boundary upon a dry surface and thin fluid film
[J]. Experiments in Fluids , 2006 , 40 (1 ): 53 - 59
DOI:10.1007/s00348-005-0045-1
[本文引用: 1]
[49]
PIERZYNA M, BURZYNSKI D A, BANSMER S E, et al Data-driven splashing threshold model for drop impact on dry smooth surfaces
[J]. Physics of Fluids , 2021 , 33 : 123317
DOI:10.1063/5.0076427
[本文引用: 1]
[50]
COSSALI G E, COGHE A, MARENGO M The impact of a single drop on a wetted solid surface
[J]. Experiments in Fluids , 1997 , 22 : 463 - 472
DOI:10.1007/s003480050073
[本文引用: 1]
[51]
RIOBOO R, BAUTHIER C, CONTI J, et al Experimental investigation of splash and crown formation during single drop impact on wetted surfaces
[J]. Experiments in Fluids , 2003 , 35 (6 ): 648 - 652
DOI:10.1007/s00348-003-0719-5
[本文引用: 1]
[53]
OKAWA T, KUBO K, KAWAI K, et al Experiments on splashing thresholds during single-drop impact onto a quiescent liquid film
[J]. Experimental Thermal and Fluid Science , 2021 , 121 : 110279
DOI:10.1016/j.expthermflusci.2020.110279
[本文引用: 1]
[54]
孙志成, 董昊, 赵世文, 等 液滴撞击移动表面动力学特性
[J]. 工程热物理学报 , 2020 , 41 (5 ): 1216 - 1218
[本文引用: 4]
SUN Zhi-cheng, DONG Hao, ZHAO Shi-wen, et al Dynamic behavior of droplet impacting on moving surface
[J]. Journal of Engineering Thermophysics , 2020 , 41 (5 ): 1216 - 1218
[本文引用: 4]
[55]
POVAROV O A, NAZAROV O I, IGNATEVSKAYA L A, et al Interaction of drops with boundary layer on rotating surface
[J]. Journal of Engineering Physics , 1976 , 31 (6 ): 1453 - 1456
DOI:10.1007/BF00860580
[本文引用: 2]
[56]
COURBIN L, BIRD J C, STONE H A Splash and anti-splash: observation and design
[J]. Chaos , 2006 , 16 (4 ): 041102
DOI:10.1063/1.2390551
[57]
孙志成. 液滴撞击移动常温和冷表面动力学特性研究[D]. 南京: 南京师范大学, 2019: 23-57.
[本文引用: 4]
SUN Zhi-cheng. Research on the dynamics of droplets impacting on the room-temperature surfaces and cold surfaces [D]. Nanjing: NanJing Normal University, 2019: 23-57.
[本文引用: 4]
Regimes of droplet train impact on a moving surface in an additive manufacturing process
1
2010
... 在液滴连续撞击移动表面的过程中,表面速度越高、液滴连续撞击频率越低,则液膜在表面的覆盖沉积越平滑[58 ] . 当需要较高的表面移动速度时,较低的频率和较高的冲击能量可以减小波动的生成,从而实现较为平滑的表面液膜覆盖[59 ] ,而铝液滴等高导热系数的液滴,则会发生逐层凝固. 液滴的凝固、铺展和回缩的耦合作用使得凝固液滴表面出现一系列“L”形隆起[60 ] . ...
1
... 在液滴连续撞击移动表面的过程中,表面速度越高、液滴连续撞击频率越低,则液膜在表面的覆盖沉积越平滑[58 ] . 当需要较高的表面移动速度时,较低的频率和较高的冲击能量可以减小波动的生成,从而实现较为平滑的表面液膜覆盖[59 ] ,而铝液滴等高导热系数的液滴,则会发生逐层凝固. 液滴的凝固、铺展和回缩的耦合作用使得凝固液滴表面出现一系列“L”形隆起[60 ] . ...
3D numerical simulation of successive deposition of uniform molten Al droplets on a moving substrate and experimental validation
1
2012
... 在液滴连续撞击移动表面的过程中,表面速度越高、液滴连续撞击频率越低,则液膜在表面的覆盖沉积越平滑[58 ] . 当需要较高的表面移动速度时,较低的频率和较高的冲击能量可以减小波动的生成,从而实现较为平滑的表面液膜覆盖[59 ] ,而铝液滴等高导热系数的液滴,则会发生逐层凝固. 液滴的凝固、铺展和回缩的耦合作用使得凝固液滴表面出现一系列“L”形隆起[60 ] . ...
3
... 旋转固体表面作为移动表面的一种特殊类型,由于其离心效应而存在一些有别于平移表面的特殊现象. 根据液滴撞击位置的不同,可以分为旋转中心撞击和非旋转中心撞击. 液滴在旋转中心撞击后的现象有铺展边缘的毛细脊、液指的发生[61 -62 ] . 液滴在非旋转中心撞击后的典型现象有如图7 所示的“月牙形”的铺展形状、几何不对称的液指拉伸、内侧的波的形成和向外推进等[29 -32 ,63 ] . ...
... 由于引入旋转带来的惯性力,液滴撞击旋转固体表面的物理过程相比于平移固体表面更为复杂. 液滴不对称铺展与惯性力共同作用,产生一些在平移固体表面观察不到的现象,如波的向外推进等. 液滴撞击旋转表面可以分为旋转中心撞击和非旋转中心撞击. 在液滴撞击旋转固体表面中心时,随着液体薄层的扩散,可以观察到边缘不稳定性以及液指的拉伸[61 -62 ] . Sahoo等[61 ] 基于线性稳定性分析得到液指数预测计算式为 ...
... [61 ]基于线性稳定性分析得到液指数预测计算式为 ...
3
... 旋转固体表面作为移动表面的一种特殊类型,由于其离心效应而存在一些有别于平移表面的特殊现象. 根据液滴撞击位置的不同,可以分为旋转中心撞击和非旋转中心撞击. 液滴在旋转中心撞击后的现象有铺展边缘的毛细脊、液指的发生[61 -62 ] . 液滴在非旋转中心撞击后的典型现象有如图7 所示的“月牙形”的铺展形状、几何不对称的液指拉伸、内侧的波的形成和向外推进等[29 -32 ,63 ] . ...
... 由于引入旋转带来的惯性力,液滴撞击旋转固体表面的物理过程相比于平移固体表面更为复杂. 液滴不对称铺展与惯性力共同作用,产生一些在平移固体表面观察不到的现象,如波的向外推进等. 液滴撞击旋转表面可以分为旋转中心撞击和非旋转中心撞击. 在液滴撞击旋转固体表面中心时,随着液体薄层的扩散,可以观察到边缘不稳定性以及液指的拉伸[61 -62 ] . Sahoo等[61 ] 基于线性稳定性分析得到液指数预测计算式为 ...
... [61 ]基于线性稳定性分析得到液指数预测计算式为 ...
Spreading dynamics of superposed liquid drops on a spinning disk
2
2018
... 旋转固体表面作为移动表面的一种特殊类型,由于其离心效应而存在一些有别于平移表面的特殊现象. 根据液滴撞击位置的不同,可以分为旋转中心撞击和非旋转中心撞击. 液滴在旋转中心撞击后的现象有铺展边缘的毛细脊、液指的发生[61 -62 ] . 液滴在非旋转中心撞击后的典型现象有如图7 所示的“月牙形”的铺展形状、几何不对称的液指拉伸、内侧的波的形成和向外推进等[29 -32 ,63 ] . ...
... 由于引入旋转带来的惯性力,液滴撞击旋转固体表面的物理过程相比于平移固体表面更为复杂. 液滴不对称铺展与惯性力共同作用,产生一些在平移固体表面观察不到的现象,如波的向外推进等. 液滴撞击旋转表面可以分为旋转中心撞击和非旋转中心撞击. 在液滴撞击旋转固体表面中心时,随着液体薄层的扩散,可以观察到边缘不稳定性以及液指的拉伸[61 -62 ] . Sahoo等[61 ] 基于线性稳定性分析得到液指数预测计算式为 ...
An experimental study of a water droplet impacting on a rotating wafer
1
2009
... 旋转固体表面作为移动表面的一种特殊类型,由于其离心效应而存在一些有别于平移表面的特殊现象. 根据液滴撞击位置的不同,可以分为旋转中心撞击和非旋转中心撞击. 液滴在旋转中心撞击后的现象有铺展边缘的毛细脊、液指的发生[61 -62 ] . 液滴在非旋转中心撞击后的典型现象有如图7 所示的“月牙形”的铺展形状、几何不对称的液指拉伸、内侧的波的形成和向外推进等[29 -32 ,63 ] . ...
An experimental study of a water droplet impinging on a liquid surface
2
2002
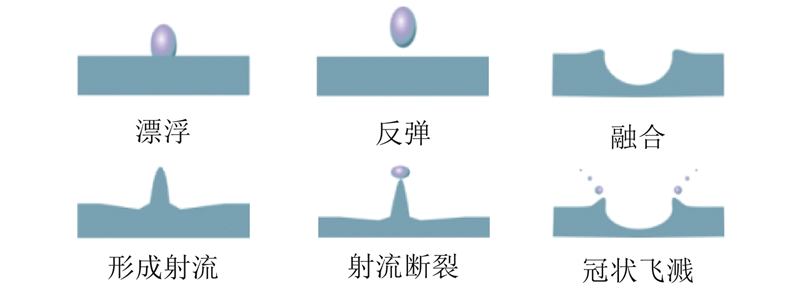
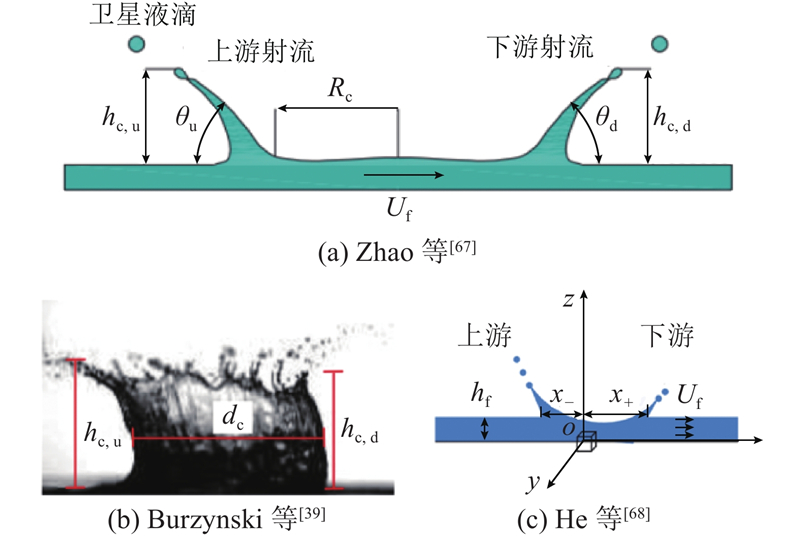
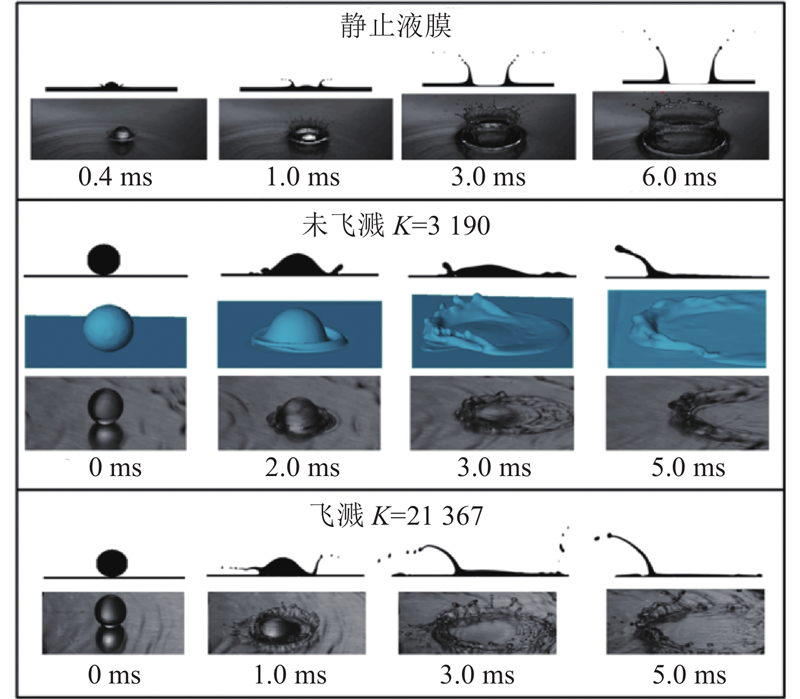
... 液滴撞击静止液膜也是一个常被讨论的物理学过程. 通常来说,液滴撞击液膜的主要现象可以分为悬浮、反弹、飞溅以及融合(如图8 ),其中飞溅又分为冠状飞溅和射流飞溅[33 ,64 -66 ] . ...
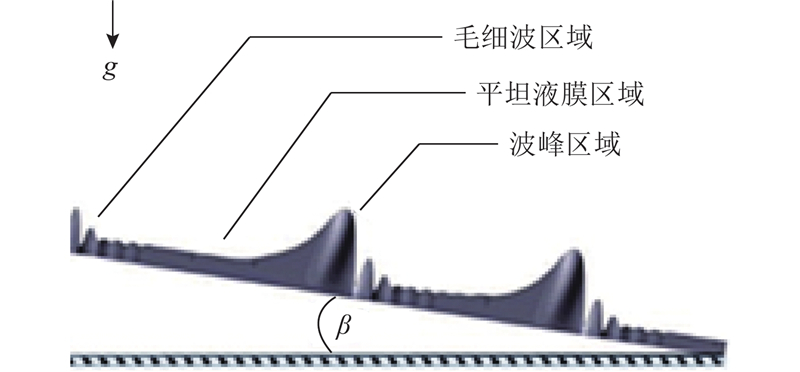
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Phenomena of liquid drop impact on solid and liquid surfaces
0
1993
1
... 液滴撞击静止液膜也是一个常被讨论的物理学过程. 通常来说,液滴撞击液膜的主要现象可以分为悬浮、反弹、飞溅以及融合(如图8 ),其中飞溅又分为冠状飞溅和射流飞溅[33 ,64 -66 ] . ...
Numerical and theoretical study on the spreading characteristics of droplet impact on a horizontal flowing liquid film
3
2021
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
... [67 ]. 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
... 在介观模拟方法中,He等[115 ] 于1999年改进LBM的相场模型. 随后Lee等[116 ] 于2005年提出模拟高密度比不可压缩两相流的格子玻尔兹曼方程的稳定离散化方法,以解决非理想气体格子玻尔兹曼方程引发的数值不稳定性. Raman等[117 ] 应用该方法研究带有液膜的移动壁对双液滴撞击行为的影响. 在较大的液滴间距下,中心射流的形成会延迟;射流高度随着液膜厚度的增加而先增加后减小;壁面运动速度增强上游射流,而抑制了中心射流和下游射流. Liu等[118 ] 基于LBM方法并使用Cahn-Hilliard式[119 ] 捕捉液滴、液膜表面及周围液体,发现控制液膜的厚度可以将液滴撞击飞溅射流的高度控制在一个范围内. He等[67 ] 采用具有可调表面张力项的格子玻尔兹曼方法(pseudopotential lattice Boltzmann method)研究液滴对运动液膜的冲击,发现液膜的运动导致上下游冠的不对称发展,上游和下游冠的不稳定性随着 $ R{e}_{{\boldsymbol{n}}} $ $ W{e}_{{\boldsymbol{n}}} $
Droplet impact on a moving thin film with pseudo potential lattice Boltzmann method
3
2020
... Liang等[110 -111 ] 基于CLSVOF方法建立液滴撞击移动液膜的三维模型,并对单液滴、双液滴先后和同时撞击等情况进行数值模拟. 流动液膜带来的剪切力使界面和热传导的对称性被打破,下游的飞溅被抑制,上游的飞溅被促进. Zhao等[68 ] 则发现液膜厚度的增加导致流入冠壁的液体量以及冠壁与液膜之间的角度增加,此外,非对称冠的迁移距离随着液膜的流动而增大. 液滴在动态液膜上的扩散速度等于上下游扩散速度的平均值,其直径与时间的1/2次成正比. 将实验结果[35 ,112 ] 与模拟结果相对照,如图18 所示,证实模拟的准确性,其中K 值使用Gao等[35 ] 的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
... 液滴撞击流动液膜的三维数值模拟与实验对比[68 ] ...
... Comparison between three-dimensional numerical simulation and experimental of droplet impingement on flowing liquid film[68 ] ...
喷雾冷却换热机理和影响换热性能的因素
1
2011
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
喷雾冷却换热机理和影响换热性能的因素
1
2011
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
Droplet impact onto moving liquids
1
2016
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
1
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
1
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Dynamics and stability of thin liquid films
1
2009
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Solitary wave dynamics of film flows
0
1994
1
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Droplet impact on shear-driven liquid films
1
2011
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Lattice Boltzmann simulation of a drop impact on a moving wall with a liquid film
1
2014
... Cheng等[75 -76 ] 分别模拟液滴倾斜撞击静止液膜和液滴垂直撞击移动表面上的液膜,发现倾斜撞击静止液膜和垂直撞击移动表面上的液膜对液滴飞溅造成一定程度上具有相似性的影响,但是两者无法完全等效. 飞溅区域气体的运动对飞溅液体尖端的形态产生扰动,使得2个系统中液滴冠状飞溅尖端的形态具有区别. 与2.1节中的倾斜和移动固体表面对比类似,不论是固体表面还是液膜,倾斜撞击和移动表面撞击之间都存在着一定的关联,但是也有着一定的差异. ...
A numerical study on splash of oblique drop impact on wet walls
1
2015
... Cheng等[75 -76 ] 分别模拟液滴倾斜撞击静止液膜和液滴垂直撞击移动表面上的液膜,发现倾斜撞击静止液膜和垂直撞击移动表面上的液膜对液滴飞溅造成一定程度上具有相似性的影响,但是两者无法完全等效. 飞溅区域气体的运动对飞溅液体尖端的形态产生扰动,使得2个系统中液滴冠状飞溅尖端的形态具有区别. 与2.1节中的倾斜和移动固体表面对比类似,不论是固体表面还是液膜,倾斜撞击和移动表面撞击之间都存在着一定的关联,但是也有着一定的差异. ...
液滴撞击固体表面过程的实验研究
1
2019
... 在液滴撞击固体表面过程的理论分析中,最常使用的手段是能量法. 其原理是液滴撞击过程中机械能、表面能、粘性耗散三者之和守恒[77 ] . 在静止表面的研究中,研究人员曾利用能量法得到了最大铺展面积等模型[78 -81 ] . ...
液滴撞击固体表面过程的实验研究
1
2019
... 在液滴撞击固体表面过程的理论分析中,最常使用的手段是能量法. 其原理是液滴撞击过程中机械能、表面能、粘性耗散三者之和守恒[77 ] . 在静止表面的研究中,研究人员曾利用能量法得到了最大铺展面积等模型[78 -81 ] . ...
On the collision of a droplet with a solid surface
2
1991
... 在液滴撞击固体表面过程的理论分析中,最常使用的手段是能量法. 其原理是液滴撞击过程中机械能、表面能、粘性耗散三者之和守恒[77 ] . 在静止表面的研究中,研究人员曾利用能量法得到了最大铺展面积等模型[78 -81 ] . ...
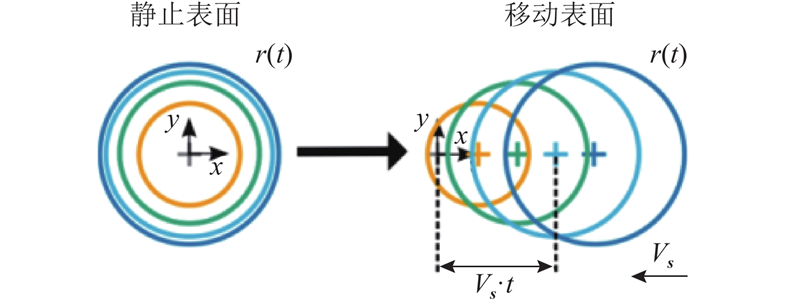
... 为了深入理解液滴在运动表面铺展的机理, Almohammadi等[23 ] 提出一个理论模型,如图11 所示,其中 $ r(t) $ [78 -86 ] . ...
Capillary effects during droplet impact on a solid surface
0
1996
On the maximum spreading diameter of impacting droplets on well-prepared solid surfaces
0
2005
1
... 在液滴撞击固体表面过程的理论分析中,最常使用的手段是能量法. 其原理是液滴撞击过程中机械能、表面能、粘性耗散三者之和守恒[77 ] . 在静止表面的研究中,研究人员曾利用能量法得到了最大铺展面积等模型[78 -81 ] . ...
An energy balance approach of ? the dynamics of drop impact on a solid surface
0
2007
The recoiling of liquid droplets upon collision with solid surfaces
0
2001
Impact of a liquid drop against a flat surface
0
1981
An improved model for droplet solidification on a flat surface
0
1997
Maximal deformation of an impacting drop
1
2004
... 为了深入理解液滴在运动表面铺展的机理, Almohammadi等[23 ] 提出一个理论模型,如图11 所示,其中 $ r(t) $ [78 -86 ] . ...
An experimental investigation of fluid-flow resulting from the impact of a water drop with an unyielding dry surface
1
1981
... 式中: $ K $ $ K=2.5 $ K =5700的情况下,预测结果与实验结果重合较好,可以简化为表面速度为0,即液滴撞击静止表面的模式,并与早期实验[47 ,87 ] 相符. 然而该模型有2个局限性:1)该模型的实验验证仅限于乙醇一种液体,因此无法体现出液体黏度、表面张力等因素对飞溅现象的影响;2)该模型对液滴几何不对称性的描述仅有一个维度,即仅考虑了液滴薄层上游端点和下游端点,而无法描述整个液滴铺展边缘其他位置的飞溅情况. ...
Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing
1
2014
... Xu等[44 ] 提出液滴的飞溅可以通过改变环境气压而抑制后,研究人员发现环境气体在液滴的飞溅过程中也起到作用. Hao等[21 ] 实验研究移动表面环境气压对液滴撞击飞溅产生的影响,通过降低气压可以抑制液滴上游的冠状飞溅,在移动表面上飞溅的临界气压小于静止表面. 根据单位长度液体薄层上升力与表面张力比值超过某阈值产生飞溅这一原理[88 -89 ] ,给出基于升力的液滴撞击移动表面的飞溅阈值模型为 ...
Effect of ambient air on liquid jet impingement on a moving substrate
1
2013
... Xu等[44 ] 提出液滴的飞溅可以通过改变环境气压而抑制后,研究人员发现环境气体在液滴的飞溅过程中也起到作用. Hao等[21 ] 实验研究移动表面环境气压对液滴撞击飞溅产生的影响,通过降低气压可以抑制液滴上游的冠状飞溅,在移动表面上飞溅的临界气压小于静止表面. 根据单位长度液体薄层上升力与表面张力比值超过某阈值产生飞溅这一原理[88 -89 ] ,给出基于升力的液滴撞击移动表面的飞溅阈值模型为 ...
1
... 詹海洋[90 ] 提出液滴在撞击超疏水表面反弹的过程中存在滑移,而滑移受到表面剪切力与升力的共同作用,他提出滑移距离 $ d $
1
... 詹海洋[90 ] 提出液滴在撞击超疏水表面反弹的过程中存在滑移,而滑移受到表面剪切力与升力的共同作用,他提出滑移距离 $ d $
Maximum spreading of droplets impacting spherical surfaces
1
2019
... 式中: $ {K}_{\boldsymbol{s}} $ $ {K}_{\mathrm{L}} $ [24 ] 的研究中被观察到. 基于在静止表面的模型[91 -92 ] ,Zhang等[24 ] 提出撞击移动超疏水表面的时间 $ {t}_{\mathrm{M}} $ $ {t}_{\boldsymbol{S}} $
Retraction dynamics of aqueous drops upon impact on non-wetting surfaces
1
2005
... 式中: $ {K}_{\boldsymbol{s}} $ $ {K}_{\mathrm{L}} $ [24 ] 的研究中被观察到. 基于在静止表面的模型[91 -92 ] ,Zhang等[24 ] 提出撞击移动超疏水表面的时间 $ {t}_{\mathrm{M}} $ $ {t}_{\boldsymbol{S}} $
Impact of a drop onto a wetted wall: description of crown formation and propagation
1
2002
... 关于液滴的冠状飞溅,在Roisman等[93 ] 的理论中,如果撞击流动液膜的液滴在变形阶段仍保持圆形,则在扩展阶段冠状的底部可以近似为一个生长的圆,随着液膜流向下游移动. Gao等[35 ] 发现上述理论在实验中有所偏差,提出当 $ H\times U\ll 1 $
Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity
1
1995
... 冠状飞溅的过程与液滴的速度、尺寸以及液膜流速有关[38 ] . Yarin等[94 ] 通过拟合实验数据得到了一个冠状水花发展的经验计算式: ...
分子动力学模拟基本原理和主要技术
2
2005
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
... 在微观尺度模拟中,Fang等[99 ] 在MD模拟中使用LJ势(Lennard–Jones potential)讨论了不同的温度、平面运动速度和射流角度下纳米液滴对移动表面的撞击. LJ势是经典的连续对势,认为原子之间的相互作用是两两之间的作用[95 ] . 当温度上升时,液体的铺展宽度会变大,液体的平均能量上升且能量波现象出现,平板上液体原子的接触角减小;随着平板速度的上升,表面液膜的厚度下降,平板运动方向前部的接触角更大. ...
分子动力学模拟基本原理和主要技术
2
2005
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
... 在微观尺度模拟中,Fang等[99 ] 在MD模拟中使用LJ势(Lennard–Jones potential)讨论了不同的温度、平面运动速度和射流角度下纳米液滴对移动表面的撞击. LJ势是经典的连续对势,认为原子之间的相互作用是两两之间的作用[95 ] . 当温度上升时,液体的铺展宽度会变大,液体的平均能量上升且能量波现象出现,平板上液体原子的接触角减小;随着平板速度的上升,表面液膜的厚度下降,平板运动方向前部的接触角更大. ...
2
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
... [96 ]. 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
2
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
... [96 ]. 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
Analysis of liquid sheet and jet flow mechanism after droplet impinging onto liquid film
1
2013
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
液氮滴撞击壁面相变行为的数值研究
1
2019
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
液氮滴撞击壁面相变行为的数值研究
1
2019
... 液滴撞击移动及旋转表面的数值模拟计算按模拟尺度可以分为微观尺度模拟、介观尺度模拟和宏观尺度模拟. 微观尺度模拟通常使用分子动力学模拟(molecule dynamics, MD). MD模拟结果准确与否的关键在于对系统内的原子之间相互作用势函数的选取[95 ] ,主要适用于纳米级别微小液滴的场景,若计算场景内分子数量过大,则会严重影响计算效率. 介观尺度模拟多使用格子玻尔兹曼方法(lattice Boltzmann method, LBM)[67 ] ,其模拟粒子的尺度比分子尺度大的多[96 ] ,可以模拟更大尺度的场景仍具有不俗的计算效率. 当前的LBM方法在高雷诺数的多相流模拟和高液气密度比的模拟中的数值稳定性存在挑战,且该方法不适合稳态计算[67 ] . 宏观尺度模拟多适用界面追踪法包括流体体积法(volume of fluid, VOF)和Level-Set方法,可以模拟宏观尺度下的液滴撞击场景. 以上两者都是流体界面的追踪方法相对容易实施,但是准确性受到对流方程解的数值耗散的限制[96 ] . 由于VOF方法和Level-Set方法各有优缺点,耦合2种方法的模拟方法也开始出现. 针对液滴撞击液膜的数值模拟中常用的耦合方法为耦合水平集流体体积法 (coupled level set and volume of fluid, CLSVOF)方法,该方法可以跟踪不可压缩两相流的相界面,有效地解决了VOF的计算收敛性、稳定性和准确性问题[97 -98 ] . ...
Effects of temperature and velocity of droplet ejection process of simulated nanojets onto a moving plate’s surface
1
2006
... 在微观尺度模拟中,Fang等[99 ] 在MD模拟中使用LJ势(Lennard–Jones potential)讨论了不同的温度、平面运动速度和射流角度下纳米液滴对移动表面的撞击. LJ势是经典的连续对势,认为原子之间的相互作用是两两之间的作用[95 ] . 当温度上升时,液体的铺展宽度会变大,液体的平均能量上升且能量波现象出现,平板上液体原子的接触角减小;随着平板速度的上升,表面液膜的厚度下降,平板运动方向前部的接触角更大. ...
A general purpose model for the condensed phases of water: TIP4P/2005
1
2005
... 2005年Abascal等[100 ] 提出一种潜在的水凝聚相通用模型即TIP4P/2005模型,该模型可以更针对性地描述水分子,并可以表现冰的微观组成. Ritos等[101 -102 ] 应用TIP4P/2005模型,设定硅、石墨和一种假想的超疏水材料进行液滴撞击的MD模拟. 硅表面上的模拟结果表明,接触线上的分子位移受固体表面相互作用的影响很大,部分受表面运动引起的黏性耗散效应的影响;对于石墨表面,前进角和后退角与静止接触角接近,黏性耗散效应可以忽略不计. 与宏观水滴润湿动力学相反,纳米尺度水滴撞击过程中具有较大影响的是固液间作用,而黏性作用反而只起到次要影响,接触角几乎不受毛细数影响. ...
Dynamics of nanoscale droplets on moving surfaces
1
2013
... 2005年Abascal等[100 ] 提出一种潜在的水凝聚相通用模型即TIP4P/2005模型,该模型可以更针对性地描述水分子,并可以表现冰的微观组成. Ritos等[101 -102 ] 应用TIP4P/2005模型,设定硅、石墨和一种假想的超疏水材料进行液滴撞击的MD模拟. 硅表面上的模拟结果表明,接触线上的分子位移受固体表面相互作用的影响很大,部分受表面运动引起的黏性耗散效应的影响;对于石墨表面,前进角和后退角与静止接触角接近,黏性耗散效应可以忽略不计. 与宏观水滴润湿动力学相反,纳米尺度水滴撞击过程中具有较大影响的是固液间作用,而黏性作用反而只起到次要影响,接触角几乎不受毛细数影响. ...
1
... 2005年Abascal等[100 ] 提出一种潜在的水凝聚相通用模型即TIP4P/2005模型,该模型可以更针对性地描述水分子,并可以表现冰的微观组成. Ritos等[101 -102 ] 应用TIP4P/2005模型,设定硅、石墨和一种假想的超疏水材料进行液滴撞击的MD模拟. 硅表面上的模拟结果表明,接触线上的分子位移受固体表面相互作用的影响很大,部分受表面运动引起的黏性耗散效应的影响;对于石墨表面,前进角和后退角与静止接触角接近,黏性耗散效应可以忽略不计. 与宏观水滴润湿动力学相反,纳米尺度水滴撞击过程中具有较大影响的是固液间作用,而黏性作用反而只起到次要影响,接触角几乎不受毛细数影响. ...
, FARMER B L, et al. Accurate simulation of surfaces and interfaces of face-centered cubic metals using 12-6 and 9-6 Lennard-Jones potentials
1
2008
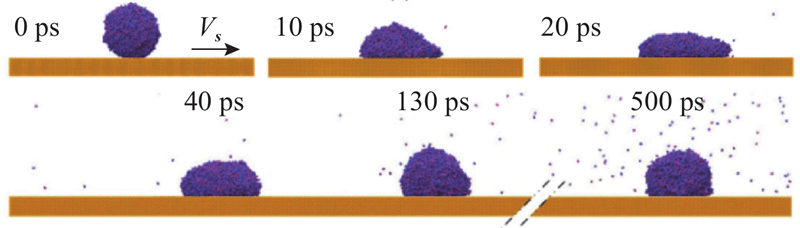
... Heinz等[103 ] 表明与嵌入原子模型(embedded atom model, EAM)和密度泛函方法相比,12-6 LJ势更加适用于大型模拟系统(106 个原子), 并证明了此势在铜上的可靠性. 图16 为Zhang等[104 ] 应用12-6LJ势模拟纳米液滴撞击平移铜表面. ...
Molecular dynamics simulation on behaviors of water nanodroplets impinging on moving surfaces
3
2022
... Heinz等[103 ] 表明与嵌入原子模型(embedded atom model, EAM)和密度泛函方法相比,12-6 LJ势更加适用于大型模拟系统(106 个原子), 并证明了此势在铜上的可靠性. 图16 为Zhang等[104 ] 应用12-6LJ势模拟纳米液滴撞击平移铜表面. ...
... 分子动力学模拟液滴撞击移动固体表面[104 ] ...
... Molecular dynamics simulation of droplet impact on moving solid surface [104 ] ...
Numerical study on impacting-freezing process of the droplet on a lateral moving cold super hydrophobic surface
3
2022
... 在宏观尺度模拟中,Hou等[105 ] 通过VOF方法获得气液界面,并利用ANSYS框架下的凝固/融化算法对过冷液滴撞击冷表面的凝固过程进行模拟. 该方法设定为过冷液滴接触冷表面的瞬间转化固液混合物,过冷度由调节混合物的参数表达[106 -107 ] . 对横向移动表面上液滴的形态演变进行模拟,在与Zhang等[24 ] 实验相似的条件下,得到了相似的结果. 图17 为对液滴撞击移动冷表面的碰撞—结冰过程进行的三维数值模拟,结果表明:液滴的初始冻结位置优先出现在液滴的上游侧,液滴下游一侧的冻结滞后于上游一侧,且滞后效应受到冷表面温度的强烈影响,同样的冻结滞后现象也在孙志成[57 ] 液滴撞击移动冷表面的实验中出现. ...
... VOF方法模拟液滴撞击移动固体表面的模型和初始条件[105 ] ...
... Model and initial conditions for simulating droplet impact on moving solid surface by VOF method[105 ] ...
Modelling the impact, spreading and freezing of a water droplet on horizontal and inclined super hydrophobic cooled surfaces
1
2017
... 在宏观尺度模拟中,Hou等[105 ] 通过VOF方法获得气液界面,并利用ANSYS框架下的凝固/融化算法对过冷液滴撞击冷表面的凝固过程进行模拟. 该方法设定为过冷液滴接触冷表面的瞬间转化固液混合物,过冷度由调节混合物的参数表达[106 -107 ] . 对横向移动表面上液滴的形态演变进行模拟,在与Zhang等[24 ] 实验相似的条件下,得到了相似的结果. 图17 为对液滴撞击移动冷表面的碰撞—结冰过程进行的三维数值模拟,结果表明:液滴的初始冻结位置优先出现在液滴的上游侧,液滴下游一侧的冻结滞后于上游一侧,且滞后效应受到冷表面温度的强烈影响,同样的冻结滞后现象也在孙志成[57 ] 液滴撞击移动冷表面的实验中出现. ...
Impacting-freezing dynamics of a supercooled water droplet on a cold surface: rebound and adhesion
1
2020
... 在宏观尺度模拟中,Hou等[105 ] 通过VOF方法获得气液界面,并利用ANSYS框架下的凝固/融化算法对过冷液滴撞击冷表面的凝固过程进行模拟. 该方法设定为过冷液滴接触冷表面的瞬间转化固液混合物,过冷度由调节混合物的参数表达[106 -107 ] . 对横向移动表面上液滴的形态演变进行模拟,在与Zhang等[24 ] 实验相似的条件下,得到了相似的结果. 图17 为对液滴撞击移动冷表面的碰撞—结冰过程进行的三维数值模拟,结果表明:液滴的初始冻结位置优先出现在液滴的上游侧,液滴下游一侧的冻结滞后于上游一侧,且滞后效应受到冷表面温度的强烈影响,同样的冻结滞后现象也在孙志成[57 ] 液滴撞击移动冷表面的实验中出现. ...
Normal and oblique droplet impingement dynamics on moving dry walls
2
2019
... Raman等[108 ] 则基于相位场不可压缩格子玻尔兹曼方法进行模拟,该模型使用2个粒子分布函数来表达不可压缩Navier-Stokes方程和宏观界面捕获相场方程,该模型分别包含应力和势形式的动量方程分子间作用力项以及序参量的相场模型[108 ] . 模拟发现液滴在回缩状态尾端会出现尾状结构,该特点在Zhan等[109 ] 的液滴撞击移动超疏水表面实验中也可以被观察到. Raman的数值模拟进一步揭示移动超疏水壁传递的动量会导致气流从中心区域转向下游方向,从而在液滴撞击后的扩散和收缩阶段导致对称性破坏的规律. ...
... [108 ]. 模拟发现液滴在回缩状态尾端会出现尾状结构,该特点在Zhan等[109 ] 的液滴撞击移动超疏水表面实验中也可以被观察到. Raman的数值模拟进一步揭示移动超疏水壁传递的动量会导致气流从中心区域转向下游方向,从而在液滴撞击后的扩散和收缩阶段导致对称性破坏的规律. ...
Horizontal motion of a super hydrophobic substrate affects the drop bouncing dynamics
1
2021
... Raman等[108 ] 则基于相位场不可压缩格子玻尔兹曼方法进行模拟,该模型使用2个粒子分布函数来表达不可压缩Navier-Stokes方程和宏观界面捕获相场方程,该模型分别包含应力和势形式的动量方程分子间作用力项以及序参量的相场模型[108 ] . 模拟发现液滴在回缩状态尾端会出现尾状结构,该特点在Zhan等[109 ] 的液滴撞击移动超疏水表面实验中也可以被观察到. Raman的数值模拟进一步揭示移动超疏水壁传递的动量会导致气流从中心区域转向下游方向,从而在液滴撞击后的扩散和收缩阶段导致对称性破坏的规律. ...
Parametric Effects on interface evolution and heat transfer in droplet impact on flowing liquid film
1
2020
... Liang等[110 -111 ] 基于CLSVOF方法建立液滴撞击移动液膜的三维模型,并对单液滴、双液滴先后和同时撞击等情况进行数值模拟. 流动液膜带来的剪切力使界面和热传导的对称性被打破,下游的飞溅被抑制,上游的飞溅被促进. Zhao等[68 ] 则发现液膜厚度的增加导致流入冠壁的液体量以及冠壁与液膜之间的角度增加,此外,非对称冠的迁移距离随着液膜的流动而增大. 液滴在动态液膜上的扩散速度等于上下游扩散速度的平均值,其直径与时间的1/2次成正比. 将实验结果[35 ,112 ] 与模拟结果相对照,如图18 所示,证实模拟的准确性,其中K 值使用Gao等[35 ] 的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
Interfacial phenomena and heat transfer associated with multi-droplet impact on flowing liquid film
1
2020
... Liang等[110 -111 ] 基于CLSVOF方法建立液滴撞击移动液膜的三维模型,并对单液滴、双液滴先后和同时撞击等情况进行数值模拟. 流动液膜带来的剪切力使界面和热传导的对称性被打破,下游的飞溅被抑制,上游的飞溅被促进. Zhao等[68 ] 则发现液膜厚度的增加导致流入冠壁的液体量以及冠壁与液膜之间的角度增加,此外,非对称冠的迁移距离随着液膜的流动而增大. 液滴在动态液膜上的扩散速度等于上下游扩散速度的平均值,其直径与时间的1/2次成正比. 将实验结果[35 ,112 ] 与模拟结果相对照,如图18 所示,证实模拟的准确性,其中K 值使用Gao等[35 ] 的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
Characteristics of secondary droplets produced by a single drop impacting on a static liquid film
1
2019
... Liang等[110 -111 ] 基于CLSVOF方法建立液滴撞击移动液膜的三维模型,并对单液滴、双液滴先后和同时撞击等情况进行数值模拟. 流动液膜带来的剪切力使界面和热传导的对称性被打破,下游的飞溅被抑制,上游的飞溅被促进. Zhao等[68 ] 则发现液膜厚度的增加导致流入冠壁的液体量以及冠壁与液膜之间的角度增加,此外,非对称冠的迁移距离随着液膜的流动而增大. 液滴在动态液膜上的扩散速度等于上下游扩散速度的平均值,其直径与时间的1/2次成正比. 将实验结果[35 ,112 ] 与模拟结果相对照,如图18 所示,证实模拟的准确性,其中K 值使用Gao等[35 ] 的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
Asymmetric heat transfer characteristics of a double droplet impact on a moving liquid film
1
2018
... Liang等[110 -111 ] 基于CLSVOF方法建立液滴撞击移动液膜的三维模型,并对单液滴、双液滴先后和同时撞击等情况进行数值模拟. 流动液膜带来的剪切力使界面和热传导的对称性被打破,下游的飞溅被抑制,上游的飞溅被促进. Zhao等[68 ] 则发现液膜厚度的增加导致流入冠壁的液体量以及冠壁与液膜之间的角度增加,此外,非对称冠的迁移距离随着液膜的流动而增大. 液滴在动态液膜上的扩散速度等于上下游扩散速度的平均值,其直径与时间的1/2次成正比. 将实验结果[35 ,112 ] 与模拟结果相对照,如图18 所示,证实模拟的准确性,其中K 值使用Gao等[35 ] 的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
Numerical study of three-dimensional droplet impact on a flowing liquid film in annular two-phase flow
1
2017
... Xie等[114 ] 采用自适应非结构网格的控制体积有限元方法(novel control volume finite element method)研究环形两相流中的三维液滴沉积过程. 该数值框架包括用于界面捕捉的VOF方法和用于自适应非结构网格上表面张力的力平衡连续介质表面力模型. ...
A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh Taylor instability
1
1999
... 在介观模拟方法中,He等[115 ] 于1999年改进LBM的相场模型. 随后Lee等[116 ] 于2005年提出模拟高密度比不可压缩两相流的格子玻尔兹曼方程的稳定离散化方法,以解决非理想气体格子玻尔兹曼方程引发的数值不稳定性. Raman等[117 ] 应用该方法研究带有液膜的移动壁对双液滴撞击行为的影响. 在较大的液滴间距下,中心射流的形成会延迟;射流高度随着液膜厚度的增加而先增加后减小;壁面运动速度增强上游射流,而抑制了中心射流和下游射流. Liu等[118 ] 基于LBM方法并使用Cahn-Hilliard式[119 ] 捕捉液滴、液膜表面及周围液体,发现控制液膜的厚度可以将液滴撞击飞溅射流的高度控制在一个范围内. He等[67 ] 采用具有可调表面张力项的格子玻尔兹曼方法(pseudopotential lattice Boltzmann method)研究液滴对运动液膜的冲击,发现液膜的运动导致上下游冠的不对称发展,上游和下游冠的不稳定性随着 $ R{e}_{{\boldsymbol{n}}} $ $ W{e}_{{\boldsymbol{n}}} $
A stable discretization of the lattice Boltzmann equation for simulation of incompressible two-phase flows at high density ratio
1
2005
... 在介观模拟方法中,He等[115 ] 于1999年改进LBM的相场模型. 随后Lee等[116 ] 于2005年提出模拟高密度比不可压缩两相流的格子玻尔兹曼方程的稳定离散化方法,以解决非理想气体格子玻尔兹曼方程引发的数值不稳定性. Raman等[117 ] 应用该方法研究带有液膜的移动壁对双液滴撞击行为的影响. 在较大的液滴间距下,中心射流的形成会延迟;射流高度随着液膜厚度的增加而先增加后减小;壁面运动速度增强上游射流,而抑制了中心射流和下游射流. Liu等[118 ] 基于LBM方法并使用Cahn-Hilliard式[119 ] 捕捉液滴、液膜表面及周围液体,发现控制液膜的厚度可以将液滴撞击飞溅射流的高度控制在一个范围内. He等[67 ] 采用具有可调表面张力项的格子玻尔兹曼方法(pseudopotential lattice Boltzmann method)研究液滴对运动液膜的冲击,发现液膜的运动导致上下游冠的不对称发展,上游和下游冠的不稳定性随着 $ R{e}_{{\boldsymbol{n}}} $ $ W{e}_{{\boldsymbol{n}}} $
On the dynamics of crown structure in simultaneous two droplets impact onto stationary and moving liquid film
1
2015
... 在介观模拟方法中,He等[115 ] 于1999年改进LBM的相场模型. 随后Lee等[116 ] 于2005年提出模拟高密度比不可压缩两相流的格子玻尔兹曼方程的稳定离散化方法,以解决非理想气体格子玻尔兹曼方程引发的数值不稳定性. Raman等[117 ] 应用该方法研究带有液膜的移动壁对双液滴撞击行为的影响. 在较大的液滴间距下,中心射流的形成会延迟;射流高度随着液膜厚度的增加而先增加后减小;壁面运动速度增强上游射流,而抑制了中心射流和下游射流. Liu等[118 ] 基于LBM方法并使用Cahn-Hilliard式[119 ] 捕捉液滴、液膜表面及周围液体,发现控制液膜的厚度可以将液滴撞击飞溅射流的高度控制在一个范围内. He等[67 ] 采用具有可调表面张力项的格子玻尔兹曼方法(pseudopotential lattice Boltzmann method)研究液滴对运动液膜的冲击,发现液膜的运动导致上下游冠的不对称发展,上游和下游冠的不稳定性随着 $ R{e}_{{\boldsymbol{n}}} $ $ W{e}_{{\boldsymbol{n}}} $
Investigation of a single droplet impact onto a liquid film with given horizontal velocity
1
2018
... 在介观模拟方法中,He等[115 ] 于1999年改进LBM的相场模型. 随后Lee等[116 ] 于2005年提出模拟高密度比不可压缩两相流的格子玻尔兹曼方程的稳定离散化方法,以解决非理想气体格子玻尔兹曼方程引发的数值不稳定性. Raman等[117 ] 应用该方法研究带有液膜的移动壁对双液滴撞击行为的影响. 在较大的液滴间距下,中心射流的形成会延迟;射流高度随着液膜厚度的增加而先增加后减小;壁面运动速度增强上游射流,而抑制了中心射流和下游射流. Liu等[118 ] 基于LBM方法并使用Cahn-Hilliard式[119 ] 捕捉液滴、液膜表面及周围液体,发现控制液膜的厚度可以将液滴撞击飞溅射流的高度控制在一个范围内. He等[67 ] 采用具有可调表面张力项的格子玻尔兹曼方法(pseudopotential lattice Boltzmann method)研究液滴对运动液膜的冲击,发现液膜的运动导致上下游冠的不对称发展,上游和下游冠的不稳定性随着 $ R{e}_{{\boldsymbol{n}}} $ $ W{e}_{{\boldsymbol{n}}} $
Diffuse Interface model for incompressible two phase flows with large density ratios
1
2007
... 在介观模拟方法中,He等[115 ] 于1999年改进LBM的相场模型. 随后Lee等[116 ] 于2005年提出模拟高密度比不可压缩两相流的格子玻尔兹曼方程的稳定离散化方法,以解决非理想气体格子玻尔兹曼方程引发的数值不稳定性. Raman等[117 ] 应用该方法研究带有液膜的移动壁对双液滴撞击行为的影响. 在较大的液滴间距下,中心射流的形成会延迟;射流高度随着液膜厚度的增加而先增加后减小;壁面运动速度增强上游射流,而抑制了中心射流和下游射流. Liu等[118 ] 基于LBM方法并使用Cahn-Hilliard式[119 ] 捕捉液滴、液膜表面及周围液体,发现控制液膜的厚度可以将液滴撞击飞溅射流的高度控制在一个范围内. He等[67 ] 采用具有可调表面张力项的格子玻尔兹曼方法(pseudopotential lattice Boltzmann method)研究液滴对运动液膜的冲击,发现液膜的运动导致上下游冠的不对称发展,上游和下游冠的不稳定性随着 $ R{e}_{{\boldsymbol{n}}} $ $ W{e}_{{\boldsymbol{n}}} $
1
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
液滴高速撞击固体板面过程的研究
1
2008
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
液滴高速撞击固体板面过程的研究
1
2008
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
Predicting droplet impingement on yawed wings
1
2015
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
Droplet impaction on a supersonic wedge- consideration of similitude
1
1990
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
旋转帽罩结冰相似准则的研究
1
2015
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
旋转帽罩结冰相似准则的研究
1
2015
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
绕轴旋转圆柱结冰特性结冰风洞试验
1
2017
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
绕轴旋转圆柱结冰特性结冰风洞试验
1
2017
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
利用自然低温的旋转叶片结冰风洞试验系统设计
0
2018
利用自然低温的旋转叶片结冰风洞试验系统设计
0
2018
绕轴旋转翼型结冰分布的结冰风洞试验研究
1
2017
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
绕轴旋转翼型结冰分布的结冰风洞试验研究
1
2017
... 液滴撞击表面现象广泛存在于人类日常生产生活中. 人们对液滴撞击有不同的要求,例如喷涂打印、喷雾冷却、农药喷洒等场景中需要液滴尽可能均匀附着在目标位置,而在风力发电机叶片结冰、飞机防除冰等场景中需要尽量减少液滴附着在表面. 液滴撞击现象的深入理解有助于优化相关工程技术,解决对应的工程问题. 随着高热流密度设备的广泛运用,传统散热方式无法满足散热需求,液滴喷雾冷却技术则可以更好地解决问题[1 ] ;喷涂打印技术可以实现数字化的零件生产[2 ] ;农药喷洒技术要求液滴需要均匀地铺展[3 ] . 许多危害现象也与液滴撞击表面的过程有关,如飞行过程中云中的水滴对飞机表面冲击附着带来的表面结冰等现象会对飞机飞行造成影响[4 -5 ] . 当水滴撞击并附着在旋转帽罩时,由于离心力以及振动对冰的影响,结出的冰可能会脱落并打坏发动机[6 ] . 旋转叶片受水滴撞击结冰后也会破坏叶片的气动特性及载荷分布,轻则降低叶片的工作效率,重则引发安全事故[7 -9 ] . ...
On the forms assumed by drops of liquids falling vertically on a horizontal plate
1
1876
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
A second paper on the forms assumed by drops of liquids falling vertically on a horizontal plate
1
1877
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
水滴撞击固体表面实验研究
1
2009
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
水滴撞击固体表面实验研究
1
2009
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
Waterdrop collisions with solid surfaces
2
1955
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
单个液滴碰击表面时的流体动力学特性
1
1985
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
单个液滴碰击表面时的流体动力学特性
1
1985
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
Analysis of impact of droplets on horizontal surfaces
1
2002
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
Phenomena of droplet-surface interactions
0
2006
Impact of droplet onto inclined surface
0
2005
Dynamic wetting angle of a spreading droplet
1
2005
... 在1876年Worthington[10 -11 ] 实验研究液滴撞击壁面及液膜的现象. 早期的研究往往选择黏度较大的液体以增加现象持续的时间[12 ] . 随着高速摄影技术的发展,研究人员对液滴撞击现象进行更深入的研究. 在1955年Engel[13 ] 使用化学方法和高速摄像机追踪撞击面内液体的流动研究液滴的铺展. 在1985年施明恒[14 ] 建立适用于润湿和非润湿接触2种情况的铺展模型. Sikalo等[15 -18 ] 于2005年进行一系列研究发现液滴撞击表面的现象受到液滴尺寸、撞击角度、速度、黏度、表面张力、壁面粗糙度等变量的影响. 在液滴撞击表面的研究中,关于静止表面(包括固体表面和液膜)的研究已经十分深入. 针对移动表面的研究仍在逐步开展,虽然目前已经有了一些优秀的研究成果,但是仍未系统、完善地建立相关的机理分析和模型体系. ...
Understanding the drop impact on moving hydrophilic and hydrophobic surfaces
5
2017
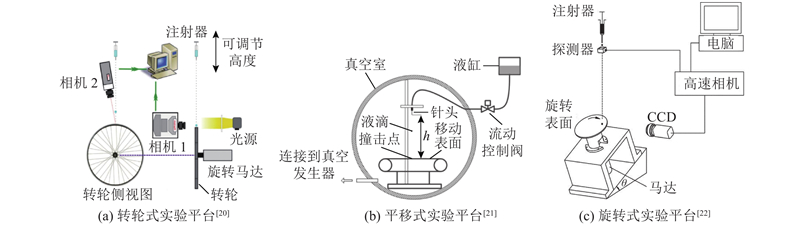
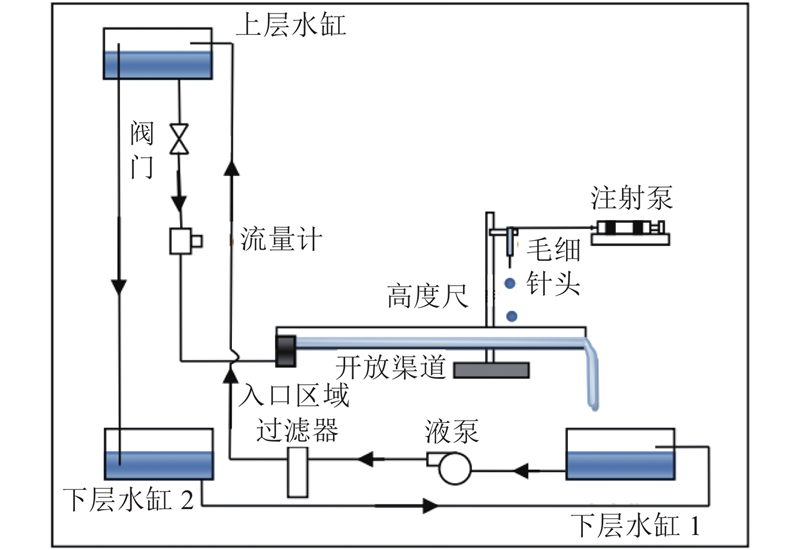
... 研究人员对液滴撞击移动固体表面设计了多种实验,常见的实验可以分为4个系统:液滴发生系统、移动表面系统、图像捕捉系统和后处理系统. 液滴发生系统用于产生液滴,控制液滴各项参数,通常使用毛细管针头产生液滴;移动表面系统用于设置移动的固体表面,控制表面各项参数;图像捕捉系统一般为高速相机,用于捕捉实验现象;后处理系统负责数据处理. 其中运动表面系统是最重要的系统之一,也体现了几种常见的设计思路,常见的运动表面平台结构可以分为3大类. 如图1 所示,分别为转轮式运动表面、平移式运动表面和旋转平台表面. 由于平移式表面实现难度往往较大,大部分实验设计者都选择转轮式和旋转平台式运动表面模拟平移平面. 在使用转轮式运动表面模拟平移平面时,通常需要保证实验景深内表面与水平面间的偏移低至可以忽略[19 ] ,否则实验表面被视为曲面将影响实验结果. ...
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
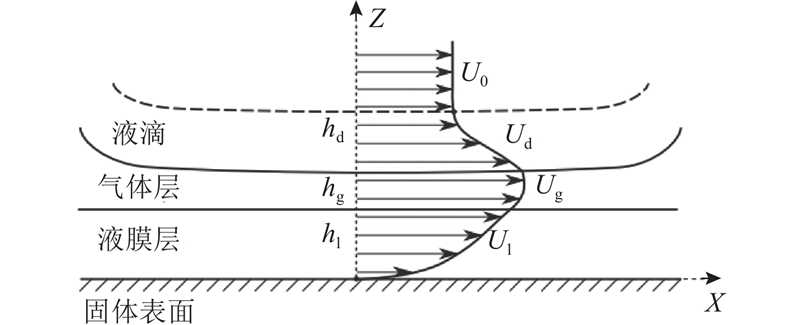
... 为了解决上述局限,Almohammadi等[19 ] 以不同比例的水和甘油的混合物进行实验,在疏水表面液体薄层脱离表面的部分多于亲水表面,且提高液体的黏性会降低飞溅阈值. 如果设定一个如图13 所示的位置角 $ \phi $ $ \phi =0° $ $ \phi =180° $
... 液体薄层边缘位置角 $ \mathit{\phi } $ [19 ] ...
... Position angle of the liquid lammella edge $ \mathit{\phi } $ [19 ] ...
Spreading of low-viscous liquids on a stationary and a moving surface
4
2019
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... Buksh等[20 ] 为了使该模型可以覆盖高张力和低张力的液体,提出改进的模型为 ...
... 椭圆形铺展模型在不同表面运动速度下的表现[20 ] ...
... Effects of elliptical spreading model under different surface velocities [20 ] ...
Splash threshold of a droplet impacting a moving substrate
3
2017
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
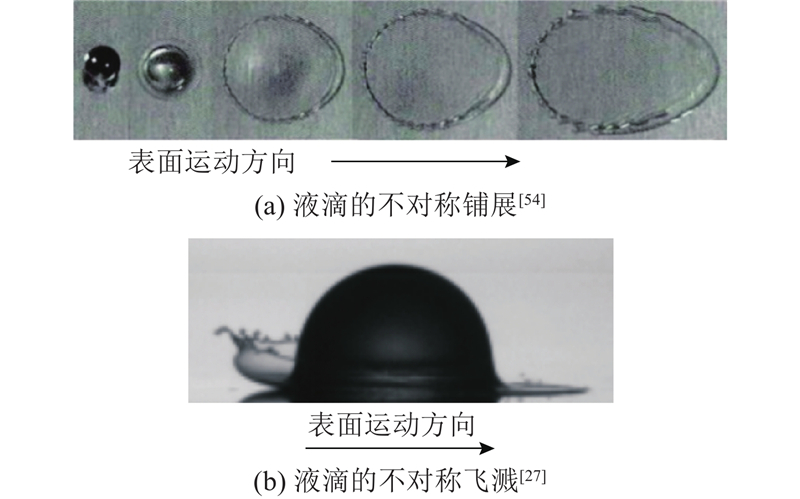
... 在移动表面上,液滴的铺展过程与静止表面最明显的不同在于铺展的不对称性,图5 列出液滴在移动固体表面上的一些典型几何不对称现象. 在运动的表面上,液滴一般会在沿表面运动方向的铺展比垂直运动方向的铺展尺度更大[54 ] . 液滴在移动表面的飞溅过程也受到一定程度的影响,例如在某些工况下,可能会在上下游两侧表现出不同的飞溅形式[27 ] ,液滴铺展后上下游的飞溅行为会受到表面速度影响[27 ] 、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... Xu等[44 ] 提出液滴的飞溅可以通过改变环境气压而抑制后,研究人员发现环境气体在液滴的飞溅过程中也起到作用. Hao等[21 ] 实验研究移动表面环境气压对液滴撞击飞溅产生的影响,通过降低气压可以抑制液滴上游的冠状飞溅,在移动表面上飞溅的临界气压小于静止表面. 根据单位长度液体薄层上升力与表面张力比值超过某阈值产生飞溅这一原理[88 -89 ] ,给出基于升力的液滴撞击移动表面的飞溅阈值模型为 ...
Ethanol drop impact on an inclined moving surface
2
2010
... 在表面选择上,大部分研究人员使用铝或不锈钢作为表面材料. 当需要研究表面性质时,多使用多晶硅[22 ] 作为表面或使用聚四氟乙烯涂层[23 ] 、SiO2 涂层[24 ] 等表面涂层进行处理. 液体选择上多使用去离子水、乙醇、甘油、硅油及其水混合物. 具体实验材料与部分工况如表1 所示. ...
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
Asymmetric spreading of a drop upon impact onto a surface
6
2017
... 在表面选择上,大部分研究人员使用铝或不锈钢作为表面材料. 当需要研究表面性质时,多使用多晶硅[22 ] 作为表面或使用聚四氟乙烯涂层[23 ] 、SiO2 涂层[24 ] 等表面涂层进行处理. 液体选择上多使用去离子水、乙醇、甘油、硅油及其水混合物. 具体实验材料与部分工况如表1 所示. ...
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 为了深入理解液滴在运动表面铺展的机理, Almohammadi等[23 ] 提出一个理论模型,如图11 所示,其中 $ r(t) $ [78 -86 ] . ...
... 液滴在平移固体表面铺展模型[23 ] ...
... Model of droplet spreading on translational solid surface [23 ] ...
... 式中: $ {V}_{\mathrm{d}} $ [23 ] 符合良好. ...
Reduced contact time of a droplet impacting on a moving superhydrophobic surface
6
2020
... 在表面选择上,大部分研究人员使用铝或不锈钢作为表面材料. 当需要研究表面性质时,多使用多晶硅[22 ] 作为表面或使用聚四氟乙烯涂层[23 ] 、SiO2 涂层[24 ] 等表面涂层进行处理. 液体选择上多使用去离子水、乙醇、甘油、硅油及其水混合物. 具体实验材料与部分工况如表1 所示. ...
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 在移动表面上,液滴的铺展过程与静止表面最明显的不同在于铺展的不对称性,图5 列出液滴在移动固体表面上的一些典型几何不对称现象. 在运动的表面上,液滴一般会在沿表面运动方向的铺展比垂直运动方向的铺展尺度更大[54 ] . 液滴在移动表面的飞溅过程也受到一定程度的影响,例如在某些工况下,可能会在上下游两侧表现出不同的飞溅形式[27 ] ,液滴铺展后上下游的飞溅行为会受到表面速度影响[27 ] 、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... 式中: $ {K}_{\boldsymbol{s}} $ $ {K}_{\mathrm{L}} $ [24 ] 的研究中被观察到. 基于在静止表面的模型[91 -92 ] ,Zhang等[24 ] 提出撞击移动超疏水表面的时间 $ {t}_{\mathrm{M}} $ $ {t}_{\boldsymbol{S}} $
... [24 ]提出撞击移动超疏水表面的时间 $ {t}_{\mathrm{M}} $ $ {t}_{\boldsymbol{S}} $
... 在宏观尺度模拟中,Hou等[105 ] 通过VOF方法获得气液界面,并利用ANSYS框架下的凝固/融化算法对过冷液滴撞击冷表面的凝固过程进行模拟. 该方法设定为过冷液滴接触冷表面的瞬间转化固液混合物,过冷度由调节混合物的参数表达[106 -107 ] . 对横向移动表面上液滴的形态演变进行模拟,在与Zhang等[24 ] 实验相似的条件下,得到了相似的结果. 图17 为对液滴撞击移动冷表面的碰撞—结冰过程进行的三维数值模拟,结果表明:液滴的初始冻结位置优先出现在液滴的上游侧,液滴下游一侧的冻结滞后于上游一侧,且滞后效应受到冷表面温度的强烈影响,同样的冻结滞后现象也在孙志成[57 ] 液滴撞击移动冷表面的实验中出现. ...
Droplet-wall collisions: experimental studies of the deformation and breakup process
2
1995
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
Effects of tangential speed on low-normal-speed liquid drop impact on a non-wettable solid surface
2
2005
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 对液滴撞击移动固体表面的模型研究大体沿着液滴撞击静止固体表面的思路进行,研究主要针对铺展、飞溅、反弹3个方面. 在液滴铺展阶段,最早可以注意到的现象便是液滴铺展的几何不对称性. Chen等[26 ] 在对去离子水撞击聚四氟乙烯表面的实验中,基于液滴撞击移动表面的几何不对称现象,对实验结果进行拟合,同时指出“部分反弹—沉积”临界态与“沉积—沉积分裂”临界态下的液滴拉伸比例(即 $ b/a $ $ W{e}_{\boldsymbol{s}} $
Inclined to splash: triggering and inhibiting a splash with tangential velocity
4
2009
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 在移动表面上,液滴的铺展过程与静止表面最明显的不同在于铺展的不对称性,图5 列出液滴在移动固体表面上的一些典型几何不对称现象. 在运动的表面上,液滴一般会在沿表面运动方向的铺展比垂直运动方向的铺展尺度更大[54 ] . 液滴在移动表面的飞溅过程也受到一定程度的影响,例如在某些工况下,可能会在上下游两侧表现出不同的飞溅形式[27 ] ,液滴铺展后上下游的飞溅行为会受到表面速度影响[27 ] 、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... [27 ]、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... 针对液滴的飞溅,Bird等[27 ] 基于液滴薄层的不稳定性提出飞溅阈值的模型. 液滴薄层的动能表达式为 ...
Impacting of droplets on moving surface and inclined surfaces
4
2021
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
... 液滴撞击倾斜与移动固体表面铺展对比[28 ] ...
... Comparison of liquid drop spreading between solid and moving surfaces [28 ] ...
Time evolutions of water drops impacting on a rotating disk
2
2012
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 旋转固体表面作为移动表面的一种特殊类型,由于其离心效应而存在一些有别于平移表面的特殊现象. 根据液滴撞击位置的不同,可以分为旋转中心撞击和非旋转中心撞击. 液滴在旋转中心撞击后的现象有铺展边缘的毛细脊、液指的发生[61 -62 ] . 液滴在非旋转中心撞击后的典型现象有如图7 所示的“月牙形”的铺展形状、几何不对称的液指拉伸、内侧的波的形成和向外推进等[29 -32 ,63 ] . ...
Impact patterns and temporal evolutions of water drops impinging on a rotating disc
1
2012
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
Effects of surface tension on drop impact on a horizontal rotating disk
1
2013
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
Droplet impact dynamics on an aluminum spinning disk
9
2021
... Experimental conditions of droplet impacting moving solid surface
Tab.1 选取的文献 测试液体 D 0 /mm V n −1 ) V max /(m·s−1 ) 表面 Mundo等[25 ] 水、乙醇 0.06~0.15 12~18 30 不锈钢 Chen等[26 ] 水 0.50~0.90 1.0~3.0 4.5 特氟龙 Bird等[27 ] 乙醇 0.80 0.8~3.6 21 铝 Zen等[22 ] 乙醇 2.30~2.50 1.4~3.9 8 多晶硅 Almohammadi等[19 ] 甘油、水 2.50 0.5~3.4 17 特氟龙 Hao等[21 ] 甘油 2.00~3.10 1.0~2.4 5 抛光不锈钢 Almohammadi等[23 ] 甘油、水 2.50 0.5~3.4 17 不锈钢、特氟龙 Buksh等[20 ] 硅油、甘油、水 2.50~2.70 0.8~2.3 2.9 不锈钢 Zhang等[24 ] 水 2.50 0.7~3.0 1.5 铝、二氧化硅 Buksh等[28 ] 硅油、甘油、水 2.50 0.4~2.9 2.9 不锈钢 Li 等[29 ] 水 4.40 1.9~3.1 14 铝 Li 等[30 ] 水 4.40 1.4~4.4 18.9 铝 Yuan 等[31 ] 水、乙醇 2.50 3.1 1.9 铝 Moghtadernejad 等[32 ] 水 2.40 1.0~2.4 10.4 铝
经过对上述文献整理发现,现有的实验对表面移动参量如 $ W{e}_{\boldsymbol{s}} $ $ {Re}_{\boldsymbol{s}} $ $ W{e}_{\boldsymbol{n}} $
... 旋转固体表面作为移动表面的一种特殊类型,由于其离心效应而存在一些有别于平移表面的特殊现象. 根据液滴撞击位置的不同,可以分为旋转中心撞击和非旋转中心撞击. 液滴在旋转中心撞击后的现象有铺展边缘的毛细脊、液指的发生[61 -62 ] . 液滴在非旋转中心撞击后的典型现象有如图7 所示的“月牙形”的铺展形状、几何不对称的液指拉伸、内侧的波的形成和向外推进等[29 -32 ,63 ] . ...
... Moghtadernejad等[32 ] 对液滴撞击旋转表面非中心位置的过程进行初步的实验研究,发现各项运动参数对液滴撞击旋转表面非中心位置的影响,其中较为特殊的有降低旋转表面的角速度会使铺展薄层上向外推移的波速度降低,提升液滴撞击点的线速度会促进二次液滴的形成等. 本文沿用文献中对各项变量的定义,即 $ {V}_{\mathrm{w}} $ $ {D}_{\mathrm{w}} $ $ {N}_{\mathrm{f}} $ $ \mathrm{L}{\mathrm{w}}_{\theta } $ $ \mathrm{L}\mathrm{w} $ $ \omega $ $ {R}_{\boldsymbol{n}} $ 表5 所示. ...
... 液滴撞击旋转平台非中心位置实验结果[32 ] ...
... Experimental results of droplet impact on non-central position of rotating platform[32 ] ...
... 当液滴撞击非旋转中心位置时,会发生如波向外侧推进以及不对称的液指拉伸等典型现象. Moghtadernejad等[32 ] 基于实验对液体径向铺展尺寸 $ \mathrm{L}\mathrm{w} $ $ {t}_{\mathrm{d}} $ $ {N}_{\mathrm{f}} $ $ {t}_{\mathrm{f}} $
... 式中:round (·) 函数为指取函数内部数值相邻最近的整数. 在液滴撞击旋转表面非中心位置的研究中,分析波推进速度等物理现象存在挑战,部分物理过程如图14 所示,其中作用力分析较为复杂,需要借助数值模拟进行辅助分析[32 ] . ...
... 波推进过程示意图[32 ] ...
... Schematic diagram of liquid wave propulsion process[32 ] ...
Normal droplet impact on horizontal moving films: an investigation of impact behaviour and regimes
6
2011
... 相较于液滴撞击静止表面的研究,液滴撞击移动液膜的实验研究起步较晚. 在2011年Alghoul等[33 ] 发表在液滴撞击移动液膜方面的实验研究成果. 如图2 所示的液滴撞击移动液膜的实验系统可以分为液滴发生系统、移动液膜系统、图像捕捉系统和后处理系统. 液滴发生系统常使用毛细管针头产生液滴,移动液膜系统常为一个横置或斜置槽,用于提供稳定的移动液膜,图像捕捉和后处理系统则使用高速相机和匹配的计算机处理软件,用于捕捉液滴撞击现象和图像处理. ...
... Experimental conditions of droplet impacting moving liquid film
Tab.2 选取的文献 液滴液体 液膜液体 D 0 /mm V n −1 ) q /(L·min−1 ) Algho等[33 ] 水 水 2.4、3.8 2.90 1.0~5.5 Che等[36 ] 水 水 3.3、 4、5.2 0.30~2.90 0.9~10.7 Gao等[35 ] 甘油, 水 甘油, 水 2.6~4.6 0.60~4.20 1.2~2.2 Gao等[37 ] 水 水 2.2~4.3 0.17~4.50 1.2~3.6 Adebayo等[38 ] 水 水 2.3~4.4 2.40~3.90 100~600 Burzynski等[39 ] 水 水 3.0 7.40~10.50 14
2. 液滴撞击静止和移动表面的行为与现象 液滴撞击移动表面的过程是在液滴撞击静止表面的过程中加入一个垂直于液滴撞击方向(或与液滴撞击方向成一定角度)的表面运动,因此液滴撞击移动表面现象与撞击静止表面现象具有一定的关联,在影响液滴撞击静止表面的变量同时,也会影响撞击移动表面的过程. 随着表面运动形式的复杂化,液滴撞击后的现象更复杂多样,但是描述液滴撞击静止表面现象的一些方法仍用在撞击移动表面上. ...
... 液滴撞击静止液膜也是一个常被讨论的物理学过程. 通常来说,液滴撞击液膜的主要现象可以分为悬浮、反弹、飞溅以及融合(如图8 ),其中飞溅又分为冠状飞溅和射流飞溅[33 ,64 -66 ] . ...
... 液滴撞击液膜主要现象[33 ] ...
... Main phenomena of droplet impacting water film[33 ] ...
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Splashing dynamics of a drop impact onto a deep liquid pool with moving film interface
3
2020
... 常见液滴撞击移动液膜实验平台[34 ] ...
... Common experiment platform of droplets impacting moving water film[34 ] ...
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
Impact of a single drop on a flowing liquid film
5
2015
... 大部分实验采用去离子水产生液滴和液膜,在考虑不同液体性质时,可选择使用不同比例的甘油和水的混合物[35 ] ,同时实验所使用的液滴和液膜液体均保持相同. 表2 为液滴撞击移动液膜的部分实验条件. 经过对上述文献整理发现,现有实验针对表面液滴撞击参量同样在较低的数值范围内,此外较多实验针对的无量纲液膜厚度 $ H $ $ H > 1 $
... Experimental conditions of droplet impacting moving liquid film
Tab.2 选取的文献 液滴液体 液膜液体 D 0 /mm V n −1 ) q /(L·min−1 ) Algho等[33 ] 水 水 2.4、3.8 2.90 1.0~5.5 Che等[36 ] 水 水 3.3、 4、5.2 0.30~2.90 0.9~10.7 Gao等[35 ] 甘油, 水 甘油, 水 2.6~4.6 0.60~4.20 1.2~2.2 Gao等[37 ] 水 水 2.2~4.3 0.17~4.50 1.2~3.6 Adebayo等[38 ] 水 水 2.3~4.4 2.40~3.90 100~600 Burzynski等[39 ] 水 水 3.0 7.40~10.50 14
2. 液滴撞击静止和移动表面的行为与现象 液滴撞击移动表面的过程是在液滴撞击静止表面的过程中加入一个垂直于液滴撞击方向(或与液滴撞击方向成一定角度)的表面运动,因此液滴撞击移动表面现象与撞击静止表面现象具有一定的关联,在影响液滴撞击静止表面的变量同时,也会影响撞击移动表面的过程. 随着表面运动形式的复杂化,液滴撞击后的现象更复杂多样,但是描述液滴撞击静止表面现象的一些方法仍用在撞击移动表面上. ...
... 关于液滴的冠状飞溅,在Roisman等[93 ] 的理论中,如果撞击流动液膜的液滴在变形阶段仍保持圆形,则在扩展阶段冠状的底部可以近似为一个生长的圆,随着液膜流向下游移动. Gao等[35 ] 发现上述理论在实验中有所偏差,提出当 $ H\times U\ll 1 $
... Liang等[110 -111 ] 基于CLSVOF方法建立液滴撞击移动液膜的三维模型,并对单液滴、双液滴先后和同时撞击等情况进行数值模拟. 流动液膜带来的剪切力使界面和热传导的对称性被打破,下游的飞溅被抑制,上游的飞溅被促进. Zhao等[68 ] 则发现液膜厚度的增加导致流入冠壁的液体量以及冠壁与液膜之间的角度增加,此外,非对称冠的迁移距离随着液膜的流动而增大. 液滴在动态液膜上的扩散速度等于上下游扩散速度的平均值,其直径与时间的1/2次成正比. 将实验结果[35 ,112 ] 与模拟结果相对照,如图18 所示,证实模拟的准确性,其中K 值使用Gao等[35 ] 的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
... [35 ]的计算方法. Wang等[113 ] 学者则使用了二维模型以提升CLSVOF方法的计算效率,同时模拟了双液滴撞击移动液膜的热传导过程,并发现非对称分布特性导致壁面热流不均匀. ...
Impact of droplets on inclined flowing liquid films
7
2015
... Experimental conditions of droplet impacting moving liquid film
Tab.2 选取的文献 液滴液体 液膜液体 D 0 /mm V n −1 ) q /(L·min−1 ) Algho等[33 ] 水 水 2.4、3.8 2.90 1.0~5.5 Che等[36 ] 水 水 3.3、 4、5.2 0.30~2.90 0.9~10.7 Gao等[35 ] 甘油, 水 甘油, 水 2.6~4.6 0.60~4.20 1.2~2.2 Gao等[37 ] 水 水 2.2~4.3 0.17~4.50 1.2~3.6 Adebayo等[38 ] 水 水 2.3~4.4 2.40~3.90 100~600 Burzynski等[39 ] 水 水 3.0 7.40~10.50 14
2. 液滴撞击静止和移动表面的行为与现象 液滴撞击移动表面的过程是在液滴撞击静止表面的过程中加入一个垂直于液滴撞击方向(或与液滴撞击方向成一定角度)的表面运动,因此液滴撞击移动表面现象与撞击静止表面现象具有一定的关联,在影响液滴撞击静止表面的变量同时,也会影响撞击移动表面的过程. 随着表面运动形式的复杂化,液滴撞击后的现象更复杂多样,但是描述液滴撞击静止表面现象的一些方法仍用在撞击移动表面上. ...
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
... 关于液滴反弹的条件如图15 所示. 由于气层和液膜的厚度相对于切向长度来说很小,可以使用润滑理论(lubrication theory)近似气层和液膜中的流动[36 ] . 推导出液滴撞击移动液膜过程中润滑力[36 ] 为 ...
... [36 ]为 ...
... 液滴下方气流和液膜流动[36 ] ...
... Air flow and water film flow under droplets[36 ] ...
... 式中:下标 $ \mathrm{a} $ $ {A}_{\mathrm{ga}} $ [36 ] 提出润滑力大于液滴重力在垂直于液膜运动方向的分量是液滴发生反弹的最小条件. ...
Heat transfer of single drop impact on a film flow cooling a hot surface
1
2017
... Experimental conditions of droplet impacting moving liquid film
Tab.2 选取的文献 液滴液体 液膜液体 D 0 /mm V n −1 ) q /(L·min−1 ) Algho等[33 ] 水 水 2.4、3.8 2.90 1.0~5.5 Che等[36 ] 水 水 3.3、 4、5.2 0.30~2.90 0.9~10.7 Gao等[35 ] 甘油, 水 甘油, 水 2.6~4.6 0.60~4.20 1.2~2.2 Gao等[37 ] 水 水 2.2~4.3 0.17~4.50 1.2~3.6 Adebayo等[38 ] 水 水 2.3~4.4 2.40~3.90 100~600 Burzynski等[39 ] 水 水 3.0 7.40~10.50 14
2. 液滴撞击静止和移动表面的行为与现象 液滴撞击移动表面的过程是在液滴撞击静止表面的过程中加入一个垂直于液滴撞击方向(或与液滴撞击方向成一定角度)的表面运动,因此液滴撞击移动表面现象与撞击静止表面现象具有一定的关联,在影响液滴撞击静止表面的变量同时,也会影响撞击移动表面的过程. 随着表面运动形式的复杂化,液滴撞击后的现象更复杂多样,但是描述液滴撞击静止表面现象的一些方法仍用在撞击移动表面上. ...
Droplet impact on flowing liquid films with inlet forcing: the splashing regime
7
2017
... Experimental conditions of droplet impacting moving liquid film
Tab.2 选取的文献 液滴液体 液膜液体 D 0 /mm V n −1 ) q /(L·min−1 ) Algho等[33 ] 水 水 2.4、3.8 2.90 1.0~5.5 Che等[36 ] 水 水 3.3、 4、5.2 0.30~2.90 0.9~10.7 Gao等[35 ] 甘油, 水 甘油, 水 2.6~4.6 0.60~4.20 1.2~2.2 Gao等[37 ] 水 水 2.2~4.3 0.17~4.50 1.2~3.6 Adebayo等[38 ] 水 水 2.3~4.4 2.40~3.90 100~600 Burzynski等[39 ] 水 水 3.0 7.40~10.50 14
2. 液滴撞击静止和移动表面的行为与现象 液滴撞击移动表面的过程是在液滴撞击静止表面的过程中加入一个垂直于液滴撞击方向(或与液滴撞击方向成一定角度)的表面运动,因此液滴撞击移动表面现象与撞击静止表面现象具有一定的关联,在影响液滴撞击静止表面的变量同时,也会影响撞击移动表面的过程. 随着表面运动形式的复杂化,液滴撞击后的现象更复杂多样,但是描述液滴撞击静止表面现象的一些方法仍用在撞击移动表面上. ...
... 液滴速度、表面速度之比以及液体性质影响液滴撞击移动液膜的现象[69 ] . 相对于撞击静止液膜,液滴撞击移动液膜时初期产生的空腔、冠状飞溅和射流呈不对称状态[34 ] . 液滴撞击后形成冠状飞溅和空腔,空腔会随着液膜的流动逐渐趋于对称,空腔缩小消失后产生向下游倾斜的射流,射流的根部会随着液膜流动逐渐靠近尖端,使得射流与液膜表面的角度逐渐向垂直发展[33 ,70 ] . 随着移动液膜流速的增加,液滴反弹的可能性也随之增大[36 ] . 当液膜流动速度超过液滴撞击速度的10%后,撞击溅起的液层出现弯曲[64 ] . 如果液滴撞击在如图10 所示的3种不同形态的流动液膜区域[71 -73 ] :在平液膜区域、毛细波区域和波峰区域上则会有不同的现象发生. 其中平滑液膜最易发生飞溅,波峰上最难发生飞溅[38 ] . 当液滴撞击液膜的上方存在剪切气流时,剪切空气通过液滴变形和限制膜厚,对碰撞前的相互作用过程产生影响[74 ] . ...
... 3种不同形态的流动液膜区域[38 ] ...
... Three different flow liquid film regions[38 ] ...
... 冠状飞溅的过程与液滴的速度、尺寸以及液膜流速有关[38 ] . Yarin等[94 ] 通过拟合实验数据得到了一个冠状水花发展的经验计算式: ...
... 式中: $ {d}_{\mathrm{c}} $ [38 ] 则在此基础上,基于努塞尔特厚度: ...
... 式中:α 为渠道倾斜角度, $ {K}_{\theta } $ [38 ] . ...
Droplet splashing on thin moving films at high Weber numbers
1
2018
... Experimental conditions of droplet impacting moving liquid film
Tab.2 选取的文献 液滴液体 液膜液体 D 0 /mm V n −1 ) q /(L·min−1 ) Algho等[33 ] 水 水 2.4、3.8 2.90 1.0~5.5 Che等[36 ] 水 水 3.3、 4、5.2 0.30~2.90 0.9~10.7 Gao等[35 ] 甘油, 水 甘油, 水 2.6~4.6 0.60~4.20 1.2~2.2 Gao等[37 ] 水 水 2.2~4.3 0.17~4.50 1.2~3.6 Adebayo等[38 ] 水 水 2.3~4.4 2.40~3.90 100~600 Burzynski等[39 ] 水 水 3.0 7.40~10.50 14
2. 液滴撞击静止和移动表面的行为与现象 液滴撞击移动表面的过程是在液滴撞击静止表面的过程中加入一个垂直于液滴撞击方向(或与液滴撞击方向成一定角度)的表面运动,因此液滴撞击移动表面现象与撞击静止表面现象具有一定的关联,在影响液滴撞击静止表面的变量同时,也会影响撞击移动表面的过程. 随着表面运动形式的复杂化,液滴撞击后的现象更复杂多样,但是描述液滴撞击静止表面现象的一些方法仍用在撞击移动表面上. ...
Drop impact dynamics: splashing, spreading, receding, bouncing…
1
2006
... 目前研究人员针对液滴撞击静止固体表面的现象和机理已经开展了十分深入的研究和讨论. 推荐读者阅读于2006年Yarin等[40 ] 发表的文献,文献中对液滴撞击静止表面的相关内容进行了详尽的总结. ...
Outcomes from a drop impact on solid surfaces
3
2001
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
... 液滴撞击硬表面的典型现象[41 ] ...
... Typical phenomenon of droplet impacting solid surfaces [41 ] ...
Formation of fingers around the edges of a drop hitting a metal plate with high velocity
1
2004
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
Spread and rebound of liquid droplets upon impact on flat surfaces
1
1997
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
Drop splashing on a dry smooth surface
2
2005
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
... Xu等[44 ] 提出液滴的飞溅可以通过改变环境气压而抑制后,研究人员发现环境气体在液滴的飞溅过程中也起到作用. Hao等[21 ] 实验研究移动表面环境气压对液滴撞击飞溅产生的影响,通过降低气压可以抑制液滴上游的冠状飞溅,在移动表面上飞溅的临界气压小于静止表面. 根据单位长度液体薄层上升力与表面张力比值超过某阈值产生飞溅这一原理[88 -89 ] ,给出基于升力的液滴撞击移动表面的飞溅阈值模型为 ...
Precursors to splashing of liquid droplets on a solid surface
1
2009
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
液滴撞击平板的铺展特征
1
2007
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
液滴撞击平板的铺展特征
1
2007
... Rioboo等[41 ] 于2001年的研究中提出液滴撞击静止硬表面广泛存在的6种现象,如图3 所示,分别为铺展、喷溅、冠状飞溅、收缩破裂、部分反弹和完全反弹. Mehdizadeh等[42 ] 还指出高速撞击下液滴铺展过程中有明显的液指生成,而表面的粗糙度[13 ] 、撞击参数[43 ] 、环境气压[44 -45 ] 、撞击角度[46 ] 等因素对液滴撞击后的现象有明显的影响. ...
液滴撞击超亲水表面的最大铺展直径预测模型
3
2021
... 在液滴撞击过程中,常被科研人员关注的行为和现象有铺展、飞溅和反弹. 它们的发生阈值和具体现象受到表面性质、液滴性质、撞击条件、环境条件等因素的影响. 在铺展过程中,研究人员主要关注的特征参数有铺展因子、铺展时间等. 目前已经有大量的实验研究及模型,推荐读者参考春江等[47 ] 针对铺展模型的详尽整理. ...
... 式中: $ K $ $ K=2.5 $ K =5700的情况下,预测结果与实验结果重合较好,可以简化为表面速度为0,即液滴撞击静止表面的模式,并与早期实验[47 ,87 ] 相符. 然而该模型有2个局限性:1)该模型的实验验证仅限于乙醇一种液体,因此无法体现出液体黏度、表面张力等因素对飞溅现象的影响;2)该模型对液滴几何不对称性的描述仅有一个维度,即仅考虑了液滴薄层上游端点和下游端点,而无法描述整个液滴铺展边缘其他位置的飞溅情况. ...
... 当液膜厚度变为0时,公式简化为 $ K=WeR{e}^{1/2} $ [47 ] . ...
液滴撞击超亲水表面的最大铺展直径预测模型
3
2021
... 在液滴撞击过程中,常被科研人员关注的行为和现象有铺展、飞溅和反弹. 它们的发生阈值和具体现象受到表面性质、液滴性质、撞击条件、环境条件等因素的影响. 在铺展过程中,研究人员主要关注的特征参数有铺展因子、铺展时间等. 目前已经有大量的实验研究及模型,推荐读者参考春江等[47 ] 针对铺展模型的详尽整理. ...
... 式中: $ K $ $ K=2.5 $ K =5700的情况下,预测结果与实验结果重合较好,可以简化为表面速度为0,即液滴撞击静止表面的模式,并与早期实验[47 ,87 ] 相符. 然而该模型有2个局限性:1)该模型的实验验证仅限于乙醇一种液体,因此无法体现出液体黏度、表面张力等因素对飞溅现象的影响;2)该模型对液滴几何不对称性的描述仅有一个维度,即仅考虑了液滴薄层上游端点和下游端点,而无法描述整个液滴铺展边缘其他位置的飞溅情况. ...
... 当液膜厚度变为0时,公式简化为 $ K=WeR{e}^{1/2} $ [47 ] . ...
The splash/non-splash boundary upon a dry surface and thin fluid film
1
2006
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
Data-driven splashing threshold model for drop impact on dry smooth surfaces
1
2021
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
The impact of a single drop on a wetted solid surface
1
1997
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
Experimental investigation of splash and crown formation during single drop impact on wetted surfaces
1
2003
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
Behavior of a water droplet impacting a thin water film
1
2021
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
Experiments on splashing thresholds during single-drop impact onto a quiescent liquid film
1
2021
... Partial splash threshold models for droplet impingement on stationary surface
Tab.3 文献来源 静止固体 模型 飞溅阈值 Mundo 等[25 ] $ K={\left({W{e}_{\boldsymbol{n}}R{e}_{\boldsymbol{n}}}^{0.5}\right)}^{0.5} $ $ {K}_{\mathrm{c}}=57.7 $ Vander Wal等[48 ] $ K=W{e}_{\boldsymbol{n}}^{0.5}R{e}_{\boldsymbol{n}}^{-0.391} $ ${K}_{\mathrm{c} }=0.845\;8$ Pierzyna等[49 ] $ K={c}_{0}+{c}_{1}{V}_{\boldsymbol{n}}+\dfrac{{c}_{2}}{\mu }+{c}_{3}\sigma +{c}_{4}{\rho }_{g} $ $ {K}_{\mathrm{c}}=0.14 $ 文献来源 静止液膜 模型 飞溅阈值 Cossali等[50 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100+5\;\mathrm{ }880{H}^{1.44} $ Rioboo等[51 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=2\;100 $ Zhu等[52 ] $ K=O{h}^{-0.4}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=1\mathrm{ }\;880+156\;\mathrm{ }122{H}^{2.017} $ Okawa等[53 ] $ K=O{h}^{-0.581}W{e}_{\boldsymbol{n}} $ $ {K}_{\mathrm{c}}=8\;\mathrm{ }123 $
值得注意的是有一种静止表面较为特殊,此静止表面与液滴下落方向之间存在夹角,即倾斜的静止表面. 如图4 所示,液滴撞击倾斜静止表面的前期现象与液滴撞击平移表面具有较高的相似性,当2个系统中液滴对表面保持相同的法向和切向速度,两者的前期铺展现象和飞溅现象几乎等效[28 ] . ...
液滴撞击移动表面动力学特性
4
2020
... 在移动表面上,液滴的铺展过程与静止表面最明显的不同在于铺展的不对称性,图5 列出液滴在移动固体表面上的一些典型几何不对称现象. 在运动的表面上,液滴一般会在沿表面运动方向的铺展比垂直运动方向的铺展尺度更大[54 ] . 液滴在移动表面的飞溅过程也受到一定程度的影响,例如在某些工况下,可能会在上下游两侧表现出不同的飞溅形式[27 ] ,液滴铺展后上下游的飞溅行为会受到表面速度影响[27 ] 、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... 由于液滴撞击移动表面具有的特殊性,研究人员引入一些定义以描述移动表面上的现象. 如图6 所示,本研究统一定义液滴铺展的最大宽度 $ a $ $ b $ $ x $ $ {t}_{\mathrm{c}} $ [54 -57 ] 如表4 所示,初步描述表面运动速度对液滴撞击后各现象的影响,其中“↑”为变量的增加、“↓”为变量的缩减. ...
... 表面运动速度与液滴铺展、飞溅、端点偏移和接触时间的关系[54 -57 ] ...
... Relationship between surface velocity and droplet spread, splash, apex offset and contact time[54 -57 ] ...
液滴撞击移动表面动力学特性
4
2020
... 在移动表面上,液滴的铺展过程与静止表面最明显的不同在于铺展的不对称性,图5 列出液滴在移动固体表面上的一些典型几何不对称现象. 在运动的表面上,液滴一般会在沿表面运动方向的铺展比垂直运动方向的铺展尺度更大[54 ] . 液滴在移动表面的飞溅过程也受到一定程度的影响,例如在某些工况下,可能会在上下游两侧表现出不同的飞溅形式[27 ] ,液滴铺展后上下游的飞溅行为会受到表面速度影响[27 ] 、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... 由于液滴撞击移动表面具有的特殊性,研究人员引入一些定义以描述移动表面上的现象. 如图6 所示,本研究统一定义液滴铺展的最大宽度 $ a $ $ b $ $ x $ $ {t}_{\mathrm{c}} $ [54 -57 ] 如表4 所示,初步描述表面运动速度对液滴撞击后各现象的影响,其中“↑”为变量的增加、“↓”为变量的缩减. ...
... 表面运动速度与液滴铺展、飞溅、端点偏移和接触时间的关系[54 -57 ] ...
... Relationship between surface velocity and droplet spread, splash, apex offset and contact time[54 -57 ] ...
Interaction of drops with boundary layer on rotating surface
2
1976
... 在移动表面上,液滴的铺展过程与静止表面最明显的不同在于铺展的不对称性,图5 列出液滴在移动固体表面上的一些典型几何不对称现象. 在运动的表面上,液滴一般会在沿表面运动方向的铺展比垂直运动方向的铺展尺度更大[54 ] . 液滴在移动表面的飞溅过程也受到一定程度的影响,例如在某些工况下,可能会在上下游两侧表现出不同的飞溅形式[27 ] ,液滴铺展后上下游的飞溅行为会受到表面速度影响[27 ] 、运动表面上液滴能够发生飞溅的最低气压值显著小于静止表面[21 ] 等. 液滴的反弹过程同样与静止表面有着区别,例如表面运动速度达到一定阈值会引起液滴撞击后反弹[55 ] 、液滴与表面接触时间缩短[24 ] 等情况. ...
... 针对液滴的反弹,Povarov等[55 ] 观察到移动表面边界层的气体升力对液滴撞击表面反弹的作用,升力系数表达式为 ...
Splash and anti-splash: observation and design
0
2006
4
... 由于液滴撞击移动表面具有的特殊性,研究人员引入一些定义以描述移动表面上的现象. 如图6 所示,本研究统一定义液滴铺展的最大宽度 $ a $ $ b $ $ x $ $ {t}_{\mathrm{c}} $ [54 -57 ] 如表4 所示,初步描述表面运动速度对液滴撞击后各现象的影响,其中“↑”为变量的增加、“↓”为变量的缩减. ...
... 表面运动速度与液滴铺展、飞溅、端点偏移和接触时间的关系[54 -57 ] ...
... Relationship between surface velocity and droplet spread, splash, apex offset and contact time[54 -57 ] ...
... 在宏观尺度模拟中,Hou等[105 ] 通过VOF方法获得气液界面,并利用ANSYS框架下的凝固/融化算法对过冷液滴撞击冷表面的凝固过程进行模拟. 该方法设定为过冷液滴接触冷表面的瞬间转化固液混合物,过冷度由调节混合物的参数表达[106 -107 ] . 对横向移动表面上液滴的形态演变进行模拟,在与Zhang等[24 ] 实验相似的条件下,得到了相似的结果. 图17 为对液滴撞击移动冷表面的碰撞—结冰过程进行的三维数值模拟,结果表明:液滴的初始冻结位置优先出现在液滴的上游侧,液滴下游一侧的冻结滞后于上游一侧,且滞后效应受到冷表面温度的强烈影响,同样的冻结滞后现象也在孙志成[57 ] 液滴撞击移动冷表面的实验中出现. ...
4
... 由于液滴撞击移动表面具有的特殊性,研究人员引入一些定义以描述移动表面上的现象. 如图6 所示,本研究统一定义液滴铺展的最大宽度 $ a $ $ b $ $ x $ $ {t}_{\mathrm{c}} $ [54 -57 ] 如表4 所示,初步描述表面运动速度对液滴撞击后各现象的影响,其中“↑”为变量的增加、“↓”为变量的缩减. ...
... 表面运动速度与液滴铺展、飞溅、端点偏移和接触时间的关系[54 -57 ] ...
... Relationship between surface velocity and droplet spread, splash, apex offset and contact time[54 -57 ] ...
... 在宏观尺度模拟中,Hou等[105 ] 通过VOF方法获得气液界面,并利用ANSYS框架下的凝固/融化算法对过冷液滴撞击冷表面的凝固过程进行模拟. 该方法设定为过冷液滴接触冷表面的瞬间转化固液混合物,过冷度由调节混合物的参数表达[106 -107 ] . 对横向移动表面上液滴的形态演变进行模拟,在与Zhang等[24 ] 实验相似的条件下,得到了相似的结果. 图17 为对液滴撞击移动冷表面的碰撞—结冰过程进行的三维数值模拟,结果表明:液滴的初始冻结位置优先出现在液滴的上游侧,液滴下游一侧的冻结滞后于上游一侧,且滞后效应受到冷表面温度的强烈影响,同样的冻结滞后现象也在孙志成[57 ] 液滴撞击移动冷表面的实验中出现. ...