近年来,诸多学者针对负载口独立控制的阀控液压缸系统进行广泛的研究. Opdenbosch等[5]设计由5个电液增压阀组成的独立计量结构,并通过基于状态轨迹的自动校准控制方法,实现对阀控缸系统的负载口独立控制. Lübbert等[6]设计由2个比例阀和5个开关阀组成的独立计量结构,并使用一个机械压力补偿器,通过SISO控制方法实现对阀控缸系统的负载口独立控制. Abuowda等[7]设计采用阶梯式旋转流量控制阀的微独立计量结构,通过操作模式的切换控制实现对阀控缸系统的负载口独立控制. Zhong等[8]提出结合高速开关先导阀的独立计量控制技术,通过模糊比例积分微分(proportion integration differentiation,PID)控制算法使得挖掘机阀控缸系统具备较好的动态性能和鲁棒性. Li等[9]针对独立计量系统中的不确定性和非线性问题,研究阀控缸系统中的非线性阀流量模型,通过自适应鲁棒控制方法使得独立计量系统具备较高的控制精度.
负载口独立控制的阀控液压缸系统具备多电液控制装置以及复杂控制逻辑等特点,往往会带来故障发生概率增加以及故障情况复杂的问题[10]. Rannow[11]针对负载口独立控制系统中出现的多传感器故障,设计了容错控制算法,提高了系统的可靠性和正常运行时间. Ding等[12]考虑到负载口独立控制系统中不同液压阀的不同程度故障,设计基于压力反馈的主动容错控制算法,保证了不同故障下的运动跟踪性能. Opdenbosch等[13]通过神经网络学习了负载口独立控制系统的逆输入-状态映射,计算其与预先建立的可接受性能边界的偏差,完成系统的异常检测. Beck等[14]根据液压缸控制腔压力信号时域特征与特定值的比较,对负载口独立控制系统进行故障检测,提高了该系统用于挖掘机臂的阀控缸系统的安全性. Bianchi等[15]根据液压缸控制腔的压力信号以及泵出口的压力信号,并结合来自控制器的附加信息,通过神经网络算法完成对负载口独立控制阀控缸系统中泵体容积效率下降、液压缸磨损故障以及计量阀开口故障的诊断工作.
针对负载口独立控制的阀控液压缸系统,现有研究多集中在系统的结构设计与控制策略设计方面. 为了实现对系统整体性能衰退的评估,极少量研究通过阈值比较或神经网络变换的方法,挖掘了系统压力信号的时域特征. 阀控液压缸系统包括先导阀、主阀、液压缸以及位移传感器等多类元件,系统整体性的衰退是由于系统中元件发生故障导致的,而不同故障在系统的状态信息表征上有着相似甚至几乎相同的特性.从高度相似的故障信息表征中识别出发生故障的具体元件有着重要的意义,这对快速发现系统故障位置并进行后续维修工作具有指导价值.
本研究提出基于独立循环神经网络和一维大核卷积神经网络(independently recurrent neural network and one-dimensional large-kernel convolution neural network,IndRNN-1DLCNN)的负载口独立控制阀控液压缸系统的故障诊断方法. 构建阀控液压缸系统状态感知方案,分别对液压缸控制腔压力信号、杆位移信号、主阀控制腔压力信号与阀芯位移信号进行感知,分析不同故障条件下的系统特性,设计基于IndRNN-1DLCNN的深度网络模型,引入残差结构增加IndRNN网络深度,并引入1DLCNN挖掘长时间跨度下的多通道特征关系,实现多源信号的特征融合与特征提取. 本研究从高度相似的故障状态信息表征中识别出发生故障的具体元件,从而完成对负载口独立控制阀控液压缸系统的故障诊断工作.
1. 阀控液压缸系统
1.1. 系统模型
本研究的负载口独立控制阀控液压缸系统原理图如图1所示,其对应的实物图如图2所示. 液压缸两腔压力独立控制,从而推动负载运行. 图2所示的阀体对应图1中的数字液压先导可编程阀,由对应的油源进行供油,先导级由4个相同的两位三通滑阀式高速开关阀构成,主级由2个相同的三位三通滑阀式液动换向阀构成,实现对液压缸两腔的独立控制,从而推动液压缸活塞杆底部连接的负载按规律运行. 系统采用HYTEK定量齿轮泵,分别对主级和先导级供油. 如图2所示,实验装置通过溢流阀和变频电机进行泵源参数设定,设定压力为10 MPa,输出流量为50 L/min,并通过减压阀实现先导油口3.2 MPa的供油. 提出负载口独立控制阀控缸系统的状态感知方案. 对于液压缸控制腔的状态,利用光栅式位置编码器实现对活塞位移的感知,利用KULITE压力传感器完成对两腔压力信号的感知. 对于主级阀芯的状态,利用集成的LVDT传感器进行阀芯位移的感知,并通过CAN总线实现数据读取.
图 1
图 1 负载口独立控制阀控液压缸系统的原理图
Fig.1 Schematic diagram of independent metering valve-controlled hydraulic cylinder system
图 2
图 2 负载口独立控制阀控液压缸系统的实物图
Fig.2 Practical diagram of independent metering valve-controlled hydraulic cylinder system
如图1所示,负载口独立控制阀控缸系统强调两级负载口的独立控制. 一级为数字液压先导可编程阀中的每2个先导高速开关阀产生不同的高频离散流体,分别控制对应主阀两端弹簧腔的压力,实现对主阀芯的负载口独立控制. 另一级为数字液压先导可编程阀中的2个主级滑阀产生不同的阀芯开度,分别控制液压缸的进、出口两腔,实现对液压缸的负载口独立控制,使得液压缸所推动的负载满足规定的运动要求. 如图2所示,液压缸活塞杆底部连接由质量块和弹性负载组成的负载,质量块的质量M为100 kg,负载刚度K为2.5×106 N/m. 负载口独立控制阀控缸系统利用先导级高速开关阀优越的启闭动态特性,完成对主级阀芯开度的独立控制;2个主级滑阀的阀芯开度独立控制液压缸进、出口两腔的状态,以满足负载的运动要求. 系统以高速开关阀为核心控制单元,使得液压缸具备较好的动态性能[16]. 系统的关键结构参数如表1所示. 表中,
表 1 阀控液压缸系统参数
Tab.1
| 参数 | 参数值 | 参数 | 参数值 | |
| | 10.00 MPa | | 0.05 kg | |
| | 3.20 MPa | | 140.00 mm | |
| | 16.00 mm | | 100.00 mm | |
| | 1.00 kg | M | 100.00 kg | |
| | 8.00 mm | K | 2.50×106 N/m |
1.2. 系统控制器
数字液压先导可编程阀的先导高速开关阀由输入驱动电压信号控制,不同阀芯开度决定主级弹簧控制腔的压力,实现对2个主阀阀芯开度的独立控制. 先导高速开关阀的驱动电压由PWM控制信号和PWM高频信号2种不同的信号组合而成. 通过激励线圈实现阀芯运动的控制. 阀芯开启时采用100%占空比控制信号,维持开启状态则采用低占空比控制信号;关闭时采用−100%占空比控制信号,维持关闭状态采用0占空比控制信号[17]. 本研究的高速开关阀采用50 Hz的控制信号与24 kHz的高频信号. 如图3所示给出维持开启状态的驱动电压示意图,图中
图 3
式中:
图 4
图 4 负载口独立控制阀控液压缸系统的控制策略
Fig.4 Control strategy of independent metering valve-controlled hydraulic cylinder system
t时刻左阀芯参考位移与实际位移的偏差
式中:
表 2 阀控液压缸系统的控制器参数
Tab.2
| 参数符号 | 参数值 |
| PID1比例环节 | 60.00 |
| PID1积分环节 | 0 |
| PID1微分环节 | 0.10 |
| PID1转换系数 | −0.01 |
| PID1转换系数 | 0.01 |
| PID2比例环节 | 100.00 |
| PID2积分环节 | 0 |
| PID2微分环节 | 0.10 |
| PID2转换系数 | 250.00 |
| PID2转换系数 | −250.00 |
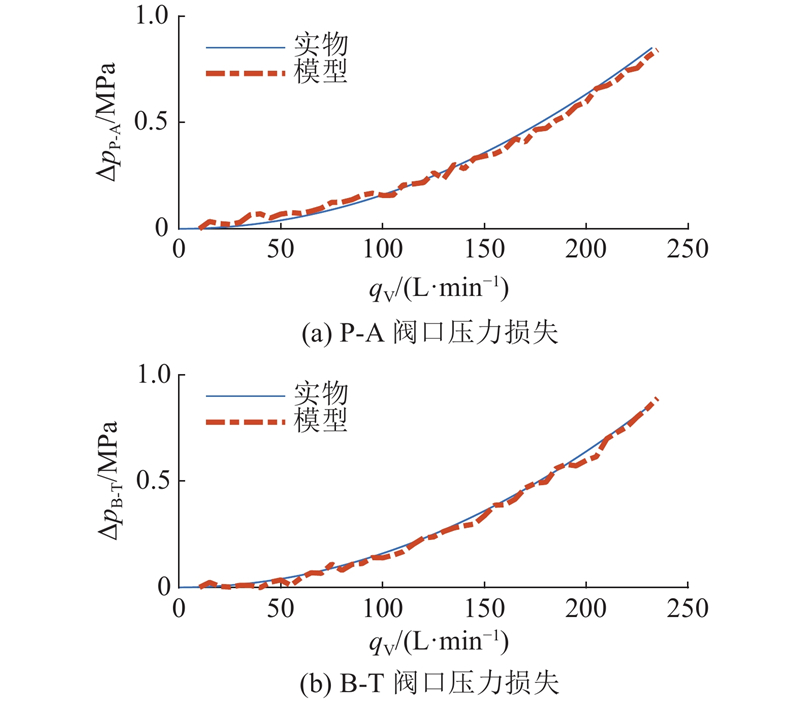
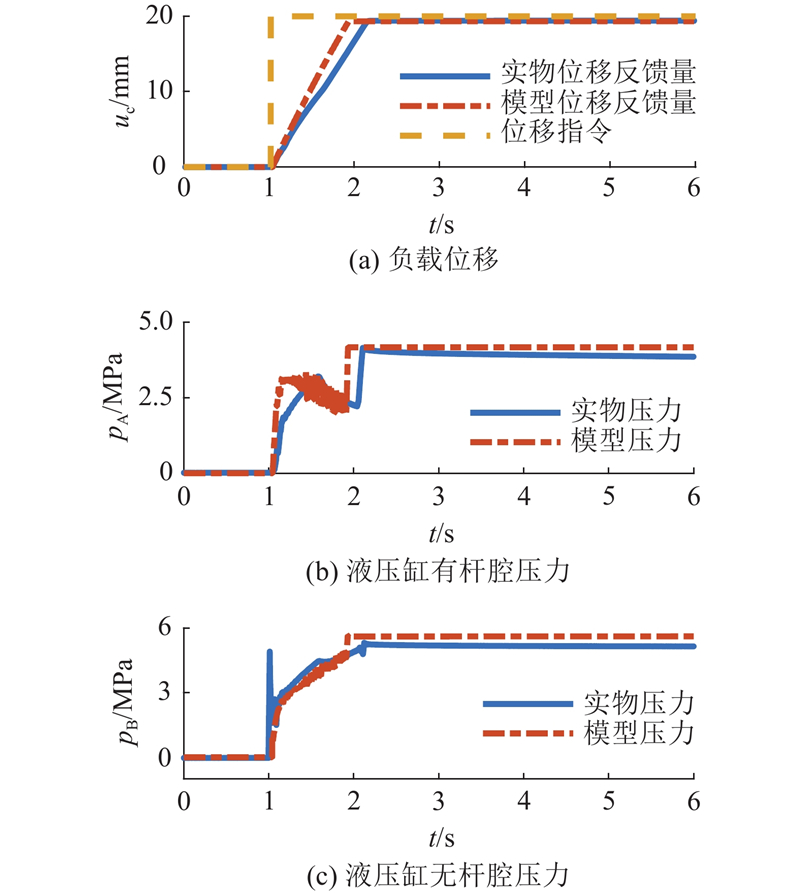
1.3. 模型验证
图 5
图 6
图 7
图 8
2. 系统故障分析
2.1. 先导级高速开关阀
高速开关阀的驱动信号由配套软硬件提供,一方面FPGA软硬件响应时间差会导致控制信号时间的滞后,另一方面控制信号频率因软硬件精度影响会导致高频离散流体频率的失准. 磁热耦合效应也会对高速开关阀的开关时间和速度产生影响[19]. 如图9所示为先导阀高速开关阀的套筒锈蚀故障, 该故障改变了高速开关阀的磁场特性,使得高速开关阀的控制信号延迟
图 9
表 3 先导阀的故障参数
Tab.3
| 类型 | 正常值区间 | 故障值区间 |
| | [0, 0.0003] | (0.0003, 0.0010] |
| | [48, 52] | [40, 48), (52, 60] |
| | [1.3, 1.5] | [0.6, 1.3) |
| kP/(N·mm−1) | [4.6, 4.8] | [3.5, 4.6) |
以图10为例,给出左先导阀1故障时的系统感知量与正常时的区别,此时左先导阀1故障为PWM控制信号延迟较高. 当负载口独立控制阀控缸系统处在正常的系统工况时,如图4所示的PID1-1和PID1-2根据负载位移指令信号与实际位移的差值,生成控制各自主阀阀芯位移的指令信号. 给定阀芯开度的最大限定值,避免负载的运行速度过快. 主级阀芯位移由其对应的2个高速开关阀控制,以左主阀为例,如图4所示的PID2-1和PID2-2根据左主阀阀芯的位移指令信号与实际位移的差值,分别生成对应先导阀的驱动电压信号,通过对高速开关阀24 kHz高频信号占空比的调节实现阀芯开度的控制. 先导级高速开关阀的阀芯开度决定了其控制的主阀弹簧腔的压力情况,从而决定了主阀阀芯位移情况. 高速开关阀存在定占空比的50 Hz控制信号,其具有开度回零的趋势,引起了主阀弹簧腔的压力波动,从而导致了主阀阀芯的位移波动. 当负载位移指令信号与实际位移的差值较小时,控制器生成的主级阀芯位移指令值较小,阀芯的正遮盖设计使其处于关闭状态.
图 10
当负载口独立控制的阀控液压缸系统存在故障时,由于控制器反馈机制调节作用的存在,系统故障对系统性能的不良影响得以削弱,使得负载位移仍能达到较好的跟踪效果[20]. 高速开关阀控制信号的延迟导致其启闭特性的变化,引起了主阀两侧弹簧腔压力特性的改变. 在系统控制器的调节下,主阀弹簧腔压力的变化不会反映出一致的延迟特性,系统的稳态特性也与正常状态存在差异. 虽然系统也能在控制器的调节下进行负载位移跟踪,但是系统特性的改变会导致系统工作状态的改变,对系统的长期运行造成不良影响,易引起阀组与液压缸的损伤.
2.2. 主级液动换向阀
表 4 主阀故障参数
Tab.4
| 参数 | 正常值区间 | 故障值区间 |
| rV/mm | [0.001, 0.015] | (0.015, 0.080] |
| lV/mm | [0.001, 0.015] | (0.015, 0.080] |
| NV/N | [133, 149] | [70, 133) |
| kV/(N·mm−1) | [13.4, 14.8] | [7.0, 13.4) |
图 11
2.3. 位移传感器
数字液压先导可编程阀的先导级与主级为一体式安装. 由于先导级高速开关阀的高速启闭特性会产生高频振动,该振动会传递到整个阀体之上,导致感知阀芯位移的LVDT位移传感器的振动. 当振动导致位移传感器的连杆固定件、密封件等松脱时,主阀阀芯位移的反馈偏差
表 5 位移传感器反馈故障参数
Tab.5
| 参数 | 正常值区间 | 故障值区间 |
| | [0, 0.03] | (0.03, 0.15] |
| | [0, 0.01] | (0.01, 0.50] |
2.4. 液压缸
阀控液压缸系统通过液压缸推动负载运动,运行过程中的元件磨损、液压冲击、温升发热等影响会导致液压缸泄漏量的增加. 液压缸泄漏量的增加可由泄漏系数的增加表示,当液压缸的泄漏系数超过制造精度所允许的泄漏系数时,液压缸发生泄漏故障[24]. 液压缸泄漏系数
3. 故障诊断模型
3.1. 独立循环神经网络
循环神经网络(recurrent neural network,RNN)是一种常用于处理时间序列问题的方法,通过循环连接将
式中:
RNN网络的权重矩阵与偏置向量具有权值共享的特点,这使得网络训练在梯度下降过程中易出现梯度爆炸与梯度消失的问题. 长短时记忆神经网络(long short term memory,LSTM)与门控循环单元(gate recurrent unit,GRU)虽然能在一定程度上解决梯度下降中存在的问题,但是只能选用tanh和sigmoid函数作为激活函数的特点导致层间梯度衰减. 引入独立循环神经网络(independently recurrent neural network,IndRNN),可以处理超过5 000时间步的时间序列问题,解决梯度爆炸与梯度消失的问题[25]. 对于式(4)稍作变化,矩阵
式中:
式(6)完成了层内神经元的解耦,因此在T时间步长内的损失函数J反向传播至时间t的梯度为
此时激活函数导数与循环权重系数独立,relu函数可以作为激活函数得:
式中:val为一个变量. 选取0~val的最大值,加快收敛并解决梯度问题.
与LSTM以及GRU不同,可以考虑采用多层IndRNN结构来探索输入的跨通道信息,如图12所示为引入残差网络的多层IndRNN的示意图. 对于第i层IndRNN网络,t时刻包括2个单独的IndRNN单元,其输入为
图 12
式中:
式中:
对于第i层IndRNN网络,t时刻的输出
3.2. 一维大核卷积神经网络
相比于传统时间序列的预测分类问题,负载口独立阀控缸系统能够判定系统是否发生故障的同时,也能区分出系统故障发生的元件,即识别出4个先导阀、2个主阀、液压缸以及位移传感器共8类元件故障. 对于既包含分类又包含定位的问题,大核卷积神经网络因其更大的感受野,能够在处理不同转换能力的同时挖掘细化特征,以保持定位性能[26].
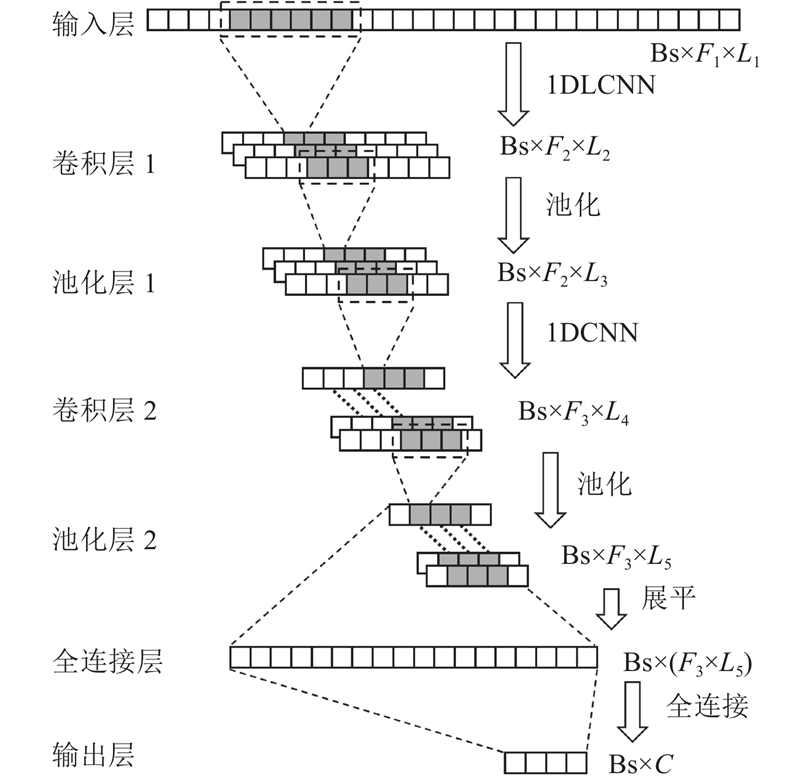
1DLCNN网络的示意图如图13所示,批尺寸大小为BS,对于一个长时间序列输入样本,特征个数为
图 13
式中:运算符
输出
式中:
式中:
3.3. 阀控液压缸系统故障诊断模型
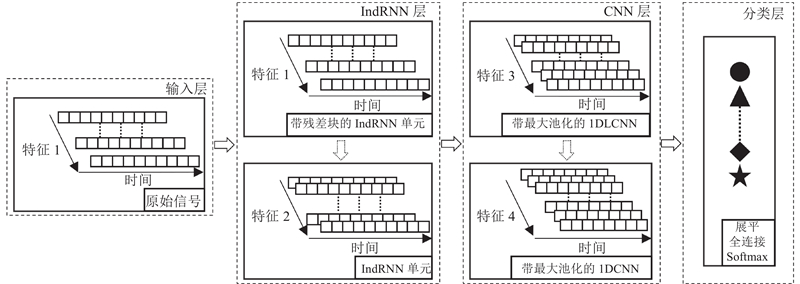
提出一种基于IndRNN-1DLCNN的负载口独立控制阀控缸系统的故障诊断模型,其结构如图14所示. 该算法通过引入残差网络增加IndRNN网络的深度,提取系统状态量在长时间维度上的特征. 同时引入1DLCNN大卷积核提升长时间跨度下的多通道特征提取能力,实现多源信号的特征融合与特征提取工作.
图 14
负载口独立控制阀控缸系统感知左、右主阀阀芯位移、弹簧腔油液压力,同时感知负载位移以及液压缸控制腔压力. 3个部件的状态量为
式中:
系统t时刻的状态量
式中:
式(17)所示的
式中:
经IndRNN网络的输出结果为
式中:
阀控缸系统状态输入量为长时间序列,可以利用IndRNN网络的特点挖掘输入序列长时间跨度下特性得到输出序列
式中:
式中:
4. 结果与分析
4.1. 故障诊断参数
表 6 系统故障类型标签
Tab.6
| 故障类型 | 标签 | 故障类型 | 标签 | 故障类型 | 标签 | ||
| 系统无故障 | 0 | 左先导阀1故障 | 3 | 右主阀故障 | 6 | ||
| 左先导阀1故障 | 1 | 左先导阀2故障 | 4 | 液压缸故障 | 7 | ||
| 左先导阀2故障 | 2 | 左主阀故障 | 5 | 传感器故障 | 8 |
参照3.3节中的IndRNN-1DLCNN算法模型,模型参数如表7所示, 阀控液压缸状态感知样本经IndRNN网络和1DLCNN网络特征提取和特征融合后,输入全连接层与Softmax分类器得到概率输出
表 7 IndRNN-1DLCNN的模型参数
Tab.7
| 网络层 | 输入维度 | 输出维度 | 关键参数 |
| IndRNN | 9×2000 | 64×2000 | IndRNN单元个数:7 |
| 隐层特征个数:64 | |||
| 残差连接个数:3 | |||
| 1DLCNN | 64×2000 | 120×39 | 卷积核大小:100 |
| 步长:50 | |||
| MaxPooling1 | 120×29 | 120×5 | 池化核大小:20 |
| 步长:4 | |||
| 1DCNN | 120×5 | 200×3 | 卷积核大小:3 |
| 步长:1 | |||
| MaxPooling2 | 200×3 | 200×1 | 池化核大小:3 |
| 步长:1 |
4.2. 故障诊断结果与分析
训练采用Adam优化器,迭代次数为2 000,批尺寸大小为128, 初始学习率为0.000 2, 学习率更新策略采用自适应学习率调整. 当验证集损失累计50次不再下降的, 学习率下降一半. 表8给出不同算法下负载口独立控制阀控缸系统故障诊断的精度.
表 8 系统的故障诊断精度
Tab.8
| 模型 | 精度/% | 模型 | 精度/% | |
| LSTM | 25.6 | IndRNN | 84.7 | |
| 2DCNN | 87.9 | 1DLCNN | 90.9 | |
| 1DCNN | 85.1 | IndRNN-1DLCNN | 96.0 |
由于阀控缸系统具备长时间序列输入信号的特点,LSTM的长期记忆能力失效, 而IndRNN的长期记忆能力得到了很好的保持, 仅通过IndRNN网络可以达到84.7%的诊断精度. 由于其多通道特征提取的欠缺, IndRNN模型的诊断精度不如2DCNN模型的87.9%、1DCNN模型的85.1%及1DLCNN模型的90.9%. 由此可以看出,卷积操作对于系统多通道传感信号的捕捉能力较强. 利用1DLCNN模型能够达到90.9%的诊断精度,是除所提出的模型外的最优模型,这体现出1DLCNN在长时间跨度下具备较高的挖掘多通道特征信息的能力. 提出的IndRNN-1DLCNN模型既发挥了独立循环单元的超长期记忆能力, 又通过一维大卷积核更大的感受野充分挖掘了系统的细化特征,模型的诊断精度能够达到96%,相较于其他模型有较大提升. 结果表明,基于提出的系统状态感知方案,设计的IndRNN-1DLCNN模型可以更好地反映出系统故障情况,提高系统故障诊断的精度. 图15 给出基于IndRNN-1DLCNN的系统的测试集混淆矩阵, 系统测试集的总精度达到96%,且单一元件的故障识别准确率均大于93%,能够较为准确地识别出系统发生故障的具体元件. 模型的误判主要发生在正常数据与故障数据之间, 这是因为系统在即将发生故障时,模型对于临界点的判定无法做到十分精确,由于4个先导阀与2个主阀构成了整个阀组, 结构上的耦合性导致了阀组内的故障定位稍有欠缺,这也是可以理解的. 对于结构上相对独立的传感器以及液压缸来说,该算法模型不会将它们的故障与阀组内部件的故障相混淆,这是较理想的结果.
图 15
4.3. 模型可视化结果与分析
为了直观地看出不同算法对系统故障诊断算法的影响,如图16给出负载口独立控制阀控液压缸系统的不同故障诊断模型的可视化结果. 采用t-SNE降维方法,通过欧氏距离衡量点对距离,将算法模型最后一层经过Softmax后的输出降维至两维进行可视化表达. 原始信号从空间分布上看,每类故障均没有鲜明的独立分布,它们的状态信息表征高度相似,出现了严重的混淆情况,因此无法区分出阀控液压缸系统故障发生的具体位置. 2DCNN、1DCNN、IndRNN以及1DLCNN这4个算法在一定程度上能够区分出阀控液压缸系统故障发生的具体位置,同时1DCNN、IndRNN以及1DLCNN对各类故障均能在一定程度上分离出来,这与表8表示的算法诊断精度具有一致性. 在不同的故障条件下,所提的IndRNN-1DLCNN算法能够提取出系统对应的故障特征,其在一定程度上呈现出更鲜明的独立分布,不同故障之间的特征分散度更高,同一类故障维持一定的聚集性.
图 16
4.4. 变工况性能分析
为了验证所提的IndRNN-1DLCNN模型针对不同工况下的负载口独立控制阀控液压缸系统的故障诊断能力,更改液压缸所推动的惯性负载的质量,分析不同负载工况下故障诊断算法的有效性.
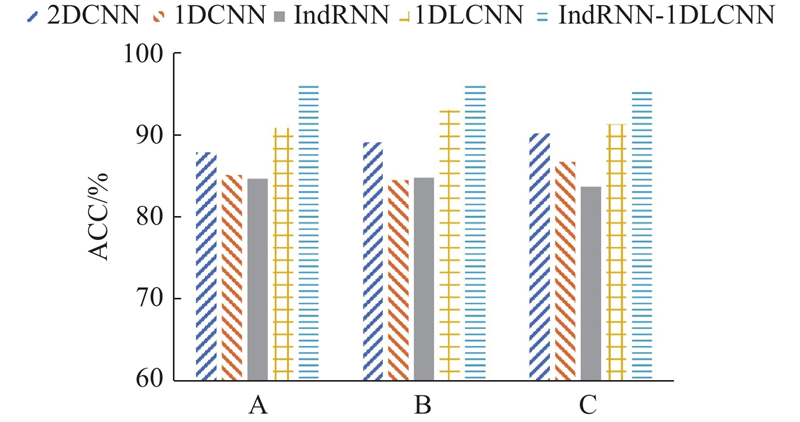
在不同工况下,图1所示的液压缸推动的负载情况不同,工况A、B、C负载质量分别取100、125、150 kg,负载刚度分别取2.50×106、2.75×106、3.00×106 N/m. 如图17给出3种工况下对应的不同故障诊断算法的精度. 如表9所示为对应的各个工况的诊断精度. 跟其余对比模型的比较中发现,所提算法的诊断精度均最高, 且均达到了95.4%以上,其余对比模型的精度均低于该水平. 本研究提出的IndRNN-1DLCNN算法在不同负载工况下均具有较好的故障诊断性能,均能较好地识别出发生故障的具体元件. 由于深度神经网络随机划分数据集的特点以及网络训练参数的差异,不同工况下的故障诊断效果有一定的偏差, 但这是可以接受的.
图 17
图 17 不同工况下的故障诊断算法精度
Fig.17 Fault diagnosis accuracy under different conditions
表 9 不同工况下的故障诊断算法精度对比
Tab.9
| 模型 | ACC/% | ||
| 工况A | 工况B | 工况C | |
| 2DCNN | 87.9 | 89.1 | 90.2 |
| 1DCNN | 85.1 | 84.5 | 86.7 |
| IndRNN | 84.7 | 84.8 | 83.7 |
| 1DLCNN | 90.9 | 93.0 | 91.3 |
| IndRNN-1DLCNN | 96.0 | 96.0 | 95.4 |
5. 结 论
(1) 提出一种适用于负载口独立控制阀控液压缸系统故障诊断的状态感知方案,基于系统压力信号与位移信号,归纳了不同元件发生故障时的系统特性.
(2) 设计基于IndRNN-1DLCNN的故障诊断算法,引入残差结构以增加IndRNN网络深度,引入1DLCNN以增强全局信息捕捉能力,从高度相似的状态信息表征中挖掘故障信息,实现了负载口独立控制阀控液压缸系统的故障元件识别.
参考文献
基于泵阀联合控制的负载口独立系统试验研究
[J].
Experiment research on individual metering systems of mobile machinery based on coordinate control of pump and valves
[J].
基于负载口独立控制的双伺服阀控缸系统
[J].
A dual servo-valved cylinder system based on load port independent control
[J].
Investigation into the independent metering control performance of a twin spools valve with switching technology-controlled pilot stage
[J].
Precision motion control of an independent metering hydraulic system with nonlinear flow modeling and compensation
[J].DOI:10.1109/TIE.2021.3102434 [本文引用: 1]
A review of electrohydraulic independent metering technology
[J].DOI:10.1016/j.isatra.2019.08.057 [本文引用: 1]
Active fault-tolerant control for electro-hydraulic systems with an independent metering valve against valve faults
[J].
Intelligent controls for electro-hydraulic poppet valves
[J].DOI:10.1016/j.conengprac.2013.02.008 [本文引用: 1]
Study on control performance of pilot high-speed switching valve
[J].
Performance analysis of a high-speed on/off valve based on an intelligent pulse-width modulation control
[J].
Energetic and dynamic impact of counterbalance valves in fluid power machines
[J].DOI:10.1016/j.enconman.2013.08.021 [本文引用: 1]
Fault diagnosis in a hydraulic directional valve using a two-stage multi-sensor information fusion
[J].DOI:10.1016/j.measurement.2021.109460 [本文引用: 1]
航空发动机燃油调节执行机构及其传感器的故障诊断与半物理仿真
[J].
Fault diagnosis and semi-physical simulation for actuator and sensor of aero-engine fuel regulator
[J].