(6) $ {C_i} = \left\{ {\begin{array}{*{20}{l}} {{\theta _1}({{\rm{ET}}_i} - {a_{i,k}}),}&{{{\rm{EET}}_i} \leqslant {a_{i,k}} \leqslant {{\rm{ET}}_i};} \\ {0,}&{ {{\rm{ET}}_i} \leqslant {a_{i,k}} \leqslant {{\rm{LT}}_i};} \\ {{\theta _2}({a_{i,k}} - {{\rm{LT}}_i}),}&{{{\rm{ET}}_i} \leqslant {a_{i,k}} \leqslant {{\rm{LLT}}_i};} \\ {\infty ,}&{其他.} \end{array}} \right.{\text{ }} $
(8) $ {U_i} = \left\{ {\begin{array}{*{20}{l}} {{{\left(\dfrac{{{a_{i,k}} - {{\rm{EET}}_i}}}{{{{\rm{ET}}_i} - {{\rm{EET}}_i}}}\right)}^\sigma },}&{{{\rm{EET}}_i} \leqslant {a_{i,k}} \leqslant {{\rm{ET}}_i};} \\ {1.0,}&{{{\rm{ET}}_i} \leqslant {a_{i,k}} \leqslant {{\rm{LT}}_i};} \\ {{{\left(\dfrac{{{{\rm{LLT}}_i} - {a_{i,k}}}}{{{{\rm{LLT}}_i} - L{T_i}}}\right)}^\sigma },}&{{{\rm{LT}}_i} \leqslant {a_{i,k}} \leqslant {{\rm{LLT}}_i};} \\ {0,}&{其他.} \end{array}} \right.{\text{ }} $
(10) $ \left.\begin{array}{l} 0 \leqslant d_{i,j}^{k,h} \leqslant {d_{i,j}}y_{i,j}^{k,h}; \\ \forall (i,j) \in N,i \ne j,k \in N,h \in H{\text{.}} \\ \end{array} \right\}$
(11) $ \sum\limits_{h = 1}^m {d_{i,j}^{k,h} = {d_{i,j}}x_{i,j}^k} {\text{ ; }}\forall (i,j) \in N,i \ne j,k \in N{\text{.}} $
(12) $\left. \begin{array}{l}{y}_{{i}_{2},{i}_{3}}^{k,{h}_{1}}\leqslant 2-{y}_{{i}_{1},{i}_{2}}^{k,{h}_{2}}-{x}_{{i}_{1},{i}_{2}}^{k}\text{; }\\ \forall k\in K,{h}_{1},{h}_{2}\in H,{h}_{1} < {h}_{2},{i}_{1}、{i}_{2}、{i}_{3}\in N\text{.}\end{array}\right\} $
(15) $ \begin{array}{cc}{t}_{i,j}^{k,h}=\dfrac{{d}_{i,j}^{k,h}}{{v}_{h}};\; \forall (i,j)\in N,i\ne j,k\in K,h\in H.\end{array} $
(17) $\left. \begin{gathered} {{l_{i,k}} \leqslant {e_h} - t_{i,j}^{k,h}+M(1 - y_{i,j}^{k,h});} \\ \forall (i,j) \in N,i \ne j,k \in K,h \in H{\text{.}} \\ \end{gathered} \right\}$
(18) $ \left.\begin{gathered} {{a_{j,k}} \geqslant {b_h} - t_{i,j}^{k,h} - M(1 - y_{i,j}^{k,h});} \\ \forall (i,j) \in N,i \ne j,k \in K,h \in H{\text{.}} \\ \end{gathered} \right\}$
(19) $ \begin{gathered} \begin{array}{*{20}{c}} {{a_{j,k}} \geqslant {l_{i,k}}+\displaystyle\sum\limits_{k = 1}^k {\displaystyle\sum\limits_{h = 1}^m {t_{i,j}^{k,h}} - M(1 - x_{i,j}^k);} }&{} \end{array} \\ \qquad \forall (i,j) \in N,k \in K{\text{.}} \\ \end{gathered} $
(25) $ \left.\begin{gathered} {0 \leqslant R_{j,k}^1 \leqslant R_{i,k}^1 - \displaystyle\sum\limits_{h = 1}^m {d_{i,j}^{k,h}\beta } +R(1 - x_{i,j}^k);} \\ k \in K,\forall i \in C,\forall j \in N,i \ne j{\text{ }}{\text{.}} \\ \end{gathered}\right\} $
(28) $\left. \begin{gathered} {y_{i,j}^{k,h} \leqslant x_{i,j}^k \leqslant \displaystyle\sum\limits_{h = 1}^m {y_{i,j}^{k,h}} }; \\ \forall (i,j) \in N,i \ne j,k \in N,h \in H{\text{.}} \\ \end{gathered} \right\}$
(29) $ \left.\begin{gathered} {x_{i,j}^k,y_{i,j}^{k,h},z_i^k \in \{ 0,1\} ;} \\ k \in K,h \in H,i \in N,j \in N{\text{.}} \\ \end{gathered}\right\} $
[1]
浙江省省政府办公厅. 关于印发《浙江省基本公共服务标准体系建设方案(2017-2020年)》的通知[EB/OL]. (2017-07-28)[2022-12-07]. http://jtyst.zj.gov.cn/art/2017/7/28/art_1676763_42409629.html.
[本文引用: 1]
[2]
张会云, 张琳琳 后疫情时代的“无接触配送”服务
[J]. 综合运输 , 2021 , 43 (8 ): 102 - 106
[本文引用: 1]
ZHANG Hui-yun, ZHANG Lin-lin "Contactless distribution" service in the post epidemic era
[J]. Comprehensive Transportation , 2021 , 43 (8 ): 102 - 106
[本文引用: 1]
[5]
李浩然 车辆路径优化问题综述
[J]. 信息与电脑: 理论版 , 2022 , 34 (3 ): 27 - 30
[本文引用: 1]
LI Hao-ran Overview of vehicle routing optimization
[J]. Information and Computer: Theoretical Edition , 2022 , 34 (3 ): 27 - 30
[本文引用: 1]
[6]
SOLOMON M M Algorithms for the vehicle routing and scheduling problems with time window constraints
[J]. Operations Research , 1987 , 35 (2 ): 254 - 265
DOI:10.1287/opre.35.2.254
[本文引用: 1]
[7]
KANG K H, LEE B K, LEE Y H, et al A heuristic for the vehicle routing problem with discrete split deliveries and time windows
[J]. European Journal of Operational Research , 2011 , 213 (3 ): 470 - 477
DOI:10.1016/j.ejor.2011.03.023
[本文引用: 1]
[8]
HOMBERGER J, GEHRING H Two evolutionary metaheuristics for the vehicle routing problem with time windows
[J]. Information Systems and Operational Research , 1999 , 37 (3 ): 297 - 318
DOI:10.1080/03155986.1999.11732386
[本文引用: 1]
[9]
FAN H, REN X X, ZHANG Y G, et al A chaotic genetic algorithm with variable neighborhood search for solving time-dependent green VRPTW with fuzzy demand
[J]. Symmetry , 2022 , 14 (10 ): 1 - 18
[本文引用: 1]
[10]
CONRAD R G, FIGLIOZZI M A The recharging vehicle routing problem
[J]. Proceedings of IIE Annual Conference , 2011 , 1 : 1 - 8
[本文引用: 1]
[12]
郭放, 杨珺, 杨超 基于货物分类配送的电动汽车路径优化与换电策略研究
[J]. 运筹与管理 , 2018 , 27 (9 ): 33 - 44
[本文引用: 1]
GUO Fang, YANG Jun, YANG Chao Research on route optimization and power exchange strategy of electric vehicles based on cargo classification and distribution
[J]. Operations Research and Management , 2018 , 27 (9 ): 33 - 44
[本文引用: 1]
[13]
肖建华, 王超文, 陈萍, 等 基于城市道路限行的多能源多车型车辆路径优化
[J]. 系统工程理论与实践 , 2017 , 37 (5 ): 1339 - 1348
DOI:10.12011/1000-6788(2017)05-1339-10
[本文引用: 1]
XIAO Jian-hua, WANG Chao-wen, CHEN Ping, et al Multi energy and multi vehicle routing optimization based on urban road restriction
[J]. System Engineering Theory and Practice , 2017 , 37 (5 ): 1339 - 1348
DOI:10.12011/1000-6788(2017)05-1339-10
[本文引用: 1]
[14]
DESAULNIERS G, ERRICO F, IRNICH S, et al Exact algorithms for electric vehiclerouting problems with time windows
[J]. Operations Research , 2016 , 64 (6 ): 1388 - 1405
DOI:10.1287/opre.2016.1535
[本文引用: 1]
[15]
YE C, HE W J, CHEN H Q Electric vehicle routing models and solution algorithms in logistics distribution: a systematic review
[J]. Environmental Science and Pollution Research International , 2022 , 29 (38 ): 57067 - 57090
DOI:10.1007/s11356-022-21559-2
[本文引用: 1]
[17]
CALVET L, FERRER A, GOMES M I, et al Combining statistical learning with metaheuristics for the multi-depot vehicle routing problem with market segmentation
[J]. Computers and Industrial Engineering , 2016 , 94 : 93 - 10
DOI:10.1016/j.cie.2016.01.016
[本文引用: 1]
[18]
马向国, 刘同娟, 杨平哲, 等 基于随机需求的冷链物流车辆路径优化模型
[J]. 系统仿真学报 , 2016 , 28 (8 ): 1824 - 1832
DOI:10.16182/j.cnki.joss.2016.08.017
[本文引用: 1]
MA Xiang-guo, LIU Tong-juan, YANG Ping-zhe, et al Vehicle routing optimization model of cold chain logistics based on random demand
[J]. Journal of System Simulation , 2016 , 28 (8 ): 1824 - 1832
DOI:10.16182/j.cnki.joss.2016.08.017
[本文引用: 1]
[19]
杨培颖, 唐加福, 于洋, 等 面向最小碳排放量的接送机场服务的车辆路径与调度
[J]. 自动化学报 , 2013 , 4 : 367 - 369
[本文引用: 1]
YANG Pei-ying, TANG Jia-fu, YU Yang, et al Vehicle routing and dispatching for airport service with minimum carbon emissions
[J]. Journal of Automation , 2013 , 4 : 367 - 369
[本文引用: 1]
[20]
王力锋, 黄斐 考虑客户等级划分的多目标冷链物流配送优化
[J]. 计算机仿真 , 2022 , 39 (9 ): 492 - 496
[本文引用: 2]
WANG Li-feng, HUANG fei Multi objective cold chain logistics distribution optimization considering customer hierarchy
[J]. Computer Simulation , 2022 , 39 (9 ): 492 - 496
[本文引用: 2]
[21]
MALANDRAKI C, DASKIN M S Time dependent vehicle routing problems: formulations, properties and heuristic algorithms
[J]. Transportation Science , 1992 , 26 (3 ): 185 - 200
DOI:10.1287/trsc.26.3.185
[本文引用: 1]
[22]
刘长石, 申立智, 盛虎宜, 等 考虑交通拥堵规避的低碳时变车辆路径问题研究
[J]. 控制与决策 , 2020 , 35 (10 ): 2486 - 2496
DOI:10.13195/j.kzyjc.2019.0257
[本文引用: 1]
LIU Chang-shi, SHEN Li-zhi, SHENG Hu-yi, et al Research on low-carbon time-varying vehicle routing problem considering traffic congestion avoidance
[J]. Control and Decision , 2020 , 35 (10 ): 2486 - 2496
DOI:10.13195/j.kzyjc.2019.0257
[本文引用: 1]
[24]
KESKIN M, CATAY B Partial recharge strategies for three electric vehicle routing problem with time windows
[J]. Transportation Review , 2016 , 89 (5 ): 111 - 127
[本文引用: 1]
[25]
ROBERTI R, WEN M The electric traveling salesman problem with time windows
[J]. Transportation Research Part E-Logistics and Transportation Review , 2016 , 89 (5 ): 32 - 52
[本文引用: 1]
[26]
张晓楠, 王陆宇, 谭昕妮, 等 时变条件下道路网的车辆路径优化
[J]. 机械科学与技术 , 2023 , 42 (2 ): 1 - 9
DOI:10.13433/j.cnki.1003-8728.20220230
[本文引用: 1]
ZHANG Xiao-nan, WANG Lu-yu, TAN Xin-ni, et al Time-dependent vehicle routing problem under road network
[J]. Mechanical Science and Technology , 2023 , 42 (2 ): 1 - 9
DOI:10.13433/j.cnki.1003-8728.20220230
[本文引用: 1]
[27]
刘秋萍. 考虑客户等级划分的多目标冷链物流配送车辆路径优化[D]. 镇江: 江苏大学, 2019: 1-92.
[本文引用: 1]
LIU Qiu-ping. Multi objective cold chain logistics distribution vehicle routing optimization considering customer ranking [D]. Zhenjiang: Jiangsu University, 2019: 1-92.
[本文引用: 1]
[28]
范定国, 贺硕, 段富, 等 一种基于云模型的综合评判模型
[J]. 科技情报开发与经济 , 2003 , 12 : 157 - 159
[本文引用: 1]
FAN Ding-guo, HE Shuo, DUAN Fu, et al A comprehensive evaluation model based on cloud-based model
[J]. Science and Technology Information Development and Economy , 2003 , 12 : 157 - 159
[本文引用: 1]
[29]
刘杰, 王宇, 李文立 基于云模型的商家信誉综合评价方法
[J]. 大连理工大学学报: 社会科学版 , 2017 , 38 (1 ): 88 - 93
[本文引用: 1]
LIU Jie, WANG Yu, LI Wen-li Comprehensive evaluation method of business reputation based on cloud-based model
[J]. Journal of Dalian University of Technology: Social Science Edition , 2017 , 38 (1 ): 88 - 93
[本文引用: 1]
[31]
HOLLAND J H. Adaptation in nature and artificial systems [M]. Cambridge: MITP, 1992: 1-211.
[本文引用: 1]
[32]
贾永基, 丁慧娜, 李嘉, 等 考虑时变速度和动态需求的电动车辆路径问题
[J]. 工业工程与管理 , 2022 , 27 (2 ): 59 - 66
DOI:10.19495/j.cnki.1007-5429.2022.02.008
[本文引用: 1]
JIA Yong-ji, DING Hui-na, LI Jia, et al Electric vehicle routing problem considering time-varying speed and dynamic demand
[J]. Industrial Engineering and Management , 2022 , 27 (2 ): 59 - 66
DOI:10.19495/j.cnki.1007-5429.2022.02.008
[本文引用: 1]
[33]
杭州市城乡建设发展研究院. 杭州市交通拥堵指数实时监测平台[EB/OL]. [2022-12-07]. https://hzjtydzs.com:801/index.html.
[本文引用: 1]
1
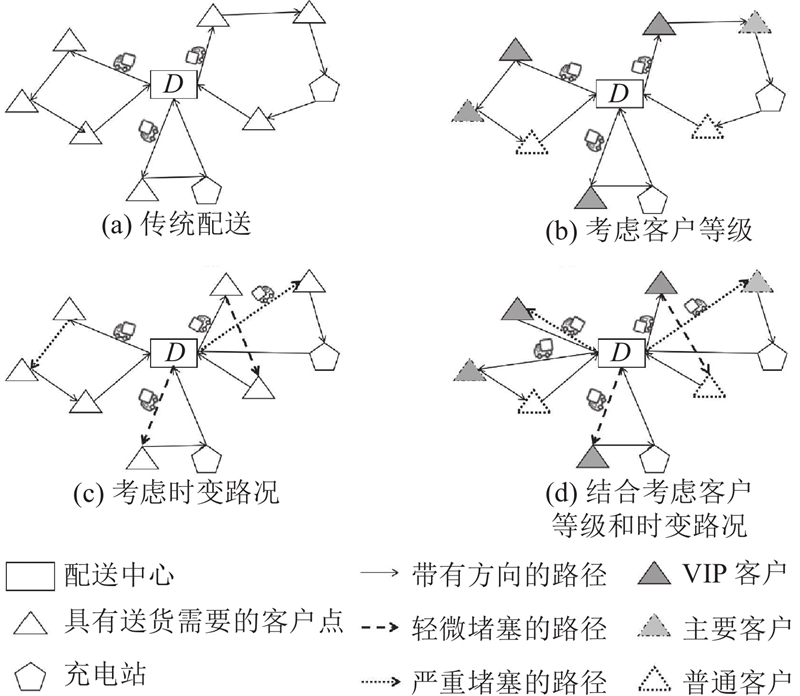
... 随着“构建智慧城市”理念的不断深入,“无人化”和“去快递员化”的配送模式脱颖而出. 物流业的发展加重交通拥堵,道路交通状况影响配送车辆行驶速度,继而影响物流运输效率,而配送的末端服务质量,会直接关联客户体验. 《浙江省基本公共服务体系建设2020年工作要点》中明确,要推进智能收投终端和末端公共服务平台建设的方针政策[1 ] ,给“无接触配送”带来发展机遇[2 ] . ...
后疫情时代的“无接触配送”服务
1
2021
... 随着“构建智慧城市”理念的不断深入,“无人化”和“去快递员化”的配送模式脱颖而出. 物流业的发展加重交通拥堵,道路交通状况影响配送车辆行驶速度,继而影响物流运输效率,而配送的末端服务质量,会直接关联客户体验. 《浙江省基本公共服务体系建设2020年工作要点》中明确,要推进智能收投终端和末端公共服务平台建设的方针政策[1 ] ,给“无接触配送”带来发展机遇[2 ] . ...
后疫情时代的“无接触配送”服务
1
2021
... 随着“构建智慧城市”理念的不断深入,“无人化”和“去快递员化”的配送模式脱颖而出. 物流业的发展加重交通拥堵,道路交通状况影响配送车辆行驶速度,继而影响物流运输效率,而配送的末端服务质量,会直接关联客户体验. 《浙江省基本公共服务体系建设2020年工作要点》中明确,要推进智能收投终端和末端公共服务平台建设的方针政策[1 ] ,给“无接触配送”带来发展机遇[2 ] . ...
The truck dispatching problem
1
1959
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
车辆路径问题的模型及算法研究综述
1
2005
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
车辆路径问题的模型及算法研究综述
1
2005
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
车辆路径优化问题综述
1
2022
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
车辆路径优化问题综述
1
2022
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
Algorithms for the vehicle routing and scheduling problems with time window constraints
1
1987
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
A heuristic for the vehicle routing problem with discrete split deliveries and time windows
1
2011
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
Two evolutionary metaheuristics for the vehicle routing problem with time windows
1
1999
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
A chaotic genetic algorithm with variable neighborhood search for solving time-dependent green VRPTW with fuzzy demand
1
2022
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
The recharging vehicle routing problem
1
2011
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
电动车辆路径优化研究与进展
1
2018
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
电动车辆路径优化研究与进展
1
2018
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
基于货物分类配送的电动汽车路径优化与换电策略研究
1
2018
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
基于货物分类配送的电动汽车路径优化与换电策略研究
1
2018
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
基于城市道路限行的多能源多车型车辆路径优化
1
2017
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
基于城市道路限行的多能源多车型车辆路径优化
1
2017
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
Exact algorithms for electric vehiclerouting problems with time windows
1
2016
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
Electric vehicle routing models and solution algorithms in logistics distribution: a systematic review
1
2022
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
A multi-objective transportation routing problem
1
2015
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
Combining statistical learning with metaheuristics for the multi-depot vehicle routing problem with market segmentation
1
2016
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
基于随机需求的冷链物流车辆路径优化模型
1
2016
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
基于随机需求的冷链物流车辆路径优化模型
1
2016
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
面向最小碳排放量的接送机场服务的车辆路径与调度
1
2013
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
面向最小碳排放量的接送机场服务的车辆路径与调度
1
2013
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
考虑客户等级划分的多目标冷链物流配送优化
2
2022
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
... 从Solomon[20 ] 标准算例(C1、R1、RC1)中分别选取25、50和100个客户点的数据,模拟形成9组测试算例. C型数据是通过聚类操作之后生成的,客户的分布区域较为集中,R型数据为随机生成的客户分布,RC型数据客户的分布则是混合R型数据和C型数据分布的. 应用Matlab R2021a,在Windows 10操作系统的环境,Intel(R) Core(TM) i7-10710U CPU @ 1.10 GHz、内存16 GB的笔记本电脑上进行仿真求解. ...
考虑客户等级划分的多目标冷链物流配送优化
2
2022
... 车辆路径问题(vehicle routing problem,VRP)是由Dantzig等[3 ] 于1959年提出的. 随着物流的不断发展,VRP得到大量关注,众多学者在VRP的基础上进行大量的延申研究,引出VRP的不同变体[4 -5 ] . 针对带时间窗的车辆路径问题(vehicle routing problem with time windows, VRPTW),Solomon[6 ] 于1987年将时间窗的约束加入到VRP中. Kang等[7 ] 将时间窗和惩罚函数相结合,对VRP进行了更全面的研究. homberger等[8 ] 基于遗传算法提出分别在变异和交叉操作上改进的2种策略来求解VRPTW. Fan等[9 ] 针对具有模糊需求的时效绿色车辆路由问题,提出自适应邻域搜索时间的策略和劣质解接受机制. 针对电动车辆配送问题(electric vehicle routing problem, EVRP),Conrad等[10 ] 在VRP上提出1个电动车能够在特定客户点进行充电的EVRP模型. 更多学者从不同方面对EVRP分析结合更多现实因素展开进一步研究[11 ] . 郭放等[12 ] 研究了货物需求的差异及电动车换电的策略. 肖建华等[13 ] 以道路限行为背景,研究电动车和燃油车的混合配送路径优化问题. Desaulniers等[14 ] 考虑带时间窗的电动车辆路径问题的4种变体. Ye等[15 ] 介绍电动车辆路径问题模型的4种类型,指出理论方法的发展趋势. 在考虑客户等级问题中,Alexiou等[16 ] 考虑配送成本与不利情况的因素相结合,不同客户等级设置相应权重,利用支树结构搜索算法确定最优路线. Calvet等[17 ] 提出考虑市场细分策略,将统计学习技术与元启发式框架相结合的混合方法. 马向国等[18 ] 研究在配送需求随机,当客户不同等重要性下,通过自适应遗传算法求解总成本最小化的数学模型. 杨培颖等[19 ] 研究减少成本的同时,并提高客户满意度的多目标VRPTW模型. 王力锋等[20 ] 在考虑客户等级划分的基础上,设计新的多目标冷链物流配送优化方法. ...
... 从Solomon[20 ] 标准算例(C1、R1、RC1)中分别选取25、50和100个客户点的数据,模拟形成9组测试算例. C型数据是通过聚类操作之后生成的,客户的分布区域较为集中,R型数据为随机生成的客户分布,RC型数据客户的分布则是混合R型数据和C型数据分布的. 应用Matlab R2021a,在Windows 10操作系统的环境,Intel(R) Core(TM) i7-10710U CPU @ 1.10 GHz、内存16 GB的笔记本电脑上进行仿真求解. ...
Time dependent vehicle routing problems: formulations, properties and heuristic algorithms
1
1992
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
考虑交通拥堵规避的低碳时变车辆路径问题研究
1
2020
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
考虑交通拥堵规避的低碳时变车辆路径问题研究
1
2020
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
考虑时变交通拥堵的污染路径优化研究
1
2020
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
考虑时变交通拥堵的污染路径优化研究
1
2020
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
Partial recharge strategies for three electric vehicle routing problem with time windows
1
2016
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
The electric traveling salesman problem with time windows
1
2016
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
时变条件下道路网的车辆路径优化
1
2023
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
时变条件下道路网的车辆路径优化
1
2023
... 针对时变路况方面,Malandraki等[21 ] 研究时变速度的VRP,提出行驶时间分段函数. 刘长石等[22 ] 设计考虑交通拥堵指数的交通拥堵规避方法. 葛显龙等[23 ] 考虑车辆配送过程中在2个客户点间路段等待的情况,以极小化碳排放量和车辆行驶时间为双目标,建立优化模型. Keskin等[24 ] 考虑部分充电下的电动车辆路径优化问题,并利用变邻域搜索算法求解. Roberti等[25 ] 提出可以在短计算时间内解决20个客户实例的混合整数线性公式,以及基于通用变量邻域搜索和动态规划的三阶段启发式算法. 张晓楠等[26 ] 结合时变旅行时间和基于关键点构建的道路网路,建立以总旅行时间最小为目标的优化模型. ...
1
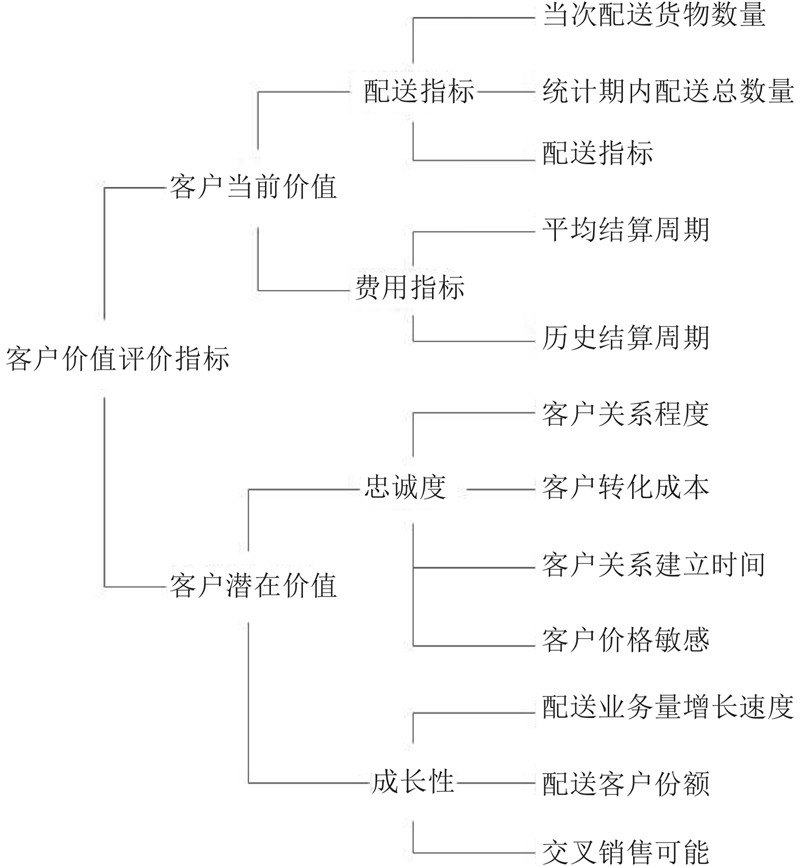
... 参考已有的客户细分理论相关研究,构建客户价值评价指标体系[27 ] 如图2 所示. ...
1
... 参考已有的客户细分理论相关研究,构建客户价值评价指标体系[27 ] 如图2 所示. ...
一种基于云模型的综合评判模型
1
2003
... 将客户等级的评分集假定为3个级别 $V = \left\{ {{V_1},{V_2},{V_3}} \right\}$ $\left[ {{C_{\min }},{C_{\max }}} \right]$ ${C_{\min }}$ ${C_{\max }}$ [28 ] 为 ...
一种基于云模型的综合评判模型
1
2003
... 将客户等级的评分集假定为3个级别 $V = \left\{ {{V_1},{V_2},{V_3}} \right\}$ $\left[ {{C_{\min }},{C_{\max }}} \right]$ ${C_{\min }}$ ${C_{\max }}$ [28 ] 为 ...
基于云模型的商家信誉综合评价方法
1
2017
... 根据公式可以计算如表1 所示. 参考二八理论,企业利润的80%是由企业20%的客户所创造,企业创造利润价值的客户数量仅为企业客户群体中的小部分. 若是客户评价值为区间边界,则该客户应取较低等级. 假设客户等级的指标集为 $U$ ${v_i}$ ${v_i} \geqslant 0$ ${v_1}+{v_2}+ \cdots + {v_m} = 1$ ${\boldsymbol{W}}$ . 通过每位专家对权重 $V$ ${X_i}$ $Ex$ $En$ $He$ ${\boldsymbol{V}}'$ . 对m 个客户等级影响指标进行打分,利用逆向云发生器计算得到相应云的数字特征 $Ex$ $En$ $He$ ${\boldsymbol{W}}'$ . 利用模糊合成算子计算综合评价结果,得到综合评价云模型,具体的云运算原理参考文献[29 ]. 通过Matlab将评价集云模型和等级综合评价云模型分别仿真显示出来,评价集云模型与综合评价云模型距离最近的,也就是最终的客户等级. ...
基于云模型的商家信誉综合评价方法
1
2017
... 根据公式可以计算如表1 所示. 参考二八理论,企业利润的80%是由企业20%的客户所创造,企业创造利润价值的客户数量仅为企业客户群体中的小部分. 若是客户评价值为区间边界,则该客户应取较低等级. 假设客户等级的指标集为 $U$ ${v_i}$ ${v_i} \geqslant 0$ ${v_1}+{v_2}+ \cdots + {v_m} = 1$ ${\boldsymbol{W}}$ . 通过每位专家对权重 $V$ ${X_i}$ $Ex$ $En$ $He$ ${\boldsymbol{V}}'$ . 对m 个客户等级影响指标进行打分,利用逆向云发生器计算得到相应云的数字特征 $Ex$ $En$ $He$ ${\boldsymbol{W}}'$ . 利用模糊合成算子计算综合评价结果,得到综合评价云模型,具体的云运算原理参考文献[29 ]. 通过Matlab将评价集云模型和等级综合评价云模型分别仿真显示出来,评价集云模型与综合评价云模型距离最近的,也就是最终的客户等级. ...
The Monte Carlo method
1
1949
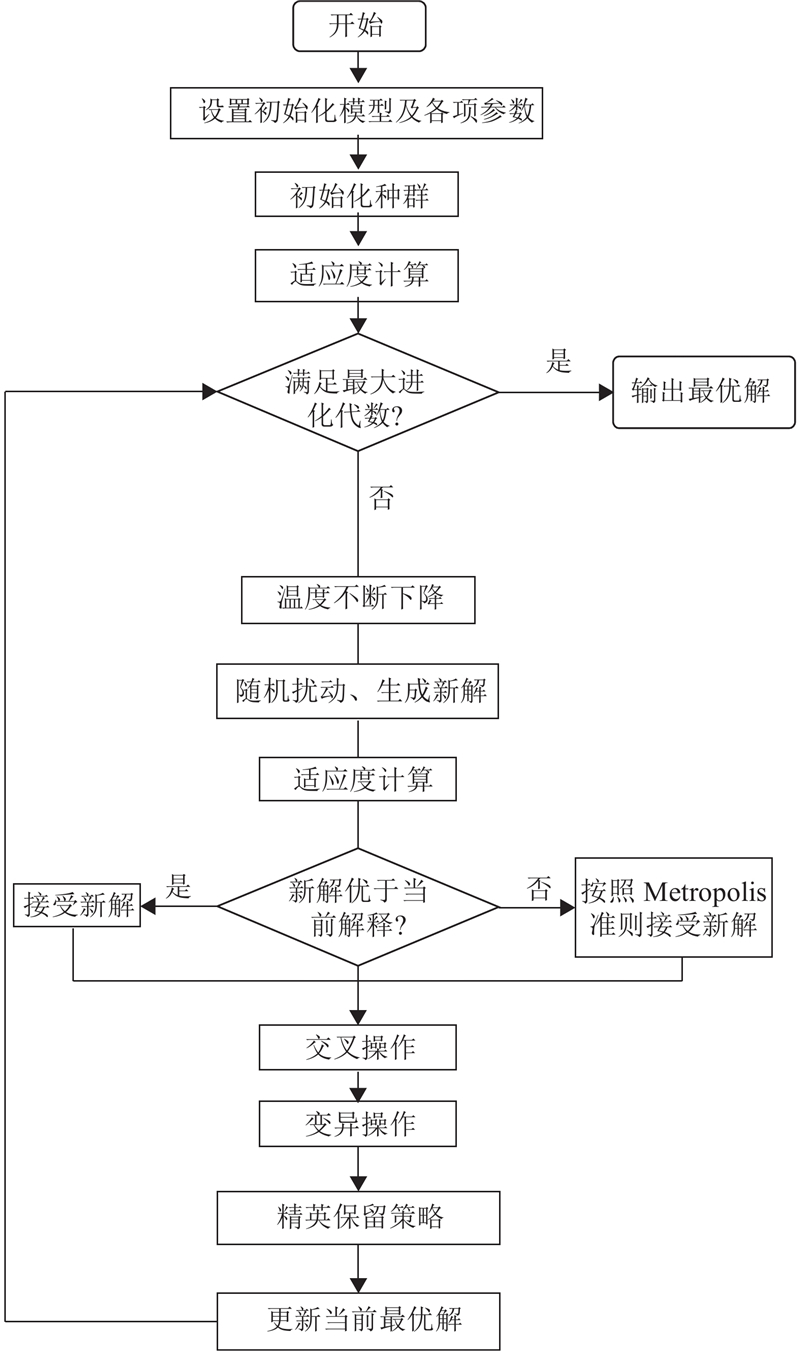
... 遗传算法和模拟退火算法都是基于概率分布的启发式搜索优化算法但是拥有不同特性. SA由Metropolis等[30 ] 于1953年提出,由于固体退火原理, 优化过程中以一定的概率接受较差解,有效防止陷入局部极值并逐渐趋于全局最优. GA是模拟生物进化过程的方法,使用达尔文的自然选择理论和遗传机制来寻找最优解,是密歇根大学的Holland[31 ] 在1975年开发的全局搜索优化算法. 混合遗传-模拟退火算法将2种方法相结合,可以一定程度上弥补2种算法的缺陷,在全局或者局部情况下都提高算法的搜索能力和效率. ...
1
... 遗传算法和模拟退火算法都是基于概率分布的启发式搜索优化算法但是拥有不同特性. SA由Metropolis等[30 ] 于1953年提出,由于固体退火原理, 优化过程中以一定的概率接受较差解,有效防止陷入局部极值并逐渐趋于全局最优. GA是模拟生物进化过程的方法,使用达尔文的自然选择理论和遗传机制来寻找最优解,是密歇根大学的Holland[31 ] 在1975年开发的全局搜索优化算法. 混合遗传-模拟退火算法将2种方法相结合,可以一定程度上弥补2种算法的缺陷,在全局或者局部情况下都提高算法的搜索能力和效率. ...
考虑时变速度和动态需求的电动车辆路径问题
1
2022
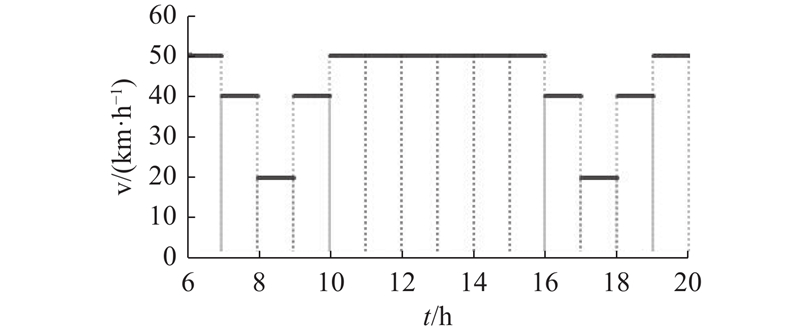
... 采取车辆在两客户点之间的配送路上不停靠策略, 即车辆从客户点 $i$ $j$ [32 ] . 参考杭州市交通拥堵大数据在线监测平台提供的数据[33 ] ,模拟不同时间段车辆行驶速度如图4 所示. 图中V 为车辆在不同时间段的行驶速度,t 为相对应的时间段. ...
考虑时变速度和动态需求的电动车辆路径问题
1
2022
... 采取车辆在两客户点之间的配送路上不停靠策略, 即车辆从客户点 $i$ $j$ [32 ] . 参考杭州市交通拥堵大数据在线监测平台提供的数据[33 ] ,模拟不同时间段车辆行驶速度如图4 所示. 图中V 为车辆在不同时间段的行驶速度,t 为相对应的时间段. ...
1
... 采取车辆在两客户点之间的配送路上不停靠策略, 即车辆从客户点 $i$ $j$ [32 ] . 参考杭州市交通拥堵大数据在线监测平台提供的数据[33 ] ,模拟不同时间段车辆行驶速度如图4 所示. 图中V 为车辆在不同时间段的行驶速度,t 为相对应的时间段. ...