服务计算与区块链、物联网、云计算等新兴技术跨界融合，催生出海量异构多模态的应用程序接口 (application programming interface, API)服务，如何有效地推荐符合用户开发需求的API服务成为当前服务计算领域的热点问题^[1]，服务推荐受到学术界和工业界的广泛关注. 早期服务推荐方法大多基于协同过滤的思想^[2-3]，根据用户或服务的相似度进行推荐. 此类方法缺乏对用户特征和服务特征的深度挖掘，推荐准确度较低. 一些研究者结合聚类技术、主题模型和因子分解机等方法^[4-7]进行改进. 虽然上述方法在一定程度上提高了推荐精确度和效率，但是仍存在以下缺陷: 1)当输入维度较高时，大部分服务推荐方法难以有效挖掘API服务之间隐式高阶关联； 2)在考虑用户行为相似性时，现有方法大多将用户与服务之间复杂的多行为交互（如调用、组合）同质化，视其为单一行为类型.

图神经网络可以较好地提取网络结构信息，是推荐系统目前的研究重点^[8-10]. 受限于图结构的度数要求，普通图神经网络只能将高阶服务关联转换为二元关系, 容易造成原始服务信息的丢失. 超图可以利用超边连接任意数量的服务节点，实现更为合理的服务特征建模^[10]. 以超图学习为基础，结合多行为推荐思想, 本研究提出基于超图卷积神经网络的多行为感知服务推荐方法(multi-behavior aware service recommendation method based on hypergraph graph convolution neural network, MBSRHGNN). 该方法构建多重超图结构对服务组合特征以及多行为依赖关系进行建模；利用双通道超图卷积网络捕获隐含的用户-服务特征；将API服务转化为嵌入向量，结合超图信号产生推荐服务的概率分布. 本研究创新点如下：1）构建行为感知超图和服务组合超图，根据超图功能结构特性，设计双通道超图卷积网络. 在超图卷积过程中，采用Chebyshev卷积算子和HG-DiffPool池化方法降低计算复杂度，减少模型过拟合风险. 2）引入多行为推荐方法对服务推荐场景中的多行为交互进行建模，结合超图自注意力机制优化目标行为表示，克服传统推荐方法中多行为交互同质化的缺陷.

协同过滤^[2-3]在服务推荐场景中的应用较为广泛，较为经典的是由Zheng等^[2]提出的一种混合式协同过滤服务推荐方法. 该方法综合考虑用户相似性和服务相似性，采用线性组合加权的方式进行服务推荐，但是传统的协同过滤服务推荐方法在应用时存在冷启动以及可拓展性差的问题. 现有研究^[4-6]表明服务功能聚类技术能够有效缩小服务搜索空间，优化API服务推荐流程. 此类方法大多利用向量空间模型将服务描述文档映射至高维特征空间，并结合余弦距离、欧式距离、马氏距离等方法计算服务相似度. Agarwal等^[4]使用长度特征权重矢量化表示API服务，结合功能词频进行服务聚类. 由于向量空间模型存在特征维度过高、语义稀疏的问题，一些工作结合自然语言处理技术来发掘服务间的语义关联^[5-6]. 笔者^[5]提出一种融合功能语义关联计算与密度峰值检测的Mashup服务聚类方法，利用功能语义权重来计算服务语义特征. 服务间语义关联的发掘需要高质量语料，然而现实中的服务描述文本容易导致大部分主题模型难以准确捕捉服务描述间的隐式语义关联^[6].

图神经网络可以有效地提取数据样本间的高阶关联和结构信息，目前在推荐系统中已得到广泛的应用^[8-10]. Wu等^[9]将会话建模为序列图结构，引入门控循环单元来生成项目嵌入和会话嵌入. 序列图、二分图、带权图等普通图结构都难以表示服务推荐场景中复杂的高阶服务组合关联. 作为一种特殊的图结构，超图能更有效地建模复杂数据样本之间的多元关系^[10]. 本研究采用构建多重超图的方式，基于双通道超图卷积神经网络深度挖掘服务组合特征.

多行为推荐方法能从异构的用户交互行为中挖掘潜在的行为语义，帮助构建更为合理、准确的用户行为表示^[11-13]. Yang等^[12]提出一种跨视图对比学习框架，利用多尺度Transformer和低秩自注意力机制捕获多行为偏好. Xia等^[13]基于图迁移学习思想，采用元学习器构建用户行为表示. 受上述工作启发，本研究将多行为推荐方法融合到服务推荐场景中，并引入超图自注意力机制动态地学习行为权重，优化行为感知超图的关联矩阵表示.

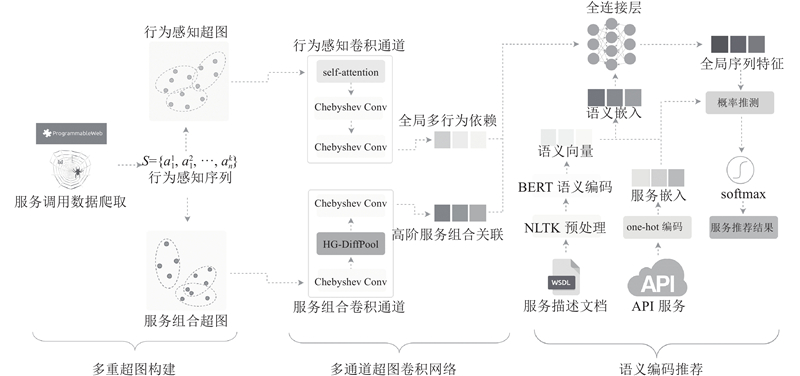
本研究提出的服务推荐模型MBSRHGNN的整体框架如图1所示，主要由以下3个模块构成. 1）多重超图构建：将爬取到的真实服务数据转化为行为感知序列和服务划分集，根据多行为交互类型和服务组合信息构建多重超图. 2）双通道超图卷积网络：基于双通道超图卷积网络捕获全局多行为依赖和高阶服务组合关联. 在行为感知卷积通道上，引入自注意力机制动态学习行为权重，将服务推荐与多行为推荐方法相结合. 在服务组合卷积通道上，增加HG-DiffPool超图池化层来降低服务特征维度. 在此模块中，self-attention为超图自注意力机制，Chebyshev Conv指的是Chebyshev近似后的卷积操作. 3）语义编码推荐：通过基于Transformer的双向编码器 (bidirectional encoder representation from transformers，BERT)编码层将功能语义信息转化为语义向量. 根据语义向量与API服务的one-hot编码结果，产生语义嵌入. 结合全局多行为依赖和高阶服务组合关联得到全局序列特征，预测推荐服务的概率.

行为感知序列和服务划分集是构建行为感知超图的基础. 将用户交互的服务项按时间顺序排列，并记录下具体的交互行为类型，可以得到行为感知序列 $ S = \{ a_1^1,a_2^1,\cdots, a_n^k\} $. 其中， $ a_n^k $多行为交互项，代表用户与API服务 $ {a_n} $之间有类型为 $ {b_k} $的交互行为. 按服务种类对 $ S $进行划分，结果定义为服务划分集 $ P = \{ {p_j} = (a_j^1,\cdots, a_j^k)\} $， $ {p_j} $为服务划分，是与 $ {a_n} $相关的所有多行为交互项的集合.

构建行为感知超图 $ {{\boldsymbol{G}}}_{{\rm{s}}}=（{V}_{{\rm{s}}},{E}_{{\rm{s}}}） $. 其中, $ {V_{\rm{s}}} $为超点集，由行为感知序列中的多行为交互项构成. $ {E_{\rm{s}}} $为超边集，超边由服务划分转换而来. $ {{\boldsymbol{G}}_{\rm{s}}} $可以用关联矩阵 $ {{\boldsymbol{H}}_{\rm{s}}} \in {{\bf{R}}^{|{V_{\rm{s}}}| \times |P|}} $表示， $ |{V_{\rm{s}}}| $和 $ |P| $分别为行为感知超图中的超点总数和超边总数，|P|=|E_s|. $ {{\boldsymbol{H}}_{\rm{s}}} $中的每个元素定义为

(1) $ {h}_{{\rm{s}}}({v}_{j}^{k},{e}_{{\rm{s}}}^{i})=\left\{\begin{array}{*{20}{l}} &1,&{a}_{j}^{k}\in {p}_{j}\text{；}\\ &0,&{其他}.\end{array}\right. $

式中： $ v_j^k $为超点， $ e_{\rm{s}}^i $为超边. 当 $ {p_j} $中存在多行为交互项 $ a_j^k $时,将 $ {h_{\rm{s}}}(v_j^k,e_{\rm{s}}^i) $记为1；否则，记为0. 在行为感知超图中，超点的度定义为 $d\left( {v_j^k} \right) =\displaystyle{\sum}_{e_{\rm{s}}^i \in {E_{\rm{s}}}} {{h_{\rm{s}}}\left( {v_j^k,e_{\rm{s}}^i} \right)}$，超边的度定义为 $\delta \left( {e_{\rm{s}}^i} \right) = \displaystyle{\sum}_{v_j^k \in {V_{\rm{s}}}} {{h_{\rm{s}}}\left( {v_j^k,e_{\rm{s}}^i} \right)}$.

基于上述定义,节点度矩阵和超边度矩阵分别以 $ {{\boldsymbol{D}}_{{\text{vs}}}} = diag\left( {d\left( {v_j^k} \right)} \right) $和 $ {{\boldsymbol{D}}_{{\text{es}}}} = diag\left( {\delta \left( {e_{\rm{s}}^i} \right)} \right) $表示. 为了避免梯度消失和梯度爆炸问题，对邻接矩阵进行归一化处理. 归一化后的邻接矩阵表述为

(2) $ {{\boldsymbol{\varTheta}} _{\rm{s}}} = {\boldsymbol{D}}_{{\rm{vs}}}^{ - {1 / 2}}{{\boldsymbol{H}}_{\rm{s}}}{\boldsymbol{D}}_{{\rm{es}}}^{ - 1}{\boldsymbol{H}}_{\rm{s}}^{\rm{T}}{\boldsymbol{D}}_{{\rm{vs}}}^{ - {1 / 2}} . $

基于API服务之间的组合关联构建服务组合超图. 首先，定义服务组合集 $ M = \{ {m_i} = \left( {{a_1},\cdots,{a_n}} \right)\} $， $ {m_i} $为服务组合，代表一系列API服务之间存在的组合关系，下标i用以区分不同的服务组合，下标n用于表示不同的API服务. 将 $ {m_i} $与行为感知序列相交，交集中的所有API服务构成超点集 $ {V_{\text{m}}} $，具体过程为

(3) $ {V_{\rm{m}}} = \bigcup {\left( {{m_i} \cap S} \right);\;{m_i} \in M} . $

当 $ {m_i} $与 $ S $中的多行为交互项相交时，考虑服务的异同. 每一组交集都将构成一条服务组合超边，将交集总数记为 $ \tau $，超边集可定义为 $ {E_{\rm{m}}} = \{ e{\rm{_m}}^1,\cdots,e_{\rm{m}}^{|\tau |}\} $. 服务组合超图可以表示为 $ {{\boldsymbol{G}}}_{\text{m}}=（{V}_{{\rm{m}}},{E}_{{\rm{m}}}） $. 在服务组合超图中，关联矩阵可以定义为 $ {{\boldsymbol{H}}_{\rm{s}}} \in {{\bf{R}}^{|{V_{\text{m}}}| \times \tau }} $，其中 $ |{V_{\text{m}}}| $为超点总数. 超点度矩阵和超边度矩阵分别定义为 $ {{\boldsymbol{D}}_{{\text{vm}}}} \in {{\bf{R}}^{|{V_{\text{m}}}| \times |{V_{\text{m}}}|}} $与 $ {{\boldsymbol{D}}_{{\text{em}}}} \in {{\bf{R}}^{\tau \times \tau }} $.

服务组合超图的归一化邻接矩阵定义为

(4) $ {{\boldsymbol{\varTheta}} _{\rm{m}}} = {\boldsymbol{D}}_{{\rm{vm}}}^{ - {1 / 2}}{{\boldsymbol{H}}_{\rm{m}}}{\boldsymbol{D}}_{{\rm{em}}}^{ - 1}{\boldsymbol{H}}_{\rm{m}}^{\rm{T}}{\boldsymbol{D}}_{{\rm{vm}}}^{ - {1 / 2}} . $

行为感知超图和服务组合超图结构不同、模态相异，难以用单一的超图卷积网络捕获其复杂异构的高阶关联信息. 因此，将超图上的近似谱卷积过程细分为2类卷积通道. 1)行为感知卷积通道：主要考虑多行为推荐方法和超图神经网络的结合，利用自注意力机制优化目标行为表示. 2)服务组合卷积通道：侧重于增强模型的泛化能力，降低高阶服务组合关联的特征维度，减少过拟合风险.

根据谱分解理论与图信号处理的思路^[14],将任意通道上的超图卷积过程定义为

(5) $ {{\boldsymbol{g}}_{\varphi} } * {\boldsymbol{x}} = {\boldsymbol{U}}\left[ {\left( {{{\boldsymbol{U}}^{\rm{T}}}{g_{\varphi} }} \right) \odot \left( {{{\boldsymbol{U}}^{\rm{T}}}{\boldsymbol{x}}} \right)} \right]. $

式中： $ {{\boldsymbol{g}}_{\varphi} } $为超图卷积核，φ为卷积核参数， $ * $为超图卷积操作运算符, $ {\boldsymbol{x}} $为超图信号, $ {\boldsymbol{U}} $为特征向量矩阵, $ \odot $为矩阵的Hadamard乘积.

由于涉及到多次特征分解和矩阵乘法运算，如式（5）定义的超图卷积过程计算代价较高，其复杂度与节点数量的平方成正比. 为此应用一阶Chebyshev多项式对卷积核 $ {{\boldsymbol{g}}_{\varphi} } $展开求解，并将拉普拉斯矩阵的最大特征值缩放为2^[15]. 近似后的超图卷积过程为

(6) $ {{\boldsymbol{g}}_{\varphi} } * {\boldsymbol{x}} \approx \varphi {\boldsymbol{D}}_{{\rm{vc}}}^{ - {1 / 2}}{{\boldsymbol{H}}_{\rm{c}}}{\boldsymbol{D}}_{{\rm{ec}}}^{ - 1}{\boldsymbol{H}}_{\rm{c}}^{\rm{T}}{\boldsymbol{D}}_{{\rm{vc}}}^{ - {1 / 2}} . $

式中： $ {{\boldsymbol{D}}_{{\rm{vc}}}} $和 $ {{\boldsymbol{D}}_{{\rm{ec}}}} $为任意卷积通道上的节点度矩阵和超边度矩阵. $ {{\boldsymbol{H}}_{\rm{c}}} $为任意卷积通道上的关联矩阵. 进一步将式（6）改写为

(7) $ {\boldsymbol{X}}_{\rm{c}}^{\left( {l+1} \right)} = \sigma \left( {{\boldsymbol{D}}_{{\rm{vc}}}^{ - {1 / 2}}{{\boldsymbol{H}}_{\rm{c}}}{\boldsymbol{D}}_{{\rm{ec}}}^{ - 1}{\boldsymbol{H}}_{\rm{c}}^{\rm{T}}{\boldsymbol{D}}_{{\rm{vc}}}^{ - {1 / 2}}{\boldsymbol{X}}_{\rm{c}}^l} \right) . $

式中： $ {\boldsymbol{X}}_{\rm{c}}^{\left( {l+1} \right)} \in {{\bf{R}}^{{\text{N}} \times {d_{l+1}}}} $和 $ {\boldsymbol{X}}_{\rm{c}}^l \in {{\bf{R}}^{{\text{N}} \times {d_l}}} $分别为第 $ l+1 $和第 $ l $层上的超图信号， $ N $和 $ d $为节点个数与特征维度. 超图上的谱卷积在近似后，无须再进行复杂的特征分解和傅里叶逆变换，拥有线性的计算复杂度. 在行为感知超图上，计算复杂度与服务划分规模相关；在服务组合超图上，计算复杂度受服务组合数量和行为感知序列长度影响.

式（7）表明超图卷积过程中的信息转移概率由关联矩阵和度矩阵所确定. 在行为感知超图上，关联矩阵的权重大小在初始化时就已经指定，因此难以度量不同服务交互的重要性差异. 为了进一步比较行为感知卷积通道上不同服务交互行为对超图信号的影响，引入自注意力机制优化行为感知超图的关联矩阵表示. 注意力分数的计算方法和关联矩阵的优化过程为

(8) $ {{\alpha }_{i}}=\frac{\exp \left( \text{LeakyReLU}\left( \mathop{{\boldsymbol{c}}}_{\text{b}}^{j}\oplus \mathop{{\boldsymbol{c}}}_{a}^{i} \right) \right)}{\displaystyle\sum\nolimits_{k\in \left| {{B}} \right|}{\exp \left( \text{LeakyReLU}\left( {{\boldsymbol{c}}}_{\text{b}}^{k}\oplus {{\boldsymbol{c}}}_{a}^{i} \right) \right)}}. $

式中： ${{\alpha }_{i}} $为学习得到的注意力分数， $\mathop{{\boldsymbol{c}}}_{\text{b}}^{j}\in {{\bf{R}}^{\text{d}}}$为行为嵌入， $\mathop{{\boldsymbol{c}}}_{\text{a}}^{i}\in {{\bf{R}}^{\text{d}}}$为服务嵌入，LeakyReLU为非线性激活函数, $\oplus $为嵌入向量的拼接操作, |B|为行为数.

(9) $ {h}_{{\rm{s}}}^{\prime }({v}_{j}^{k},{e}_{{\rm{s}}}^{i})=\left\{\begin{array}{*{20}{l}} &{\alpha }_{j},&{a}_{j}^{k}\in {p}_{j}\text{；}\\ &0,&{其他}.\end{array}\right. $

式中： $ h_{\rm{s}}^\prime (v_j^k,e_{\rm{s}}^i) $为自注意力机制优化后的行为感知关联矩阵的元素.

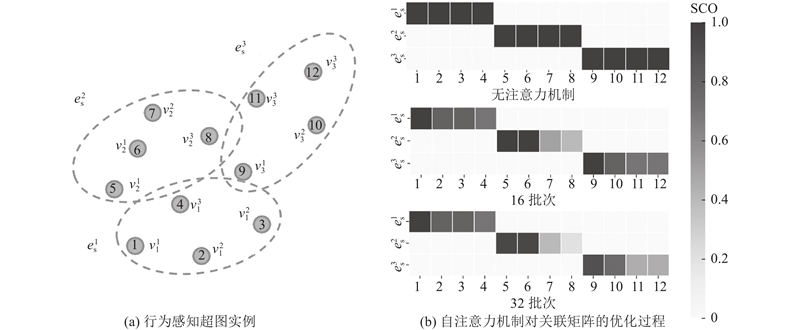
超图自注意力机制提高了节点间信息传播过程的可解释性. 如图2（a）所示为一个基于真实服务数据构建的行为感知超图实例. 图中 $ {v_1} $、 $ {v_2} $、 $ {v_3} $分别为Google Map、Open Weather和Facebook服务. 节点上标1、2、3分别为调用行为、浏览行为和组合行为，调用行为是目标行为. $ e_{\rm{s}}^1 $、 $ e_{\rm{s}}^2 $、 $ e_{\rm{s}}^3 $为构建的超边实例. 如图2（b）所示通过热力图展示自注意力机制对 $ {{\boldsymbol{H}}_{\rm{s}}} $的优化过程. 色块颜色的深浅代表注意力分数的高低，也反映了不同行为类型的重要性差异. 当未引入自注意力机制时，所有色块颜色相同，这代表矩阵元素取值只能为0或1，节点间信息转移概率是固定的. 当训练16轮次后，具有目标行为类型的节点 1、5、6、9取得了更高的注意力分数；当训练32轮次后，色块颜色区分更为明显. 以节点7、8为例，虽然两者均拥有辅助行为类型，但是节点7的色块颜色更深，对应的浏览行为拥有更重要的影响力，说明模型通过自注意力机制学习到多行为交互间更细微的差异.

引入超图自注意力机制后，行为感知超图通道上的超图卷积过程为

(10) $ {\boldsymbol{X}}_{\rm{c}}^{\left( {l+1} \right)} = \sigma \left( {{\boldsymbol{D}}_{{\rm{vs}}}^{ - {1 / 2}}{\boldsymbol{H}}_{\rm{s}}^\prime {\boldsymbol{D}}_{{\rm{es}}}^{ - 1}{\boldsymbol{H}}_{\rm{s}}^{\prime {\rm{T}}}{\boldsymbol{D}}_{{\rm{vs}}}^{ - {1 / 2}}{\boldsymbol{X}}_{\rm{c}}^l} \right) . $

由于在服务组合超图上，按式（4）构建的邻接矩阵较为稠密，直接进行特征学习存在较高的过拟合风险，而均值池化、最大池化、随机池化等常用池化方法在超图上所起到的降维效果有限，并且容易造成结构信息的丢失^[16]. 本研究根据超图结构特性，在DiffPool^[17]的基础上进行改良，提出超图池化方法HG-DiffPool.

该方法将服务组合通道上的第 $ l $层的邻接矩阵和超图信号输入到超图神经网络 $ {\text{HGNN}}_{{\rm{pool}}}^l $部件中进行学习，得到赋值矩阵 $ {{\boldsymbol{A}}^l} \in {{\bf{R}}^{{N_l} \times {N_{l+1}}}} $. 利用得到的赋值矩阵对邻接矩阵进行池化：

(11) $ {{\boldsymbol{A}}^l} = {\rm{soft}}\max \left( {{\rm{HGNN}}_{{\rm{pool}}}^l({\boldsymbol{\varTheta}} _{\rm{m}}^l,{\boldsymbol{X}}_{\rm{m}}^l)} \right) . $

式中： $ {\boldsymbol{\varTheta}} _{\rm{m}}^l $和 $ {\boldsymbol{X}}_{\rm{m}}^l $为服务组合卷积通道第 $ l $层上的邻接矩阵和超图信号， $ {\rm{soft}}\max $为激活函数. 赋值矩阵 $ {{\boldsymbol{A}}^l} $的矩阵元素表示第 $ l $层上的节点被分配到下一层的概率大小.

(12) $ {\boldsymbol{\varTheta}}_{\text{m}}^{\left( l+1 \right)}={{\left( {{{\boldsymbol{A}}}^{l}} \right)}^{{\rm{T}}}}{\boldsymbol{\varTheta}}_{\text{m}}^{l}{{{\boldsymbol{A}}}^{l}}. $

式中： ${\boldsymbol{\varTheta}} _{\rm{m}}^{(l+1)}$为池化后的超图邻接矩阵.

在完成对邻接矩阵的池化后，可以利用 ${\text{HGNN}}_{{\rm{embed}}}^l$部件对第 $ l $层上的邻接矩阵和超图信号进行采样,生成特征向量 $ {{\boldsymbol{Z}}^l} $. 在此基础上,利用采样特征向量生成池化后的超图信号 ${\boldsymbol{X}}_{\rm{m}}^{(l+1)}$. 特征采样过程和超图池化过程如下：

(13) $ {{\boldsymbol{Z}}^l} = {\rm{HGNN}}_{{\rm{embed}}}^l({\boldsymbol{\varTheta}} _{\rm{m}}^l,{\boldsymbol{X}}_{\rm{m}}^l) \text{，} $

(14) $ {{\boldsymbol{X}}}_{\text{m}}^{\left( l+1 \right)}={{\left( {{{\boldsymbol{A}}}^{l}} \right)}^{{\rm{T}}}}{{{\boldsymbol{Z}}}^{l}}. $

式中： $ {{\boldsymbol{Z}}^l} \in {{\bf{R}}^{{N_l} \times d}} $是经过特征采样后生成的特征向量, $ {\boldsymbol{X}}_{\rm{m}}^{(l+1)} \in {{\bf{R}}^{{N_{l+1}} \times d}} $是池化后的超图信号.

为了最大程度地利用服务语义信息，分2步构建API服务的嵌入向量. 首先利用one-hot编码将每个API服务转化为服务嵌入 ${\boldsymbol{c}}_{\rm{a}}^n \in {{\bf{R}}^d}$；使用自然语言处理工具包 (natural language toolkit，NLTK) 对训练样本中的服务描述文本和功能标签进行分词、去停、词频统计等操作，再利用BERT将处理后的描述文本和功能标签转化为相应的语义向量. 拼接语义向量和服务嵌入，得到语义嵌入 $ {{\boldsymbol{s}}_i} \in {{\bf{R}}^d} $.

行为感知序列的局部序列特征可以定义为 ${{\boldsymbol{S}}_{\text{p}}} = \displaystyle{\sum}_{i = 0} {{{\boldsymbol{s}}_i}}$. 通过全连接层融合局部序列特征与超图信号，得到全局序列特征 $ {{\boldsymbol{S}}_{\text{g}}} $. 计算全局序列特征和服务嵌入之间的乘积，得到推荐分数. 具体过程为

(15) $ {{\boldsymbol{S}}_{\rm{g}}} = {\boldsymbol{W}}\left( {{{\boldsymbol{x}}_{\text{m}}} \oplus {{\boldsymbol{x}}_{\text{s}}} \oplus {{\boldsymbol{S}}_{\rm{p}}}} \right) \text{，} $

(16) $ r\left( {{{\boldsymbol{S}}_{\text{g}}},{{\boldsymbol{c}}_{\rm{a}}^n}} \right) = {\left( {{\boldsymbol{S}}{}_{\text{g}}} \right)^{\rm{T}}}{{\boldsymbol{c}}_{\rm{a}}^n} . $

式中： $ {{\boldsymbol{x}}_{\text{m}}} $和 $ {{\boldsymbol{x}}_{\text{s}}} $分别为超图卷积得到的高阶服务组合关联和全局多行为依赖； $ {\boldsymbol{W}} $为可以学习的模型参数，即 $ {\boldsymbol{W}} \in {{\bf{R}}^{d \times 3d}} $；r为推荐分数.

为了消除超图卷积神经网络中的过平滑效应，所有的高阶特征均取多层卷积的平均值作为最终结果^[18]. 在得到推荐分数后,每个API服务被推荐的预测概率定义为

(17) $ y_i^\prime = \frac{{\exp \left( {r\left( {{{\boldsymbol{S}}_{\text{g}}},{{\boldsymbol{c}}_{\rm{a}}^i}} \right)} \right)}}{{\displaystyle\sum\limits_{j = 0} {\exp (r\left( {{{\boldsymbol{S}}_{\text{g}}},{{\boldsymbol{c}}_{\rm{a}}^j}} \right))} }} . $

通过构造交叉熵损失函数来训练和学习MBSRHGNN模型：

(18) $ L = - \sum\limits_{i = 1} {\left[ {{y_i}\ln \left( {y_i^\prime } \right)+\left( {1 - {y_i}} \right)} \right]\ln \left( {1 - y_i^\prime } \right)} . $

式中： $ {y_i} $为API服务被推荐的真实值.

通过多组实验来验证MBSRHGNN模型的有效性，给出实验数据集、基线方法、评估指标以及超参设置的介绍. 通过基线实验、消融实验、超参数实验回答以下3个问题：1）与现有的服务推荐方法、基于图神经网络的推荐方法和多行为推荐方法相比,模型的推荐性能如何？2）多重超图结构在模型中起何种作用？3）不同的超参数设置(例如：行为感知序列长度、特征向量维度大小)对模型的性能有什么影响？

本研究爬取了2019—2020年ProgrammableWeb网站上真实的用户交互记录和服务信息进行实验. 其中包括3 102位用户的11 032条多行为交互记录，6 206种服务组合以及13 329项API服务信息. 为了验证MBSRHGNN模型和现有推荐方法在数据高度稀疏场景下的性能表现，将预处理后的数据划分为稀疏数据集和稠密数据集，表1所示为2种实验数据集的具体统计信息. 表中，μ为用户数量，ε为服务组合数量，λ为API服务数量，l为服务描述文档的平均长度，ς为API服务被调用数，ρ为数据集的密度，Z为交互类型。

将MBSRHGNN模型与现有的10种推荐方法进行比较. 在实验过程中，各基线方法的参数设置基本保持和原文一致. 当出现梯度下降速度较慢、收敛时间过长、模型难以收敛等问题时，适当地调整学习率、批大小等参数. 基线方法中的前2种为服务推荐方法，第3、4种为基于图神经网络的推荐方法，其余方法为多行为推荐方法. 基线方法的详细介绍如下.

1）AFMRec^[7]. 采用注意力分解机挖掘多维特征向量之间的隐式服务关联. 超参设置为：注意力网络大小64，批大小512，学习率0.001.

2）WR-MSN^[5]. 基于密度峰值检测聚类算法进行服务聚类，利用服务邻域进行推荐. 超参设置为：词向量维度300，聚类划分数9，局部密度0.4.

3）DHCN^[8]. 基于双通道超图卷积网络提取序列特征嵌入. 超参设置为：特征维度100，批大小128，学习率0.000 1.

4）HyperRec^[19]. 将用户交互视为连接项目的超边，构建超图捕捉用户的动态短期兴趣. 超参设置为：特征维度64，批大小256，学习率0.001.

5）MBHT^[12]. 利用多尺度 Transformer 结合低秩自注意力对多行为序列进行编码. 超参设置为：特征维度64，批大小32，学习率0.001.

6）MB-GCN^[13]. 基于图卷积神经网络捕获用户—项目交互图上的多行为交互信息. 超参设置为：特征维度128，批大小64，学习率0.003.

为了保持和现有工作一致的评估设置，采用以下评估指标：命中率(hit ratio, HR)、归一化折损累计增益 (normalized discounted cumulative gain, NDCG)和平均倒数排名 (mean reciprocal rank, MRR). HR指标越高，说明服务推荐的精确性越好；NDCG指标与MRR指标越高，说明服务推荐的相关性越强.

在实验过程中, MBSRHGNN模型的主要超参设置如下：1）服务嵌入特征维度和语义嵌入特征维度在{16,32,64,96,128}中选择；2）行为感知序列长度在{10,20,30,40,60,100}中选取；3）学习率的取值为{0.001,0.003,0.006}；4）在{0.05,0.10,0.15,0.20}调整学习率衰减系数；5）使用基于最小批的ADAM优化器优化模型参数，取最小批大小为128.

根据参数实验结果,模型性能在特征维度为96，序列长度为40时达到最优. 依据实际经验，学习率初始取值为0.006，根据模型收敛情况进行分段衰减. 此外，在模型训练过程中执行提前停止策略. 如果在连续10个时间段内，测试数据上的HR指标、NDCG指标和MRR指标没有增加，则提前终止训练.

针对实验部分提出的问题1），将MBSRHGNN模型与基线方法进行比较，以验证性能优势. 每组基线实验在相同的实验设置下重复10次，取平均值作为最终实验结果，实验结果如表2所示. 表中，IMP为MBSRHGNN相较于最优基线方法的性能提升幅度，表中对所提出的MBSRHGNN方法进行加粗，具体分析如下.

1）在服务推荐方法中，基于服务聚类的WR-MSN方法受数据稀疏性问题影响较大. 基于注意力分解机的AFMRec方法能较好地适应数据稀疏的推荐场景，HR@5指标达到了0.381. 在稠密数据集上,WR-MSN方法的推荐精确度和相关性提升较大. 对比AFMRec方法，WR-MSN方法的HR@5指标提高了12.8%，MRR指标提高了11.7%.

2）在基于图神经网络的推荐方法中，HyperRec方法的性能表现最佳. 在多行为推荐方法中, MBHT模型的HR@5、MRR指标在所有基准方法中最优. MBHT模型在多尺度Transformer的基础上融入超图卷积神经网络，并利用跨视图对比学习方法进一步提高用户交互嵌入向量的表征能力.

3）所提的MBSRHGNN模型在不同密度的实验数据集上均取得了更好的推荐结果. 相较于最优的基准方法，MBSRHGNN的HR@5指标提高了4.5%~8.3%, NDCG@5指标和MRR指标分别提高了3.2%~8.8%和4.9%~6.9%，说明MBSRHGNN模型拥有更高的推荐精确度和推荐相关性.

MBSRHGNN模型的推荐性能优势具体分析如下：1）根据多重超图功能结构特性设计的双通道超图卷积网络能有效捕获高阶服务组合关联和全局多行为依赖；2）多行为权重并非事先指定，而是利用自注意力在模型训练过程中动态学习得到的；3）将API服务的one-hot编码与BERT语言模型相融合，克服了服务嵌入语义稀疏的问题.

针对实验部分提出的问题2），构造3种MBSRHGNN的变体模型进行消融实验，变体模型的详细介绍如下：1)MH-Behavior：移除行为感知超图，屏蔽行为感知卷积通道上的超图信号. 2)MH-Mashup：移除服务组合超图，屏蔽服务组合卷积通道上的超图信号. 3)MH-HyperGraph：移除多重超图结构.

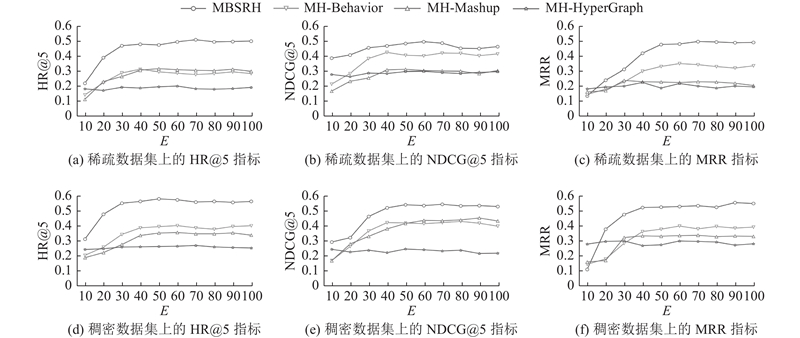
在消融实验过程中,所有变体模型取相同的超参数设定，在2类服务数据规模（见表1）下进行10次实验. 实验结果如图3所示，图中，E为模型训练批次. 可以看出：1）移除多重超图结构的MH-HyperGraph变体表现出较差的学习能力，各项指标没有随着训练轮次的增加而提升，综合推荐质量也较低；2）保留了部分超图结构的MH-Behavior和MH-Mashup变体表现出更强的数据样本学习能力. 从实验结果看，在经过30~40轮次训练后，两者的HR@5、NDCG@5和MRR指标均超过了MH-HyperGraph变体. 3）相较于各种变体，拥有多重超图结构的原模型MBSRHGNN表现出最好的推荐性能. 综上可知，所提的多重超图结构是有效的，能够实现对用户-服务特征的合理建模.

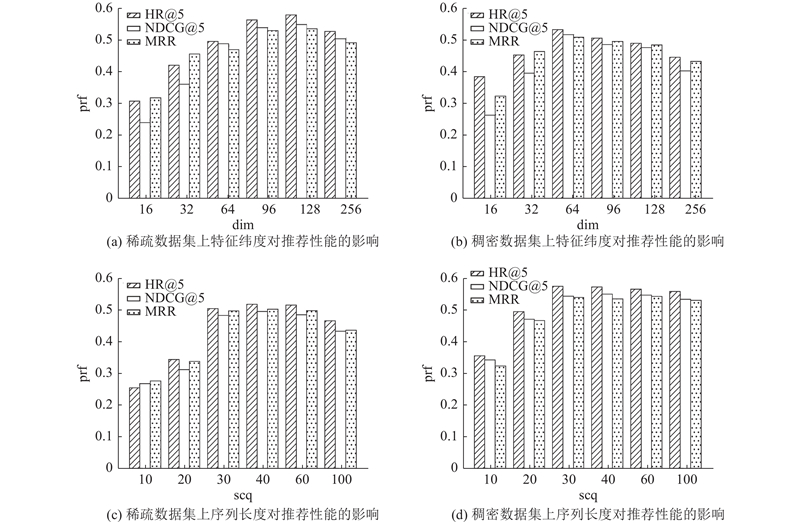
针对实验部分提出的问题3），验证特征维度和行为感知序列长度对推荐性能的影响. 特征维度在{16,32,64,96,128}中选择，序列长度在{10,20,30,40,60,100}中选取. 超参数实验结果如图4所示. 图中dim为特征维度，seq为序列长度，prf为推荐性能.

特征维度决定服务嵌入和语义嵌入的表征能力，并且对模型的学习能力也有重要的影响. 过小的特征维度将导致模型不能充分地学习数据样本间的非线性关系，造成欠拟合问题. 随着特征维度的增高，模型的学习能力逐渐增强，但是过强的学习能力容易造成过拟合现象. 特征维度不是越大越好. 对比图4（a）、（b），当特征维度取值较低时，模型的推荐性能较差. 随着特征维度的上升，模型的推荐性能逐渐增强. 当特征维度取值为128时，模型在稀疏数据集上的推荐性能达到最优. 当特征维度取值为64时，模型在稠密数据集上的推荐性能达到最优. 随着特征维度的上升，模型的推荐性能略有下降，MBSRHGNN模型具有一定的鲁棒性，推荐性能不会因为超参数细微的变化发生大幅波动.

行为感知序列长度主要对多重超图构建过程有较大的影响. 当行为感知序列较短时，产生的服务划分数量会变少，并且与服务组合集的相交部分也会变小,导致构建的行为感知超图和服务组合超图变得更为稀疏,不利于全局多行为依赖和高阶服务组合关联的提取. 当行为感知序列较长时,虽然能够引入更多的用户交互样本，但是也会带来一定的噪声，造成推荐准确率的下降. 对比图4（c）、（d）可以看出，序列长度的合理取值应该在[30,60]. 在稀疏数据集上，用户交互的API服务数量较少, 需要更长的序列来引入额外的交互信息. 在稠密数据集上，交互信息较丰富，即使序列长度较短，模型也有较高的推荐质量.

本研究提出基于超图卷积神经网络的多行为感知服务推荐方法. 通过自注意力机制，为不同的服务交互行为赋予权重. 相比较于普通的图神经网络，通过多重超图结构能够有效地表示全局多行为依赖和高阶服务组合关联2种特征. 在不同稀疏度的数据集上，本研究相比其他主流推荐方法在精度评价指标和相关度评价指标上能够获得更好的效果. 不足之处在于提出的多重超图结构仍不够完善，没有考虑服务质量信息，超图信号与嵌入向量的融合过程还有待改进. 在下一阶段的工作主要包括: 丰富多重超图结构，以便可以更准确、合理地表示服务特征；探索超图信号与嵌入向量的自适应地融合方法；在图神经网络框架的基础上，构造不同类型的神经网络，从多个侧面提取、整合服务特征.