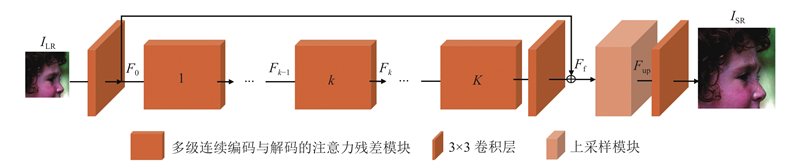
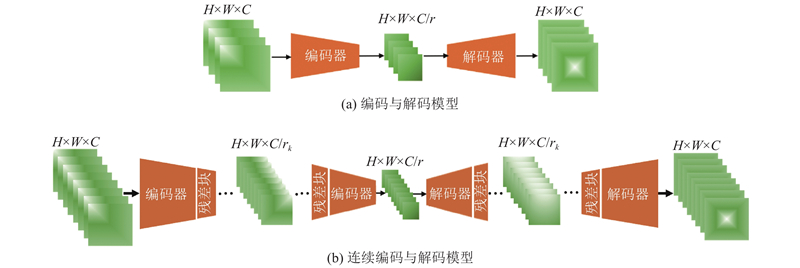
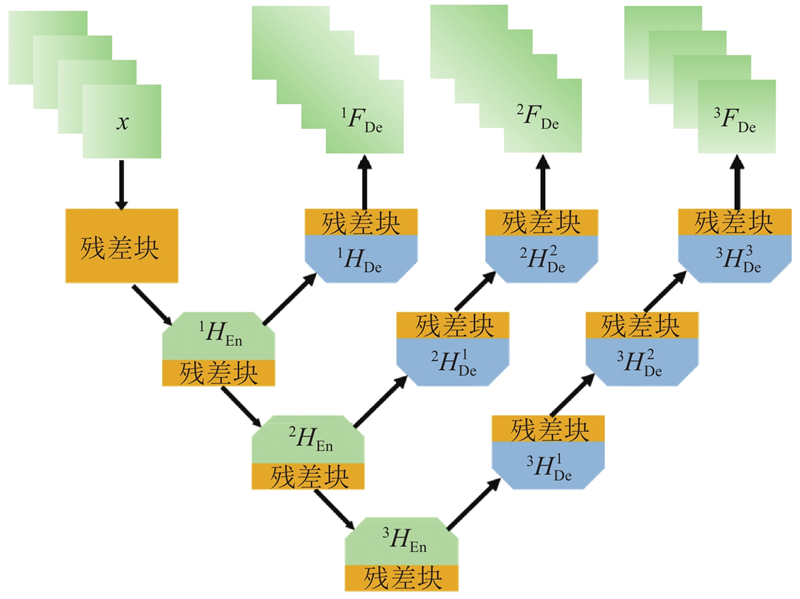
基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题。基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息.
[20]
ZHANG Y, TIAN Y, KONG Y, et al. Residual dense network for image super-resolution [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 2472-2481.
[本文引用: 1]
[21]
ZHANG Y, LI K, LI K, et al. Image super-resolution using very deep residual channel attention networks [C]// European Conference on Computer Vision . [S.l.]: Springer, 2018: 294-301.
[本文引用: 1]
[22]
CHEN H, GU J, ZHANG Z. Attention in attention network for image super-resolution [EB/OL]. [2022-04-21]. https://arxiv.org/pdf/2104.09497.pdf.
[本文引用: 5]
[23]
AGUSTSSON E, TIMOFTE R. NTIRE 2017 challenge on single image super-resolution: dataset and study [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops . Honolulu: IEEE, 2017: 126-135.
[本文引用: 1]
[24]
BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding [C]// Proceedings British Machine Vision Conference . Surrey: [s.n.], 2012: 1-10.
[本文引用: 1]
[25]
ZEYDE R, ELAD M, PROTTER M, et al. On single image scale-up using sparse-representations [C]// International Conference on Curves and Surfaces . [S.l.]: Springer, 2010: 711-730.
[本文引用: 1]
[26]
MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics [C]// Proceedings of the IEEE International Conference on Computer Vision . Vancouver: IEEE, 2001: 416-423.
[本文引用: 1]
[27]
HUANG J, SINGH A, AHUJA N, et al. Single image super-resolution from transformed self-exemplars [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Boston: IEEE, 2015: 5197-5206
[本文引用: 1]
[28]
KINGMA D P, BA J L. ADAM: a method for stochastic optimization [EB/OL]. [2022-04-21]. https://arxiv.org/pdf/1412.6980.pdf.
[本文引用: 1]
[29]
WANG Z, BOVIK A C, SHEIKH H R, et al Image quality assessment: from error visibility to structural similarity
[J]. IEEE Transactions on Image Processing , 2004 , 13 (4 ): 600 - 612
DOI:10.1109/TIP.2003.819861
[本文引用: 1]
[30]
HARIS M, SHAKHNAROVICH G, UKITA N Deep back-projection networks for super-resolution
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2021 , 43 (12 ): 4323 - 4337
DOI:10.1109/TPAMI.2020.3002836
[本文引用: 3]
[31]
LIU J, TANG J, WU G. Residual feature distillation network for lightweight image super-resolution [C]// European Conference on Computer Vision . [S.l.]: Springer, 2020: 41-55.
[本文引用: 4]
[2]
REBECQ H, RANFTL R, KOLTUN V, et al. Events-to-video: bringing modern computer vision to event cameras [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 3857-3866.
[本文引用: 1]
[4]
LIU H, GU Y, WANG T, et al Satellite video super-resolution based on adaptively spatiotemporal neighbors and nonlocal similarity regularization
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2020 , 58 (12 ): 8372 - 8383
DOI:10.1109/TGRS.2020.2987400
[6]
DENG L, YU D. Deep learning: methods and applications [M]. [S.l.]: Now Foundations and Trends, 2014: 197-387.
[本文引用: 1]
[7]
JORDAN M I, MITCHELL T M Machine learning: trends, perspectives, and prospects
[J]. Science , 2015 , 349 (6245 ): 255 - 260
DOI:10.1126/science.aaa8415
[9]
ANWAR S, KHAN S, BARNES N A deep journey into super-resolution: a survey
[J]. ACM Computing Surveys , 2020 , 53 (3 ): 1 - 34
[本文引用: 1]
[10]
WANG Z, CHEN J, HOI S C H Deep learning for image super-resolution: a survey
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2021 , 43 (10 ): 3365 - 3387
DOI:10.1109/TPAMI.2020.2982166
[11]
SONG Z, ZHAO X, JIANG H Gradual deep residual network for super-resolution
[J]. Multimedia Tools and Applications , 2021 , 80 : 9765 - 9778
DOI:10.1007/s11042-020-10152-9
[12]
SONG Z, ZHAO X, HUI Y, et al Progressive back-projection network for COVID-CT super-resolution
[J]. Computer Methods and Programs in Biomedicine , 2021 , 208 : 106193
DOI:10.1016/j.cmpb.2021.106193
[本文引用: 1]
[13]
DONG C, LOY C C, HE K, et al Image super-resolution using deep convolutional networks
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 38 (2 ): 295 - 307
[本文引用: 5]
[14]
DONG C, LOY C C, TANG X, et al. Accelerating the super-resolution convolutional neural network [C]// European Conference on Computer Vision . [S.l.]: Springer, 2016: 391-407.
[本文引用: 5]
[15]
SHI W, CABALLERO J, HUSZÁR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 1874-1883.
[本文引用: 1]
[16]
KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 1646-1654.
[本文引用: 5]
[17]
KIM J, LEE J K, LEE K M. Deeply-recursive convolutional network for image super-resolution [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 1637-1645.
[本文引用: 1]
[18]
LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 136-144.
[本文引用: 1]
[19]
TONG T, LI G, LIU X, et al. Image super-resolution using dense skip connections [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 4799-4807.
[本文引用: 1]
1
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
1
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
5
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
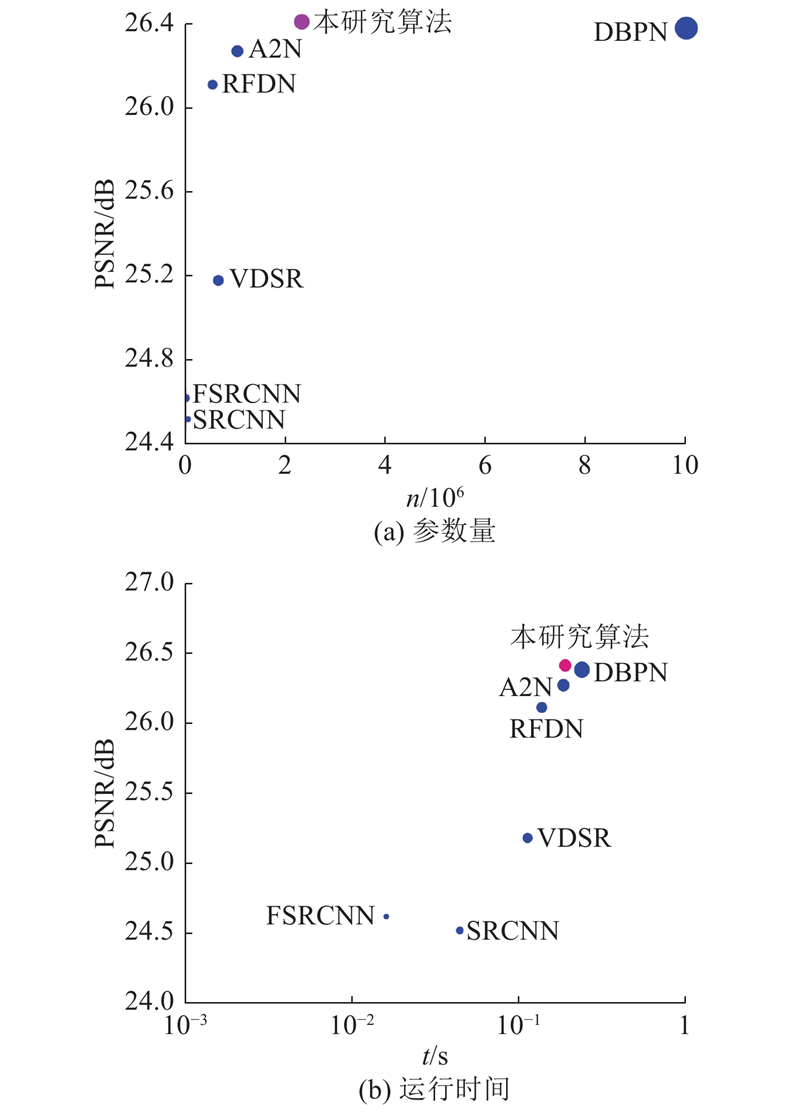
... 将主流的7种算法(Bicubic、SRCNN[13 ] 、FSRCNN[14 ] 、VDSR[16 ] 、DBPN[30 ] 、RFDN[31 ] 和A2N[22 ] )与所提算法进行算法性能的对比测试. 分别在放大倍数为2、3和4的情况下,使用不同算法测试Set5、Set14、BSD100和Urban100数据集, 测试结果如表1 ~3 所示. 相比主流算法, 在放大倍数为2、3的情况下,所提算法测试4个数据集的性能评价指标均为最优, 实现了PSNR、SSIM的较大提升.相比主流算法, 在放大倍数为4的情况下,所提算法测试Urban100数据集的性能评价指标最优. 具体来说, 对于测试集Set5、Set14、BSD100、Urban100,当放大倍数为2时, 所提算法获得的PSNR比DBPN算法获得的次优PSNR分别提升0.08、0.09、0.01、0.19 dB;当放大倍数为3时, 所提算法获得的PSNR比A2N算法获得的次优PSNR分别提升0.11、0.07、0.06、0.25 dB.当放大倍数为4时,对于Urban100测试集, 所提算法获得的PSNR比DBPN算法获得的次优PSNR值提升0.03 dB;当放大倍数为2、4时, 所提算法获得的SSIM比DBPN算法获得的次优SSIM分别提升0.001 8、0.002 8;当放大倍数为3时, 所提算法获得的SSIM比A2N算法获得的次优SSIM提升0.006 4. 所提算法在特征提取过程中通过多级连续编码与解码的注意力残差块,获取不同层级的图像特征信息, 为不同层级的图像特征信息分配不同计算量的权重, 能够尽可能多地获得图像内部丰富的细节特征, 因此相比7种主流算法, 所提算法具有较好的超分辨率重建性能, 能够实现PSNR、SSIM的较大提升. ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 2)
Tab.1 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 33.66 0.929 9 30.24 0.868 8 29.56 0.843 1 26.88 0.840 3 SRCNN[13 ] 36.66 0.954 2 32.45 0.906 7 31.36 0.887 9 29.50 0.894 6 FSRCNN[14 ] 37.05 0.956 0 32.66 0.909 0 31.53 0.892 0 29.88 0.902 0 VDSR[16 ] 37.53 0.959 0 33.05 0.913 0 31.90 0.896 0 30.77 0.914 0 DBPN[30 ] 38.09 0.960 0 33.85 0.919 0 32.27 0.900 0 32.55 0.932 4 RFDN[31 ] 38.05 0.960 6 33.68 0.918 4 32.16 0.899 4 32.12 0.927 8 A2N[22 ] 38.06 0.960 8 33.75 0.919 4 32.22 0.900 2 32.43 0.931 1 本研究 38.17 0.961 0 33.94 0.920 8 32.28 0.901 0 32.74 0.934 2
表 2 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为3) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 3)
Tab.2 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 30.39 0.868 2 27.55 0.774 2 27.21 0.738 5 24.46 0.734 9 SRCNN[13 ] 32.75 0.909 0 29.30 0.821 5 28.41 0.786 3 26.24 0.798 9 FSRCNN[14 ] 33.18 0.914 0 29.37 0.824 0 28.53 0.791 0 26.43 0.808 0 VDSR[16 ] 33.67 0.921 0 29.78 0.832 0 28.83 0.799 0 27.14 0.829 0 RFDN[31 ] 34.41 0.927 3 30.34 0.842 0 29.09 0.805 0 28.21 0.852 5 A2N[22 ] 34.47 0.927 9 30.44 0.843 7 29.14 0.805 9 28.41 0.857 0 本研究 34.58 0.928 8 30.51 0.845 6 29.20 0.807 9 28.66 0.863 4
表 3 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为4) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 4)
Tab.3 算法 Set5 Set14 BSD100 Urban100 PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM Bicubic 28.42 0.810 4 26.00 0.702 7 25.96 0.667 5 23.14 0.657 7 SRCNN[13 ] 30.48 0.862 8 27.50 0.751 3 26.90 0.710 1 24.52 0.722 1 FSRCNN[14 ] 30.72 0.866 0 27.61 0.755 0 26.98 0.715 0 24.62 0.728 0 VDSR[16 ] 31.35 0.883 0 28.02 0.768 0 27.29 0.725 1 25.18 0.754 0 DBPN[30 ] 32.47 0.898 0 28.82 0.786 0 27.72 0.740 0 26.38 0.794 6 RFDN[31 ] 32.24 0.895 2 28.61 0.781 9 27.57 0.736 0 26.11 0.785 8 A2N[22 ] 32.30 0.896 6 28.71 0.784 2 27.61 0.737 4 26.27 0.792 0 本研究 32.37 0.897 1 28.76 0.785 7 27.55 0.734 0 26.41 0.797 4
为了测试所提算法的重建图像的视觉效果, 在放大倍数为4的情况下对Urban100测试集中的3张图像(img004、img061和img096)进行不同算法的对比测试, 对比测试的视觉效果图如图5 ~7 所示. 图5 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的小孔存在模糊问题, DBPN、RFDN和A2N算法图像重建的小孔存在严重的变形问题(如DBPN算法图像重建的小孔存在变小和变圆问题, RFDN、A2N算法图像重建的小孔存在变弯问题), 所提算法图像重建的小孔基本保持了原形状. 图6 中, Bicubic、SRCNN、和FSRCNN算法图像重建的楼层存在严重的模糊问题, VDSR算法图像重建的高楼层存在严重的变形问题, DBPN、RFDN和A2N算法图像重建的楼层存在严重的锐化问题, 所提算法图像重建的楼层存在轻微的锐化问题, 不存在变形问题. 图7 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的大楼外侧竖条出现严重的模糊不清问题, DBPN、RFDN和A2N算法图像重建的大楼外右侧竖条存在较严重的模糊问题, 重建的大楼外左侧竖条存在轻微的扭曲问题, 所提算法图像重建的大楼外侧基本没有模糊问题和扭曲问题. 综上所述, 所提算法相比主流算法不仅在性能测试指标方面实现较大提升, 而且在重建图像的细节方面也具体较好的视觉效果. ...
1
... 训练集为DIV2K[23 ] 数据集, 该数据集包含800张高清的HR图像, 100张验证图像和100张测试图像. 使用Bicubic算法处理HR图像, 生成对应的放大倍数分别为2、3、4的LR图像. 为了扩展数据集, 先对HR图像和不同放大倍数下的LR图像按照旋转角度分别为90°、180°、270°进行旋转, 再按照比例系数分别为0.6、0.7、0.8、0.9进行缩放, 最后对这些图像进行裁剪. ...
1
... 测试集为Set5[24 ] 、Set14[25 ] 、BSD100[26 ] 和Urban100[27 ] 数据集, 分别包含5、14、100、100张不同风格的图像(如人像、动物、风景、建筑物等). 使用Bicubic算法生成和HR图像对应的放大倍数分别为2、3、4的LR图像. ...
1
... 测试集为Set5[24 ] 、Set14[25 ] 、BSD100[26 ] 和Urban100[27 ] 数据集, 分别包含5、14、100、100张不同风格的图像(如人像、动物、风景、建筑物等). 使用Bicubic算法生成和HR图像对应的放大倍数分别为2、3、4的LR图像. ...
1
... 测试集为Set5[24 ] 、Set14[25 ] 、BSD100[26 ] 和Urban100[27 ] 数据集, 分别包含5、14、100、100张不同风格的图像(如人像、动物、风景、建筑物等). 使用Bicubic算法生成和HR图像对应的放大倍数分别为2、3、4的LR图像. ...
1
... 测试集为Set5[24 ] 、Set14[25 ] 、BSD100[26 ] 和Urban100[27 ] 数据集, 分别包含5、14、100、100张不同风格的图像(如人像、动物、风景、建筑物等). 使用Bicubic算法生成和HR图像对应的放大倍数分别为2、3、4的LR图像. ...
1
... 所提算法在深度特征提取中使用64个多级连续编码与解码的注意力残差模块. 本研究使用的损失函数为 $ L_1^{} $ [28 ] 优化算法对损失函数进行优化. 网络训练过程中设置的批次大小为16, 迭代轮次epoch=1 000, 学习率初始为0.000 1;epoch每隔200,学习率降为原来的一半. 所提算法在测试过程中使用的性能评价指标为峰值信噪比(peak signal to noise ratio, PSNR)和结构相似度[29 ] (structural similarity index, SSIM), 在YCbCr通道中的Y通道进行测试图像性能测试. ...
Image quality assessment: from error visibility to structural similarity
1
2004
... 所提算法在深度特征提取中使用64个多级连续编码与解码的注意力残差模块. 本研究使用的损失函数为 $ L_1^{} $ [28 ] 优化算法对损失函数进行优化. 网络训练过程中设置的批次大小为16, 迭代轮次epoch=1 000, 学习率初始为0.000 1;epoch每隔200,学习率降为原来的一半. 所提算法在测试过程中使用的性能评价指标为峰值信噪比(peak signal to noise ratio, PSNR)和结构相似度[29 ] (structural similarity index, SSIM), 在YCbCr通道中的Y通道进行测试图像性能测试. ...
Deep back-projection networks for super-resolution
3
2021
... 将主流的7种算法(Bicubic、SRCNN[13 ] 、FSRCNN[14 ] 、VDSR[16 ] 、DBPN[30 ] 、RFDN[31 ] 和A2N[22 ] )与所提算法进行算法性能的对比测试. 分别在放大倍数为2、3和4的情况下,使用不同算法测试Set5、Set14、BSD100和Urban100数据集, 测试结果如表1 ~3 所示. 相比主流算法, 在放大倍数为2、3的情况下,所提算法测试4个数据集的性能评价指标均为最优, 实现了PSNR、SSIM的较大提升.相比主流算法, 在放大倍数为4的情况下,所提算法测试Urban100数据集的性能评价指标最优. 具体来说, 对于测试集Set5、Set14、BSD100、Urban100,当放大倍数为2时, 所提算法获得的PSNR比DBPN算法获得的次优PSNR分别提升0.08、0.09、0.01、0.19 dB;当放大倍数为3时, 所提算法获得的PSNR比A2N算法获得的次优PSNR分别提升0.11、0.07、0.06、0.25 dB.当放大倍数为4时,对于Urban100测试集, 所提算法获得的PSNR比DBPN算法获得的次优PSNR值提升0.03 dB;当放大倍数为2、4时, 所提算法获得的SSIM比DBPN算法获得的次优SSIM分别提升0.001 8、0.002 8;当放大倍数为3时, 所提算法获得的SSIM比A2N算法获得的次优SSIM提升0.006 4. 所提算法在特征提取过程中通过多级连续编码与解码的注意力残差块,获取不同层级的图像特征信息, 为不同层级的图像特征信息分配不同计算量的权重, 能够尽可能多地获得图像内部丰富的细节特征, 因此相比7种主流算法, 所提算法具有较好的超分辨率重建性能, 能够实现PSNR、SSIM的较大提升. ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 2)
Tab.1 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 33.66 0.929 9 30.24 0.868 8 29.56 0.843 1 26.88 0.840 3 SRCNN[13 ] 36.66 0.954 2 32.45 0.906 7 31.36 0.887 9 29.50 0.894 6 FSRCNN[14 ] 37.05 0.956 0 32.66 0.909 0 31.53 0.892 0 29.88 0.902 0 VDSR[16 ] 37.53 0.959 0 33.05 0.913 0 31.90 0.896 0 30.77 0.914 0 DBPN[30 ] 38.09 0.960 0 33.85 0.919 0 32.27 0.900 0 32.55 0.932 4 RFDN[31 ] 38.05 0.960 6 33.68 0.918 4 32.16 0.899 4 32.12 0.927 8 A2N[22 ] 38.06 0.960 8 33.75 0.919 4 32.22 0.900 2 32.43 0.931 1 本研究 38.17 0.961 0 33.94 0.920 8 32.28 0.901 0 32.74 0.934 2
表 2 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为3) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 4)
Tab.3 算法 Set5 Set14 BSD100 Urban100 PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM Bicubic 28.42 0.810 4 26.00 0.702 7 25.96 0.667 5 23.14 0.657 7 SRCNN[13 ] 30.48 0.862 8 27.50 0.751 3 26.90 0.710 1 24.52 0.722 1 FSRCNN[14 ] 30.72 0.866 0 27.61 0.755 0 26.98 0.715 0 24.62 0.728 0 VDSR[16 ] 31.35 0.883 0 28.02 0.768 0 27.29 0.725 1 25.18 0.754 0 DBPN[30 ] 32.47 0.898 0 28.82 0.786 0 27.72 0.740 0 26.38 0.794 6 RFDN[31 ] 32.24 0.895 2 28.61 0.781 9 27.57 0.736 0 26.11 0.785 8 A2N[22 ] 32.30 0.896 6 28.71 0.784 2 27.61 0.737 4 26.27 0.792 0 本研究 32.37 0.897 1 28.76 0.785 7 27.55 0.734 0 26.41 0.797 4
为了测试所提算法的重建图像的视觉效果, 在放大倍数为4的情况下对Urban100测试集中的3张图像(img004、img061和img096)进行不同算法的对比测试, 对比测试的视觉效果图如图5 ~7 所示. 图5 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的小孔存在模糊问题, DBPN、RFDN和A2N算法图像重建的小孔存在严重的变形问题(如DBPN算法图像重建的小孔存在变小和变圆问题, RFDN、A2N算法图像重建的小孔存在变弯问题), 所提算法图像重建的小孔基本保持了原形状. 图6 中, Bicubic、SRCNN、和FSRCNN算法图像重建的楼层存在严重的模糊问题, VDSR算法图像重建的高楼层存在严重的变形问题, DBPN、RFDN和A2N算法图像重建的楼层存在严重的锐化问题, 所提算法图像重建的楼层存在轻微的锐化问题, 不存在变形问题. 图7 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的大楼外侧竖条出现严重的模糊不清问题, DBPN、RFDN和A2N算法图像重建的大楼外右侧竖条存在较严重的模糊问题, 重建的大楼外左侧竖条存在轻微的扭曲问题, 所提算法图像重建的大楼外侧基本没有模糊问题和扭曲问题. 综上所述, 所提算法相比主流算法不仅在性能测试指标方面实现较大提升, 而且在重建图像的细节方面也具体较好的视觉效果. ...
4
... 将主流的7种算法(Bicubic、SRCNN[13 ] 、FSRCNN[14 ] 、VDSR[16 ] 、DBPN[30 ] 、RFDN[31 ] 和A2N[22 ] )与所提算法进行算法性能的对比测试. 分别在放大倍数为2、3和4的情况下,使用不同算法测试Set5、Set14、BSD100和Urban100数据集, 测试结果如表1 ~3 所示. 相比主流算法, 在放大倍数为2、3的情况下,所提算法测试4个数据集的性能评价指标均为最优, 实现了PSNR、SSIM的较大提升.相比主流算法, 在放大倍数为4的情况下,所提算法测试Urban100数据集的性能评价指标最优. 具体来说, 对于测试集Set5、Set14、BSD100、Urban100,当放大倍数为2时, 所提算法获得的PSNR比DBPN算法获得的次优PSNR分别提升0.08、0.09、0.01、0.19 dB;当放大倍数为3时, 所提算法获得的PSNR比A2N算法获得的次优PSNR分别提升0.11、0.07、0.06、0.25 dB.当放大倍数为4时,对于Urban100测试集, 所提算法获得的PSNR比DBPN算法获得的次优PSNR值提升0.03 dB;当放大倍数为2、4时, 所提算法获得的SSIM比DBPN算法获得的次优SSIM分别提升0.001 8、0.002 8;当放大倍数为3时, 所提算法获得的SSIM比A2N算法获得的次优SSIM提升0.006 4. 所提算法在特征提取过程中通过多级连续编码与解码的注意力残差块,获取不同层级的图像特征信息, 为不同层级的图像特征信息分配不同计算量的权重, 能够尽可能多地获得图像内部丰富的细节特征, 因此相比7种主流算法, 所提算法具有较好的超分辨率重建性能, 能够实现PSNR、SSIM的较大提升. ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 2)
Tab.1 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 33.66 0.929 9 30.24 0.868 8 29.56 0.843 1 26.88 0.840 3 SRCNN[13 ] 36.66 0.954 2 32.45 0.906 7 31.36 0.887 9 29.50 0.894 6 FSRCNN[14 ] 37.05 0.956 0 32.66 0.909 0 31.53 0.892 0 29.88 0.902 0 VDSR[16 ] 37.53 0.959 0 33.05 0.913 0 31.90 0.896 0 30.77 0.914 0 DBPN[30 ] 38.09 0.960 0 33.85 0.919 0 32.27 0.900 0 32.55 0.932 4 RFDN[31 ] 38.05 0.960 6 33.68 0.918 4 32.16 0.899 4 32.12 0.927 8 A2N[22 ] 38.06 0.960 8 33.75 0.919 4 32.22 0.900 2 32.43 0.931 1 本研究 38.17 0.961 0 33.94 0.920 8 32.28 0.901 0 32.74 0.934 2
表 2 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为3) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 3)
Tab.2 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 30.39 0.868 2 27.55 0.774 2 27.21 0.738 5 24.46 0.734 9 SRCNN[13 ] 32.75 0.909 0 29.30 0.821 5 28.41 0.786 3 26.24 0.798 9 FSRCNN[14 ] 33.18 0.914 0 29.37 0.824 0 28.53 0.791 0 26.43 0.808 0 VDSR[16 ] 33.67 0.921 0 29.78 0.832 0 28.83 0.799 0 27.14 0.829 0 RFDN[31 ] 34.41 0.927 3 30.34 0.842 0 29.09 0.805 0 28.21 0.852 5 A2N[22 ] 34.47 0.927 9 30.44 0.843 7 29.14 0.805 9 28.41 0.857 0 本研究 34.58 0.928 8 30.51 0.845 6 29.20 0.807 9 28.66 0.863 4
表 3 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为4) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 4)
Tab.3 算法 Set5 Set14 BSD100 Urban100 PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM Bicubic 28.42 0.810 4 26.00 0.702 7 25.96 0.667 5 23.14 0.657 7 SRCNN[13 ] 30.48 0.862 8 27.50 0.751 3 26.90 0.710 1 24.52 0.722 1 FSRCNN[14 ] 30.72 0.866 0 27.61 0.755 0 26.98 0.715 0 24.62 0.728 0 VDSR[16 ] 31.35 0.883 0 28.02 0.768 0 27.29 0.725 1 25.18 0.754 0 DBPN[30 ] 32.47 0.898 0 28.82 0.786 0 27.72 0.740 0 26.38 0.794 6 RFDN[31 ] 32.24 0.895 2 28.61 0.781 9 27.57 0.736 0 26.11 0.785 8 A2N[22 ] 32.30 0.896 6 28.71 0.784 2 27.61 0.737 4 26.27 0.792 0 本研究 32.37 0.897 1 28.76 0.785 7 27.55 0.734 0 26.41 0.797 4
为了测试所提算法的重建图像的视觉效果, 在放大倍数为4的情况下对Urban100测试集中的3张图像(img004、img061和img096)进行不同算法的对比测试, 对比测试的视觉效果图如图5 ~7 所示. 图5 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的小孔存在模糊问题, DBPN、RFDN和A2N算法图像重建的小孔存在严重的变形问题(如DBPN算法图像重建的小孔存在变小和变圆问题, RFDN、A2N算法图像重建的小孔存在变弯问题), 所提算法图像重建的小孔基本保持了原形状. 图6 中, Bicubic、SRCNN、和FSRCNN算法图像重建的楼层存在严重的模糊问题, VDSR算法图像重建的高楼层存在严重的变形问题, DBPN、RFDN和A2N算法图像重建的楼层存在严重的锐化问题, 所提算法图像重建的楼层存在轻微的锐化问题, 不存在变形问题. 图7 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的大楼外侧竖条出现严重的模糊不清问题, DBPN、RFDN和A2N算法图像重建的大楼外右侧竖条存在较严重的模糊问题, 重建的大楼外左侧竖条存在轻微的扭曲问题, 所提算法图像重建的大楼外侧基本没有模糊问题和扭曲问题. 综上所述, 所提算法相比主流算法不仅在性能测试指标方面实现较大提升, 而且在重建图像的细节方面也具体较好的视觉效果. ...
Real-world single image super-resolution: a brief review
1
2022
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
1
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
Ultra-dense GAN for satellite imagery super-resolution
1
2020
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
Satellite video super-resolution based on adaptively spatiotemporal neighbors and nonlocal similarity regularization
0
2020
Image super-resolution: the techniques, applications, and future
1
2016
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
1
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
Machine learning: trends, perspectives, and prospects
0
2015
Deep learning
1
2015
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
A deep journey into super-resolution: a survey
1
2020
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
Deep learning for image super-resolution: a survey
0
2021
Gradual deep residual network for super-resolution
0
2021
Progressive back-projection network for COVID-CT super-resolution
1
2021
... 图像超分辨率重建旨在从低分辨率(low-resolution, LR)图像中重建出一副对应的高分辨率(high-resolution, HR)图像, 是计算机视觉的重要分支[1 -2 ] , 在生活中具有广泛的应用场景[3 -5 ] . 许多深度学习[6 -8 ] 的算法致力于通过构建更深或更宽的神经网络模型来学习LR图像和HR图像之间复杂的映射关系[9 -12 ] . ...
Image super-resolution using deep convolutional networks
5
2015
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
... 将主流的7种算法(Bicubic、SRCNN[13 ] 、FSRCNN[14 ] 、VDSR[16 ] 、DBPN[30 ] 、RFDN[31 ] 和A2N[22 ] )与所提算法进行算法性能的对比测试. 分别在放大倍数为2、3和4的情况下,使用不同算法测试Set5、Set14、BSD100和Urban100数据集, 测试结果如表1 ~3 所示. 相比主流算法, 在放大倍数为2、3的情况下,所提算法测试4个数据集的性能评价指标均为最优, 实现了PSNR、SSIM的较大提升.相比主流算法, 在放大倍数为4的情况下,所提算法测试Urban100数据集的性能评价指标最优. 具体来说, 对于测试集Set5、Set14、BSD100、Urban100,当放大倍数为2时, 所提算法获得的PSNR比DBPN算法获得的次优PSNR分别提升0.08、0.09、0.01、0.19 dB;当放大倍数为3时, 所提算法获得的PSNR比A2N算法获得的次优PSNR分别提升0.11、0.07、0.06、0.25 dB.当放大倍数为4时,对于Urban100测试集, 所提算法获得的PSNR比DBPN算法获得的次优PSNR值提升0.03 dB;当放大倍数为2、4时, 所提算法获得的SSIM比DBPN算法获得的次优SSIM分别提升0.001 8、0.002 8;当放大倍数为3时, 所提算法获得的SSIM比A2N算法获得的次优SSIM提升0.006 4. 所提算法在特征提取过程中通过多级连续编码与解码的注意力残差块,获取不同层级的图像特征信息, 为不同层级的图像特征信息分配不同计算量的权重, 能够尽可能多地获得图像内部丰富的细节特征, 因此相比7种主流算法, 所提算法具有较好的超分辨率重建性能, 能够实现PSNR、SSIM的较大提升. ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 2)
Tab.1 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 33.66 0.929 9 30.24 0.868 8 29.56 0.843 1 26.88 0.840 3 SRCNN[13 ] 36.66 0.954 2 32.45 0.906 7 31.36 0.887 9 29.50 0.894 6 FSRCNN[14 ] 37.05 0.956 0 32.66 0.909 0 31.53 0.892 0 29.88 0.902 0 VDSR[16 ] 37.53 0.959 0 33.05 0.913 0 31.90 0.896 0 30.77 0.914 0 DBPN[30 ] 38.09 0.960 0 33.85 0.919 0 32.27 0.900 0 32.55 0.932 4 RFDN[31 ] 38.05 0.960 6 33.68 0.918 4 32.16 0.899 4 32.12 0.927 8 A2N[22 ] 38.06 0.960 8 33.75 0.919 4 32.22 0.900 2 32.43 0.931 1 本研究 38.17 0.961 0 33.94 0.920 8 32.28 0.901 0 32.74 0.934 2
表 2 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为3) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 3)
Tab.2 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 30.39 0.868 2 27.55 0.774 2 27.21 0.738 5 24.46 0.734 9 SRCNN[13 ] 32.75 0.909 0 29.30 0.821 5 28.41 0.786 3 26.24 0.798 9 FSRCNN[14 ] 33.18 0.914 0 29.37 0.824 0 28.53 0.791 0 26.43 0.808 0 VDSR[16 ] 33.67 0.921 0 29.78 0.832 0 28.83 0.799 0 27.14 0.829 0 RFDN[31 ] 34.41 0.927 3 30.34 0.842 0 29.09 0.805 0 28.21 0.852 5 A2N[22 ] 34.47 0.927 9 30.44 0.843 7 29.14 0.805 9 28.41 0.857 0 本研究 34.58 0.928 8 30.51 0.845 6 29.20 0.807 9 28.66 0.863 4
表 3 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为4) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 4)
Tab.3 算法 Set5 Set14 BSD100 Urban100 PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM Bicubic 28.42 0.810 4 26.00 0.702 7 25.96 0.667 5 23.14 0.657 7 SRCNN[13 ] 30.48 0.862 8 27.50 0.751 3 26.90 0.710 1 24.52 0.722 1 FSRCNN[14 ] 30.72 0.866 0 27.61 0.755 0 26.98 0.715 0 24.62 0.728 0 VDSR[16 ] 31.35 0.883 0 28.02 0.768 0 27.29 0.725 1 25.18 0.754 0 DBPN[30 ] 32.47 0.898 0 28.82 0.786 0 27.72 0.740 0 26.38 0.794 6 RFDN[31 ] 32.24 0.895 2 28.61 0.781 9 27.57 0.736 0 26.11 0.785 8 A2N[22 ] 32.30 0.896 6 28.71 0.784 2 27.61 0.737 4 26.27 0.792 0 本研究 32.37 0.897 1 28.76 0.785 7 27.55 0.734 0 26.41 0.797 4
为了测试所提算法的重建图像的视觉效果, 在放大倍数为4的情况下对Urban100测试集中的3张图像(img004、img061和img096)进行不同算法的对比测试, 对比测试的视觉效果图如图5 ~7 所示. 图5 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的小孔存在模糊问题, DBPN、RFDN和A2N算法图像重建的小孔存在严重的变形问题(如DBPN算法图像重建的小孔存在变小和变圆问题, RFDN、A2N算法图像重建的小孔存在变弯问题), 所提算法图像重建的小孔基本保持了原形状. 图6 中, Bicubic、SRCNN、和FSRCNN算法图像重建的楼层存在严重的模糊问题, VDSR算法图像重建的高楼层存在严重的变形问题, DBPN、RFDN和A2N算法图像重建的楼层存在严重的锐化问题, 所提算法图像重建的楼层存在轻微的锐化问题, 不存在变形问题. 图7 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的大楼外侧竖条出现严重的模糊不清问题, DBPN、RFDN和A2N算法图像重建的大楼外右侧竖条存在较严重的模糊问题, 重建的大楼外左侧竖条存在轻微的扭曲问题, 所提算法图像重建的大楼外侧基本没有模糊问题和扭曲问题. 综上所述, 所提算法相比主流算法不仅在性能测试指标方面实现较大提升, 而且在重建图像的细节方面也具体较好的视觉效果. ...
5
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
... 将主流的7种算法(Bicubic、SRCNN[13 ] 、FSRCNN[14 ] 、VDSR[16 ] 、DBPN[30 ] 、RFDN[31 ] 和A2N[22 ] )与所提算法进行算法性能的对比测试. 分别在放大倍数为2、3和4的情况下,使用不同算法测试Set5、Set14、BSD100和Urban100数据集, 测试结果如表1 ~3 所示. 相比主流算法, 在放大倍数为2、3的情况下,所提算法测试4个数据集的性能评价指标均为最优, 实现了PSNR、SSIM的较大提升.相比主流算法, 在放大倍数为4的情况下,所提算法测试Urban100数据集的性能评价指标最优. 具体来说, 对于测试集Set5、Set14、BSD100、Urban100,当放大倍数为2时, 所提算法获得的PSNR比DBPN算法获得的次优PSNR分别提升0.08、0.09、0.01、0.19 dB;当放大倍数为3时, 所提算法获得的PSNR比A2N算法获得的次优PSNR分别提升0.11、0.07、0.06、0.25 dB.当放大倍数为4时,对于Urban100测试集, 所提算法获得的PSNR比DBPN算法获得的次优PSNR值提升0.03 dB;当放大倍数为2、4时, 所提算法获得的SSIM比DBPN算法获得的次优SSIM分别提升0.001 8、0.002 8;当放大倍数为3时, 所提算法获得的SSIM比A2N算法获得的次优SSIM提升0.006 4. 所提算法在特征提取过程中通过多级连续编码与解码的注意力残差块,获取不同层级的图像特征信息, 为不同层级的图像特征信息分配不同计算量的权重, 能够尽可能多地获得图像内部丰富的细节特征, 因此相比7种主流算法, 所提算法具有较好的超分辨率重建性能, 能够实现PSNR、SSIM的较大提升. ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 2)
Tab.1 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 33.66 0.929 9 30.24 0.868 8 29.56 0.843 1 26.88 0.840 3 SRCNN[13 ] 36.66 0.954 2 32.45 0.906 7 31.36 0.887 9 29.50 0.894 6 FSRCNN[14 ] 37.05 0.956 0 32.66 0.909 0 31.53 0.892 0 29.88 0.902 0 VDSR[16 ] 37.53 0.959 0 33.05 0.913 0 31.90 0.896 0 30.77 0.914 0 DBPN[30 ] 38.09 0.960 0 33.85 0.919 0 32.27 0.900 0 32.55 0.932 4 RFDN[31 ] 38.05 0.960 6 33.68 0.918 4 32.16 0.899 4 32.12 0.927 8 A2N[22 ] 38.06 0.960 8 33.75 0.919 4 32.22 0.900 2 32.43 0.931 1 本研究 38.17 0.961 0 33.94 0.920 8 32.28 0.901 0 32.74 0.934 2
表 2 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为3) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 3)
Tab.2 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 30.39 0.868 2 27.55 0.774 2 27.21 0.738 5 24.46 0.734 9 SRCNN[13 ] 32.75 0.909 0 29.30 0.821 5 28.41 0.786 3 26.24 0.798 9 FSRCNN[14 ] 33.18 0.914 0 29.37 0.824 0 28.53 0.791 0 26.43 0.808 0 VDSR[16 ] 33.67 0.921 0 29.78 0.832 0 28.83 0.799 0 27.14 0.829 0 RFDN[31 ] 34.41 0.927 3 30.34 0.842 0 29.09 0.805 0 28.21 0.852 5 A2N[22 ] 34.47 0.927 9 30.44 0.843 7 29.14 0.805 9 28.41 0.857 0 本研究 34.58 0.928 8 30.51 0.845 6 29.20 0.807 9 28.66 0.863 4
表 3 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为4) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 4)
Tab.3 算法 Set5 Set14 BSD100 Urban100 PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM Bicubic 28.42 0.810 4 26.00 0.702 7 25.96 0.667 5 23.14 0.657 7 SRCNN[13 ] 30.48 0.862 8 27.50 0.751 3 26.90 0.710 1 24.52 0.722 1 FSRCNN[14 ] 30.72 0.866 0 27.61 0.755 0 26.98 0.715 0 24.62 0.728 0 VDSR[16 ] 31.35 0.883 0 28.02 0.768 0 27.29 0.725 1 25.18 0.754 0 DBPN[30 ] 32.47 0.898 0 28.82 0.786 0 27.72 0.740 0 26.38 0.794 6 RFDN[31 ] 32.24 0.895 2 28.61 0.781 9 27.57 0.736 0 26.11 0.785 8 A2N[22 ] 32.30 0.896 6 28.71 0.784 2 27.61 0.737 4 26.27 0.792 0 本研究 32.37 0.897 1 28.76 0.785 7 27.55 0.734 0 26.41 0.797 4
为了测试所提算法的重建图像的视觉效果, 在放大倍数为4的情况下对Urban100测试集中的3张图像(img004、img061和img096)进行不同算法的对比测试, 对比测试的视觉效果图如图5 ~7 所示. 图5 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的小孔存在模糊问题, DBPN、RFDN和A2N算法图像重建的小孔存在严重的变形问题(如DBPN算法图像重建的小孔存在变小和变圆问题, RFDN、A2N算法图像重建的小孔存在变弯问题), 所提算法图像重建的小孔基本保持了原形状. 图6 中, Bicubic、SRCNN、和FSRCNN算法图像重建的楼层存在严重的模糊问题, VDSR算法图像重建的高楼层存在严重的变形问题, DBPN、RFDN和A2N算法图像重建的楼层存在严重的锐化问题, 所提算法图像重建的楼层存在轻微的锐化问题, 不存在变形问题. 图7 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的大楼外侧竖条出现严重的模糊不清问题, DBPN、RFDN和A2N算法图像重建的大楼外右侧竖条存在较严重的模糊问题, 重建的大楼外左侧竖条存在轻微的扭曲问题, 所提算法图像重建的大楼外侧基本没有模糊问题和扭曲问题. 综上所述, 所提算法相比主流算法不仅在性能测试指标方面实现较大提升, 而且在重建图像的细节方面也具体较好的视觉效果. ...
1
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
5
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
... 将主流的7种算法(Bicubic、SRCNN[13 ] 、FSRCNN[14 ] 、VDSR[16 ] 、DBPN[30 ] 、RFDN[31 ] 和A2N[22 ] )与所提算法进行算法性能的对比测试. 分别在放大倍数为2、3和4的情况下,使用不同算法测试Set5、Set14、BSD100和Urban100数据集, 测试结果如表1 ~3 所示. 相比主流算法, 在放大倍数为2、3的情况下,所提算法测试4个数据集的性能评价指标均为最优, 实现了PSNR、SSIM的较大提升.相比主流算法, 在放大倍数为4的情况下,所提算法测试Urban100数据集的性能评价指标最优. 具体来说, 对于测试集Set5、Set14、BSD100、Urban100,当放大倍数为2时, 所提算法获得的PSNR比DBPN算法获得的次优PSNR分别提升0.08、0.09、0.01、0.19 dB;当放大倍数为3时, 所提算法获得的PSNR比A2N算法获得的次优PSNR分别提升0.11、0.07、0.06、0.25 dB.当放大倍数为4时,对于Urban100测试集, 所提算法获得的PSNR比DBPN算法获得的次优PSNR值提升0.03 dB;当放大倍数为2、4时, 所提算法获得的SSIM比DBPN算法获得的次优SSIM分别提升0.001 8、0.002 8;当放大倍数为3时, 所提算法获得的SSIM比A2N算法获得的次优SSIM提升0.006 4. 所提算法在特征提取过程中通过多级连续编码与解码的注意力残差块,获取不同层级的图像特征信息, 为不同层级的图像特征信息分配不同计算量的权重, 能够尽可能多地获得图像内部丰富的细节特征, 因此相比7种主流算法, 所提算法具有较好的超分辨率重建性能, 能够实现PSNR、SSIM的较大提升. ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 2)
Tab.1 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 33.66 0.929 9 30.24 0.868 8 29.56 0.843 1 26.88 0.840 3 SRCNN[13 ] 36.66 0.954 2 32.45 0.906 7 31.36 0.887 9 29.50 0.894 6 FSRCNN[14 ] 37.05 0.956 0 32.66 0.909 0 31.53 0.892 0 29.88 0.902 0 VDSR[16 ] 37.53 0.959 0 33.05 0.913 0 31.90 0.896 0 30.77 0.914 0 DBPN[30 ] 38.09 0.960 0 33.85 0.919 0 32.27 0.900 0 32.55 0.932 4 RFDN[31 ] 38.05 0.960 6 33.68 0.918 4 32.16 0.899 4 32.12 0.927 8 A2N[22 ] 38.06 0.960 8 33.75 0.919 4 32.22 0.900 2 32.43 0.931 1 本研究 38.17 0.961 0 33.94 0.920 8 32.28 0.901 0 32.74 0.934 2
表 2 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为3) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 3)
Tab.2 算法 Set5 Set14 BSD100 Urban100 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM Bicubic 30.39 0.868 2 27.55 0.774 2 27.21 0.738 5 24.46 0.734 9 SRCNN[13 ] 32.75 0.909 0 29.30 0.821 5 28.41 0.786 3 26.24 0.798 9 FSRCNN[14 ] 33.18 0.914 0 29.37 0.824 0 28.53 0.791 0 26.43 0.808 0 VDSR[16 ] 33.67 0.921 0 29.78 0.832 0 28.83 0.799 0 27.14 0.829 0 RFDN[31 ] 34.41 0.927 3 30.34 0.842 0 29.09 0.805 0 28.21 0.852 5 A2N[22 ] 34.47 0.927 9 30.44 0.843 7 29.14 0.805 9 28.41 0.857 0 本研究 34.58 0.928 8 30.51 0.845 6 29.20 0.807 9 28.66 0.863 4
表 3 不同图像重建算法在4个测试集上的性能评价指标(放大倍数为4) ...
... Performance evaluation indicators of different image resolution algorithms on four test sets (magnification is 4)
Tab.3 算法 Set5 Set14 BSD100 Urban100 PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM PSNR/ dB SSIM Bicubic 28.42 0.810 4 26.00 0.702 7 25.96 0.667 5 23.14 0.657 7 SRCNN[13 ] 30.48 0.862 8 27.50 0.751 3 26.90 0.710 1 24.52 0.722 1 FSRCNN[14 ] 30.72 0.866 0 27.61 0.755 0 26.98 0.715 0 24.62 0.728 0 VDSR[16 ] 31.35 0.883 0 28.02 0.768 0 27.29 0.725 1 25.18 0.754 0 DBPN[30 ] 32.47 0.898 0 28.82 0.786 0 27.72 0.740 0 26.38 0.794 6 RFDN[31 ] 32.24 0.895 2 28.61 0.781 9 27.57 0.736 0 26.11 0.785 8 A2N[22 ] 32.30 0.896 6 28.71 0.784 2 27.61 0.737 4 26.27 0.792 0 本研究 32.37 0.897 1 28.76 0.785 7 27.55 0.734 0 26.41 0.797 4
为了测试所提算法的重建图像的视觉效果, 在放大倍数为4的情况下对Urban100测试集中的3张图像(img004、img061和img096)进行不同算法的对比测试, 对比测试的视觉效果图如图5 ~7 所示. 图5 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的小孔存在模糊问题, DBPN、RFDN和A2N算法图像重建的小孔存在严重的变形问题(如DBPN算法图像重建的小孔存在变小和变圆问题, RFDN、A2N算法图像重建的小孔存在变弯问题), 所提算法图像重建的小孔基本保持了原形状. 图6 中, Bicubic、SRCNN、和FSRCNN算法图像重建的楼层存在严重的模糊问题, VDSR算法图像重建的高楼层存在严重的变形问题, DBPN、RFDN和A2N算法图像重建的楼层存在严重的锐化问题, 所提算法图像重建的楼层存在轻微的锐化问题, 不存在变形问题. 图7 中, Bicubic、SRCNN、FSRCNN和VDSR算法图像重建的大楼外侧竖条出现严重的模糊不清问题, DBPN、RFDN和A2N算法图像重建的大楼外右侧竖条存在较严重的模糊问题, 重建的大楼外左侧竖条存在轻微的扭曲问题, 所提算法图像重建的大楼外侧基本没有模糊问题和扭曲问题. 综上所述, 所提算法相比主流算法不仅在性能测试指标方面实现较大提升, 而且在重建图像的细节方面也具体较好的视觉效果. ...
1
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
1
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...
1
... 基于卷积神经网络的图像超分辨率重建算法(super-resolution convolutional neural network, SRCNN)[13 ] 率先通过建立卷积神经网络来学习LR图像到HR图像的映射关系. 虽然该算法较传统算法的性能有较大提升, 但是算法建立的神经网络模型结构比较简单(仅有3个卷积层), 导致该网络模型的学习性能有限. 有研究者在卷积神经网络的基础上提出一系列基于神经网络的图像超分辨率重建算法, 如基于快速的卷积神经网络图像超分辨率重建算法(fast super-resolution convolutional neural network, FSRCNN)[14 ] 和基于高效的亚像素卷积网络图像超分辨率重建算法(Efficient sub-pixel convolutional neural network, ESPCN)[15 ] . 虽然这些算法拥有较强的学习复杂映射关系的能力, 但是在训练过程中容易造成梯度爆炸. 基于深度卷积网络的图像超分辨率重建算法(very deep convolution network super-resolution, VDSR)[16 ] 在加深网络深度和扩大网络感受野的同时引入残差学习. 基于递归神经网络的图像超分辨率重建算法(deeply-recursive convolutional network, DRCN)[17 ] 在残差学习的基础上引入全局残差网络. 基于增强的深度残差网络图像超分辨率重建算法(enhanced deep residual network for single image super-resolution, EDSR)[18 ] 引入局部残差并去除了残差块中的批归一化层,能够构建更深的神经网络来学习复杂映射关系. 基于密集跳线连接的图像超分辨率重建算法(super-resolution using dense network, SRDenseNet)[19 ] 将密集连接网络应用于图像超分辨率重建, 有效抑制了梯度消失问题.基于残差密集网络的图像超分辨率重建算法(residual dense network, RDN)[20 ] 在密集块的开头和结尾增加残差连接和卷积运算进行特征降维, 使模型具有更强的学习能力. 这些算法同等对待图像的低、高频特征, 耗费了大量的计算量却未获得图像的深层特征. 受深度神经网络蓬勃发展的影响, 有研究者提出用各种网络结构和学习机制来实现更好的图像重建性能. 如1)基于深度残差通道注意力网络的图像超分辨率重建算法(residual channel attention network, RCAN)[21 ] 引入通道注意机制来重点关注图像的高频特征并获得更好的性能, 2)基于注意力网络的注意力图像超分辨率图像算法(attention in attention network, A2N)[22 ] 引入注意力丢失机制来动态调整注意力的权重. 这些算法难以获取LR内部的多层次信息. ...