[1]
WANG J, CHENG J. Truss decomposition in massive networks [C]// proceedings of the VLDB Endowment . [S.l.]: VLDB Endowment, 2012, 5(9): 812–823.
[本文引用: 1]
[2]
KAIRAM S R, WANG D J, LESKOVEC J. The life and death of online groups: predicting group growth and longevity [C]// Proceedings of the Fifth ACM International Conference on Web Search and Data Mining . [S.l.]: ACM, 2012: 673–682.
[本文引用: 1]
[3]
PÉREZ J, ARENAS M, GUTIERREZ C. Semantics and complexity of sparql [C]// ACM Transactions on Database Systems , 2009, 16: 1-45.
[本文引用: 1]
[4]
CHRISTOPHIDES V. Resource description framework (RDF) schema (RDFS) [M]// LIU L, ÖZSU M T. Encyclopedia of database systems . Boston: Springer, 2009: 2425-2428.
[6]
YAN X F, YU P S, HAN J W. Graph indexing: a frequent structure-based approach [C]// Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data . [S.l.]: ACM, 2004: 335-346.
[本文引用: 1]
[7]
LIU H B, BLOUIN C, KEŠELJ V. Biological event extraction using subgraph matching [EB/OL]. [2022-06-01]. https://ceur-ws.org/Vol-714/ShortPaper03_Liu.pdf.
[本文引用: 1]
[8]
GAREY M R, JOHNSON D S. Computers and intractability: a guide to the theory of NP-completeness [M]. [S.l.]: W. H. Freeman and Company, 1979.
[本文引用: 1]
[9]
CONTE D, FOGGIA P, SANSONE C, et al Thirty years of graph matching in pattern recognition
[J]. International Journal of Pattern Recognition and Artificial Intelligence , 2004 , 18 (3 ): 265 - 298
DOI:10.1142/S0218001404003228
[本文引用: 1]
[10]
LIN H, ZHU X W, YU B W, et al. ShenTu: processing multi-trillion edge graphs on millions of cores in seconds [C]// SC18: International Conference for High Performance Computing, Networking, Storage and Analysis . Dallas: IEEE, 2018: 706-716.
[本文引用: 1]
[11]
MENG K, LI J J, TAN G M, et al. A pattern based algorithmic autotuner for graph processing on GPUs [C]// Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming . [S.l.]: ACM, 2019: 201-213.
[本文引用: 1]
[12]
KHORASANI F, VORA K, GUPTA R, et al. CuSha: vertex-centric graph processing on GPUs [C]// Proceeding of the 23rd International Symposium on High-Performance Parallel and Distributed Computing . [S.l.]: ACM, 2014: 239-252.
[本文引用: 1]
[13]
ULLMANN J R. An algorithm for subgraph isomorphism [J] Journal of the ACM, 1976, 23(1): 31-42.
[本文引用: 1]
[14]
CORDELLA L P, FOGGIA P, SANSONE C, et al A (sub)graph isomorphism algorithm for matching large graphs
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2004 , 26 (10 ): 1367 - 1372
DOI:10.1109/TPAMI.2004.75
[本文引用: 1]
[15]
CARLETTI V, FOGGIA P, SAGGESE A, et al Challenging the time complexity of exact subgraph isomorphism for huge and dense graphs with VF3
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2018 , 40 (4 ): 804 - 818
DOI:10.1109/TPAMI.2017.2696940
[本文引用: 1]
[16]
HAN W S, LEE J, LEE J H. TurboISO : towards ultrafast and robust subgraph isomorphism search in large graph databases [C]// Proceedings of the ACM SIGMOD International Conference on Management of Data . [S.l.]: ACM, 2013: 337-348.
[本文引用: 1]
[17]
HE H, SINGH A K. Graphs-at-a-time: query language and access methods for graph databases [C]// Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data . [S.l.]: ACM, 2008: 405-418.
[本文引用: 1]
[18]
SUN Z, WANG H Z, WANG H X, et al. Efficient subgraph matching on billion node graphs [C]// Proceedings of the VLDB Endowment . [S.l.]: VLDB Endowment, 2012, 5(9): 788-799.
[本文引用: 1]
[19]
ZHANG S J, LI S R, YANG J. GADDI: distance index based subgraph matching in biological networks [C]// Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology . [S.l.]: ACM, 2009: 192-203.
[本文引用: 1]
[20]
LEE J, HAN W S, KASPEROVICS R, et al. An in-depth comparison of subgraph isomorphism algorithms in graph databases [C]// Proceedings of the VLDB Endowment . [S.l.]: VLDB Endowment, 2012, 6(2): 133-144.
[本文引用: 1]
[21]
徐周波, 李珍, 刘华东, 等 基于邻居信息聚合的子图同构匹配算法
[J]. 计算机应用 , 2021 , 41 (1 ): 43 - 47
[本文引用: 1]
XU Zhou-bo, LI Zhen, LIU Hua-dong, et al Subgraph isomorphism matching algorithm based on neighbor information aggregation
[J]. Journal of Computer Applications , 2021 , 41 (1 ): 43 - 47
[本文引用: 1]
[22]
MOORMAN J D, CHEN Q Y, TU T K, et al. Filtering methods for subgraph matching on multiplex networks [C]// Proceedings of the 2018 IEEE International Conference on Big Data . Seattle: IEEE, 2018: 3980-3985.
[本文引用: 1]
[23]
TRAN H N, KIM J J, HE B S. Fast subgraph matching on large graphs using graphics processors [C]// Proceedings of the 2015 International Conference on Database Systems for Advanced Applications . [S.l.]: Springer, 2015: 299-315.
[本文引用: 2]
[24]
WANG L, OWENS J D. Fast Gunrock subgraph matching (GSM) on GPUs [EB/OL]. [2022-06-01]. https://arxiv.org/pdf/2003.01527.pdf.
[本文引用: 1]
[25]
WANG Y Z H, DAVIDSON A, PAN Y C, et al. Gunrock: a high-performance graph processing library on the GPU [C]// Proceedings of the 20th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming . [S.l.]: ACM, 2015: 265-266
[本文引用: 1]
[26]
ZENG L, ZOU L, ÖZSU M T, et al. GSI: GPU-friendly subgraph isomorphism [C]// Proceedings of the 2020 IEEE 36th International Conference on Data Engineering . Dallas: IEEE, 2020: 1249-1260.
[本文引用: 4]
[27]
BONNICI V, GIUGNO R, BOMBIERI N. An efficient implementation of a subgraph isomorphism algorithm for GPUs [C]// Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine . Madrid: IEEE, 2018: 2674-2681.
[本文引用: 1]
[28]
汪洋, 江世杰, 曹宇聪, 等 多编码树GPU并行轴心子图匹配
[J]. 计算机应用 , 2022 , 42 (1 ): 132 - 139
[本文引用: 1]
WAGN Yang, JIANG Shi-jie, CAO Yu-cong, et al Parallel pivoted subgraph matching with multiple coding trees on GPU
[J]. Journal of Computer Applications , 2022 , 42 (1 ): 132 - 139
[本文引用: 1]
[29]
KIRK D. NVIDIA CUDA software and GPU parallel computing architecture [C]// Proceedings of the 6th International Symposium on Memory Management . [S.l.]: ACM, 2007: 103–104.
[本文引用: 1]
[30]
NVIDIA: CUDA Toolkit documentation v10.2 [CP/OL]. (2019-11-28)[2022-06-01]. https://docs.nvidia.com/cuda/archive/10.2/.
[本文引用: 2]
[31]
ASHARI A, SEDAGHATI N, EISENLOHR J, et al. Fast sparse matrix-vector multiplication on GPUs for graph applications [C]// Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis . New Orleans: IEEE, 2014: 781-792.
[本文引用: 1]
[32]
李岑浩, 崔鹏杰, 袁野, 等 面向大图子图匹配的多GPU编程模型
[J]. 计算机科学与探索 , 2023 , 17 (7 ): 1576 - 1585
[本文引用: 1]
LI Cen-hao, CUI Peng-jie, YUAN Ye, et al Muti-GPU programming model for subgraph matching in large graphs
[J]. Journal of Frontiers of Computer Science and Technology , 2023 , 17 (7 ): 1576 - 1585
[本文引用: 1]
[33]
LESKOVEC J. Stanford large network dataset collection [DS/OL]. (2021-09-17)[2022-06-01]. http://snap.stanford.edu/data/.
[本文引用: 1]
[34]
REZA T, RIPEANU M, TRIPOUL N, et al. PruneJuice: pruning trillion-edge graphs to a precise pattern-matching solution [C]// Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis . Dallas: IEEE, 2018: 1-17.
[本文引用: 1]
[35]
Boost Library: VF2 (Sub)Graph Isomorphism-master [CP/OL]. (2013-04-26) [2022-06-01]. https://www.boost.org/doc/libs/master/libs/graph.
[本文引用: 1]
[36]
HU Y F, WANG W J, YU Y Graph matching beyond perfectly-overlapping Erdős-Rényi random graphs
[J]. Statistics and Computing , 2022 , 32 : 19
DOI:10.1007/s11222-022-10079-1
[本文引用: 1]
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
Redesign of the gstore system
1
2018
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
Thirty years of graph matching in pattern recognition
1
2004
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 图作为重要的数据结构,能清晰地表示系统内各部分之间的复杂联系. 子图匹配是基础的图数据挖掘算法,目的是在数据图中找到与查询图结构相同的子图,在社交网络分析[1 -2 ] 、知识图谱检索[3 -5 ] ,化合物发现[6 ] 、生物事件提取[7 ] 等领域都有重要应用. 子图匹配被证明是NP-hard问题[8 ] ,传统的解决方法通常基于树的搜索和回溯实现[9 ] . 随着信息时代的发展,图数据规模急剧增大,上百万条边的图已十分常见[10 ] ,传统的串行子图匹配算法难以应对. 以图形处理器(graphic processing unit, GPU)为中心的中央处理器(center processing unit, CPU)-GPU异构图处理系统不断涌现[11 -12 ] ,英伟达推出的计算机统一设备架构(computer unified device architecture,CUDA)编程模型进一步方便了GPU的使用. 相比于以CPU为主的图计算系统,GPU有更高的带宽和并发度,为子图匹配问题的解决带来了新的思路. ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
A (sub)graph isomorphism algorithm for matching large graphs
1
2004
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
Challenging the time complexity of exact subgraph isomorphism for huge and dense graphs with VF3
1
2018
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
基于邻居信息聚合的子图同构匹配算法
1
2021
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
基于邻居信息聚合的子图同构匹配算法
1
2021
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
1
... 根据算法的执行环境,对子图匹配算法的研究可以分为2个类别:基于CPU和基于GPU. 基于CPU的串行算法由Ullmann[13 ] 提出,使用基于深度优先搜索的策略,VF2[14 ] 在此基础上利用结点间的连接性进行剪枝,VF3[15 ] 改进VF2,由此出现更多的剪枝策略,如启发式确定匹配顺序、结点分类. 为了降低候选集的规模,减少冗余的匹配,TurboISO [16 ] 提出邻居等价类的概念.还有许多算法预先建立关于图的结构索引,以减少搜索空间和优化匹配顺序,如QuickSI[17 ] 、GraphQL[18 ] 、GADDI[19 ] 等,这些算法的优化细节[20 -21 ] 各有不同,但基本思路都是通过增强候选集的过滤能力来提升算法的执行效率[22 ] . ...
2
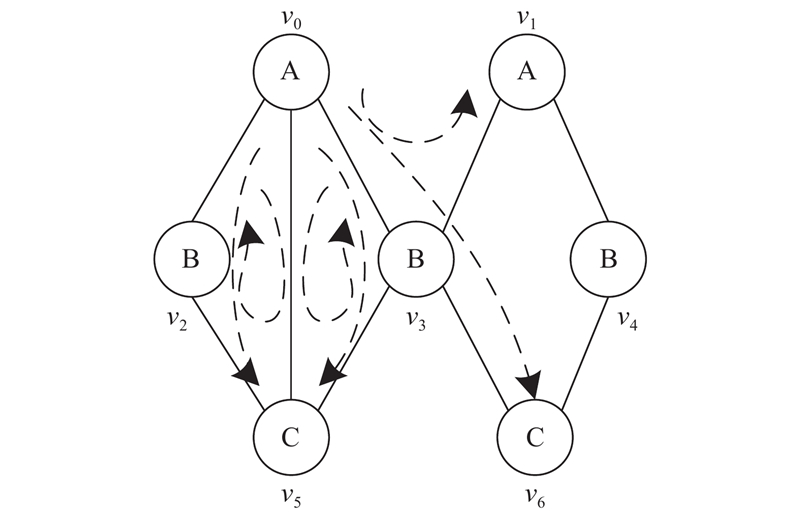
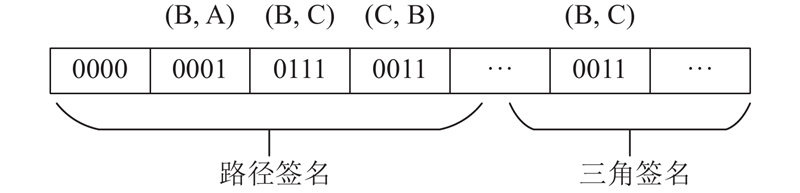
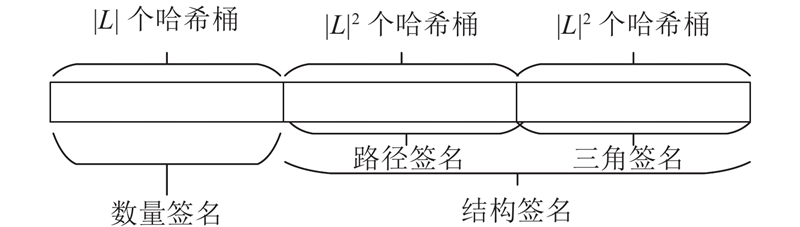
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
... [23 ,26 ],占用大量线程资源且在时间上带来额外开销. ...
1
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
1
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
4
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
... ,26 ],占用大量线程资源且在时间上带来额外开销. ...
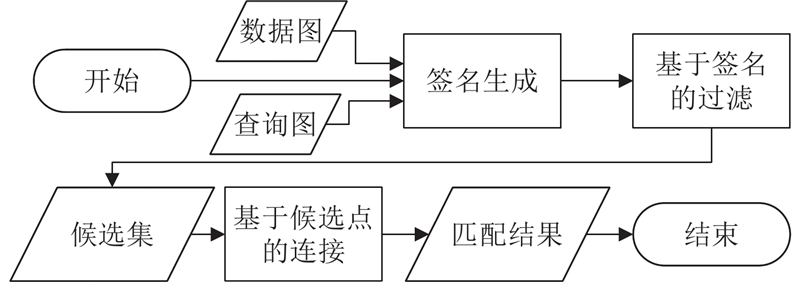
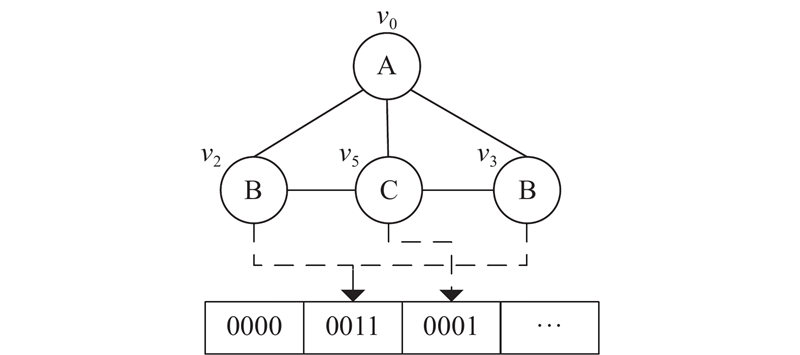
... 针对以上挑战和已有算法的不足,本研究提出基于GPU的子图匹配算法GpSI,对过滤和连接的2阶段模型进行优化. 过滤阶段,综合考虑结点局部的数量特征和结构特征,将这些特征编码生成结点签名,利用GPU并行验证,高效过滤候选集;连接阶段,采用基于候选点的连接策略[26 ] ,预分配空间并设计高效的集合运算以避免边连接策略因重复连接带来的额外时空开销. 通过在真实数据集与合成数据集上的多个算法对比实验来证明GpSI的优越性. ...
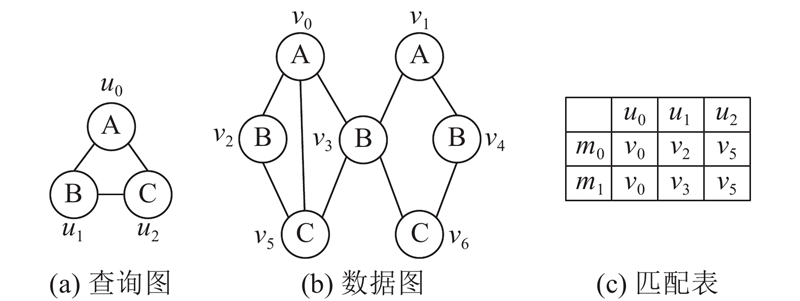
... 换言之,作为必要条件,若式(3)不成立,则 $v \notin C(u)$ [26 ] ,综合利用结点局部的结构和数量特征的复合签名具有更强的过滤能力. 以图1 (a)中的 ${u_1}$ $C({u_1}) = \{ {v_2},{v_3},{v_4}\} $ ${v_4} \notin C({u_1})$ $C({u_1}) = \{ {v_2},{v_3}\} $ [30 ] ,时间复杂度为 $O(|{V_q}|{\rm{lb}}\;|{V_g}|)$ $|{V_q}|$
1
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
多编码树GPU并行轴心子图匹配
1
2022
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
多编码树GPU并行轴心子图匹配
1
2022
... 随着GPU相关技术的发展,研究者开始尝试寻求子图匹配在GPU上的并行解决方案. Tran等[23 ] 提出GpSM,采用基于边的连接策略,利用生成树和非树结构2次过滤候选集以提升匹配效率. 同样是以候选边为连接单元,GunrockSM[24 ] 基于Gunrock[25 ] 图计算平台, 采用广度优先的并行处理方式. 不同于基于边的连接实现,Zeng等[26 ] 提出的GPU友好子图匹配算法(GPU-friendly subgraph isomorphism algorithm,GSI)采用基于点的连接策略,并针对图的边标签设计数据结构以提升访存效率. Bonnici等[27 ] 提出GRASS算法,采用混合广度优先和深度优先的方式,通过 GPU并行过滤候选集. 汪洋等[28 ] 提出多编码树结构,使生成的搜索空间树的尺寸减小. 当前子图匹配算法在GPU上的实现主要由过滤和连接2个阶段组成. 在过滤阶段,为每个查询图中的结点确定在数据图中可供匹配的候选集,GpSM利用生成树且分2步过滤候选集,并行性不高;GSI将邻边和邻接点的标签数量编码为签名以方便并行验证,但忽略了结点的所处局部的结构特征,过滤能力不强. 在连接阶段,GpSM由候选点生成候选边,再基于候选边进行连接运算,但这样不能确定中间结果表的大小和写入地址,需要进行重复连接[23 ,26 ] ,占用大量线程资源且在时间上带来额外开销. ...
1
... CUDA由NVIDIA在2007年推出[29 ] . 在CUDA模型下,GPU的线程按组织粒度由大到小分为线程格(grid)、线程块(block)以及线程(thread),同一个线程块内每32个线程组织成线程束(warp),工作在单指令多线程(single instruction multiple threads, SIMT)模式下,是GPU最小的调度单元. GPU内部包含一组固定的流式多处理器(streaming multiprocessor, SM),线程块按一定策略被调度到处理器上执行. GPU内存被划分为多个层次和类型,各部分容量和访问延迟均有较大差异. 其中最外层为全局内存(global memory),可供所有的线程访问,大小通常为GB级别,访问延迟在400~600个时间片;其次为每个线程块内的共享内存(shared memory),只能由块内线程访问,大小通常为48 KB,访问延迟为32个时间片;线程块内还设有L1缓存,特性与共享内存类似. GPU上内存总线读写全局内存和L1缓存每次都传输连续的128 B[30 ] ,因此对同一个线程束内的线程而言,访问一段连续的内存可以进行合并访存优化,显著降低访存频率从而降低访存延迟. ...
2
... CUDA由NVIDIA在2007年推出[29 ] . 在CUDA模型下,GPU的线程按组织粒度由大到小分为线程格(grid)、线程块(block)以及线程(thread),同一个线程块内每32个线程组织成线程束(warp),工作在单指令多线程(single instruction multiple threads, SIMT)模式下,是GPU最小的调度单元. GPU内部包含一组固定的流式多处理器(streaming multiprocessor, SM),线程块按一定策略被调度到处理器上执行. GPU内存被划分为多个层次和类型,各部分容量和访问延迟均有较大差异. 其中最外层为全局内存(global memory),可供所有的线程访问,大小通常为GB级别,访问延迟在400~600个时间片;其次为每个线程块内的共享内存(shared memory),只能由块内线程访问,大小通常为48 KB,访问延迟为32个时间片;线程块内还设有L1缓存,特性与共享内存类似. GPU上内存总线读写全局内存和L1缓存每次都传输连续的128 B[30 ] ,因此对同一个线程束内的线程而言,访问一段连续的内存可以进行合并访存优化,显著降低访存频率从而降低访存延迟. ...
... 换言之,作为必要条件,若式(3)不成立,则 $v \notin C(u)$ [26 ] ,综合利用结点局部的结构和数量特征的复合签名具有更强的过滤能力. 以图1 (a)中的 ${u_1}$ $C({u_1}) = \{ {v_2},{v_3},{v_4}\} $ ${v_4} \notin C({u_1})$ $C({u_1}) = \{ {v_2},{v_3}\} $ [30 ] ,时间复杂度为 $O(|{V_q}|{\rm{lb}}\;|{V_g}|)$ $|{V_q}|$
1
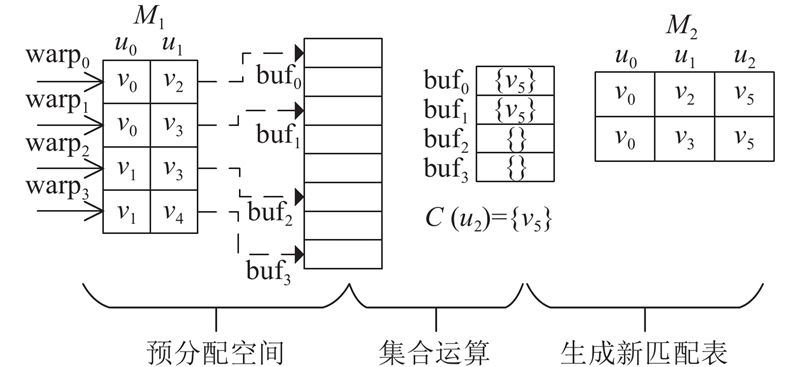
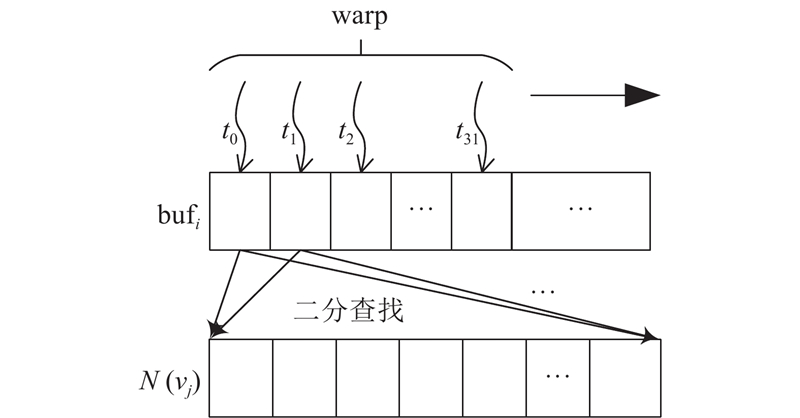
... 算法3为 ${\text{join}}$ ${m_i}$ $ {\text{bu}}{{\text{f}}_i} $ ${m_i}$ $C(u)$ $O(1)$ $C(u)$ . 行9~10是对 ${\tilde m_i}$ [31 ] 进行存储. 不同于传统的邻接表和邻接矩阵的图数据表现形式,CSR具有节省空间、存储结构对GPU友好的优点. 使用CSR, $O(1)$
面向大图子图匹配的多GPU编程模型
1
2023
... 负载不均衡不但会导致线程资源的浪费,而且会影响整体执行耗时. 为此,结合GPU的线程模型,采用线程的三级调度策略[32 ] ,即在并行场景下,当任务量较大时,优先采用线程块执行;任务量中等时,使用线程束;若仍有剩余则使用线程并行处理. 如算法3的行6~10,若 $ 32 \leqslant |N({v_{\rm{s}}})| < 1\;024 $ $ 1\;024 \leqslant |N({v_{\rm{s}}})| $
面向大图子图匹配的多GPU编程模型
1
2023
... 负载不均衡不但会导致线程资源的浪费,而且会影响整体执行耗时. 为此,结合GPU的线程模型,采用线程的三级调度策略[32 ] ,即在并行场景下,当任务量较大时,优先采用线程块执行;任务量中等时,使用线程束;若仍有剩余则使用线程并行处理. 如算法3的行6~10,若 $ 32 \leqslant |N({v_{\rm{s}}})| < 1\;024 $ $ 1\;024 \leqslant |N({v_{\rm{s}}})| $
1
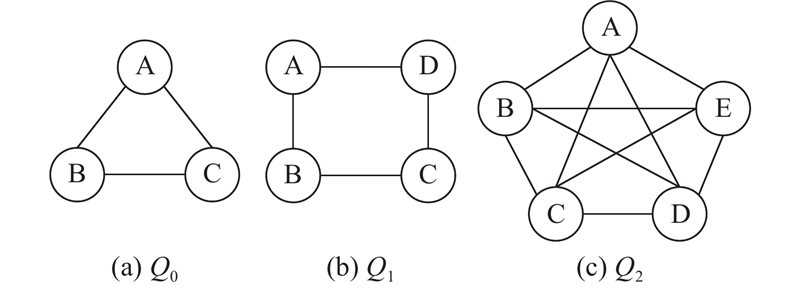
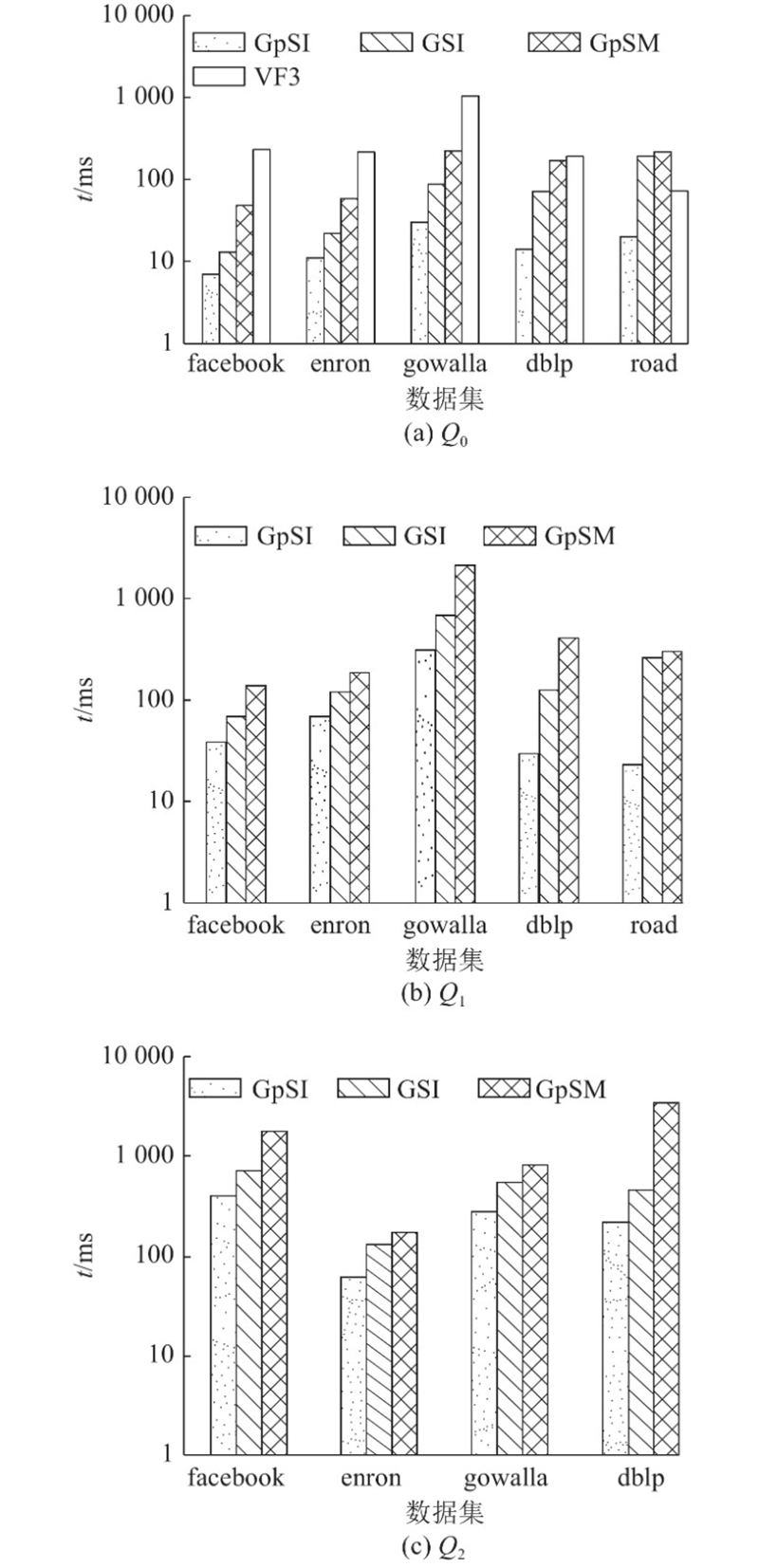
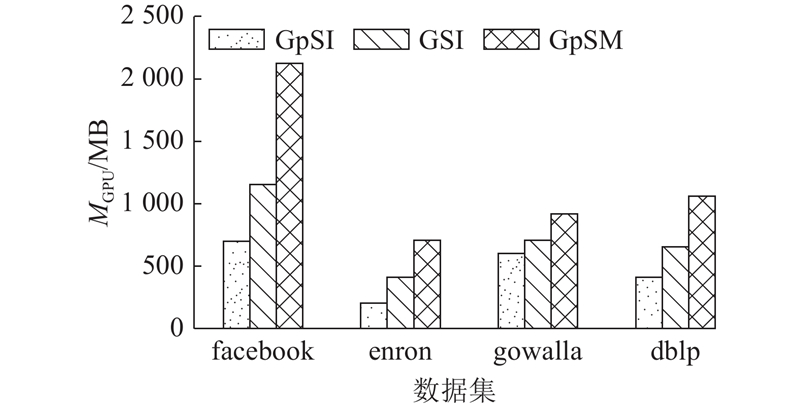
... 对本研究提出的算法GpSI进行实验,并对比GPU上先进的算法GSI、基于边连接的算法GpSM和CPU上广泛使用的串行算法VF3. 实验采用真实数据集和合成数据集进行测试. 真实数据集来自斯坦福大规模网络数据集SNAP[33 ] ,包括脸书社交圈网络(facebook)、联邦能源委员会邮件通信网络(enron)、地理位置社交网络(gowalla)、DBLP协作网络(dblp)以及美国得州道路网(road),各数据集详细信息如表1 所示. 表中,MD为最大结点度数,N V 为结点数,N E 为边数. 设置相关研究中普遍使用的3个查询图[34 ] 进行实验,如图9 所示. 稳定性测试中,采用模型生成或随机游走的方式生成数据图、查询图以验证算法的鲁棒性. 真实数据集上结点一般不带标签,因此预处理阶段进行随机设置,下文若不作特殊说明,数据图中结点标签种类均设定为5. 算法代码均采用C++编写,使用CUDA Toolkit 10.9,操作系统为Ubuntu20.04. CPU为Intel i5-9400,GPU为NVIDIA GTX1650,显存4 GB,拥有896个流处理器,内存为DDR4 16 GB,SSD大小为512 GB. 所有实验均重复10次,以平均值作为实验结果. 算法输出经过Boost-VF2lib[35 ] 提供的子图匹配算法程序的正确性验证. ...
1
... 对本研究提出的算法GpSI进行实验,并对比GPU上先进的算法GSI、基于边连接的算法GpSM和CPU上广泛使用的串行算法VF3. 实验采用真实数据集和合成数据集进行测试. 真实数据集来自斯坦福大规模网络数据集SNAP[33 ] ,包括脸书社交圈网络(facebook)、联邦能源委员会邮件通信网络(enron)、地理位置社交网络(gowalla)、DBLP协作网络(dblp)以及美国得州道路网(road),各数据集详细信息如表1 所示. 表中,MD为最大结点度数,N V 为结点数,N E 为边数. 设置相关研究中普遍使用的3个查询图[34 ] 进行实验,如图9 所示. 稳定性测试中,采用模型生成或随机游走的方式生成数据图、查询图以验证算法的鲁棒性. 真实数据集上结点一般不带标签,因此预处理阶段进行随机设置,下文若不作特殊说明,数据图中结点标签种类均设定为5. 算法代码均采用C++编写,使用CUDA Toolkit 10.9,操作系统为Ubuntu20.04. CPU为Intel i5-9400,GPU为NVIDIA GTX1650,显存4 GB,拥有896个流处理器,内存为DDR4 16 GB,SSD大小为512 GB. 所有实验均重复10次,以平均值作为实验结果. 算法输出经过Boost-VF2lib[35 ] 提供的子图匹配算法程序的正确性验证. ...
1
... 对本研究提出的算法GpSI进行实验,并对比GPU上先进的算法GSI、基于边连接的算法GpSM和CPU上广泛使用的串行算法VF3. 实验采用真实数据集和合成数据集进行测试. 真实数据集来自斯坦福大规模网络数据集SNAP[33 ] ,包括脸书社交圈网络(facebook)、联邦能源委员会邮件通信网络(enron)、地理位置社交网络(gowalla)、DBLP协作网络(dblp)以及美国得州道路网(road),各数据集详细信息如表1 所示. 表中,MD为最大结点度数,N V 为结点数,N E 为边数. 设置相关研究中普遍使用的3个查询图[34 ] 进行实验,如图9 所示. 稳定性测试中,采用模型生成或随机游走的方式生成数据图、查询图以验证算法的鲁棒性. 真实数据集上结点一般不带标签,因此预处理阶段进行随机设置,下文若不作特殊说明,数据图中结点标签种类均设定为5. 算法代码均采用C++编写,使用CUDA Toolkit 10.9,操作系统为Ubuntu20.04. CPU为Intel i5-9400,GPU为NVIDIA GTX1650,显存4 GB,拥有896个流处理器,内存为DDR4 16 GB,SSD大小为512 GB. 所有实验均重复10次,以平均值作为实验结果. 算法输出经过Boost-VF2lib[35 ] 提供的子图匹配算法程序的正确性验证. ...
Graph matching beyond perfectly-overlapping Erd?s-Rényi random graphs
1
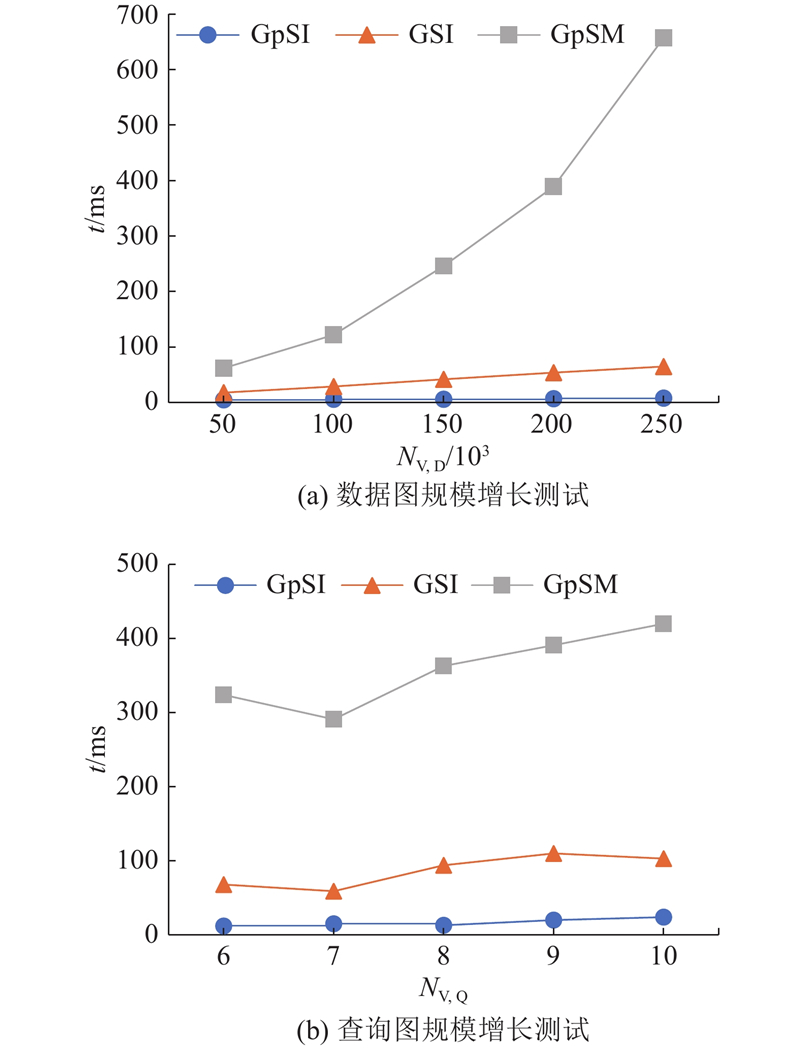
2022
... 为了测试GpSI的稳定性,记录算法随数据图和查询图规模增长时的总执行用时. 数据图规模增长测试中,采用Erdős-Rényi模型[36 ] 生成随机的数据图进行实验,初始时 $N_{\rm{V}}= 5.0 \times {10^4}$ $N_{\rm{E}} = 2.0 \times {10^5}$ $N_{\rm{V}}= 2.5 \times {10^5}$ $N_{\rm{E}} = 1.0 \times {10^6}$ ${Q_0}$ . 在查询图规模增长测试中,使用Erdős-Rényi模型生成 $N_{\rm{V}}= 1.0 \times {10^5}$ $N_{\rm{E}} = 4.0 \times {10^5}$ 图12 所示,图中,N V, D 为数据图结点数,N V, Q 为查询图结点数. 由于候选集和匹配表规模庞大,随着数据图规模的增长,GpSM耗时急剧增加,GpSI和GSI的执行用时都维持着线性增长. GpSI有高强的候选集过滤能力和高效的连接策略,在执行用时上始终优于GpSM和GSI,且对图数据规模的增长不敏感,稳定性最好. ...