2020年,我国建筑能耗占所有行业总能耗的31%[1]. 基于天然气的冷热电联供(combined cooling, heating and power microgrid,CCHP)系统为建筑提供多种类型的能源,能够实现电、热、冷等多种形式能源的灵活转化和综合利用. CCHP中多种形式的能源间存在多时间尺度特性,为建筑能源的高效优化调度带来挑战. 在微网的优化调度中,有多种技术能够提升调度经济性和供能稳定性:需求响应作为供给侧和需求侧的互动方法,能够提升微网系统的灵活性,保障供能的稳定性;日前-日内调度能够降低由于日前负荷预测不准确导致的调度偏差,减少负荷不确定性对调度结果带来的影响[2].
建筑作为柔性虚拟储能,能够有效参与冷热负荷的调度过程[3]. 楼宇虚拟储能作为重要的需求响应资源被广泛应用于微网优化调度中. 靳小龙等[4]通过约束温度舒适性区间,构建基于楼宇虚拟储能的调度模型;楼宇虚拟储能有保证低压配电网系统电压稳定性和降低运行成本的双重作用[5];葛少云等[6]通过构建综合考虑室内空气和建筑围护结构的精细化虚拟储能模型,全面分析了楼宇虚拟储能的需求响应效果;陈厚合等[7]基于热阻热容网络提出考虑太阳辐射方向性的多区域建筑虚拟储能模型. 尽管已有研究推进了建筑模型的发展,预测了动态环境条件的建筑热惯性,也提出了楼宇虚拟储能作为需求响应方法参与能源系统优化调度的方法,但很少有研究关注室内含湿量变化对楼宇虚拟储能的作用. 室内含湿量变化将导致室内湿空气的焓值(即潜热焓值)发生变化,建筑中因潜热焓值变化造成的室内暖通系统(heating, ventilation, and air conditioning, HVAC)额外运行能耗占比可达39%[8]. 当HVAC同时控制室内温度和相对湿度时,由于室内相对湿度发生变化,相应的除湿或加湿过程将产生湿负荷,湿负荷的变化能够引起水蒸气携带的潜热焓值变化,最终导致热负荷或冷负荷的计算偏差[9]. 因此仅考虑室内温度约束的方法,不适用于热/湿负荷同时参与需求响应的场景,需要额外将湿负荷引入需求响应中,发挥潜热在调度中的价值.
模型预测控制(model predictive control, MPC)被广泛应用于微网日内调度. 预测时域的选择是MPC的关键,它对日内调度结果有显著影响. 预测时域越长,用于优化调度的信息越充足,得到的经济性越好,但计算成本将大幅上升;预测时域越短,模型计算成本越低,调度结果却不令人满意[10-12]. 预测时域主要有滚动预测时域[13-18]和缩短预测时域[19-20]2种,其中滚动预测时域采用固定值,缩短预测时域采用的时域长度随时间逐渐减小. 上述文献均未提出均衡计算成本和调度结果的预测时域确定方法,且少有研究针对不同负荷随机性下的预测时域长度变化问题展开讨论. 自适应预测时域方法能够在室内热/湿负荷波动较大时自动拓宽预测时域,保证用户热舒适得到满足并降低系统运行经济成本;该方法还能够在室内热/湿负荷波动减小时自动减少预测时域,降低整体计算成本. 本研究提出基于考虑湿负荷的冷负荷需求响应和自适应预测时域的冷热电联供微网日前-日内优化调度模型. 探索冷负荷的潜热和显热部分协同作用下微网系统经济成本和设备供能灵活性的影响. 采用改进粒子群优化算法 (particle swarmoptimization, PSO)求解优化调度计算模型. 以杭州某典型商业建筑的夏季制冷工况为例,验证所提模型的性能.
1. 冷热电联供微网系统结构及建模
1.1. 冷热电联供微网系统结构
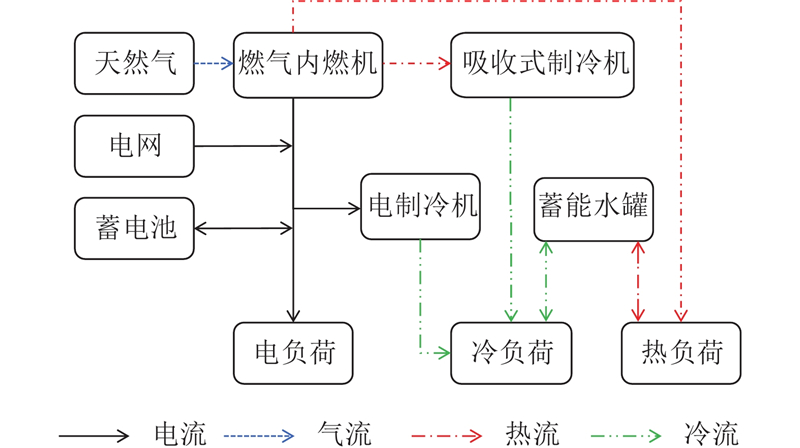
如图1所示,本研究构建的冷热电联供微网系统为楼宇型微网. 电负荷主要由燃气内燃机消耗天然气进行发电来承担,多余电力可以送入蓄电池,不足部分由电网或蓄电池供应。夏季冷负荷主要由燃气内燃机排放的烟气驱动吸收式制冷机制冷来承担,不足部分由电制冷机和蓄能水罐补充;冬季热负荷主要由燃气内燃机的余热和蓄能水罐供应. 本研究仅考虑夏季工况下的多时间尺度优化调度问题,因此仅对冷负荷和电负荷进行建模.
图 1
图 1 冷热电联供微网系统结构
Fig.1 Schematic of combined cooling, heating and power microgrid
1.2. 冷热电联供微网系统建模
1.2.1. 燃气内燃机
燃气内燃机的发电效率ηgt(τ)和余热回收效率ηht(τ)均为机组负荷率ωgt(τ)的函数,
式中:Pgt,e(τ)为燃气内燃机出力,
式中:ζ为天然气热值,取ζ=38 931 kJ/m3. 燃气内燃机满足约束:
1.2.2. 吸收式制冷机和电制冷机
采用溴化锂吸收式制冷机和电制冷机作为冷源满足冷负荷,其中溴化锂吸收式制冷功率Pac,c(τ)和电制冷机制冷功率Pec,c(τ)分别为各自制冷系数e的函数,
式中:Pac(τ)、Pec,e(τ)分别为τ时刻从燃气内燃机中得到的吸热功率和电功率;eac、e,ec分别为吸收式制冷机和电制冷机的制冷系数,其中eac为常数,eec为电制冷机负荷率ωec(τ)的函数,
吸收式制冷机和电制冷机的约束分别为
式中:
1.2.3. 蓄电池和蓄能水罐
蓄电池和蓄能水罐分别提供储电和储冷,τ时刻的蓄电量Wbt(τ)和蓄冷量Wwt(τ)分别由上一时刻Wbt(τ−1)和Wwt(τ−1)得到,
式中:Pbt、Pwt分别为蓄电池和蓄能水罐的充放电功率,正值代表充电,负值代表放电;δwt为蓄能水罐能量损失率,假设蓄能水罐为理想状况,即δwt = 0;下标bt_c、bt_d分别代表蓄电池充、放电过程,下标wt_c、wt_d分别代表蓄能水罐储冷、释冷过程. 蓄电池和蓄能水罐分别满足的约束为
式中:
1.3. 电负荷与包含湿负荷的冷负荷建模
典型的日前建筑逐时电负荷Pe_l(τ)和逐时冷负荷Pc_l(τ)计算均以恒定室内温湿度设定值为前提. 为了充分挖掘建筑柔性储能参与需求响应的潜力,本研究提出包含湿负荷的冷负荷建模方法,使日前建筑负荷能够在调度中同时调整室内温湿度设定值以响应分时电价.
1.3.1. 包含湿负荷的日前冷负荷分布
湿负荷为根据室内相对湿度设定值进行相对湿度调控产生的供湿量或除湿量. 在传统考虑热负荷的需求响应基础上,根据HVAC湿度控制的特点,1)将室内热负荷的平衡式由温度自变量改写为比焓值(显热部分)自变量,2)将湿负荷通过湿空气的水蒸气潜热效应等效转换为比焓值(潜热部分)的形式. 因此,本研究构建的冷负荷由2个部分构成:文献中广泛采用的显热部分和本研究提出的由湿负荷产生的潜热部分. 在满足文献[21]规定的室内热舒适温湿度区间内,通过调整室内温湿度设定值,达到充分利用建筑围护结构热湿惯性并使得冷负荷进行削峰填谷,最终减少系统运行成本的作用. 基于湿空气中水蒸气的高汽化潜热这一特性,考虑湿惯性能够进一步发挥建筑作为虚拟储能单元的需求响应潜力. 在基于额定室内温湿度得到的冷负荷基础上,通过包含湿负荷,可以起到进一步平移负荷的作用.
基于热湿平衡方程得到显热和潜热平衡分别为
式中:Psen(τ)、M(τ)分别为室内冷负荷的显热部分和湿负荷,cp、ρ分别为比定压热容和密度,V为室内容积,vS为回风体积流量,
式中:
1.3.2. 日内负荷预测分布
根据文献[23],由于天气和人员活动具有不确定性,建筑负荷的波动范围为10%~20%. 因此,设置室内电/冷负荷服从方差为10%的正态分布,即N(μ, 0.1μ),其中μ为日前预测的负荷期望值.
2. 日内自适应预测时域模型预测控制
在日内阶段,由于负荷的不确定性,经典的MPC一般采用恒定的控制时域和预测时域修正日前调度结果. 虽然预测时域长度对日内调度结果的影响较大,但现有文献对最佳预测时域长度尚无定论. 预测时域长度对日内调度结果的影响表现为1)拓宽预测时域虽然能获取全面的预测数据和最佳经济成本,但会产生高昂的计算成本,不利于日内调度的实施;2)减小预测时域虽然能够加快系统调度响应,但往往以损失系统经济成本为代价. 本研究提出自适应预测时域MPC方法,旨在寻找最优的预测时域,使计算时间和经济成本均达到较小值.
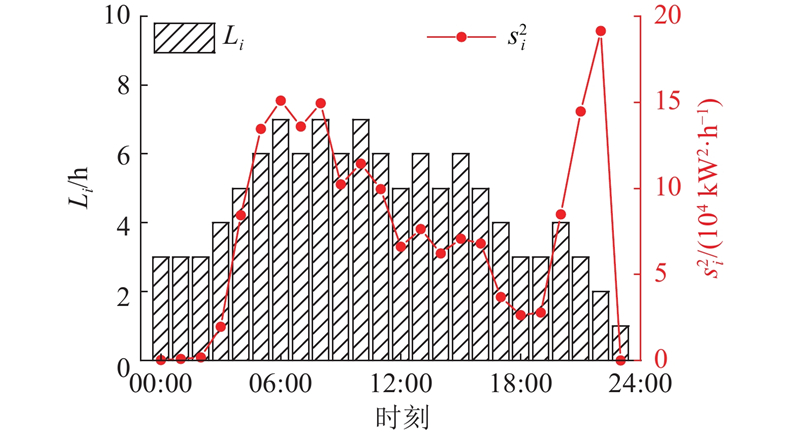
根据负荷的波动情况,假设单位预测时域长度为1 h,预测时域总长为Li,定义从i 至i+Li 的预测负荷方差
式中:
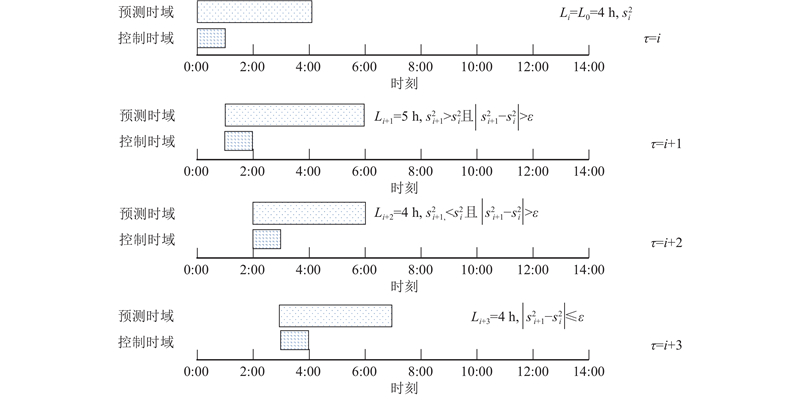
如图2所示为自适应预测时域模型预测控制示意图,其中控制时域为1 h,
图 2
图 2 自适应预测时域模型预测控制示意图
Fig.2 Schematic of adaptive prediction horizon for model predictive control
1)当控制时域为τ = i 时刻(如0∶00)时,给定初始预测时域长度L0,并指定Li = L0,计算
2)当控制时域为τ = i +1 时刻(如1∶00)时,给定预测时域长度Li+1 = Li,计算
3)对比
4)保持预测时域长度不变,即Li+1 = Li,执行步骤7).
5)负荷波动在增大,因此增大预测时域为Li+1 = Li +1,以提供全面的预测信息,执行步骤7).
6)负荷波动在减小,因此减小预测时域为Li+1 = Li −1,以增加优化计算效率,执行步骤7).
7)随控制时域进行滚动执行步骤2)~6),直至i+Li时刻到达日内调度周期停止.
日内优化调度不考虑次日情形,因此在滚动执行步骤2)~6)过程中,当模型预测时域超出日前调度周期时,预测时域长度需要相应缩短,即截断超出日前调度周期的预测时域长度.
3. 模型求解
3.1. 日前优化调度数学模型及约束
日前优化调度使得系统达到最小运行成本,包括燃料成本Cgas(τ)、购电成本Cgrid(τ)以及运行维修成本
式中:Rgas为天然气价,Rgrid(τ)为τ时刻电网分时电价,Rom_gt、Rom_ac、Rom_ec、Rom_bt和Rom_wt分别为燃气内燃机、吸收式制冷机、电制冷机、蓄电池和蓄能水罐的运行维修价格. 日前调度除了满足各设备运行约束和上下限约束外,还要满足各负荷平衡约束,包括
3.2. 日内优化调度数学模型及约束
日内优化调度在日前调度结果上使系统在满足负荷需求的前提下进一步降低运行成本,根据自适应预测时域,有目标函数:
此外,系统的约束条件与日前调度保持一致.
3.3. 改进粒子群优化算法
采用改进的粒子群优化算法对优化模型进行求解. 传统粒子群优化算法虽然广泛用于优化调度问题求解,但其求解速度较慢,且如早熟收敛和陷入局部极值的问题导致其收敛能力较差[24]. 为了提升搜寻全局最优值的能力,进行如下改进.
1) 优化惯性权重(Opt1):对惯性权重w进行更新,表达式为
式中:wk为第k次迭代采用的惯性权重,wa、wz分别为初始惯性权重和终止惯性权重;k、kmax分别为第k次迭代数和总迭代次数. 惯性权重能够使优化在迭代初期拥有较大的搜索惯性和搜索空间,并在迭代后期能够快速收敛至全局最优值.
2) 设置罚函数(Opt2):通过在目标函数式(18)、(20)中各自额外增加罚函数项m·G快速过滤不满足约束的粒子,使带约束问题转变为无约束问题. 其中m为罚函数权重,G为罚函数. 罚函数的形式定义如下:对于等式约束f(A) = a,G = [f(A) − a]2,对于不等式约束f(B) ≤ b,G = max[0, f(B) − b].
3) 设置自调节设备出力(Opt3):针对等式约束难以满足的问题,在粒子群优化中计算粒子适应度步骤前,加入自调节步骤以增大可行解比例[25]. 由于同一设备可能既能提供冷负荷也能提供电负荷,优先对供冷设备进行自调节过程,即优先保障冷负荷平衡.
4) 引入粒子突变(Opt4):粒子突变是避免传统粒子群算法存在早熟收敛和局部最优的改进方法,其特点为牺牲部分效率换取更大的搜索空间[26]. 粒子突变规则:若种群最优解变化连续k次迭代均小于一定值εk,则从种群中随机抽取部分粒子进行突变.
4. 算例分析
4.1. 算例数据
图 3
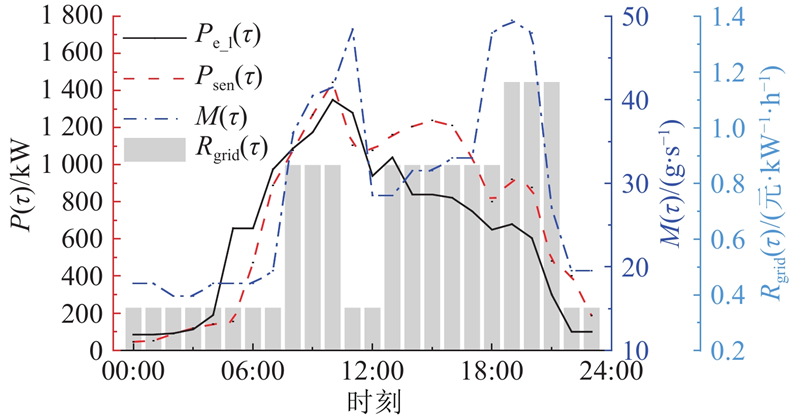
图 3 日前阶段电、冷(显热部分)、湿负荷及分时电价
Fig.3 Electricity, cold (sensible heat part), humidity load and time-of-use tariff during day-ahead scheduling
表 1 微网系统各设备的相关参数设置
Tab.1
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | ||
| | 1 000 | | 1 300 | | 600 | ||
| | 500 | | 0 | | 500 | ||
| | 0 | | 2 000 | eac | 1.2 | ||
| | 2 000 | ηbt_c | 0.8 | ηbt_d | 0.8 | ||
| ηwt_c | 0.8 | ηwt_d | 0.8 | — | — |
表 2 湿负荷参与需求响应和经济成本的相关参数设置
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| | 24 | | 28 | |
| | 0.4 | | 0.7 | |
| Rgas / (元·m−3) | 2.8 | Rrm_gt/ (元·kW−1·h−1) | 0.03 | |
| Rrm_ac/ (元·kW−1·h−1) | 0.025 | Rrm_ec/(元·kW−1·h−1) | 0.01 | |
| Rrm_bt/ (元·kW−1·h−1) | 0.02 | Rrm_wt/ (元·kW−1·h−1) | 0.13 |
为了对比本研究提出的考虑湿负荷后的冷负荷需求响应在日前阶段中的作用,除了包含湿负荷的冷负荷需求响应方案S2外,在日前阶段计算中平行设置以下方案:无负荷需求响应方案S0(室内无任何负荷需求响应)和仅考虑传统冷负荷需求响应方案S1(仅冷负荷参与需求响应,湿负荷不参与需求响应). 为了对比自适应预测时域模型预测控制在日内阶段中的作用,在日内阶段设置固定预测时域进行对比.
4.2. 算例结果与分析
4.2.1. 改进粒子群优化算法效果分析
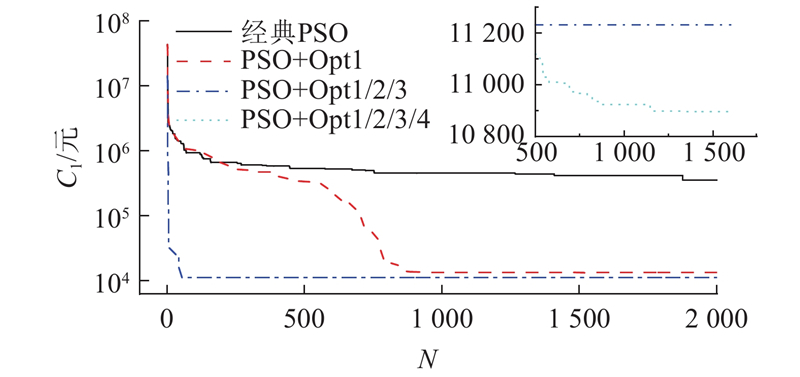
在日前阶段采用经典粒子群算法和各种改进粒子群算法的比较如图4所示. 可以看出,经典粒子群算法的收敛效果较差,仅采用优化惯性权重(Opt1)改进后,约迭代次数N = 800后可得到较好的收敛效果. 进一步采用优化惯性权重(Opt1)、设置罚函数(Opt2)和自调节设备出力(Opt3)后,在N = 100内即可达到收敛(收敛时间较经典PSO缩短约72%). 增加粒子突变(Opt4)后,虽然可在N = 1500跳出局部最优解并达到全局最优值,但对目标函数降低范围有限但收敛时间较经典PSO延长87%,因此针对本研究涉及的优化调度问题不建议采用粒子突变方法.
图 4
图 4 不同粒子群优化算法的日前阶段优化结果比较
Fig.4 Comparisons between optimization results obtained by different particle swarm optimization algorithms for day-ahead scheduling
4.2.2. 日前阶段包含湿负荷的冷负荷需求响应结果与分析
需求响应方案S0、S1和S2的日前总运行成本分别为12028、11341、11096元. 在包含室内湿负荷参与冷负荷需求响应后,总运行成本相比方案S0下降了7.75%,且比方案S1额外下降了2.04%. 这一结果表明,在暖通设计中,考虑空调等设备的热/冷、湿负荷并使之同时参与需求响应,可以达到更好的经济效益. 原因是湿空气中的水蒸气具有较高的潜热,被视为建筑中的虚拟储能,这一举措在高湿地区有较好的经济效益.
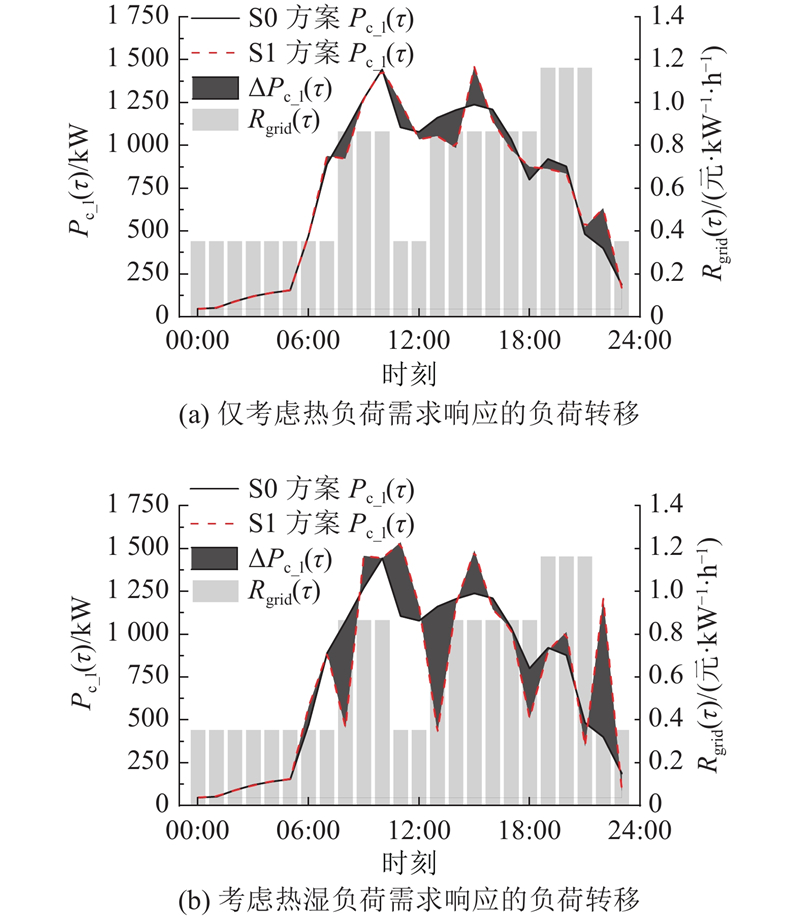
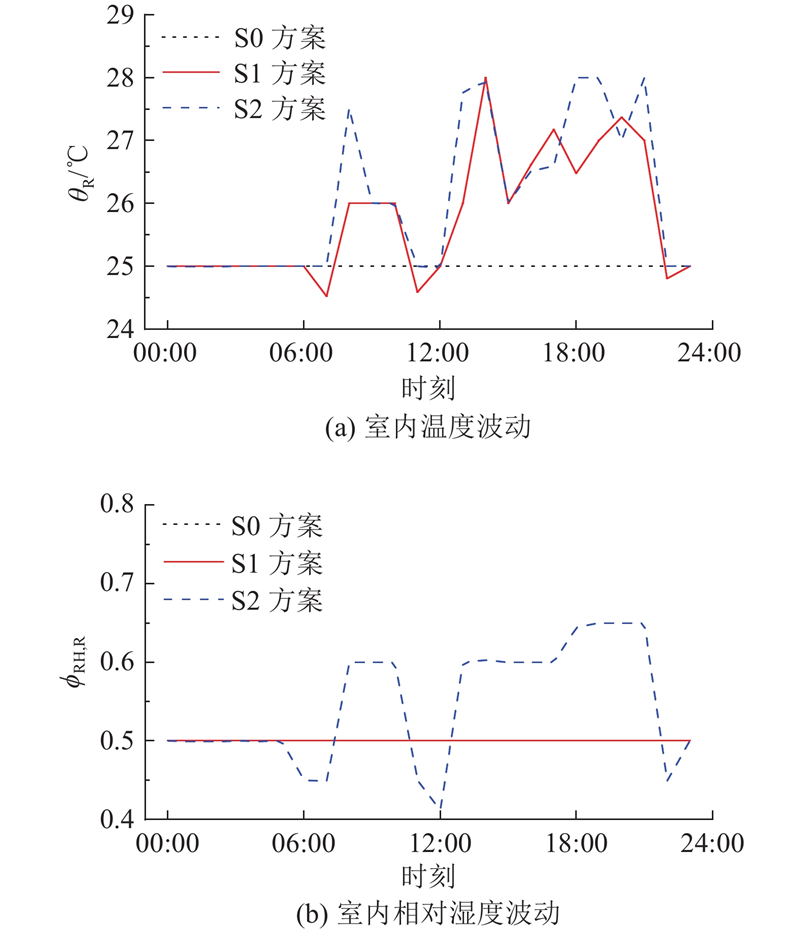
以方案S0为参照,方案S1和S2日前调度中冷负荷的负荷转移情况对比如图5所示. 不同需求响应方案根据分时电价进行相应的冷负荷转移,日总冷负荷均为17456 kW·h. 可以看到,考虑湿负荷参与冷负荷需求响应后,冷负荷转移量明显增大,因而较大的负荷转移量使得冷负荷能够有效避开分时电价中高峰电价时段,降低了日前阶段总经济成本. 图5中在低谷电价时段冷负荷出现回弹效应,但是总体经济成本并未上升,反而最大化“移峰填谷”的作用. 3种方案的室内温湿度波动情况如图6所示. 可以看出,室内温湿度在夏季考虑湿负荷作为冷负荷的一部分参与需求响应后呈上升趋势,但未超过文献[21]规定的热舒适温度和相对湿度区间,因此方案S2能够在保证热舒适要求的前提下共同转移冷负荷中的显热和潜热负荷(湿负荷).
图 5
图 5 日前阶段各需求响应方案的冷负荷转移情况
Fig.5 Cooling load shifting of each case during day-ahead scheduling
图 6
图 6 日前阶段各需求响应方案的室内温湿度情况
Fig.6 Indoor temperature and relative humidity of each case during day-ahead scheduling
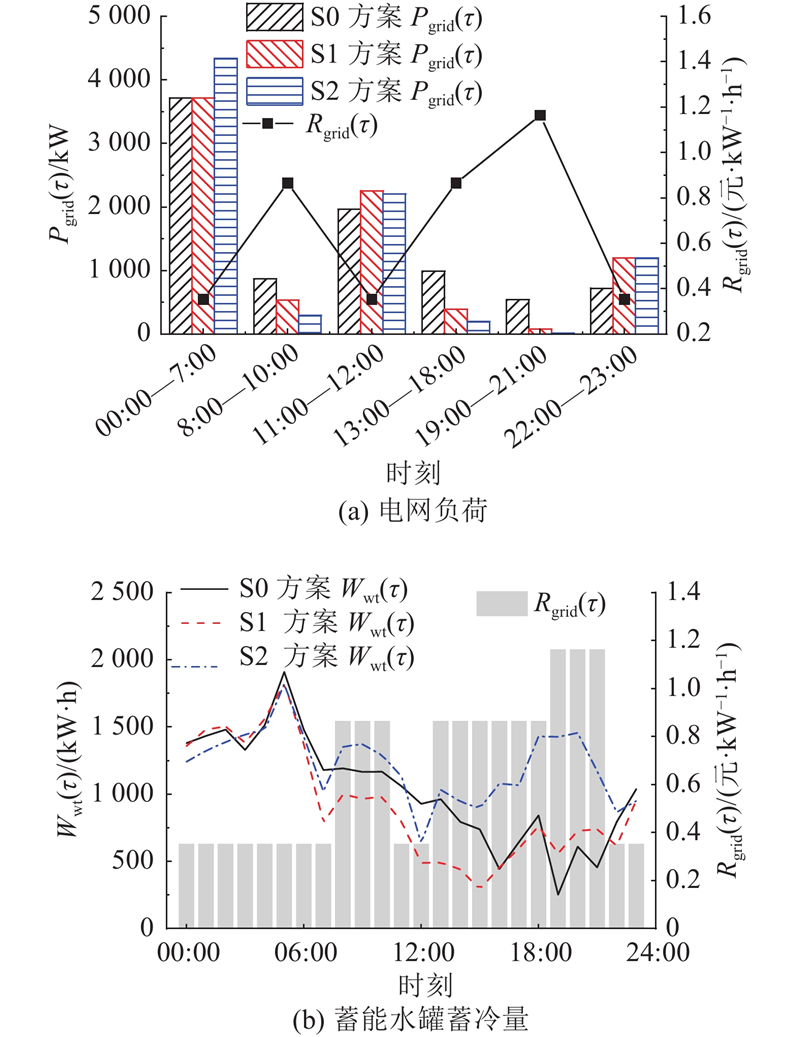
3种方案的电网负荷变化和蓄能水罐蓄冷量变化如图7所示. 考虑包含湿负荷的冷负荷需求响应后,方案S2在高峰电价时段平均购电量仅为方案S0的2.5% (19:00—21:00的平均值),几乎可以实现高峰时段离网运行,缓解了电网压力. 方案S2在平峰电价时段的购电量也大幅下降,与方案S0相比平均下降幅度为26.3%. 在高峰和平峰电价时段,方案S2中蓄能水罐的蓄冷量相比方案S0、S1也呈现大幅提升的效果,原因是湿空气潜热较大,在高峰时段适当放松室内相对湿度要求后,其冷负荷能够大幅降低,使蓄能水罐在高峰时段也能进行蓄冷,保证了蓄能水罐的工作稳定性. 如果考虑式(10)的蓄能水罐能量损失率,蓄能水罐的蓄冷量Wwt(τ)将随时间进一步降低,方案S0、S1中的蓄冷量可能无法满足用户冷负荷, 方案S2能够在实际工况下保证蓄能水罐的工作稳定性和冷负荷的满足.
图 7
图 7 日前各需求响应方案的电网负荷和蓄能水罐蓄冷量
Fig.7 Grid electricity load and stored cooling energy in water tank of each case during day-ahead scheduling
4.2.3. 日内阶段考虑自适应预测时域结果与分析
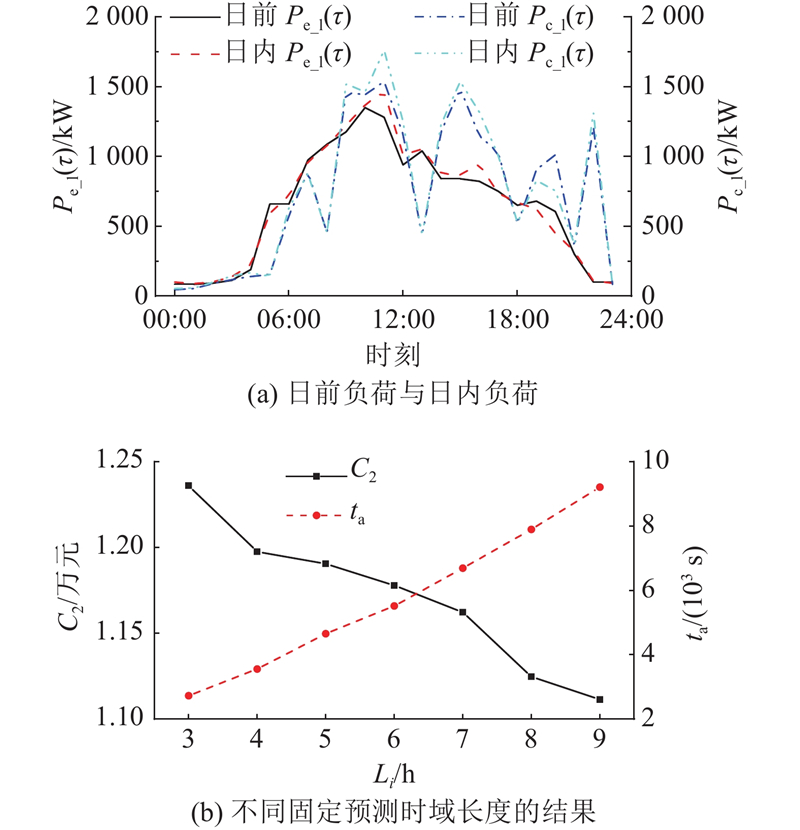
图 8
图 8 日前/日内负荷和不同固定预测时域结果
Fig.8 Day-ahead/intra-day loads and results of different constant prediction horizons
图 9
图 9 自适应预测时域方案在日内的预测时域长度变化
Fig.9 Intra-day change of prediction horizon with adaptive prediction horizon length scheme
表 3 自适应预测时域与不同固定预测时域的结果对比
Tab.3
| 预测时域方案 | C2/ (元·d−1) | ta/s | ψ |
| 自适应 | 11 777 | 4 481 | 4.76 |
| 固定3 h | 12 360 | 2 725 | 5.08 |
| 固定7 h | 11 623 | 6 688 | 4.92 |
式中:w1、w2为权重系数,均取0.5;
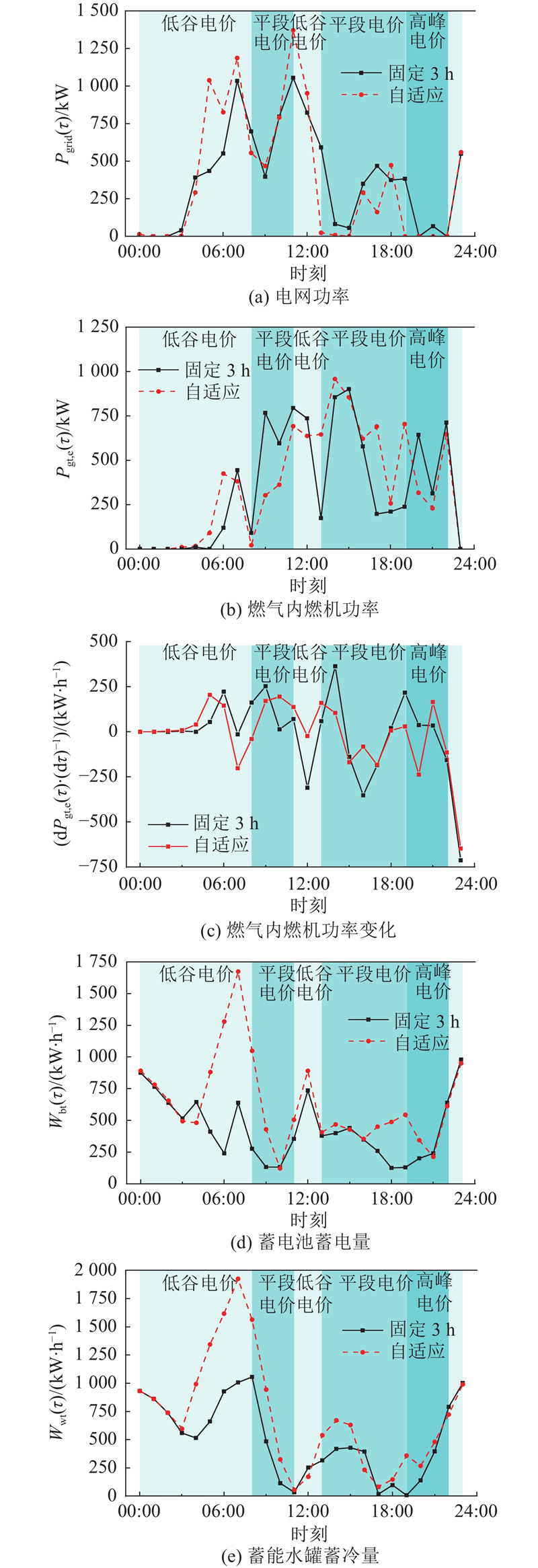
进一步从各设备层面对自适应预测时域进行评估. 采用自适应预测时域模型预测控制与3 h固定预测时域模型预测控制的结果对比如图10所示. 图10(a)显示采用本研究提出的自适应预测时域后,电网在高峰电价时段的功率下降,有助于进一步降低电网负荷,并且在低谷和平段电价时段有较高的功率,有助于电网在日内各时段达到稳定负荷. 图10(b)显示在自适应预测时域中燃气内燃机在高峰时段出力大幅降低,同时在整个调度周期上(特别是9:00—18:00)有更平稳的输出功率);图10(d)、(e)显示蓄电池和蓄能水罐的蓄能量波动,可以看出自适应预测时域使得蓄电量和蓄冷量在低谷电价和平段电价时段大幅上升,即自适应预测时域能够预测到更长时间范围内的负荷波动以及电价变化,从而提前进行蓄能设备的蓄能或者释能,有效增加了储能设备的利用率,并在考虑蓄能水罐能量损失后更能确保在高峰用冷时段(图10(e)中10:00—12:00和16:00—20:00)的供冷稳定性.
图 10
图 10 各设备结果在自适应与固定预测时域中的对比
Fig.10 Comparison of results for each device by adaptive and constant prediction horizons
5. 结 论
(1) 引入湿负荷作为新的负荷需求响应方法,有效降低系统在日前阶段的总运行成本7.75%;湿负荷的需求响应有效地降低了分时电价下对电网的负荷压力,大幅提升了蓄能水罐蓄冷量和稳定性.
(2) 提出新的自适应预测时域模型预测控制方法,该方法能够基于负荷波动方差自动调整预测时域,对合理选择预测时域有指导意义.
(3) 所提出的自适应预测时域模型预测控制方法在日内阶段平衡了计算时间和经济性成本;自适应模型预测控制方法对减少对电网负荷、平稳燃气内燃机输出功率、增加蓄能水罐和蓄电池等储能设备的利用率等有一定贡献;为了对比自适应预测时域与固定时域的效果,提出预测时域选择评价因子.
(4)所提的湿负荷需求响应方法和自适应预测时域模型预测控制方法对于不同微网形式、不同季节和不同负荷状况下均适用. 后续研究计划基于不同微网形式/季节/工况考察湿负荷需求响应的能力,在不同负荷状况下评估自适应预测时域模型预测控制方法的作用.
参考文献
综合能源系统优化运行技术研究综述
[J].
Review of research on optimal operation technology of intergrated energy system
[J].
基于柔性负荷的孤立多能互补建筑能源系统优化设计
[J].
Design of isolated multi-energy complementary building energy system based on flexible load
[J].
融合需求侧虚拟储能系统的冷热电联供楼宇微网优化调度方法
[J].
Optimal scheduling method for a combined cooling, heating and power building microgrid considering virtual storage system at demand side
[J].
考虑空调群虚拟储能的配电网电压无功协同控制研究
[J].
Coordinated control research for voltage and reactive power of distribution network considering virtual energy storage of air-conditionings
[J].
需求响应机制下含建筑虚拟储能的能源站经济调度
[J].
Economic dispatch of energy station with building virtual energy storage in demand response mechanism
[J].
集成智能楼宇的主动配电网建模及优化方法
[J].
Modeling and optimization of active distribution network with integrated smart buildings
[J].
A temperature and humidity setback demand response strategy for HVAC systems
[J].DOI:10.1016/j.scs.2021.103393 [本文引用: 1]
基于能耗模拟的精密空调温湿度协同优化控制
[J].
Cooperative optimal control on temperature and humidity of precision air conditioning based on energy consumption simulation
[J].
Model predictive control: past, present and future
[J].
Lifetime optimization framework for a hybrid renewable energy system based on receding horizon optimization
[J].DOI:10.1016/j.energy.2018.02.158 [本文引用: 1]
基于模型预测控制的冷热电联供型微网动态优化调度
[J].
Optimal dynamic dispatch for combined cooling heating and power microgrid based on model predictive control
[J].
融合虚拟储能系统的楼宇微网模型预测调控方法
[J].DOI:10.13334/j.0258-8013.pcsee.171707 [本文引用: 1]
Model predictive scheduling method for a building microgrid considering virtual storage system
[J].DOI:10.13334/j.0258-8013.pcsee.171707 [本文引用: 1]
计及多类型需求响应的风-火-荷两阶段协同调度
[J].
A two-stage coordinated dispatch of wind power, thermal power and system load with multi-type demand response
[J].
含混合储能的独立微电网多时间尺度协调控制策略
[J].
Multi-time scale coordination control strategy of isolated microgrid with hybrid energy storage
[J].
基于差异化需求响应模型预测控制的微网时域滚动优化调度
[J].DOI:10.13335/j.1000-3673.pst.2020.1507
Time-domain rolling optimal scheduling of microgrid based on differential demand response model predictive control
[J].DOI:10.13335/j.1000-3673.pst.2020.1507
A two-stage optimization and control for CCHP microgrid energy management
[J].DOI:10.1016/j.applthermaleng.2017.05.188
Hierarchical microgrid energy management in an office building
[J].DOI:10.1016/j.apenergy.2017.10.002 [本文引用: 1]
基于预测控制的含风电滚动优化调度
[J].DOI:10.19595/j.cnki.1000-6753.tces.161373 [本文引用: 1]
A rolling dispatch model for wind power integrated power system based on predictive control
[J].DOI:10.19595/j.cnki.1000-6753.tces.161373 [本文引用: 1]
Demand reduction in building energy systems based on economic model predictive control
[J].DOI:10.1016/j.ces.2011.07.052 [本文引用: 1]
A review on the prediction of building energy consumption
[J].DOI:10.1016/j.rser.2012.02.049 [本文引用: 1]
基于改进粒子群算法的冷热电联供微网优化调度
[J].
Optimal scheduling of micro grid with CCHP systems based on improved particle swarm optimization algorithm
[J].
电热联合系统多时间尺度滚动调度策略
[J].
Multi-time scale rolling scheduling method for combined heat and power system
[J].
带可变随机函数和变异算子的粒子群优化算法(英文)
[J].DOI:10.1016/S1874-1029(14)60015-X [本文引用: 1]
A particle swarm optimization algorithm with variable random functions and mutation
[J].DOI:10.1016/S1874-1029(14)60015-X [本文引用: 1]