钢筋机械锚固是指通过设置在钢筋端部的锚具的承压机制将受力钢筋锚固于混凝土[1]. 锚具的形式有焊接锚固板、螺纹连接锚固板、冷挤压套管、钢筋墩头、贴焊锚筋等[2-3]. 近年来,机械锚固钢筋在房屋和桥梁领域的应用不断增多[4–6]. 相较于传统的锚固方式如直锚、末端带弯钩锚固,钢筋的机械锚固可以减小钢筋锚固长度,解决节点区域因钢筋拥挤造成绑扎安装困难、混凝土浇筑质量差的问题,从而有效保证施工质量[7]. 过去,国内外学者较多采用试验的手段从宏观的角度对机械锚固钢筋的锚固性能进行研究. 美国Caltrans、SINTEF、Texas等[3]大学和机构、日本大成建设公司[8]、中国建筑科学研究院、天津大学和哈尔滨工业大学等单位[2,9–11]先后对各种机械锚固钢筋进行一系列基础拔出试验,主要研究机械锚固钢筋的一般性能,集中于对锚固长度和锚固能力的研究,对于机械锚固钢筋细观工作机理的研究较少.
随着计算机技术的快速发展,有限元分析方法已在土木领域得到广泛应用[12-13]. 它不仅能有效减少试验所带来的高昂成本,还能验证试验并提取丰富的数据结果. 采用有限元软件对机械锚固钢筋的拔出试验进行数值仿真分析,可以对试件内部的裂缝发展情况、复杂的应力状态进行全程可视化,从而准确地揭示其细观工作机理. 通常,机械锚固钢筋在混凝土中除锚具外,还有一定长度的直锚段与之共同受力,因此,所建立的有限元模型除了反映机械锚固作用外,还须准确反映黏结作用. 目前,关于钢筋与混凝土之间黏结作用机理研究的有限元模型主要有杆尺度模型[14–16]和肋尺度模型[17–19]2种. 杆尺度模型将钢筋简化为具有公称直径的圆柱体,不体现钢筋表面横肋的几何形状. Aragão等[16]采用杆尺度模型分析带锚固板钢筋在混凝土中的锚固性能,该模型通过假定黏结滑移关系来定义钢筋与混凝土之间的应力传递,然而,现有的黏结滑移关系往往是在某些特定试验条件下得到的结果,并不具有普适性,难以准确地反映其他研究问题的真实应力状态. 肋尺度模型通过对钢筋表面横肋的几何形状进行精细化建模来实现钢筋与混凝土之间的应力传递. 与杆尺度模型相比,肋尺度模型能准确地反映变形钢筋与混凝土之间的机械咬合作用,无须人为假定黏结滑移关系,在研究直钢筋在混凝土中的黏结作用机理时被一些学者所采用. Jiang等[17]采用肋尺度模型研究侧向拉伸荷载作用下变形钢筋与混凝土之间的黏结性能. Seok等[18]采用肋尺度模型研究单调荷载作用下钢筋混凝土梁中纵向搭接钢筋黏结区域的力学行为. 过去采用肋尺度模型进行的研究主要针对单一黏结锚固的情况,然而,钢筋的机械锚固通常与黏结锚固同时存在,两者共同工作时内部的应力传递机理较复杂,很少有学者将肋尺度模型应用于机械锚固与黏结锚固共同工作机理的研究中.
为了揭示混凝土中钢筋机械锚固与黏结锚固共同工作的机理,以减小锚具大小和锚固长度,提高锚固效率,提出一种肋尺度精细化建模方法,采用DIANA 10.4有限元软件分别对机械锚固单独工作的带锚固板钢筋拔出试验、黏结锚固单独工作的U形弯钩钢筋拔出试验进行建模和分析,将模拟结果与各自的试验结果进行对比,验证单一机制下2种有限元模型的有效性. 其次,同时使用上述2种建模方法对黏结和机械锚固共同工作下的冷挤压套管钢筋拔出试验进行模拟分析,并与试验结果进行多方面对比,进一步验证2种机制共同工作下肋尺度模型的有效性. 根据有限元分析结果,探讨机械锚固和黏结锚固各自的工作机理、损伤演化和破坏模式以及2种方式共同工作的荷载分担比例.
1. 试验概况
分别对3组试验进行模拟. A组:带锚固板钢筋拔出试验;B组:U形弯钩钢筋拔出试验;C组:冷挤压套管直钢筋拔出试验.
1.1. 带锚固板钢筋拔出试验
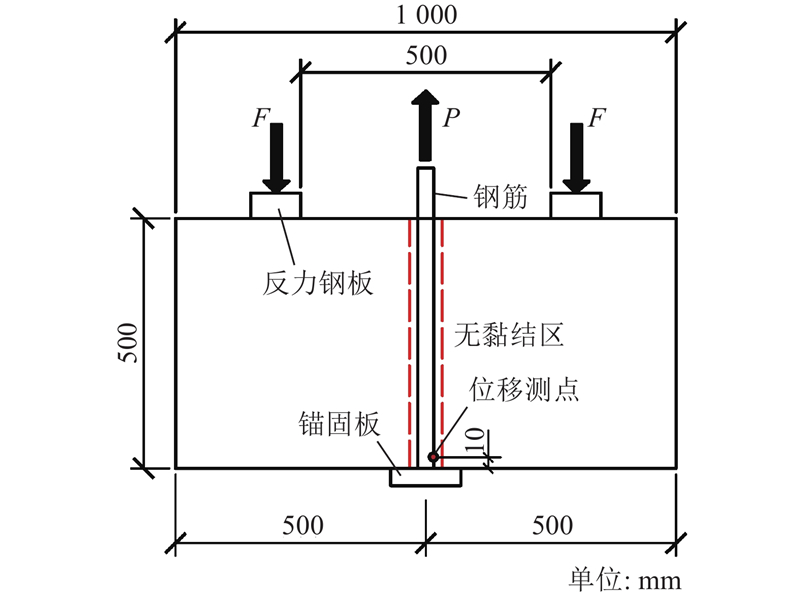
畑明仁等[20]对3种不同强度的摩擦焊接锚固板钢筋进行了拔出试验,试验所采用的摩擦焊接锚固板钢筋如图1所示.试件的几何尺寸及详细参数分别如图2和表1所示. 图中,P为拔出荷载,F为反力. 表中,d为锚固板的直径,t为锚固板的厚度,D为钢筋的直径. 试验共包括3种工况,各工况的锚固板尺寸不同,混凝土块的尺寸均为1000 mm×1000 mm×500 mm,3种工况下混凝土抗压强度试验结果平均值分别为32.4、32.1、33.2 MPa. 混凝土顶面的2块反力作用钢板的尺寸均为500 mm×100 mm×50 mm,钢板关于模型中心线对称分布. 为了消除钢筋与混凝土之间的黏结作用,如图1所示,预先对埋置于混凝土中的钢筋段(见图2红色虚线标注区段)进行表面处理,方法是用黏土填平钢筋表面肋与肋之间的沟槽,然后用乙烯基塑料胶带进行包裹. 带锚固板钢筋的直径均为32 mm,锚固板为圆形. 锚固板的弹性模量为182 GPa,泊松比为0.3,屈服强度为370 MPa. 钢筋的材料性能参数如表2所示. 表中,E为弹性模量,ν为泊松比,fy为屈服强度,fyk为屈服强度标准值,fu为抗拉强度,fuk为抗拉强度标准值. 试验加载装置如图3所示,采用单调加载的方式对带锚固板钢筋执行加载,采用力传感器测得钢筋所受到的拉力. 利用位移计检测距钢筋根部以上10 mm处的位移(见图2).
图 1
图 2
图 2 带锚固板钢筋拔出试件的几何尺寸
Fig.2 Geometric dimensions of pullout specimen of headed bar
表 1 带锚固板钢筋拔出试件的详细参数
Tab.1
| 工况 | 锚固板 | 钢筋 | |||
| 形状 | d/mm | t/mm | D/mm | ||
| 1 | 圆形 | 65 | 19 | 32 | |
| 2 | 圆形 | 70 | 22 | 32 | |
| 3 | 圆形 | 70 | 26 | 32 | |
表 2 钢筋的材料性能参数(A组)
Tab.2
| 工况 | E/GPa | ν | fy(fyk)/MPa | fu(fuk)/MPa |
| 1 | 191 | 0.3 | 384(345) | 605(490) |
| 2 | 191 | 0.3 | 431(390) | 653(560) |
| 3 | 191 | 0.3 | 529(490) | 714(620) |
图 3
1.2. U形弯钩钢筋拔出试验
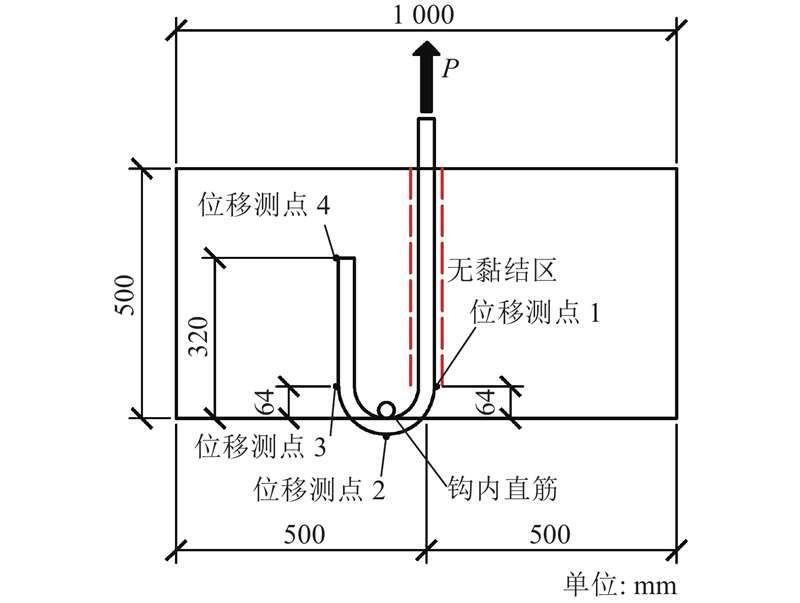
文献[21]、[22]对不同直径的U形(180°)弯钩钢筋进行了拔出试验. 为了便于与A组(带锚固板钢筋拔出试验)对比,选择钢筋直径为32 mm的工况进行模拟. 试件的几何尺寸如图4所示. 混凝土块的尺寸为1000 mm×1000 mm×500 mm,混凝土的抗压强度试验结果平均值为35 MPa. U形弯钩钢筋、弯钩内侧直钢筋的直径均为32 mm. 钢筋的弹性模量为200 GPa,泊松比为0.3,屈服强度为394 MPa,抗拉强度为600 MPa. 定义U形弯钩锚固的起始点为点1,终点为点4,测量1~4各点的位移,加载端至位移测点1的埋入段钢筋与混凝土之间的黏结作用已消除(见图4红色虚线标注区段). 试验的加载装置与A组试验相同,采用单调加载的方式对U形弯钩钢筋执行加载.
图 4
图 4 U形弯钩钢筋拔出试件的几何尺寸
Fig.4 Geometric dimensions of pullout specimen of U-shape hooked bar
1.3. 冷挤压套管钢筋拔出试验
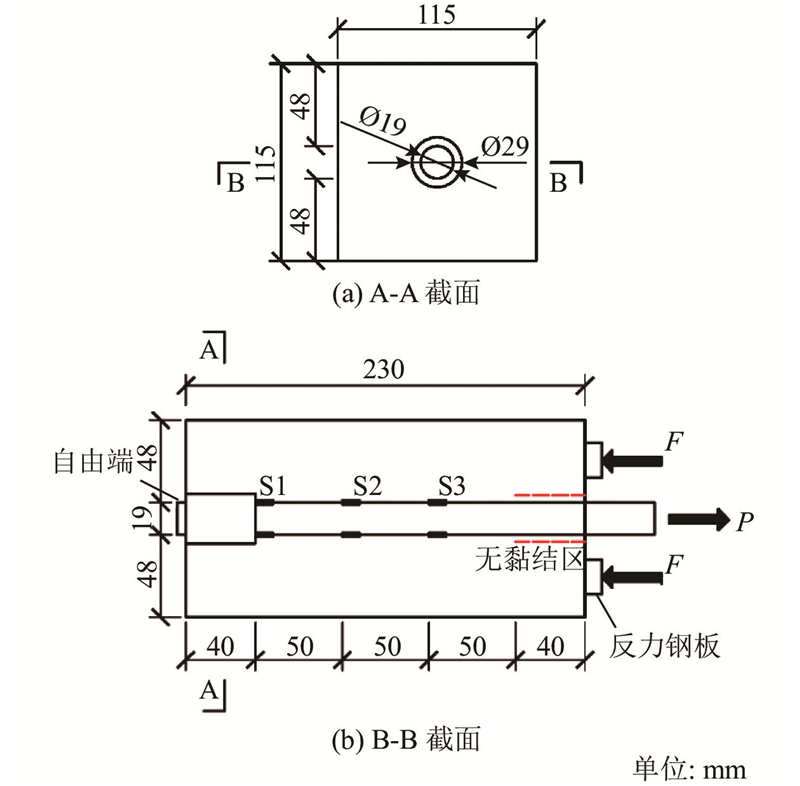
原健悟等[23]为了研究预制混凝土桥面板中纵向钢筋的连接,进行了无黏结段和有黏结段的冷挤压套管钢筋的拔出试验,试验采用的冷挤压套管钢筋如图5所示.试件的几何尺寸如图6所示,混凝土为截面115 mm×115 mm、长230 mm的棱柱体,钢筋的直径为19 mm,套管的外径为29 mm. 钢筋和套管的弹性模量均为200 GPa,泊松比均为0.3,钢筋的屈服强度和抗拉强度分别为385、580 MPa,套管的屈服强度和抗拉强度分别为240、400 MPa. 套管及钢筋表面涂有环氧树脂防锈层,混凝土顶面的2块反力作用钢板的尺寸均为115 mm×20 mm×20 mm,钢板关于模型中心线对称分布,S1、S2、S3分别为应变片的黏贴位置. 试验包括2种情况:1)埋入段钢筋与混凝土之间无黏结作用;2)埋入段钢筋与混凝土之间有黏结作用(除了无黏结区). 混凝土的抗压强度试验结果平均值为46.1 MPa. 采用单调加载的方式对冷挤压套管钢筋执行加载,利用位移计测量如图6(b)所示钢筋自由端的位移.
图 5
图 6
图 6 冷挤压套管钢筋拔出试件的几何尺寸
Fig.6 Geometric dimensions of pullout specimen of cold extruded casing reinforcement
2. 精细化有限元模型
采用DIANA 10.4有限元软件,对上述3种钢筋拔出试验进行建模和数值仿真分析.
2.1. 有限元模型的建立
1)带锚固板钢筋拔出试验的有限元模型.对如图2所示带锚固板钢筋拔出试验进行有限元建模,由于试验不考虑钢筋与混凝土之间的黏结作用,在建模时将钢筋简化为具有公称直径的圆柱体,不体现钢筋表面横肋的形状. 考虑到模型的对称性,为了减小网格数量并提高计算效率,采用轴对称单元建模. 所有部件均采用基于线性插值和高斯积分的四节点四边形轴对称单元(Q8AXI).
由于DIANA 10.4在划分网格后,会自动将接触面两侧不同材料单元的节点自由度进行耦合,即共节点[24]. 因此,为了消除钢筋与混凝土之间的黏结作用,引入界面单元并将其切向刚度设置为0. 为了实现锚固板顶面与混凝土之间的相互作用,引入界面单元并设置其法向受压刚度为无穷大,以保证两者在互不嵌入的前提下能有效传递压应力,切向刚度同样设置为0.
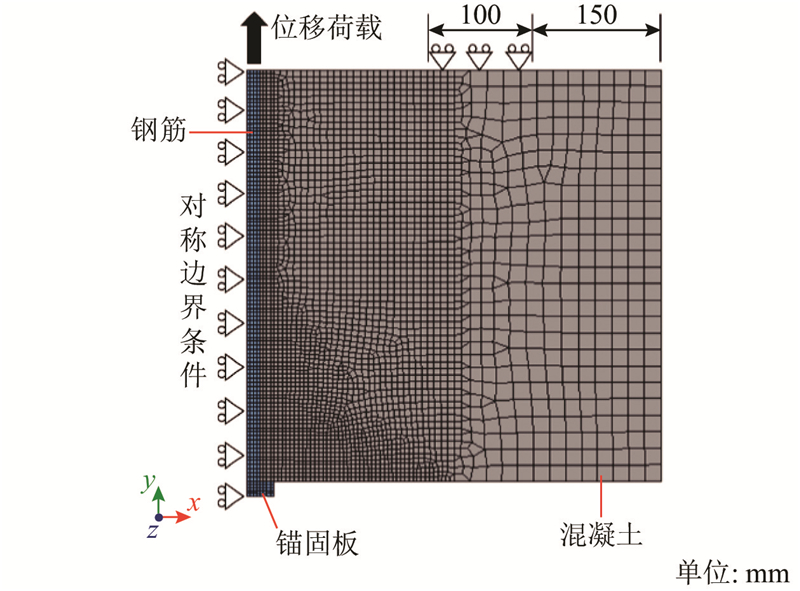
网格划分采用分区域播种,根据区域的重要性分别采用不同的网格大小,钢筋、锚固板以及混凝土受力关键区域的网格大小为5 mm,控制混凝土网格最大尺寸为20 mm. 采用位移加载的方式,对钢筋顶面中心点施加竖直向上的位移,顶面所有节点绑定于中心点,使其具备相同的竖向位移. 采用自定义荷载步的方式执行加载. 模型的网格划分、边界条件、荷载条件如图7所示.
图 7
图 7 带锚固板钢筋拔出试验的有限元模型(A组)
Fig.7 FE model of pullout test of headed bar (group A)
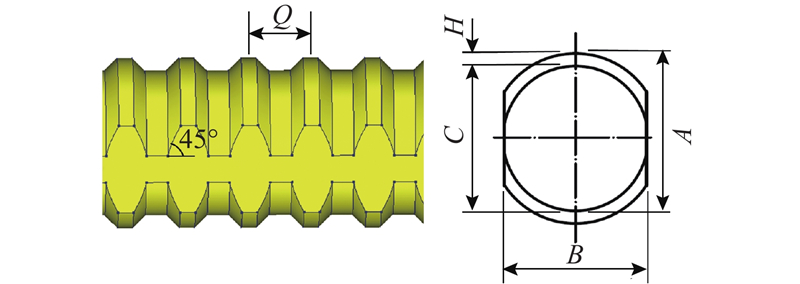
2)U形弯钩钢筋拔出试验的有限元模型.对如图4所示U形弯钩钢筋拔出试验进行有限元建模. 混凝土和钢筋均采用三维实体单元,考虑到模型的对称性,建立1/2模型. 模型所包含的各部件主要采用基于线性插值和高斯积分的八节点六面体单元(HX24L),由于钢筋肋的几何形状较复杂,钢筋肋以及肋附近的混凝土采用边界适应性较好的四节点四面体单元(TE12L)、五节点锥形单元(PY15L)、六节点三棱柱单元(TP18L). 图4中无黏结区按A组试验的模拟方法消除黏结作用,即引入界面单元并将其切向刚度设置为0. 图4中位移测点1~4的埋入段钢筋与混凝土之间存在黏结作用,为了真实地再现变形钢筋与混凝土之间的机械咬合作用,避免人为假定黏结滑移关系,采用体现钢筋表面几何形状的肋尺度精细化建模方法. 钢筋表面肋的形状尺寸参考钢筋生产厂家日本东京铁钢株式会社的螺纹钢筋产品规格[25],并将螺旋肋简化为环形肋. 肋的几何形状如图8所示. 图中,A=35.7 mm,B=29.8 mm,C=30.4 mm,Q=13.0 mm,H=2.65 mm.
图 8
在肋尺度精细化模型中,有学者采用库伦摩擦界面模型定义钢筋与混凝土接触面的切向行为,这种方法须假定摩擦系数和凝聚力,这些参数的取值往往依赖于经验,模型的适用性较差. 为了避免人为假定以上参数,分别采用以下2种简化处理钢筋与混凝土接触面的方法,并在模拟结果与讨论中对2种方法进行对比. (a)节点耦合法:综合考虑变形钢筋与混凝土之间的化学胶着力、摩擦力和机械咬合力,利用DIANA 10.4自动耦合功能[24]实现钢筋单元与混凝土单元节点自由度的耦合,即通常所说的“共节点”,接触面两侧材料单元的节点不产生相对滑动. (b)界面单元法:基于变形钢筋与混凝土之间的黏结力主要为机械咬合力,本方法忽略界面的化学胶着力和摩擦力,仅考虑机械咬合作用. 具体方法是通过引入界面单元,来源面选择与混凝土相接触的所有钢筋表面,目标面选择相应的混凝土表面,界面单元的计算参数设置为法向受压刚度无穷大,法向受拉刚度为0,切向刚度为0,以保证钢筋与混凝土在法向上的相对位置并阻止其嵌入,同时允许法向分离和切向的相对滑移. 2种界面定义方法的概念如图9所示.
图 9
图 9 钢筋与混凝土接触面连接特性示意图
Fig.9 Schematic view of connection properties at concrete-bar surface
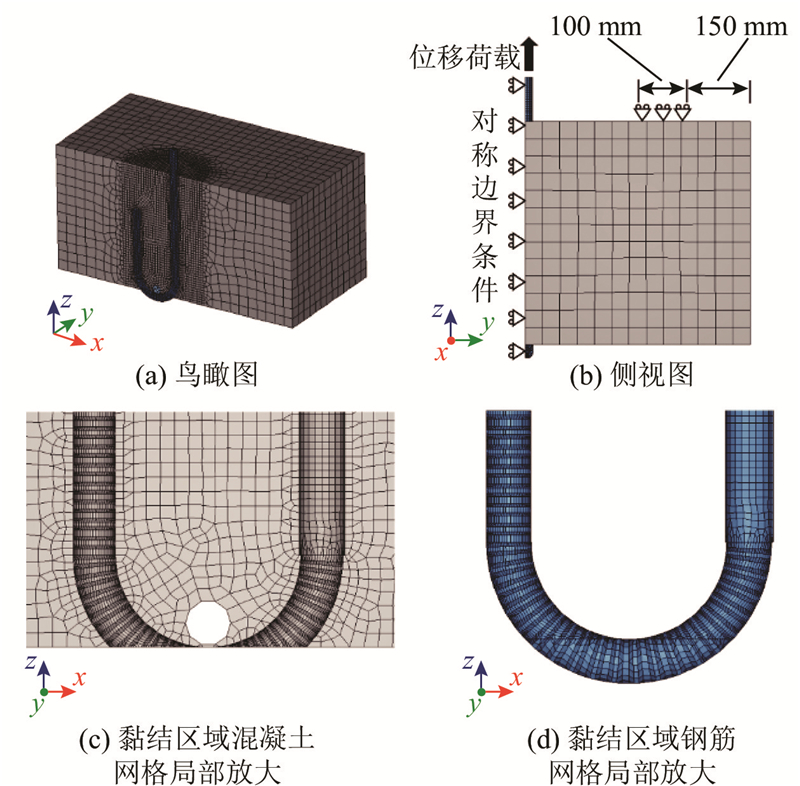
由于该模型为三维肋尺度精细化模型,钢筋横肋尺寸较小且为U形弯钩,网格划分较复杂. 综合考虑构件的几何形状特点以及计算精度和效率的要求,网格划分采用分区域播种,对于受力关键区域,控制钢筋网格最小尺寸为2 mm,钢筋肋附近的混凝土网格最小尺寸为2 mm,非受力关键区域的混凝土网格最大尺寸为40 mm. 采用自定义荷载步的方式执行位移加载. 模型的网格划分、边界条件、荷载条件如图10所示.
图 10
图 10 U形弯钩钢筋拔出试验的有限元模型(B组)
Fig.10 FE model of pullout test of hooked bar (group B)
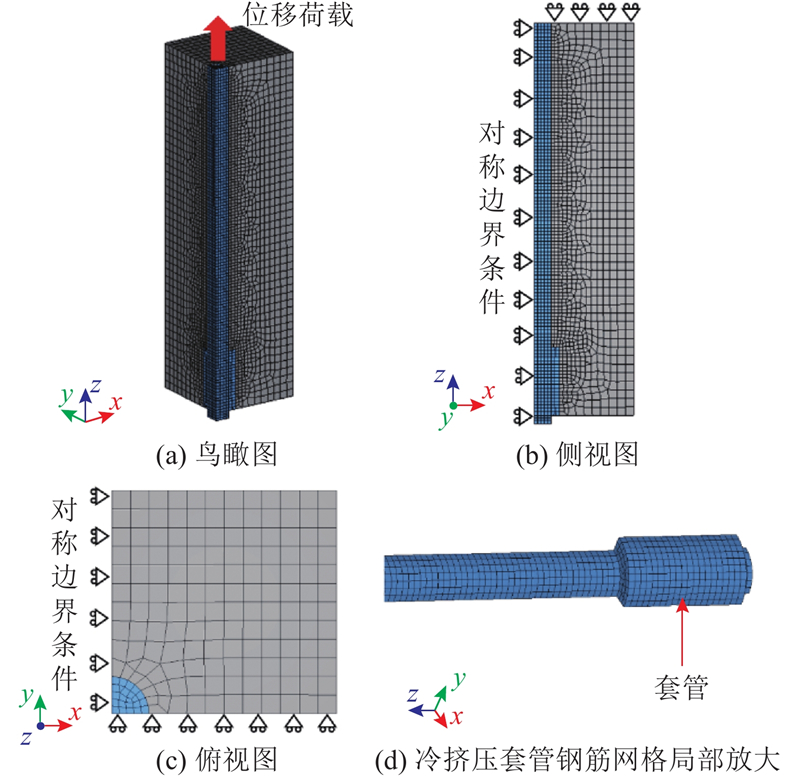
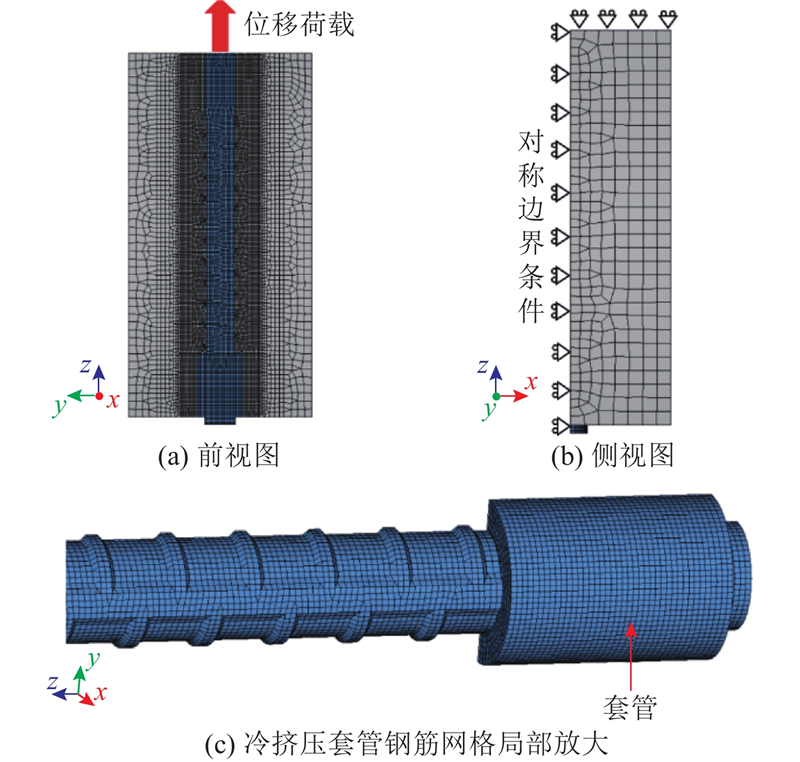
3)冷挤压套管钢筋拔出试验的有限元模型.对如图6所示的冷挤压套管钢筋拔出试验进行有限元建模. 混凝土、钢筋、套管均采用三维实体单元,套管和钢筋材料不同,但几何上视为一个整体. 套管建模采用与模型1)中的锚固板相类似的方法. 对埋入段直钢筋分别对应试验的2种情况进行建模:(a)埋入段钢筋与混凝土之间无黏结作用. 同模型1),钢筋简化为具有公称直径的圆柱体,不体现钢筋表面形状. 利用模型对称性,建立1/4模型;(b)埋入段钢筋与混凝土之间有黏结作用(除了图6的无黏结区),同模型2),采用肋尺度精细化建模方法,对钢筋表面横肋的几何形状进行建模. 由于该试验采用的钢筋表面肋的几何形状不同于前述U形弯钩钢筋的螺旋肋,故采用1/2模型. 钢筋表面形状尺寸参考了钢筋生产厂家大阪制铁株式会社的变形钢筋的产品规格[25],横肋间距为13.4 mm,肋高为1.0 mm,倾角(肋坡与钢筋轴线的夹角)为45°. 采用模型2)所提到的界面单元法定义钢筋与混凝土接触面的连接特性. 采用与模型2)相类似的方法分区域播种网格,由于钢筋的肋高仅1 mm,控制钢筋网格最小尺寸为1 mm,钢筋肋附近的混凝土网格同样为1 mm. 采用自定义荷载步的方式执行位移加载. 以上2种情况所对应的模型的网格划分、边界条件、荷载条件分别如图11、12所示.
图 11
图 11 冷挤压套管钢筋拔出试验的有限元模型(C组-无黏结)
Fig.11 FE model of pullout test of cold extruded casing reinforcement (group C- without bond)
图 12
图 12 冷挤压套管钢筋拔出试验的有限元模型(C组-有黏结)
Fig.12 FE model of pullout test of cold extruded casing reinforcement (group C- with bond)
2.2. 材料本构关系
钢筋、锚固板、套管均采用DIANA 10.4中Von Mises塑性材料模型,3组拉拔试验所采用的钢材分别按照相应的材料性能参数进行取值.
钢筋与套管均采用双折线模型,锚固板采用理想弹塑性模型. 2种模型表达式分别为
式中:σ和ε分别为钢材的应力和应变;
混凝土的单轴受压应力-应变关系采用日本土木学会混凝土结构设计规范建议的模型[26],其表达式如下:
式中:σc和εc分别为混凝土的压应力和压应变,Ec为弹性模量,fcm为混凝土的抗压强度试验结果平均值.
混凝土的单轴受拉应力-应变关系采用Hordijk[27]模型,其表达式如下:
式中:fctm为混凝土抗拉强度,
表 3 混凝土的材料性能参数
Tab.3
| 分组 | 工况 | Ec/GPa | ν | fcm/MPa | fctm/MPa | Gf/(N·mm−1) |
| A组 | 1 | 29.4 | 0.2 | 32.4 | 2.52 | 0.137 |
| 2 | 29.1 | 0.2 | 32.1 | 2.50 | 0.137 | |
| 3 | 30.1 | 0.2 | 33.2 | 2.58 | 0.137 | |
| B组 | − | 31.8 | 0.2 | 35.0 | 2.70 | 0.138 |
| C组 | − | 41.9 | 0.2 | 46.1 | 3.40 | 0.145 |
3. 模拟结果与讨论
3.1. 带锚固板钢筋拔出试验的模拟结果分析
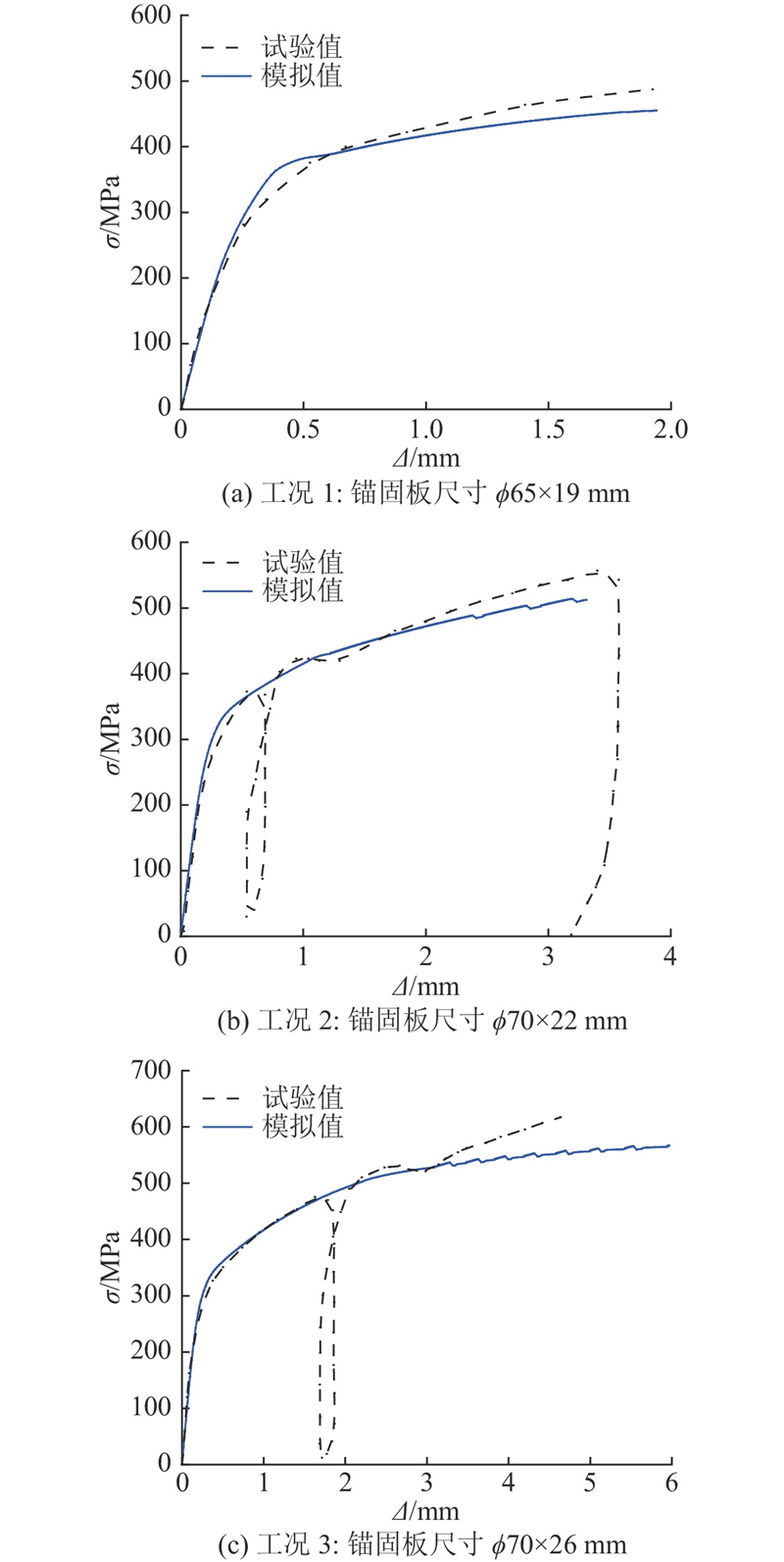
如图13所示为不同工况下钢筋应力-位移曲线的模拟结果与试验结果的对比. 图中,钢筋应力σ等于拔出荷载除以钢筋公称面积,Δ为位移. 可以看出,模拟结果与试验结果较一致,说明模型较好地反映了带锚固板钢筋在轴向拔出荷载作用下的局部承压机制. 在3种工况下,钢筋的屈服强度分别为384、431、529 MPa,试验最终在加载至钢筋的抗拉强度标准值(见表2)时主动卸载. 该锚固板的设计目标是当钢筋应力达到抗拉强度标准值时,锚固板未发生屈服,锚固板下混凝土未发生局部承压破坏,以及锚固区未发生锥状冲切破坏,带锚固板钢筋拉拔试验主要用于对前2种性能进行评估. 从荷载(钢筋应力)-位移曲线可知,至试验加载结束为止,试验和模拟的钢筋应力仍处于上升阶段,没有发生破坏. 在钢筋屈服后,模拟曲线斜率略低于试验曲线,这是由于钢筋采用双折线模型,与实际存在一定偏差,钢筋屈服后的斜率取值可能偏低.
图 13
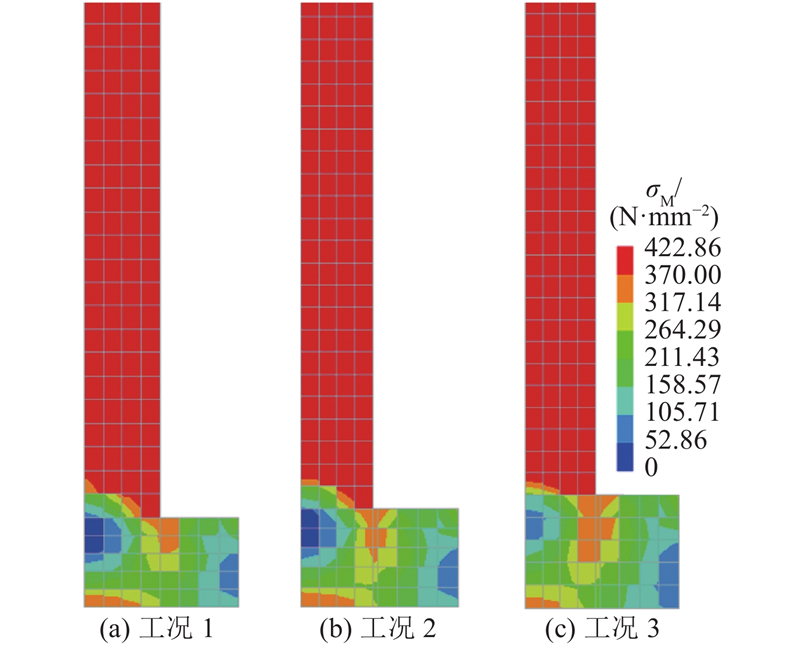
如图14所示为不同工况下钢筋达到屈服强度时,锚固板附近混凝土的主压应力云图. 图中,σ3为主压应力. 锚固板附近混凝土单元的主压应力大于100 MPa,远远超过其单轴抗压强度. 该压应力呈球状扩散,随着至锚固板距离的增大而快速递减,呈现出明显的局部承压状态. 由于钢筋与混凝土之间无黏结作用,拔出荷载全部由锚固板承压方式传递至其下混凝土,混凝土块的尺寸远大于锚固板,锚固板附近混凝土局部受压产生纵向压缩和横向膨胀变形,横向变形受到周围混凝土的约束,导致其处于三轴受压应力状态,锚固承载力大幅度提高.
图 14
图 15
图 16
以上结果表明,在拔出荷载作用下,带锚固板钢筋的锚固机制是局部承压,锚固板下的混凝土处于三轴受压应力状态,在锚固区周围存在足够约束的条件下,锚固板下混凝土的抗压强度可以提高3倍以上,因此较小的锚固板可以提供较大的锚固力.
3.2. U形弯钩钢筋拔出试验模拟结果分析
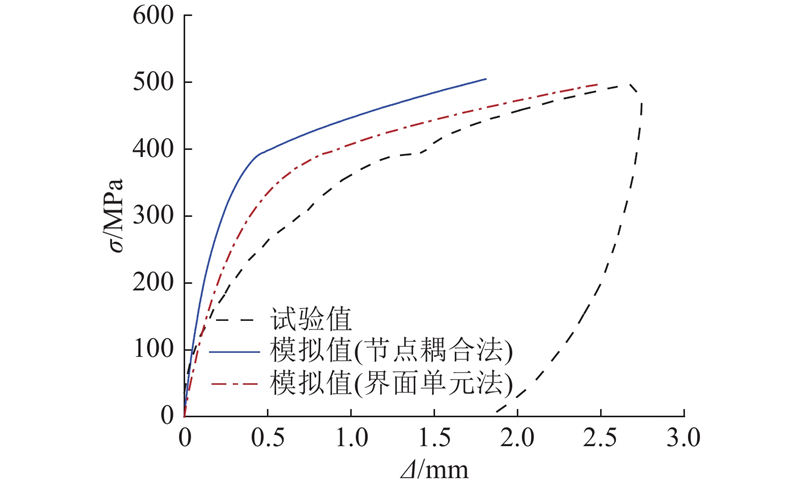
如图17所示为钢筋应力-位移曲线,位移采用U形弯钩起始点(位移测点1)的位移. 分别采用节点耦合法和界面单元法定义钢筋与混凝土的接触面. 由图17可知,相较于节点耦合法,界面单元法的模拟结果与试验结果更接近. 节点耦合法初始刚度偏大,但与试验的初始刚度较一致. 随着荷载的增大,试验曲线刚度开始降低,位移逐渐增大,可以推测此时钢筋与混凝土接触面的化学胶着力和摩擦力开始逐渐减弱和消失,黏结力的主要来源逐渐转变为机械咬合作用. 然而节点耦合法是共节点,意味着直至钢筋表面附近的混凝土破坏为止化学胶着力和摩擦力始终存在,因此模拟的抗拔刚度到钢筋屈服为止一直居高不下,逐渐远离试验结果. 与之相反,界面单元法在钢筋与混凝土之间插入了界面单元并假定切向刚度为0,即假定钢筋与混凝土之间仅存在机械咬合作用,忽略了化学胶着力和摩擦力. 其结果是界面单元法的初始刚度偏低,但从整体上看更接近于试验结果. 相较于试验结果,采用界面单元法的曲线在钢筋屈服以前刚度仍然有些偏大,这可能是由于弯钩起点钢筋肋与混凝土之间的黏结作用并未完全劣化,与试验情况有一定的偏差. 以上结果表明,在肋尺度精细化模型中,除了加载初期以外,节点耦合法过于强化化学胶着力和摩擦力的作用,与试验结果不符. 界面单元法能够较好地体现钢筋与混凝土之间的机械咬合作用和伴随机械咬合作用的相对滑移,化学胶着力和摩擦力对黏结性能的影响较小,可以忽略不计.
图 17
如图18所示为在不同荷载水平下采用主拉应变云图所表示的混凝土裂缝分布形态. 图中,ε1表示主拉应变. 可以看出,在弹性阶段(钢筋应力209 MPa),弯钩起始点(位移测点1)附近混凝土最先出现裂缝,当钢筋屈服时(钢筋应力394 MPa),裂缝已发展至弯钩中点(位移测点2)附近,在钢筋进入强化阶段后(钢筋应力498 MPa),弯钩终点(位移测点3)附近出现细微裂缝. 在整个加载过程裂缝主要分布于钢筋弯起点附近,该区域混凝土损伤较严重. 上述现象与直钢筋拔出试验结果较一致,属于黏结锚固机制,在拔出荷载作用下,弯钩钢筋横肋之间的混凝土齿键发生剪切破坏,从而导致该区域钢筋与混凝土之间产生相对滑移. 剪切破坏取决于混凝土的抗拉强度,为了防止锚固失效,通常需要较大的弯钩和较长的锚固长度.
图 18
图 18 黏结区域混凝土主拉应变(B组)
Fig.18 Principal tensile strain of concrete in bond zone (group B)
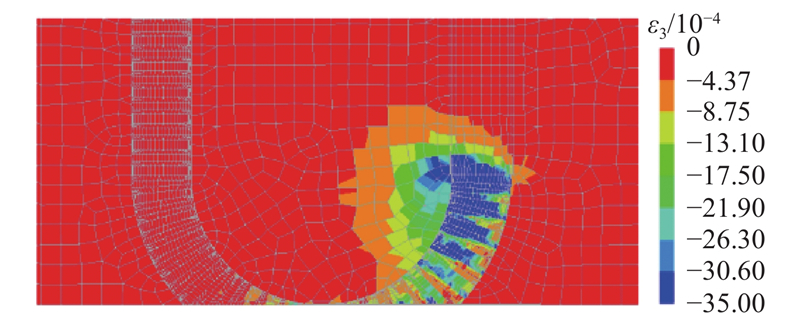
与直钢筋黏结锚固有所不同的是,由于弯钩钢筋是弯曲的,在拉拔荷载作用下,弯钩起点附近的应力状态并非沿钢筋轴线对称分布,如图19所示为张拉端钢筋应力为209 MPa时混凝土主压应变云图. 图中,ε3表示主压应变. 可以看出,在弯钩起始点附近,弯钩内侧存在局部受压区域,弯钩外侧则以受拉为主. 因此,现有的在某些特定试验条件下得到的黏结滑移关系难以准确地反映本研究对象的真实应力状态,这是本研究采用肋尺度精细化有限元模型的主要原因之一. 肋尺度模型只须提供材料单轴受拉和受压本构关系,无须假定界面的黏结滑移本构模型.
图 19
3.3. 冷挤压套管钢筋拔出实验模拟结果分析
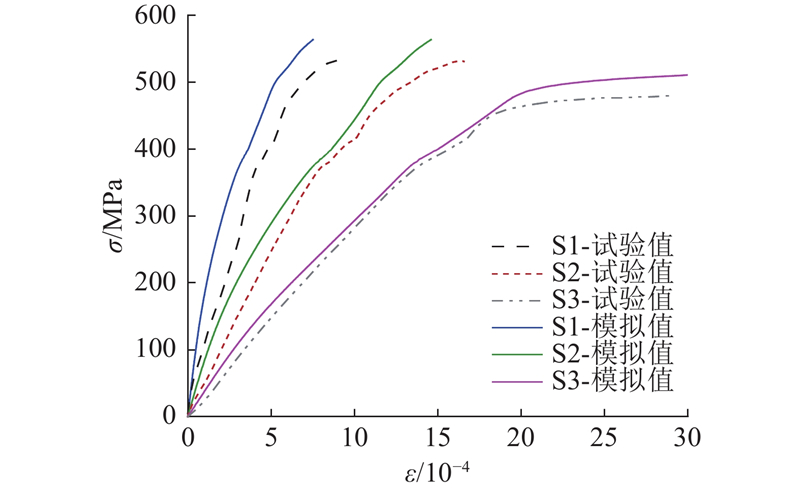
对于机械锚固和黏结共同工作的冷挤压套管钢筋,分别对2种情况进行模拟:1)埋入段钢筋与混凝土之间无黏结作用;2)埋入段钢筋与混凝土之间有黏结作用(除图6的无黏结区). 如图20所示为2种情况下的钢筋应力-位移曲线模拟结果与试验结果的对比,位移采用钢筋自由端的位移. 对于情况1),试件发生了混凝土局部劈裂破坏导致的承载力下降[23],虽然峰值荷载对应的位移有所不同,但峰值荷载较接近,在达到峰值荷载时,加载端钢筋应力试验值为288 MPa,模拟值为305 MPa,误差为6%. 对于情况2),试验加载至钢筋的标准抗拉强度490 MPa后卸载,不论是试验还是模拟,试件均未破坏,钢筋自由端的位移都几乎为0.
图 20
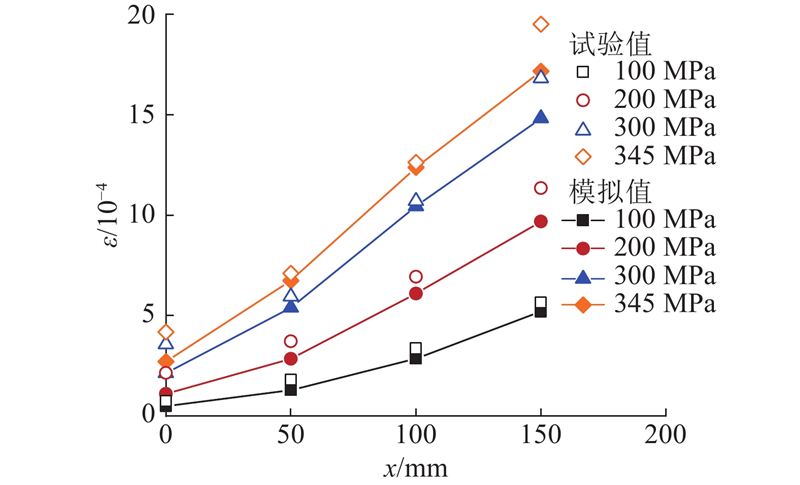
对于情况2),试验测量了多点的钢筋应变. 基于钢筋应变测量结果,可以从细观层面对本研究提出的肋尺度模型进行验证. 如图21所示为张拉端钢筋应力与各测点应变关系曲线. 图中,σ为张拉端钢筋应力,ε为应变. 可以看出,模拟结果略小于试验结果,但应变随荷载的发展趋势基本一致. 显而易见,距离加载端越远,钢筋的应变越小. 当钢筋进入强化阶段后,测点S3的应变剧增,测点S1和S2的应变也随之快速增大. 这是由于加载端附近钢筋屈服而黏结退化,随后钢筋强化又进一步导致钢筋屈服范围的扩大(至少扩大到测点S3以左),黏结应力分布逐渐向锚固端后移,套管承担的荷载开始快速增加.
图 21
图 21 钢筋应力-应变曲线(C组-情况2:有黏结)
Fig.21 Reinforcement stress-strain curves (group C-case 2: with bond)
图 22
图 22 钢筋轴向应变分布(C组-情况2:有黏结)
Fig.22 Axial strain distribution of reinforcement (group C-case 2: with bond)
图 23
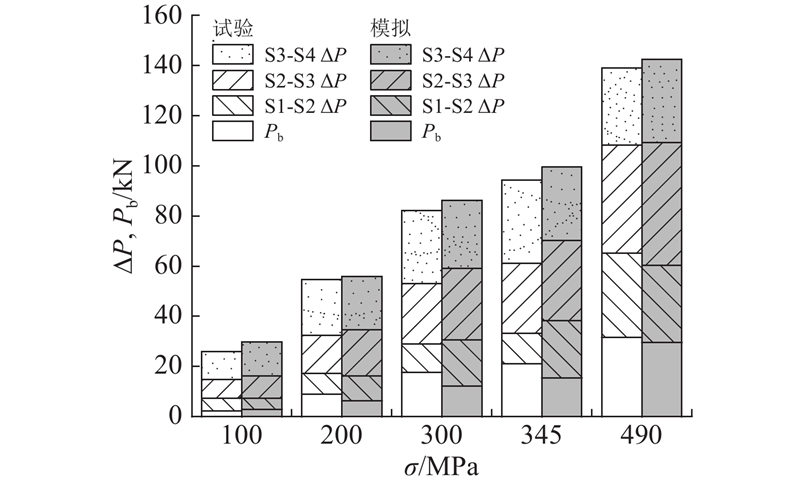
图 23 锚固区荷载分担比例的演化过程
Fig.23 Evolution process of load distribution ratio in anchorage zone
各测点间的黏结力表达式如下:
式中:
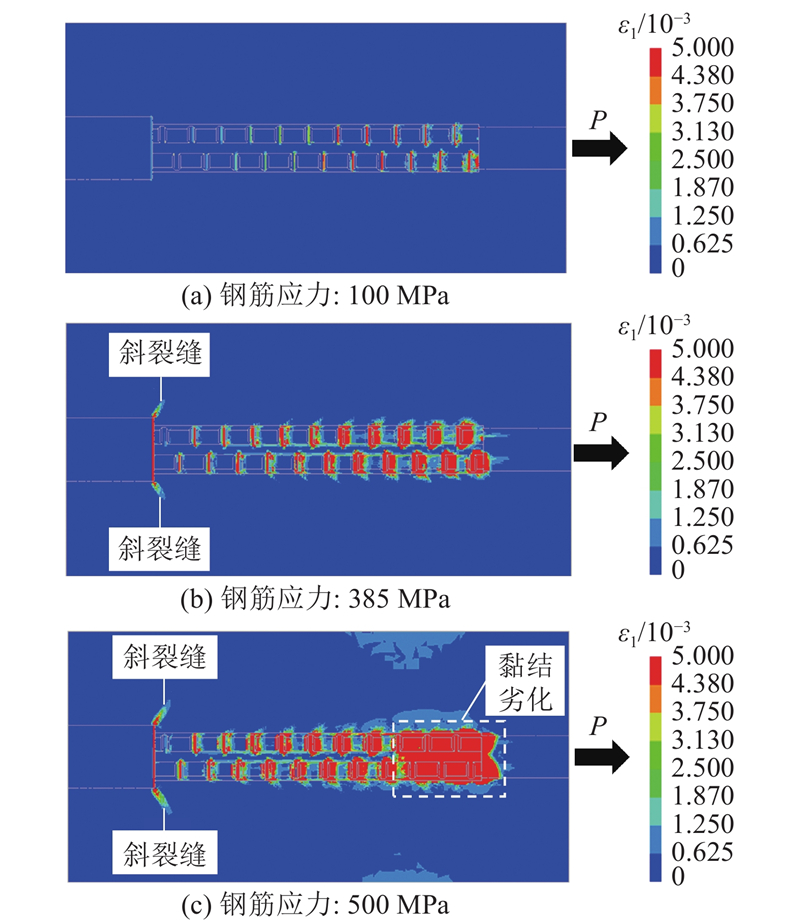
如图24所示为情况2)在不同荷载水平下混凝土的主拉应变云图. 图中,红色区域表示主拉应变超过5×10−3的区域. 在弹性阶段(钢筋应力100 MPa),混凝土的应力水平较低,仅在靠近加载端的钢筋表面横肋附近混凝土产生细微裂缝,套管附近混凝土无明显裂缝. 当荷载达到钢筋屈服时(钢筋应力385 MPa),加载端附近以肋为中心的各个裂缝区域逐渐扩大,说明发生黏结损伤. 同时黏结区域的裂缝逐渐由加载端向钢筋锚固端发展,能明显地看到钢筋肋附近混凝土产生45°斜向裂缝. 这是由于钢筋在拔出荷载作用下,黏结应力平行于钢筋轴向的切向分力使混凝土齿槽受剪,产生斜向裂缝. 在该荷载水平下,还可以看到套管局部承压面外边缘附近的混凝土开始产生锥状斜裂缝. 这是由于套管承压面对混凝土的局部承压作用伴随混凝土的局部沉降变形,该作用使局部承压面边缘发生冲切锥裂[29]. 当钢筋进入强化阶段后(钢筋应力500 MPa),从加载端至S3附近的范围内,开裂区域已连成一片,说明钢筋与混凝土之间的黏结已经显著劣化. 拉拔力(锚固力)由加载端向锚固端转移,局部承压面附近产生的锥状斜裂缝逐渐变宽并向外延伸.
图 24
以上3组拔出试验的模拟结果表明,在无须假定黏结滑移关系的情况下,本研究所提出的肋尺度精细化有限元模型不仅对单一锚固方式有效,而且能够较为准确地反映2种锚固方式共同工作的细观机理,合理地描述和预测机械锚固钢筋在拔出荷载作用下的宏观力学行为,可以用于钢筋机械锚固相关研究.
4. 结 论
(1)所提出的肋尺度精细化有限元模型,在无须假定黏结滑移关系的情况下,能准确地体现变形钢筋的横肋与混凝土的机械咬合作用,适用于黏结锚固单一方式和黏结锚固与机械锚固共同工作方式的数值分析. 钢筋应力-位移曲线、钢筋应力-应变曲线、黏结力与局部承压力的荷载分担比例等均与试验结果较吻合. 节点耦合法过大评价化学胶着力和摩擦力的作用,建议采用界面单元法来实现钢筋与混凝土接触面的设置.
(2)弯钩钢筋的锚固机制主要为黏结锚固,钢筋横肋之间的混凝土齿键发生剪切破坏是导致黏结劣化和失效的原因. 带锚固板钢筋的机械锚固是通过钢筋端头锚固板的局部承压作用来实现的,锚固区内混凝土处于三轴受压状态,在锚固区周围存在足够约束的条件下,锚固板下混凝土的抗压强度可以提高3倍以上,机械锚固的效果显著优于弯钩黏结锚固.
(3)当机械锚固和黏结段共存时,由于前后的位置关系,锚固区将发生加载初期以张拉端为主到加载后期向锚固端内移、加载初期以黏结锚固为主到加载后期黏结与机械锚固共同工作的应力重分布,荷载分担比例主要取决于黏结段长度和荷载水平. 肋尺度模型能够较好地反映机械锚固与黏结的细观共同工作机理和宏观力学响应,可以用于钢筋机械锚固相关研究.
参考文献
钢筋机械锚固性能的试验研究
[J].DOI:10.13204/j.gyjz1991.11.007 [本文引用: 2]
Experimental research mechanical anchorage properties of bars in concrete
[J].DOI:10.13204/j.gyjz1991.11.007 [本文引用: 2]
Flexural behaviour of headed bar connections between precast concrete panels
[J].DOI:10.1016/j.conbuildmat.2017.07.146 [本文引用: 1]
Performance of R. C. slabs with lap splices using headed bars
[J].
带锚固板钢筋的机械锚固性能试验及其最新研究成果
[J].DOI:10.3969/j.issn.1002-8528.2007.11.010 [本文引用: 1]
Experiment in anchorage behavior of headed reinforcement and its latest research results
[J].DOI:10.3969/j.issn.1002-8528.2007.11.010 [本文引用: 1]
锚固力在钢筋黏结和端板承压间的分配规律
[J].DOI:10.11918/j.issn.0367-6234.201710053
Distribution regulation of the reinforcement force between bond and headed bars
[J].DOI:10.11918/j.issn.0367-6234.201710053
带锚固板高强热轧钢筋与混凝土黏结锚固性能试验研究
[J].DOI:10.14006/j.jzjgxb.2018.04.014 [本文引用: 1]
A study on anchoring behavior between high strength hot-rolled reinforcement with headed bars and concrete
[J].DOI:10.14006/j.jzjgxb.2018.04.014 [本文引用: 1]
有限元法的发展现状及应用
[J].
Development and application of finite element method
[J].
Development of a plasticity bond model for steel reinforcement
[J].DOI:10.1002/(SICI)1099-1484(199804)3:2<155::AID-CFM45>3.0.CO;2-S [本文引用: 1]
Reinforcement-concrete bond behavior: experimentation in drying conditions and meso-scale modeling
[J].DOI:10.1016/j.engstruct.2015.07.028
Three-dimensional nonlinear finite element modeling for bond performance of ribbed steel bars in concrete under lateral tensions
[J].DOI:10.1007/s40999-019-00488-1 [本文引用: 2]
High-resolution finite element modeling for bond in high-strength concrete beam
[J].DOI:10.1016/j.engstruct.2018.06.068 [本文引用: 1]
3D nonlinear finite-element modeling of lap splices in UHPFRC
[J].
钢筋直锚与机械锚固的异同
[J].DOI:10.3969/j.issn.1001-523X.2014.07.012 [本文引用: 1]
Similarities and differences between straight and mechanically anchoraged
[J].DOI:10.3969/j.issn.1001-523X.2014.07.012 [本文引用: 1]