(1) $ {\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{{{s}}_{{{i,j}}}}}&{{{{s}}_{{{i,j}}+1}}}&{ \cdots }&{{{{s}}_{{{i,m}} - 1}}}&{{{{s}}_{{{i}}{{,m}}}}} \\ {{{{s}}_{{{i}}+1{{,j}}}}}&{{{{s}}_{{{i}}+1{{,j}}+1}}}&{ \cdots }&{{{{s}}_{{{i}}+{{1,m}} - 1}}}&{{{{s}}_{{{i}}+1{{,m}}}}} \\ { \vdots }&{ \vdots }&{ }&{ \vdots }&{ \vdots } \\ {{{{s}}_{{{n}} - 1{{,j}}}}}&{{{{s}}_{{{n}} - 1{{,j}}+1}}}&{ \cdots }&{{{{s}}_{{{n}} - 1{{,m}} - 1}}}&{{{{s}}_{{{n}} - 1{{,m}} - 1}}} \\ {{{{s}}_{{{n,j}}}}}&{{{{s}}_{{{n,j}}+1}}}&{ \cdots }&{{{{s}}_{{{n,m}} - 1}}}&{{{{s}}_{{{n,m}}}}} \end{array}} \right]. $
[1]
祁朵, 毛政元 基于自适应时序剖分与KNN的短时交通流量预测
[J]. 地球信息科学学报 , 2022 , 24 (2 ): 339 - 351
[本文引用: 1]
QI Duo, MAO Zheng-yuan Short-term traffic flow prediction based on adaptive time Slice and KNN
[J]. Journal of Geo-Information Science , 2022 , 24 (2 ): 339 - 351
[本文引用: 1]
[2]
康军, 段宗涛, 唐蕾, 等 一种LS-SVM在线式短时交通流预测方法
[J]. 计算机应用研究 , 2018 , 35 (10 ): 2965 - 2968
[本文引用: 1]
KANG Jun, DUAN Zong-tao, TANG Lei, et al LS-SVM online shrot traffic flow prediction method
[J]. Computer Application Research , 2018 , 35 (10 ): 2965 - 2968
[本文引用: 1]
[3]
林浩, 李雷孝, 王慧, 等 基于相关向量机和模糊综合评价的路况预测模型
[J]. 浙江大学学报: 工学版 , 2021 , 55 (6 ): 1072 - 1082
[本文引用: 1]
LIN Hao, LI Lei-xiao, WANG Hui, et al Model based on relevance vector machine and fuzzy comprehensive evaluation for road condition prediction
[J]. Journal of ZheJiang University: Engineering Science , 2021 , 55 (6 ): 1072 - 1082
[本文引用: 1]
[4]
KANG D Q, LV Y S, CHEN Y Y. Short-term traffic flow prediction with LSTM recurrent neural network[C]// 2017 IEEE 20th International Conference on Intelligent Transportation Systems . Yokohama: IEEE, 2017: 1-6.
[本文引用: 1]
[5]
GAO Y, ZHOU C J, RONG J, et al, Short-term traffic speed forecasting using a deep Learning method based on multitemporal traffic flow volume[J]. IEEE Access , 2022, 10: 82384-82395.
[6]
ZHENG Z, CHEN W, WU X, et al LSTM network: a deep learning approach for short-term traffic forecast
[J]. Intelligent Transport Systems , 2017 , 11 (2 ): 68 - 75
DOI:10.1049/iet-its.2016.0208
[本文引用: 1]
[7]
SHI X, CHEN Z, WANG H, et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting[J]. MIT Press , 2015, 1: 802-810.
[本文引用: 1]
[8]
晏臻, 于重重, 韩璐, 等 基于CNN+LSTM的短时交通流量预测方法
[J]. 计算机工程与设计 , 2019 , 40 (9 ): 2620 - 2624+2659
DOI:10.16208/j.issn1000-7024.2019.09.038
[本文引用: 1]
YAN Zhen, YU Chong-chong, HAN Lu, et al Short-term traffic flow forecasting method based on CNN+LSTM
[J]. Computer Engineering and Design , 2019 , 40 (9 ): 2620 - 2624+2659
DOI:10.16208/j.issn1000-7024.2019.09.038
[本文引用: 1]
[9]
王婧娟, 陈庆奎 一种时空注意力网络的交通预测模型
[J]. 小型微型计算机系统 , 2021 , 42 (2 ): 303 - 307
[本文引用: 1]
WANG Jin-juan, CHEN Qing-kui Traffic prediction model based on spationtemporal attention network
[J]. Mini Microcomputer System , 2021 , 42 (2 ): 303 - 307
[本文引用: 1]
[12]
THOMAS N, KIP T, WELLING M. Semi-supervised classification with graph convolutional networks [C]// International Conference on Learning Representations . Toulon: ICLR Institute, 2017.
[本文引用: 1]
[13]
SEO Y, DEFFER M, VANDERG P, et al. Structured sequence modeling with graph convolutional recurrent networks [C]// Processing of the 25th International Conference (ICONIP 2018) . Siem Reap: Asia Pacific Neural Network Society, 2018: 362-373.
[本文引用: 1]
[14]
LI Y , YU R , SHAHABI C , et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting[C]// International Conference on Learning Representations . Vancouver: ICLR Institute, 2018.
[本文引用: 1]
[15]
冯宁, 郭晟楠, 宋超, 等 面向交通流量预测的多组件时空图卷积网络
[J]. 软件学报 , 2019 , 30 (3 ): 759 - 769
DOI:10.13328/j.cnki.jos.005697
[本文引用: 6]
FENG Ning, GUO Sheng-nan, SONG Chao, et al Multi-component spatial-temporal graph convolution networks for traffic flow forecasting
[J]. Journal of Software , 2019 , 30 (3 ): 759 - 769
DOI:10.13328/j.cnki.jos.005697
[本文引用: 6]
[16]
杨建喜, 郁超顺, 李韧, 等 基于多周期组件时空神经网络的路网通行速度预测
[J]. 交通运输系统工程与信息 , 2021 , 21 (3 ): 112 - 119+139
[本文引用: 1]
YANG Jian-xi, YU Chao-shun, LI Ren, et al Traffic network speed prediction via multi-periodic-component spatialtemporal neural network
[J]. Journal of Transportation Systems Engineering and Information Technology , 2021 , 21 (3 ): 112 - 119+139
[本文引用: 1]
[17]
闫旭, 范晓亮, 郑传潘, 等 基于图卷积神经网络的城市交通态势预测算法
[J]. 浙江大学学报: 工学版 , 2020 , 54 (6 ): 1147 - 1155
[本文引用: 1]
YAN Xu, FAN Xiao-liang, ZHENG Chuan-pan, et al Urban traffic flow prediction algorithm based on graph convolutional neural networks
[J]. Journal of ZheJiang University: Engineering Science , 2020 , 54 (6 ): 1147 - 1155
[本文引用: 1]
[18]
LI C , CUI Z , ZHENG W, et al. Spatio-temporal graph convolution for skeleton based action recognition [C]// 32th Association for the Advancement of Artificial Intelligence . New Orleans: AAAI Institute. 2018: 938-946.
[本文引用: 4]
[19]
SONG C, LIN Y, GUO S, et al. Spatial-temporal synchronous graph convolutional networks: a new framework for spatial-temporal network data forecasting [C]// 34th Association for the Advancement of Artificial Intelligence . New York: AAAI Institute, 2020: 914-921.
[本文引用: 4]
[20]
GUO S , LIN Y , FENG N , et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting [C]// National Conference on Artificial Intelligence. 33th Association for the Advancement of Artificial Intelligence . Hawaii State: AAAI Institute, 2019: 922-929.
[本文引用: 4]
[21]
HU Y. Research on city traffic flow forecast based on graph convolutional neural network [C]// 2021 IEEE 2nd International Conference on Big Data . NanChang: Artificial Intelligence and Internet of Things Engineering, 2021: 269-273.
[本文引用: 1]
[22]
LV M Q, HONG Z X, CHEN L, et al Temporal multi-graph convolutional network for traffic flow prediction
[J]. Intelligent Transportation Systems , 2021 , 22 (6 ): 3337 - 3348
[本文引用: 1]
基于自适应时序剖分与KNN的短时交通流量预测
1
2022
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
基于自适应时序剖分与KNN的短时交通流量预测
1
2022
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
一种LS-SVM在线式短时交通流预测方法
1
2018
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
一种LS-SVM在线式短时交通流预测方法
1
2018
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
基于相关向量机和模糊综合评价的路况预测模型
1
2021
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
基于相关向量机和模糊综合评价的路况预测模型
1
2021
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
1
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
LSTM network: a deep learning approach for short-term traffic forecast
1
2017
... 城市路网错综复杂,科学准确的交通流量预测在道路拥堵评判、路径规划领域起到重要作用. 交通流量具有较强的周期性,且与上一时刻的状态紧密相连. 一些研究者关注序列在时间维的逻辑关系,通过历史均值法、时间序列模型、K-最近邻算法(K-nearest neighbor,KNN)[1 ] 、支持向量机(support vector machine, SVM)[2 ] 、相关向量机(relevance vector machine,RVM)[3 ] 等机器学习模型以及适用于序列预测的长短期记忆神经网络(long short-term memory,LSTM)[4 -6 ] 等深度学习模型进行交通流量预测. ...
1
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
基于CNN+LSTM的短时交通流量预测方法
1
2019
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
基于CNN+LSTM的短时交通流量预测方法
1
2019
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
一种时空注意力网络的交通预测模型
1
2021
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
一种时空注意力网络的交通预测模型
1
2021
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
基于CNN-SVR混合深度学习模型的短时交通流预测
1
2017
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
基于CNN-SVR混合深度学习模型的短时交通流预测
1
2017
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
基于CNN-XGBoost的短时交通流预测
1
2020
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
基于CNN-XGBoost的短时交通流预测
1
2020
... 实际上,单纯考虑时间维关系较为局限. 准确的交通流量预测的难点在于一个路段当前状态同时会影响邻居路段的未来状态. 通过加入空间维信息,合理地剖析交通流量的时空特征信息对提高模型的预测精度有较大影响. Shi等[7 ] 提出ConvLSTM概念,通过卷积运算代替LSTM网络中部分哈达玛积运算,从而挖掘空间性信息,减小预测误差. 另一种方法是将在二维空间上提取特征的卷积神经网络(convolutional neural networks,CNN)与序列预测算法相结合. 诸如CNN与循环神经网络(recurrent neural network,RNN)的组合[8 -9 ] 、CNN与传统机器学习算法的组合[10 -11 ] . 以上方法均作用于传统的二维时空矩阵,事实上只能考虑到上下游路段空间关系的影响,在错综复杂的道路环境下并不能较好地适用. ...
1
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
1
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
1
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
面向交通流量预测的多组件时空图卷积网络
6
2019
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
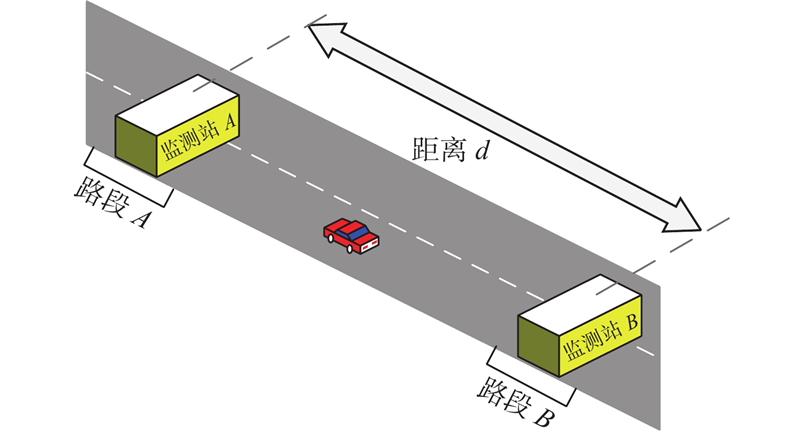
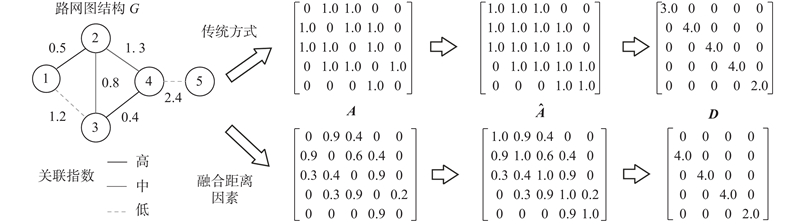
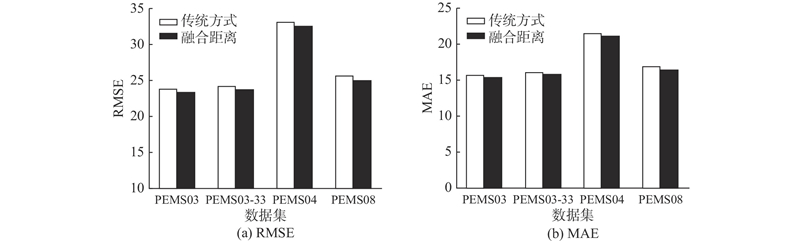
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... [15 ,20 ]设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... 对比实验选取时序预测常用的LSTM、GRU模型作为基准模型,并选取了目前应用于交通流量预测的图卷积网络模型,包括STGCN[18 ] 、MCSTGCN[15 ] 、STSGCN[19 ] 、ASTGCN[20 ] ,分别比较其在PEMS04、PEMS08数据集下的预测性能. 为了综合评判模型的预测性能,对每一个模型分别记录其在5~60 min内的12组数据,时间间隔为5 min,将12组结果进行平均计算,最终得到模型的综合预测误差结果. 对比模型概念如下. ...
... 4)MCSTGCN[15 ] :多组件时空图卷积网络,设计时、日、周3个独立的卷积模块进行分别预测,最后将3个组件的预测结果进行加权运算得到最终输出. ...
... Error of different models on PEMS04 and PEMS08 datasets
Tab.4 模型 PEMS04 PEMS08 RMSE MAE RMSE MAE LSTM 43.17 28.83 33.18 23.30 GRU 42.83 28.32 32.97 23.15 STGCN[18 ] 38.29 25.15 27.87 18.88 MCSTGCN[15 ] 35.64 22.73 26.47 17.47 STSGCN[19 ] 33.65 21.19 26.80 17.13 ASTGCN[20 ] 32.82 21.80 25.27 16.63 本研究模型 32.51 21.04 24.92 16.41
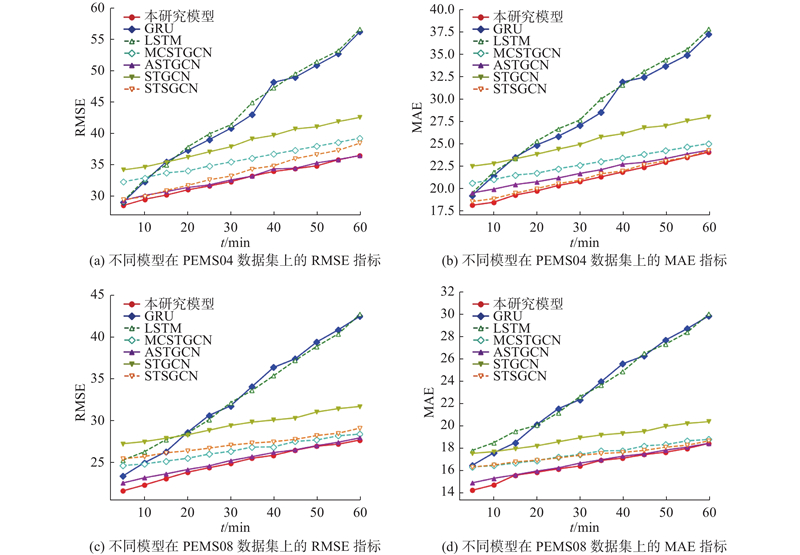
由于未考虑空间性信息,LSTM、GRU这2种循环神经网络只能捕获时间维的相关性,相比其他图卷积构建的网络模型误差更大,并且,随着预测时间范围的增加,差异性更加明显. 同时考虑了空间维与时间维的特征信息的STGCN模型的预测误差较LSTM、GRU有明显的降低;考虑周期性因素的MCSTGCN、ASTGCN通过设置时、日、周独立预测组件,预测误差进一步降低. STSGCN通过网络架构的改善提出时空同步建模机制,体现出较大的优势. 本模型分别设立空间图卷积模块与时间序列预测模块,同时考虑距离因素构造新型邻接矩阵,并在网络层级中添加融合周期性信息的序列,模型的预测性能表现最优. 由图7 可以看出,在5~15min短时时间范围内本模型优势较明显,但随着预测时间范围的增加,与其他模型的差异逐渐减小. ...
面向交通流量预测的多组件时空图卷积网络
6
2019
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... [15 ,20 ]设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... 对比实验选取时序预测常用的LSTM、GRU模型作为基准模型,并选取了目前应用于交通流量预测的图卷积网络模型,包括STGCN[18 ] 、MCSTGCN[15 ] 、STSGCN[19 ] 、ASTGCN[20 ] ,分别比较其在PEMS04、PEMS08数据集下的预测性能. 为了综合评判模型的预测性能,对每一个模型分别记录其在5~60 min内的12组数据,时间间隔为5 min,将12组结果进行平均计算,最终得到模型的综合预测误差结果. 对比模型概念如下. ...
... 4)MCSTGCN[15 ] :多组件时空图卷积网络,设计时、日、周3个独立的卷积模块进行分别预测,最后将3个组件的预测结果进行加权运算得到最终输出. ...
... Error of different models on PEMS04 and PEMS08 datasets
Tab.4 模型 PEMS04 PEMS08 RMSE MAE RMSE MAE LSTM 43.17 28.83 33.18 23.30 GRU 42.83 28.32 32.97 23.15 STGCN[18 ] 38.29 25.15 27.87 18.88 MCSTGCN[15 ] 35.64 22.73 26.47 17.47 STSGCN[19 ] 33.65 21.19 26.80 17.13 ASTGCN[20 ] 32.82 21.80 25.27 16.63 本研究模型 32.51 21.04 24.92 16.41
由于未考虑空间性信息,LSTM、GRU这2种循环神经网络只能捕获时间维的相关性,相比其他图卷积构建的网络模型误差更大,并且,随着预测时间范围的增加,差异性更加明显. 同时考虑了空间维与时间维的特征信息的STGCN模型的预测误差较LSTM、GRU有明显的降低;考虑周期性因素的MCSTGCN、ASTGCN通过设置时、日、周独立预测组件,预测误差进一步降低. STSGCN通过网络架构的改善提出时空同步建模机制,体现出较大的优势. 本模型分别设立空间图卷积模块与时间序列预测模块,同时考虑距离因素构造新型邻接矩阵,并在网络层级中添加融合周期性信息的序列,模型的预测性能表现最优. 由图7 可以看出,在5~15min短时时间范围内本模型优势较明显,但随着预测时间范围的增加,与其他模型的差异逐渐减小. ...
基于多周期组件时空神经网络的路网通行速度预测
1
2021
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
基于多周期组件时空神经网络的路网通行速度预测
1
2021
... 为了表征路段之间复杂的邻接关系,可以通过图的形式存储复杂的拓扑结构. 图卷积神经网络(graph convolutional network,GCN)[12 ] 的出现为深度学习模型挖掘图结构的特征信息奠定了基础. Seo等[13 ] 提出图卷积递归网络(graph convolutional recurrent network,GCRN),将图卷积网络与循环神经网络相结合,为挖掘时空序列特征提供了理论基础. Li等[14 ] 提出扩散卷积递归神经网络(diffusion convolutional recurrent neural network,DCRNN),将交通流的变化趋势建模为有向图上的扩散过程,通过图的双向随机游动性获取空间特征. 交通流量在日、周周期上具有较强的周期规律,在考虑交通流量的周期性特性上,冯宁等[15 -16 ] 设计多组件时空图卷积网络,通过时、日、周3个子组件分别进行训练及预测,最终将3个组件的预测结果加权组合得到最终输出. ...
基于图卷积神经网络的城市交通态势预测算法
1
2020
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
基于图卷积神经网络的城市交通态势预测算法
1
2020
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
4
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... 对比实验选取时序预测常用的LSTM、GRU模型作为基准模型,并选取了目前应用于交通流量预测的图卷积网络模型,包括STGCN[18 ] 、MCSTGCN[15 ] 、STSGCN[19 ] 、ASTGCN[20 ] ,分别比较其在PEMS04、PEMS08数据集下的预测性能. 为了综合评判模型的预测性能,对每一个模型分别记录其在5~60 min内的12组数据,时间间隔为5 min,将12组结果进行平均计算,最终得到模型的综合预测误差结果. 对比模型概念如下. ...
... 3)STGCN[18 ] :建立纯卷积的预测模型,设计空间卷积层与时间卷积层进行特征提取,以更少的参数以获取更快的收敛速度. ...
... Error of different models on PEMS04 and PEMS08 datasets
Tab.4 模型 PEMS04 PEMS08 RMSE MAE RMSE MAE LSTM 43.17 28.83 33.18 23.30 GRU 42.83 28.32 32.97 23.15 STGCN[18 ] 38.29 25.15 27.87 18.88 MCSTGCN[15 ] 35.64 22.73 26.47 17.47 STSGCN[19 ] 33.65 21.19 26.80 17.13 ASTGCN[20 ] 32.82 21.80 25.27 16.63 本研究模型 32.51 21.04 24.92 16.41
由于未考虑空间性信息,LSTM、GRU这2种循环神经网络只能捕获时间维的相关性,相比其他图卷积构建的网络模型误差更大,并且,随着预测时间范围的增加,差异性更加明显. 同时考虑了空间维与时间维的特征信息的STGCN模型的预测误差较LSTM、GRU有明显的降低;考虑周期性因素的MCSTGCN、ASTGCN通过设置时、日、周独立预测组件,预测误差进一步降低. STSGCN通过网络架构的改善提出时空同步建模机制,体现出较大的优势. 本模型分别设立空间图卷积模块与时间序列预测模块,同时考虑距离因素构造新型邻接矩阵,并在网络层级中添加融合周期性信息的序列,模型的预测性能表现最优. 由图7 可以看出,在5~15min短时时间范围内本模型优势较明显,但随着预测时间范围的增加,与其他模型的差异逐渐减小. ...
4
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... 对比实验选取时序预测常用的LSTM、GRU模型作为基准模型,并选取了目前应用于交通流量预测的图卷积网络模型,包括STGCN[18 ] 、MCSTGCN[15 ] 、STSGCN[19 ] 、ASTGCN[20 ] ,分别比较其在PEMS04、PEMS08数据集下的预测性能. 为了综合评判模型的预测性能,对每一个模型分别记录其在5~60 min内的12组数据,时间间隔为5 min,将12组结果进行平均计算,最终得到模型的综合预测误差结果. 对比模型概念如下. ...
... 5)STSGCN[19 ] :构建局部时空图,局部时空图由3个相邻的时间片组成,在不同时间段部署多个STSGCN模型,以解决长时间时空网络数据的异质性. ...
... Error of different models on PEMS04 and PEMS08 datasets
Tab.4 模型 PEMS04 PEMS08 RMSE MAE RMSE MAE LSTM 43.17 28.83 33.18 23.30 GRU 42.83 28.32 32.97 23.15 STGCN[18 ] 38.29 25.15 27.87 18.88 MCSTGCN[15 ] 35.64 22.73 26.47 17.47 STSGCN[19 ] 33.65 21.19 26.80 17.13 ASTGCN[20 ] 32.82 21.80 25.27 16.63 本研究模型 32.51 21.04 24.92 16.41
由于未考虑空间性信息,LSTM、GRU这2种循环神经网络只能捕获时间维的相关性,相比其他图卷积构建的网络模型误差更大,并且,随着预测时间范围的增加,差异性更加明显. 同时考虑了空间维与时间维的特征信息的STGCN模型的预测误差较LSTM、GRU有明显的降低;考虑周期性因素的MCSTGCN、ASTGCN通过设置时、日、周独立预测组件,预测误差进一步降低. STSGCN通过网络架构的改善提出时空同步建模机制,体现出较大的优势. 本模型分别设立空间图卷积模块与时间序列预测模块,同时考虑距离因素构造新型邻接矩阵,并在网络层级中添加融合周期性信息的序列,模型的预测性能表现最优. 由图7 可以看出,在5~15min短时时间范围内本模型优势较明显,但随着预测时间范围的增加,与其他模型的差异逐渐减小. ...
4
... 基于图结构挖掘交通流量的时空特征已成为研究热点[17 -18 ] ,但目前基于图神经网络所构建的模型尚存在一些问题,例如在图邻接矩阵的构造中,传统方式只单纯考虑路段之间是否邻接. 因此可考虑距离因素,分析路网拓扑关系中当前节点邻接节点以及次邻接节点影响程度的大小,通过设置不同的权重矩阵使模型尽可能考虑更远路段的信息,旨在一定程度上提高预测精度. 但每个节点之间距离存在差异,已有研究忽略了节点间距离的远近直接造成的空间相关性不同的问题. 在网络模型构建上,多数模型只通过图卷积层提取时空特征[15 ,19 ] ,忽略了空间维与时间维信息的差异性. 在考虑周期性因素问题上,传统模型[15 ,20 ] 设计时、日、周独立组件分别进行训练及测试,最终将多个子组件结果加权输出,加大了时间与空间开销成本. ...
... 对比实验选取时序预测常用的LSTM、GRU模型作为基准模型,并选取了目前应用于交通流量预测的图卷积网络模型,包括STGCN[18 ] 、MCSTGCN[15 ] 、STSGCN[19 ] 、ASTGCN[20 ] ,分别比较其在PEMS04、PEMS08数据集下的预测性能. 为了综合评判模型的预测性能,对每一个模型分别记录其在5~60 min内的12组数据,时间间隔为5 min,将12组结果进行平均计算,最终得到模型的综合预测误差结果. 对比模型概念如下. ...
... 6)ASTGCN[20 ] :在时间卷积与空间卷积模块中引入注意力机制,最后通过图卷积运算得到最终输出. ...
... Error of different models on PEMS04 and PEMS08 datasets
Tab.4 模型 PEMS04 PEMS08 RMSE MAE RMSE MAE LSTM 43.17 28.83 33.18 23.30 GRU 42.83 28.32 32.97 23.15 STGCN[18 ] 38.29 25.15 27.87 18.88 MCSTGCN[15 ] 35.64 22.73 26.47 17.47 STSGCN[19 ] 33.65 21.19 26.80 17.13 ASTGCN[20 ] 32.82 21.80 25.27 16.63 本研究模型 32.51 21.04 24.92 16.41
由于未考虑空间性信息,LSTM、GRU这2种循环神经网络只能捕获时间维的相关性,相比其他图卷积构建的网络模型误差更大,并且,随着预测时间范围的增加,差异性更加明显. 同时考虑了空间维与时间维的特征信息的STGCN模型的预测误差较LSTM、GRU有明显的降低;考虑周期性因素的MCSTGCN、ASTGCN通过设置时、日、周独立预测组件,预测误差进一步降低. STSGCN通过网络架构的改善提出时空同步建模机制,体现出较大的优势. 本模型分别设立空间图卷积模块与时间序列预测模块,同时考虑距离因素构造新型邻接矩阵,并在网络层级中添加融合周期性信息的序列,模型的预测性能表现最优. 由图7 可以看出,在5~15min短时时间范围内本模型优势较明显,但随着预测时间范围的增加,与其他模型的差异逐渐减小. ...
1
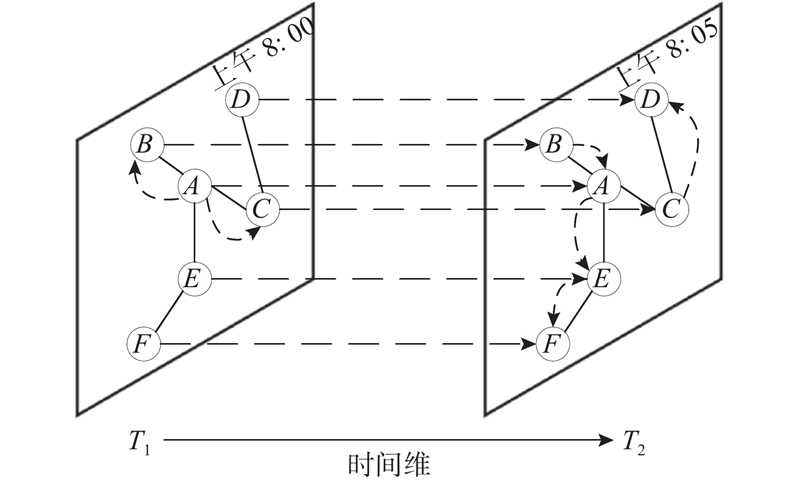
... 路网结构日益复杂,因道路交叉口与分岔口的存在,某一路段的邻接路段会存在多个. 传统二维矩阵的存储方式并不能表征目前路网中复杂的空间拓扑关系. 图结构[21 -22 ] 的形式可以最直观地存储路网间各路段的邻接关系,因此基于图结构进行交通路网建模. ...
Temporal multi-graph convolutional network for traffic flow prediction
1
2021
... 路网结构日益复杂,因道路交叉口与分岔口的存在,某一路段的邻接路段会存在多个. 传统二维矩阵的存储方式并不能表征目前路网中复杂的空间拓扑关系. 图结构[21 -22 ] 的形式可以最直观地存储路网间各路段的邻接关系,因此基于图结构进行交通路网建模. ...