在典型的区块链应用中,用户发起大量交易,节点通过对每笔交易进行验签来判定交易是否有效. 由于交易验签是计算密集型工作,随着交易数量的增加,大量验签操作会占用节点的CPU资源,严重影响区块链系统的峰值TPS[4],因此交易验签效率在将来会成为区块链系统的性能瓶颈. 研究者们通常使用专为计算密集型工作设计的硬件加速器来减轻CPU的负担. 区块链中使用的主流硬件加速器包括可编程逻辑门阵列(field programmable gate array, FPGA)、专用集成电路(application specific integrated circuit, ASIC)和图形处理器(graphics processing unit, GPU),其中FPGA和ASIC这类专用硬件加速器存在设计制造难度较大、开发周期过长、升级维护困难、制造成本昂贵等问题,而GPU的硬件实现对上层开发者几乎透明,大大降低了开发难度,而且GPU具有良好的兼容性,支持以极小的开发代价对硬件设备进行迭代更新. 此外,GPU相较于FPGA和ASIC在价格上更具优势. 因此,使用GPU加速区块链交易验签具有广阔的研究前景和实用价值.
针对上述问题,采用GPU来加速区块链系统性能,充分发挥GPU多核并行的高性能,相较于CPU能以更低的延迟实现更高的吞吐量,还能释放CPU资源供区块链其他模块使用,从而提升区块链系统的整体性能. 本研究主要贡献如下:1)提出基于GPU的区块链交易验签加速技术,将区块链交易验签过程划分为数据准备与传输、GPU多线程并行验签、结果更新与确认3个阶段并分别进行优化,可以在不修改协议的情况下提升区块链系统的性能,并以插件形式支持验签算法的热插拔替换. 2)结合GPU计算能力强而分支预测能力弱的特性提出基于同时多点乘的改进算法. 该算法将滑动窗口大小置为1,并使用具有相同Z坐标的点表示法[5],加速交易验签算法中最耗时的多点乘操作,提高GPU多线程并行度.
1. 相关工作
1.1. 区块链硬件加速技术
区块链中使用的主流硬件加速器包括FPGA、ASIC和GPU.
FPGA被用于区块链交易验签、区块链搜索、网络传输等领域. 在区块链交易验签领域,Agrawal等[6]提出基于FPGA的椭圆曲线数字签名算法(elliptic curve digital signature algorithm, ECDSA)签名验证引擎,对有限域模运算和椭圆曲线点乘运算进行优化,并引入预处理. 在区块链搜索领域,Sakakibara等[7]在FPGA上基于块随机存取存储器(block random access memory,BRAM)设计并实现了带有键值存储(key-value store,KVS)的原型系统,提供数字资产转移的基本命令. 在网络传输领域,Javaid等[8]使用带有网络连接的FPGA直接从网络接口读取数据,有效降低了内核网络协议栈带来的通信延迟.
ASIC须设计专用逻辑电路,然后交由芯片制造厂家流片,设计制造难度大、周期长,且流片后功能固定不可更改,灵活性差,适合成熟应用的批量生产使用. FPGA作为一种半定制电路,弥补了定制电路的不足,但是相比于GPU仍存在峰值性能和接口带宽太低的问题. 另外,GPU还可以通过统一计算设备架构(compute unified device architecture, CUDA)编程框架调用,更便于软件开发人员使用GPU进行并行应用开发. 此外,GPU在价格和易得性方面明显优于FPGA和ASIC. 综上,本研究选用GPU作为区块链系统硬件加速器.
在区块链交易验签领域已有研究者引入硬件加速平台. Agrawal等[6]提出的签名验证引擎严重依赖Javaid等[8]提出的协议解析处理模块,从而导致通用性大幅下降. 朱立等[11]提出的椭圆曲线点运算并行算法需要多线程协作对同一个签名进行验证,这会带来额外的线程间通信开销,且会有部分线程轮空,造成资源浪费. 另外,现有研究缺乏对CPU-GPU异构平台整体性能的优化,未能充分发挥GPU作为协处理器的优势. 本研究提出的基于GPU的区块链交易验签加速技术,无须修改协议,侵入性较低;采用为每个交易验签任务分配一个独立处理线程的方式,规避了多线程协作验签的额外通信开销和资源浪费;不仅关注GPU,而是基于CPU-GPU异构平台整体优化的视角进行设计实现,有效提升了区块链系统整体性能表现.
1.2. 区块链签名算法
公有区块链和国外主流许可区块链如比特币、以太坊和Hyperledger Fabric等采用ECDSA对交易进行签名. 许可区块链主要用于企业应用,须符合所在国家法律监管要求,因此国产许可区块链均使用或支持由中国国家密码局提出的基于椭圆曲线密码学(ellipse curve cryptography, ECC)的SM2算法对交易进行签名.
基于SM2算法的数字签名验证过程中最核心也最耗时的步骤是多点乘法. 表达式如下:
式中:
1)先分别计算点乘
2)同时多点乘法[24]. 该方法只需要2轮次循环:在线预计算表构建、主循环,因此在GPU上可能有更好的优化效果. 朴素同时多点乘法首先在线构建一个二维预计算表,然后通过滑动窗口法循环计算点倍和点加结果,但须注意的是,二维预计算表的在线构建需要额外的计算和存储资源,依然会限制GPU并行规模. 本研究对朴素同时多点乘算法进行了改进,使其更适合GPU特性,从而实现更高的计算性能.
2. 基于GPU的区块链交易验签加速技术
2.1. 方法概述
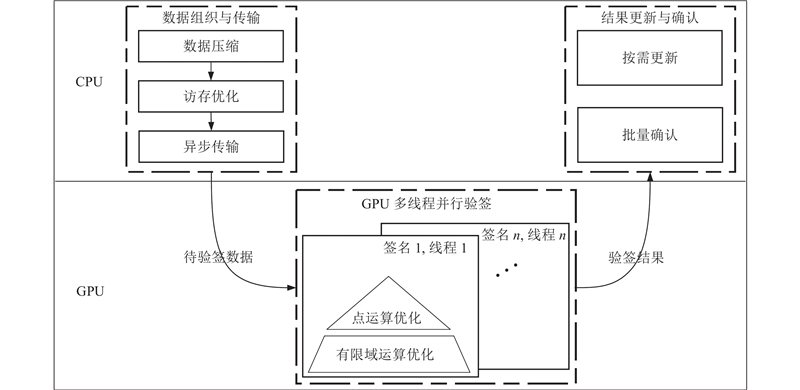
基于上述调研,提出基于GPU的区块链交易验签加速技术,对交易签名的验证过程进行多阶段优化,既可以充分发挥GPU多核并行的高性能,在不增加额外延迟的前提下相较于CPU大幅提升交易验签的吞吐量,同时还可以释放CPU资源供其他模块使用,从而提高区块链系统整体性能. 本研究方案的技术框架如图1所示.
图 1
图 1 基于GPU的区块链交易验签加速技术框架
Fig.1 Framework for GPU-based acceleration technology for signature verification of blockchain transactions
CPU端显示了CPU的处理以及主机内存中的数据,GPU端显示了GPU的处理和GPU全局内存中的数据,整体处理流程共分3个阶段:1)数据组织与传输:该阶段由CPU负责,从交易中提取待验签数据并拷贝至GPU显存. 2)GPU多线程并行验签:该阶段在GPU内完成,实现多线程并行验签. 3)结果更新与确认:该阶段由CPU负责,对验签结果进行确认以实施相应交易处理步骤.
2.2. 数据组织与传输
将第1阶段数据组织与传输分为3个流程:首先将待验签数据进行压缩,然后在内存中按照“列优先”方式对数据进行排布,最后以流水线方式进行数据异步传输和GPU内核异步调用. 不仅降低了数据传输量,实现了GPU全局内存的合并访问,降低了IO开销,而且对上层隐藏了数据传输环节.
2.2.1. 数据压缩
为了降低待验签数据由主机内存传输到GPU显存带来的IO开销,利用公钥坐标是椭圆曲线上的点这一事实,对公钥长度进行压缩. 具体地,在主机端提取公钥Y坐标时仅保留最低位,使数据传输量降低19.9%. 在GPU内恢复公钥时,由于SM2曲线参数
公钥恢复算法的伪代码如算法1所示.
算法1 公钥恢复算法
输入:公钥X坐标x,公钥Y坐标最低位d
输出:公钥Y坐标y
1:
2:
3:
4:
5:
6:
7: y=p−y
8: endif
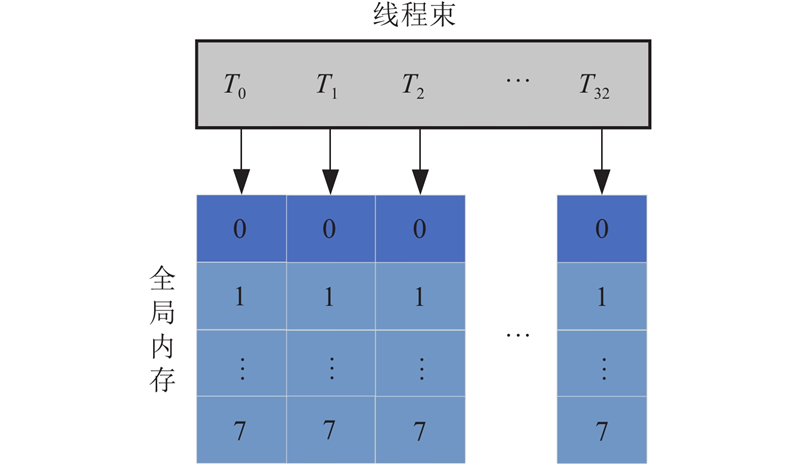
2.2.2. 访存优化
图 2
2.2.3. 异步传输
考虑GPU内核调用的异步性,即允许一个GPU设备上的多个内核使用不同的流[23]复制数据并同时执行计算,而且当前的GPU设备通常具有多个数据复制引擎,因此基于多流技术以类流水线机制设计实现异构设备间的数据传输与处理,将CPU与GPU间数据传输过程和GPU内计算过程相互重叠,一方面从上层“隐藏”了数据拷贝开销,充分利用了GPU的并行性,另一方面也让主机端的任务调度大大简化,使用先来先服务模式无需维护任务队列,进一步提高了本研究方案的通用性和易集成性.
2.3. GPU多线程并行验签
针对第2阶段GPU多线程并行验签,采用为每个交易验签任务分配一个独立线程进行处理的方式,而不是多线程协作完成单笔交易的验签. 这是因为验签流程多个步骤之间前后依赖性强,无法直接并行化. 即使在椭圆曲线域和多精度大数域具备并行化的条件,线程间通信也会引入额外开销. 并且线程间同步会导致部分线程轮空,不能充分利用计算资源. 此外,还针对交易验签算法在椭圆曲线点运算和有限域运算2个层面进行了优化,不仅加速了交易验签算法中最耗时的点乘操作,而且对GPU分支预测能力弱而计算能力强的特征具有更强的适应性.
2.3.1. 椭圆曲线点运算优化
针对交易验签算法中最耗时的多点乘法,现有大多数文献都采用先分别计算固定点乘
综上,在GPU上使用时,改进算法从多个维度上降低了复杂度,减少了单个线程资源占用,从而增加了多线程并行规模,尽可能规避了GPU分支预测能力差的弱点,充分利用了GPU的高算力. 改进后的同时多点乘算法伪代码如算法2所示.
算法2 改进后的同时多点乘算法
输入:大整数
大整数
待验签交易公钥
输出:椭圆曲线点
1:
2:
//G为椭圆曲线基点,坐标固定
3:
4:
5:
6:
7:
8:
9:
//
10:
11: endfor
步骤2)计算椭圆曲线基点
2.3.2. 有限域运算优化
对GPU上的有限域运算进行了定制实现. 总体而言,使用内联并行线程执行指令集架构(parallel thread execution instruction set architecture, PTX ISA)实现有限域上多精度运算. 其中add.cc、sub.cc、addc、subc等指令使开发人员可以直接控制进位寄存器,避免模运算中大量冗余比较. mad指令可以在一个周期内完成乘法和加法,降低多精度乘法和平方计算运算耗时. shf.r.clamp指令实现2个32位整数拼接后向右移位,有效优化二进制扩展欧几里得算法中除以2的运算效率,该算法主要用于计算模逆. 此外,PTX提供了一个稳定的编程模型和指令集,能够跨越多种GPU,并且能够优化代码的编译,也让本研究方案具备独立于硬件的优势,确保可以在各种NVIDIA GPU上执行.
2.4. 结果更新与确认
针对第3阶段结果更新与确认,使用位图数据结构存储验签结果,在大幅降低IO开销的同时,支持CPU端批量确认. 此外还利用GPU统一内存架构实现了验签结果按需更新.
2.4.1. 批量确认
考虑到验签结果只需1 bit即可表示,使用位图结构进行存储组织,并通过共享内存对所有线程的验签结果进行收集后统一写入全局内存. 这样原本N个线程需要的N次访存可以减少为1次访存,且数据传输量大幅下降,进一步降低IO开销. 同时,考虑到许可区块链中绝大部分签名是有效的,主机端可以使用64位长整型对返回值进行转换,通过判断其是否为0实现验签结果1∶64的批量确认,在Go语言中该类型为
2.4.2. 按需更新
考虑到区块链系统对验签结果的访存只须进行一次GPU写入和一次CPU读取,使用NVIDIA提出的统一内存[23]技术对验签结果进行存储管理,使得区块链系统的交易验签和共识过程可以并发执行,在交易执行前按需进行验签结果更新. 由于统一内存的特性,在此过程中发生的数据迁移由操作系统自动完成,进一步优化了CPU-GPU异构平台整体的内存性能.
3. 实验分析
为了验证提出的基于GPU的区块链交易验签加速技术,在RTX3080平台上进行相关实验.
3.1. 实验设置
通过构造并发送大量模拟交易的方式,对基于GPU的区块链交易验签加速技术进行性能评估,实验环境配置为16核心Intel(R) Xeon(R) W-1290 CPU,主频3.2 GHz,内存32 G,GPU型号为NVIDIA RTX 3080,主频1.44 GHz,显存10 G.
验签吞吐量是指单位时间内验证交易签名的次数,本研究所有测试均未使用聚合签名和批量签名,因此也等价于单位时间内验签完成的交易数量. 验签吞吐量表达式如下:
式中:
TPS是指单位时间内区块链系统中已上链的交易数量,表达式如下:
式中:
3.2. 验签加速技术优化效果评估实验
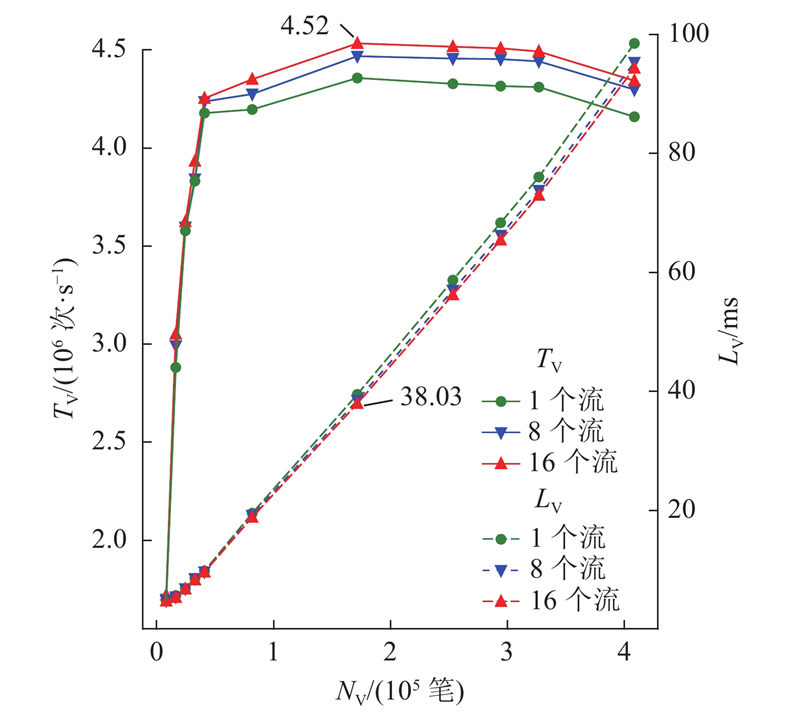
首先对研究方案进行整体优化效果评估,实验结果如图3所示.可以看出:1)本研究方案在使用16个流对172032笔交易验签时,峰值吞吐量为 4.52×106 次/s,延迟为37.95 ms. 在同等条件下,使用CPU的交易验签吞吐量为1.59×105 次/s,延迟为1.08 s,性能表现相差28倍以上. 本研究方案能够以较低的延迟实现尽可能高的吞吐量,一方面是因为本方案有效提升了GPU多线程并行验签算法的性能,同时还对整体IO开销和访存均进行了优化. 另一方面是因为GPU架构的特殊性,使其具备较高的并行性,并支持异步调用,在执行大批量任务时性能表现优异. 2)本研究方案的峰值吞吐量随着使用异步流数量的增加而上升,但是相较于从8个流增至16个流带来的峰值吞吐量的提升,从1个流增加至8个流带来的吞吐量增幅更明显,这是因为GPU内数据复制引擎的数量有限,当并发异步流的数量超过数据复制引擎数量时,部分流会进入串行处理队列. 3)随着验证签名数量的不断增加,本研究方案的吞吐量也逐渐提升,在达到4.25×106 次/s后趋于稳定,不再显著提升,在达到极限性能4.52×106 次/s后开始呈现下降趋势,这是因为此时GPU内计算资源使用已充分饱和,未分配到计算资源的验签任务只能同步等待,从而导致延迟显著增长和吞吐量下降.
图 3
图 3 验签加速技术吞吐量与延迟
Fig.3 Throughput and latency of signature verification acceleration technology
考虑区块链系统实际使用场景中,交易数量总是持续增加,几乎不可能出现图3中数十万笔交易瞬时到达的情况,如果使用单流模式,为了实现高吞吐量,部分预先到达的待验签交易须等待后续交易,这无疑会增加延迟并降低吞吐量,而多流模式的类流水线架构允许待验签交易即到即处理,可以在交易瞬时并发量不高而总量较大的场景中实现好于单流模式的整体性能,因此更符合区块链系统的实际使用场景.
对本研究方案进行分阶段优化效果评估,该部分采用控制变量的方式进行对比实验,即在评估某一阶段优化效果时另外2阶段均使用相同的设置.在进行第2阶段优化效果评估时,考虑到其他2个阶段主要针对CPU与GPU间IO开销和访存技巧进行优化,实验设计为仅使用本研究方案中GPU多线程并行验签阶段优化的实现与基于CPU验签的主流实现进行对比. 其中CPU上的实现基于GmSSL[29]实现,并使用Go语言协程实现了16的并发度以充分利用CPU核心. 实验结果如表1所示. 表中,
表 1 各阶段优化效果评估
Tab.1
| 优化阶段 | 是否优化 | | | |
| 数据组织与传输 | 优化 | 45.2 | 38.03 | 11.06 |
| 未优化 | 40.7 | 34.33 | ||
| GPU多线程 并行验签 | 优化 | 39.6 | 28.91 | 2490.00 |
| 未优化 | 1.59 | 1080 | ||
| 结果更新与确认 | 优化 | 45.2 | 38.03 | 3.91 |
| 未优化 | 43.5 | 36.09 |
3.3. GPU加速效果对比实验
图 4
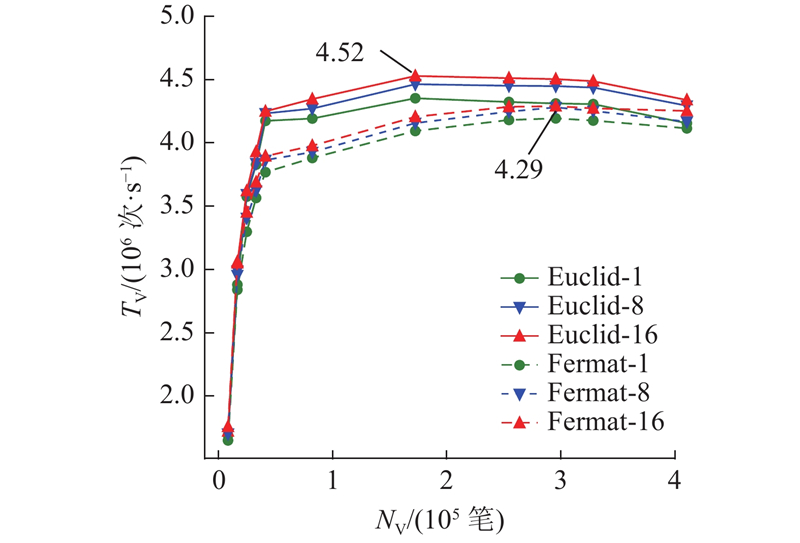
图 4 Euclid和Fermat验签方案吞吐量对比
Fig.4 Throughput comparison of Euclid and Fermat signature verification solutions
实验发现Fermat验签方案在GPU线程块大小设置为128时,无论交易验签数量是否大于32768,均实现了超过其他线程块大小设置的验签吞吐量,因此Fermat验签方案线程块大小均设置为128,Euclid验签方案则仍采用3.2节中基于交易验签数量自适应的线程块大小设置.可以看出:1)Euclid验签方案在交易验签数量为172032、流数量为16时达到峰值验签吞吐量4.52×106 次/s,Fermat验签方案在交易验签数量为294912、流数量为16时达到峰值验签吞吐量4.29×106 次/s. 2)当交易验签数量不大于32768时,Euclid验签方案略优于Fermat验签方案,当交易验签数量大于32768时,Euclid验签方案相较于Fermat验签方案有明显优势.
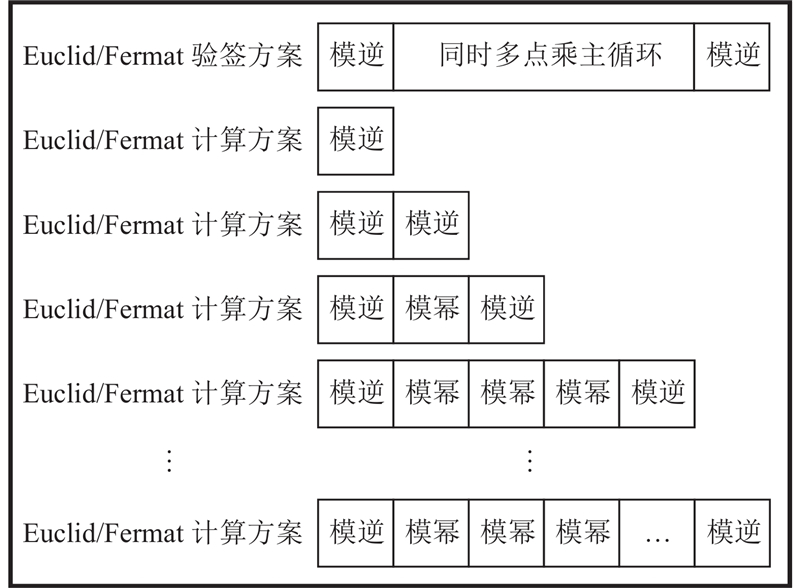
为了深入探究基于不同算法的模逆运算集成到验签方案后的整体表现,进行如图5所示的实验,其中Euclid计算方案中模逆运算基于二进制扩展欧几里得方法,Fermat计算方案中模逆运算基于费马小定理. 具体地,因为在Euclid和Fermat验签方案中的GPU多线程并行验签阶段,2次模逆运算和同时多点乘法运算中的主循环占用了大部分时间开销,本研究通过增加Euclid和Fermat计算方案中模幂运算次数的方式,逐步逼近并超过Euclid和Fermat验签方案的计算量,观察基于不同模逆算法的计算方案峰值吞吐量的变化情况,实验结果如图6所示. 图中,
图 5
图 5 Euclid和Fermat计算方案实验设计
Fig.5 Experimental design of Euclid and Fermat computational solutions
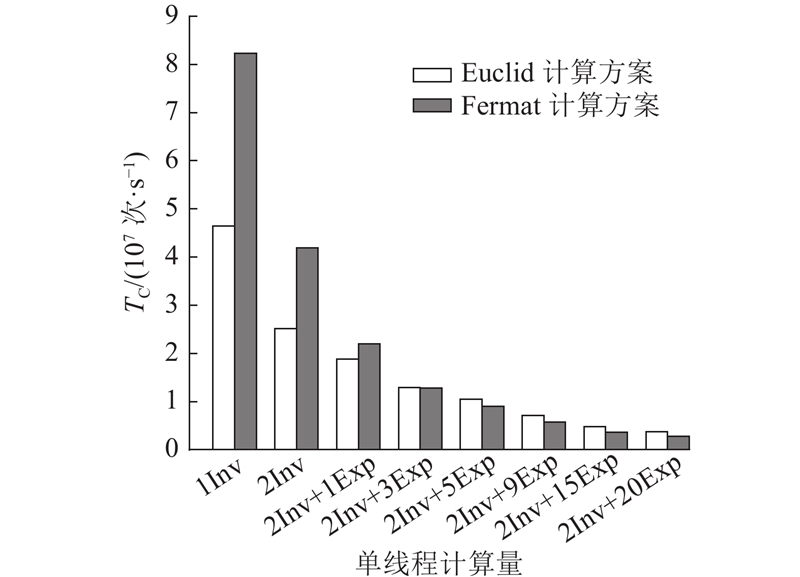
图 6
图 6 Euclid和Fermat计算方案峰值吞吐量对比
Fig.6 Comparison of peak throughput of Euclid and Fermat computing solutions
出现这种现象的原因如下. 1)相比于Euclid计算方案,Fermat计算方案需要更多的硬件资源. 具体地,Euclid计算方案使用寄存器数量为48个,Fermat计算方案的为64个. 此外实验测得在仅计算1次模逆,线程块大小步进128的情况下,Euclid计算方案最大支持线程块大小为1024,Fermat计算方案最大支持线程块大小为896,进一步佐证了Fermat计算方案消耗更多硬件资源的事实. 因此当GPU线程仅计算模逆时,使用更多硬件资源的Fermat计算方案性能更佳(类比算法思想中的“用空间换时间”理论),但随着引入模幂运算后计算量逐渐增加,GPU线程内分配给模逆运算的资源会逐渐减少,资源需求量相对较少的Euclid计算方案优势逐渐显现,并最终超越Fermat计算方案. 2)虽然随着总计算量的增加,Euclid计算方案实现了超过Fermat计算方案的峰值吞吐量,但相较于仅计算模逆时Fermat计算方案超过Euclid计算方案的峰值吞吐量,前者的差距低了2个数量级,这是因为2次模逆的计算量占总计算量的比例逐渐下降,从而对整体方案性能的影响也大幅下降.
进一步地,Euclid和Fermat验签方案中,同时多点乘法主循环的开销远超2次模逆运算的,同样存在类似于Euclid和Fermat计算方案实验中硬件资源分配的实际情况,因此资源需求量更少的Euclid验签方案实现了更高的的峰值验签吞吐量.
考虑到对比方案的实现均采用常规多倍点乘法,对本研究方案优化后的同时多点乘法和常规多倍点乘法进行性能对比实验. 同时多点乘法一次性完成多点乘法
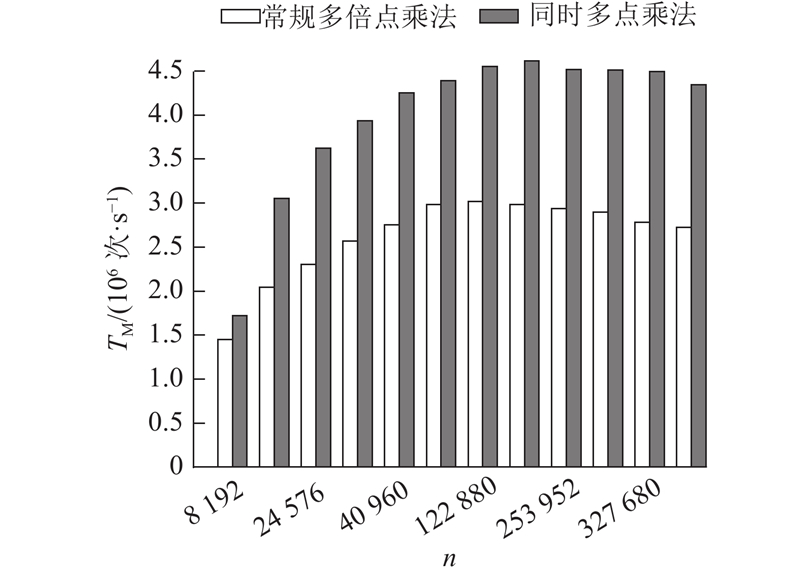
图 7
图 7 同时多点乘法和常规多倍点乘法峰值吞吐量对比
Fig.7 Comparison of peak throughput of simultaneous multipoint multiplication and standard multipoint multiplication
原因如下:1)在常规多倍点乘法中,固定点乘法和未知点乘法均须频繁访问位于全局内存的预计算表,且在同一个线程束内对预计算表无法合并访存,大幅增加了GPU设备内的访存IO开销. 而优化后的同时多点乘法则规避了这些访存开销. 2)多点乘法主循环为验签过程中最主要的计算开销,常规多倍点乘法相较于同时多点乘法具有更复杂的逻辑判断,更加可能使同一个线程束内各线程间出现互相等待的情况,从而拉低多点乘法整体吞吐量. 因此本研究最终选用了同时多点乘法.
最后,将本研究方案集成于国产许可区块链Hyperchain中进行优化效果验证,实验结果如表2所示.可以看出:在集成本研究方案后,Hyperchain平台上链TPS提升15.81%,上链延迟下降6.56%. 经测算,国产区块链Hyperchain平台中验签模块耗时约占30%,根据阿姆达尔定律(Amdahl’s Law)可知使用本研究方案后Hyperchain平台中验签模块性能提升约为83.55%. 这说明提出的方法有效提升了许可区块链平台的整体性能,实现了更高的吞吐量和更低的延迟. 但是相比于本研究方案的峰值验签吞吐量4.52×106 次/s,优化后的Hyperchain平台上链TPS为45410 次/s,远未达到本研究方案的上限,这是因为区块链系统的性能受多模块影响,优化后的验签模块已不再是性能瓶颈,但共识、网络、虚拟机等核心模块的瓶颈依然存在,从而导致集成性能测试期间,Hyperchain平台处理的瞬时交易数量无法达到如图3所示的模拟交易数量,未能发挥GPU全部算力. 因此在数据组织与传输阶段使用数据压缩方法,虽然会引入公钥恢复的计算量,但并不会带来额外的GPU计算开销.
表 2 集成优化效果验证
Tab.2
| 实验方案 | | |
| Hyperchain(使用本研究方案) | 45410 | 58.42 |
| Hyperchain(不使用本研究方案) | 39209 | 62.52 |
4. 结 语
随着交易数量的不断增加,交易验签效率已逐渐成为许可区块链系统性能瓶颈. 本研究提出基于GPU的区块链交易验签加速技术,从数据组织与传输、GPU多线程并行验签、结果更新与确认3个阶段分别进行了优化,不仅提升了验签吞吐量,而且释放了CPU资源,最终实现了4.52×106 次/s的极限验签性能, 高于现有已发布的CPU和基于GPU的实现. 之后将该研究方案应用于国产许可区块链Hyperchain平台中,实验结果表明关键性能指标上链TPS提升15.81%,延迟下降6.56%. 本研究方案方法只须做少许改动,即可适用于使用ECDSA签名的区块链系统.
实验结果表明上述将GPU用于加速区块链交易验签环节还未用尽GPU算力,后续可以将交易哈希计算操作也卸载至GPU处理,进一步释放CPU资源. 同时,GPUDirect RDMA技术的蓬勃发展,也使得通过GPU完成节点间交易及区块转发成为现实,并且能够更好地与本研究方案深度结合. 后续将进一步挖掘区块链中使用GPU作为硬件加速器的场景,不断优化区块链系统性能.
参考文献
Double SHA-256 hardware architecture with compact message expander for bitcoin mining
[J].DOI:10.1109/ACCESS.2020.3012581 [本文引用: 1]
BCA: a 530-mW multicore blockchain accelerator for power-constrained devices in securing decentralized networks
[J].DOI:10.1109/TCSI.2021.3102618 [本文引用: 1]
高性能联盟区块链技术研究
[J].DOI:10.13328/j.cnki.jos.005737 [本文引用: 2]
Research on high-performance consortium blockchain technology
[J].DOI:10.13328/j.cnki.jos.005737 [本文引用: 2]
GPU accelerated blockchain over key-value database transactions
[J].DOI:10.1049/blc2.12011 [本文引用: 1]
An efficient elliptic curve cryptography signature server with GPU acceleration
[J].DOI:10.1109/TIFS.2016.2603974 [本文引用: 4]
一种基于图形处理器的高吞吐量SM2数字签名计算方案
[J].DOI:10.11999/JEIT211049 [本文引用: 5]
A high throughput SM2 digital signature computing scheme over graphics processing unit platform
[J].DOI:10.11999/JEIT211049 [本文引用: 5]
Fixed-base comb with window-non-adjacent form (NAF) method for scalar multiplication
[J].DOI:10.3390/s130709483 [本文引用: 1]
Speeding-up P-256 ECDSA verification on x86-64 servers
[J].DOI:10.1109/LOCS.2019.2911063 [本文引用: 1]
Efficient fixed-base exponentiation and scalar multiplication based on a multiplicative splitting exponent recoding
[J].DOI:10.1007/s13389-018-0196-7 [本文引用: 1]
Low-latency elliptic curve scalar multiplication
[J].DOI:10.1007/s10766-012-0198-5 [本文引用: 1]