[1]
SI W, HAN J, YANG Z, et al. Research on key techniques for super-resolution reconstruction of satellite remote sensing images of transmission lines [C]// Journal of Physics: Conference Series . Sanya: ICAACE, 2021: 012092.
[本文引用: 1]
[2]
DEEBA F, KUN S, DHAREJO F A, et al Sparse representation based computed tomography images reconstruction by coupled dictionary learning algorithm
[J]. IET Image Processing , 2020 , 14 (11 ): 2365 - 2375
DOI:10.1049/iet-ipr.2019.1312
[本文引用: 1]
[3]
ZHANG F, LIU N, CHANG L, et al Edge-guided single facial depth map super-resolution using CNN
[J]. IET Image Processing , 2020 , 14 (17 ): 4708 - 4716
DOI:10.1049/iet-ipr.2019.1623
[本文引用: 1]
[4]
LI W, LIAO W Stable super-resolution limit and smallest singular value of restricted Fourier matrices
[J]. Applied and Computational Harmonic Analysis , 2021 , 51 : 118 - 156
DOI:10.1016/j.acha.2020.10.004
[本文引用: 1]
[5]
吴世豪, 罗小华, 张建炜, 等 基于FPGA的新边缘指导插值算法硬件实现
[J]. 浙江大学学报: 工学版 , 2018 , 52 (11 ): 2226 - 2232
[本文引用: 1]
WU Shi-hao, LUO Xiao-hua, ZHANG Jian-wei, et al FPGA-based hardware implementation of new edge-directed interpolation algorithm
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (11 ): 2226 - 2232
[本文引用: 1]
[6]
段然, 周登文, 赵丽娟, 等 基于多尺度特征映射网络的图像超分辨率重建
[J]. 浙江大学学报: 工学版 , 2019 , 53 (7 ): 1331 - 1339
[本文引用: 1]
DUAN Ran, ZHOU Deng-wen, ZHAO Li-juan, et al Image super-resolution reconstruction based on multi-scale feature mapping network
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (7 ): 1331 - 1339
[本文引用: 1]
[7]
DONG C, LOY C C, HE K, et al. Learning a deep convolutional network for image super-resolution [C]// European Conference on Computer Vision . Zurich: ECCV, 2014: 184-199.
[本文引用: 1]
[8]
DONG C, LOY C C, HE K, et al Image super-resolution using deep convolutional networks
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 38 (2 ): 295 - 307
[本文引用: 1]
[9]
LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops . Honolulu: CVPRW, 2017: 136-144.
[本文引用: 3]
[10]
TAI Y, YANG J, LIU X, et al. Memnet: a persistent memory network for image restoration [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: ICCV, 2017: 4539-4547.
[本文引用: 2]
[11]
AHN N, KANG B, SOHN K A. Fast, accurate, and lightweight super-resolution with cascading residual network [C]// Proceedings of the European Conference on Computer Vision . Munich: ECCV, 2018: 252-268.
[本文引用: 2]
[12]
WANG C, LI Z , SHI J. Lightweight image super-resolution with adaptive weighted learning network [EB/OL]. [2019-04-04]. https://arxiv.org/abs/1904.02358.
[本文引用: 1]
[13]
WOO S, PARK J, LEE J Y, et al. Cbam: convolutional block attention module [C]// Proceedings of the European Conference on Computer Vision . Munich: ECCV, 2018: 3-19.
[本文引用: 1]
[14]
DAI T, CAI J, ZHANG Y, et al. Second-order attention network for single image super-resolution [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: CVPR, 2019: 11065-11074.
[本文引用: 1]
[15]
ZHANG Y, LI K, LI K, et al. Residual non-local attention networks for image restoration[EB/OL]. [2019-03-24]. https://arxiv.org/abs/1903.10082.
[本文引用: 1]
[16]
JIA X, BRABANDERE D B, TUYTELAARS T, et al. Dynamic filter networks for predicting unobserved views [C]// Proceedings of the European Conference on Computer Vision 2016 Workshops . Amsterdam: ECCVW, 2016: 1-2.
[本文引用: 1]
[17]
YANG B, BENDER G, LE Q V, et al. Condconv: conditionally parameterized convolutions for efficient inference [C]// Advances in Neural Information Processing Systems . 2019, 32: 767-779.
[本文引用: 1]
[18]
CHEN Y, DAI X, LIU M, et al. Dynamic convolution: attention over convolution kernels [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: CVPR, 2020: 11030-11039.
[本文引用: 2]
[19]
ZHANG Y, ZHANG J, WANG Q, et al. Dynet: dynamic convolution for accelerating convolutional neural networks [EB/OL]. [2020-04-22]. https://arxiv.org/abs/2004.10694.
[本文引用: 2]
[20]
ZHANG Y, LI K, LI K, et al. Image super-resolution using very deep residual channel attention networks [C]// Proceedings of the European Conference on Computer Vision . Munich: ECCV, 2018: 286-301.
[本文引用: 1]
[21]
CHEN H, GU J, ZHANG Z. Attention in attention network for image super-resolution [EB/OL]. [2021-04-19]. https://arxiv.org/abs/2104.09497.
[本文引用: 1]
[22]
TIMOFTE R, AGUSTSSON E, VAN G L, et al. Ntire 2017 challenge on single image super-resolution: methods and results [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops . Hawaii: CVPRW, 2017: 114-125.
[本文引用: 1]
[23]
BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding [C]// Proceedings British Machine Vision Conference . Surrey: Springer, 2012: 1-10.
[本文引用: 1]
[24]
ZEYDE R, ELAD M, PROTTER M. On single image scale-up using sparse-representations [C]// International Conference on Curves and Surfaces . Avignon: ICCS, 2010: 711-730.
[本文引用: 1]
[25]
MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics [C]// Proceedings 18th IEEE International Conference on Computer Vision . Vancouver: ICCV, 2001: 416-423.
[本文引用: 1]
[26]
HUANG J B, SINGH A, AHUJA N. Single image super-resolution from transformed self-exemplars [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Santiago: IEEE, 2015: 5197-5206.
[本文引用: 1]
[27]
MATSUI Y, ITO K, ARAMAKI Y, et al Sketch-based manga retrieval using manga109 dataset
[J]. Multimedia Tools and Applications , 2017 , 76 (20 ): 21811 - 21838
DOI:10.1007/s11042-016-4020-z
[本文引用: 1]
[28]
FEI Y, LIAN F H, YAN Y. An improved PSNR algorithm for objective video quality evaluation [C]// 2007 Chinese Control Conference . Zhangjiajie: CCC, 2007: 376-380.
[本文引用: 1]
[29]
WANG Z, BOVIK A C, SHEIKH H R, et al Image quality assessment: from error visibility to structural similarity
[J]. IEEE Transactions on Image Processing , 2004 , 13 (4 ): 600 - 612
DOI:10.1109/TIP.2003.819861
[本文引用: 1]
[30]
KINGMA D P, BA J. Adam: a method for stochastic optimization [EB/OL]. [2014-12-22]. https://arxiv.org/abs/1412.6980.
[本文引用: 1]
[31]
HUI Z, GAO X, YANG Y, et al. Lightweight image super-resolution with information multi-distillation network [C]// Proceedings of the 27th ACM International Conference on Multimedia . Ottawa: ACM, 2019: 2024-2032.
[本文引用: 1]
[32]
FANG F, LI J, ZENG T Soft-edge assisted network for single image super-resolution
[J]. IEEE Transactions on Image Processing , 2020 , 29 : 4656 - 4668
DOI:10.1109/TIP.2020.2973769
[本文引用: 1]
[33]
LIU Y, JIA Q, FAN X, et al Cross-srn: structure-preserving super-resolution network with cross convolution
[J]. IEEE Transactions on Circuits and Systems for Video Technology , 2021 , 32 (8 ): 4927 - 4939
[本文引用: 1]
[34]
ZHANG K, ZUO W, ZHANG L. Learning a single convolutional super-resolution network for multiple degradations [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Salt lake city: CVPR, 2018: 3262-3271.
[本文引用: 1]
1
... 单幅图像超分辨率(single image super-resolution, SISR)重建是计算机视觉领域中一项重要的图像处理技术,在卫星遥感[1 ] 、医学成像[2 ] 和人脸识别[3 ] 等诸多领域有着广泛应用,其目的主要为从低分辨率(low resolution, LR)图像中重建出高分辨率(high resolution, HR)图像. ...
Sparse representation based computed tomography images reconstruction by coupled dictionary learning algorithm
1
2020
... 单幅图像超分辨率(single image super-resolution, SISR)重建是计算机视觉领域中一项重要的图像处理技术,在卫星遥感[1 ] 、医学成像[2 ] 和人脸识别[3 ] 等诸多领域有着广泛应用,其目的主要为从低分辨率(low resolution, LR)图像中重建出高分辨率(high resolution, HR)图像. ...
Edge-guided single facial depth map super-resolution using CNN
1
2020
... 单幅图像超分辨率(single image super-resolution, SISR)重建是计算机视觉领域中一项重要的图像处理技术,在卫星遥感[1 ] 、医学成像[2 ] 和人脸识别[3 ] 等诸多领域有着广泛应用,其目的主要为从低分辨率(low resolution, LR)图像中重建出高分辨率(high resolution, HR)图像. ...
Stable super-resolution limit and smallest singular value of restricted Fourier matrices
1
2021
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
基于FPGA的新边缘指导插值算法硬件实现
1
2018
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
基于FPGA的新边缘指导插值算法硬件实现
1
2018
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
基于多尺度特征映射网络的图像超分辨率重建
1
2019
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
基于多尺度特征映射网络的图像超分辨率重建
1
2019
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
1
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
Image super-resolution using deep convolutional networks
1
2015
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
3
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
... 网络训练所用平台为Ubuntu18.04,编程框架为Pytorch,处理器为Intel Core i9-9900K,显卡为RTX2080Ti,11 G显存,系统内存为64 G. 网络使用Adam算法[30 ] 进行优化,其具体参数设置为 $ \,\beta _1 = 0.9 $ $ \,\beta _2 = 0.999 $ $ \varepsilon = {10^{ - 8}} $ . 使用 $ {L_1} $ [9 ] 大小设置为16,整个网络共训练1000个epoch,初始学习率为0.0001,每200个epoch减少一半. ...
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...
2
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...
2
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...
1
... 图像降质是一个病态过程,高-低分辨率图像之间不存在一一对应的关系,即同一张HR图像在不同环境下有不同退化方向. 早期基于插值[4 ] 的方法使用同一个插值核而忽略图像的局部结构,无法分辨图像中存在的局部复杂结构;基于重建[5 ] 的方法容易受到输入数据和随机噪声的影响,导致重建效果提升不显著,因此这2类方法都难以改善图像超分辨率重建的效果. 近些年,随着深度学习[6 ] 的快速发展,Dong等[7 ] 在图像超分辨率重建领域中运用深度学习方法,提出了基于卷积神经网络的SRCNN (super resolution using convolutional neural network)算法,实现了网络端对端的学习,但由于只进行了3层卷积操作,该算法提取的图像信息有限. 针对此问题,Dong等[8 ] 在SRCNN算法的基础上提出FSRCNN (accelerating the super-resolution convolutional neural network)算法,该算法在上采样操作中使用反卷积层代替双三次插值,并且将网络由3层加深为8层. 随后,许多研究者在此基础上,致力于研究重建效果更好的算法. 网络的加深会带来大量参数的计算,针对此问题,Lim等[9 ] 提出基于增强型深度残差网络的EDSR (enhanced deep residual network for single image super-resolution) 算法,该算法在残差网络的基础上将批标准化层移除,加快网络收敛速度. Tai等[10 ] 提出基于持续记忆网络的MemNet (persistent memory network)算法,其利用密集连接结构构建了一个深度神经网络,使算法具有较强的学习LR图像与HR图像之间映射函数的能力. Ahn等[11 ] 提出基于级联残差网络的CARN(cascading residual network)算法,通过使用局部和全局的级联模块来避免以往使用递归网络造成的信息损失. Wang等[12 ] 提出基于自适应加权网络的AWSRN(adaptive weighted super-resolution network)算法,提出一种自适应加权多尺度重构模块,在不减少性能的情况下,通过自适应权值去除一些贡献较低的分支,来减少网络参数. ...
1
... 尽管上述基于深度学习的图像超分辨率算法取得了较好的重建效果,但仍存在一些问题,比如这些算法大多都通过增加网络的宽度和深度来实现更好的重建效果. 在现实世界中,高昂的计算成本限制了它们的应用[13 ] . 为此,一些使用注意力机制的超分辨率重建算法被提出,Dai等[14 ] 提出基于二阶注意力网络的SAN(second-order attention network)算法,利用二阶特征的分布自适应地学习特征的内部依赖关系. Zhang等[15 ] 提出将基于残差非局部注意网络的RNAN (residual non-local attention network)算法用于图像修复,通过在分支中提出残差局部和非局部注意力块,进一步增强网络表征能力. 上述大多数方法都专注于开发复杂的注意力模块以获得更好的性能或采用均等处理的方式来运用各种注意力机制,但是不同注意力机制所提取的特征存在不同的重要程度,均等处理的方式会使得大量计算资源分配到无用特征上,从而导致计算资源无法得到有效利用. ...
1
... 尽管上述基于深度学习的图像超分辨率算法取得了较好的重建效果,但仍存在一些问题,比如这些算法大多都通过增加网络的宽度和深度来实现更好的重建效果. 在现实世界中,高昂的计算成本限制了它们的应用[13 ] . 为此,一些使用注意力机制的超分辨率重建算法被提出,Dai等[14 ] 提出基于二阶注意力网络的SAN(second-order attention network)算法,利用二阶特征的分布自适应地学习特征的内部依赖关系. Zhang等[15 ] 提出将基于残差非局部注意网络的RNAN (residual non-local attention network)算法用于图像修复,通过在分支中提出残差局部和非局部注意力块,进一步增强网络表征能力. 上述大多数方法都专注于开发复杂的注意力模块以获得更好的性能或采用均等处理的方式来运用各种注意力机制,但是不同注意力机制所提取的特征存在不同的重要程度,均等处理的方式会使得大量计算资源分配到无用特征上,从而导致计算资源无法得到有效利用. ...
1
... 尽管上述基于深度学习的图像超分辨率算法取得了较好的重建效果,但仍存在一些问题,比如这些算法大多都通过增加网络的宽度和深度来实现更好的重建效果. 在现实世界中,高昂的计算成本限制了它们的应用[13 ] . 为此,一些使用注意力机制的超分辨率重建算法被提出,Dai等[14 ] 提出基于二阶注意力网络的SAN(second-order attention network)算法,利用二阶特征的分布自适应地学习特征的内部依赖关系. Zhang等[15 ] 提出将基于残差非局部注意网络的RNAN (residual non-local attention network)算法用于图像修复,通过在分支中提出残差局部和非局部注意力块,进一步增强网络表征能力. 上述大多数方法都专注于开发复杂的注意力模块以获得更好的性能或采用均等处理的方式来运用各种注意力机制,但是不同注意力机制所提取的特征存在不同的重要程度,均等处理的方式会使得大量计算资源分配到无用特征上,从而导致计算资源无法得到有效利用. ...
1
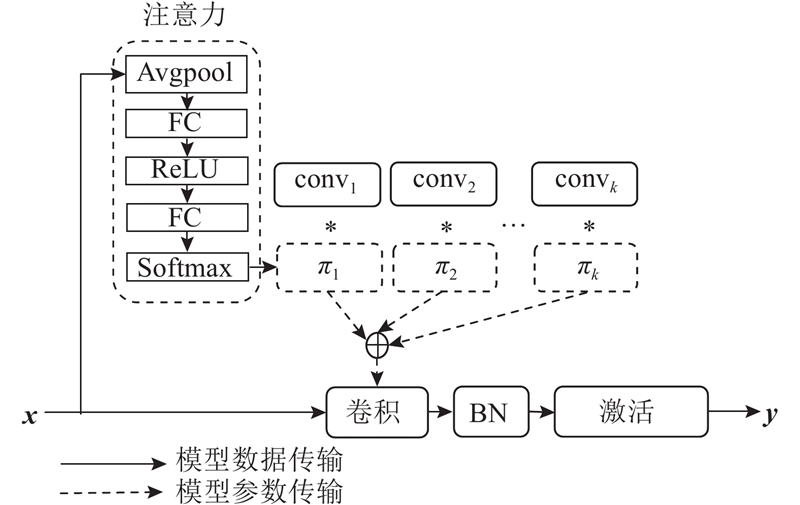
... Jia等[16 ] 首次将动态学习的概念引入到深度学习之中,提出一种新的学习框架. Yang等[17 ] 提出条件参数卷积,可以为每个特征学习一个特定的卷积核参数,在提升模型的尺寸与容量的同时保持高效推理. Chen等[18 ] 提出动态卷积,与普通卷积不同的是,动态卷积没有使用单个卷积核,而是根据输入的关注度动态地聚合多个并行卷积核. Zang等[19 ] 提出用于加速卷积神经网络的自适应卷积,基于图像内容生成可调节的卷积核,以解决卷积核之间存在冗余信息的问题. 其中,动态卷积[18 ] 的框架图如图1 所示. 图中,FC、BN分别表示全连接层和批归一化层. ...
1
... Jia等[16 ] 首次将动态学习的概念引入到深度学习之中,提出一种新的学习框架. Yang等[17 ] 提出条件参数卷积,可以为每个特征学习一个特定的卷积核参数,在提升模型的尺寸与容量的同时保持高效推理. Chen等[18 ] 提出动态卷积,与普通卷积不同的是,动态卷积没有使用单个卷积核,而是根据输入的关注度动态地聚合多个并行卷积核. Zang等[19 ] 提出用于加速卷积神经网络的自适应卷积,基于图像内容生成可调节的卷积核,以解决卷积核之间存在冗余信息的问题. 其中,动态卷积[18 ] 的框架图如图1 所示. 图中,FC、BN分别表示全连接层和批归一化层. ...
2
... Jia等[16 ] 首次将动态学习的概念引入到深度学习之中,提出一种新的学习框架. Yang等[17 ] 提出条件参数卷积,可以为每个特征学习一个特定的卷积核参数,在提升模型的尺寸与容量的同时保持高效推理. Chen等[18 ] 提出动态卷积,与普通卷积不同的是,动态卷积没有使用单个卷积核,而是根据输入的关注度动态地聚合多个并行卷积核. Zang等[19 ] 提出用于加速卷积神经网络的自适应卷积,基于图像内容生成可调节的卷积核,以解决卷积核之间存在冗余信息的问题. 其中,动态卷积[18 ] 的框架图如图1 所示. 图中,FC、BN分别表示全连接层和批归一化层. ...
... [18 ]的框架图如图1 所示. 图中,FC、BN分别表示全连接层和批归一化层. ...
2
... Jia等[16 ] 首次将动态学习的概念引入到深度学习之中,提出一种新的学习框架. Yang等[17 ] 提出条件参数卷积,可以为每个特征学习一个特定的卷积核参数,在提升模型的尺寸与容量的同时保持高效推理. Chen等[18 ] 提出动态卷积,与普通卷积不同的是,动态卷积没有使用单个卷积核,而是根据输入的关注度动态地聚合多个并行卷积核. Zang等[19 ] 提出用于加速卷积神经网络的自适应卷积,基于图像内容生成可调节的卷积核,以解决卷积核之间存在冗余信息的问题. 其中,动态卷积[18 ] 的框架图如图1 所示. 图中,FC、BN分别表示全连接层和批归一化层. ...
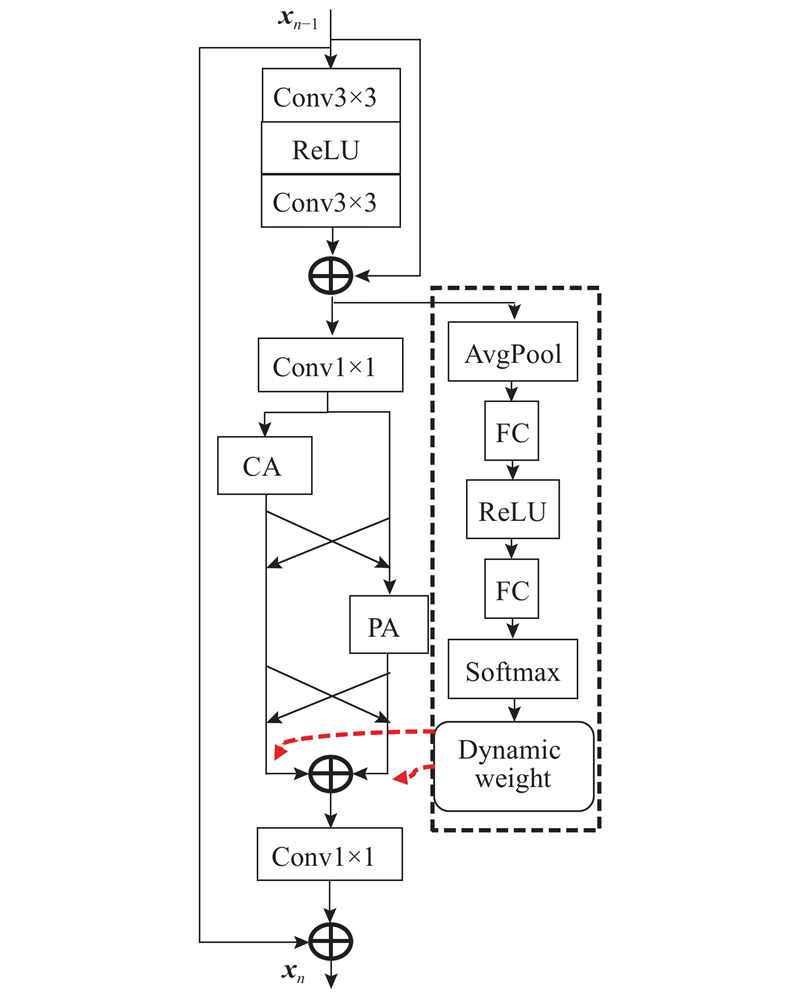
... 式中: $ {f_{{\rm{am}}}} $ $ {f_{{\rm{am}}}} $ 图3 所示, $ {{{\boldsymbol{x}}}_{n - 1}} $ 19 ]所述,通过约束动态权重可以促进动态模块的学习,即定义了一个约束 $ \pi _{n - 1}^{{{\rm{ca}}} }+\pi _{n - 1}^{{{\rm{pa}}} } = 1 $
1
... 式中: $ f_{{{\rm{DA}}} }^i $ $ i $ $ {{\boldsymbol{x}}_n} $ $ n $ [20 ] 的方式进行连接,以此简化学习过程,增强梯度传播,同时缓解梯度爆炸问题,具体操作如下: ...
1
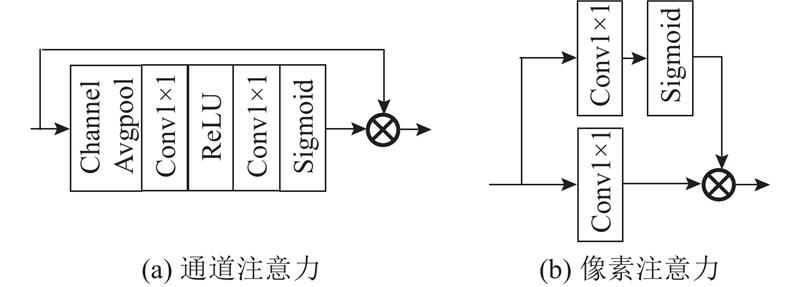
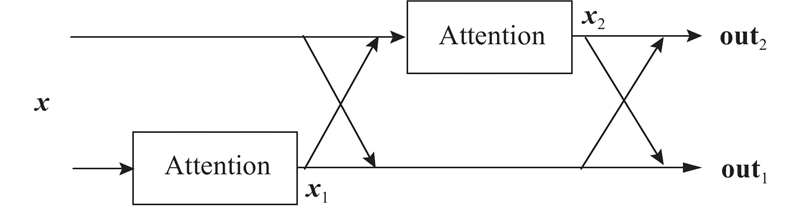
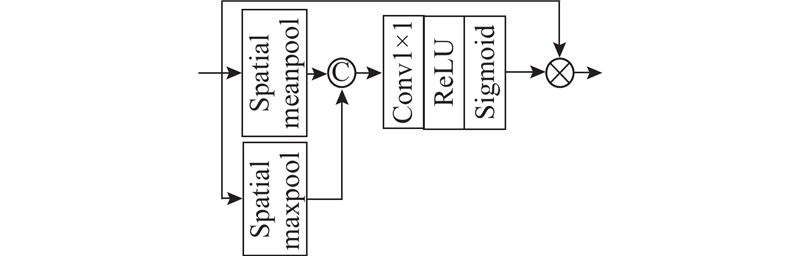
... 先前的文献[21 ] 表明,低分辨率图像中的信息具有丰富的低频和有价值的高频成分,使用注意力机制可以帮助网络更加关注高频特征,避免所有特征都被平等对待. 通常,在使用不同注意力机制的过程中,都是采取均等处理的方式,即通过简单的串联或并联,直接将产生的不同特征图融合,而没有考虑到不同注意力机制所提取的图像特征具有不同的重要程度,以及花费大量计算资源在相似的特征信息上的问题. 为此,本研究提出了一种可学习的DA模块,如图3 所示. 图中,CA和PA分别表示通道注意力块和像素注意力块. 2种注意力结构图如图4 所示. ...
1
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
1
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
1
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
1
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
1
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
Sketch-based manga retrieval using manga109 dataset
1
2017
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
1
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
Image quality assessment: from error visibility to structural similarity
1
2004
... 在训练阶段,使用公开的DIV2K[22 ] 数据集作为训练数据集,其包含了800张2K分辨率的高清图像,对这些高分辨率图像进行90°、180°、270°旋转以及比例缩放来进行数据增强. 训练所用的低分辨率图像由高分辨率图像经过双三次下采样获得,将高分辨率图像和对应的低分辨率图像分别裁剪成尺寸为 $ 48s \times 48s $ $ 48 \times 48 $ $ s $ [23 ] 、Set14[24 ] 、BSD100[25 ] 、Urban100[26 ] 和Manga109[27 ] . 本研究在RGB通道上训练网络,在YCrCb空间中的Y通道上进行批次测试,同时使用峰值信噪比(peak signal-to-noise ratio, PSNR)[28 ] 和结构相似度(structural similarity, SSIM)[29 ] 进行评估. ...
1
... 网络训练所用平台为Ubuntu18.04,编程框架为Pytorch,处理器为Intel Core i9-9900K,显卡为RTX2080Ti,11 G显存,系统内存为64 G. 网络使用Adam算法[30 ] 进行优化,其具体参数设置为 $ \,\beta _1 = 0.9 $ $ \,\beta _2 = 0.999 $ $ \varepsilon = {10^{ - 8}} $ . 使用 $ {L_1} $ [9 ] 大小设置为16,整个网络共训练1000个epoch,初始学习率为0.0001,每200个epoch减少一半. ...
1
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...
Soft-edge assisted network for single image super-resolution
1
2020
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...
Cross-srn: structure-preserving super-resolution network with cross convolution
1
2021
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...
1
... 为了验证本研究算法的有效性,进行客观效果的评估,在Set5、Set14、BSD100、Urban100和Manga109标准测试集上,将本研究算法的重建结果与当前先进的超分辨率算法Bicubic、EDSR-baseline[9 ] 、MemNet[10 ] 、CARN[11 ] 、IMDN[31 ] 、SeaNet-baseline[32 ] 、Cross-SRN[33 ] 和SRMDNF[34 ] 进行2倍、3倍、4倍放大倍数下的PSNR性能对比,对比结果如表1 所示. 表中,加粗的为最优结果,下划线为次优结果. 可以看出,本研究所提出的DAN的平均PSNR和SSIM均显著优于其他主流对比方法的,在Set14测试集的放大2、3、4倍的情况下,与次优结果相比,平均PSNR分别提升了0.02、0.04、0.07 dB;而在BSD100测试集的放大2、3、4倍情况下,与次优结果相比,平均PSNR提升了0.01、0.01、0.04 dB. 同时,横向来看,当放大系数为4时,在5个测试集上,与次优结果相比,平均PSNR分别提升了0.08、0.07、0.04、0.15、0.15 dB. 在参数量方面,DAN算法能够在付出较小参数量提升的情况下,获得较高的重建性能提升幅度,例如,在放大系数为4的情况下,与次优结果相比,在参数量上仅提高了41 K. 这些实验结果表明,DAN对于不同放大系数及不同类型的图像均有良好的重建效果,但其能更好地适应重建难度更大的放大倍数较大的图像,也更善于重建存在不同频段细节特征的图片,同时可以在图像超分辨率性能和模型复杂度之间取得更好的平衡. ...