在电力系统运行中,系统频率在微小范围内保持稳定至关重要. 作为有利的辅助技术,负荷频率控制 ( load frequency control, LFC ) 通过维持电力系统供需间的动态平衡来保证系统频率运行在额定值,能够迅速抑制外界扰动所引发的频率变化[1-4]. 智能电网将信息网、电力网深度交互融合,实现了对电力系统的网络控制,通信网络成为信息传输的媒介[5-6]. 在网络带宽资源有限的情况下实现高效通信是研究的重点. 为了降低通信负担,事件触发机制应运而生.“事件”表示与系统状态有关的一种判断条件,当条件成立时,传感器更新并向控制器发送信号,从而实现控制的目的. 事件触发控制主要依据系统状态来判断触发时刻,实现了“按需通信”[7-9].
针对LFC系统的事件触发控制问题, Zhang等[10-12]进行了一系列研究,事件触发控制既能够有效地减少数据传输量,也能够保证系统的稳定运行. 在网络攻击下,通过事件触发机制筛选出关键的控制信号,可以防御攻击,保证LFC系统的稳定性[13-15]. 通过将新能源电动汽车接入电网中,应用弹性事件触发机制,能够消除DoS攻击导致数据包丢失的不利影响[16]. 针对开放式通信网络具有通信延迟的问题, Yue等[17]提出延迟系统方法,设计事件触发控制器. 自适应事件触发机制的阈值可以随时间动态调整,以减少不必要的通信[18]. 为了节约网络资源,本文在系统的反馈通道和前向通道中,分别设计加入指数衰减项和状态模拟项的事件触发机制,以降低触发频率.
LFC需要借助通信网络完成被控量的采集和控制量的下发,当信道的传输码率有限时,需要对信号进行量化处理. 量化误差会削弱系统的控制性能,甚至导致系统失去稳定,因此对量化控制系统的稳定性分析一直是研究的重点. 当基于动态量化的线性不确定系统受到未知、有界的扰动输入时,自适应控制器能够保证闭环系统的稳定性[19]. 对于基于动态量化控制的连续时间系统,借助稳定性理论可以推导得到闭环系统全局渐近稳定的充分性条件[20]. 当网络传输存在通信延迟时,利用基于时间触发的动态量化缩放算法能够保证系统的指数稳定性[21]. 对于量化误差对系统产生的不利影响, Zhou等[22]的研究表明,事件触发机制对量化误差具有一定的鲁棒性. 当系统状态不易通过直接测量得到时,应用基于观测器的输出反馈控制器,利用量化器参数缩放算法能够保证线性系统的渐近稳定性[23]. 量化控制不仅能够改变系统输出,也能够改变控制输入. 本文采用输入输出的量化控制方式,设计基于事件触发的动态量化器参数缩放算法,对量化控制系统进行稳定性分析.
本文研究基于动态量化的事件触发LFC问题. 根据系统状态和动态量化参数,针对反馈通道和前向通道,设计加入指数衰减项和状态模拟项的事件触发通信机制,降低了触发频率,节约了网络资源. 在反馈通道和前向通道中应用动态量化器,对测量输出和控制输入的触发采样信号进行量化控制,实现了信号的网络传输. 利用基于事件触发的动态量化器参数缩放算法,保证了闭环系统输入到状态稳定,缩放变量异步更新,自由度更高.
1. 系统模型
1.1. LFC系统
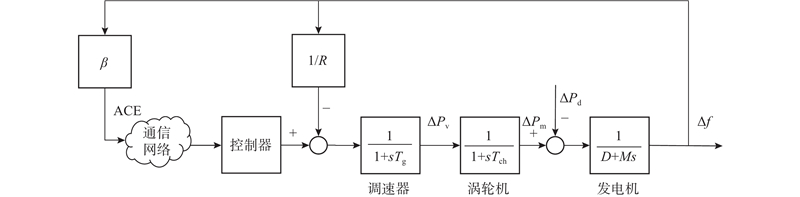
LFC系统的动态模型如图1所示. 该模型是在科学假设下的区域单机等值等效模型,由发电机、涡轮机、调速器、控制器及通信网络等模块组成.图1中,
图 1
图 1 单区域负荷频率控制系统的动态模型
Fig.1 Dynamic model of one-area load frequency control system
相对于电压和功角快速变化的过程, LFC下的频率响应较缓慢,因此采用简化的低阶线性系统来表征平衡点附近的动态特性. 频率调节过程可以简述如下: 电网的负荷变化造成系统频率偏离额定值,反馈机制根据频率偏差产生控制信号,调节涡轮机的输出功率增量补偿负荷变化量,从而控制系统频率回到设定值. 基于各环节的传递函数和信号流向,得到频域下系统状态变量的动态方程组:
对式(1)进行拉普拉斯反变换,得到时域下系统状态变量的微分方程组:
对于单区域LFC电力系统, 区域控制误差(area control error, ACE)仅以维持区域内系统频率稳定为目标, 只包含频率偏差变量.
选择系统的状态向量和输出向量为
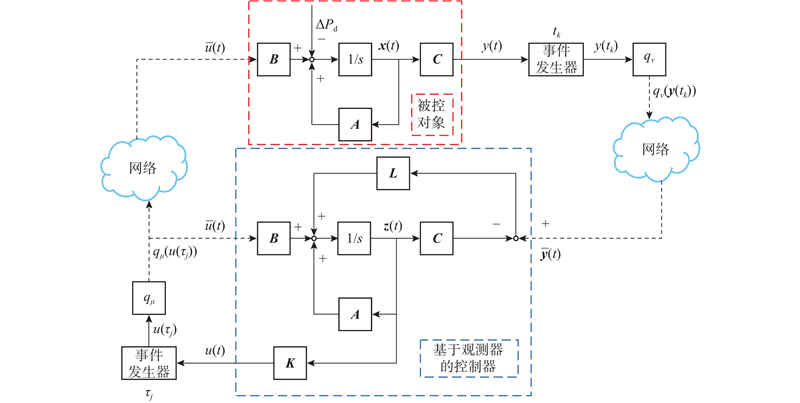
基于量化控制的LFC系统动态模型如图2所示,系统的状态空间表达式为
图 2
图 2 基于量化控制的负荷频率控制系统动态模型
Fig.2 Dynamic model of load frequency control system based on quantization control
式中:
考虑系统状态存在不易直接测量得到的情况,采用基于观测器的输出反馈控制器,选择状态估计向量为
式中:
为了得出相关的结论,假设如下.
1)
2)
1.2. 动态量化器
量化控制可将连续信号离散化,只需传输量化处理后的少量数值信号,可以大大降低对网络带宽的需求[20]. 在系统的反馈通道和前向通道设置动态量化器,对信号进行量化处理.
输出量化器可以刻画为分段函数
1) 若
2) 若
式中:
设置在反馈通道的动态量化器的数学模型为
式中:
类似地,输入量化器
设置在前向通道的动态量化器的数学模型为
式中:
注1 信号在带宽有限的网络中传输,须经过量化处理. 量化器能够把采样信号转换成在有限集合中取值的数字信号. 应用动态量化器不可避免地带来了量化误差, 削弱了系统的控制性能, 甚至导致系统不稳定. 对于信号量化产生的不利影响, Zhou等[22]的研究表明,事件触发机制对量化误差具有一定的鲁棒性.
1.3. 系统运行分析
网络化控制的LFC系统动态模型如图2所示. 图中,
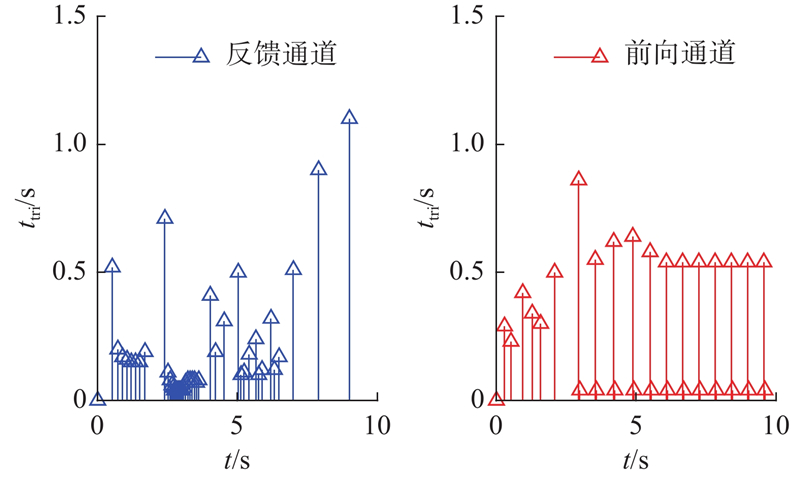
当电网的负荷发生变化时,反馈通道的传感器检测到电网频率的变化,事件发生器判断出触发时刻
当控制器下发控制信号时,前向通道的事件发生器判断出触发时刻
2. 稳定性分析
利用李雅普诺夫稳定性理论,对基于动态量化的事件触发LFC系统进行稳定性分析, 证明触发过程中不会产生Zeno现象,对初始条件进行约束. 为了便于分析,对观测器和控制器的设计过程分别进行讨论.
引理1[23] 对于矩阵指数函数
定义1[24] 考虑误差系统
则
2.1. 观测器设计
定义状态估计误差为
基于LFC系统(3)和观测器(4), 反馈通道的事件触发机制设计如下.
1) 通过加入指数衰减项的事件触发条件
2) 缩放变量
定理1 基于反馈通道的事件触发机制,可得如下结论.
1) 状态估计误差
2) 任意2次连续触发之间存在最小的间隔时间
证明: 选取
定义
若
当
根据定义1可知, 状态估计误差
接下来证明当
由引理1可知,存在常数
对式(13)两端积分,可得
计算可得
化简可得
间隔时间
注2 在有效的控制过程中,尽管系统输出
注3 在反馈通道连续2次触发之间, 指数衰减项的持续作用可能使动态量化器对采样测量输出信号进行多次处理,所以动态量化器的更新由事件触发机制和动态量化算法共同作用决定.
2.2. 控制器设计
控制器对发电机组的输出进行调整,平衡电量供给与负荷需求,从而稳定系统状态. 前向通道的事件触发机制设计如下.
1) 通过带有状态模拟项的事件触发条件
2) 缩放变量
定理2 基于前向通道的事件触发机制,可得如下结论.
1) 观测器状态
2) 任意2次连续触发之间存在最小的间隔时间
证明: 以下的证明过程讨论了2类情况. 第1类情况是
首先讨论第1类情况,当
选取
由状态观测器的设计过程可知,当
定义
当
根据定义1可知, 观测器状态
接下来证明当
定义
其中
由引理1可知,存在常数
定 义
对式(22)两端积分,可得
计算可得
化简可得
式中:
再讨论第2类情况,当
选取
当
注4 在前向通道中设计加入状态模拟项的事件触发机制,判断触发时刻
注5 相较于文献[22],本文在LFC系统的反馈通道设计加入指数衰减项的事件触发机制,在前向通道设计加入状态模拟项的事件触发机制,既能够保证系统稳定运行,又能够降低触发频率, 节约网络和计算资源.
2.3. 初始条件
基于区域单机等值等效模型,利用稳定性理论分析基于动态量化的事件触发LFC系统的稳定性,得到闭环系统输入到状态稳定的充分性条件,排除了Zeno现象. 由于动态量化器的量化范围是有限的,系统初始值须在量化范围内,初始条件的设定对系统稳定性分析十分关键.
定理3 设定初始条件满足
证明: 在定理3的限定下,系统初始值在动态量化器的量化范围内. 由定理1和定理2的证明过程可知,闭环控制系统输入到状态稳定.
3. 仿真案例及分析
表 1 电力负荷频率控制系统的参数
Tab.1
| 参数 | 参数值 | 参数 | 参数值 | |
| M/Hz−1 | 10 | Tg/s | 0.1 | |
| D/Hz−1 | 1 | R/Hz | 0.05 | |
| Tch/s | 0.3 | | 21 |
根据系统参数可知,系统矩阵、输入矩阵、输出矩阵、扰动矩阵分别为
反馈增益矩阵和观测器增益矩阵分别设定为
系统的初始条件设定为
动态量化器的相关参数设定为
图 3
图 4
图 5
图 6
图 7
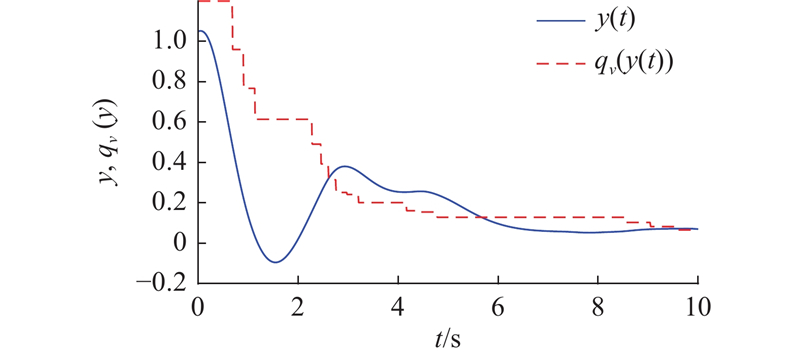
图 7 测量输出信号和输出量化器的响应曲线
Fig.7 Response curve of output signal and output quantizer
图 8
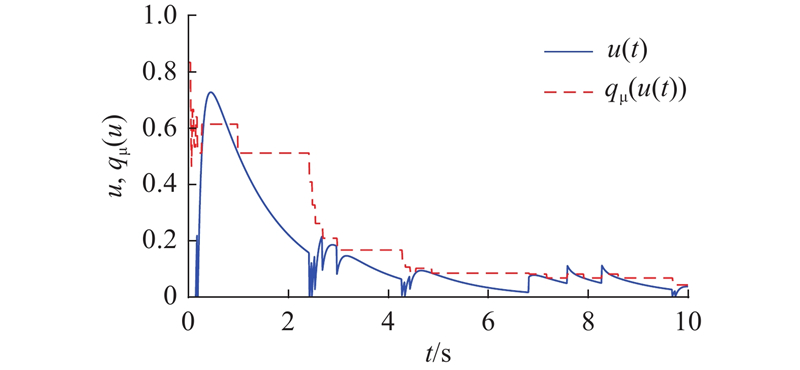
图 8 控制输入信号和输入量化器的响应曲线
Fig.8 Response curve of input signal and input quantizer
图 9
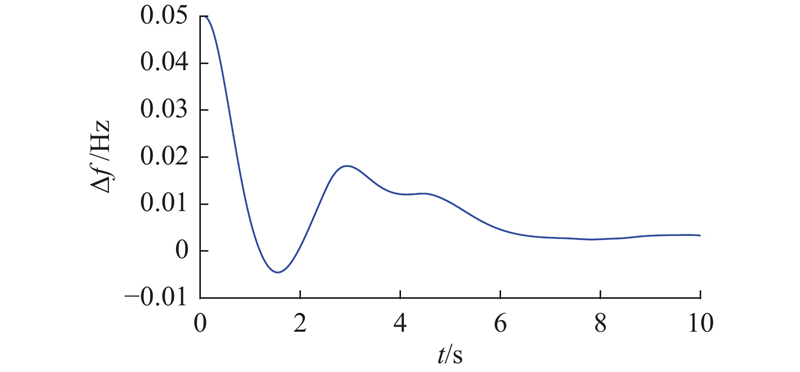
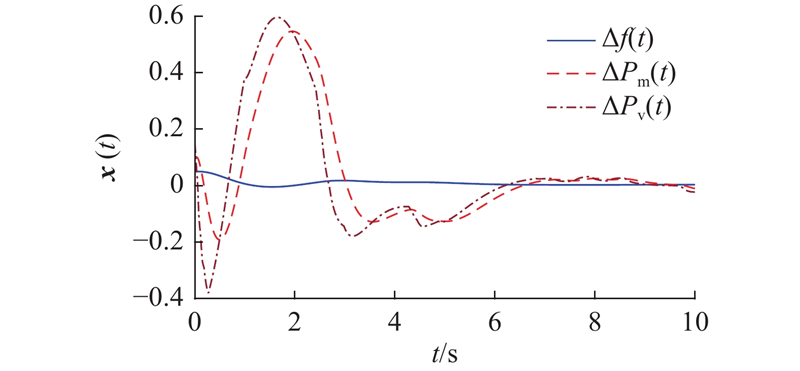
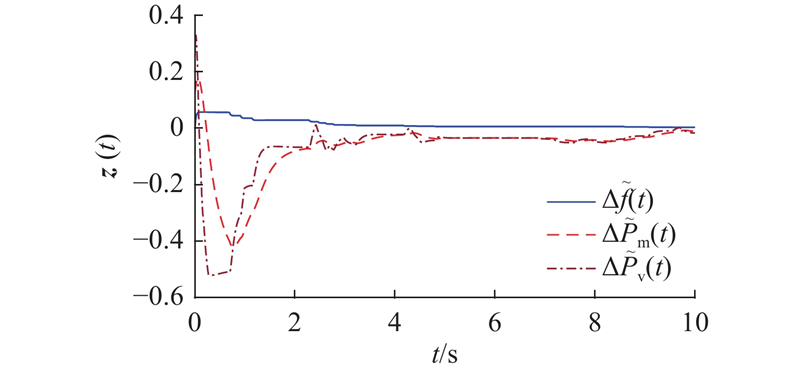
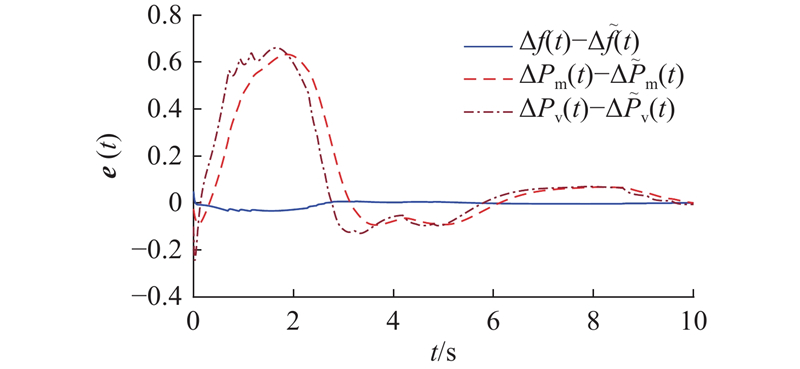
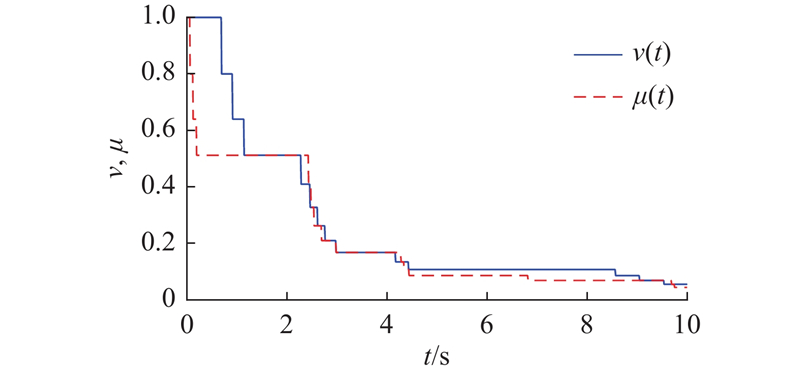
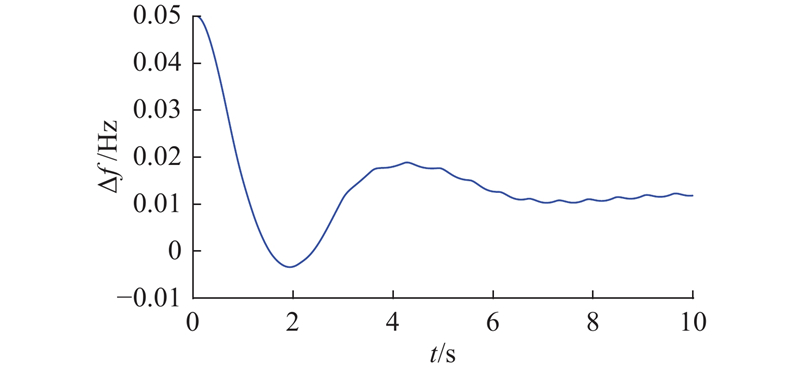
在有界负荷扰动信号的输入下,从图3可知,
在初始阶段,负荷扰动信号和量化误差会共同加剧系统的振荡程度,但LFC具有自动修正系统频率偏离给定值的作用,因而能够消除内外扰动所引起的偏差,达成自动控制的目的.
图 10
图 11
图 12
对比的仿真实验验证了加入指数衰减项和状态模拟项的事件触发机制在动态量化下,既能够保证系统良好的控制性能,也能够节约更多的网络资源,因而综合性能更优.
4. 结 语
新能源高比例并网给电力系统带来了二次调频通信负荷增加的问题. 为了节约网络和计算资源,在反馈通道中设计加入指数衰减项的事件触发机制,在前向通道中设计加入状态模拟项的事件触发机制,应用动态量化器实现了测量输出和控制输入信号的量化控制. 利用李雅普诺夫稳定性理论,分析基于动态量化的事件触发LFC系统的稳定性,得到闭环系统输入到状态稳定的充分条件, 排除了Zeno现象. 通过仿真验证了加入指数衰减项和状态模拟项的事件触发机制具备更好的综合性能.
参考文献
Delay-dependent robust load frequency control for time delay power systems
[J].DOI:10.1109/TPWRS.2012.2228281 [本文引用: 1]
Robust load frequency control of power systems against random time-delay attacks
[J].
Control performance standards-oriented event-triggered load frequency control for power systems under limited communication bandwidth
[J].
Robust load frequency control for power system considering transmission delay and sampling period
[J].DOI:10.1109/TII.2020.3026336 [本文引用: 1]
基于贝叶斯序贯博弈模型的智能电网信息物理安全分析
[J].DOI:10.16383/j.aas.2018.c180336 [本文引用: 1]
Cyber-physical security analysis of smart grids with Bayesian sequential game models
[J].DOI:10.16383/j.aas.2018.c180336 [本文引用: 1]
信息物理融合系统研究综述
[J].
Cyber-physical systems: a survey
[J].
基于事件触发机制的网络控制研究综述
[J].DOI:10.13195/j.kzyjc.2017.0531 [本文引用: 1]
A survey of networked event-triggered control
[J].DOI:10.13195/j.kzyjc.2017.0531 [本文引用: 1]
Relaxed resilient fuzzy stabilization of discrete-time Takagi-Sugeno systems via a higher order time-variant balanced matrix method
[J].DOI:10.1109/TFUZZ.2022.3145809
Event-triggered stabilization of a class of nonlinear time-delay systems
[J].DOI:10.1109/TAC.2020.2979828 [本文引用: 1]
Practical stability and event- triggered load frequency control of networked power systems
[J].DOI:10.1109/TSMC.2022.3143853 [本文引用: 1]
Dynamic event-triggered output feedback control for load frequency control in power systems with multiple cyber attacks
[J].
Event-triggering load frequency control for multi-area power systems with communication delays
[J].DOI:10.1109/TIE.2015.2399394 [本文引用: 1]
Hybrid dynamic event-triggered load frequency control for power systems with unreliable transmission networks
[J].DOI:10.1109/TCYB.2022.3163271 [本文引用: 1]
Model-based dynamic event-triggered control for cyber-physical systems subject to dynamic quantization and DoS attacks
[J].
Resilient event-triggering H∞ load frequency control for multi-area power systems with energy limited DoS attacks
[J].DOI:10.1109/TPWRS.2016.2634122 [本文引用: 1]
网络攻击下信息物理融合电力系统的弹性事件触发控制
[J].DOI:10.16383/j.aas.c180388 [本文引用: 2]
Resilient event-triggered control of grid cyber-physical systems against cyber attack
[J].DOI:10.16383/j.aas.c180388 [本文引用: 2]
A delay system method for designing event-triggered controllers of networked control systems
[J].DOI:10.1109/TAC.2012.2206694 [本文引用: 1]
Adaptive event-triggering H∞ load frequency control for network-based power systems
[J].DOI:10.1109/TIE.2017.2726965 [本文引用: 1]
Adaptive control of passifiable linear systems with quantized measurements and bounded disturbances
[J].DOI:10.1016/j.sysconle.2015.12.001 [本文引用: 1]
Hybrid feedback stabilization of systems with quantized signals
[J].DOI:10.1016/S0005-1098(03)00151-1 [本文引用: 2]
Dynamic quantization of uncertain linear networked control systems
[J].DOI:10.1016/j.automatica.2015.06.041 [本文引用: 1]
Self-triggered and event-triggered control for linear systems with quantization
[J].DOI:10.1109/TSMC.2018.2833114 [本文引用: 10]
Observer-based feedback stabilization of linear systems with event-triggered sampling and dynamic quantization
[J].DOI:10.1016/j.sysconle.2016.05.008 [本文引用: 2]
On the input-to-state stability property
[J].DOI:10.1016/S0947-3580(95)70005-X [本文引用: 2]