处理多目标优化问题常用的方法有NSGA-II、多目标遗传算法、多目标粒子群算法、非支配邻域免疫算法等. 其中NSGA-II是基于帕雷托(Pareto)最优解的多目标优化算法. 由于该算法具有计算复杂度低、寻优速度快、计算精度高等优点,被广泛应用于多目标优化问题中. 将NSGA-II算法应用于可调旋转式流体阻尼器结构参数的多目标优化设计,其最优解集可为设计人员提供多种结构参数的选择[11].
目前,大多数阻尼器的优化目标主要是力学性能,极少考虑阻尼器因关键公差设计而出现的制造成本问题[12]. 为了以最小几何公差制造成本实现直升机操纵系统的阻尼减振,本文开发新型的可调旋转式流体阻尼器,对其关键的几何参数进行多目标优化. 通过阻尼器样机的力学性能测试,验证了阻尼器参数多目标优化结果的正确性.
1. 阻尼器结构及工作原理
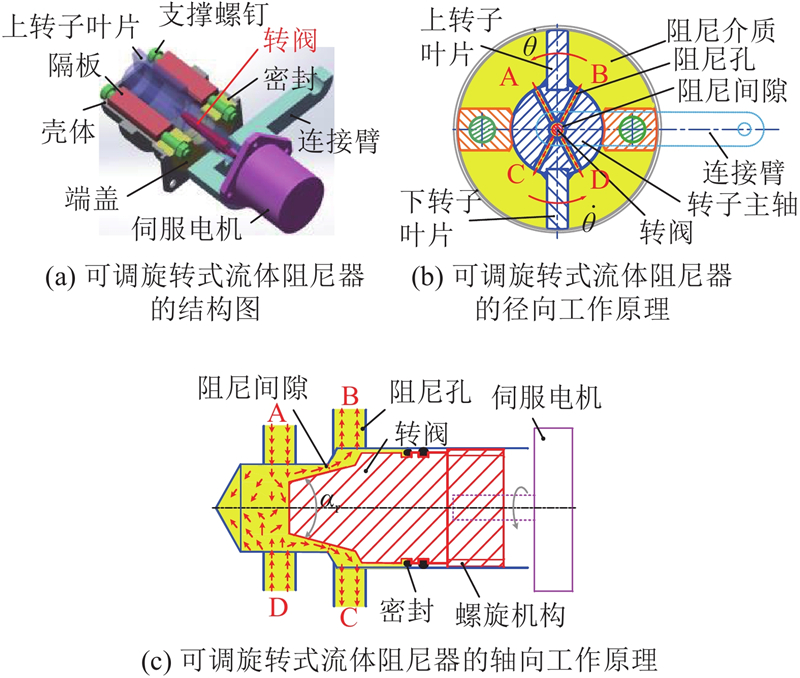
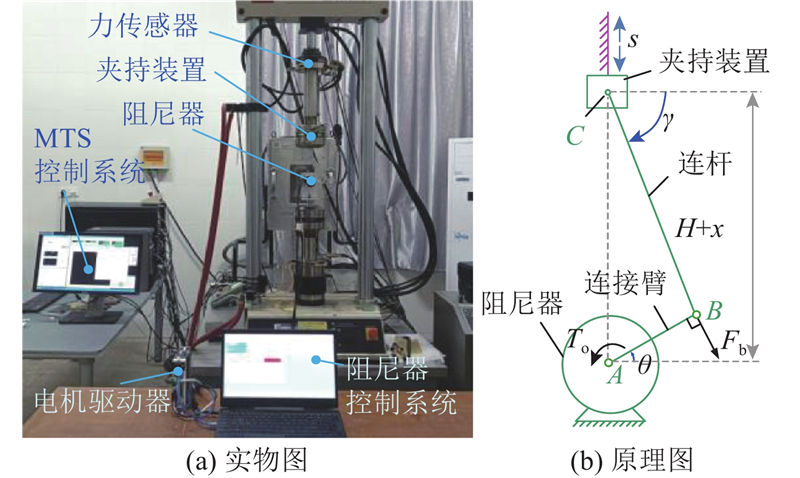
开发具有重量轻、阻尼连续可调、吸能效率高等优点的新型可调旋转式流体阻尼器,并将该阻尼器安装在直升机操纵系统的纵向、横向及总距操纵线系中,起到吸收振动和限制操纵速度的作用. 该阻尼器主要由壳体、转子叶片、隔板、转阀、支撑螺钉、端盖、连接臂、伺服电机等组成,如图1(a)所示. 壳体、隔板和转子叶片将阻尼器内腔划分为4个腔室(A、B、C、D腔). 在可调旋转式流体阻尼器的工作腔内填充黏温特性较好的液压油,作为阻尼介质. 为了减少阻尼介质的泄露,端盖及转阀上开设有密封装置. 阻尼器的径向工作原理如图1(b)所示,当转子叶片逆时针旋转时,左上腔(A腔)和右下腔(D腔)阻尼介质受到叶片挤压,成为高压腔. 右上腔(B腔)和左下腔(C腔)被转子叶片拉伸,成为低压腔. 油液自A、D腔通过阻尼孔流向转子轴心,在轴心处形成绕转阀的环流,然后分流流向B、C腔. 反之,则A、D腔形成低压腔,B、C腔变为高压腔,油液自B、C腔流向A、D腔. 阻尼器的轴向工作原理如图1(c)所示(图中的A、B、C、D与图1(b)对应),阻尼器通过伺服电机带动转子主轴中心孔处的转阀(转阀末端为锥形结构)旋转,从而改变阻尼间隙的大小,以便调节阻尼介质的流动速度及方向,获得理想的目标阻尼. 主体结构的振动带动连接臂上下摆动和转子叶片正、逆时针转动,使得阻尼介质在4个腔室间交替流动,不断地产生阻尼力矩,达到衰减操纵系统主体结构振动的目的.
图 1
2. 阻尼器的准静态模型
图 2
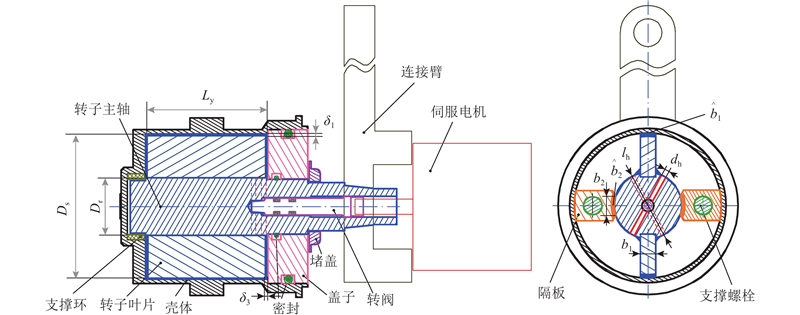
图 2 可调旋转式流体阻尼器的结构参数图
Fig.2 Structural parameter diagram of adjustable rotary fluid damper
式中:∆p为转子叶片两侧的压强差;Tf为转子主轴与密封件相对运动时的库仑摩擦力矩[14],
其中,fc为密封件压缩而产生的轴周单位长度的摩擦力, fc = 87.5 N/mm;Lo为密封件摩擦面的轴周长度;fh为流体压力作用在密封件单位投影面积上产生的摩擦力,fh ≈ 0;Ar为密封投影面积.
当阻尼器的结构参数不变时,Td与∆p近似呈线性关系,而∆p可以通过阻尼器内流场的体积流量计算获得. 工作腔内阻尼介质的总流量等于单位时间内转子叶片所扫过的体积. 阻尼器内流场的总体积流量[15]如下:
式中:ω为阻尼器旋转的角速度.
1)转子叶片上常通阻尼孔的体积流量. 当转阀可调间隙大于转子叶片上阻尼孔过流面积时,阻尼器具有最小的阻尼力矩. 阻尼孔的直径与流通长度之比lh/dh > 4,因此可以采用细长小孔的节流方程计算,阻尼孔的体积流量 [16]为
2)转子叶片与壳体径向之间的缝隙. 转子叶片与壳体内径轴向之间缝隙的体积流量为
3)隔板与转子主轴之间缝隙的体积流量. 基于平行平板缝隙流量公式可知,隔板与转子主轴之间缝隙的体积流量为
4)转子叶片轴向两端面与壳体之间缝隙的体积流量. 基于平行平板缝隙流量公式可知,转子叶片端面与壳体之间缝隙的体积流量为
阻尼器内流场的总体积流量等于各个缝隙体积流量之和,由流体过流量守恒方程可得
式中:qVr为转阀间隙的体积流量. 将式(3)~(7)代入式(8),可得不同状态下的∆p.
将∆p代入式(1),可得阻尼器不同状态下的输出阻尼力矩Td.
当转阀处于全闭合时,此时流过转阀处的体积流量为0,可得转阀全闭时的内流场压强∆pc为
此时阻尼器内流场压强最大,相应的阻尼输出力矩最大,将∆pc代入式(1),可得转阀全闭时的阻尼器输出力矩:
当转阀处于全开时,此时流过转阀处的体积流量为阻尼孔的总体积流量,基于式(2)~(8),可得转阀全开时的内流场压强∆po为
将∆po代入式(1),可得转阀全开时的阻尼器输出力矩:
此时,阻尼器的输出力矩最小.
3. 响应面及灵敏度分析
可调旋转式流体阻尼器的力学特性主要包括最大阻尼力矩Tdc(转阀闭合状态下的出力)及阻尼力矩可调范围
表 1 可调旋转式流体阻尼器的结构参数初值
Tab.1
| 参数 | 初始值 |
| Ds/mm | 46 |
| Dr/mm | 22 |
| Ly/mm | 38 |
| μ /(kg·m−1·s−1) | 1.17×10−2 |
| b1/mm | 5 |
| b2/mm | 6 |
| dh/mm | 1.5 |
| δ1/mm | 初始值0.03 公差(0.01~0.03) |
| δ2/mm | 初始值0.03 公差(0.01~0.03) |
| δ3/mm | 初始值0.03 公差(0.01~0.03) |
| lr/mm | 3 |
| αr/(°) | 9 |
| ω/(rad·s−1) | 0.229 |
3.1. 最大阻尼力矩响应面及灵敏度分析
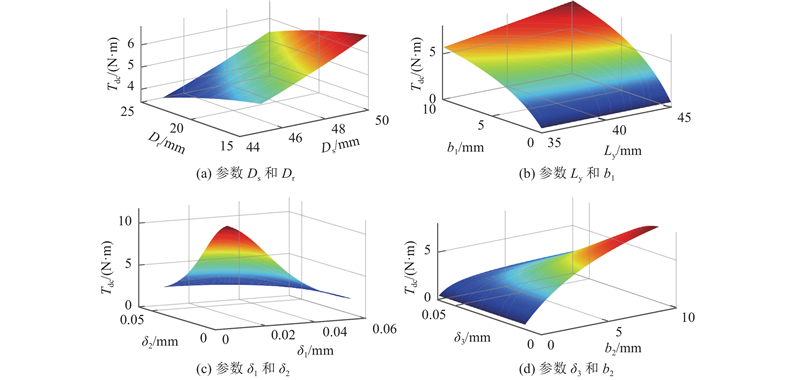
当可调旋转式流体阻尼器转阀处于闭合状态时,输出阻尼最大. 对于可控流体阻尼器而言,一般要求最大阻尼力矩尽可能大. 如图3(a)~(d)所示为转阀闭合状态下阻尼器力矩随各结构参数变化的响应图. 随着Ds、Ly、b1、b2的增加,阻尼器的最大输出阻尼力矩逐渐增大. 随着Dr、δ1、δ2、δ3的增加,阻尼器最大输出阻尼力矩逐渐减小. 其中Ds、δ1、δ2、δ3的变化最明显,说明其尺寸变化对阻尼器最大力矩的影响较大.
图 3
图 3 转阀全闭时结构参数对阻尼力矩的影响
Fig.3 Influence of structural parameters on damping torque when rotary valve is fully closed
式中:f(z)为灵敏度分析的目标函数,zi为结构参数z在i点的值,
式中:Sz表示设计变量z在区间[zimin, zimax]上的灵敏度,N为变化参数数据采样点的总个数. 为了便于对比分析,各个模型参数灵敏度所占百分比SPzj[18]可以表示为
式中:Szj为第j个参数的灵敏度,n为参数的总个数.
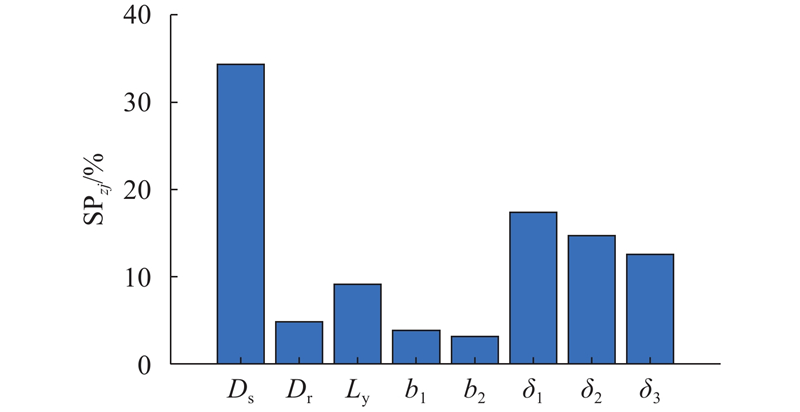
各结构参数的灵敏度百分比分析结果如图4所示,Ds的灵敏度百分比为34.35%,占比最高,与图3所示的结果对应. 增加Ds,阻尼器最大出力将显著提高. 尽管Ds、Ly对阻尼器最大出力的影响较大,Ds、Ly的增加将导致阻尼器体积及质量的增加,这对于低质量、小体积零部件要求较高的直升机来说具有极大的局限性. 阻尼器结构优化时,需要对Ds、Ly的最大值加以限定. δ1、δ2、δ3的灵敏度百分比分别为17.41%、14.70%、12.55%,其灵敏度百分比较高,表明调整δ1、δ2、δ3将快速改变阻尼器的最大阻尼力矩. 改变各个间隙尺寸δ1、δ2、δ3,基本不增加阻尼器的质量. 当优化可调旋转式流体阻尼器最大阻尼力矩时,需要重点考虑缝隙尺寸δ1、δ2、δ3. b1、b2的灵敏度百分比分别为3.83%、3.17%,说明增加b1、b2仅能够小幅提高最大阻尼输出力矩,但这将导致阻尼器的可动行程减小. 可动行程对阻尼器非常重要,直接关系着系统的振动幅值.
图 4
图 4 转阀全闭时的结构参数灵敏度分析
Fig.4 Sensitivity analysis of structural parameters when rotary valve is fully closed
3.2. 阻尼力矩可调倍数响应面及灵敏度分析
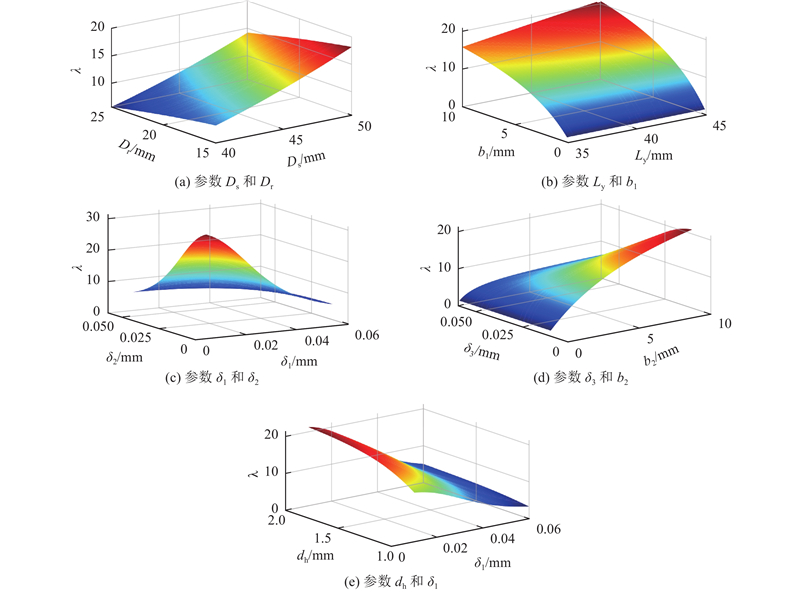
可调旋转式流体阻尼器可调倍数为转阀闭合状态与全开状态下阻尼力矩的比值,一般要求可调倍数尽可能大. 如图5(a)~(e)所示为阻尼器力矩可调倍数随各结构参数变化的响应面图. 随着b1、b2、dh的增加,阻尼器最大输出阻尼力矩逐渐增加. 随着Ds、Dr、Ly、δ1、δ2、δ3的增加,阻尼器力矩可调倍数逐渐减小.
图 5
图 5 结构参数对阻尼力矩可调范围的影响
Fig.5 Influence of structural parameters on adjustable range of damping moment
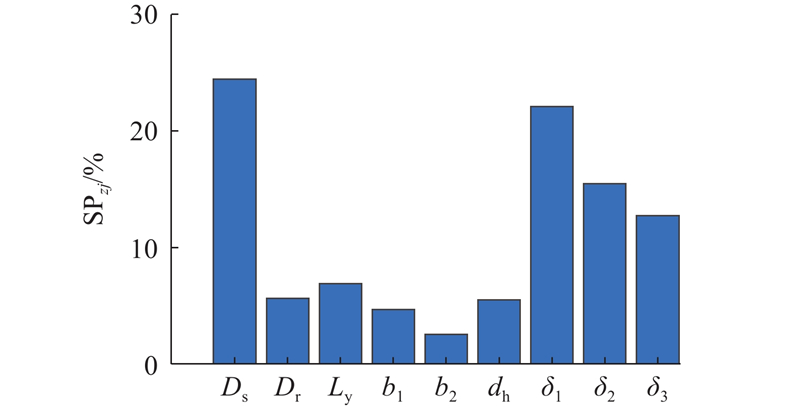
各参数对阻尼力矩可调范围的灵敏度百分比分析如图6所示,其中Ds灵敏度百分比为24.43%,占比最高,说明在优化阻尼力矩可调倍数时需要重点关注Ds. δ1、δ2、δ3的灵敏度百分比分别为22.10%、15.49%、12.75%,占比也较高,说明改变这些结构参数,能够快速改变阻尼器力矩的可调范围. dh、Dr、Ly、b1、b2的灵敏度百分比分别为5.50%、5.64%、6.89%、4.67%、2.53%,总体占比较低,对阻尼器力矩可调范围的影响不明显.
图 6
图 6 结构参数对阻尼力矩可调范围影响的灵敏度分析
Fig.6 Sensitivity analysis of influence of structural parameters on adjustable range of damping moment
4. 阻尼器结构参数的多目标优化
4.1. 设计需求
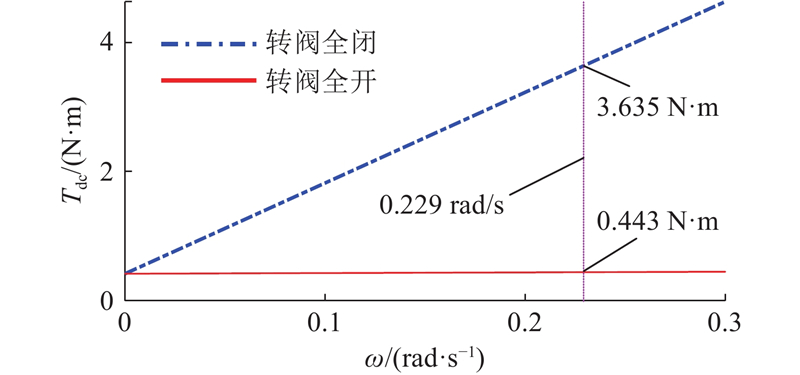
所设计的可调旋转式流体阻尼器主要用于直升机操纵系统的减振控制. 在实际的应用环境中,直升操纵系统的1阶共振频率约为3 Hz. 根据实际工程的要求可知,当激励幅值为1 mm、频率为3 Hz(相应的可调旋转式流体阻尼器角速度幅值为0.229 rad/s)的正弦信号时,需要至少3.5 N·m的阻尼力矩才能抑制共振区域的振动. 在阻尼器转动角速度为0.229 rad/s的条件下,旋转式流体阻尼器的最大阻尼力矩需要大于3.5 N·m. 当操纵系统处于非共振区时,阻尼力矩越小,系统的振动响应越小,因此阻尼力矩可调倍数越大,表明阻尼器对直升机操纵系统在不同振动工况下的适应能力越强,相应的控制性能越好,可调倍数至少满足6倍以上的设计要求. 在满足最大阻尼力矩、可调倍数的前提下,阻尼器关键配合公差制造成本越小越好.
4.2. 优化目标
阻尼器的主要优化目标包括3个:最大阻尼力矩、阻尼力矩可调倍数、公差制造成本.
1)最大阻尼力矩Tdc. Tdc尽可能取大值,即转阀闭合状态下的阻尼力矩取最大值,则目标函数f1可以表示为
2)阻尼力矩可调倍数λ. λ应尽可能大,则目标函数f2可以表示为
3)关键配合公差制造成本. 阻尼器内流场的配合间隙对阻尼器性能的影响至关重要. 若活动配合间隙依靠传统的橡胶类材料进行密封,一旦密封圈失效,则阻尼器无法提供应有的阻尼力,这将直接危害直升机的飞行安全. 对于安全性要求较高的直升机操纵系统阻尼器来说,使用阻尼器金属零件间配合间隙进行内流场密封是最安全、可靠的,但给加工制造带来了极大的挑战. 由于阻尼器内流场各个配合零件间不允许出现固体结构件间(固体-固体间)的摩擦,否则将极大影响阻尼器的最小阻尼出力,一般要求阻尼器内活动零件间的最小配合间隙为0.01 mm,而最大配合公差需要满足阻尼器的最大阻尼出力及阻尼可调范围的要求. 由于航空零部件对于结构尺寸及质量具有较高的要求,该配合公差的精度要求较高,需要进行多次修配才能达到理想的阻尼出力效果. 阻尼器内流场的配合公差范围设计得越小,则修配及测试的次数越多,这将极大地延长阻尼器的制造周期. 阻尼器零部件的合格率下降,导致加工成本相应提高. 在阻尼器设计阶段,对可调旋转式流体阻尼器内流场各配合零部件间的公差进行综合考虑. 在满足阻尼器性能要求的前提下,尽可能地增大内流场各配合尺寸的公差(包括δ1、δ2、δ3),实现并行公差的优化设计,可以有效地解决配合公差带来的问题. 采用公差评价系数ηt,评估各设计变量的公差水平[19-20]:
式中:k为设计公差变量的个数;∆xi、xiC分别为第i个设计变量的设计公差和基本尺寸;p理论上可以取任意正整数,在实际应用中p可取1或无穷大. 当p = 1时,ηt为设计变量的平均公差;当p取无穷大时,ηt为各设计变量的最大公差. 为了简化计算,取p = 1. 从式(18)可以看出,ηt越大,说明阻尼器允许的变量设计公差越大,相应的制造成本越小. 定义阻尼器的公差制造成本目标函数为
对于平板间的缝隙,可以将其量化为类似于圆柱面配合的形式. 由于平板类的间隙配合比圆柱面的间隙配合容易,构建阻尼器加工成本函数为
式中:δ1U为转子叶片-壳体径向缝隙配合尺寸的上偏差,δ1L为转子叶片-壳体径向配合缝隙尺寸的下偏差,δ2U为转子叶片与隔板径向缝隙配合尺寸的上偏差,δ2L为转子叶片与隔板径向缝隙配合尺寸的下偏差,δ3U为转子叶片端面与壳体轴向缝隙尺寸的上偏差,δ3L为转子叶片端面与壳体轴向缝隙尺寸的下偏差. 综合目标函数可以表示为
4.3. 约束条件
b1、b2直接影响阻尼器的转动角度,且这2个参数对最大阻尼力矩、可调范围的灵敏度影响均较小,因此设置这2个参数为表1中的初值. 鉴于直升机操纵系统的减振特性需求,μ不作为优化对象,取初始设计值. 基于阻尼器的实际工况要求,当阻尼器角速度为0.229 rad/s时,阻尼器最大阻尼力矩须满足
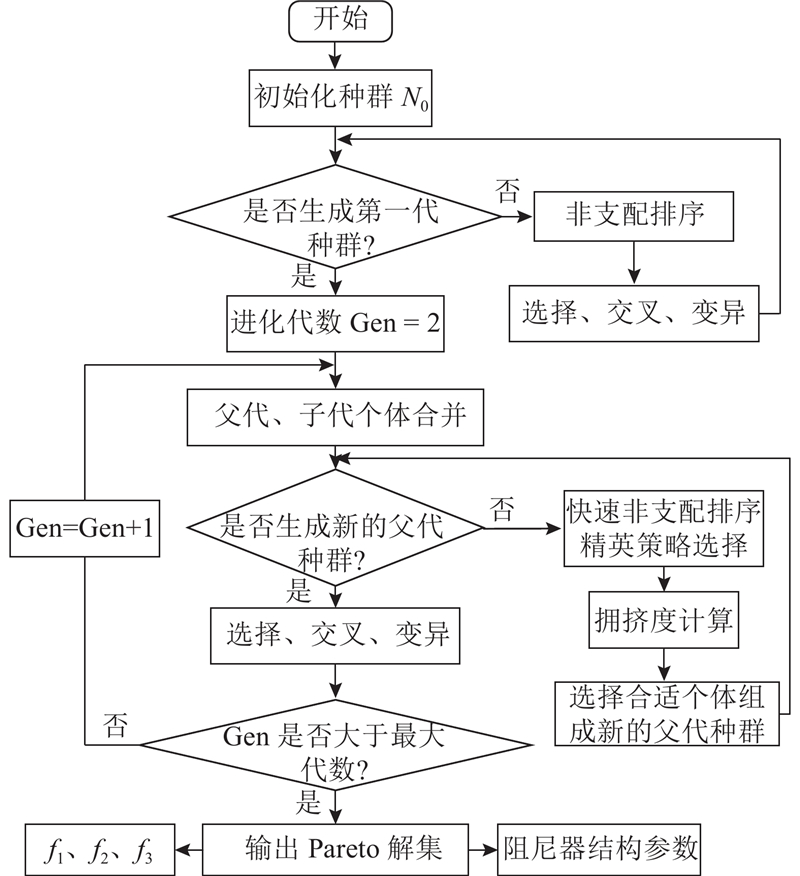
4.4. 基于NSGA-II算法的多目标优化设计
由于可调旋转式流体阻尼器待优化的目标函数最大阻尼力力矩f1、可调范围f2、阻尼器配合公差成本f3之间是相互矛盾的,其中某一个子目标函数值的进一步减少都可能会使另外一个或几个子目标函数值升高. 在3个子目标函数之间进行折中处理,根据具体的限制条件选取综合性能较优的解. 多目标优化问题求得的解不是唯一的,而是一组由众多Pareto解组成的非劣解集.
图 7
图 8
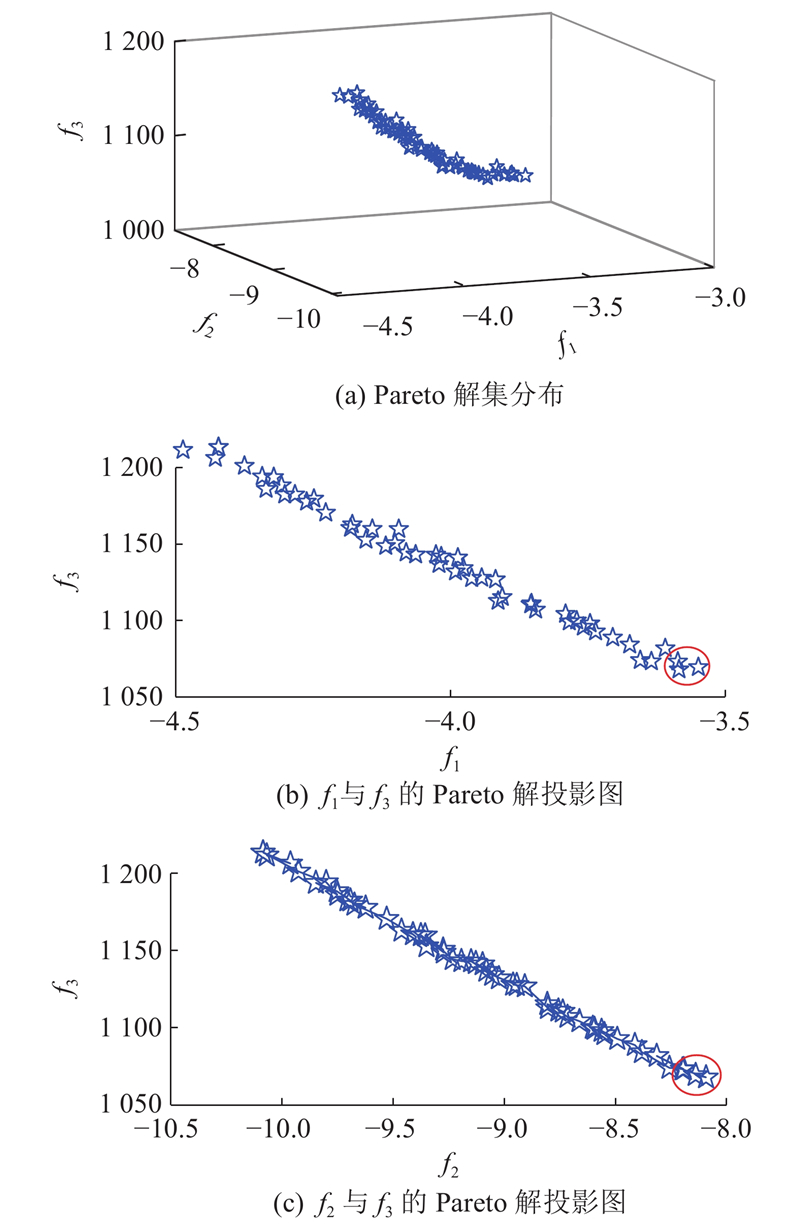
图 8 Pareto解集的分布及投影图
Fig.8 Distribution and projection graph of Pareto solution set
结合直升机操纵系统减振控制的实际工况,要求可调旋转式流体阻尼器转阀闭合状态下的阻尼力矩不能小于3.5 N·m,需要从Pareto解集中筛除f1 >−3.5的解,将剩余的Pareto解集分别投影到( f1, f3)平面和(f2, f3)平面内,可得非劣解子集的投影,如图8(b)、(c)所示. f1与f3之间近似为线性关系,随着f1的减小,f3总体上呈增大的趋势,说明优化后的阻尼器力矩与阻尼器公差成本存在一定的负相关性. 随着f2的减小,f3总体上呈增大的趋势(除个别非劣解外),说明优化的阻尼器力矩与阻尼器公差成本之间存在一定的负相关性.
表 2 选取的Pareto解
Tab.2
| 序号 | f1 | f2 | f3 |
| 1 | −3.549 | −8.139 | 1069.473 |
| 2 | −3.584 | −8.093 | 1067.954 |
| 3 | −3.586 | −8.198 | 1073.108 |
| 修正后 | −3.635 | −8.205 | 1067.954 |
表 3 选取的Pareto解的结构参数值
Tab.3
| mm | |||||||
| 序号 | δ1U | δ2U | δ3U | dh | Ds | Dr | Ly |
| 1 | 0.042 | 0.040 | 0.046 | 1.981 | 48.86 | 20.13 | 38.97 |
| 2 | 0.042 | 0.039 | 0.047 | 1.995 | 48.77 | 20.07 | 38.89 |
| 3 | 0.041 | 0.040 | 0.047 | 1.979 | 48.63 | 20.20 | 39.09 |
| 修正后 | 0.042 | 0.039 | 0.047 | 2 | 49 | 20 | 39 |
经过多目标优化后,阻尼器的理论最大阻尼力矩为3.635 N·m (>3.5 N·m),阻尼器的理论可调倍数为8.205(>6)倍,满足阻尼器力学性能的设计要求. 阻尼器的公差制造成本为1 067.954,在Pareto解集的可行域中属于比较小的值(见图8(b)、(c)),表明阻尼器的关键公差设计在满足力学性能要求的前提下达到最优解.
图 9
图 10
5. 力学性能试验研究
5.1. 测试装置与测试方法
为了验证优化后半主动旋转式流体阻尼器的最大阻尼力矩、可调倍数是否满足要求,基于阻尼器优化后的结构参数制作阻尼器样机,如图11所示. 该样机主要由阻尼器本体、连接臂、伺服电机、支座等组成.
图 11
图 12
当滑块的初始位置为水平位置时,θ = 0,滑块质心到A点的垂直距离H = 114.89 mm. 当滑块位移为x时(x为位移传感器测得的位移),曲柄滑块机构的运动学公式可以表示为
式中:LAB为连接臂AB的长度,LAB = 80 mm;LBC为连杆BC的长度,LBC = 140 mm.
利用MATLAB可以解得不同时刻的θ、γ. 激振力F在A点施加的外力矩为
式中:F为连杆LBC传给减振器拉臂的激振力.
5.2. 试验结果及分析
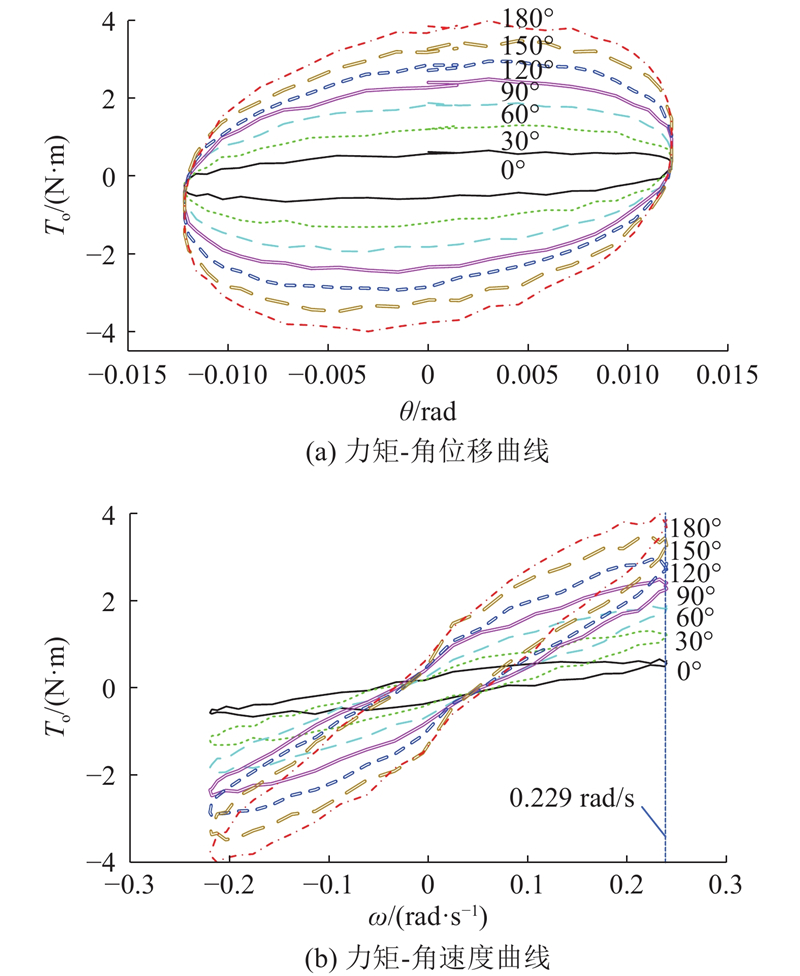
采用振幅为1 mm、频率为3 Hz的正弦信号作为激励. 伺服电机的角位移为0°、30°、60°、90°、120°、150°、180°,其中0°为转阀全开时的角度,180°为转阀全闭时的角度. 不同电机角位移下的动态响应测试结果如图13所示. 从图13(a)可以看出,阻尼器最大阻尼力矩随着电机角位移的增加而逐渐增大,这是因为转阀处节流间隙的减小导致阻尼器内流场压强增大,从而使阻尼力矩变大. 通过对实验数据的分析可知,0°时的最大阻尼力矩为0.617 N·m,180°时的最大阻尼力矩为3.997 N·m,由此可以计算得到最大阻尼力矩可调倍数为6.478倍,满足设计要求. 从图13(b)可知,阻尼器力矩-角速度曲线存在一定的非线性和滞回特性,这主要是因为阻尼介质的剪切稀化特性和液压油中气体的可压缩性造成的. 当阻尼器的角速度为0.229 rad/s时,0°时的阻尼力矩为0.561 N·m,180°时的阻尼力矩为3.855 N·m,由此可以计算得到角速度为0.229 rad/s时的可调倍数为6.872倍. 通过以上分析可知,阻尼器的力学性能均满足设计需求.
图 13
本文所使用的优化方法突破了传统阻尼器优化设计仅关注阻尼器最大出力和可调范围的局限,为阻尼器在满足力学性能要求的前提下降低制造成本提供了设计方法.
6. 结 论
(1)针对传统直升机操纵系统被动阻尼器减振效果差的缺点,本文提出新型的可调旋转式流体阻尼器. 该阻尼器通过伺服电机带动转阀实时调节阻尼器出力,实现直升机操纵系统的阻尼减振控制.
(2)基于质量守恒定律建立阻尼器的准静态模型,分析阻尼器结构参数对最大阻尼力矩、可调倍数的影响规律. 其中,壳体内径对最大阻尼力矩和可调倍数的影响均较大,灵敏度占比分别为34.35%、24.43%.
(3)为了协调阻尼器最大阻尼出力、动态可调范围及阻尼器公差制造成本之间的关系,建立阻尼器的优化目标和约束条件. 运用NSGA-II算法对阻尼器进行多目标优化设计,确定阻尼器的最优设计参数.
(4)基于优化后的设计参数,制作阻尼器样机,开展力学性能的测试. 当角速度为0.229 rad/s时,阻尼器最大力矩为3.855 N·m,可调倍数为6.872,验证了多目标优化结果满足设计要求.
参考文献
直升机操纵杆振动特性测量与分析
[J].
Measurement and analysis of helicopter control stick vibration characteristics
[J].
Modeling and experimental verification of a semi-rotary fluid damper based on an improved Kelvin model
[J].DOI:10.1007/s13369-021-05414-z [本文引用: 1]
A design and modelling review of rotary magnetorheological damper
[J].DOI:10.1016/j.matdes.2013.04.042 [本文引用: 1]
Modeling and control of helicopter flight control system with a controllable semi-rotary fluid viscous damper
[J].DOI:10.1016/j.aej.2022.06.035 [本文引用: 2]
Hydrodynamic optimized vibration damper
[J].DOI:10.1016/j.jsv.2018.10.008 [本文引用: 1]
第Ⅱ类机器人混流装配线的平衡与排序联合决策
[J].
Joint decision-making of balancing and sequencing for type-Ⅱ robotic mixed-model assembly line
[J].
Multi-objective optimal design and performance of magnetorheological damper
[J].DOI:10.1002/mawe.202000175 [本文引用: 1]
Multi-objective system optimization method and experimental validation of a centralized squeeze film damper using a cell mapping method considering dynamic constraints
[J].DOI:10.1080/0305215X.2020.1759577 [本文引用: 1]
Uncertainty analysis and optimization of automotive driveline torsional vibration with a driveline and rear axle coupled model
[J].DOI:10.1080/0305215X.2017.1421952 [本文引用: 1]
A comprehensive optimal design method for magnetorheological dampers utilized in DMU power package
[J].
Optimal design of magnetorheological fluid-based dampers for front-loaded washing machines
[J].DOI:10.1177/0954406213485908 [本文引用: 1]
履带车辆肘内式半主动油气悬挂性能研究
[J].
Study on the performance of semi-active in-arm hydro-pneumatic suspension for tracked vehicle
[J].
节流方式对扭转减振器的影响
[J].
Effect of the throttle on the torsion damp shock absorber
[J].
A review of techniques for parameter sensitivity analysis of environmental models
[J].DOI:10.1007/BF00547132 [本文引用: 1]
Parameter sensitivity analysis and optimum model of the magnetorheological damper's Bouc-Wen model
[J].
基于区间分析的汽车平顺性优化
[J].
Vehicle ride comfort optimization based on interval analysis
[J].
考虑公差的扭转动力吸振器不确定性优化设计
[J].DOI:10.3969/j.issn.1004-132X.2018.14.002 [本文引用: 1]
Uncertain optimization of torsional vibration damper considering tolerant design
[J].DOI:10.3969/j.issn.1004-132X.2018.14.002 [本文引用: 1]
Multi-objective optimization design for a magnetorheological damper
[J].DOI:10.1177/1045389X211006907 [本文引用: 1]
Design of bypass rotary vane magnetorheological damper for prosthetic knee application
[J].DOI:10.1177/1045389X20942577 [本文引用: 1]
基于遗传算法的汽车磁流变减振器多目标优化
[J].DOI:10.3969/j.issn.1000-680X.2016.07.013 [本文引用: 1]
Multi-objective optimization of vehicle MR damper based on genetic algorithm
[J].DOI:10.3969/j.issn.1000-680X.2016.07.013 [本文引用: 1]
面向高速的磁流变缓冲器多目标优化设计及性能研究
[J].DOI:10.3901/JME.2014.05.127 [本文引用: 1]
Multi-objective optimization and performance research of magneto-rheological absorber under high speed
[J].DOI:10.3901/JME.2014.05.127 [本文引用: 1]