近年来,环境振动问题日益突出[1-2],利用桩-土周期结构设计的地基隔振屏障得到了成功应用[3-4]. 早期学者们沿用传统的周期结构理论,将土体视为理想线弹性材料,对单层[5]或多层[6]土体排桩周期结构的禁振带隙和振动衰减规律进行研究. 最近几年,Shi等[7-10]借助COMSOL有限元软件中的多孔弹性波模块,研究两相饱和土中周期性排桩的带隙和振动传输规律. 简单的散射型声子晶体产生的带隙位于高频段,很难覆盖实际中地震和交通荷载引起的低频振动. Pu等[11-12]通过填充软材料,研究具有局域共振性质的套管桩隔振结构. 陈晓斌等[13]利用有限元软件,模拟更复杂的四组元开孔套管桩周期结构的隔振性能. 实际土体由于松弛和蠕变效应,应力作用下土颗粒的重新排列和骨架错动具有明显的时间效应[14-15]. 蔡袁强等[16]基于Terzaghi一维固结理论,分析循环荷载作用下土体应力-应变在时间效应下的非线性渐变过程. 曾庆有等[17]采用Mesri蠕变模型考虑土体的流变性,计算黏弹性土中桩基的长期沉降. 艾志勇等[18-19]采用有限元-边界元耦合的方法,研究层状黏弹性地基与桩以及梁共同作用的时变行为. 何利军等[20]提出黏弹性土的蠕变模型,对土体应力-应变的时间效应进行精确分析. 汪磊等[21]研究半透水边界下分数阶黏弹性饱和土的固结时效行为. 吴奎等[22]研究流变性岩体中深埋隧道的力学响应问题. 张婉洁等[23]基于分数阶Bingham模型的线性刚度系统,研究磁流变液阻尼器的时滞问题. 上述研究表明,流变性土的应力-应变对于时间具有依赖性.
为了探究流变性土排桩周期结构的带隙特征以及土体流变性的影响规律,本文采用时间依赖性模量描述土体流变效应,构建桩-土周期结构的连续介质动力学模型. 采用多重散射法推导周期系统的体波弥散方程,通过搜索布里渊域得出周期性排桩地基的频率域弥散曲线,利用模型退化验证算法的正确性. 分析流变性土排桩地基的禁振带隙及核心参数的影响规律.
1. 分析模型
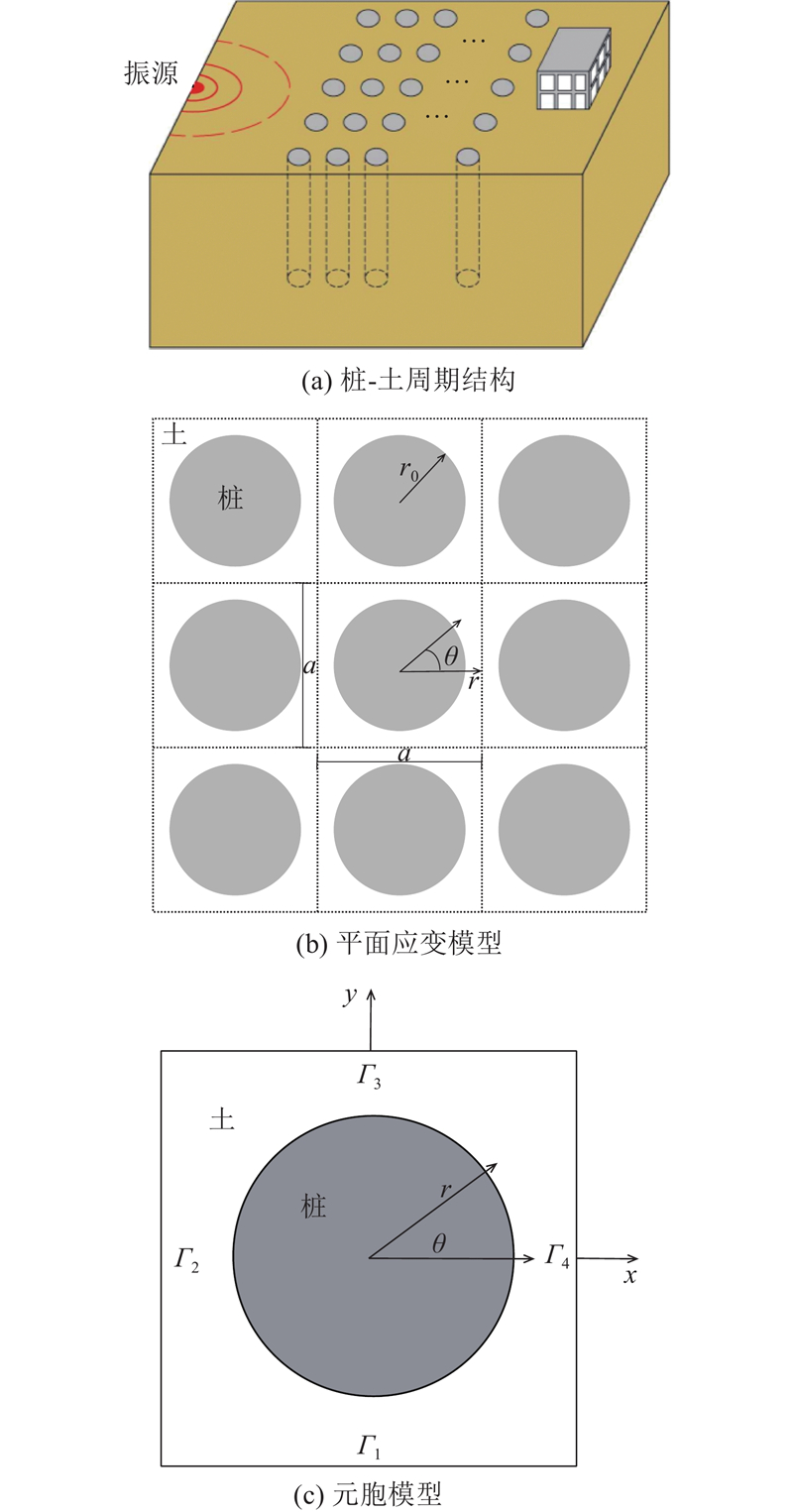
图 1
2. 土体流变性描述
采用具有时间依赖性的模量描述土体的流变效应,积分形式的本构方程[24]为
式中:σs、εs分别为土体的应力和应变,δij为Kronecker delta函数;ζs为体应变;λs = λs(t)、μs = μs(t)为Lamé常数,由于考虑土体模量的时间依赖性, λs、μs均为时间t的函数;τ为松弛时间.
根据Lamé常数的定义,可知
式中:vs为泊松比(本文中假定vs不随时间变化);E(t)为弹性模量,松弛函数形式[24]为
式中:E0、E∞分别为初始和最终稳定状态的弹性模量.
对式(3)引入时间t的Fourier变换,可以得到频率域的表达式:
式中:ω为角频率;i为虚数单位;
对式(1)进行时间t的Fourier变换,可以得到频率域的本构方程:
式中:λs(ω)、μs(ω)为频率域中对应的Lamé常数,表达式为
其中η为初始和最终状态的模量比,η = E∞/E0;λ0、μ0为初始Lamé常数,
根据黏性理论,可得滞回阻尼比为
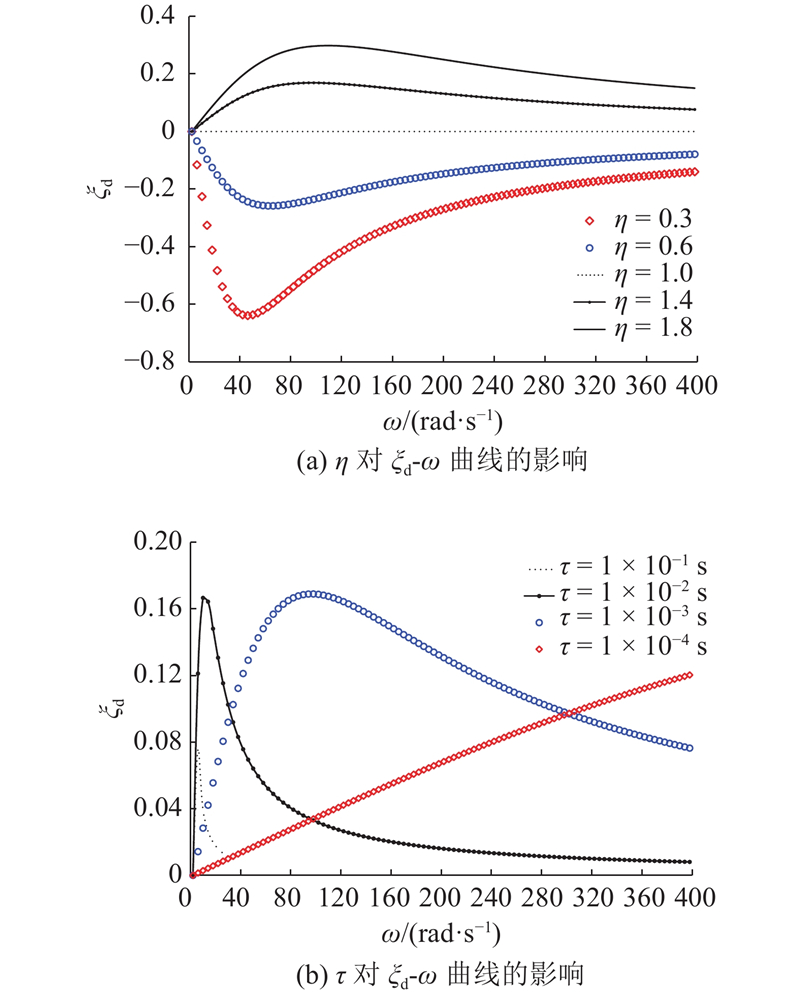
图 2
通过对式(8)求极值,可得阻尼比的峰值和峰值对应的频率:
从图2及式(9)可知,η决定阻尼比的幅值,τ决定阻尼比随频率的变化速率. 在实际工程中,土体受载后被压密,变形模量将增大(E∞ > E0),因此不会出现η < 1的情况,不再讨论该情况.
3. 波动方程求解
根据弹性波动理论可知,土体和桩基的频率域Navier波动方程为
式中:us、up、ρs、ρp分别为土体和桩基的位移矢量和密度;与流变性土体不同,桩基为均质弹性材料,其Lamé常数λp、μp为常数.
引入势函数
将式(12)代入式(10),可得
式中:kl1、kt1分别为土体中压缩波和剪切波的波数,kl1 = ω/cl1、kt1= ω/ct1,其中cl1、ct1为2种波的波速.
将式(12)代入本构方程(5),可得
引入势函数
式中:kl2、kt2分别为桩基中压缩波和剪切波的波数.
根据弹性波散射理论[25],将土体和桩体的势函数
式中:Am1、Am2、Bm1、Bm2、Cm1、Cm2为待定积分常数,通过桩-土界面条件确定;Jm、Ym分别为m阶第1类和第2类Bessel函数,其中m为整数.
将式(17)代入式(12)、(14)、(16),可得土体和桩基位移场及应力场的级数表达式:
式中:系数矩阵Fm、Gm、fm、gm、Dm、dm均为已知的二阶矩阵,具体表达式见附录.
根据桩-土界面处(r = r0)的位移和应力连续,得到界面条件如下:
将式(18)代入式(19),可得待定系数Am1、Am2与Bm1、Bm2的关系:
将式(20)代入式(18),可以将土体位移写为
式中:Pm、Qm为已知的二阶矩阵,表达式见附录.
为了推导桩-土周期结构的弥散方程,须将极坐标系中的土体位移转换到元胞系统的直角坐标系(x-y)中,转换关系如下:
式中:
将图1(c)中元胞4个边界上的法向位移表示为
式中:n= [nx, ny, −nx, −ny]为4个边界对应的单位法向量;系数矩阵Ω为8N×8N阶矩阵,矩阵元素由
式中:
根据Bloch–Floquet定理可知,周期结构中的所有场量Φ均满足如下周期条件:
式中:X为坐标矢量,X = [x, y];k为波矢,k = [kx, ky].
对元胞边界上的位移运用周期条件(25),可得
将式(26)代入式(23),可得桩-土系统的特征方程:
式中:Ω31、Ω32、Ω41、Ω42为Ω中的二维分块矩阵;
将式(27)进一步整理为标准方程形式:
式(28)为8N×8N阶矩阵方程,其中I为4N×4N阶单位矩阵;
利用非凡解条件,可得
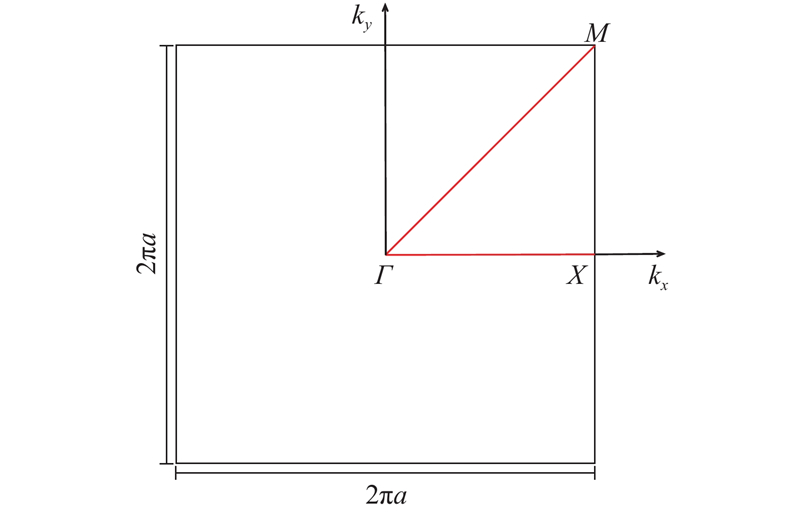
式(29)为桩-土周期结构的弥散方程,det表示取行列式. 对方程给定角频率ω,在第一不可约布里渊域Γ-X-M(见图3)中搜索满足方程的波矢kx、ky,可得周期系统中压缩波和剪切波的弥散曲线(频率-波数关系). 当搜索Γ-X边界时(0 ≤ kx ≤ π/a),方程中的指数项取
图 3
4. 算例分析
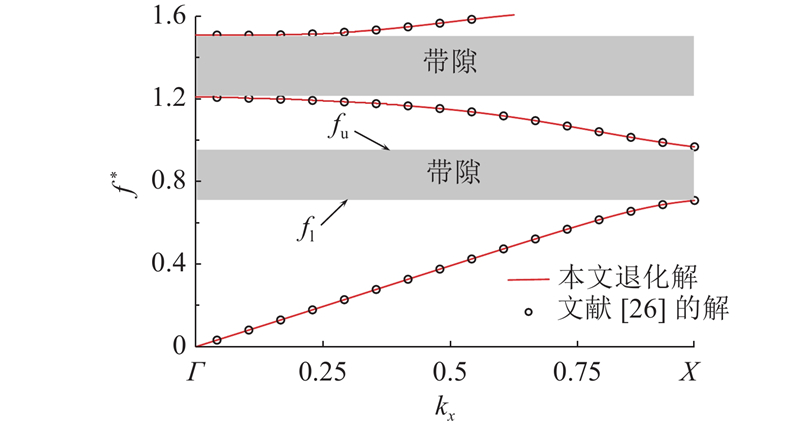
图 4
表 1 土和桩的计算参数表
Tab.1
| 参数 | 参数值 |
| ρs/(kg·m−3) | 1 900 |
| μ0/ MPa | 30 |
| vs | 0.25 |
| ρp/(kg·m−3) | 2 500 |
| λp/GPa | 8.3 |
| μp/GPa | 12.5 |
| r0/m | 0.65 |
| a/m | 2 |
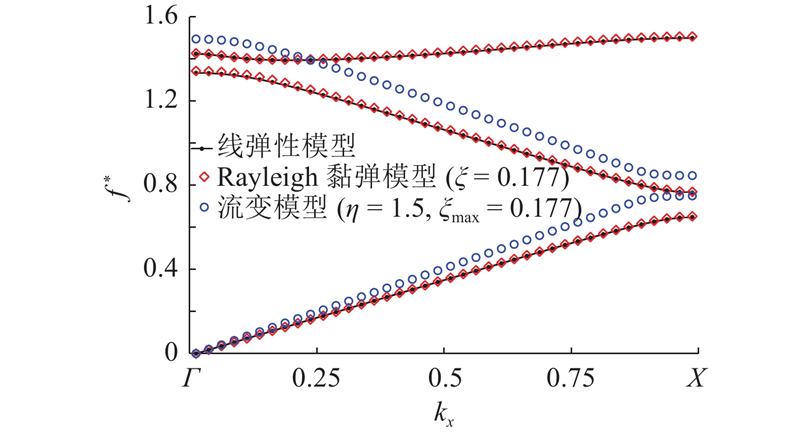
图 5
图 5 常阻尼模型与流变模型的带隙结果对比
Fig.5 Band gap results comparison between constant damping model and rheological model
表 2 不同阻尼比取值下的带隙结果
Tab.2
| η | (ξd)max | Rayleigh模型 | 流变模型(τ = 0.001 s) | |||
| [fl, fu] | fu− fl | [fl, fu] | fu− fl | |||
| 1 | 0 | [0.619, 0.730] | 0.111 | [0.619, 0.730] | 0.111 | |
| 1.2 | 0.083 | [0.620, 0.731] | 0.111 | [0.704, 0.781] | 0.077 | |
| 1.4 | 0.149 | [0.621, 0.732] | 0.111 | [0.719, 0.788] | 0.069 | |
| 2.0 | 0.283 | [0.626, 0.737] | 0.111 | [0.760, 0.809] | 0.049 | |
| 10 | 0.606 | [0.648, 0.759] | 0.111 | [0.915, 1.096] | 0.181 | |
| 100 | 0.697 | [0.657, 0.765] | 0.108 | [1.165, 1.608] | 0.443 | |
| 200 | 0.702 | [0.659, 0.766] | 0.107 | [1.383, 1.790] | 0.407 | |
图 6
图 7
图 8
5. 结 论
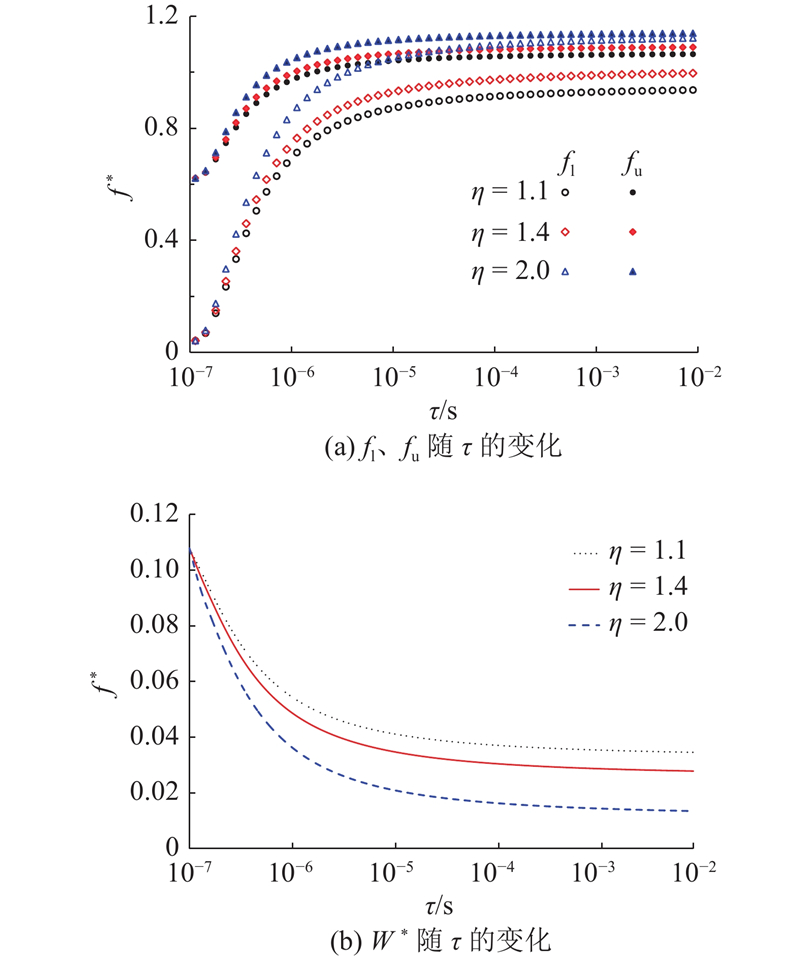
(1)流变性土的阻尼比随频率发生非单调性变化,始终态模量比决定阻尼比的幅值,而松弛时间决定阻尼比随频率的变化速率. 阻尼比的幅值随着模量比的增大而增大,松弛时间越大,阻尼比随频率的变化速率越大.
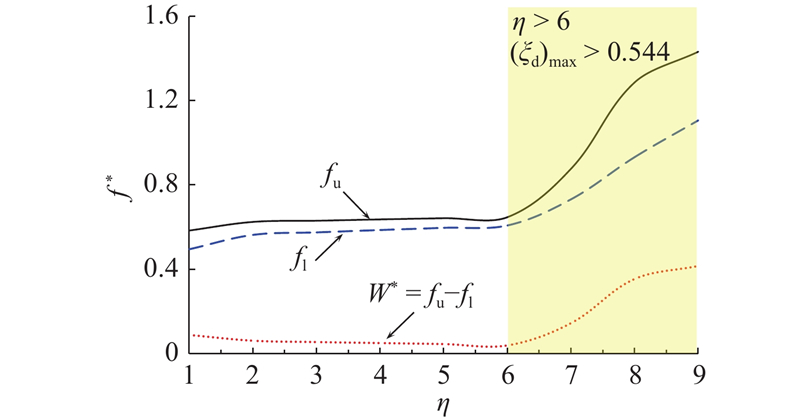
(2)土体流变性引起排桩地基的带隙位置上移,且带宽减小. 模量比和松弛时间越大,则带隙位置上移,带宽减小越明显. 松弛时间对带隙的影响程度显著大于模量比,这是土体流变性影响带隙的主要因素.
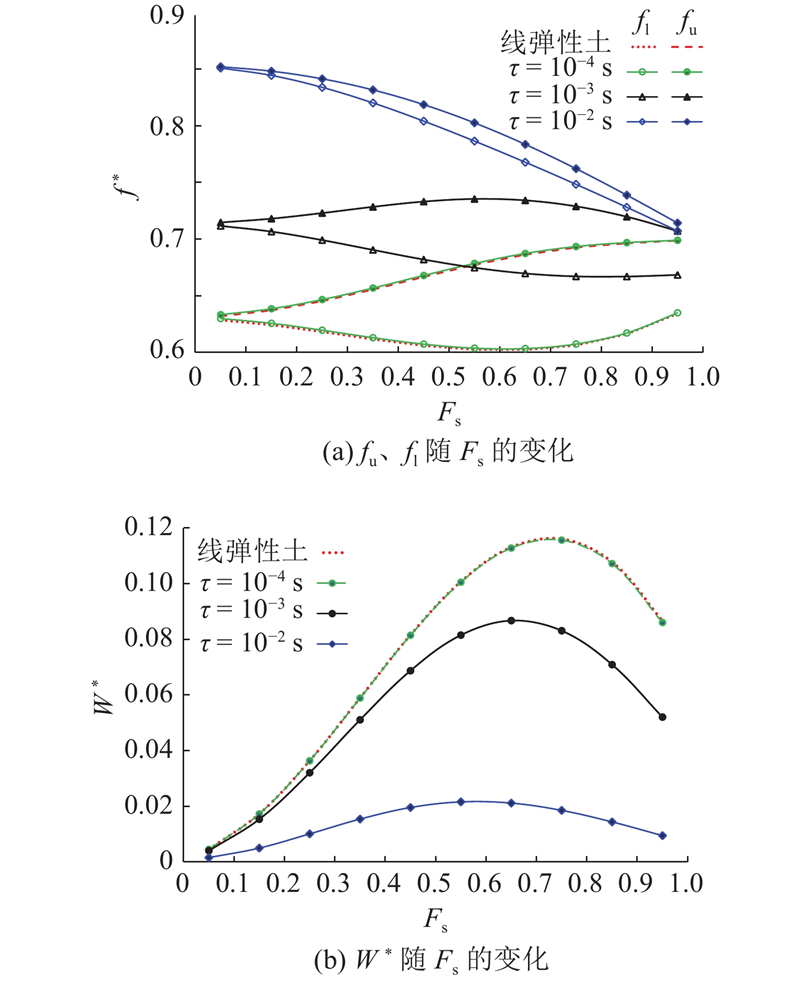
(3)流变性减弱了桩基填充率对带隙的影响,土体流变性越强,带隙随填充率的变化幅度越小.
(4)受土体流变性的影响,实际工程中排桩地基的带隙频率高于理论值,且带宽减小,减弱了排桩的隔振效果,消除桩周土的流变性将有利于排桩发挥隔振作用.
参考文献
Efficient mitigation of high-speed trains induced vibrations of railway embankments using expanded polystyrene blocks
[J].
汽车行驶诱发地表振动的解析研究
[J].
Analytical research on surface vibration induced by vehicle driving
[J].
Experimental study on attenuation zone of soil-periodic piles system
[J].DOI:10.1016/j.soildyn.2019.105738 [本文引用: 1]
Surface-wave attenuation by periodic pile barriers in layered soils
[J].
2D dynamic structure-soil-structure interaction for twin buildings in layered half-space II: incident SV-waves
[J].
Propagation attenuation of plane waves in saturated soil by pile barriers
[J].DOI:10.1061/(ASCE)GM.1943-5622.0000963 [本文引用: 2]
Vibration isolation of plane waves by periodic pipe pile barriers in saturated soil
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000938
基于周期理论和COMSOL PDE的排桩减振特性研究
[J].
Study on vibration reduction characteristics of piles based on period theory and COMSOL PDE
[J].
饱和土中周期性排桩隔离体波的性能研究
[J].DOI:10.13465/j.cnki.jvs.2020.24.025 [本文引用: 2]
Study on the performance of periodic piles to isolate body waves in saturated soil
[J].DOI:10.13465/j.cnki.jvs.2020.24.025 [本文引用: 2]
Feasibility of ambient vibration screening by periodic geo-foam-filled trenches
[J].
Vibration mitigation in saturated soil by periodic in-filled pipe pile barriers
[J].
周期性四组元局域共振桩带隙特征及隔振性能研究
[J].DOI:10.16285/j.rsm.2021.0727 [本文引用: 1]
Study on band gap characteristics and vibration isolation of local resonance pile with periodic four component
[J].DOI:10.16285/j.rsm.2021.0727 [本文引用: 1]
In situ and laboratory stress-strain relationships
[J].
Viscous behaviour of soft clay and inducing factors
[J].DOI:10.1007/s10706-012-9535-0 [本文引用: 1]
半透水边界的黏弹性土层在循环荷载下的一维固结
[J].DOI:10.3321/j.issn:1000-131X.2003.08.016 [本文引用: 1]
One-dimensional consolidation of viscoelastic soil layer with semi-permeable boundaries under cyclic loading
[J].DOI:10.3321/j.issn:1000-131X.2003.08.016 [本文引用: 1]
考虑应力应变时间效应的桩基长期沉降计算方法
[J].DOI:10.3969/j.issn.1000-7598.2005.08.019 [本文引用: 1]
Method for long-term settlement prediction of pile-foundation in consideration of time effect of stress-strain relationship
[J].DOI:10.3969/j.issn.1000-7598.2005.08.019 [本文引用: 1]
层状分数阶黏弹性饱和地基与梁共同作用的时效研究
[J].DOI:10.6052/0459-1879-20-447 [本文引用: 1]
Aging study on the interaction between layered fractional viscoelastic saturated foundation and beam
[J].DOI:10.6052/0459-1879-20-447 [本文引用: 1]
Time-dependent response of laterally loaded piles and pile groups embedded in transversely isotropic saturated viscoelastic soils
[J].
采用分数阶导数描述软黏土蠕变的模型
[J].DOI:10.16285/j.rsm.2011.s2.022 [本文引用: 1]
A description of creep model for soft soil with fractional derivative
[J].DOI:10.16285/j.rsm.2011.s2.022 [本文引用: 1]
半透水边界下分数阶黏弹性饱和土一维固结特性分析
[J].DOI:10.16285/j.rsm.2017.0659 [本文引用: 1]
Analysis of one-dimensional consolidation of fractional viscoelastic saturated soils with semi-permeable boundary
[J].DOI:10.16285/j.rsm.2017.0659 [本文引用: 1]
流变岩体中让压支护作用下隧道力学行为研究
[J].
Study on mechanical behavior of tunnel under the action of yielding support in rheological rock mass
[J].
含分数阶Bingham模型的阻尼减振系统时滞半主动控制
[J].DOI:10.6052/0459-1879-21-467 [本文引用: 1]
Time-delay semi-active control of damping and vibration reduction system with fractional Bingham model
[J].DOI:10.6052/0459-1879-21-467 [本文引用: 1]
Vibration reduction of plane waves using periodic in-filled pile barriers
[J].DOI:10.1061/(ASCE)GT.1943-5606.0001301 [本文引用: 3]