浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(6): 1251-1256 doi: 10.3785/j.issn.1008-973X.2023.06.021

航空航天技术

基于GRU的扑翼非定常气动特性快速预测

赵嘉墀,, 王天琪, 曾丽芳,, 邵雪明

1. 浙江大学工程师学院，浙江 杭州 310058

2. 浙江大学 航空航天学院，浙江 杭州 310058

Rapid prediction of unsteady aerodynamic characteristics of flapping wing based on GRU

ZHAO Jia-chi,, WANG Tian-qi, ZENG Li-fang,, SHAO Xue-ming

1. Polytechnic Institute, Zhejiang University, Hangzhou 310058, China

2. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310058, China

通讯作者: 曾丽芳，女，助理研究员. orcid.org/0000-0001-5378-1208. E-mail： lifang_zeng@zju.edu.cn

收稿日期: 2022-06-10  

基金资助: 国防基础科研计划资助项目（JCKY2019205A006）

Received: 2022-06-10  

Fund supported: 国防基础科研计划资助项目（JCKY2019205A006）

作者简介 About authors

赵嘉墀（1999—），男，硕士生，从事智能无人机研究.crcid.org/0000-0003-2404-3104.E-mail：jczhao@zju.edu.cn , E-mail：jczhao@zju.edu.cn

摘要

为了克服传统计算流体力学代理模型不能有效模拟流体力学高度非线性系统的困难，解决现有基于深度学习的代理模型难以有效处理时间顺序信息的问题，以扑翼飞行器的二维翼型为研究对象，基于门控循环单元（GRU）与多层感知机，建立扑翼非定常气动参数的快速预测模型，实现对扑翼扑动时高度非定常、非线性气动参数的实时预测. 使用计算流体力学方法获得扑翼二维翼型扑动时的气动参数，以该参数为样本训练预测模型. 将扑翼的扑动振幅、频率、摆动角度与运动时间输入预测模型，快速得到扑翼在对应扑动状态下的升力、阻力与力矩. 实验结果表明，所建立的预测模型精度高、计算速度快，能够实现对扑翼非定常气动参数变化的实时高精度预测.

关键词： 门控循环单元（GRU） ; 多层感知机 ; 扑翼 ; 气动参数预测 ; 深度学习 ; 计算流体力学

Abstract

Traditional computational fluid dynamics surrogate model cannot effectively simulate the highly nonlinear fluid, and existed deep learning-based surrogate models are difficult to deal with temporal sequence information effectively. Based on the gated recurrent units (GRU) and the multilayer perceptron, a two-dimensional airfoil of a flapping-wing aircraft was studied to establish a model for rapid predict unsteady aerodynamic parameters of the flapping-wing. The real-time prediction for the highly unsteady and nonlinear aerodynamic parameters of the flapping wing was realized. The computational fluid dynamics method was used to obtain the aerodynamic parameters of the flapping two-dimensional airfoil and the parameters were used as samples to train the prediction model. The flapping amplitude, the frequency, the swing angle and the motion time of the flapping wing were fed into the prediction model, and the lift, the drag and the moment in the relevant condition could be quickly output. Experimental results showed that the established prediction model has high accuracy and fast calculation speed. The prediction model could realize real-time high-precision prediction for unsteady aerodynamic parameters of flapping wings.

Keywords： gated recurrent units (GRU) ; multilayer perceptron ; flapping wing ; aerodynamic parameter prediction ; deep learning ; computational fluid dynamics

PDF (2600KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

赵嘉墀, 王天琪, 曾丽芳, 邵雪明. 基于GRU的扑翼非定常气动特性快速预测. 浙江大学学报(工学版)[J], 2023, 57(6): 1251-1256 doi:10.3785/j.issn.1008-973X.2023.06.021

ZHAO Jia-chi, WANG Tian-qi, ZENG Li-fang, SHAO Xue-ming. Rapid prediction of unsteady aerodynamic characteristics of flapping wing based on GRU. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(6): 1251-1256 doi:10.3785/j.issn.1008-973X.2023.06.021

仿生扑翼飞行器在扑动过程中产生的气动力具有强非定常、非线性特性，了解气动特性是进行扑翼优化设计与控制的基础，如何快速获得准确的气动特性，是扑翼飞行器的设计难点[1]. 计算流体力学（computational fluid dynamics，CFD）方法是扑翼气动模拟的主要方法，该方法的准确性依赖计算网格. 由于扑翼扑动过程涉及复杂的动网格或变形网格问题，容易导致CFD计算失败，且非定常过程模拟的耗时长[2-3]. 在扑翼飞行器的优化设计阶段，往往需要开展大规模的算例计算和实验分析[4-5]，CFD的优化工作耗时长达数十天. 气动参数的实时预测对气动模型的计算效率有很高的要求. 为了解决传统CFD方法求解速度慢的问题，研究者常采用代理模型或降阶模型，尽可能实现气动参数的快速预测[6-7]，但常见的CFD代理模型不能有效模拟高度非线性系统.

发展迅速的深度学习技术已经在许多领域有广泛应用[8]. 相较于浅层的神经网络，深度神经网络（deep neural network，DNN）能够应用于复杂非线性系统的建模. 随着DNN准确且迅速处理非线性数据的能力受到流体力学领域的研究者关注，深度学习方法已被成功应用在气动参数快速预测上. Sekar等[9]通过深度学习技术建立数据驱动的模型，实现对翼型形状的数值化与翼型气动特性的快速预测. 基于卷积神经网络考虑机翼变攻角和浮沉，吕召阳等[10]建立的多变量多输出模型实现机翼气动参数的快速预测. Han等[11]设计混合深度网络结构，直接从高维非定常流场中提取非定常流的时空特征，并对圆柱绕流和某种翼型绕流进行预测，预测结果与CFD仿真结果基本一致. Peng等[12]提出的数据驱动的降阶模型使用卷积神经网络作为编码器，反卷积神经网络作为解码器，训练后的模型可以准确快速预测测试集流场数据. 陈海等[13]使用卷积神经网络建立气动参数预测模型，在迎角、马赫数和雷诺数一定的情况下，仅根据翼型图像就能够预测出翼型的气动参数. Jin等[14]使用卷积神经网络训练圆柱绕流的CFD数据，建立圆柱体上的压力波动与圆柱体周围速度场之间的映射关系，在不同雷诺数下对训练后的模型进行测试，该模型的预测结果与CFD结果吻合良好.

上述研究使用深度学习方法实现对气动参数的高精度快速预测，预测速度远超传统的CFD方法. 但扑翼的状态变化迅速，具有较强的非定常特性，前后时刻的气动参数会因流场而相互影响，若使用传统的DNN模型对扑翼飞行器翼型的气动参数进行预测，流场的时序影响将被忽略，导致预测精度低. 循环神经网络（recurrent neural network, RNN）对变长序列数据有较好处理能力[15]，适合处理时序相关数据. 门控循环单元（gated recurrent units, GRU）[16]是RNN的变体，能够解决普通RNN中出现的梯度消失问题，相比于普通RNN具有更好的性能. 针对扑翼扑动时气动参数的强非定常、非线性特性，本研究以扑翼的二维翼型剖面为典型研究对象，基于GRU与多层感知机（multilayer perceptron，MLP），建立数据驱动的二维扑翼气动参数快速预测模型. 通过对该预测模型输入振幅、频率、摆动角度等扑动运动参数的方式，快速获得二维扑翼当前状态下的气动力与力矩特性.

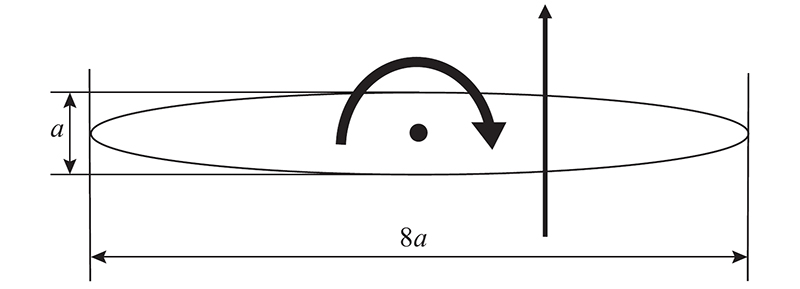
1. 物理模型

如图1所示为本研究选取的翼型[17]，翼型轮廓为上下对称的椭圆形，最大相对厚度为12.5%. 翼型的弦长c=100 mm，a为翼型的最大厚度. 翼型的扑动分为平动与转动2个部分，运动表达式为

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   椭圆形翼型示意图

Fig.1   Elliptic airfoil diagram


$ \left.\begin{array}{l}v (t)=-2\text{π}f (0.8aA)\mathrm{sin}\;(2\text{π}f t)\text{，}\\ \omega(t)=2\text{π}f \alpha \mathrm{cos}\;(2\text{π}f t).\end{array}\right\} $

式中： $ v (t) $为平动速度； $ \omega(t) $为转动速度； $ f $为扑动频率， $ f $∈[10, 30] Hz； $ A $为扑动振幅， $ A $∈[1.0, 2.0] mm； $ \alpha $为摆动角度幅值， $ \alpha $∈[10°, 60°]，本研究关注的 $ \alpha $取值范围为[10°, 40°]，因此以5∶1分别从[10°, 40°]与(40°, 60°)取值. 平动部分运动方式为上下平动，振幅 $ A $越大，翼型上下扑动范围越大；频率 $ f $越大，翼型上下平动速度越快. 转动部分的运动方式为绕翼型质心的转动， $ \alpha $越大，翼型转动角度越大. 选定取值范围后，随机从上述工况中抽取共1 368种特征组合，以保证模型数据集的均匀性与随机性，选取的扑动运动参数的组合分布如图2所示. 在1 368种特征组合中，随机选取168种特征组合作为预测模型的测试集数据，其余1 200种特征组合作为预测模型的训练集数据. 每种特征组合选取流场稳定后的196个仿真时间节点（每个扑动周期划分为100个仿真时间点）作为数据集，数据集共包含1 368×196种数据组合.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   扑动参数组合分布

Fig.2   Combination distribution of flapping parameters


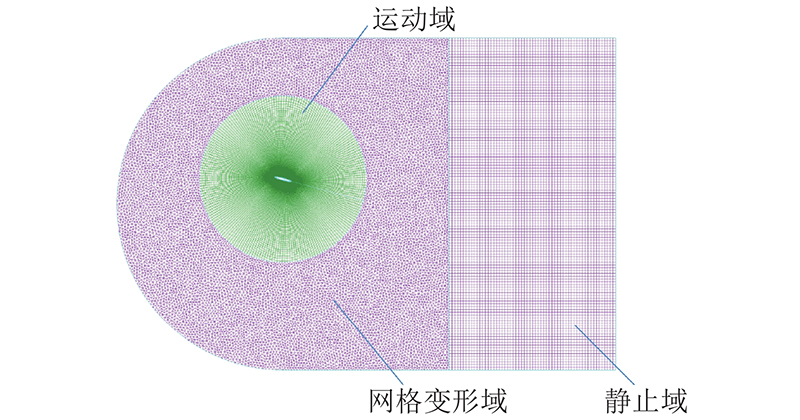
为了得到训练预测模型所需要的气动参数（升力、阻力、力矩）数据集，采用CFD方法对不同振幅、频率、摆动角度组合下的翼型扑动时气动参数进行仿真求解，计算流场区域及其网格划分如图3所示. 计算区域整体采用C形网格，计算域的大小为30c×20c. 为了模拟扑翼的运动，网格采用变形动网格技术，包含运动域、变形网格域与静止域，其中运动域随翼型扑动，非结构的变形网格域随运动域边界的运动不断更新以形成高质量的计算网格. 翼型表面设置边界层，整个计算域的网格数量为8.8×104.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   CFD计算域与网格划分

Fig.3   CFD calculation area and grid distribution


流体域外边界的左侧及上下侧设置为速度入口，来流方向为水平向右，速度为1 m/s，右侧设置为压力出口，翼型表面采用无滑移壁面边界条件.流体域的控制方程为非定常不可压缩黏性流体的连续性方程及基于雷诺平均的N-S方程，湍流模型采用低雷诺数k-ε模型，对控制方程中的对流项和扩散性分别采用二阶迎风格式和二阶中心差分格式进行离散，并采用SIMPLEC算法对压力和速度的耦合方程进行分离求解. 对每种扑动参数组合，采用CFD方法计算2个扑动周期中椭圆形翼型的升力 $L$、阻力 $D$、力矩 $M$，作为深度网络预测模型的训练标签，某一扑动参数组合下的气动参数如图4所示，其中扑动周期

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   气动参数CFD计算结果

Fig.4   CFD calculation results of aerodynamic parameters


$ T = \frac{1}{f}. $

2. 深度网络模型与训练方法

2.1. 深度网络模型

本研究建立的深度网络预测模型核心由GRU层与MLP层构成，该结构能够更好地提取时序影响数据的特征，并对该特征进行进一步处理，以实现更精准的气动参数预测. 为了减少不同气动参数预测网络的相互影响，分别对3个气动参数使用3个相同的预测模型并进行独立训练，气动参数预测模型结构如下.

1）输入层. 对预测模型输入扑动时翼型的振幅、频率、摆动角度，与当前时间点组成序列信息. 每组序列信息长度为196，对应原始数据中196个等时间间隔仿真结果. 归一化处理4种原始数据，使其数据均分布在[0, 1]，以加快深度网络的训练并提高预测精度. 在振幅、频率、摆动角度与当前时间点状态下，分别将经过CFD计算得到的升力、阻力、力矩作为标签，进行有监督学习训练.

2）GRU部分. GRU层是预测模型的核心，虽然GRU层数越多，深度网络对输入特征抽象的层次越深，但是会出现过拟合、网络计算速度慢的问题. 考虑到实时性的预测需求，经过反复调试，建立的预测模型采用2层GRU结构，第1层含96个节点 (nodes)，第2层含64个节点. 非线性激活函数是神经网络实现非线性映射的基础，双曲正切tanh激活函数具备较强的非线性映射性能，能够将输入参数映射至(−1, 1)，使预测模型对输入特征具有更强的映射表征能力，因此在GRU层选用tanh作为激活函数.

3）MLP部分. MLP是典型的前馈神经网络，通常由多个全连接层组成，上一层节点的输出通过激活函数传到下一层各节点. 与GRU层类似，MLP层数越多虽然对输入特征的处理效果越好，但也会带来过拟合问题. 经过调整，建立的预测模型采用含有4个隐含层的MLP结构，以第2层GRU的输出特征作为MLP层的输入，并对输入特征进行多层非线性映射，最后将结果输出至输出层. 由于泄露整流线性单元(leaky rectified linear unit, Leaky-ReLU)具备较快收敛速度且可以解决神经元“死亡”的问题，在MLP层选用Leaky-ReLU作为激活函数，表达式为

$ f(x)=\left\{\begin{array}{l}bx,\text{ }x < 0\text{；}\\ x,\text{ }x \geqslant 0.\end{array} \right.$

经过反复调整，取系数 $ b $=0.3.

4）输出层. 输出层将经过MLP层处理后的特征值进行累加，传递至预测模型最末层的神经元，输出模型预测值，每个预测模型的输出层含1个节点. 气动参数预测属于回归问题，因此输出层不设置激活函数.

气动参数预测模型结构与超参数设置如表1所示. 表中，NN为节点数量.

表 1   气动参数预测模型结构与超参数

Tab.1  Structure and hyperparameters of aerodynamic parameter prediction model

层名称 NN 激活函数
输入层
GRU层1
GRU层2
全连接层1
全连接层2
全连接层3
全连接层4
输出层 		4
96
64
128
128
64
16
1 		—
tanh
tanh
Leaky-ReLU
Leaky-ReLU
Leaky-ReLU
Leaky-ReLU
—

新窗口打开| 下载CSV


2.2. 模型训练方法

预测模型训练采用反向传播算法，优化器使用自适应矩估计(adaptive moment estimation, Adam). 在训练开始时学习率设置为0.001，以加快训练初期深度网络收敛速度；在训练过程中学习率逐渐减小为1×10−5，以获得更高的预测准确率. 为了提高训练效率，将训练数据以每批10组序列信息，分120批输入预测模型中训练，训练共迭代10 000个回合. 使用CFD仿真结果作为升力、阻力、力矩预测网络模型的训练标签. 模型训练损失函数使用均方误差计算，表达式为

$ {{\rm{MSE}}} = \frac{1}{N}\sum\limits_{i = 1}^N {({C_i} - \hat {C_i}} ). $

式中： $ {C_i} $为深度网络预测值； $\hat {{C_i}}$为CFD仿真结果，在模型训练中作为真实值， $N $为每批次中的训练数据量.

3. 二维扑翼气动参数预测模型性能评估

3.1. 模型预测精度

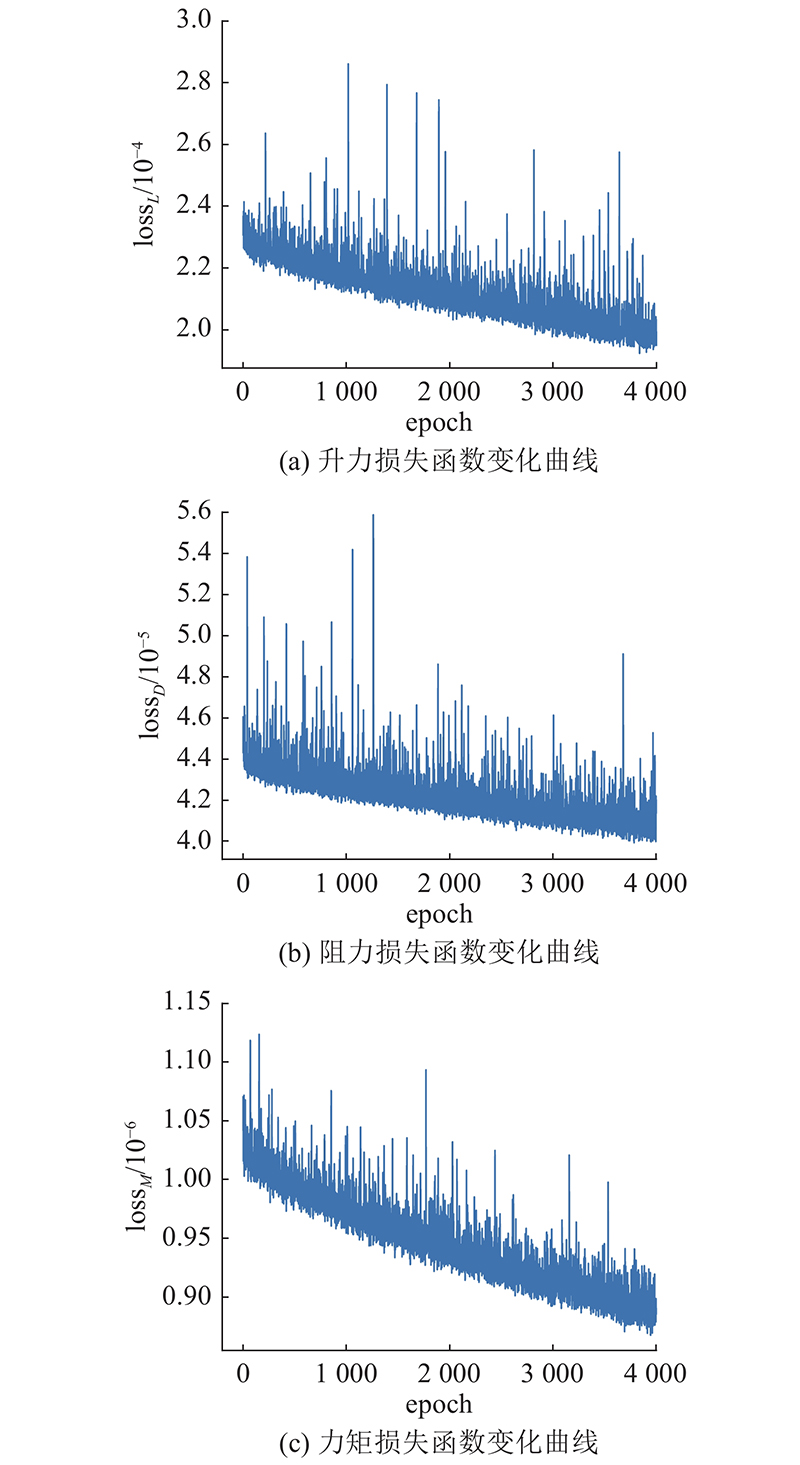
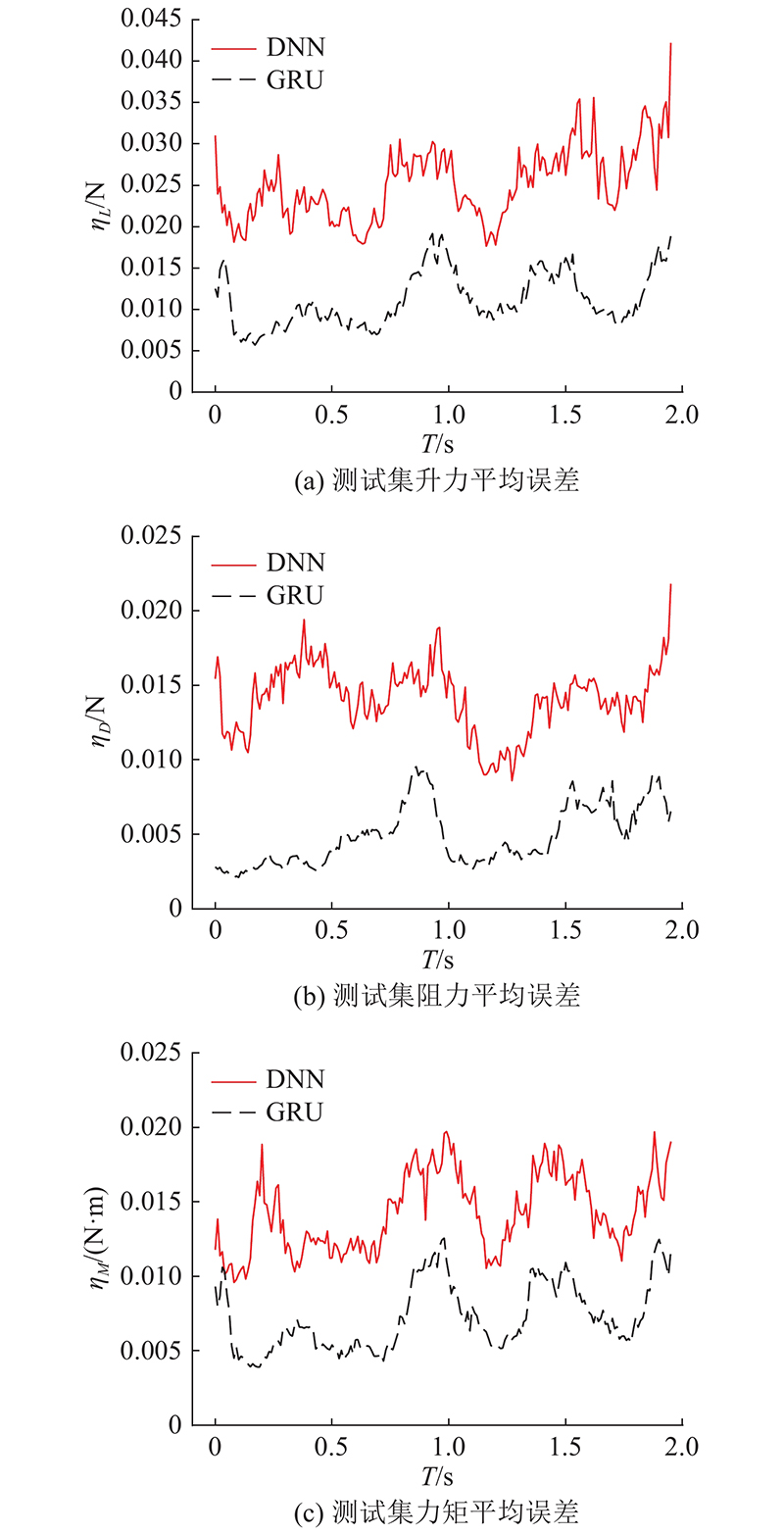
在二维扑翼气动参数预测模型的训练过程中，升力损失函数MSE降低至2×10−4，阻力损失函数MSE降低至4×10−5，力矩损失函数MSE降低至8.8×10−7. 当损失函数连续100个迭代回合无明显降低时，停止模型的训练. 训练过程中最后4 000个训练迭代回合的损失函数变化曲线如图5所示. 图中，epoch为迭代轮次，lossL、lossD、lossM分别为升力、阻力、力矩的损失函数. 模型训练完成后，将不包含在训练集中的168组扑动参数组合作为测试集，验证预测模型的性能. 训练基于传统DNN的预测模型用以对比，验证基于GRU的模型的预测效果. 2种预测模型在测试集中气动参数预测结果，沿时间轴的平均误差 η 如图6所示. 对于基于GRU模型的预测结果，升力平均误差不超过0.02 N，阻力平均误差不超过0.01 N，力矩平均误差不超过0.001 3 N·m.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   训练过程损失函数变化曲线

Fig.5   Loss function curve during training


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   测试集预测值误差曲线

Fig.6   Test dataset prediction error curve


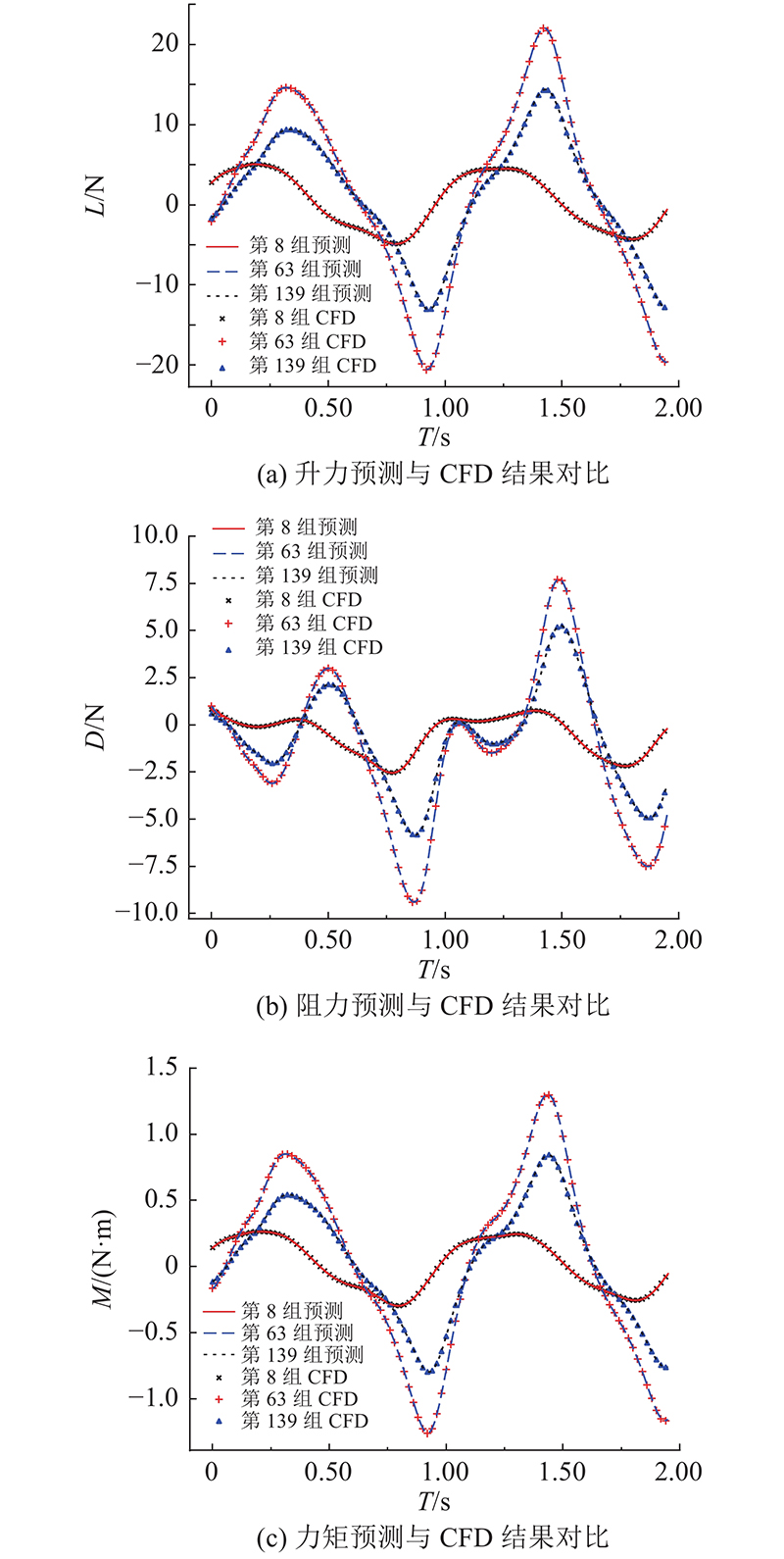
从测试集数据中随机抽取第8、63、139组特征组合，将其特征输入预测模型，得到的气动参数预测结果与CFD仿真结果对比如图7所示.对于不同类型和不同范围的气动参数波动，模型预测值与CFD仿真结果基本重合，说明气动参数预测模型预测效果较好.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   预测模型输出与CFD结果对比

Fig.7   Comparison of prediction model outputs and CFD results


3.2. 模型预测速度

采用深度学习方法进行气动参数预测的核心目标是大幅提升计算效率，因此该模型的预测速度至关重要. 如表2所示为各类运算的耗时 $ {T}_{{\rm{c}}} $统计，包括模型训练耗时、模型预测1种运动模式下3种气动参数的预测耗时、1种运动模式下CFD计算耗时. 所提预测模型极大提高了气动参数的计算速度，传统的CFD仿真方法计算2个扑动周期大约需要10 min，本研究提出的气动参数预测模型耗时0.03 s. 可以看出，所提预测模型极大提高了计算效率，能够满足扑翼飞行器优化设计与控制的实时性要求.

表 2   预测模型和CFD计算时长

Tab.2  Prediction model and CFD operation time

运算类型 ${\mathit{T} }_{\rm{c} }$/s 运算设备
模型训练
模型预测
CFD计算 		36 000
0.03
600 		NVIDIA GeForce RTX 2080ti
NVIDIA GeForce RTX 2080ti
AMD Ryzen 7 5800H

新窗口打开| 下载CSV


4. 结　语

本研究基于GRU与MLP构建扑翼飞行器二维翼型的气动参数快速预测模型，相比于传统的CFD计算方法，所提预测模型极大提高了气动参数的计算速度，预测耗时低至0.03 s，满足实时预测的要求. 得益于GRU对时序信息强大的处理能力，通过与CFD方法计算出的气动参数对比验证，所提预测模型精度高，计算速度快，能够实现对扑翼非定常气动参数变化的实时高精度预测. 设计预测模型精度对比实验，通过基于GRU预测模型和基于传统DNN预测模型的实验对比，验证基于GRU的模型在时序特征强烈的流场预测方面相比DNN预测模型更具优势. 提出的预测模型以CFD仿真结果作为训练样本，对CFD仿真的数据量及数据可靠性要求较高. 如果非定常气动参数变化复杂，则需要更多的CFD计算结果，预测模型的独立性较差、对CFD结果的依赖性较强. 如何基于有限的气动参数训练样本得到普遍适用的预测模型，是下一步计划开展的研究.

参考文献

宋笔锋, 稂鑫雨, 薛栋, 等

鸟翼空气动力学机理的研究现状和进展综述

[J]. 中国科学:技术科学, 2022, 52 (6): 893- 910

DOI:10.1360/SST-2020-0515      [本文引用: 1]

SONG Bi-feng, LANG Xin-yu, XUE Dong, et al

A review of the research status and progress on the aerodynamic mechanism of bird wings

[J]. Scientia Sinica Technologica, 2022, 52 (6): 893- 910

DOI:10.1360/SST-2020-0515      [本文引用: 1]

杨茂, 徐珊珊

耦合运动的襟翼-翼型气动特性数值仿真

[J]. 浙江大学学报: 工学版, 2014, 48 (1): 149- 153

[本文引用: 1]

YANG Mao, XU Shan-shan

Numerical simulation of aerodynamics of coupled flapping-pitching airfoil with trailing-edge flap

[J]. Journal of Zhejiang University: Engineering Science, 2014, 48 (1): 149- 153

[本文引用: 1]

张志君, 陈默, 杨贺捷, 等

基于XFlow的仿生扑翼飞行器机翼气动特性分析

[J]. 东北大学学报: 自然科学版, 2021, 42 (6): 821- 828

[本文引用: 1]

ZHANG Zhi-jun, CHEN Mo, YANG He-jie, et al

Analysis of aerodynamic characteristics of bionic flapping wing aircraft based on XFlow

[J]. Journal of Northeastern University: Natural Science, 2021, 42 (6): 821- 828

[本文引用: 1]

ZHU Z G, ZHAO J T, HE Y Y, et al

Aerodynamic analysis of insect-like flapping wings in fan-sweep and parallel motions with the slit effect

[J]. Biomimetic Intelligence and Robotics, 2022, 2 (2): 100046

DOI:10.1016/j.birob.2022.100046      [本文引用: 1]

CHEN S, WANG L, HE Y Y, et al

Aerodynamic performance of a flyable flapping wing rotor with passive pitching angle variation

[J]. IEEE Transactions on Industrial Electronics, 2021, 69 (9): 9176- 9184

[本文引用: 1]

HUANG R, HU H, ZHAO Y

Nonlinear reduced-order modeling for multiple-input/multiple output aerodynamic systems

[J]. AIAA Journal, 2014, 52 (6): 1219- 1231

DOI:10.2514/1.J052323      [本文引用: 1]

LUCIA D J, BERAN P S, SILVA W A

Reduced-order modeling: new approaches for computational physics

[J]. Progress in Aerospace Sciences, 2004, 40 (1/2): 51- 117

[本文引用: 1]

YANG L C, YOSHUA B, GEOFFREY H

Deep learning

[J]. Nature, 2015, 521: 436- 444

DOI:10.1038/nature14539      [本文引用: 1]

SEKAR V, JIANG Q H, SHU C, et al

Fast flow field prediction over airfoils using deep learning approach

[J]. Physics of Fluids, 2019, 31: 057103

DOI:10.1063/1.5094943      [本文引用: 1]

吕召阳, 聂雪媛, 赵奥博

基于CNN机翼气动系数预测

[J]. 北京航空航天大学学报, 2023, 49 (3): 674- 680

DOI:10.13700/j.bh.1001-5965.2021.0276      [本文引用: 1]

LYU Zhao-yang, NIE Xue-yuan, ZHAO Ao-bo

Prediction of wing aerodynamic coefficient based on CNN

[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49 (3): 674- 680

DOI:10.13700/j.bh.1001-5965.2021.0276      [本文引用: 1]

HAN R K, WANG Y X, ZHANG Y, et al

A novel spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural network

[J]. Physics of Fluids, 2019, 31: 127101

DOI:10.1063/1.5127247      [本文引用: 1]

PENG J Z, CHEN S H, AUBRY N, et al

Time-variant prediction of flow over an airfoil using deep neural network

[J]. Physics of Fluids, 2020, 32: 123602

DOI:10.1063/5.0022222      [本文引用: 1]

陈海, 钱炜祺, 何磊

基于深度学习的翼型气动系数预测

[J]. 空气动力学学报, 2018, 36 (2): 294- 299

[本文引用: 1]

CHEN Hai, QIAN Wei-qi, HE Lei

Aerodynamic coefficient prediction of airfoils based on deep learning

[J]. Acta Aerodynamica Sinica, 2018, 36 (2): 294- 299

[本文引用: 1]

JIN X W, CHENG P, CHEN W L, et al

Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder

[J]. Physics of Fluids, 2018, 30: 047105

DOI:10.1063/1.5024595      [本文引用: 1]

李亚超, 熊德意, 张民

神经机器翻译综述

[J]. 计算机学报, 2018, 41 (12): 2734- 2755

[本文引用: 1]

LI Ya-chao, XIONG De-yi, ZHANG Min

A survey of neural machine translation

[J]. Chinese Journal of Computers, 2018, 41 (12): 2734- 2755

[本文引用: 1]

CHO K, VAN MERRIËNBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation [C]// Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing. Doha: Association for Computational Linguistics, 2014: 1724-1734.

[本文引用: 1]

WANG Z J, BIRCH J M, DICKINSON M H

Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments

[J]. The Journal of Experimental Biology, 2004, 207 (3): 449- 460

[本文引用: 1]

/

〈 〉