调频连续波(frequency modulated continuous wave, FMCW)雷达距离测量的常规步骤是先通过快速傅里叶变换(fast Fourier transform, FFT)估计雷达中频(intermediate frequency, IF)信号的频率, 再将频率转换成目标的距离. 但FFT固有的栅栏效应可能会导致测量误差较大[3]. 针对这个问题, 许多学者提出基于FFT离散频谱的两步法[4-6]:1)对信号进行FFT得到目标所在频谱区间的粗略估计, 2)利用频谱矫正算法对区间内的目标所在频率进行精确估计. 例如, Gong等[4]提出利用线性调频Z变换(chirp Z-transform, CZT)来处理中频信号的方法, CZT在Z平面上用任意选取的螺线采样取代FFT固定的单位圆采样, 因此自由度和灵活性大. Zheng等[5]根据窗函数离散功率谱的能量中心无穷逼近坐标原点的特性提出能量重心法, 通过功率谱主瓣内的谱线估计出的主瓣中心位置即为目标所在的精确位置. Ai-Qudsi等[6]通过细化快速傅里叶变换(zoom-FFT, ZFFT)对中频信号复调制、低通滤波和降采样,实现频谱局部细化, ZFFT在相同变换点数下比FFT的频谱分辨率更高.这些频率矫正算法大多针对单目标进行精确估计, 一旦多个目标在频谱上的位置分散, 算法不但会失去灵活性, 计算量也会大大增加.
除了上述基于傅里叶变换的方法, 学者们还提出基于谱估计的超分辨算法[7-10]. 多重信号分类(multiple signal classification, MUSIC)算法是具有代表性的超分辨算法之一[7]. MUSIC算法通过信号子空间和噪声子空间的正交性来估计信号参数,缺点是必须将信号中目标的个数作为先验信息, 即无法适用于目标个数未知的情况. Liepins[8]提出的拓展离散傅里叶变换(extended discrete Fourier transform, EDFT)无需预先知道目标个数即可实现超分辨. EDFT通过优化的方法找到适用于有限时间内带限信号的变换基, 尽可能逼近理想傅里叶变换的变换基, 最终使得有限长时间信号的傅里叶变换更趋近理想信号的傅里叶变换. Yu等[9]利用自回归(autoregressive, AR)模型对分离的子频带进行插值以弥补缺失的快时间数据, 进而利用多子带线性调频合成 (mutiband chirp synthesis, MCS)技术将几个不相连的频带回波组合以获得更大的带宽, 以此提高雷达的距离分辨率. Kim等[10]使用AR模型对信号进行外推以获得更高的距离分辨率, 将MUSIC算法应用于多普勒方向进行二维联合参数估计, 使得距离-多普勒图(range-doppler map, RDM)达到超分辨的效果. 现实应用中的雷达信号往往受到噪声和杂波的影响, 以MUSIC为代表的超分辨算法在低信噪比和低快拍数的情况下普遍存在稳健性较差的缺陷[11-12].
神经网络由于其强大的表示能力被广泛应用于雷达目标识别、参数估计和状态预测[13-15]等任务. 现有的雷达超分辨算法难以有效地应用于现实场景, 本研究利用具有非线性拟合能力的深度神经网络(deep neural network, DNN)来有效处理雷达信号, 提出基于DNN的FMCW雷达距离超分辨的方法. 采用快速傅里叶变换结合离散时间傅里叶变换(fast Fourier transform+discrete time Fourier transform, FFT+DTFT)算法预处理雷达的中频信号; 将得到的时域信号输入DNN进行递归预测以外推时域信号的长度, 对时域外推后的信号进行FFT, 得到高分辨的目标距离像; 使用恒虚警率(constant false alarm rate, CFAR)检测在排除杂波的干扰同时清晰地提取目标的距离信息. 实验采用实测数据和仿真生成数据进行验证, 将所提方法与现有超分辨算法进行比较, 以验证所提出方法的有效性.
1. 距离分辨率
式中:
显然, 只要带宽足够, 就有可能以任意精细的分辨率区分目标. 然而增加系统带宽需要考虑硬件上的可实现性和高昂的成本, 因此通过信号处理的方式来提高距离分辨率就显得尤为重要.
2. 信号外推
连续傅里叶变换虽然可以对连续信号进行频率估计, 但在实际应用中得到的都是有限长度的离散信号(相当于连续信号的截断离散信号, 只能在离散域分析). 当实际得到的信号频谱仅仅为连续信号频谱的近似时, FFT的栅栏效应将不可避免. 栅栏效应表现为FFT的谱线被限制在基频的整数倍, 只能在部分离散点看到频率分量[18], 导致算出的频谱与真实频谱存在偏差. 本研究提出的时域信号外推方法本质上是对信号的频域进行插值, 频域插值可以有效地降低栅栏效应带来的影响. 以此方法提高信号的频率分辨率, 就对应提高了FMCW雷达的距离分辨率.
在FMCW雷达信号处理中, 单个目标的中频信号可以看成单频的正弦信号. 包含
式中:
可以看出, 距离分辨率随着
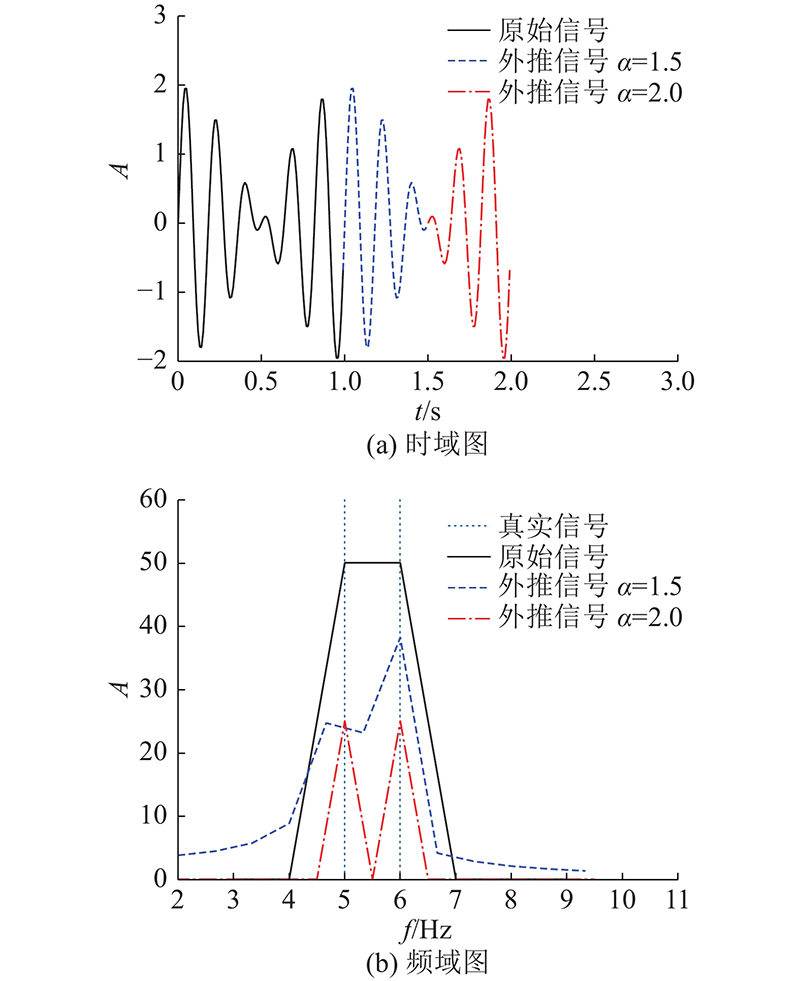
图 1
图 1 外推信号的时域图和频域图
Fig.1 Time domain and frequency domain of extrapolated signal
3. 距离超分辨
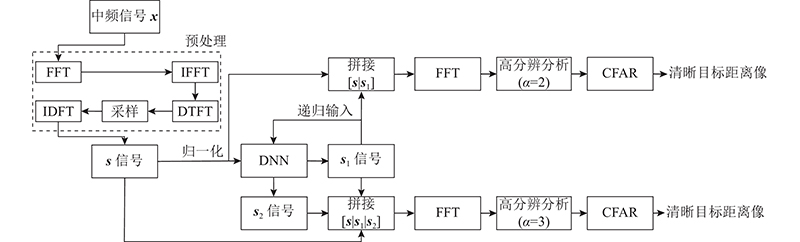
本研究所提方法的信号处理流程如图2所示. 1)中频信号
图 2
图 2 基于深度神经网络的雷达距离超分辨方法的信号处理流程图
Fig.2 Signal processing flowchart of radar range super-resolution method based on deep neural network
3.1. FFT+DTFT预处理
FFT+DTFT算法预处理可以分为2个步骤:1)对模数转换器采样后的中频信号
式中:
3.2. DNN预测
本研究所提方法采用DNN预测时域信号. DNN为单向多层结构, 可以分为输入层、隐藏层和输出层, 每层包含若干个神经元. 层间的信息单向传送, 上一层的输出被当作下一层的输入, 每层的输出不断向前传递. 通过信息的前向传播和误差反向传播算法不断优化神经网络权重, 合理的网络权重可以有效提取输入数据的潜在特征[19].
由于神经网络无法直接处理FMCW雷达采集的复数数据[20], 而复数数据所包含的相位信息并不会影响测距结果, 因此将雷达采集的复数数据取实部后再进行后续处理. 从输入层开始, 将信号
式中:
误差反向传播算法可以将网络中的残差传递到输入层, 利用误差反馈不断地调整和优化网络的权值并尽量使得网络的损失最小化. 通过损失函数对网络参数求偏导, 采用梯度下降法更新每层的参数. 采用链式求导法则计算第
式中:
可以得到
由递推关系式得到
采用逐后层至前层的方式算出
式中:
4. 实验设计与验证
4.1. 实验数据
通过2组实测数据和4组仿真生成数据验证所提出方法的有效性. 实测数据的采集基于TI公司毫米波雷达IWR1642BOOST和数据采集卡DCA1000EVM套件. 如图3所示为雷达正面和实测场景图. 为了尽量避免周围物体对待测目标的影响,使用雷达采集1组无目标的空白场景数据,再采集有待测目标的场景数据. 利用有待测目标的场景数据减去空白场景的数据, 得到较为干净的信号. 在雷始开始采集前, 设置距离分辨率
图 3
表 1 雷达实测参数设置
Tab.1
| 参数 | 数值 |
| 起始频率 | 77 |
| 调频斜率 | 25 |
| 调频时间 | 30 |
| 采样点数 | 128 |
| 采样率 | 5 |
4.2. 模型设置
实验基于Python编程语言实现, 利用Adam优化器优化模型参数. Adam优化器拥有收敛快、易调参的优点, 是广泛应用的优化器. 现实采集的实测数据大多呈现复杂的非线性. 为了使得DNN能够充分挖掘数据的潜在特征, 通过观察模型训练和测试过程中的损失和误差的变化趋势, 在避免出现过拟合的情况下, 尽可能地提高DNN的网络层数和隐藏层单元数, 最终选取较为合适的网络层数为8层和隐藏层单元数为500个. ReLU函数可以提高反向传播的效率, 还能够克服DNN中容易出现的梯度消失, 因此选取ReLU函数作为DNN的激活函数. 在模型的训练过程中, 学习率直接影响模型的性能. 过大的学习率有可能导致网络收敛到局部最优点, 过小的学习率会导致模型拥有较低的收敛速度.为了更好地训练模型, 实验中通过交叉验证法选择合适的学习率为0.001, 训练次数设定为100次.
4.3. 模型训练和测试
训练集采用3个具有随机幅度、频率和相位的正弦信号组合
将输入信号
式中:
式中:
4.4. 实验结果和分析
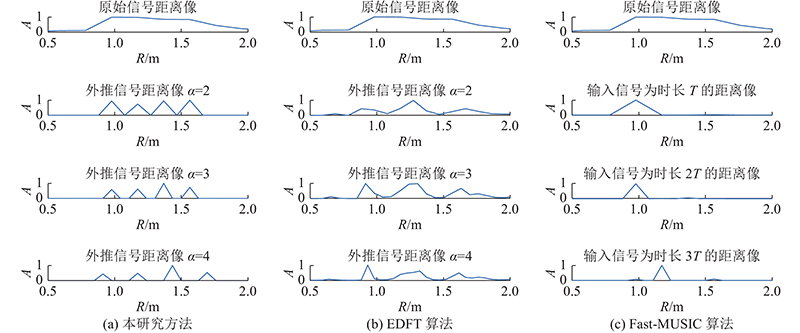
分别选取EDFT[8]、AR模型[9]和Fast-MUSIC[21]作为对比算法, 如图4、5所示为所提方法和对比算法用于2组实测数据的处理结果. 由于AR模型不能有效作用于2组实测数据, 因此图中没有给出相应的处理结果. 可以看出, 2组数据的原始信号距离像中的4个目标相互耦合, 无法被直接区分. 所提方法中的外推信号的距离分辨率随着
图 4
图 4 不同超分辨方法处理实测数据1的结果图
Fig.4 Results of processing measured data 1 with different super-resolution methods
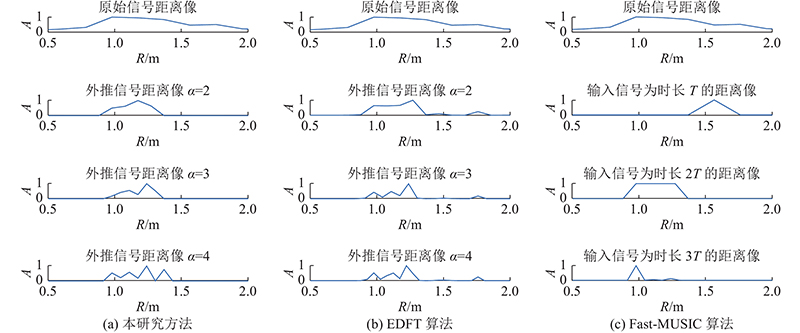
图 5
图 5 不同超分辨方法处理实测数据2的结果图
Fig.5 Results of processing measured data 2 with different super-resolution methods
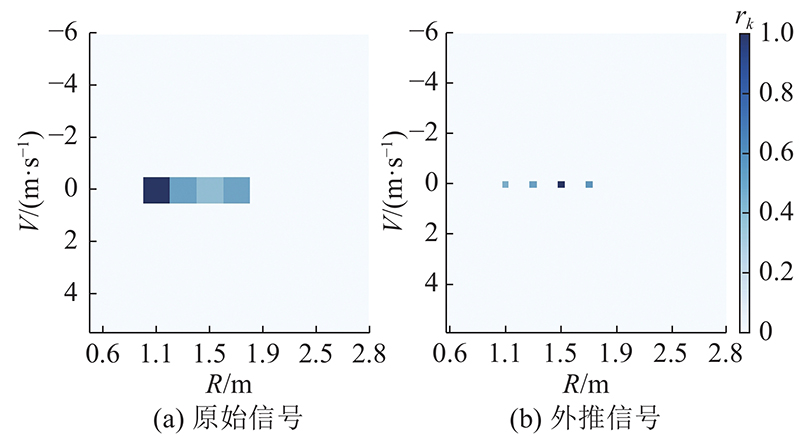
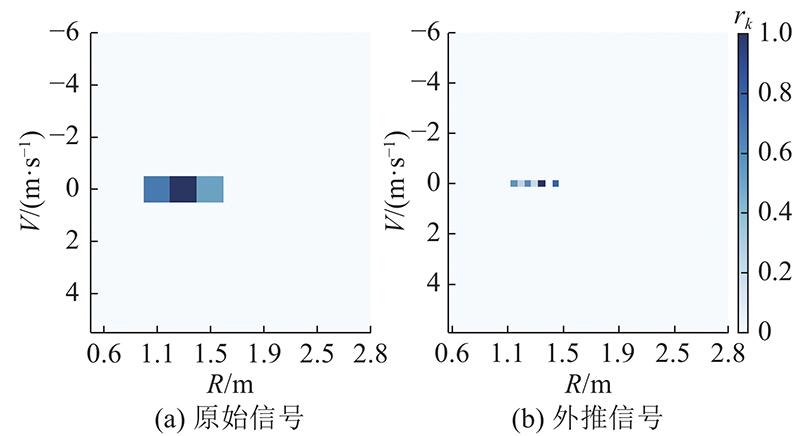
在现实的雷达系统中, RDM可以显示目标的距离和速度信息,因此被作为常用的成像图. 将2组实测数据的原始信号与基于所提方法的外推信号
图 6
图 6 实测数据1的原始信号和外推信号的距离-速度图对比
Fig.6 Comparison of range-doppler map between original signal and extrapolated signal of measured data 1
图 7
图 7 实测数据2的原始信号和外推信号的距离-速度图对比
Fig.7 Comparison of Range-doppler map between original signal and extrapolated signal of measured data 2
所提方法和对比算法的误差结果如表2~4所示. 表中,下标M1、M2、S1、S2、S3和S4分别代表实测数据1、实测数据2、仿真数据1、仿真数据2、仿真数据3和仿真数据4. 可以看出, 所提方法较对比算法在实测数据和仿真生成数据整体上拥有更低的误差、较好的性能. 雷达在现实场景中采集的数据会受到噪声和杂波的影响, 信号组成上可以认为是较为复杂的非线性信号. DNN拥有强大的非线性拟合能力, 可以提取输入信号的潜在特征并进行非线性预测, 因此更适合用于现实场景中的实测数据. 在小部分数据(主要集中于
表 2 实测数据的距离像在不同外推长度下的误差
Tab.2
| 算法 | | | |||||
| | | | | | | ||
| EDFT | 0.0847, 0.1083 | 0.2145, 0.2518 | 0.3456, 0.4010 | 0.3187, 0.4178 | 0.3486, 0.4211 | 0.2500, 0.3402 | |
| Fast-MUSIC | 0.4640, 0.5551 | 0.4279, 0.5099 | 0.4121, 0.5291 | 0.4318, 0.5419 | 0.3731, 0.4599 | 0.3652, 0.4614 | |
| 本研究 | 0.1926, 0.2134 | 0.1784, 0.2580 | 0.2426, 0.3280 | 0.2169, 0.2614 | 0.3165, 0.3513 | 0.2427, 0.2989 | |
表 3 仿真数据1和仿真数据2的距离像在不同外推长度下的误差
Tab.3
| 算法 | | | |||||
| | | | | | | ||
| AR模型 | 0.0228, 0.0386 | 0.0315, 0.0487 | 0.0559, 0.1016 | 0.1174, 0.1425 | 0.2591, 0.3135 | 0.4397, 0.4887 | |
| EDFT | 0.0289, 0.0384 | 0.0369, 0.0421 | 0.0502, 0.0728 | 0.1844, 0.2236 | 0.2010, 0.2667 | 0.1758/0.2479 | |
| Fast-MUSIC | 0.1275, 0.2742 | 0.1050, 0.2149 | 0.1107, 0.2280 | 0.2736, 0.3700 | 0.2235, 0.2903 | 0.1698, 0.2507 | |
| 本研究 | 0.0631, 0.1042 | 0.0580, 0.0715 | 0.0559, 0.1042 | 0.1314, 0.1617 | 0.1651, 0.2295 | 0.1256, 0.1937 | |
表 4 仿真数据3和仿真数据4的距离像在不同外推长度下的误差
Tab.4
| 算法 | | | |||||
| | | | | | | ||
| AR模型 | 0.2142, 0.2733 | 0.2305, 0.2802 | 0.2849, 0.3410 | 0.1459, 0.1749 | 0.2203, 0.3063 | 0.2272, 0.3177 | |
| EDFT | 0.2697, 0.3562 | 0.2483, 0.3312 | 0.2298, 0.3192 | 0.1544, 0.2024 | 0.2067, 0.2838 | 0.2172, 0.3069 | |
| Fast-MUSIC | 0.2897, 0.3491 | 0.2877, 0.3512 | 0.2379, 0.3487 | 0.2782, 0.3642 | 0.2862, 0.3682 | 0.2901, 0.3805 | |
| 本文方法 | 0.2693, 0.3357 | 0.1719, 0.2598 | 0.1482, 0.2225 | 0.1314, 0.1617 | 0.1651, 0.2295 | 0.1928, 0.2589 | |
5. 结 语
本研究提出基于DNN的FMCW雷达距离超分辨的方法, 通过信号时域的外推来提高频域的分辨率, 对应地提高FMCW雷达的距离分辨率. 仿真实验表明, 与现有的超分辨方法相比,所提基于DNN的方法更适用于复杂信号的情况, 能够有效地应用于处理雷达所采集的现实场景数据. 未来的研究工作计划从以下2个角度出发: 1)信号递归输入神经网络预测的方式会产生误差累积效应, 减小误差累积可以提高外推精度, 达到更好的距离超分辨成像效果; 2)在距离超分辨的基础上, 进一步考虑角度超分辨或速度超分辨, 实现距离-角度超分辨或距离-速度超分辨.
参考文献
Decoupling the doppler ambiguity interval from the maximum operational range and range-resolution in FMCW radars
[J].DOI:10.1109/JSEN.2020.2972152 [本文引用: 1]
High-resolution range-doppler maps by coherent extension of narrowband pulses
[J].DOI:10.1109/TAES.2020.2965754 [本文引用: 1]
A quantitative study of pitfalls in the FFT
[J].DOI:10.1109/TAES.1980.308971 [本文引用: 1]
Low-complexity joint extrapolation-MUSIC-based 2-D parameter estimator for vital FMCW radar
[J].
DOI:10.1109/TSP.2013.2263502 [本文引用: 1]
基于MUSIC及其改进算法的DOA估计研究
[J].DOI:10.3969/j.issn.1002-0802.2021.06.012 [本文引用: 1]
Research on DOA estimation based on MUSIC and its improved algorithm
[J].DOI:10.3969/j.issn.1002-0802.2021.06.012 [本文引用: 1]
Radar HRRP target recognition model based on a stacked CNN–Bi-RNN with attention mechanism
[J].
Spatial–temporal convolutional gated recurrent unit network for significant wave height estimation from shipborne marine radar data
[J].
Convolutional neural network for convective storm nowcasting using 3-D doppler weather radar data
[J].DOI:10.1109/TGRS.2019.2948070 [本文引用: 1]
Toward ant-sized moving object localization using deep learning in FMCW radar: a pilot study
[J].
Spectral estimation: an overdetermined rational model equation approach
[J].DOI:10.1109/PROC.1982.12424 [本文引用: 2]
一种深度神经网络多站雷达系统干扰鉴别方法
[J].DOI:10.19665/j.issn1001-2400.2021.02.017 [本文引用: 1]
Method for discrimination of false targets in multistation radar systems based on the deep neural network
[J].DOI:10.19665/j.issn1001-2400.2021.02.017 [本文引用: 1]