在生产精密零件过程中，高精数控机床的加工精度受多种误差源影响，其中由机床运转与外界环境引起的热误差占加工精度总误差的40%~70%，是最大的误差源^[1-3]. 热误差建模及补偿是减少机床热误差的基础，常用的建模方法有多元线性回归^[4]、人工神经网络^[5]、支持向量机^[6]等. Ma等^[7]采用遗传算法(genetic algorithm, GA)和粒子群优化（particle swarm optimization, PSO）算法对反向传递（back propagation, BP）神经网络参数进行优化，该方法容易陷入局部极小，收敛性能有待提高. Cheng等^[8]使用径向基函数（radial basis function，RBF）神经网络进行热误差建模，与传统的BP神经网络相比，RBF神经网络具有更高的预测精度. Zhu等^[9]提出基于随机森林的热误差建模方法，采用与交叉验证相结合的网格搜索方法，此搜索方法易于优化模型的超参数. Li等^[10]提出基于综合温度信息的温度敏感点选择方法，建立采用鲸鱼优化算法进行优化的支持向量回归（support vector regression, SVR）模型，该方法具有较高的精度和鲁棒性.

建立准确的热误差模型，常规的做法是通过布置大量传感器获得机床的温度场分布情况^[11]. 机床整体温度场具有非线性和时变性，大量的传感器使数据处理量变大，实验成本提高，同时温度测点间存在的复共线性将使热误差建模的效果不理想. 温度测点的优化是保证模型准确性和可靠性的重要手段，有许多学者采用聚类算法研究温度测点优化问题. Fu等^[12]采用基于相关分析K-means聚类方法，得到不同K值对应的温度敏感点组合；通过建立残差和均方根误差的均值来评价RBF模型的结果，筛选出最优的温度敏感点组合；设置不同的聚类数目建立一系列热误差模型，通过对这些模型分配权重和阈值建立组合预测模型，得到最佳分类数目^[13]. Yang等^[14]通过模糊C均值聚类方法从原始温度数据中选择代表的温度点导出，将测温点从9个减少到2个. Zhou等^[15]为了提高预测模型的性能，提出基于密度峰聚类的关键测温点选择方法，该方法能够快速地对大量的温度测点进行聚类，并自动选取具有各聚类共同特征的关键温度测点. 李逢春等^[16]使用兼顾欧氏距离和相关系数的系统聚类准则，降低了温度测点间的共线性，减少了温度测点的数量.

为了更好地删减具有冗余特征的传感器，提高建模质量，降低研究成本，并提高测点优化方法对不同机床在不同环境下的适用程度，本研究通过建立欧氏距离与相关系数的融合矩阵，深入挖掘温度变量之间的相关性，并通过灰色关联分析对机床温度测点进行优化，建立基于GA优化的SVR模型来实现有效的热误差建模. 融合矩阵的权重系数和聚类数，采用GA建立多转速条件下的适应度函数自动寻找出最佳分类与选择方案. 在多机床上进行热误差测试试验以验证该方法的有效性，为提高机床加工精度提供参考.

合理的温度传感器布置可以降低模型的复杂性，提高模型的准确性和鲁棒性. 因此优化机床上布置传感器的数量，减少冗余信息对机床热误差建模的影响是本研究的主要目的. 根据文献[17]，需要构建衡量传感器之间差异的指标，以便更好地区分不同传感器在热误差建模中的影响. 同时需要从每类传感器集群中筛选出最有代表性、与热误差的关联性最大的传感器作为建模的输入对象，以便建立准确而稳定的热误差模型.

传统的系统聚类分析法将传感器之间的差异性笼统地定义为距离. 距离代表着不同温度传感器在机床上的不同位置，每个时刻所测得的温度值存在差异，距离越大差异越明显，因此通过传感器数据之间距离指标可以找到最能包含机床整体温度场信息的传感器. 由于传统的系统聚类分析法未考虑各测点的相关性对机床热误差建模产生的不利影响，仅考虑传感器间距离得到的聚类结果仍然存在冗余数据. 若仅考虑温度变量之间的相关性，则可能没有得到机床本身温度场的全部信息，从而丢失一些比较关键的测点数据，这同样对热误差建模不利.

为了实现多个传感器的有效聚类，本研究采用融合欧氏距离和相关系数的差异指标，该差异指标获得过程如下.

1）设 ${{{\boldsymbol{X}}}_i}$、 ${{{\boldsymbol{X}}}_j}$分别为第i、j个温度传感器的信号序列向量，共有n个传感器，推导出各温度传感器信号之间的距离 ${d_{ij}} = \left\| {{{{\boldsymbol{X}}}_i} - {{{\boldsymbol{X}}}_j}} \right\|$，建立欧氏距离矩阵 $ {{\boldsymbol{D}}} = {[{d_{ij}}]_{n \times n}} $.

2）计算得到基于相关系数的矩阵 ${{\boldsymbol{R}}} = {[{r_{ij}}]_{n \times n}}$，

(1) $ {r_{i j}} = \frac{{\displaystyle\sum\limits_{k = 1}^l {\left( {{x_{ik}} - \overline {{x_i}} } \right)\left( {{x_{jk}} - \overline {{x_j}} } \right)} }}{{\sqrt {\displaystyle\sum\limits_{k = 1}^l {{{({x_{ik}} - \overline {{x_i}} )}^2}} } \sqrt {\displaystyle\sum\limits_{k = 1}^l {{{({x_{jk}} - \overline {{x_j}} )}^2}} } }}. $

式中： $ {r_{ij}} $为相关系数； $ \overline {{x_i}} $ 、 $ \overline {{x_j}} $ 分别为对应编号传感器的温度序列均值，即 $ \overline {{x_i}} = {\displaystyle\sum\limits}_{k = 1}^l {{x_{ik}}/l} $ ， $\overline {{x_j}} = {\displaystyle\sum\limits}_{k = 1}^l {{x_{jk}}/l}$；式(1)的分母为对应编号传感器温度序列的协方差；l为信号数据长度； $ {x_{ik}} $为第i个传感器的第k个值； $ {x_{jk}} $为第j个传感器的第k个值.

3）相关系数矩阵的元素属于[−1, 1]，距离矩阵的元素属于[0,p]，其中p为最大距离. 在进行矩阵融合前，须同时对2个矩阵进行预处理. 将欧氏距离矩阵和相关系数矩阵分别更新为新的矩阵： ${{{\boldsymbol{D}}}_u} = {[{d_{ui j}}]_{n \times n}}$、 $ {{{\boldsymbol{R}}}_u} = {[{r_{uij}}]_{n \times n}} $，其中

(2) $ {d_{ui j}} = \frac{{{d_{i j}} - {d_{i j\min }}}}{{{d_{i j\max }} - {d_{i j\min }}}}, $

(3) $ {r_{ui j}} = 1 - \left| {{r_{i j}}} \right|. $

式中： $ {d_{i j\min }} $、 $ {d_{i j\max }} $分别为距离矩阵 $ {{\boldsymbol{D}}} $中的最小元素和最大元素. 更新后的相关系数矩阵与欧氏距离矩阵中的元素分别与差异性建立等价关系，即数值越大，传感器之间的差异性越大.

4）融合2个矩阵为传感器差异指标矩阵 ${{\boldsymbol{S}}}$，以 ${{\boldsymbol{S}}}$作为系统聚类法的改进距离矩阵，进行聚类.

(4) $ {{\boldsymbol{S}}} = \lambda {{{\boldsymbol{D}}}_u}+(1 - \lambda ){{{\boldsymbol{R}}}_u}. $

式中： $\lambda $为线性权重， $\lambda $∈[0, 1]. 当 $\lambda $较大时，欧氏距离占据主导地位；当 $\lambda $较小时，相关系数占主导地位. 建立的新差异性指标将代替传统的距离指标进行系统聚类，在得到差异指标矩阵后，寻找该矩阵中上三角区域内的最小元素 ${t_{i j\min }}$，对应的第i、j个传感器并为一类，其余传感器各为一类. 将此元素略去后继续寻找最小元素 ${t_{pq\min }}$，若此元素与 ${t_{i j\min}}$位于同行或同列，则合并为一类；否则，第p个传感器与第q个传感器分为一类. 以此循环往复，直至将N个温度传感器分为一类结束循环，获得系统聚类树.

本研究采集的温度测点数据对于整机温度场来讲具有小样本、贫信息的特点，采用灰色系统模型^[18]研究温度测点与热误差之间的内在联系较为合适，便于找出最优代表性的温度测点进行热误差建模.

对采集的原始数据进行规范化处理，实现温度与温度序列、温度与热误差序列之间的“等权”^[19]. 本研究对原始数据采取极差化变换法，设有原始温度序列 ${x^{(0)}} = \left\{ {{x^{(0)}}\left. {(v)} \right|v = 1,2,\cdots,u} \right\}$，原始热误差序列 ${x^{(m)}} = \left\{ {{x^{(m)}}(v)\left| {v = 1,2,\cdots,u} \right.} \right\}$，其中u为序列长度，通过极差变换后得到归一化序列为

(5) $ x(v) = \frac{{\max {x^{(0)}}(v) - {x^{(0)}}(v)}}{{\max {x^{(0)}}(v) - \min {x^{(0)}}(v)}}. $

式中： $x(v)$为归一化数据，热误差序列处理方法与温度序列处理方法相同. 在第v个点得到的关联系数为

(6) $ {r^{(0m)}}(v) = \frac{{ \mathop {\min }\limits_m \mathop {\min }\limits_v {\varDelta _{0m}}(v)+\mathop {\max }\limits_m \mathop {\max }\limits_v {\varDelta _{0m}}(v)}}{{{\varDelta _{0m}}(v)+\rho \mathop {\max }\limits_m \mathop {\max }\limits_v {\varDelta _{0m}}(v)}}. $

式中： $ {\varDelta _{0m}}(v) = \left| {{x^{(0)}}(v) - {x^{(m)}}(v)} \right| $； $ \mathop {\min }\limits_m \mathop {\min }\limits_v {\varDelta _{0m}}(v) $为两级最小差； $ \mathop {\max }\limits_m \mathop {\max }\limits_v {\varDelta _{0m}}(v) $为两级最大差； $\; \rho $为分辨系数，一般取 $\; \rho $=0.5. 根据求得的各时刻关联系数，得到某温度传感器测得温度序列与位移传感器所测得热误差序列之间的灰色关联度为

(7) $ {r^{(0m)}} = \frac{1}{u}\sum\limits_{v = 1}^u {{r^{(0m)}}(v)} . $

将各个温度测点计算得到的关联度从大到小排列，得到各个温度测点对热误差影响的大小.

在SVR建立热误差模型过程中，给定集合 $ \left\{ {(x_{_i}^{(1)}, x_{_i}^{(2)}, \cdots, x_{_i}^{(n)},{y_i}),i = 1,2,\cdots,l} \right\} $， 其中 [ $ x_{_i}^{(1)},x_{_i}^{(2)},\cdots,x_{_i}^{(n)} $]为输入矩阵， ${y_i}$为目标值. 将样本映射到高维空间，计算高维特征空间回归方程 $y = f({\boldsymbol{x}})$，SVR模型可以概况为以下方程式：

(8) $ f({\boldsymbol{x}}){ = {\boldsymbol{w}}}{\boldsymbol{\phi}} ({\boldsymbol{x}})+b. $

式中： $ {\boldsymbol{\phi}} ({\boldsymbol{x}}) $为非线性映射函数, $ {{\boldsymbol{w}} = }\left[ {{w_1},{w_2},\cdots,{w_l}} \right] $为权值向量，b为偏差. 引入松弛因子后，求解 $ {{\boldsymbol{w}}} $、b. 建立约束优化问题：

(9) $ \left. \begin{split} & \min \;\frac{1}{2}{\left\| {{\boldsymbol{w}}} \right\|^2}+C\sum\limits_{i = 1}^n {({\xi _i}} +{\xi _i}^*). \\ & {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{array}{l} f({{\boldsymbol{x}}_i}) - {y_i} \leqslant \varepsilon +{\xi _i}; \\ {y_i} - f({{\boldsymbol{x}}_i}) \leqslant \varepsilon +{\xi _i}^*; \\ {\xi _i} \geqslant 0,\;{\xi _i}^* \geqslant 0. \\ \end{array} \right. \end{split} \right\} $

式中：y_i为实际输出值，ε为不敏感边界的宽度，C为惩罚参数， $ {\xi _i} $、 $ {\xi _i}^* $均为松弛因子. 引入拉格朗日函数并转化为对偶问题：

(10) $ \left. \begin{split} & \min \;\frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {({\alpha _i}^* - {\alpha _i})} } ({\alpha _j}^* - {\alpha _j})\kappa ({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) - \\ & \qquad \sum\limits_{i = 1}^l {({\alpha _i}^*+{\alpha _i})} \varepsilon +\sum\limits_{i = 1}^l {({\alpha _i}^* - {\alpha _i})} {y_i}. \\ & {\rm{s.t.}}\left\{ \begin{array}{l} \displaystyle\sum\limits_{i = 1}^l {({\alpha _i}^* - {\alpha _i})} = 0; \\ 0 \leqslant {\alpha _i} \leqslant C,\;0 \leqslant {\alpha _i}^* \leqslant C. \\ \end{array} \right. \end{split} \right\} $

式中： $ {\alpha _i}^{} $、 $ {\alpha _i}^* $均为拉格朗日乘子，x_i、x_j分别为第i、j个输入样本， $ \kappa ({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) $为核函数. 选择径向基函数作为核函数，表示为

(11) $ \kappa ({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) = \exp \left( - \frac{{{{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}^2}}}{{2{\sigma ^2}}}\right). $

SVR对核参数以及核函数的选择比较敏感，核函数参数 $\sigma $影响样本映射到高维特征空间的分布情况；惩罚参数C影响模型的复杂度和稳定性，因此这2个参数的好坏决定了SVR预测模型的精度和稳定性. 为了提高预测精度，采用GA对模型系数进行优化. 根据文献[20]，本研究的模型系数优化的具体流程如下. 1）设定初始值：种群规模、交叉概率、变异概率、最大迭代次数以及适应度函数等. 2）设定惩罚参数C和核函数参数 $\sigma $的搜索范围，使用随机函数对初始父代的各个体进行染色体基因编码. 3）将父代种群用SVR模型进行训练，并采用三折交叉验证获取此时输入的C、 $\sigma $得到的最小预测误差，作为初始父代种群的适应度. 4）根据交叉概率进行交配，实现基因序列部分交替生成子代，并根据步骤3）进一步得到子代的适应度值，按一定规则在初始的2代中选出优秀的个体并对部分个体进行变异操作. 5）进行迭代，重复步骤2）~ 4），直到达到预先设定的最大迭代次数，挑选出最优个体，其基因序列便是最优的C、 $\sigma $.

为了验证所提出方法的适用性和有效性，在多机床上进行实验，并列举其中的3台由不同厂家研发的机床：VM-850L立式加工中心（机床Ⅰ）、SUKCES-G1160立式加工中心（机床Ⅱ）和VMC-850E立式加工中心（机床Ⅲ）. 实验均在空转条件下进行，环境温度变化通过温度传感器监测得到.

以机床Ⅰ为例，搭建数控机床热态特性采集测试实验平台如图1所示. 平台的主要硬件设备如下：加工中心本体、数控机床主轴系统智能热特性测试与补偿仪、Fluke TiS50热成像仪器（测量范围为10~50 ℃，测量精度为±2 ℃，测量距离为1.5 m）、磁吸式温度传感器PT100（测温精度为0.4%）、电容位移传感器CPL230（工作温度范围为4~50 ℃）、五点法专用夹具和检验棒. 参照ISO 230-3中的五点法布置安装测量仪器.

机床Ⅰ的主要热源有主轴电机、主轴轴承和环境温度. 在进行温度测点选择时，先根据热模态理论中热敏感点的选择办法寻找原始测点，然后采用Fluke TiS50热成像仪进一步确定机床温度敏感点部位，从而确定原始测点的布置. 在机床达到热稳态的情况下，在电机与轴承处温升最为明显，尤其是主轴下部轴承安装处的温升对热误差影响最大（影响权重也最大）. 因此本研究主要在主轴、主轴箱和电机处预设温度测点，共设置16个磁吸式温度传感器获取机床的温度场信息，具体安装位置如表1所示. 由于Z方向热误差对机床精度的影响明显，本研究以获取的主轴Z方向的热位移作为热误差进行分析，温度传感器与Z向位移传感器安装位置如图2所示.

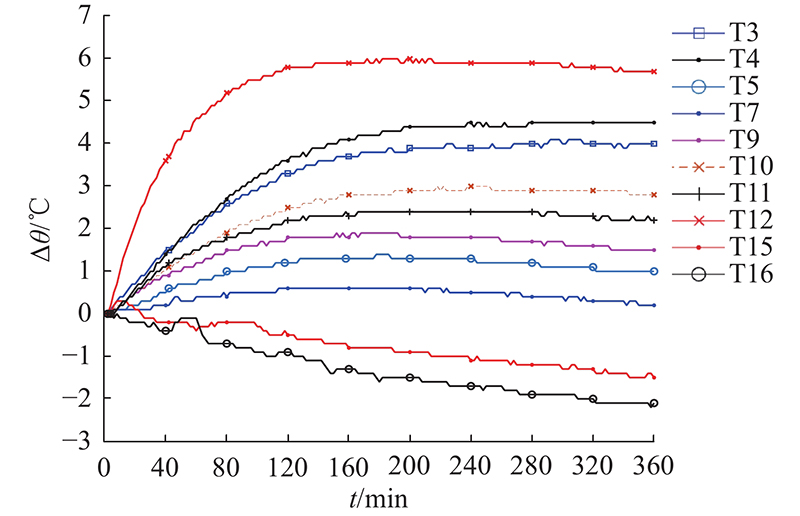
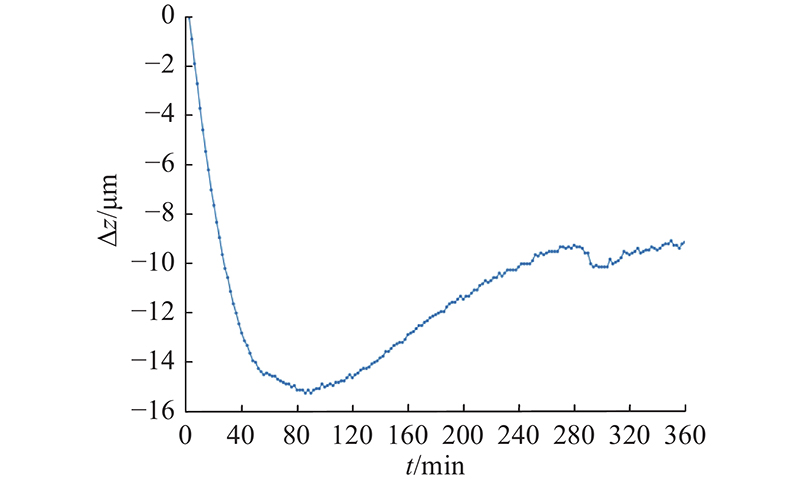
加工中心主轴系统启动后，使用智能热特性测试与补偿仪通过温度和位移传感器采集外部温度和热位移信号，将采样获得的多路信号数据存储在计算机中. 本实验采集温度信号与热位移信号的传感器采样间隔为2 min，采集主轴在空转条件下恒定转速分别为2 000、3 000、3 500、4 000 r/min的温度、热位移信号，并在达到热平衡后使机床主轴停转，每组转速试验均进行6 h的温升位移数据采集. 以4 000 r/min为例，实验获得温度测点的温升 $\Delta \theta$和Z向的热误差 $\Delta z$随时间t的变化曲线分别如图3、4所示. 由于一些温度测点的温升趋势接近，图3中没有列举T1、T2、T6、T8和T14的温升-时间曲线.

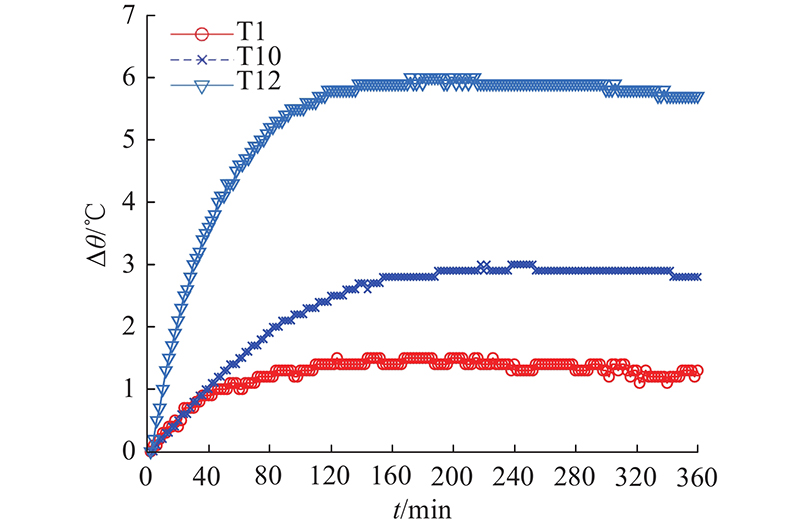
如图5所示为以4 000 r/min实验的部分温升-时间曲线. 数控机床的温度场变化具有以下特点. 1）某些测点的温升-时间曲线差距较大（如T10、T12），若仅根据欧氏距离进行系统聚类，会被分为不同的类别，但是在相同时间情况下T12的温升大致是T10的2倍. 这就会导致模型的输入量存在共线性的问题，从而使模型的预测精度降低. 2）某些测点的温升-时间曲线虽然相关性大（如T1、T12），仅根据温度测点间的相关系数它们将归为同类，但它们的温升差距较大，且相互位置较远. 若将这些测点聚为一类，则可能导致无法监测整个机床的温度场信息，关键信息缺失将影响建模精度.

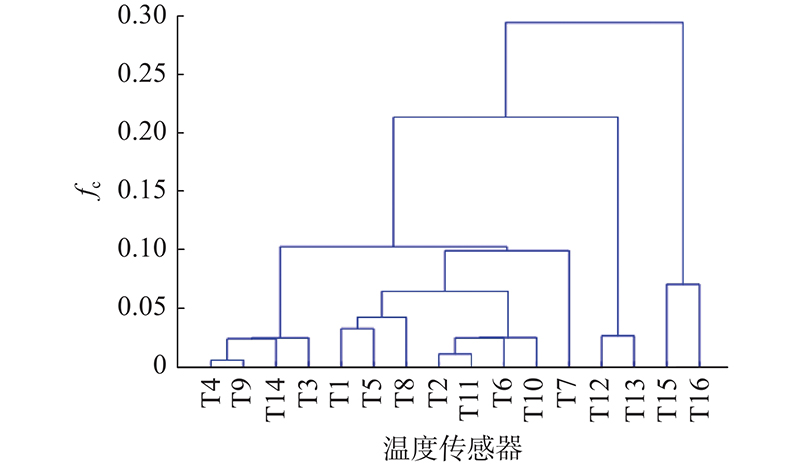
对采集的各测点温升序列构造欧氏距离矩阵和相关系数矩阵，按一定权重系数 $\lambda $ 融合矩阵后进行系统聚类. 共将16个温度传感器分为K类，使用灰色关联度分析排序所有温度序列对热误差序列的影响程度，挑选出K个代表性的传感器作为热误差模型的输入. GA-SVR模型的参数设定如下：令自定义参数 $g = 1/2{\sigma ^2}$、 C∈(0, 100]、 g∈ (0, 1 000]，搜索最优解即找到误差最小值，设定种群数为20，变异概率为0.95，交换概率为0.8，最大迭代次数为200. 权重系数 $\lambda $和聚类数K均为可选参数，其中 $\lambda $ 的变化将改变最终的聚类树，得到不同的聚类情况；K将直接决定参与热误差建模的温度传感器个数. 为了自动得到合适的 $\lambda $ 、K，也为了避免与SVR参数寻优方式混淆，使用GA进行寻优并称其为外层GA（outer genetic algorithm, OGA），对应地SVR参数寻优为内层GA（inner genetic algorithm, IGA）. 为了实现在不同转速下的通用性，定义OGA适应度函数为

(12) $ f=(R_{x}+R_{y})/2 $

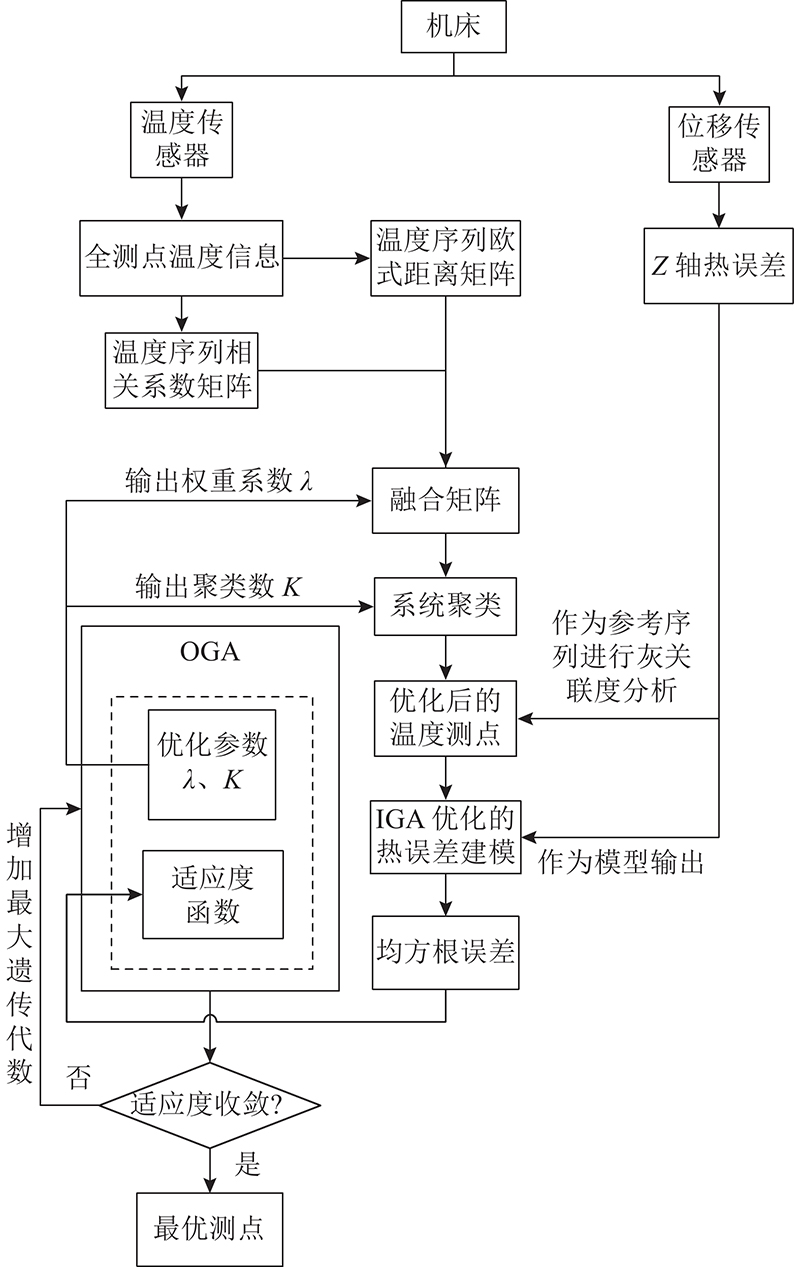
式中：R_x、R_y为热误差模型预测转速分别为x、y的位移得到的均方根误差. 在机床Ⅰ中，采用4 000 r/min实验得到的热误差模型预测2 000、3 000 r/min实验的热误差，迭代获得最优的 $\lambda $、K，使适应度值最小，即获得多转速下的预测模型最优解. 综上所述，测点优化方法的流程如图6所示.

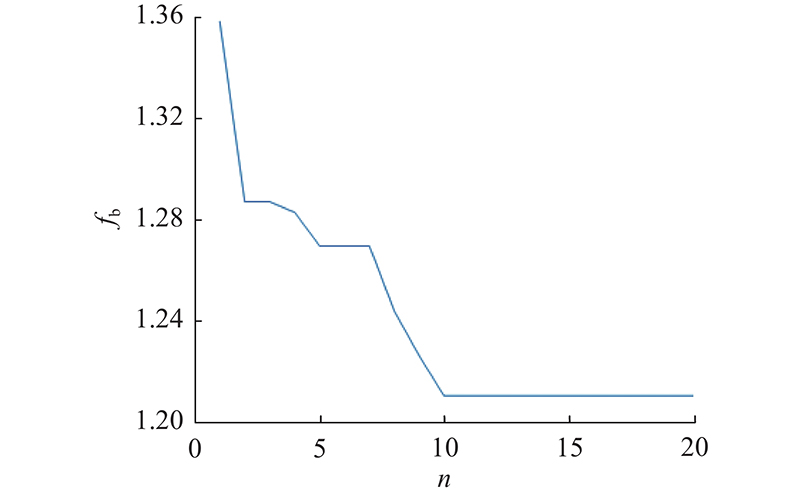
工程经验表明，温度特征点过多会增加温度测量、数据处理和热误差建模的工作量和费用；温度特征点太少可能导致重要信息的丢失^[2]. 对于OGA，设定聚类数 $K\in [4, 12] $的自然数， $\lambda $ 的变化范围为[0, 1.0]，设定种群数为20，变异概率为0.95，交换概率为0.8，最大迭代次数为20. 由转速为4 000 r/min的各温度序列和热误差序列进行灰色关联度分析，结果如图7所示. 图中，f_a为灰色关联度值. 由OGA得到的最优参数分别为 $\lambda $=0.4、K=5，迭代过程如图8所示，其中n为迭代次数，f_b为适应度值. 当 $ \lambda=0.4 $、 $K=5 $时，对应的聚类树如图9所示，其中f_c为截断值.

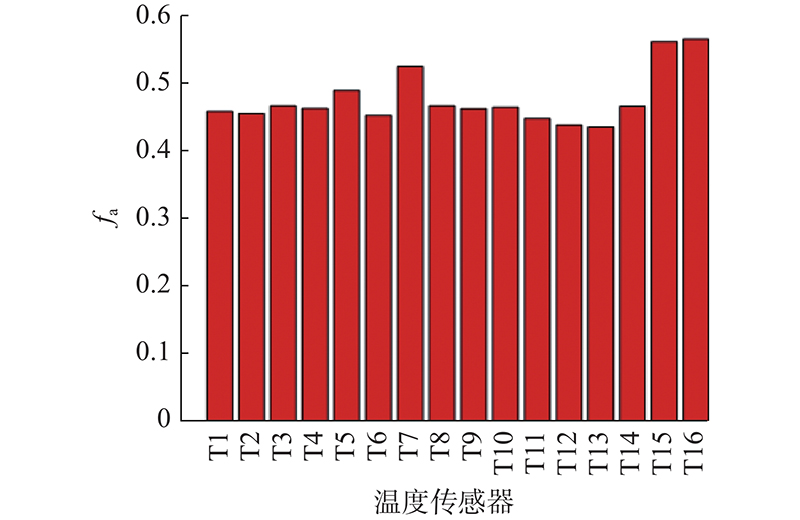
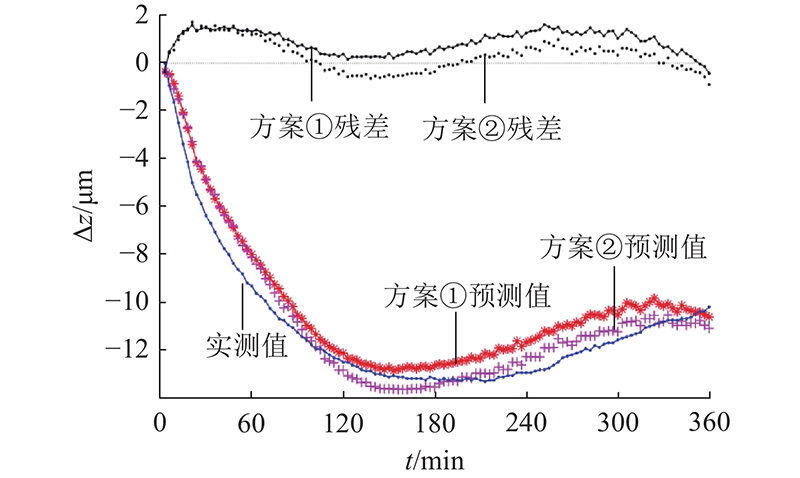
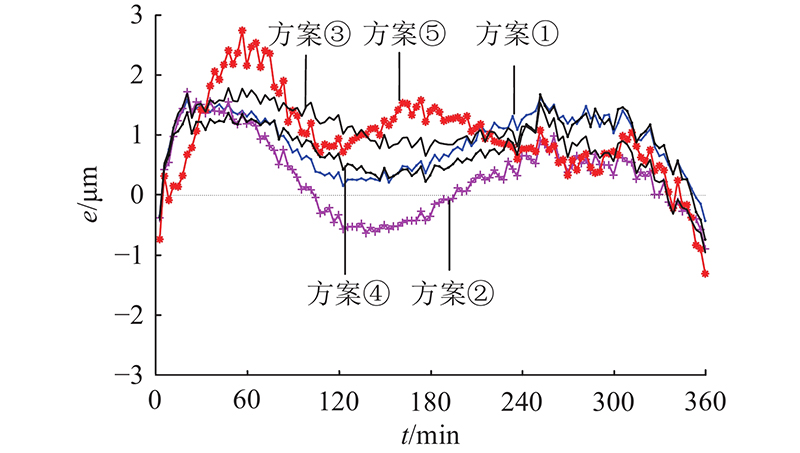
在所有传感器分为5类的情况下，提取每类中具有最高灰色关联度的温度测点，得到的最终结果为传感器T3、T5、T7、T12、T16. 为了验证测点优化结果在机床Ⅰ不同工况下的热误差建模效果，使用转速为2 000 r/min的数据进行建模，预测转速为3 500 r/min的热误差变化，如图10所示为使用原始全部测点和使用所提方法选出的测点的预测结果对比图. 不同测点选择方案下机床Ⅰ的热误差模型预测残差e比对图如图11所示. 其中方案①为通过原始全部测点进行热误差建模；方案②为同时考虑温度传感器间的欧氏距离和相关系数，即本研究所提方法；方案③为仅考虑温度测点之间的欧氏距离；方案④为仅考虑温度测点之间的相关系数；方案⑤为仅考虑各温度测点的灰色关联度，取前几个关联度高的点作为热误差模型输入. 各方案建立的模型采用均方根误差（root mean squared error, RMSE）与平均残差（mean absolute error, MAE）进行评估，结果如表2所示. 可以看到，方案②在不同工况下的热误差预测性能（RMSE和MAE最小）较好. 与原始采用16个测点所建立的热误差模型（方案①）相比，方案②选出的优化测点不但大大减少了实验所需的传感器数量，而且拥有更高的预测精度，降低了实验成本和模型的复杂程度. 相比较方案③、④、⑤的建模预测结果，融合了欧氏距离和相关系数后的传感器差异性聚类有更好的预测效果.

图8~11的分析结果表明，本研究所提方法不仅提高了模型预测精度，通过GA还能够自动选出最佳的权重系数和聚类个数，避免了传统经验选点方式的不确定性. 从表2中可以看出，与使用全部测点的方案①相比，所提方法的RMSE=0.770 μm，模型的预测精度提高了24%.

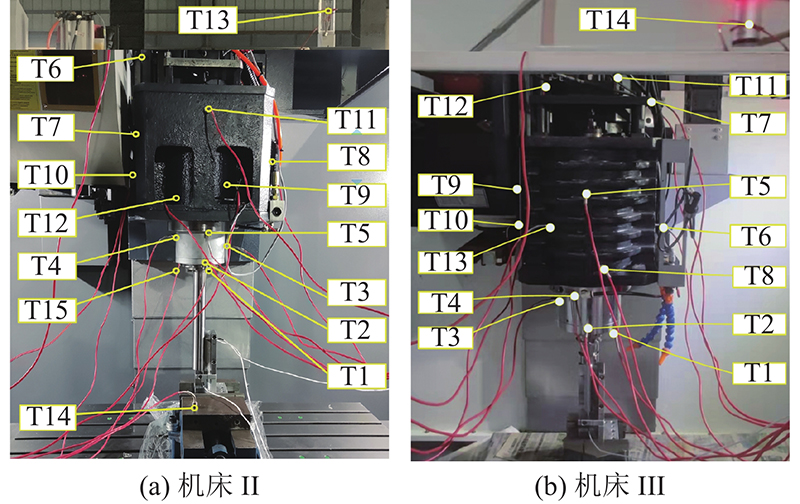
采用机床Ⅱ、Ⅲ对图6所示的测点优化流程进行验证. 2台验证机床的实验平台设置如图12所示，其中位移传感器布置与机床Ⅰ的相同，温度传感器布置分别如表3、4所示，温度传感器安装位置如图13所示. 对机床Ⅱ，在转速为2 000~8 000 r/min的工况下进行多次热误差实验，记录温度和热误差从机床启动到热平衡的时间段数据. 以转速为8 000 r/min的实验数据为基础，实现改进的系统聚类过程，根据灰色关联分析的结果筛选重要测点作为GA-SVR模型的输入. IGA与OGA的具体参数设置如下：C∈(0,100]、 g∈(0,1000]，种群数为20，变异概率为0.95，交换概率为0.8，最大迭代次数为200. 设置OGA的适应度函数为 $f ={{\left( {{R_{4\;000}} + {R_{6\;000}}} \right)}}/{2}$，迭代找到最小适应度对应的最佳温度测点. 经分析计算，选取的最优测点为T1、T2、T6、T14. 机床Ⅲ进行相同的多转速实验，设置OGA的适应度函数为 $f ={{\left( {{R_{3\;000}} + {R_{4\;000}}} \right)}}/{2}$，经分析处理计算得到的最佳分类数为5，最优的权重系数为0.46，最优测点为T1、T8、T11、T12、T14. 可以看出，虽然不同型号机床的内部结构和工作条件不同，同时受到预先布置测点位置的影响，得到的最优测点不同，但是3台机床的最优测点均含主轴轴承位置和电机所在的位置的热敏感点以及与机床自身发热关系较小的点位（如机床Ⅰ的T16、机床Ⅱ的T14以及机床Ⅲ的T14），说明这些测点对于热误差建模的精度有积极的作用.

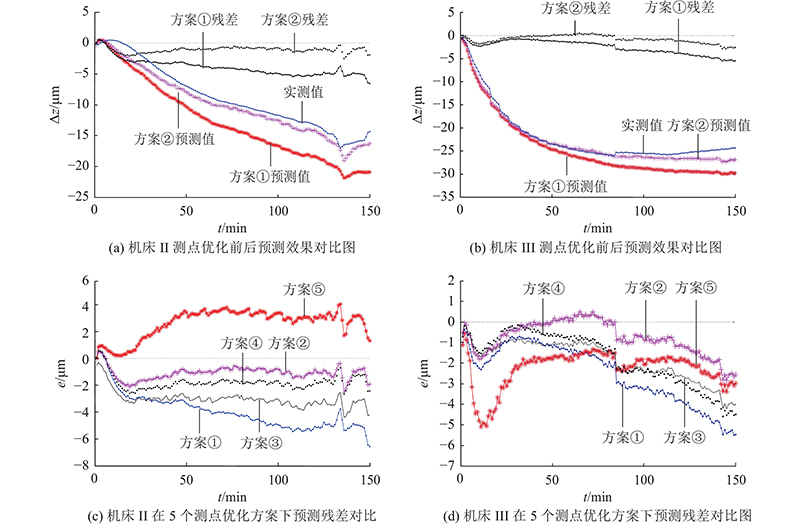
以6 000 r/min工况下建立的机床Ⅱ、Ⅲ热误差模型预测4 000 r/min的热误差， 5种测点选择方式的预测模型评估结果如表5所示，2台验证机床的预测效果比对图和残差比对如图14所示.多机床下的热误差实验表明，由于温度传感器之间的相关性过高，预设的温度传感器中的冗余信号多，对热误差建模产生不利影响，导致与测点优化后的结果相比预测误差较大. 采用方案②选取温度测点作为热误差模型的输入，在机床Ⅱ、Ⅲ的实验中，分别使预测均方误差从4.162 μm降到1.200 μm、2.883 μm降到1.106 μm，精度分别提高了71%和62%，与机床Ⅰ的实验结果类似，方案②是5种方案中预测性能最好的. 分析机床Ⅱ的数据，使用方案④的预测误差小于使用方案③的，根据GA迭代结果中的最优权重系数可以看出，机床Ⅱ的温度传感器聚类是以相关系数为主导，因此该机床测点用相关系数聚类的效果优于欧氏距离聚类. 对于方案⑤，从3台机床实验结果中均可以看出，仅采用灰色关联度排序得到的各温度测点均得不到较好的预测模型. 原因是没有考虑温度测点之间的相关性和距离的因素导致信息缺失或者冗余. 通过列举的3台机床的实验研究结果可知，构建融合相关系数和欧氏距离的差异性矩阵进行系统聚类分析具有多机床适用性，不仅大大减少了温度传感器的布置量，还有效地提高了预测模型精度.

结合改进的系统聚类方法和灰色关联度分析优化机床主轴系统的温度测点，通过在不同工况条件下多机床的实验，验证了所提方法的有效性和通用性. 实验结果表明，优化后的机床温度测点数大幅减少，并均能够得到较优的热误差模型. 在3组机床试验中，与采用未经优化的测点建立的热误差模型预测精度相比，使用本研究提出的优化测点方法建立的热误差模型预测精度分别提升了24%、71%和62%. 与其他选点方案相比，所提测点选择方法不仅在模型的预测精度上最优，还能够适应不同工况下的热误差模型预测，避免温度变量耦合的影响，提高热误差模型的鲁棒性. 采用双层GA分别对聚类个数，组合权重系数，SVR模型的惩罚参数、核参数进行寻优；本研究所提方法可以自适应地选出最优的测点；建立最优的热误差模型；避免了传统的经验选择法带来的不确定性. 为了检验所提出方法的有效性和普适性，本研究仅选用不同型号相同类型的机床进行验证，下一步计划将所提方法应用于如数控车床、车铣复合机床的不同类型数控机床，并开展相关研究.