受断层破裂方向性效应和滑移效应的影响，脉冲型地震动常发生在近断层区域，表现出高幅值、短持时和典型的长周期特性^[1-2]. 建筑结构在脉冲型地震动作用下易发生严重破坏^[3-4]. 钢框架结构已普遍应用于住宅、厂房、桥梁等多种建筑形式. 研究钢框架结构在脉冲型地震动作用下的特性对指导断层区钢框架结构的抗震设计具有重要意义^[5]. 结构在地震作用下的状态水平，既取决于结构固有的抗力水平，更受地震引起的荷载效应的影响. 结构地震需求概率模型旨在通过输入地震环境参数和结构参数获取结构内力或变形反应的概率分布^[6]. 由地震易损性曲线可以得到结构或构件在给定地震动参数下结构发生或达到预定状态失效的条件概率^[7]. 由于能够充分考虑影响结构荷载效应各因素的随机性，结构地震需求概率模型在结构地震易损性分析中扮演着重要角色^[8]. 建立脉冲型地震动作用下钢框架结构的地震需求概率模型对断层区钢框架结构基于可靠度的抗震设计具有重要意义.

在结构易损性分析中，采用增量动力分析法（incremental dynamic analysis，IDA）、云图法建立的地震需求概率模型已被广泛用于钢框架结构的易损性分析^[9]. 王伟等^[10]基于增量动力分析法，研究节点性能对多层梁贯式支撑钢框架地震易损性的影响. 乔云龙等^[11]基于Open SEES有限元分析软件，采用增量动力分析法研究黏滞阻尼器对高层钢结构地震易损性的影响. 李钢等^[12]基于Abaqus有限元软件采用增量动力分析法，研究地震作用下人字形中心支撑钢框架结构因支撑部分失效导致的长耗能梁-偏心支撑机制对结构抗震性能的影响. 郑文豪^[13]基于Etabs有限元软件采用非线性动力时程分析方法，研究不同位置薄弱层对钢框架抗震性能的影响. 徐善华等^[14]基于静力弹塑性分析和增量动力分析法，提出锈蚀钢框架地震易损性的评估方法. 这些研究为揭示钢框架结构在脉冲型地震动作用下的破坏机理和模式做出重要贡献；多种可行的钢框架结构设计优化方案对提高钢框架结构的抗震安全水平具有重要意义. 在这些研究中，地震需求模型通常简化为荷载效应与地震动参数或与谱加速度参数的简单线性函数，不能充分反映结构地震需求的潜在随机性. 由于地震需求模型形式过于简单，当结构参数或地震动参数变化时，易损性曲线并不能做出相应调整.

本研究选用文献[15]中介绍的9层和20层钢框架结构，建立钢框架结构的Abaqus有限元模型，计算钢框架结构在65条典型脉冲型地震动作用下的最大底部剪力、最大底部弯矩、最大层间位移角和顶层位移反应. 文献[16]建议采用底部剪力法或振型分解反应谱法计算钢框架结构的地震作用，基于力学原理计算钢框架结构的地震反应. 不能体现参数随机性的方法在可靠度的分析中常被称为确定性方法，力学模型、材料性质与实际结构存在差异是不可避免的，因此确定性方法结果常存在固有偏差. 为了获取具有明确力学和物理意义的地震需求概率模型，本研究以确定性方法为基础，通过增加具有实际物理意义的修正项消除固有偏差，建立钢框架结构的地震需求概率模型，并基于贝叶斯方法优化模型和估计模型参数. 以20层钢框架结构为例，采用所提出的地震需求概率模型估计钢框架结构的地震易损性曲线，并对比已有的分析结果.

地震需求概率模型是通过已知的结构参数和地震作用参数来估计结构地震荷载效应大小的数学表达式. 在结构地震易损性分析中，地震需求是易损性曲线的重要随机性来源. 为了使地震需求概率模型参数具有明确的物理意义，Gardoni等^[17-18]提出在已知确定性模型的基础上增加修正项来建立结构的无偏估计抗震能力和地震需求概率模型. 确定性模型与概率模型不同，概率模型获得的是概率分布，确定性模型仅得到确切的值. 为了使用方便，确定性模型通常为由力学原理导出的，具有明确物理含义的表达式，如规范中规定的公式. Gardoni等^[17-18]所提方法已被应用于多种结构形式的地震易损性分析^[19-20]，本研究将基于此方法建立脉冲型地震动作用下钢框架结构的地震需求概率模型：

(1) $ \ln \;[D({\boldsymbol{x}},{\boldsymbol{\theta}} )]{\text{ = ln\;[}}\hat d({\boldsymbol{x}})]+\gamma ({\boldsymbol{x}},{\boldsymbol{\theta}} )+\sigma \varepsilon . $

式中： $D({\boldsymbol{x}},{\boldsymbol{\theta}} )$为地震需求， $ \hat d({\boldsymbol{x}}) $为确定性方法计算的地震需求， $ \gamma ({\boldsymbol{x}},{\boldsymbol{\theta}} ) $为用于修正确定性方法固有偏差的修正项， $ {\boldsymbol{x}} $为模型的输入参数， ${\boldsymbol{ \theta}} $ = [θ₁, θ₂, ···, θ_p]为模型参数向量，ε为服从标准正态分布的随机变量，σ为模型的标准差. 式（1）中的 $ D({\boldsymbol{x}},{\boldsymbol{\theta }}) $采用对数形式是为了满足3条特性假设：同方差性（σ不依赖 $ {\boldsymbol{x}} $）、正态性（ε服从标准正态分布）、可加性（σε可线性添加至模型）. 除对数变换外，其他变换形式也可以满足这3条假设，也可以通过综合对比分析确定最优的变换形式. 在文献[17]中， $ \gamma ({\boldsymbol{x}},{\boldsymbol{\theta}} ) $被表示为解释项 $ {h_i}({\boldsymbol{x}}) $(i = 1, 2, ···, p)的线性组合：

(2) $ \gamma ({\boldsymbol{x}},{\boldsymbol{\theta}} ){\text{ = }}\sum\limits_{i = 1}^p {{{{\theta}} _i}{h_i}({\boldsymbol{x}})} . $

为了充分考虑不同因素的潜在影响，在进行模型预估时，通常先尽可能多地选择解释项，再通过分析剔除贡献较小的解释项. 本研究通过贝叶斯方法估计模型参数并优化解释项，以获取形式更为简洁的地震需求概率模型，主要步骤如下. 1）赋予 ${\boldsymbol{ \theta}} $ = [θ₁, θ₂, ···, θ_p]、σ先验分布. 由于尚未获知各参数的相关信息，给各参数赋均值等于0、标准差等于100的正态分布. 建立贝叶斯回归分析模型，输入观测数据，计算各参数的后验分布和变异系数. 2）若解释项h_k在模型中贡献较大，则对应参数θ_k的变异系数较小，反之亦然. 因此，将变异系数最大的参数θ_m对应的项h_m从模型中剔除. 3）重复步骤1）、2），若在某次删除解释项时模型的标准差σ比前一步增大10%或比初始值增大20%，σ发生显著增长，说明该解释项对模型具有显著的贡献，则停止剔除解释项，并保留最后剔除的解释项. 当θ_i与θ_j（i≠j）间的皮尔逊相关系数绝对值 $\left| {{\rho _{{\theta _i}{\theta _j}}}} \right| \geqslant 0.7$时，认为 $ {h_i}({\boldsymbol{x}}) $、 $ {h_j}({\boldsymbol{x}}) $高度相关. 为了获取更为简洁的地震需求概率模型将 $ {h_i}({\boldsymbol{x}}) $、 $ {h_j}({\boldsymbol{x}}) $合并.

(3) $ {\hat \theta _i} = {\mu _{{\theta _i}}}+{\rho _{{\theta _i}{\theta _j}}}\frac{{{\sigma _{{\theta _i}}}}}{{{\sigma _{{\theta _j}}}}}({\theta _j} - {\mu _{{\theta _j}}}). $

式中： ${\mu _{{\theta _i}}}$、 ${\sigma _{{\theta _i}}}$分别为θ_i的后验分布均值和标准差. 参考文献[17]，当 $\left| {{\rho _{{\theta _i}{\theta _j}}}} \right| \geqslant 0.7$时采用式（3），用θ_j替代θ_i.

根据式（1），在基于力学原理的确定性方法基础上增加修正项，得到钢框架结构地震需求概率模型. 文献[16]规定了2种计算地震作用的方法：底部剪力法和振型分解反应谱法. 本研究采用具有普遍适用性的振型分解反应谱法计算地震作用，基于力学基本原理计算结构的地震反应，以此作为确定性方法. 1）计算结构的前n阶振型和周期，建立振型向量、质量矩阵、振型参与系数等；计算地震动加速度反应谱，得到结构前n阶振型对应的加速度反应谱值. 2）基于振型分解反应谱法计算钢框架结构在每阶振型下各质点的水平地震作用. 3）由各振型各质点的水平地震作用力依次求出各振型的层间剪力，按照SRSS（square root of the sum of the squares）组合方法，获得组合后的层间剪力：

(4) $ {V_i} = \sqrt {\sum\limits_{j = 1}^n {{V_{ij}}^2} } . $

式中：V_ij为第i层j振型的层间剪力值. 若采用时程分析方法可以获取底部剪力V₁的时程，通常取最大值作为代表值. 本研究采用非线性时程分析方法计算框架结构最大底部剪力V_max. 考虑楼板的约束作用，假设每层水平面刚度无穷大，可认为梁柱线刚度比无穷大，满足反弯点法的适用条件. 假定底层反弯点位于支座高度H的2/3处，底部最大弯矩为

(5) $ {M_{\max }} = \frac{{2H}}{3}{V_{\max }}. $

根据反弯点法，分别计算第i层第j个柱子的抗推刚度d_tj和每层的抗推刚度D_ti：

(6) $ {d_{tj}} = \frac{{12{i_{cj}}}}{{{h_i}^2}},\;{D_{ti}}{\text{ = }}\sum\limits_{j = 1}^k {{d_{tj}}} . $

式中：i_cj为第i层第j个柱子的线刚度；h_i为第i层柱子的高度，即i层层高.

(7) $ { \varDelta_i}={\frac{V_i}{D_{t i}}},\; \delta_i={\frac{\varDelta_i}{h_i}}. $

式中：Δ_i为层间位移，δ_i为层间位移角. 从各层层间位移角中选取最大值，作为最大层间位移角δ_max. 将求得的层间位移Δ_i逐层累加，得到顶层位移为

(8) $ d{\text{ = }}\sum\limits_{i = 1}^n {{\varDelta _i}} . $

使用Abaqus建立钢框架结构有限元分析模型，通过非线性动力时程分析获取式（1）中的地震需求 $ D({\boldsymbol{x}},{\boldsymbol{\theta}}) $，以此为数据基础进行模型优化和模型参数标定. 选用9、20层钢框架结构模型^[15]作为建模分析对象. 这2个结构模型分别对应实际工程中的中层和高层钢框架结构. 在2种钢框架结构模型中，梁采用A36钢（屈服强度为248 MPa），柱采用A992Fy50钢材（屈服强度为345 MPa）. 9层钢框架梁截面为1~2层W36×160、3~6层W36×135、7层W30×99、8层W27×84、9层W24×68；柱子采用I形截面；柱底与基础刚接，柱间距为9.15 m；1层层高为5.49 m，2~9层的层高均为3.96 m. 20层钢框架梁截面为1~4层W30×99、5~10层W30×108、11~16层W30×99、17~18层W27×84、19层W24×62、20层W21×50；柱间距为6.10 m；1层层高为5.49 m，2~20层层高均为3.96 m；内柱采用I形截面，边柱采用箱型截面. 这2种钢框架结构的具体信息参阅文献[15]. 考虑材料非线性和几何非线性，在动力时程反应分析时，模型采用二维梁单元建立，钢框架阻尼比设为0.05，阻尼模型采用瑞利（Rayleigh）阻尼. 9层框架模型的前3阶振型对应的自振周期分别为2.26、0.85、0.49 s，20层框架模型的前3阶振型对应的自振周期分别为3.75、1.28、0.74 s，数值与文献[15]提供的参考值基本一致.

在传统的分析中，通常通过视觉检查判断地震动是否为脉冲型地震动. 为了消除人工识别过程中的主观性误差，学者们提出多种定量识别脉冲型地震动的方法^[21-23]，并给出大量可供选取的脉冲型地震动记录. 如Baker^[21]基于小波分析方法提出定量识别脉冲型地震动的方法，并从NGA-West 1地震动数据库中选取91条脉冲型地震动数据. 但在这些数据中，一些被划分为脉冲类别的数据表现出较弱的脉冲特性. 本研究旨在分析钢框架结构在典型的强脉冲型地震动作用下的地震需求. 鉴于脉冲型地震动易出现在大震级地震的近场区域，Zhao等 ^[24]从文献[21]选取的91条数据和文献[25]搜集的54条数据中选取65条矩震级不小于5级，断层距不超过20 km，且速度时程中包含显著脉冲的典型脉冲型地震动数据. 本研究以这65条典型脉冲型地震动记录为数据基础，构建钢框架结构在脉冲型地震动作用下的4种不同形式的地震需求概率模型.

分别采用确定性方法和有限元方法计算2种钢框架结构模型在65条脉冲型地震动作用下的最大底部剪力、最大底部弯矩、最大层间位移角和顶层位移反应，并以此为数据基础，建立4种地震需求概率模型，并估计模型参数.

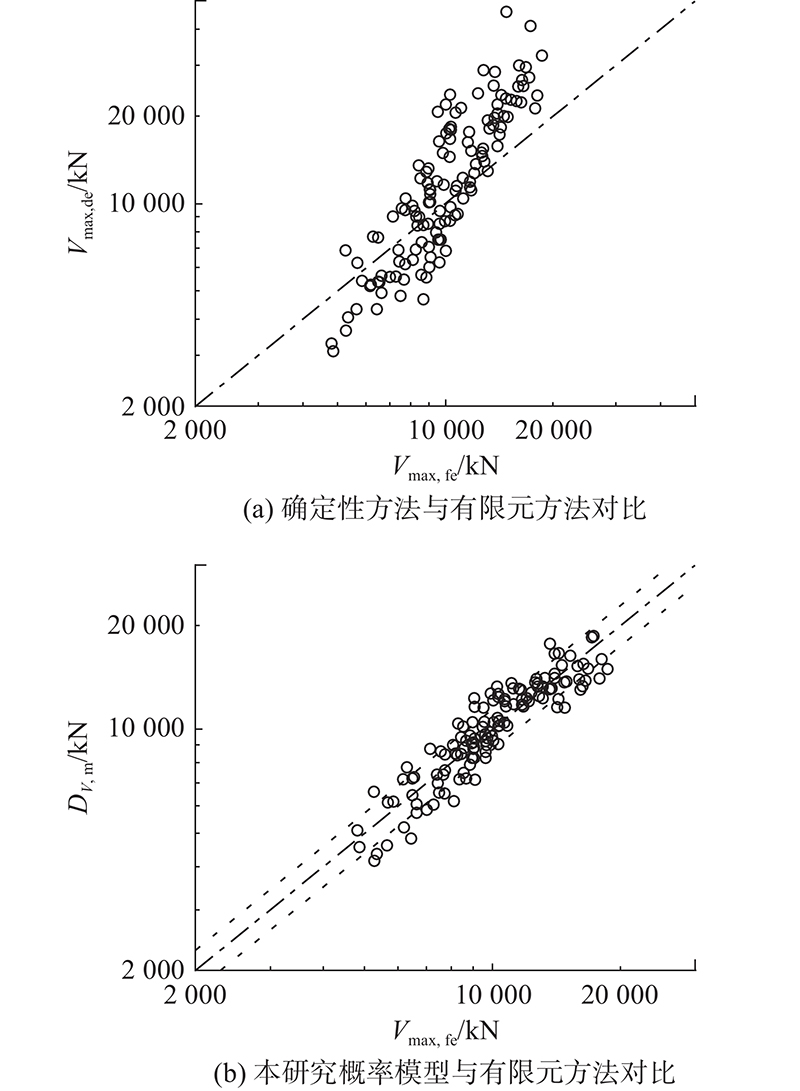
如图1（a）所示为采用确定性方法计算的最大底部剪力V_max,de与有限元数值解V_max,fe的对比. 当结构的最大底部剪力反应较小时，确定性方法结果偏小，当最大底部剪力反应较大时，确定性方法结果偏大. 因此采用确定性方法计算的结构最大底部剪力存在固有偏差. 为了修正模型的固有偏差，并综合考虑不同因素的潜在影响，应尽可能多地选取解释项. 为了修正模型中独立于变量之外的潜在偏差，取 $ {h_1}({\boldsymbol{x}}){\text{ = }}1 $；考虑层数N对模型的影响，取 $ {h_2}({\boldsymbol{x}}){\text{ = }}N $；考虑脉冲型地震动的影响，选取多个地震动参数作为解释项：断层距R为 $ {h_3}({\boldsymbol{x}})$、剪切波速 ${V_{{\text{s}},30}} $为 $ {h_4}({\boldsymbol{x}}) $、脉冲周期 ${T_{\text{p}}}为 $ $ {h_5}({\boldsymbol{x}}) $、峰值加速度 ${\text{ PGA}} $为 $ {h_6}({\boldsymbol{x}}) $、峰值速度 ${\text{ PGV}} $为 $ {h_7}({\boldsymbol{x}}) $、峰值位移 ${\text{ PGD}} $为 $ {h_8}({\boldsymbol{x}}) $、里氏烈度 ${I_{\text{a}}} $为 $ {h_9}({\boldsymbol{x}}) $、结构自振周期对应的5%阻尼比时的加速度反应谱值 ${S_a}({T_1},5 \text{%} ) $为 $ {h_{10}}({\boldsymbol{x}})$.

如表1所示为模型进行优化和参数估计的筛选过程. 在分析步1中，10个解释项均参与计算，模型标准差后验分布的均值μ(σ_V)=0.127. 此时在所有参数中θ_V3的变异系数最大. 为了简化模型，在分析步2中舍弃 $ {h_3}({\boldsymbol{x}}) $. 模型标准差后验分布的均值μ(σ_V)=0.128，说明 $ {h_3}({\boldsymbol{x}}) $对模型的贡献量可忽略不计，即不能为模型提供有效的信息. 在分析步7中，当将 $ {h_7}({\boldsymbol{x}}) $删除后，模型标准差后验分布均值μ(σ_V)发生显著变化，由0.136增长至0.165. 因此， $ {h_7}({\boldsymbol{x}}) $能够为模型提供不可忽略的有效信息. 最终的模型采取分析步6的分析结果，即模型中包含5个解释项.

通过分析各参数之间的相关性，发现 $ {\theta _{_{{V1}}}} $与 $ {\theta _{_{{V2}}}} $、 $ {\theta _{_{{V7}}}} $与 $ {\theta _{_{{V8}}}} $之间的线性相关系数分别为−0.81和−0.75，存在显著的相关性. 为了获取更为简洁的模型形式，根据式（3）对参数进行替代，选取层数的系数 $ {\theta _{_{{V2}}}} $代替常数的系数 $ {\theta _{_{{V1}}}} $，选取峰值地面速度PGV的系数 $ {\theta _{_{{V7}}}} $代替峰值地面位移PGD的系数 $ {\theta _{_{{V8}}}} $，即 ${\hat \theta _{_{{V1}}}} = 0.403\;4 - 15.052\;5{\theta _{_{{V2}}}}$和 ${\hat \theta _{_{{V8}}}} = 0.000\;815 - 0.45{\theta _{_{{V7}}}}$, 最终的最大底部剪力概率模型为

(9) $ \begin{split} \ln \;[{D_{{_V}}}({\boldsymbol{x}},&{{\boldsymbol{\theta}} _{{_V}}})] = {{\ln\;[}}{{\hat d}_{{_V}}}({\boldsymbol{x}})]+0.403\;4 - 15.052\;5{\theta _{_{{V2}}}}+\\ & {\theta _{_{{V2}}}}N+{\theta _{_{{V7}}}}{\text{PGV}}+(0.000\;815 -\\ &{\theta _{_{{V10}}}}{S_{\text{a}}}{\text{(}}{T_{\text{1}}}{\text{,5\% )}}+0.45{\theta _{_{{V7}}}}){\text{PGD}} + {\sigma _{{_V}}}{\varepsilon _{{_V}}}. \end{split} $

式中同时包含PGV和PGD项，而PGD/PGV可作为描述地震动频率成分的重要参数，因此式（9）中虽未包含脉冲周期，但在一定程度上也考虑了地震动频率成分的影响. 模型参数的均值μ，标准差σ和相关系数ρ信息如表2所示. 如图1（b）所示为基于式（9）概率模型估计的中值D_v,m与有限元数值解的对比，其中虚线为模型中值±1倍的模型标准差. 图1（b）的数据点规律分布在45°线附近，比图1（a）数据点的离散程度更小，表明所提概率模型修正了确定性方法中的固有偏差，可以获取有限元数值解的无偏估计.

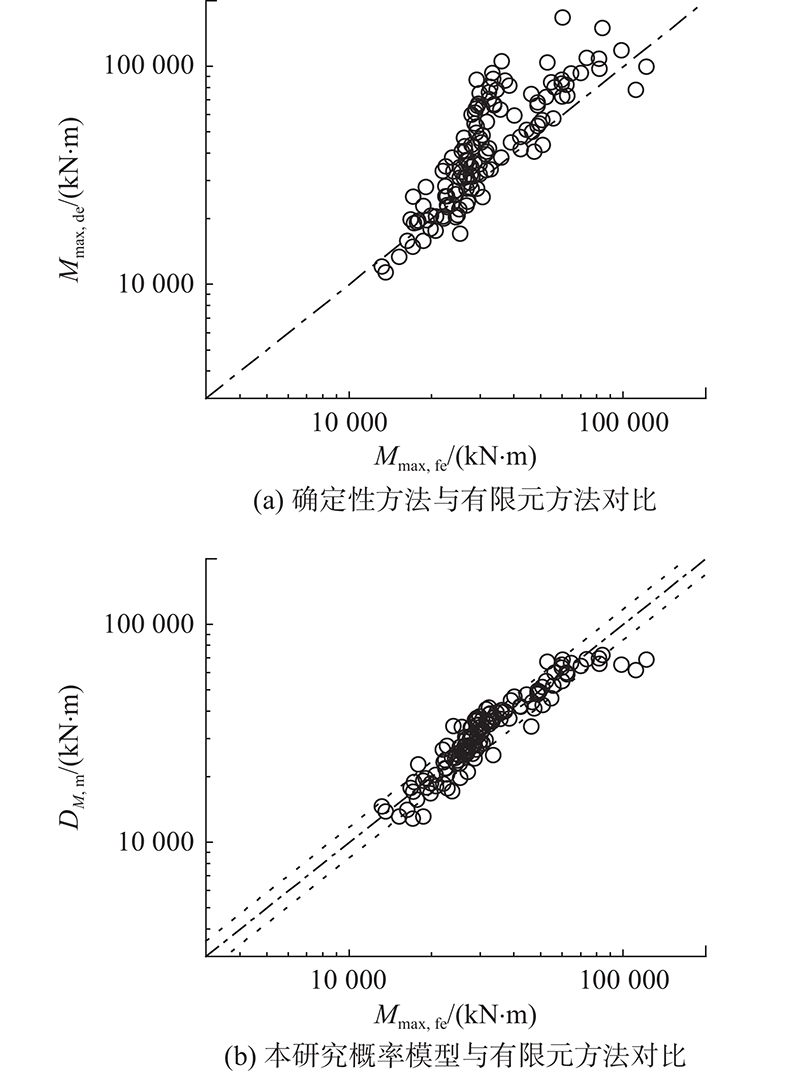
如图2（a）所示为采用确定性方法计算的最大底部弯矩M_max,de与有限元数值解M_max,fe的对比. 可以看出，确定性方法与有限元结果之间存在较大的差异，整体上按规范的计算结果显著偏大. 确定性方法采用的力学假设与结构实际的受力状态之间存在差异，未考虑材料的非线性性质均是导致这一差异的主要原因. 结构的内力及位移反应通常受同一组参数的影响，因此使用底部剪力模型中使用的解释项修正后续概率模型，同时将确定性方法计算出的最大底部剪力值V_max作为修正项 $ {h_{11}}({\boldsymbol{x}}) $以提高模型的精度. 通过基于分析各参数的后验分布的模型优化，最终保留的解释项为h₁、h₂、h₁₀和h₁₁. 分析表明 $ {\theta _{_{{M1}}}} $与 $ {\theta _{_{{M2}}}} $、 $ {\theta _{_{{M10}}}} $与 $ {\theta _{_{{M11}}}} $之间的线性相关系数分别为−0.83和−0.98，存在显著的相关性. 为了简化模型形式，根据式（3），选取层数的系数 $ {\theta _{_{{M2}}}} $代替常数的系数 $ {\theta _{_{{M1}}}} $，选取谱加速度值的系数 $ {\theta _{_{{M10}}}} $代替最大底部剪力的系数 $ {\theta _{_{{M11}}}} $，即 ${\hat \theta _{_{{M1}}}} = 0.221\;0 - 13.772\;8{\theta _{M2}}$ 和 ${\hat \theta _{_{{M11}}}} = - 0.029\;52 - 0.205\;7{\theta _{_{{M10}}}}$. 最终的最大底部弯矩概率模型为

(10) $ \begin{split} \ln\; [{D_{{_M}}}({\boldsymbol{x}},&{{\boldsymbol{\theta}} _{{_M}}})] ={{\ln\;[}}{{\hat d}_{{_{M}}}}({\boldsymbol{x}})]+(0.221\;0 - 13.772\;8{\theta _{_{{M2}}}})+ \\ &{\theta _{_{{M2}}}}N+{\theta _{_{{M10}}}}{S_{\text{a}}}{\text{(}}{T_1}{\text{,5\% ) }}+ \\ &( - 0.029\;52 - 0.205\;7{\theta _{_{{M10}}}}){V_{\max }} +{\sigma _{_{{M}}}}{\varepsilon _{_{{M}}}}. \\[-9pt] \end{split} $

如表3所示为最大底部弯矩概率模型参数的详细信息. 如图2（b）所示为采用所提概率模型估计的最大底部弯矩中值 $D_{{_{M,m}}} $与有限元数值解的对比，其中虚线为模型中值±1倍的模型标准差. 图2（b）的数据点整体分布在45°线处，未出现明显的偏离和波动，表明所提概率模型可以修正确定性方法的固有偏差，且经修正后估计值的离散程度显著降低.

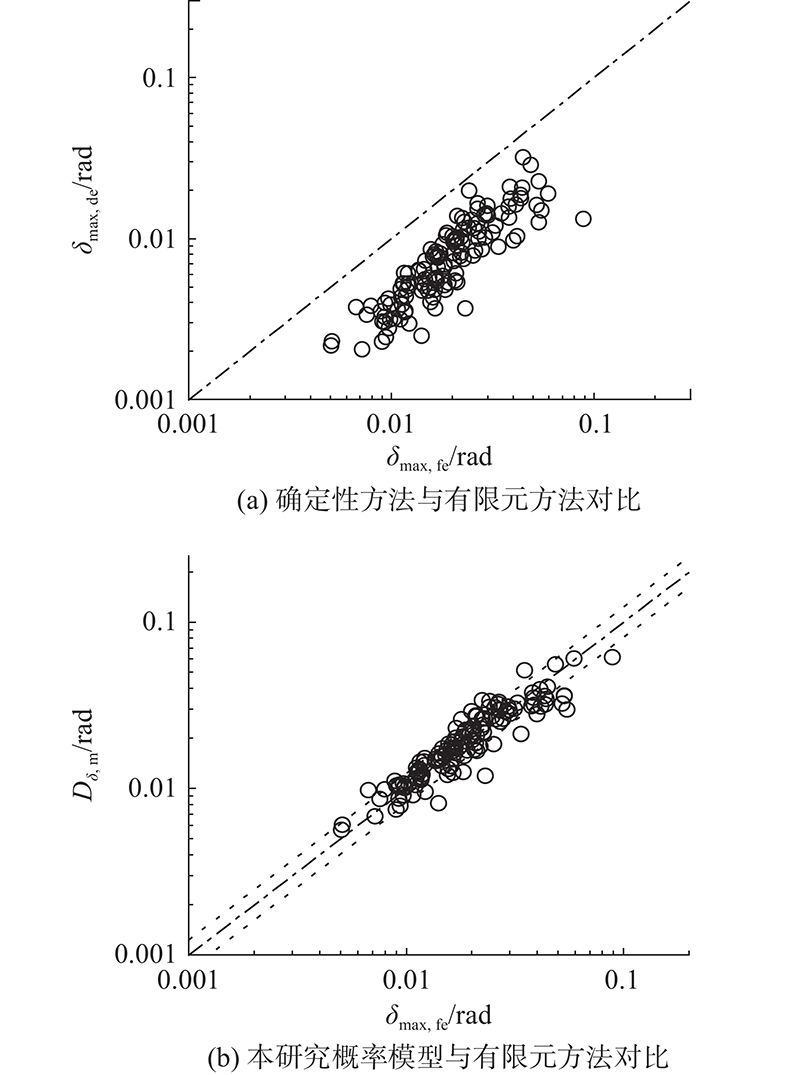
如图3（a）所示为采用确定性方法计算的最大层间位移角 $\delta _{{\rm{max,de}}} $与有限元数值解 $\delta _{{\rm{max,fe}}} $的对比. 可以看出，确定性方法结果显著小于有限元数值解. 有限元分析考虑了确定性方法未考虑材料的塑性，是导致这一差异的本质原因. 因此，采用确定性方法会显著低估结构的最大层间位移角. 通过模型优化，最终保留的解释项为h₁、h₂、h₈和h₁₀，且分析发现 $ {\theta _{{\delta} 1}} $与 $ {\theta _{{\delta} 2}} $之间存在显著的相关性. 根据式（3），选取层数的系数 $ {\theta _{{{\delta} 2}}} $代替常数的系数 $ {\theta _{{\delta} 1}} $，即 $\hat \theta _{{{\delta}1}} = 1.094 - 15.008 \theta _{{{\delta} 2}}$. 最终的最大层间位移角的概率模型为

(11) $ \begin{split} \ln \;[{D_{\delta} }({\boldsymbol{x}}, &{{\boldsymbol{\theta}} _{\delta} })] = {{\ln \;[}}{{\hat d}_{\delta} }({\boldsymbol{x}})]+(1.094 - 15.008{\theta _{{\delta} 2}}) +{\theta _{{\delta} 2}}N+\\ & {\theta _{{\delta} 8}}{\text{PGD}} + {\theta _{{\delta} 10}}{S_{\text{a}}}{\text{(}}{T_{\text{1}}}{\text{,5\% )}}+{\sigma _{\delta} }{\varepsilon _{\delta} }. \\[-9pt] \end{split} $

如表4所示为最大层间位移角概率模型的详细参数信息. 如图3（b）所示为所提模型求取的最大层间位移角中值 $D_{{\delta},m} $与有限元数值解的对比. 可以看出，所提概率模型能够较好地估计结构的最大层间位移角，有效修正了确定性方法中的固有偏差，且估计值的离散程度比确定性方法更小.

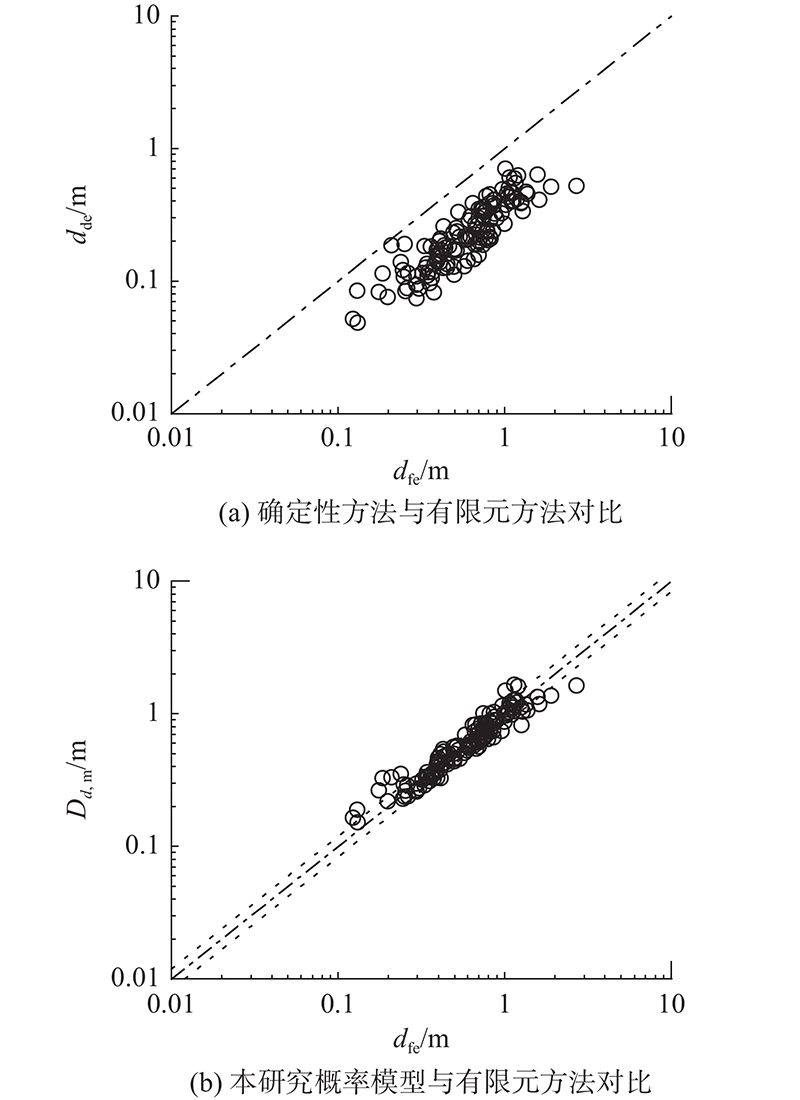
如图4（a）所示为采用确定性方法计算的顶层位移d_de与有限元数值解d_fe的对比. 可以看出，确定性方法计算得到的顶层位移明显小于有限元数值结果，且呈现出较大的离散性. 确定性方法未考虑材料的塑性性质是导致这一差异的主要原因. 通过模型优化，最终保留的解释项为h₁、h₂、h₅、h₆、h₁₀和h₁₁. 通过参数分析发现， $ {\theta _{{{d6}}}} $与 $ {\theta _{{{d9}}}} $、 $ {\theta _{{{d10}}}} $与 $ {\theta _{{{d11}}}} $之间线性相关系数分别为−0.7和−0.99，存在显著的相关性. 选取峰值地面加速度PGA的系数 $ {\theta _{{{d6}}}} $代替里氏烈度的系数 $ {\theta _{{{d9}}}} $，选取反应谱值的系数 $ {\theta _{{{d10}}}} $代替剪力的系数 $ {\theta _{{{d11}}}} $，即 ${\hat \theta _{{{d9}}}} = - 0.032 - 0.077{\theta _{{{d6}}}}$和 ${\hat \theta _{{{d11}}}} = - 0.012\;8 - 0.222\;4{\theta _{{{d10}}}}$. 最终的顶层位移概率模型为

(12) $ \begin{split} {D_{{d}}}({\boldsymbol{x}},&{{\boldsymbol{\theta}} _{{d}}}) = {{}}{{\hat d}_{{d}}}({\boldsymbol{x}})+{\theta _{{{d1}}}}+{\theta _{{{d2}}}}N+{\theta _{{{d5}}}}{T_{\text{p}}}+{\theta _{{{d6}}}}{\text{PGA}} +\\ &( - 0.032 - 0.077{\theta _{{{d6}}}}){I_{\text{a}}}+{\theta _{{{d10}}}}{S_{\rm{a}}}({T_1},5{\text{% }}) +\\ &( - 0.012\;8 - 0.222\;4{\theta _{{{d10}}}}) {V_{\max }}+{\sigma _{{d}}}{\varepsilon _{{d}}}. \\ \end{split} $

顶层位移概率模型参数详细信息如表5所示. 如图4（b）所示为采用概率模型估计的顶层位移中值D_d,m与有限元数值解的对比. 可以看出，所提概率模型能够修正确定性方法中的固有偏差，且模型增加修正后项后能够降低结果的离散性.

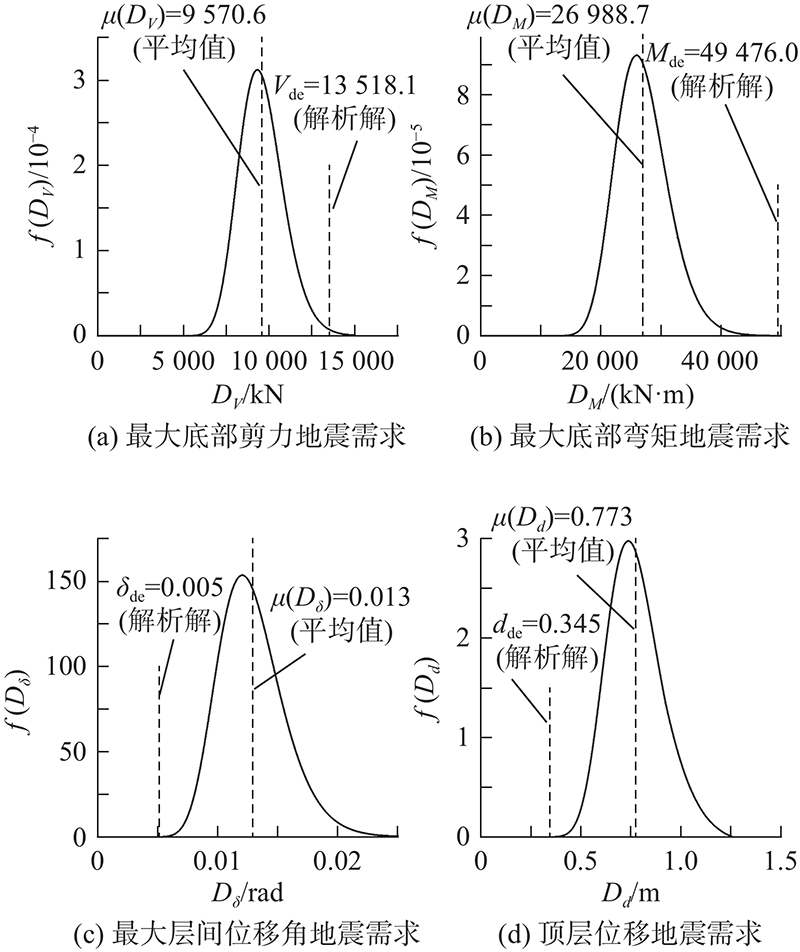
本研究基于贝叶斯方法提出的钢框架结构4种地震反应的无偏估计概率模型不需要进行有限元动力分析，即可得到与有限元分析一致的结果. 以20层钢框架为目标结构，以1971年San Fernando地震（矩震级M_w = 6.6）Pacoima Dam台站数据为例，计算其相关参数作为荷载参数，采用所提概率模型估计4种不同地震需求，并与确定性方法得到的解析解进行对比，如图5所示. 可以看出，采用确定性方法可以获取地震需求的1个估计值，所提方法可以获取地震需求的概率分布. 对于最大底部剪力和底部弯矩的地震需求，采用确定性方法计算的结果明显偏于保守. 由于确定性方法中未能考虑材料的非线性，其最大层间位移角和顶层位移的估计值明显小于所提方法的概率估计均值.

易损性曲线能够直观反映目标结构在不同地震强度指标下的失效概率，已被广泛应用于各种结构形式的地震安全分析. 地震需求是易损性曲线的重要随机因素来源. 本研究结合所提地震动需求模型和文献[26]、[27]给出的结构能力参数，计算20层钢框架的易损性曲线. 结构的失效概率计算式为

(13) $ {P_{\rm{_f}}}({\mu _{\rm{_D}}} \geqslant {\mu _{\rm{_C}}}|{S_{\rm{a}}}({T_1}) = x) = \varPhi \left(\frac{{\ln \;({{\bar \mu }_{\rm{_D}}}/{{\bar \mu }_{\rm{_C}}})}}{{\sqrt {\beta _{\rm{_C}}^2+\beta _{\rm{_D}}^2} }}\right). $

式中： $ \;{\mu _{\rm{_D}}} $为结构地震需求均值， $ \;{\mu _{\rm{_C}}} $为能力参数均值， $ {S_{\rm{a}}}({T_1}) $为结构第一振型周期T₁对应的谱加速度， $\;\beta _{\rm{_C}} $、 $\;\beta _{\rm{_D}} $分别为结构能力参数和需求参数的对数标准差，Φ为标准正态分布的分布函数. 在框架结构的易损性分析中，通常采用层间位移角作为破坏指标，对于不同的破坏状态通常定义不同的层间位移角阈值. 本研究采用式（11）计算20层钢框架结构的地震需求. 为了获取目标结构在脉冲型地震动作用下更具代表性的易损性曲线，采用65条脉冲型地震动的平均加速度反应谱确定式（11）中的谱加速度. 经过统计分析，对于本研究所选脉冲型地震动，当PGA=1g时，PGD的平均值为133 cm，按照该比例确定式（11）中PGD的取值. 李玉占等^[26-27]建立了20层钢框架结构^[15]有限元分析模型，并给出最终的结构易损性曲线，但所选地震数据为普通类型地震动，未考虑脉冲型地震动的影响. 李玉占等^[26]定义了3种破坏状态：不需修理仍可继续使用（IO）、结构的主体倒塌临界状态（CP）、整体动力失稳状态（GI）；对应的能力参数阈值分别为 $ \delta _{\max }^{{\text{IO}}} = 0.007 $、 $ \delta _{\max }^{{\text{CP}}} = 0.029 $、 $ \delta _{{\text{max}}}^{{\text{GI}}} = 0.036 $. Guo等^[27]定义的结构倒塌的能力参数阈值为 $ {\delta _{\max }} = 0.02 $.

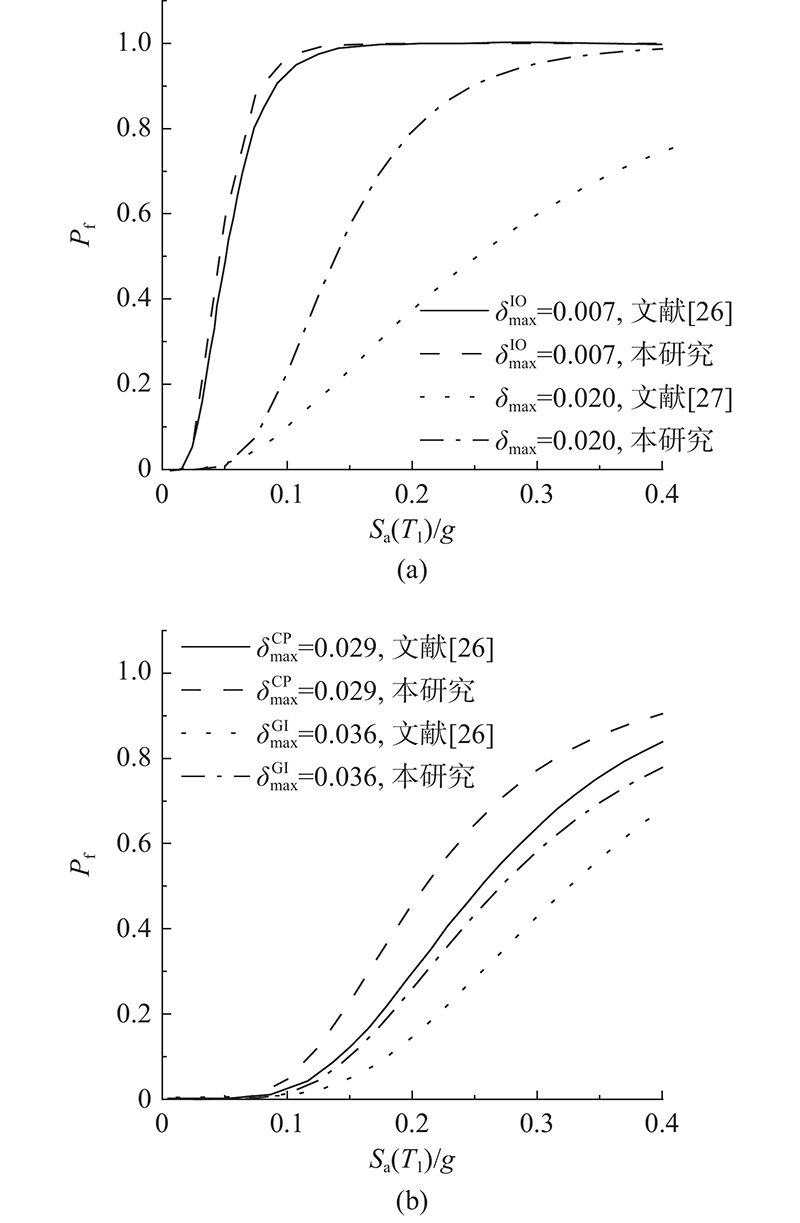
如图6所示为采用所提地震需求模型并结合能力参数获取的易损性曲线与其他文献中的易损性曲线. 可以看出，在不同破坏状态下，即当能力参数阈值δ_max取不同值时，钢框架结构在脉冲型地震动作用下的失效概率均大于其在普通类型地震动作用下的失效概率. 当层间位移角限值较小时，如 $ \delta _{\max }^{{\text{IO}}} = 0.007 $，结构处于弹性阶段. 由于结构未发生塑性变形和累积损伤，当谱加速度一致时，结构在脉冲型地震动作用下和普通类型地震动作用下的状态应接近. 因此，对于 $ \delta _{\max }^{{\text{IO}}} = 0.007 $，本研究所得的易损性曲线与文献[26]的易损性曲线接近. 这也可以作为所提地震需求概率模型具有可靠性的例证. 此外，所提地震需求模型还与结构参数相关，当结构参数发生变化时，所提模型不需要重新通过有限元计算结构的地震需求即可获取新的结构易损性曲线.

（1）基于力学原理得到钢框架结构4种地震需求的确定性方法计算结果. 分析表明，相对于有限元模拟结果，确定性方法计算结果通常偏于保守且未能考虑各参数的随机性. 在确定性方法的基础上增加修正项，得到地震需求概率模型，使模型参数具有明确的物理意义. 采用贝叶斯方法进行模型优化和参数估计以充分考虑各参数的不确定性，最终获取了4种地震需求的无偏估计概率模型.

（2）4种地震需求概率模型均与层数相关，即当框架结构层数改变时，结构的响应将发生明显变化. 除顶层位移概率模型外，其余3种地震需求概率模型均与PGA无关. 当选择谱加速度作为解释变量之一时，增加PGA不再提供显著的有效信息以提高模型的精度. 脉冲周期、脉冲幅值是衡量脉冲型地震动特性的重要参数. 顶层位移概率模型与脉冲周期显著相关，其余3种概率模型均直接或间接与脉冲幅值（PGV或PGD）相关. 脉冲地震动的特征参数是影响脉冲型地震动作用下钢框架结构地震反应的重要因素，在模型中考虑脉冲参数的影响能够提高模型的精度.

（3）所提地震需求概率模型可以为科学评估脉冲型地震动作用下钢框架结构的地震需求、分析地震易损性提供方法参考和理论依据. 案例分析表明，钢框架结构在脉冲型地震动作用下的易损性曲线明显大于其在非脉冲型地震动作用下的易损性曲线. 与普通类型地震动相比，钢框架结构在脉冲型地震动作用下更易发生破坏. 所提地震需求概率模型可以应用于与美国土木工程师协会提出的9层和20层钢框架基准模型相近的钢框架结构. 所提模型是否能够在参数差别较大的钢框架结构中应用，须结合结构实例进行深入讨论与分析后决定.

（4）本研究侧重于钢框架结构的地震需求概率模型. 地震需求、抗震能力和损伤指标是影响结构地震易损性分析结果的3个重要因素. 在后续的研究中将开展有关抗震能力概率模型和考虑不同破坏状态的损伤指标的研究工作，以在钢框架结构的地震易损性分析中，充分应对各因素的潜在随机性影响.