半监督学习(semi-supervised learning, SSL)方法有效利用标签和无标签样本,改善模型的分类准确性和泛化性,成为近年来模式识别领域中关注和研究的重点之一.
为了防止半监督学习任务被单一损失主导,当前多采用损失权重分配方法,主流方法有关联函数法与人工先验调整法. 利用人工先验方法计算权值相对比较简单,但流程较复杂. Laine等[9]在π-model模型中通过多次实验,将最优检测准确率的参数设置为损失的权值. Lee[4]提出Pseudo Label方法,在平衡熵最小化损失和分类交叉熵损失的过程中,提出调节系数α作为熵最小化损失的权值. Tarvainen等[5]提出Meanteacher方法,通过多次实验确定一致性约束权重. Laine等[9,16]提出利用关联函数的方法进行动态调节权值参数,如无监督数据增强 (unsupervised data augmentation, UDA)方法. 然而人工调整权重系数的方法过于依赖先验知识,基于关联函数的方法需要对各个约束项间的关联进行建模, 流程较复杂.
1. 统一的半监督损失函数框架
根据分类交叉熵损失、熵最小化损失、一致性损失函数在优化目标上基于距离度量差值的共性,将各个损失函数转换为基于余弦距离度量的半监督损失函数. 提出基于伪标签的一致性损失,在一致性损失函数中加入标签作为评价指标,与其他损失函数在计算形式上达成一致,合并得到统一的半监督损失函数. 传统的分类交叉熵损失、熵最小化损失、一致性损失公式如下所示:
式(1)为分类交叉熵损失函数. 式中:f为模型
式(2)为熵最小化损失函数. 式中:y'为无标签数据对应的伪标签,
式(4)为一致性损失函数. 式中:
1.1. 基于余弦距离度量的半监督损失函数构建
余弦距离度量采用夹角余弦值评估数据间的相似性,表达式为
式中:X1、X2为2个不同的向量. 与传统距离度量相比,余弦距离度量方式更加注重2个向量在方向上的差异,数学意义满足本文统一函数的构造要求,可以实现交叉熵损失函数、熵最小化损失函数、一致性损失函数公式的统一.
引入基于余弦度量的类内相似度sp与类间相似度sn,用于描述嵌入向量和类别特征向量之间的相似度. 模型嵌入向量
将分类交叉熵损失、熵最小化损失与一致性损失统一转换为类内相似度和类间相似度的表达式. 分类交叉熵损失函数的转换过程如下:
基于余弦度量的分类交叉熵损失函数
基于余弦度量的分类交叉熵损失函数
1.2. 基于伪标签的一致性损失函数
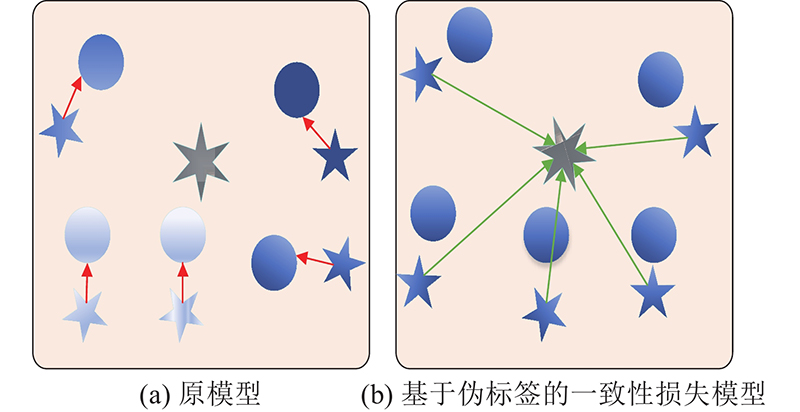
一致性损失函数表示扰动前、后嵌入向量的输出差值,在计算过程中无须考虑伪标签类别,这与分类交叉熵损失函数和熵最小化损失函数的形式不统一. 提出基于伪标签的一致性损失函数,在已知嵌入向量的伪标签类别及熵最小化损失约束的条件下,嵌入向量将靠近对应伪标签类别的proxy向量. 将扰动后的嵌入向量和对应伪标签类别的proxy向量的距离度量作为一致性损失,保证嵌入向量扰动前、后的输出值差异最小化. 基于伪标签的一致性损失构建示意图如图1所示. 图1(a) 中,有向线段表示一致性损失,不同圆点表示不同无标签数据对应的嵌入向量,五角星表示对应扰动后的嵌入向量. 图1(b) 中,有向线段表示伪标签一致性损失,圆点表示已知伪标签的嵌入向量,五角星表示数据扰动后的嵌入向量. 图1中,六角星表示伪标签所对应的嵌入向量. 基于伪标签的一致性损失可以视为扰动后嵌入向量的熵最小化损失,公式可以表示为
图 1
图 1 一致性损失与熵最小化损失的示意图
Fig.1 Schematic diagram of entropy minimization and consistency loss
式中:
基于伪标签的一致性损失函数的优化目标可以表示为
综上所述,基于伪标签的一致性损失函数为基于带标签信息的余弦相似度差值,其形式与分类交叉熵损失(式(6))及熵最小损失函数(式(7))相同. 以上损失函数可以统一为基于度量的损失框架,最终框架如式(9)所示. 本文专注于优化度量损失中优化目标的设定,提升了半监督学习效果.
2. 损失函数框架优化
2.1. 特征向量和嵌入向量优化映射方法
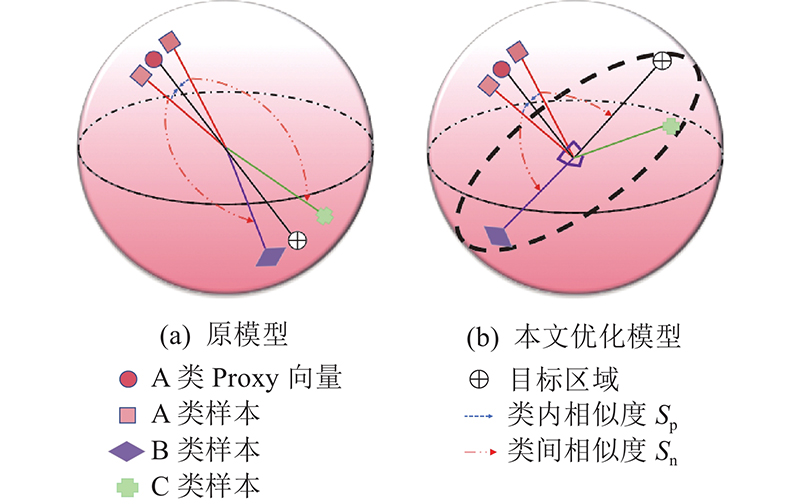
目前,基于距离度量的损失函数在对嵌入向量进行优化时,与当前标签不同类别的嵌入向量的优化目标均被设定为与当前类别proxy特征向量相反的区域. 如图2(a) 所示,优化类别A的嵌入向量被定位于对应的proxy特征向量附近,类别B与类别C的样本会被优化至类别A的proxy特征向量相反的附近位置,造成类别B与C的样本嵌入向量的冲突,模型的分类性能下降. 通过改进特征向量和嵌入向量映射的方法来消除冲突,思路如图2(b) 所示. 将不同类别嵌入向量的优化目标定位为正交于当前类别proxy特征向量的位置,既保证了非同类嵌入向量的分离性,又避免了嵌入向量优化过程的冲突问题,以获得具备较强鲁棒性的半监督分类模型.
图 2
图 2 嵌入向量与特征向量优化方法的示意图
Fig.2 Schematic diagram of optimization method of embedd-ing vector and feature vector
设计自适应类内相似度权重
根据模型优化的要求可知,同类嵌入向量越靠近越好,类间嵌入向量需要正交,即
2.2. 间距系数和缩放因子
损失用于分类时,分类决策面为
当使用余弦相似度作为度量时,对分类权重与分类向量w、 f进行归一化处理,余弦相似度数值范围将缩小,梯度范围相应减小,导致模型更新速率减慢. 添加
2.3. Unify Loss函数
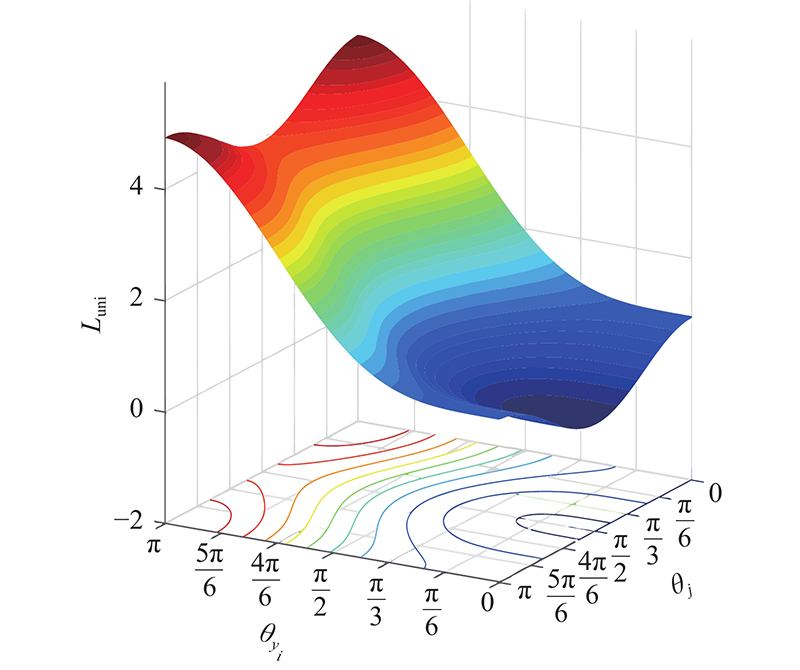
在式(9)的基础上,经过上述改进,得到完整的Unify Loss函数,形式如下.
本文得到的Unify Loss函数专注于优化
图 3
3. 实验与分析
3.1. 梯度分析
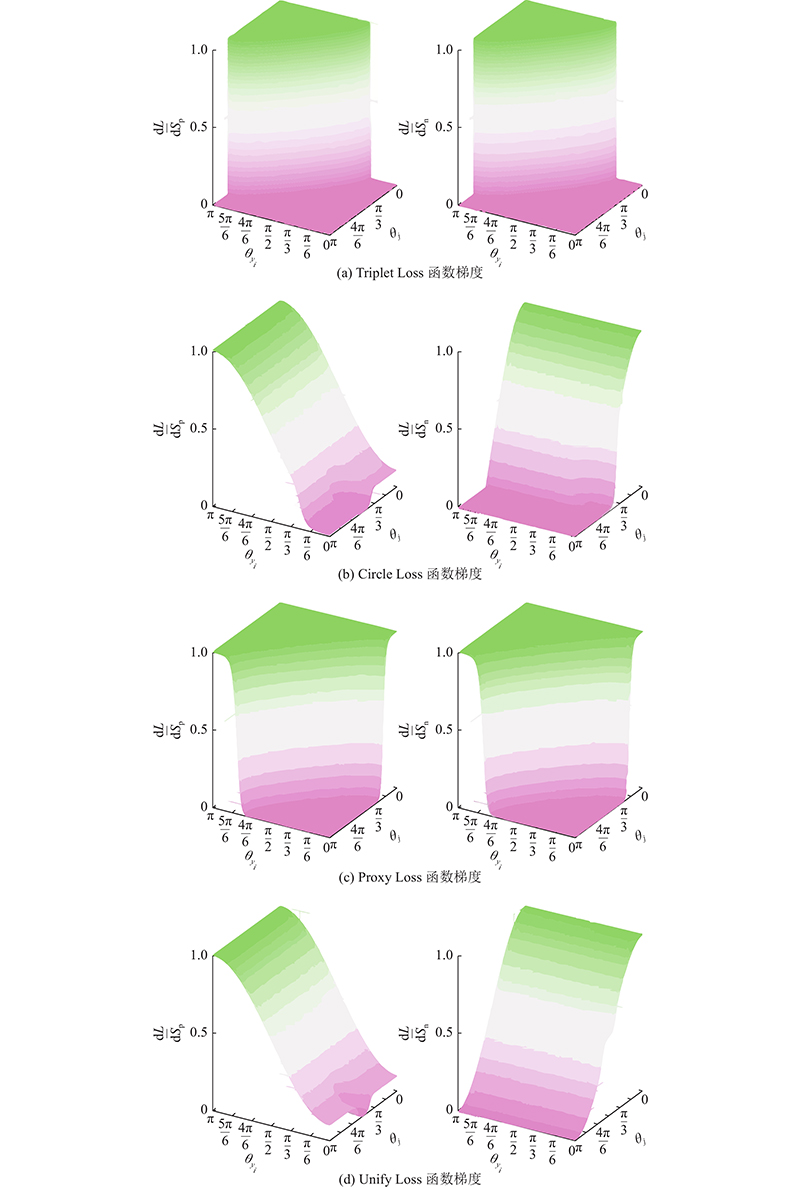
由于模型的优化速率与函数求解过程中的梯度直接相关. 对常用的Triplet Loss、Proxy Loss、Circle Loss函数与Unify Loss函数进行梯度分析,结果如图4所示. 对
图 4
3.2. 实验数据集
表 1 各数据集的训练及测试样本分布
Tab.1
| 数据集 | N | Nt | |
| Nl | Nu | ||
| SVHN | 40 | 70 000 | 26 000 |
| 250 | 70 000 | ||
| 4 000 | 70 000 | ||
| CIFAR-10 | 40 | 50 000 | 5 000 |
| 250 | 50 000 | ||
| 4 000 | 50 000 | ||
| CIFAR-100 | 400 | 40 000 | 10 000 |
| 1 000 | 40 000 | ||
| 10 000 | 40 000 | ||
| STL-10 | 1 000 | 10 000 | 8 000 |
| 5 000 | 10 000 | ||
| Pneumonia Chest X-ray | 250 | 4 750 | 600 |
| 500 | 4 500 | ||
| 1 000 | 4 000 | ||
3.3. 实验设计
实验采用MeanTeacher、MixMatch、UDA、Remixmatch、Fixmatch、Flexmatch、虚拟对抗网络(virtual adversarial training, VAT)算法[5-7,22-25],与本文算法进行对比. VAT算法结合半监督思想与对抗网络(generative adversarial network, GAN),运用GAN网络中生成器与判别器2类模块生成器相互博弈学习的方式,提高样本利用率. MeanTeacher与UDA算法模型均采用一致性正则方法,通过一致性损失提高无标签样本的利用率,其中UDA算法使用无监督数据增强策略,分类准确性较MeanTeacher有一定的提高. MixMatch与Fixmatch是整合一致性正则、多视图训练优势的混合方法. 其中MixMatch利用数据增强方法与无监督损失函数,提高无标签样本的利用率;Fixmatch对无标签样本进行增强,使用交叉熵形式的正则化损失计算增强后样本的损失. 这2类方法整合多方优势,均取得较好的结果. Flexmatch算法在Fixmatch的基础上,提出课程伪标签方法(curriculum pseudo labeling, CLP),通过动态调节伪标签置信度阈值,增加模型不同训练阶段获得的伪标签样本数量. 为了对比各算法的性能,各算法均采用小规模网络CNN13[5]和大规模网络ResNet18,用于训练CIFAR-10、CIFAR-100、SVHN、STL-10数据集与Pneumonia Chest X-ray数据集. 不同算法使用相同的网络结构,优化器、学习率及batch size都设置为相同值. 其中优化器使用默认的SGD算法,学习率选用cosine衰减方法,初始学习率设定为0.03,衰减速率
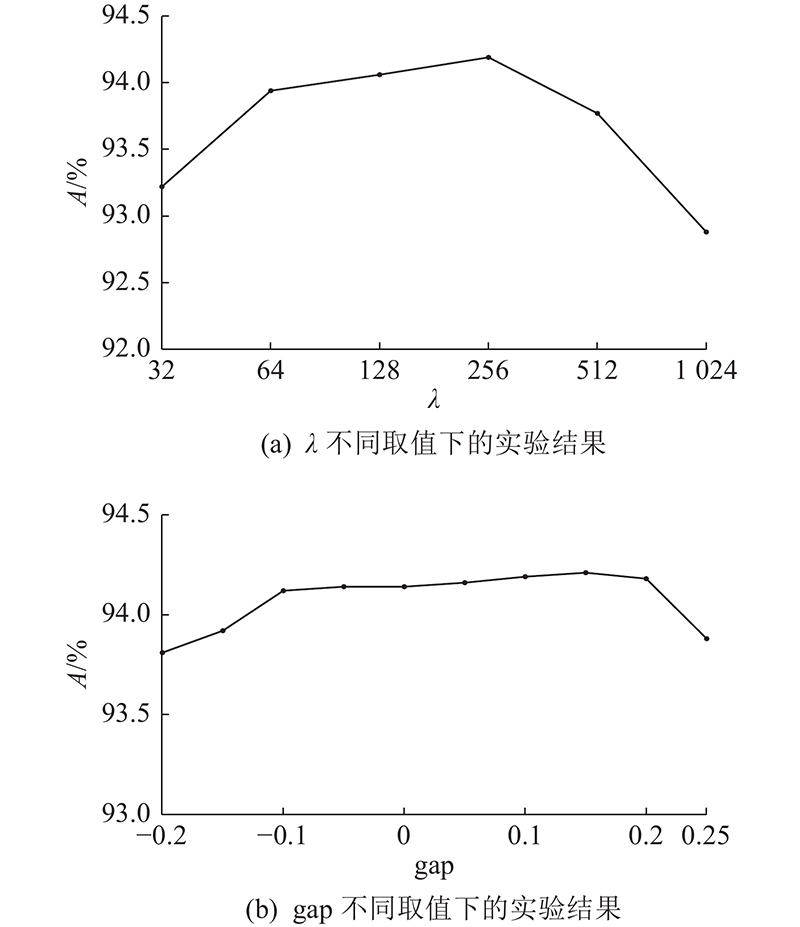
3.4. 参数对比
对Unify Loss函数中的2个超参数
如图5所示为标签数为4 000时参数在各取值下的分类结果. 图中,A为准确率. 如图5(a)所示为
图 5
3.5. 仿真结果分析
表 2 各方法在CIFAR-10、CIFAR-100、SVHN、STL-10数据集中的准确率
Tab.2
| 方法 | CIFAR-10 | CIFAR-100 | SVHN | STL-10 | ||||||||||
| Nl = 40 | Nl = 250 | Nl = 4000 | Nl = 400 | Nl = 1000 | Nl = 10000 | Nl = 40 | Nl = 250 | Nl = 4000 | Nl = 1000 | Nl = 5000 | ||||
| VAT | 27.41 | 53.97 | 82.59 | 5.12 | 12.89 | 53.20 | 35.64 | 79.78 | 90.06 | 68.77 | 81.26 | |||
| MeanTeacher | 26.54 | 55.52 | 83.79 | 4.94 | 12.13 | 55.13 | 36.45 | 78.43 | 93.58 | 69.01 | 82.80 | |||
| MixMatch | 41.47 | 74.08 | 90.74 | 9.15 | 32.39 | 65.87 | 47.45 | 76.02 | 93.50 | 79.59 | 88.41 | |||
| Remixmatch | 42.32 | 78.71 | 92.20 | 12.98 | 44.56 | 72.33 | 52.55 | 81.92 | 94.67 | 84.33 | 92.89 | |||
| UDA | 44.55 | 81.66 | 92.45 | 10.66 | 40.72 | 71.18 | 47.37 | 84.31 | 95.54 | 82.34 | 92.74 | |||
| UDA_unify | 49.69 | 84.22 | 93.87 | 18.06 | 46.12 | 72.67 | 53.14 | 87.32 | 95.77 | 87.21 | 94.34 | |||
| Fixmatch | 50.17 | 86.28 | 93.11 | 12.65 | 42.95 | 72.08 | 56.41 | 88.75 | 95.94 | 89.68 | 94.58 | |||
| Fixmatch_unify | 55.24 | 89.94 | 94.74 | 18.51 | 47.79 | 73.38 | 65.86 | 90.09 | 96.02 | 93.44 | 95.25 | |||
| Flexmatch | 52.70 | 85.08 | 93.97 | 27.22 | 55.12 | 77.84 | 62.03 | 90.42 | 95.83 | 92.36 | 96.06 | |||
| Unify Loss | 61.19 | 90.33 | 94.25 | 35.35 | 61.75 | 78.11 | 67.35 | 92.47 | 96.17 | 93.42 | 96.51 | |||
表 3 各方法在 Pneumonia Chest X-ray 数据集中的验证结果
Tab.3
| 方法 | A/% | ||
| Nl/N = 5% | Nl/N = 10% | Nl/N = 20% | |
| VAT | 8.62 | 25.71 | 67.12 |
| MeanTeacher | 10.72 | 27.92 | 69.46 |
| MixMatch | 12.24 | 31.62 | 73.86 |
| Remixmatch | 15.07 | 33.78 | 74.02 |
| UDA | 11.87 | 31.89 | 75.31 |
| UDA_unify | 17.66 | 36.46 | 76.55 |
| Fixmatch | 19.12 | 37.22 | 77.54 |
| Fixmatch_unify | 23.55 | 40.91 | 77.67 |
| Flexmatch | 23.38 | 40.67 | 78.76 |
| Unify Loss | 26.57 | 42.26 | 79.24 |
在对CIFAR-10数据集的测试中,当标签数为40时,VAT与MeanTeacher算法的分类准确率分别为27.41%、26.54%,MixMatch、Remixmatch与UDA算法的分类准确率较前2个算法提升了约20%. 5类算法的数据增强方式不同,导致模型的分类准确率差异较大. VAT算法利用标签样本生成对抗样本,在标签数极少的情况下,对抗样本可生成的数量有限,模型分类性能下降. MeanTeacher方法采用一致性约束扩充训练数据,但在标签数严重不足的情况下,为了保证扰动前、后样本的输出一致性,数据扰动范围较小,产生的训练样本有限. MixMatch算法、Remixmatch算法与UDA算法分别采用Weak Augment、CTAugment与RandAugment的数据扩充方式,与传统一致性约束下扩充数据的方法相比,提升了标签数据与无标签数据的有效利用率,获得较好的分类结果. Fixmatch算法综合了UDA与Remixmatch算法中的Strong Augmentation数据增强策略,引入带阈值的交叉熵损失,实现更优的分类效果. 该算法在标签样本数为40时得到了50.17%的分类准确率. Flexmatch算法在Fixmatch的基础上提出CLP方法,给无标签样本设定可动态调整的置信度阈值,以充分利用低置信度样本,方法在标签样本数为40时得到了52.70%的分类准确率. Unify Loss算法保留了Flexmatch的CLP方法,引入本文的损失框架,以取代原算法中的损失函数,方法在标签数为40时得到61.19%的最优分类准确率,与Flexmatch算法相比,分类准确率提高了8.49%. 为了体现本文损失框架的有效性,实验部分在UDA与Fixmatch算法中引入本文损失框架. 改进后的算法与原算法相比,分类效果均有所提升,特别是在标签样本严重匮乏的情况下,分类准确率可以提高5%以上. 在CIFAR-100数据集测试中,图像数量与类别较CIFAR-10大幅增加. 当标签数不足时,VAT模型无法利用足量的标签信息生成对抗样本,导致分类错误率增大. 在MeanTeacher模型中,参数更新过程依赖于标签数量,当标签数量不足以满足模型参数的更新需求时,易导致分类效果降低. 相较于前2种模型对样本标签的依赖性,MixMatch、Remixmatch与UDA算法通过数据增强,提升了在无标签样本上的分类准确性. Fixmatch与Flexmatch方法整合MixMatch、Remixmatch与UDA算法的优势,简化了无标签数据标记方式,以提高模型性能. 当标签样本数为400时,UDA、Fixmatch、Flexmatch算法在引入本文损失后的分类准确率分别提高了7.50%、5.86%与8.13%,当标签样本数量为1 000与10 000时,各改进算法的分类准确率均有所提高.
在SVHN数据集的测试中,当标签数为40时,由于极度缺乏标签信息,导致7种算法对简单数字识别任务的效果不理想. 当标签数为250时,算法的分类检测性能具有明显的提升,均超过75%. 本文的Unify Loss方法分类准确率为92.47%,较VAT算法提升了12.69%,较原Flexmatch方法提升了2.05%. 当标签数由250增加到4 000时,不同算法的提升效果不明显. 这是因为SVHN为门牌号数字,数据变化区域为统一可识别的标准范围. 数字图像的变化程度小,减少了算法对标签的依赖性. 与CIFAT-100相比,分类难度降低,导致标签数超过250以后,不同算法的差异性较小. 相比于VAT和MeanTeacher算法,其余算法在标签数较低时能够有接近50%的分类准确率. 这是因为MixMatch、Remixmatch、UDA等算法运用了特定的数据增强策略,通过在训练过程中合理划分标签和非标签数据,提高样本信息的利用率. 本文的统一损失框架在标签数极度缺乏的情况下,可以有效地提高算法分类性能. 当标签数为40时,与原算法相比,改进后的UDA_unify、Fixmatch_unify、Unify Loss的图像分类准确率分别提高了5.77%、9.45%与5.32%,提升效果明显.
STL-10数据集与SVHN数据集同为10分类数据集,与SVHN数据集相比,STL-10具有更丰富的图像特征,因此模型训练过程中对标签的依赖程度提升. 对比2类数据集的实验结果可知,STL-10数据集需要1 000张带标签数据,才能达到与SVHN标签数为250时相近的分类准确率. 在STL-10数据集测试中,当标签样本数目为1 000时,UDA_unify、Fixmatch_unify、Unify Loss算法相对于原算法的分类准确率分别提高了1.06%、3.76%、4.87%. 实验结果表明,提出的损失应用于特征丰富的图像时具有一定的分类优势.
Pneumonia Chest X-ray为胸腔X射线透视图数据集. 数据集中包含正常与肺炎2类样本,相较于CIFAR-10、CIFAR-100、SVHN与STL-10数据集,Pneumonia Chest X-ray图像的分辨率增大,图像特征丰富,因此分类难度提升. 分析Pneumonia Chest X-ray训练集测试结果可知,当标签样本占比为5%、10%与20%时,本文Unify Loss方法的分类准确率为26.57%、42.26%与79.24%,较原Flexmatch算法的分类准确率分别提高了3.19%、1.59%与0.48%. 在标签样本极少的情况下,本文方法的分类优势明显. 本文方法可以在特定标签难以获取的任务中(如医学图像检测)得到较好的应用,方法具有实用性.
综上所述,Unify Loss方法在5个公开数据集上均获得了最优的分类结果. 仿真结果表明,统一损失后的Unify Loss方法能够有效整合3类损失,避免任务被单一损失主导,提升了模型整体的分类准确率.
4. 结 语
本文提出基于距离度量损失框架的半监督学习方法. 该方法以分类交叉熵损失、熵最小化损失和一致性损失为基础,构建统一损失框架函数(unify loss函数),将其作为半监督任务中的核心损失函数,能够避免多种损失函数的超参数调节. 对比Unify Loss方法与典型半监督学习方法的算法性能,实验结果表明,在不同的图像数据集中,Unify Loss方法只需要少量标签数据就能获得较好的分类结果,具有更好的泛化性和实用性.
下一步将针对实际工程问题展开研究,尤其是对于乳腺癌检测中标签数据缺乏的实际问题,尝试采用本文提出的方法来提高识别准确性.
参考文献
基于图神经网络的地表水水质预测模型
[J].
Surface water quality prediction model based on graph neural network
[J].
Mean teachers are better role models: weight-averaged consistency targets improve semi-supervised deep learning results
[J].
Unsupervised data augmentation for consistency training
[J].
Virtual adversarial training: a regularization method for supervised and semi-supervised learning
[J].
Additive margin softmax for face verification
[J].DOI:10.1109/LSP.2018.2822810 [本文引用: 2]
Regularization with stochastic transformations and perturbations for deep semi-supervised learning
[J].
Semi-supervised learning by entropy minimization
[J].
Interpolation consistency training for semi-supervised learning
[J].DOI:10.1016/j.neunet.2021.10.008 [本文引用: 1]
Labeled optical coherence tomography (oct) and chest X-ray images for classification
[J].
Mixmatch: a holistic approach to semi-supervised learning
[J].
Fixmatch: simplifying semi-supervised learning with consistency and confidence
[J].