时序网络是当前动态复杂网络特征多属性研究的重要领域,时序网络可以更加准确地描述网络演化进程,刻画现实生活中存在的生物网络、社交网络、交通网络和蛋白质网络等[1-5]复杂网络系统的时序演化交互关系. 时序网络研究始于静态网络,经典静态网络节点重要性序结构的研究方法有度中心性[6]、介数中心性[7]、特征向量中心性[8-9]等. 杨松青等[10]结合节点K-shell中心性和结构洞特征,提出基于Tsallis熵的复杂网络节点重要性评估方法. Lu[11]利用相对熵并引入灰色关联度量曲线边缘耦合度,提出基于结构洞和改进TOPSIS的节点重要性评估方法. 苏晓萍等[12]提出基于节点及其邻域结构洞的局部中心性测量方法,可以准确地评价节点传播能力. Zeng等[13]考虑节点混合度和剩余度,提出混合度分解方法. Sun等[14]提出基于熵的自适应节点重要性评估方法,客观地评估节点重要性. 杨杰等[15]提出基于覆盖范围和结构洞影响力最大化算法,挖掘使信息在网络中传播范围最大化的种子节点.
时序多层网络节点重要性辨识是目前网络系统研究的难点,对时序网络中节点的时序化分层提取属性特征,可以有效地表征动态复杂网络的演化过程,揭示动态复杂网络的拓扑结构与动力学系统的内在规律. 在现实生活中,网络包含时间属性,网络节点活跃程度随着时间不断变化. 时序网络节点全时间段内的属性信息变更规律及节点全时间段内的重要性排序结果较静态网络的准确性更高. Kim等[16]将时序图转化为有向静态网络,定义有向时序网络度中心性、介数中心性和紧密度中心性. Taylor等[17]考虑网络多层耦合的方法,分析网络时间层内和层间关系,建立超邻接矩阵,定义基于特征向量中心性指标和节点重要性的评判指标(SAM). 杨剑楠等[18]使用邻居拓扑重叠系数对层间关系进行度量,计算相邻层间的相似性,提出基于节点层间相似性的超邻接矩阵时序网络节点重要性识别方法. 笔者等[19]提出基于时序网络层间同构率动态演化的超邻接矩阵建模重要节点辨识方法,分析时序网络多时间层内节点交互信息对节点重要性排序的影响. 曹连谦等[20]分析节点异质性、层间耦合、层内耦合对网络能控性的影响,给出网络系统能控的充分条件或必要条件.
时序网络领域研究取得初步成果,应注意到在动态多层复杂网络的时序演化过程中,不同时序网络层间节点交互关联信息集结存在冗余,同一时间段内多层网络、层与层之间、层内之间的关联关系存在冗余. 为了有效地剔除动态网络时序演化的大量冗余交互关联信息,提高时序网络节点重要性的辨识准确性,本文提出熵值结构洞时序网络(entropy-valued structural holes temporal networks, ESHT)节点重要性辨识模型. 给出时序网络K-shell广义邻接信息熵、熵值投入比、熵值结构洞等相关定义. 提出熵值结构洞模型,给出相应的算法. 利用SIR模型与Kendall相关系数进行验证,说明模型的有效性及优越性.
1. 理论基础
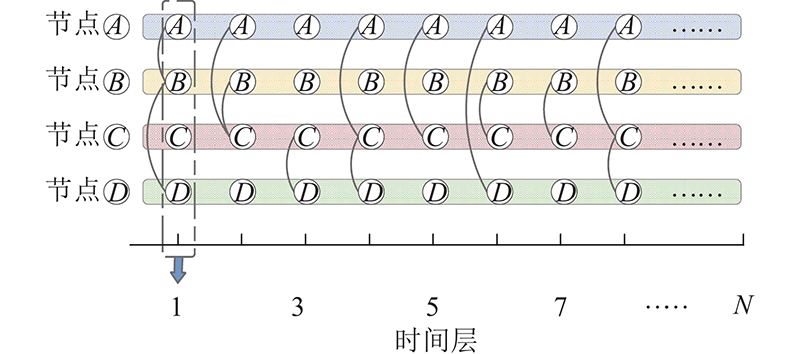
时序网络节点的重要性排序结果在不同时间层内是动态变化的. 在静态多层网络中,节点的邻接信息熵可以提供准确的节点重要性排序信息. 将其延伸至时序网络,则节点在相邻时间层和多个连续时间层内的交互关系会随着时间的推进而不断间断和重连,网络拓扑结构不断演化,如图1所示,静态网络无法描述这一过程. 本文针对动态多层无向无权时序网络节点的重要性进行演化分析,使用邻接度和邻接度概率函数表征节点属性信息. 基于网络K-shell分解,构建K-shell广义邻接信息熵. 本文提出节点熵值结构洞重要性序结构辨识方法,并延伸至时序网络,提出对应的时序网络节点重要性辨识模型.
图 1
图 1 时序多层网络节点信息演化图
Fig.1 Evolution diagram of temporal multilayer network node information
1.1. 广义邻接信息熵
节点邻接信息熵通过研究节点及其直接和间接节点间交互关联关系,利用节点信息熵刻画不同节点在网络中局部影响力的重要性. 网络节点交互关联属性信息通过局部信息熵集结表述更加精准.
设无向网络
邻接度为
其中
邻接度概率函数为
信息熵[21]由香农在1948年提出,指出任何信息都存在冗余,冗余大小与信息中每个符号的出现概率或不确定性有关. 利用概率与统计的方法,表征样本空间所体现的无序化程度.
式中:
节点邻居概率函数. 为了描述不同节点的邻居节点对节点的影响力大小,根据信息熵理论,定义节点邻居概率函数如下:
广义邻接信息熵为
节点邻接信息熵通过集结网络节点多属性度偏好信息,比较全面有效地表征网络各个节点的重要性权重.
1.2. K-shell分解
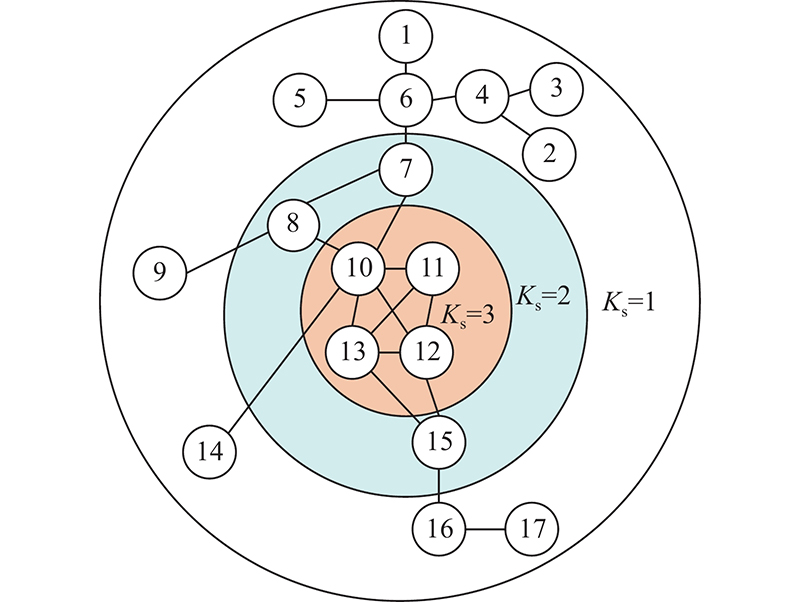
K-shell分解的核心思想是将整个网络划分为从边缘至核心的不同层次,递归地删除网络中节点度值小于或等于
图 2
1.3. K-shell广义邻接信息熵
节点的广义邻接信息熵表征各个节点在网络中不同层间的局部交互关联信息. 在时序网络演化过程中,节点会被网络局部信息影响,网络整体关联信息对每个节点的演化进程起到主导作用. K-shell分解是对网络整体信息等级划分处理的方式,节点
K-shell广义邻接信息熵为
式中:
1.4. 结构洞理论
图 3
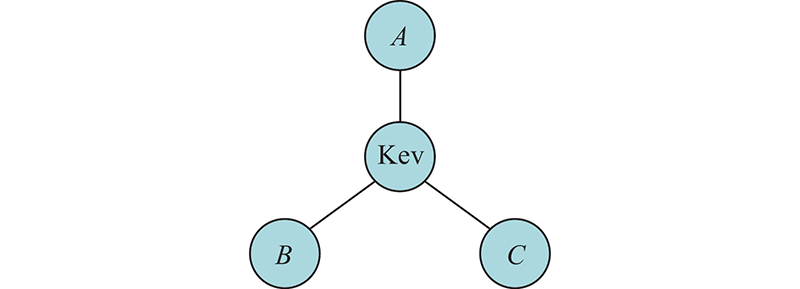
Burt为了衡量网络节点形成结构洞时所受到的约束,提出网络约束系数[22]:
式中:节点
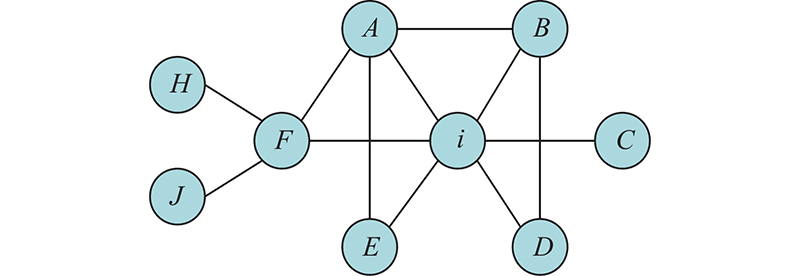
如图4所示,计算节点
图 4
图 4 结构洞约束系数计算的示意图
Fig.4 Schematic diagram of structural hole constraint coefficient calculation
同理可以继续求得
1.5. 熵值结构洞
结构洞理论为寻找网络中的重要枢纽节点提供理论基础. 结构洞计算结合网络中节点的自身度和所计算节点的共同邻居数目,计算出每个节点与共同邻居节点间的贡献程度,得到每个节点的结构洞约束系数. K-shell邻接信息熵可以快速约简,加速网络分层分块,但K-shell信息熵带来较多的冗余信息. 为了有效地解决节点信息的冗余性问题,基于结构洞投入比提出节点熵值投入比:
网络K-shell分解得到节点
基于结构洞理论,提出节点熵值结构洞:
时序多层网络熵值结构洞在计算过程中,将结构洞投入比转换成节点K-shell邻接信息熵投入比,节点K-shell邻接信息熵信息包含网络整体拓扑结构属性和节点局部拓扑信息属性,使得节点在网络全局计算上更加精准.
1.6. 时序多层网络节点重要性的计算模型
熵值结构洞的时序化网络节点重要性计算考虑节点累计效应的影响,将时序多层网络节点在每个时间层内的排序结果进行归一化无量纲处理. 基于以上分析可知,时序网络节点熵值结构洞的重要性系数为
式中:
式(11)中
式(11)中
式(11)中
熵值结构洞计算节点在时序网络中的活跃性系数,根据熵增定律可知,在确定时间层划分长度的情况下,每个时间层内的熵总值为定值. 计算时间层内节点熵值结构洞系数在本层内的占比,可以直观地表述该节点在本层的活跃性占比. 网络时间层依据时间间隔进行均值划分,单一时间层的时间长度比例相等,节点随着时间推进演化,累计节点熵值结构洞系数占比更加合理. 熵值结构洞时序网络计算模型反映节点在一个或多个时间层内节点重要性排序结果的演化规律,避免单一时间层节点活跃性突变导致重要性排序在短时间内发生巨大变化,降低节点影响力突变效应在全时间层内的消极影响.
2. 实证数据分析
2.1. SIR传播模型
使用SIR传播模型,模拟真实网络节点受到感染后的传播过程,统计在时序网络层内稳定状态下的免疫节点数量,计算该节点在当前时间层内的影响力大小. SIR模型将网络中的节点分为以下3类. 1)易感者,其数量记为
2.2. 数据集及相关参数
实验采用Workspace数据集和Email-Eu-core数据集,验证时序多层网络熵值结构洞节点重要性的排序结果. Workspace数据集[23]是2013年6月24日至7月3日在法国一栋办公楼测量到的个人之间面对面交互联系数据集. 面对面接触记录是按照交流时长进行统计,每个场景的总时长不同,因此Workspace数据的单位时间层划分长度为“一天”,即每个时间层的时间范围是24 h. Email-Eu-core数据集[24]利用欧洲一家大型研究机构的电子邮件数据生成的网络数据集,电子邮件时序网络数据包含986个匿名ID在历时803天中产生的交互信息,本文以30 d为一个时间尺度进行划分,截取其中360 d的交互信息进行仿真实验. 网络的基本特征如表1、2所示. 表中,
表 1 Workspace网络的基本特征统计
Tab.1
| T | N | Na | E | 时间段 | | | |
| 1 | 92 | 72 | 188 | 第1~10天 | 4.09 | 28.41 | 0.14 |
| 2 | 92 | 70 | 152 | 第11~20天 | 3.30 | 18.83 | 0.18 |
| 3 | 92 | 59 | 123 | 第21~30天 | 2.67 | 15.39 | 0.17 |
| 4 | 92 | 70 | 186 | 第31~40天 | 4.04 | 28.61 | 0.14 |
| 5 | 92 | 62 | 103 | 第41~50天 | 2.24 | 10.46 | 0.21 |
| 6 | 92 | 68 | 147 | 第51~60天 | 3.20 | 17.93 | 0.18 |
| 7 | 92 | 69 | 151 | 第61~70天 | 3.28 | 19.83 | 0.17 |
| 8 | 92 | 69 | 160 | 第71~80天 | 3.48 | 23.65 | 0.15 |
| 9 | 92 | 68 | 158 | 第81~90天 | 3.43 | 21.54 | 0.16 |
| 10 | 92 | 62 | 94 | 第91~100天 | 2.04 | 8.30 | 0.25 |
表 2 Email-Eu-core网络的基本特征统计
Tab.2
| T | N | Na | E | 时间段 | | | |
| 1 | 851 | 664 | 2863 | 第1~30天 | 62.24 | 1206.43 | 0.05 |
| 2 | 851 | 646 | 2505 | 第31~60天 | 54.46 | 903.61 | 0.06 |
| 3 | 851 | 607 | 1770 | 第61~90天 | 38.48 | 493.30 | 0.08 |
| 4 | 851 | 633 | 2170 | 第91~120天 | 47.17 | 688.20 | 0.07 |
| 5 | 851 | 665 | 3053 | 第121~150天 | 66.37 | 1300.28 | 0.05 |
| 6 | 851 | 676 | 3110 | 第151~180天 | 67.61 | 1364.50 | 0.05 |
| 7 | 851 | 689 | 3236 | 第181~210天 | 70.35 | 1537.57 | 0.05 |
| 8 | 851 | 648 | 2602 | 第211~240天 | 56.57 | 976.17 | 0.06 |
| 9 | 851 | 675 | 2822 | 第241~270天 | 61.35 | 1115.15 | 0.06 |
| 10 | 851 | 671 | 2590 | 第271~300天 | 56.30 | 1008.50 | 0.06 |
| 11 | 851 | 696 | 3198 | 第301~330天 | 69.52 | 1483.78 | 0.05 |
| 12 | 851 | 694 | 3290 | 第331~360天 | 71.52 | 1493.76 | 0.05 |
假设传染者为节点
2.3. 评价方法
实验采用肯德尔相关系数(Kendall’s
式中:
其中
2.4. 实验结果分析
为了验证本文方法的有效性,基于实证网络数据集,使用SIR模型得到节点免疫数量排序分析, 利用
图 5
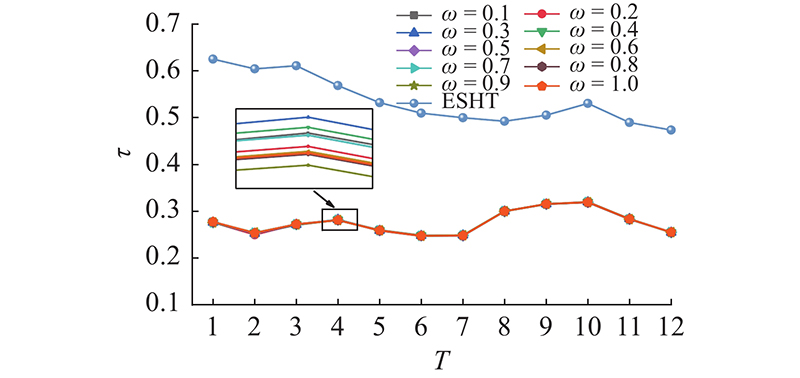
图 5 Workspace数据节点使用ESHT方法与SAM方法排序结果的Kendall相关性系数分析对比
Fig.5 Comparative analysis of Kendall correlation coefficients between sorting results of ESHT and SAM methods for Workspace data nodes
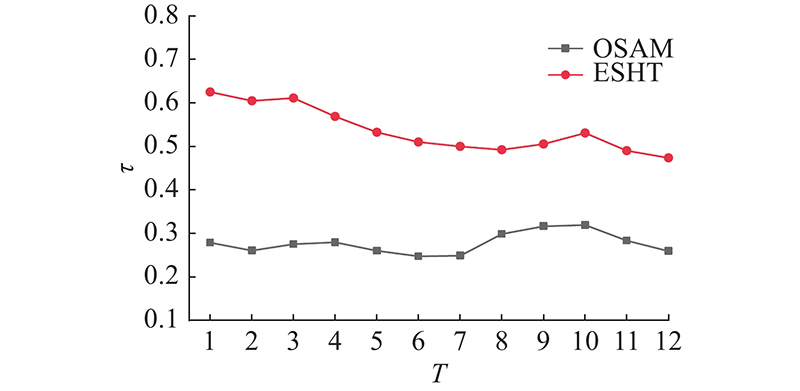
图 6
图 6 Workspace数据节点使用ESHT方法与OSAM方法排序结果的Kendall相关性系数分析对比
Fig.6 Comparative analysis of Kendall correlation coefficients between sorting results of ESHT and OSAM methods for Workspace data nodes
图 7
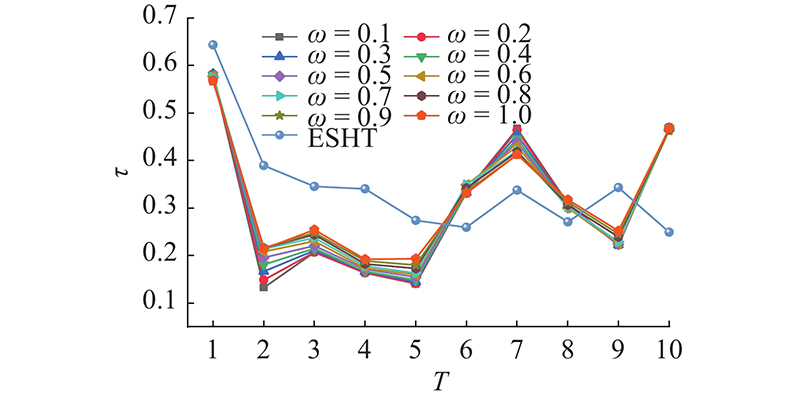
图 7 Email-Eu-core数据节点使用ESHT方法与SAM方法排序结果的Kendall相关性系数分析对比
Fig.7 Comparative analysis of Kendall correlation coefficients between sorting results of ESHT and SAM methods for Email-Eu-core data nodes
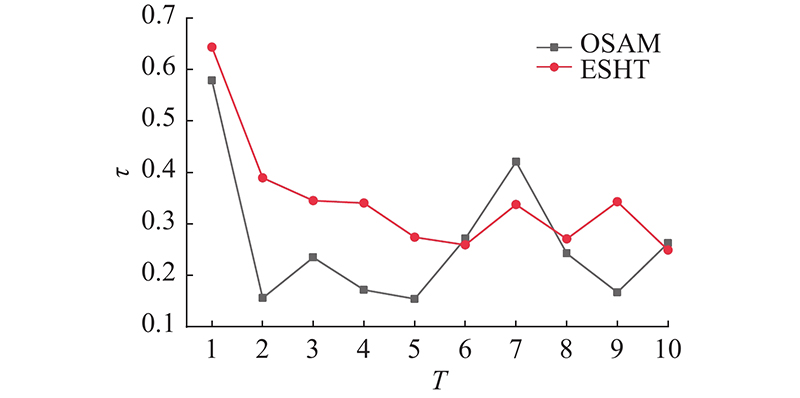
图 8
图 8 Email-Eu-core数据节点使用ESHT方法与OSAM方法排序结果的Kendall相关性系数分析对比
Fig.8 Comparative analysis of Kendall correlation coefficients between sorting results of ESHT and OSAM methods for Email-Eu-core data nodes
3. 结 语
本文提出熵值结构洞时序网络的节点重要性序结构辨识方法,可以有效地对复杂网络中的节点重要性进行排序. 该方法综合考虑了网络节点局部信息熵属性变化和节点K-shell全局拓扑信息,利用时序网络计算模型将网络节点时序化,揭示了节点重要性序结构随时间的演化规律,通过仿真建模分析验证了相关结论. 未来应进一步探讨动态多层网络熵值结构洞节点重要性的辨识方法,并将其推广到时序演化节点重要性的预测分析中.
参考文献
LPA-MNI: an improved label propagation algorithm based on modularity and node importance for community detection
[J].
基于Google Earth Engine与复杂网络的黄河流域土地利用/覆被变化分析
[J].
Land ues/cover change in the Tellow River Basin based on Google Earth Engine and complex network
[J].
Mobile device data reveal the dynamics in a positive relationship between human mobility and COVID-19 infections
[J].
Non-compulsory measures sufficiently reduced human mobility in Tokyo during the COVID-19 epidemic
[J].DOI:10.1038/s41598-019-56847-4 [本文引用: 1]
Factoring and weighting approaches to status scores and clique identification
[J].
Structural equivalence of individuals in social networks
[J].
Centrality and network flow
[J].DOI:10.1016/j.socnet.2004.11.008 [本文引用: 1]
Rethinking centrality: methods and examples
[J].DOI:10.1016/0378-8733(89)90016-6 [本文引用: 1]
基于Tsallis熵的复杂网络节点重要性评估方法
[J].
A method for evaluating the importance of nodes in complex network based on Tsallis entropy
[J].
Node importance evaluation based on neighborhood structure hole and improved TOPSIS
[J].
Ranking spreaders by decomposing complex networks
[J].DOI:10.1016/j.physleta.2013.02.039 [本文引用: 1]
An entropy-based self-adaptive node importance evaluation method for complex networks
[J].
融合节点覆盖范围和结构洞的影响力最大化算法
[J].
Influence maximization algorithm based on node coverage and structural holes
[J].
Temporal node centrality in complex networks
[J].
Eigenvector-based centrality measures for temporal networks
[J].DOI:10.1137/16M1066142 [本文引用: 1]
基于层间相似性的时序网络节点重要性研究
[J].DOI:10.7498/aps.67.20172255 [本文引用: 1]
Node importance idenfication for temporal network based on inter-layer similarity
[J].DOI:10.7498/aps.67.20172255 [本文引用: 1]
基于时序网络层间同构率动态演化的重要节点辨识
[J].
Identification of important nodes based on dynamic evolution of inter-layer isomorphism rate in temporal networks
[J].
基于重连机制的复杂网络鲁棒性分析
[J].
Robustness analysis of complex network based on rewiring mechanism
[J].
Structural holes: the social structure of competition
[J].
Can co-location be used as a proxy for face-to-face contacts?
[J].DOI:10.1140/epjds/s13688-018-0140-1 [本文引用: 1]
Thresholds for epidemic spreading in networks
[J].DOI:10.1103/PhysRevLett.105.218701 [本文引用: 1]
A new rank correlation measure
[J].DOI:10.1007/s00362-011-0423-0 [本文引用: 1]
基于网络超链接信息熵的节点重要性序结构演化建模分析
[J].
The model to analyses of node importance order structure evolution based on network hyperlink information entropy
[J].