交流电网静态电压稳定研究与多直流馈入(multi-infeed DC, MIDC)系统电压稳定研究经常采用同样的分析理论和方法,归纳前者的发展规律有助于理清后者的发展趋势[3-12]. 一方面,复杂系统电压稳定的研究核心在于,找到稳健的模型降阶方法,将复杂系统的电压稳定转化为简单系统的电压稳定问题,再利用射频电路的阻抗匹配[3]和无功负荷/电压(或有功/电流)灵敏度[8]这2个基本原理进行稳定性评估. 所用到的模型降阶方法主要有电路等值(功率等值[9]、阻抗等值[10])和模态解耦[11]. 复杂交流系统静态电压稳定研究经历从电路等值-局部指标[13]到模态解耦-全局指标[14]的发展过程. 另一方面,直流侧与交流侧耦合复杂[15-19],难以直观刻画交直流系统电压稳定的物理机理,因此国内外学者将单直流母线接入无穷大电网或单馈入(single-infeed HVDC, SIDC)系统作为反映电压稳定机理的最小系统,并致力于将在SIDC系统中所发现的规律推广到MIDC系统. 在SIDC系统中,交流侧的短路比(short circuit ratio, SCR)对交直流系统的无功/电压、有功/电流灵敏度影响最为明显,因此被作为具有良好可观性的电压稳定裕度评估指标. 但是,在将SCR推广应用到MIDC系统时遇到如下研究难题:1)在MIDC系统中,不同LCC-HVDC通过交流电网发生耦合,交直流系统间的相互作用不再存在一一对应性,导致SIDC系统的稳定机理在推广到MIDC系统时缺乏理论保证;2)不同控制方式下的LCC-HVDC对MIDC系统的电压稳定性或灵敏度特性存在显著影响,SCR只与交流系统的拓扑结构、参数相关,缺乏LCC-HVDC控制方式与电压稳定性的本质联系,因而弱化了SCR指标在实际工程中的实用性. 为此,国内外学者借鉴交流系统静态电压稳定研究思路,从有功/电流[15-16]或无功/电压[17-18]灵敏度出发,提出多种类型的多馈入短路比(multi-infeed short circuit ratio, MISCR). 该类研究的共同点是,将MIDC系统转化为SIDC系统后,再回归电路等值(功率等值[19])或模态解耦(网络模态解耦[15,17]),这跟复杂交流系统电压稳定的研究思路无异. 以广义短路比(Generalized short circuit ratio, gSCR)[15,17]为代表的研究引入模态解耦的思路,针对LCC-HVDC存在同构性的标称MIDC系统,借鉴文献[12]的思路将交流网络解耦,可以获得与MIDC系统稳定性保持一致的SIDC系统,从理论层面指出MISCR存在稳健临界值的条件.
尽管不同LCC-HVDC控制方式的影响效果已经有了数值计算和动态仿真的确认,但是大部分计及LCC-HVDC控制方式的SCR计算仍立足于电路等值类的方法,未能建立LCC-HVDC控制方式与系统雅克比矩阵奇异性的本质联系. 为此,本研究提出基于交流系统雅克比矩阵主导模式灵敏度性质的定性分析方法. 统一LCC-HVDC不同控制方式下直流侧电压稳定雅克比矩阵(voltage stability Jacobian matrix, VSJM)的建模方法,得到不同控制方式下直流端口特性的数值特征[20],同时揭示此类研究的建模思路本质.
1. 单馈入系统准稳态模型
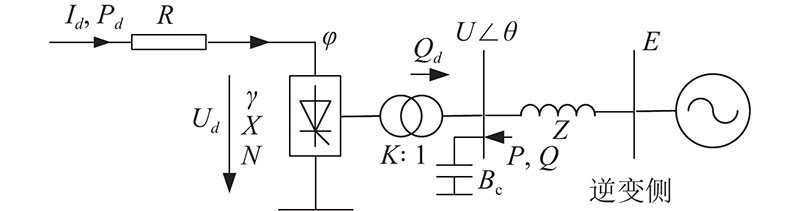
交直流系统电压稳定研究采用的LCC-HVDC单馈入系统等效电路如图1所示,该电路包含直流逆变器与交流电网2个部分. 其中直流侧有功功率、电压、电流、关断角和换相电抗,分别用
图 1
图 1 LCC-HVDC单馈入系统准稳态模型
Fig.1 Quasi-steady-state model of single-infeed LCC-HVDC system
式中:k为直流侧电压基准值与交流测电压基准值的比值,其余变量定义见文献[21]、[22]. 式(1)~(4)均表示逆变器端口特性,式(5)、(6)表示交直流系统耦合特性. 式(1)~(6)可以直接代入各变量标幺值进行计算. LCC-HVDC存在4种主要控制方式:定功率定息弧角(constant power constant extinction angle, CP-CEA),定电流定息弧角(constant current constant extinction angle, CC-CEA),定功率定电压(constant power constant voltage, CP-CV)和定电流定电压(constant current constant voltage, CC-CV),本研究具体分析LCC-HVDC控制方式对直流侧雅克比矩阵的影响.
2. 定功率/定电流定息弧角下的电压稳定雅克比矩阵
LCC-HVDC交直流系统电压稳定的前提是节点吸收的无功功率与交流电压存在负反馈关系,若当增加直流并网点无功补偿时交流电压下降,则认为发生电压失稳. 文献[19]提出二阶雅克比矩阵奇异作为交直流系统临界电压稳定判据:
式中:
CP-CEA、CC-CEA控制下的直流端口灵敏度及其推导过程分别如下. 1)在CP-CEA控制方式下,直流传输功率
式中:
式(11)、(12)的推导过程详见附录A.
根据本研究选择的无功正方向,当电压稳定时,有下列条件成立:
式中:
3. 雅克比矩阵的统一建模方法
3.1. LCC-HVDC单馈入系统的四阶雅克比矩阵
补充变量的方式不是唯一的,为了简化雅克比矩阵的建模过程,须遵循的原则如下. 1)成对补充具有相关性的变量. 如当
3.2. 基于四阶雅克比矩阵的电压稳定矩阵建模
CP-CV/CC-CV控制方式下的VSJM均通过对相应四阶雅克比矩阵进行消元变换得到. 对于CP-CV控制方式,
其中
对于CC-CV控制方式,
2)删除矩阵
对比式(15)和(17)可知,CP-CV/CC-CV控制方式下的VSJM完全一致. Lee等[19, 23]大多从控制特性出发,启发式地认为CP-CV/CC-CV控制方式下的VSJM一致,并利用CP-CV控制方式进行简化推导,缺乏严格的数学理论基础. 本研究基于消元法思路系统地通过CP-CV/CC-CV下的VSJM,揭示这2种控制方式下VSJM一致的原因:当
四阶雅克比矩阵推导CP-CEA/CC-CEA控制方式下VSJM的过程如下:1)针对CP-CEA,可以直接由
3.3. 基于四阶雅克比矩阵的直流外特性分析
4种控制方式下的LCC-HVDC端口外特性具有3种表达式,对应3种数值特征. 本研究采用CIGRE标准直流测试系统参数[20],将系统参数代入所得外特性矩阵式(9)~(12)和(15)、(17),得到外特性数值特征列表. 观察并总结发现:只有CP-CEA控制方式下的无功/电压灵敏度是正数,其余都是负数;只有当该灵敏度为正时,配合弱电网才有可能导致电压不稳定.
4. 多馈入系统电压稳定的定性分析
以MIDC系统交流电网部分的雅克比矩阵为标称矩阵,把接入的直流雅克比矩阵当作对标称矩阵的摄动,研究摄动后标称矩阵主导特征值的运动方向,即定性分析不同控制方式下的直流接入对系统电压稳定主导模式的影响.
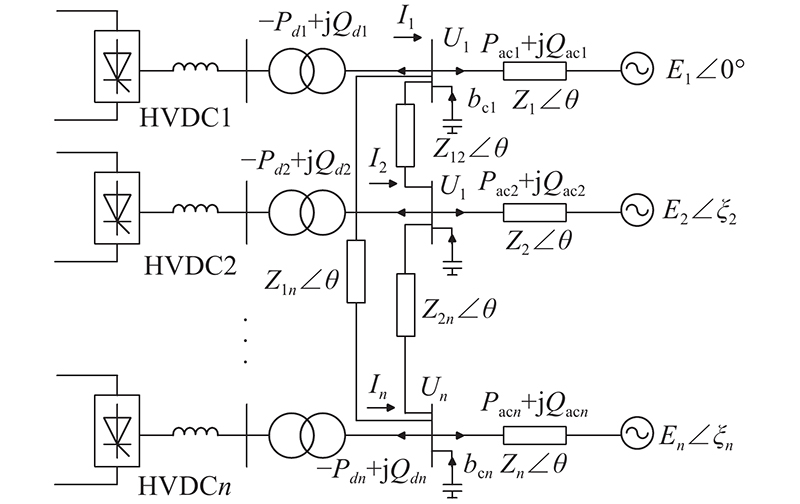
4.1. 交流网络雅克比矩阵建模
图 2
4个分块矩阵的元素分别为
考虑额定运行时直流并网点的电压幅值约为1p.u.(
对角矩阵
注1:B为对角占优的负定(对称)矩阵,
4.2. 交流网络雅克比矩阵模态灵敏度的符号分布
分析交流雅克比矩阵
1)定义矩阵
式中:
特征值对矩阵元素的灵敏度由特征向量构成[20],将特征值
工程上LCC-HVDC单馈入系统的短路比近似满足条件[22]:
式(30)等价于B的元素(
式中:
4.3. 不同直流控制方式下MIDC系统电压稳定分析
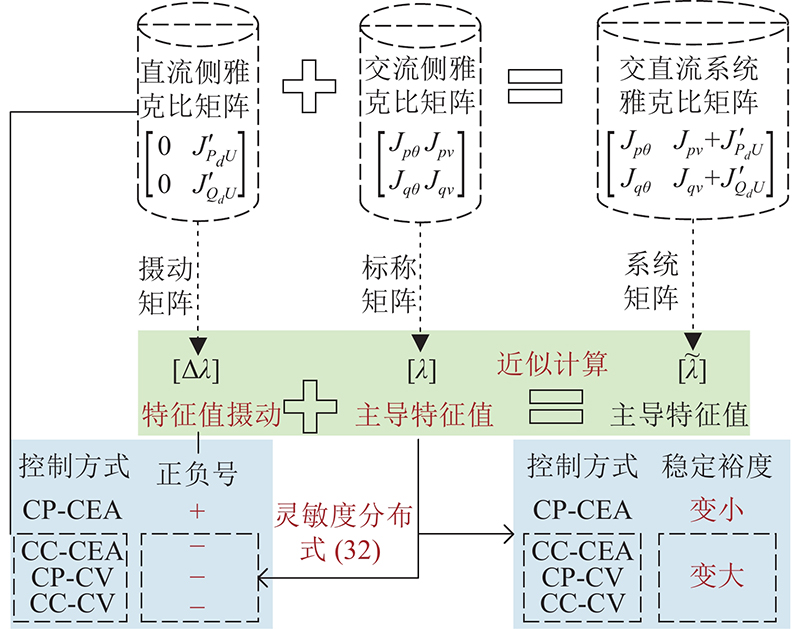
本研究所提的定性分析方法的全部内容如图3所示. 由图可知,定性分析的基本思路是将交流侧雅克比矩阵视为标称矩阵,将直流侧雅克比矩阵作为摄动矩阵,二者相加得到交直流系统的雅克比矩阵;利用交流侧雅克比矩阵的主导特征值,加上特征值摄动,以近似计算交直流系统的主导特征值;利用式(32)中标称矩阵主导模态灵敏度的符号分布特征,可以直接得到在不同控制方式下特征值摄动量的正负符号,据此可知交流系统在接入CP-CEA控制方式下的LCC-HVDC后,系统电压稳定裕度下降;接入其余3种控制方式下的LCC-HVDC后(已忽略滤波电容),系统电压稳定裕度上升. 定性分析的具体过程如下. CP-CEA控制方式下的直流侧雅克比矩阵的符号与式(32)的符号分布一致,导致标称矩阵主导特征值
图 3
5. 算例分析
5.1. 系统模型
为了对本研究所提矩阵建模方法和主导模态灵敏度符号分布性质进行有效性分析,采用如图1、2所示的LCC-HVDC单/多馈入系统准稳态模型进行算例分析. LCC-HVDC采用CIGRE标准直流测试系统参数[20],直流侧额定功率为1 000 MW,额定电压为500 kV,交流侧额定线电压有效值为230 kV,变压器变比K=211.42/230,交直流电压基准值的比例k=500/230. 假定直流端口电压
5.2. 4种控制方式下单馈入系统电压稳定性分析
LCC-HVDC交直流系统电压稳定性受到逆变侧有功功率和无功功率对换相电压幅值灵敏度的影响,因此需要对单馈入系统在4种控制方式下的电压灵敏度
表 1 CIGRE标准直流测试系统在4种控制方式下的电压灵敏度计算结果
Tab.1
| 控制方式 | | |
| CP-CEA | 0 | 0.4830 |
| CC-CEA | 1.1032 | −0.3645 |
| CP-CV | 0 | −2.3664 |
| CC-CV | 0 | −2.3664 |
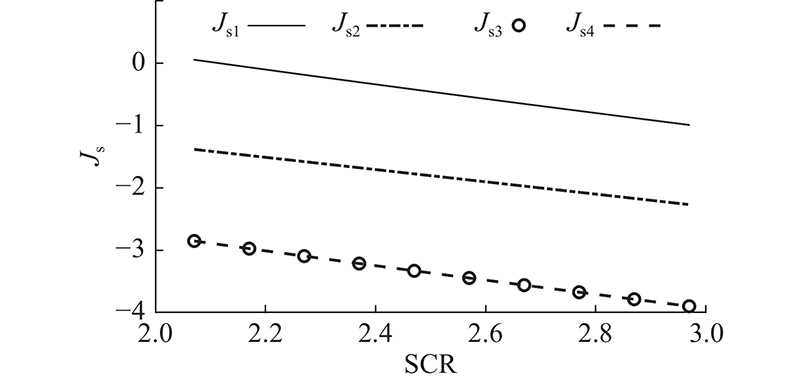
如图4所示为4种控制方式下
图 4
图 4 雅可比矩阵奇异性与短路比关系
Fig.4 Relationship between singularity of Jacobian matrix and short circuit ratio
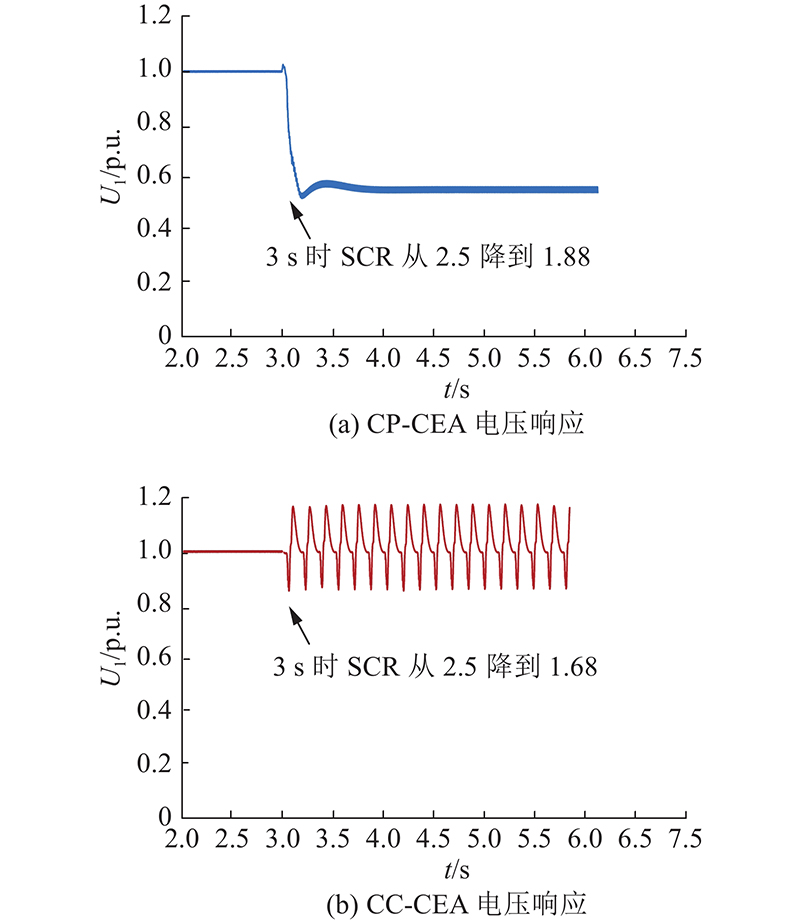
图 5
图 5 不同控制下LCC-HVDC馈入系统交流电压响应
Fig.5 AC voltage response of LCC-HVDC infeed system with different control mode
5.3. 主导模态灵敏度符号分布数值性质分析
在灵敏度矩阵符号分布性质的推导过程中对交流网络潮流提出假设条件,为此通过数值计算分析当假设条件不完全满足时,所得结论的有效性. 给出交流网络参数,按照图2中的图示,设置三馈入系统的外电网等值电压幅值
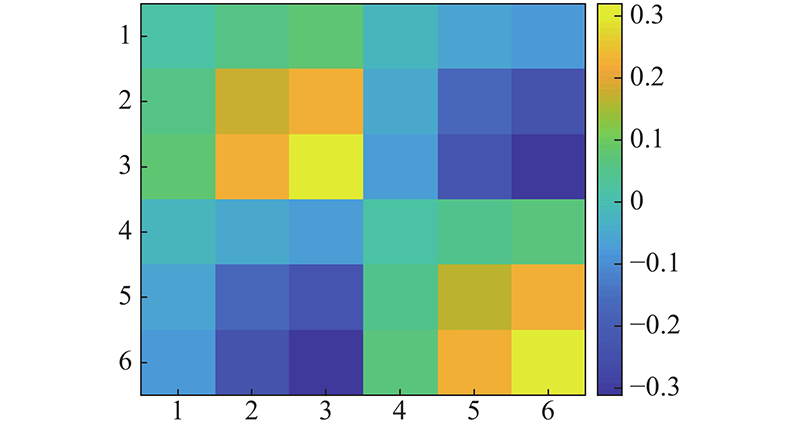
直流并网点的电压相角分别为5.2°、10.5°和12.8°. 代入简化前的雅克比矩阵式(18)后,得到灵敏度矩阵的分布特性如图6所示. 当考虑直流馈入节点之间的相角差存在时,通过近似雅克比矩阵分析得到的网络侧主导模态灵敏度的符号分布特性依然存在,说明了所提定性分析方法的有效性.
图 6
5.4. 含不同控制方式直流的两馈入系统仿真分析
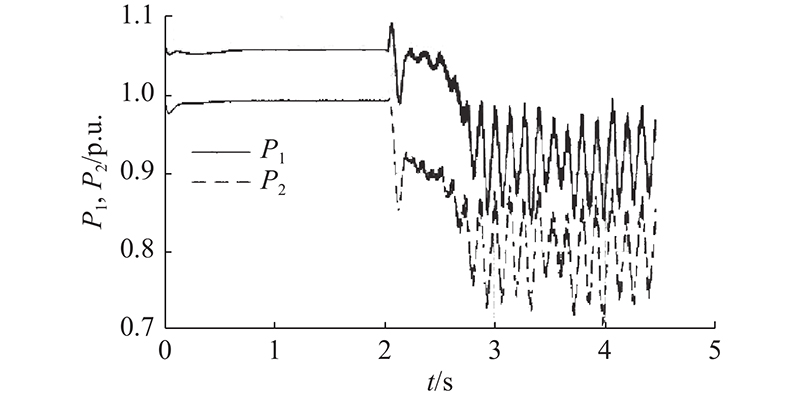
采用基于PSCAD仿真平台的时域仿真进一步说明定性分析所得结论的有效性. 为了说明LCC-HVDC不同控制方式对系统电压稳定裕度的影响,采用电磁暂态仿真分析含CP-CEA和CC-CV2种控制方式直流的两馈入系统临界稳定条件. 仿真设置情况如下:P1为CP-CEA控制下的LCC-HVDC输出有功功率,P2为CC-CV控制下的LCC-HVDC输出有功功率,动态模型采用PSCAD自带的CIGRE标准模型. 两馈入系统的节点导纳矩阵为
图 7
6. 结 论
(1)为了统一分析LCC-HVDC的4种常规控制方式对交直流系统电压稳定性的影响,提出基于四阶雅克比矩阵的建模方法和基于网络灵敏度的定性分析方法,取得如下分析结果. 1)直流不同控制方式下的电压稳定雅克比矩阵均可由同个四阶雅克比矩阵通过消元法思路转化而来. 2)通过本研究所提四阶雅克比矩阵,从方程组消元角度提出CP-CV/CC-CV控制方式下电压灵敏度的推导过程,发现2种控制下的VSJM或电压灵敏度完全一致,数学机理在于四阶雅克比矩阵经一次消元所对应的三阶雅克比矩阵的第1行中有2个零元素. 3)通过对单馈入系统电压稳定性分析和对多馈入系统网络模态灵敏度的定性分析,给出CP-CEA控制方式下系统更易发生电压失稳的数学机理,为多馈入系统的电压稳定裕度判断提供定性分析的思路.
(2)鉴于当前直流多馈入系统的评估方法研究普遍采用电路等值+局部指标的研究思路,未能建立不同控制方式与系统雅克比矩阵奇异性之间的联系,导致评估指标缺乏稳健的临界值. 广义短路比等模态解耦类指标尚未覆盖全部4种控制方式,本研究在一定程度上推动了模态分析在多馈入短路比研究中的应用,未来将根据本研究的定性分析结果研究多馈入短路比的实用计算方法.
参考文献
考虑高比例可再生能源的交直流输电网规划挑战与展望
[J].
Challenges and prospects for AC/DC transmission expansion planning considering high proportion of renewable energy
[J].
Voltage stability monitoring based on the concept of coupled single-port circuit
[J].DOI:10.1109/TPWRS.2011.2154366 [本文引用: 2]
Searching for the shortest path to voltage instability boundary: from Euclidean space to algebraic manifold
[J].DOI:10.1016/j.ijepes.2021.107127
Voltage stabilization in microgrids via quadratic droop control
[J].
Intrinsic geometric analysis of the network reliability and voltage stability
[J].DOI:10.1016/j.ijepes.2012.08.032
Voltage collapse in complex power grids
[J].
Control of voltage stability using sensitivity analysis
[J].DOI:10.1109/59.141694 [本文引用: 1]
Voltage stability assessment using equivalent nodal analysis
[J].DOI:10.1109/TPWRS.2015.2402436 [本文引用: 1]
Strength evaluation of multi-infeed LCC-HVDC systems based on the virtual impedance concept
[J].DOI:10.1109/TPWRS.2019.2960298 [本文引用: 1]
基于改进模态分析法的柔性多端交直流混联系统静态电压稳定性评估
[J].DOI:10.19595/j.cnki.1000-6753.tces.201031 [本文引用: 1]
Static voltage stability assessment on hybrid alternating current/voltage source converter-multiple terminal direct current system using improved modal analysis
[J].DOI:10.19595/j.cnki.1000-6753.tces.201031 [本文引用: 1]
A network decoupling transform for phasor data based voltage stability analysis and monitoring
[J].DOI:10.1109/TSG.2011.2163175 [本文引用: 2]
Estimating the voltage stability of a power system
[J].DOI:10.1109/TPWRD.1986.4308013 [本文引用: 1]
Voltage stability indices for stressed power systems
[J].DOI:10.1109/59.221224 [本文引用: 1]
直流多馈入系统的广义短路比: 影响因素分析
[J].
Generalized short circuit ratio for multi-infeed DC systems: influence factors
[J].
A general steady-state voltage stability analysis for hybrid multi-infeed HVDC systems
[J].DOI:10.1109/TPWRD.2020.3006027 [本文引用: 1]
多馈入直流系统广义短路比: 定义与理论分析
[J].
Generalized short circuit ratio for multi-infeed DC system: definition and theoretical analysis
[J].
Evaluation of strength measure for static voltage stability analysis of hybrid multi-infeed DC systems
[J].DOI:10.1109/TPWRD.2019.2901831 [本文引用: 1]
考虑直流输电系统外特性影响的多直流馈入短路比实用计算方法
[J].
Practical calculation method for multi-infeed short circuit ratio influenced by characteristics of external characteristics of DC system
[J].