Timoshenko 等[3]针对杆间有支撑两端简支压杆的稳定承载力问题进行了理论推导. 谢鹏[2]对Timoshenko 等[3]的理论推导结果进行了试验验证. 王祖能[1]的研究表明,压杆稳定承载力随着拉压弹簧刚度的增加而线性增加,在拉压弹簧刚度达到一定值后,压杆稳定承载力达到峰值,此时杆间的拉压弹簧支撑可视作无穷刚度的横向支撑. Foster等[4]通过计算机程序计算验证了钢结构设计中支撑构件的作用. 王述红等[5] 使用稳定函数计算并分析了带支撑结构的整体稳定性. 石永久等[6-7]提出高性能钢材未来的发展方向以及稳定设计方法. Bleich[8]补充了压杆失稳理论计算的方法. Peng[9]研究了具有支撑结构系统的整体失稳性能. 刘占科等[10]系统归纳了不同国家和地区的现行钢结构设计规范,分析了钢结构稳定设计的研究现状. 于春海等[11]通过试验研究了Q420角钢构件轴心受压承载力. 在压杆失稳方面,许多学者针对构件几何初始缺陷、残余应力、杆间约束等因素进行了理论计算及有限元分析[12-18].
1. 工程模型简化及理论推导
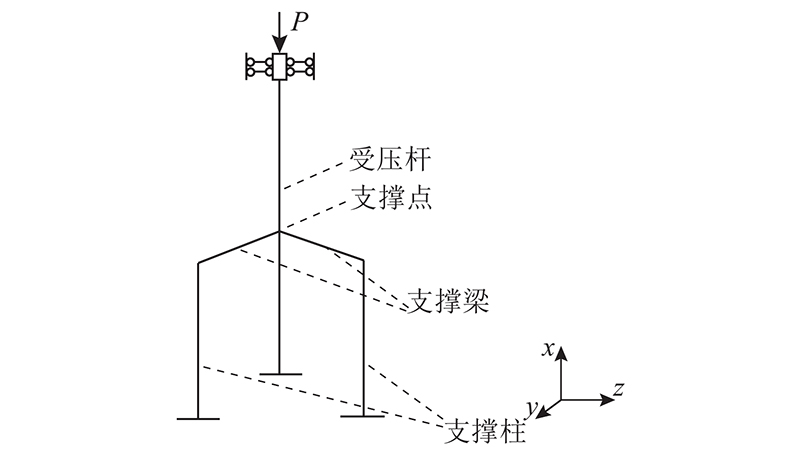
1.1. 工程模型简化
图 1
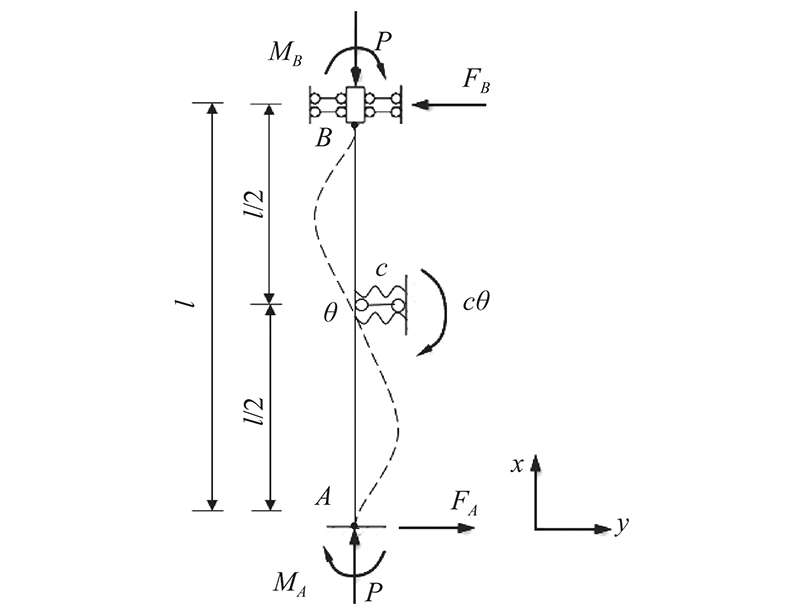
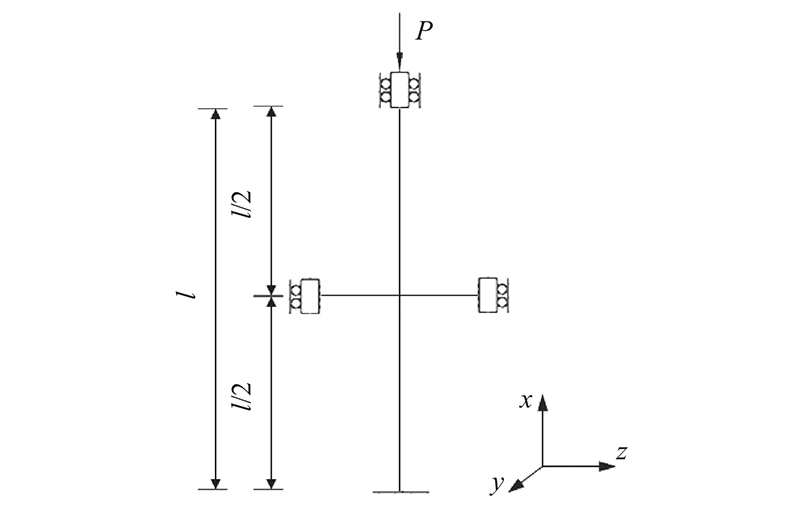
图 2
1.2. 理论推导
轴压杆件的稳定性问题本质上属于整体变形效应,宜在微小弯曲平衡状态下计算. 因此,基于小挠度理论,运用挠度曲线微分方程推导压杆稳定承载力与扭转弹簧刚度的关系. 确定坐标系如下:杆件轴向为x方向,杆件挠度变形方向为y方向,弯矩cθ以逆时针方向为正方向. 以扭转弹簧约束为界限,截取上下侧截面作为隔离体分别讨论.
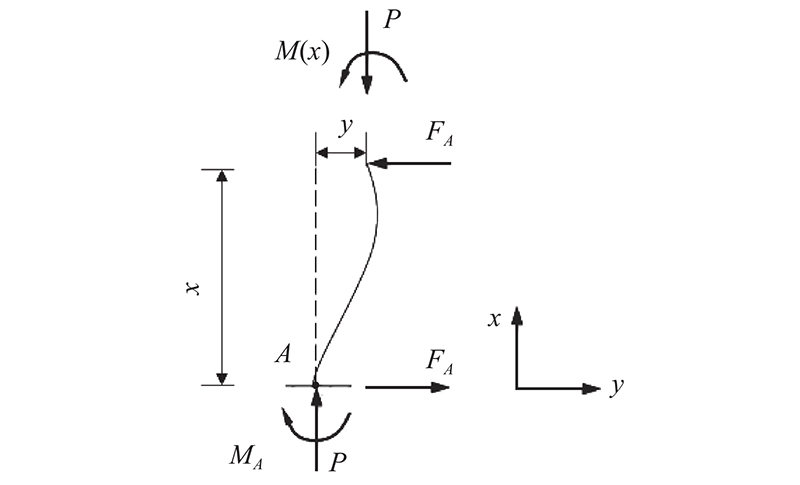
情况1:截取隔离体的截面在扭转弹簧约束下侧,即0≤x≤l/2时,如图3所示. 根据隔离体建立平衡方程,对点A取矩,计算式为
图 3
将挠度的二次微分等效为曲率,得到
令
求解式(3),得到杆件挠度曲线为
利用边界条件:
将边界条件
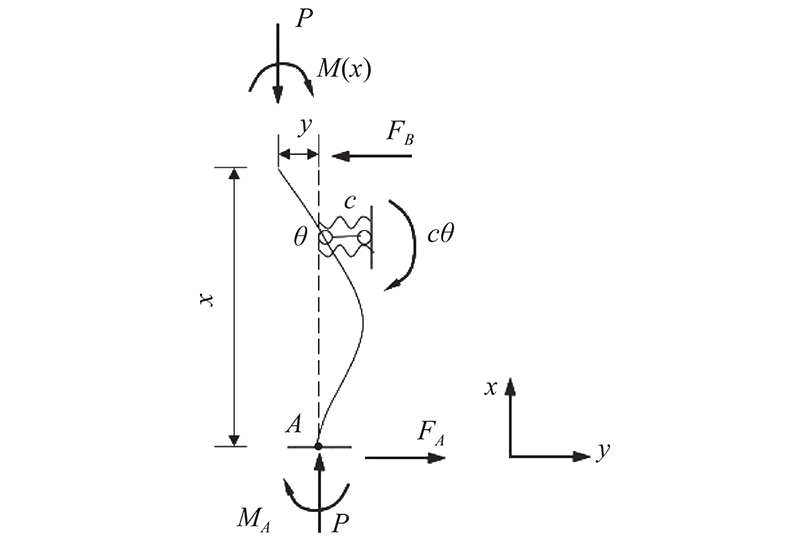
情况2:截取隔离体的截面在扭转弹簧约束上侧,即l/2≤x≤l时,如图4所示. 对隔离体的顶点取矩,此时隔离体的平衡方程为
图 4
参照情况1,得到微分方程
求解式(8),得到杆件挠度曲线为
常数A2、B2由边界条件求得,代入
代入A2,B2及边界条件
对式(9)求导,并代入边界条件
结合式(6)、(10),得到
结合式(11)、(12),得到
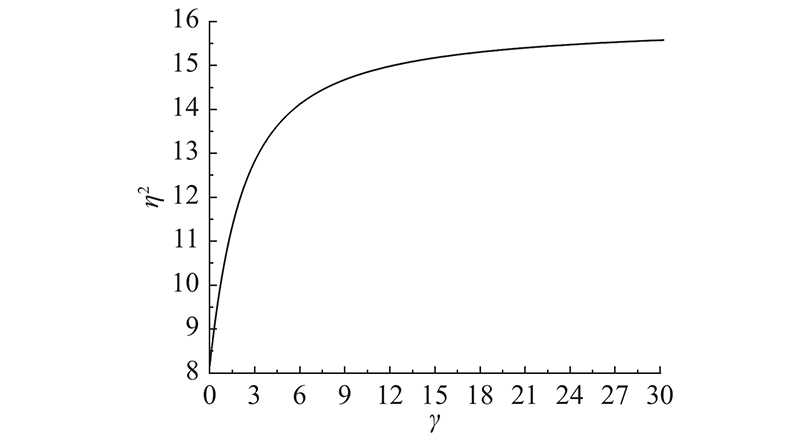
为了方便、直观地绘制两端固定压杆在杆间有扭转弹簧约束情况下的稳定承载力与扭转弹簧刚度的关系曲线,进行如下简化:规定杆间无任何约束时两端简支压杆稳定承载力
求解不同弹簧扭转刚度系数时对应的
图 5
图 5 压杆稳定承载力与扭转弹簧刚度关系曲线
Fig.5 Relation curve between stable bearing capacity of compression bar and torsional spring stiffness
2. 压杆稳定性试验
2.1. 试验目的及设计
设计具有杆间横梁支撑的压杆稳定性试验,验证理论关系公式. 如图6所示,受压杆件采用截面尺寸为Φ16 mm×5 mm的无缝圆钢管,计算长度l=1 600 mm,材料采用Q235钢. 无缝圆钢管满足文献[19]的初始缺陷要求. 使用5根钢管样本进行抗弯刚度测定试验,取其中3根钢管样本的有效结果,分别为642.3、630.4、634.6 N·m2,取平均值,得到试验压杆的抗弯刚度EI=635.8 N·m2. 由EI得到对应扭转弹簧刚度基本值
图 6
图 7
2.2. 试验平台及试验装置
依托烟台新天地试验技术有限公司YJ-IIA-W 型结构力学组合试验装置,本试验模型如图8所示. 试验模型对应的理论模型如图9所示. 压杆中部具有横梁支撑,且无竖向位移约束,存在横向约束和扭转约束(试验结果表明,压杆在平面x-y发生失稳). 当横梁对压杆的横向约束达到一定刚度值后(经计算,6种横梁支撑均大于该刚度值),可以将杆间横梁视为无穷刚度的约束[1],即图9的理论模型可以对应为图2的理论模型,扭转弹簧的刚度c对应为横梁截面的扭转刚度GJ,2根横梁的截面抗扭刚度
图 8
图 8 具有杆间横梁支撑的两端固定压杆
1-刹车块;2-随动小车平台;3-电动缸;4-YC-4-50型力传感器;5-导向装置;6-固定支座;7-YWD-50型位移传感器;8-滑轨;9-支撑横梁;10-压杆. Two-end fixed compression bar with cross beam support between bar
图 9
图 9 具有杆间横梁支撑的两端固定压杆试验模型对应的理论模型
Fig.9 Theoretical model corresponding to test model of two-end fixed compression bar with cross beam support between bar
2.3. 材料拉伸试验
图 10
拉伸试验开始时,使用YDD-2数据采集分析系统同时采集2组应变片的应变和拉力. 根据力-应变曲线得到钢材的弹性模量E,由纵向应变和横向应变的比值得到钢材的泊松比
表 1 压杆拉伸试验结果
Tab.1
| 试验编号 | E/GPa | | G/GPa |
| 1 | 202 | 0.306 | 77 |
| 2 | 204 | 0.298 | 79 |
| 3 | 206 | 0.301 | 79 |
| 平均值 | 204 | 0.302 | 78 |
2.4. 量测内容与加载方案
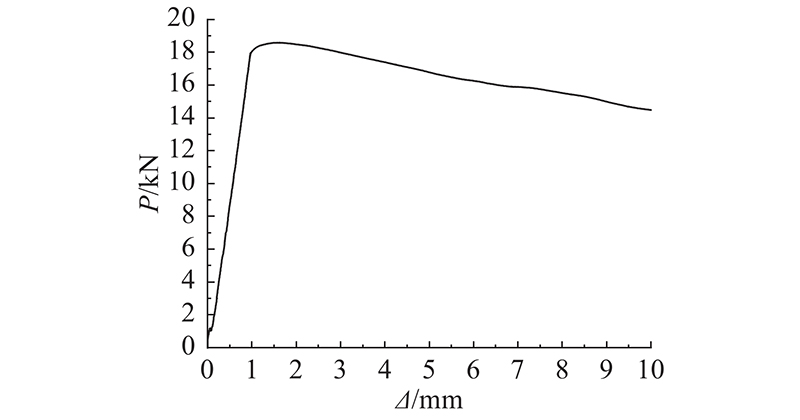
当轴压杆件失稳时,顶端位移继续增加,荷载开始下降. 本研究量测杆端力和杆件顶端位移,绘制荷载-位移曲线. 试验采用5 t电动缸进行加载,按照位移控制单调加载,使用YDD-2数据采集分析系统、力与位移信号,当荷载下降到峰值的65%~75%时停止加载,存储数据、卸载、更换杆件,重复以上加载步骤.
2.5. 试验结果
图 11
图 12
图 13
表 2 不同试验模型压杆试件的稳定承载力
Tab.2
| 模型编号 | 横梁截面尺寸/mm | GJ/(N·m) | Pe/kN | |||
| n=1 | n=2 | n=3 | 平均值 | |||
| MX-1 | Φ10×1 | 274 | 18.47 | 18.52 | 18.59 | 18.53 |
| MX-2 | Φ22×1 | 3 446 | 23.56 | 23.25 | 22.82 | 23.21 |
| MX-3 | Φ22×2 | 6 000 | 24.99 | 25.76 | 25.78 | 25.51 |
| MX-4 | Φ26×2 | 10 336 | 26.97 | 27.63 | 28.27 | 27.62 |
| MX-5 | Φ26×4 | 16 336 | 29.07 | 29.35 | 29.35 | 29.26 |
| MX-6 | Φ26×8 | 20 744 | 30.51 | 29.99 | 31.10 | 30.53 |
表 3 不同试验模型的压杆承载力试验值与理论值对比
Tab.3
| 模型编号 | | | Pe/kN | Pt/kN | e/% |
| MX-1 | 0.07 | 2.90 | 18.53 | 20.61 | +11.2 |
| MX-2 | 0.88 | 3.22 | 23.21 | 25.42 | +9.5 |
| MX-3 | 1.53 | 3.37 | 25.51 | 27.84 | +9.1 |
| MX-4 | 2.64 | 3.54 | 27.62 | 30.72 | +11.2 |
| MX-5 | 4.17 | 3.67 | 29.26 | 33.01 | +12.8 |
| MX-6 | 5.29 | 3.73 | 30.53 | 34.10 | +11.7 |
图 14
2.6. 误差分析
由表3可以得到,试验值和理论值误差在9%~13%,且试验值普遍低于理论值. 分析产生误差的原因,有两个方面:支座约束和初始缺陷. 试验采用的两端刚接支座,没有达到理论模型中的完全刚接,是介于刚性支座和铰支座间的约束. 为了验证支座未达到完全刚接,同时为了证明误差与横梁约束无关,设计第7组试验模型,去掉横梁约束,杆间不存在任何约束,进行两端刚接的压杆失稳试验. 试验流程同前6组试验,得到3次有效试验结果,极限承载力分别为9.17、9.08、9.01 kN,取平均值,得到Pe=9.09 kN,Pt=4P0=4×2451.2 N=9.80 kN,e=−7.2%. 另外,理论推导得到的压杆稳定承载力不考虑初始缺陷的屈曲荷载,试验中的压杆是存在初始缺陷的不完善杆,考虑初始缺陷后压杆的试验承载力比理论承载力小.
3. 有限元分析
3.1. 试验模型的有限元计算值
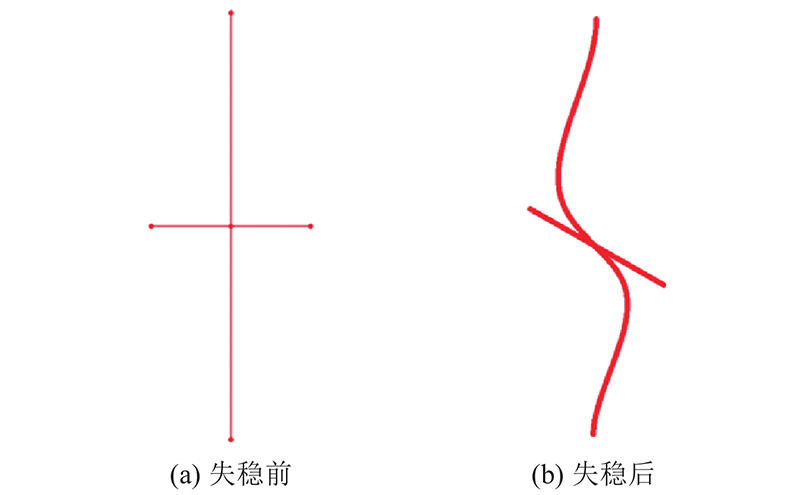
使用有限元软件Abaqus 进行数值分析,计算压杆稳定承载力. 根据试验模型MX-1~MX-6建立有限元模型,杆长l=1.6 m,截面尺寸为Φ16 mm×5 mm,设置材料的E=204 GPa,v=0.3. 横梁尺寸根据试验模型设置(边界条件同图9),使用Abaqus进行特征值屈曲分析,压杆失稳前后形态如图15所示. 将压杆稳定承载力与试验值和理论值进行比较,如表4所示. 表中,Pf为压杆承载力的有限元值,ef为Pf与Pe的误差,et为Pt与Pe的误差. 可以看出, 6种试验模型的试验值与有限元值误差在11%~16%,且试验值普遍低于有限元值,误差原因与前述误差分析相同. 试验中的压杆由于存在初始缺陷,得到的承载力低于理论推导中不考虑初始缺陷的压杆稳定承载力. 本研究为了验证理论公式,有限元模型未设置初始缺陷. 与et相比,6种试验模型的ef更接近,试验模型的有限元值和理论值互为验证. 对比6种试验模型的试验值、理论值、有限元值,使在误差允许范围内有限元模型的准确性得以验证.
图 15
表 4 不同试验模型压杆承载力的试验值、理论值与有限元值对比
Tab.4
| 试验编号 | Pe/kN | Pt/kN | Pf /kN | ef /% | et /% |
| MX-1 | 18.53 | 20.61 | 20.82 | +12.4 | +11.2 |
| MX-2 | 23.21 | 25.42 | 25.95 | +11.8 | +9.5 |
| MX-3 | 25.51 | 27.84 | 28.62 | +12.2 | +9.1 |
| MX-4 | 27.62 | 30.72 | 31.50 | +14.0 | +11.2 |
| MX-5 | 29.26 | 33.01 | 33.74 | +15.3 | +12.8 |
| MX-6 | 30.53 | 34.10 | 34.75 | +13.8 | +11.7 |
3.2. 理论公式验证
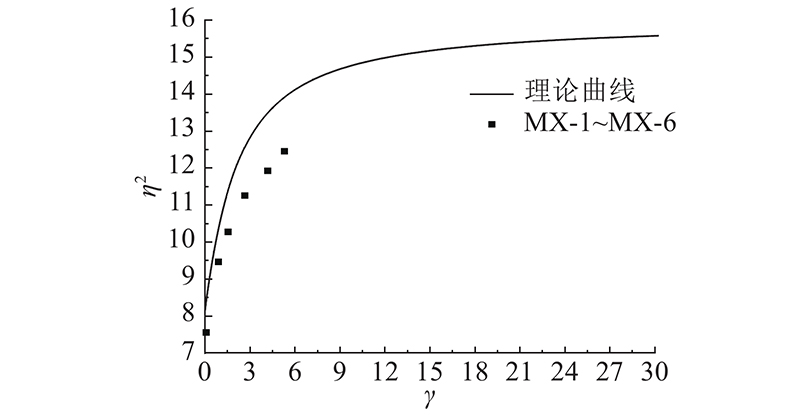
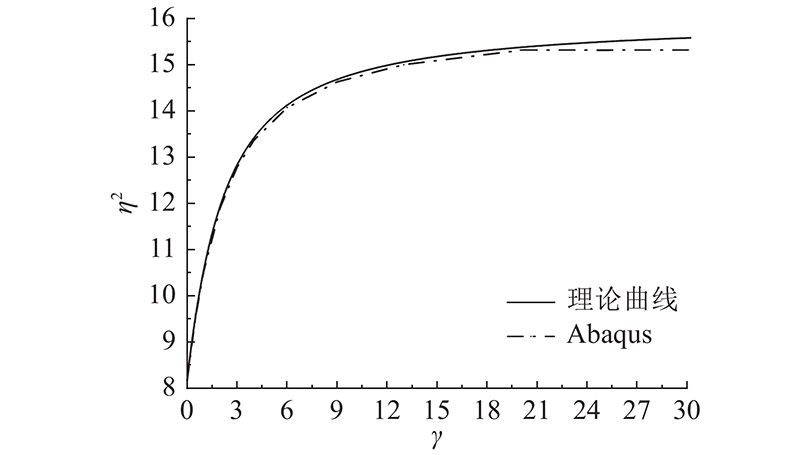
由于试验数据有限,为了验证理论公式的正确性,使用经试验模型结果验证的有限元模型,通过特征值屈曲分析方法计算压杆稳定承载力. 使用扭转弹簧约束和横向约束代替图15(a)中的支撑横梁(边界条件同图2). 根据图5所示的理论关系曲线,取12种不同扭转弹簧刚度,使用Abaqus求解压杆的稳定承载力,对比理论解和有限元解,结果如表5所示. 可以看出,不同弹簧刚度下的有限元解与理论解误差绝对值均不超过0.5%,有限元结果验证了理论曲线的正确性. 将有限元结果绘制到理论关系曲线中进行比较,如图16所示. 可以看出,2条曲线基本吻合. 调整截面参数及杆件材料进行重复计算,依然可以得到理论曲线与有限元曲线吻合较好的结论,说明此结论具有可靠性.
表 5 压杆承载力在不同弹簧刚度下的理论解和有限元解对比
Tab.5
| c/(N·m) | | Pt/kN | Pf/kN | e/% |
| 0.000 1 | 0 | 20.29 | 20.25 | −0.2 |
| 1 984 | 0.5 | 23.66 | 23.59 | −0.3 |
| 3 968 | 1 | 26.19 | 26.12 | −0.3 |
| 7 936 | 2 | 29.66 | 29.56 | −0.3 |
| 11 904 | 3 | 31.82 | 31.71 | −0.3 |
| 15 872 | 4 | 33.26 | 33.14 | −0.4 |
| 23 808 | 6 | 35.02 | 34.89 | −0.4 |
| 35 712 | 9 | 36.41 | 36.27 | −0.4 |
| 51 584 | 13 | 37.35 | 37.20 | −0.4 |
| 79 360 | 20 | 38.12 | 37.97 | −0.4 |
| 3 968 000 | 1 000 | 39.66 | 39.48 | −0.5 |
| 3 968 000 000 | 1 000 000 | 39.68 | 39.51 | −0.4 |
图 16
图 16 压杆承载力理论曲线与有限元曲线对比
Fig.16 Comparison between theoretical curve and finite element curve of compression bar capacities
4. 结 语
在具有杆间扭转弹簧约束的情况下,对两端固定压杆进行稳定承载力与杆间扭转弹簧刚度关系的理论推导,弥补了理论研究的不足,提出了可供工程设计使用的简化计算公式:已知杆间扭转弹簧的刚度,可以得到两端固定压杆的稳定承载力. 通过6组试验模型探究理论推导的正确性,在误差允许范围内,认为理论推导的结果是正确的. 根据试验结果验证有限元模型的可靠性,基于经过验证的模型进行大量算例分析,与理论曲线比较,得到有限元分析结果与理论关系曲线拟合较好的结论,进一步验证了理论推导结果的正确性. 试验中发现,两端简支或两端固定压杆的两端支座均无法达到理想的铰接或者刚接支座,实际工程中也是如此,后续计划进行关于弹性支座的深入研究.
参考文献
Ultimate behavior of continuous steel beams with discrete lateral restraints
[J].DOI:10.1016/j.tws.2014.11.018 [本文引用: 1]
基于稳定函数的支撑结构系统临界力计算方法
[J].
Calculation method of the critical force of support structure system based on stability function
[J].
高性能结构钢材与钢结构体系研究与应用
[J].DOI:10.19701/j.jzjg.2021.17.021 [本文引用: 1]
Research and application on high performance structural steel and its structural system
[J].DOI:10.19701/j.jzjg.2021.17.021 [本文引用: 1]
复合型高性能钢材轴压构件整体稳定性能研究
[J].DOI:10.15951/j.tmgcxb.2021.09.011 [本文引用: 1]
Research on overall buckling behavior of superior high-performance steel columns
[J].DOI:10.15951/j.tmgcxb.2021.09.011 [本文引用: 1]
Experiment and stability analysis on heavy-duty scaffold systems with top shores
[J].
钢构件整体稳定直接分析法研究现状及展望
[J].DOI:10.14006/j.jzjgxb.2020.C335 [本文引用: 1]
State-of-the-art on research of direct analysis method of steel members with global instability
[J].DOI:10.14006/j.jzjgxb.2020.C335 [本文引用: 1]
Q420高强度角钢轴心受压承载力试验研究
[J].DOI:10.19701/j.jzjg.2020.03.018 [本文引用: 1]
Experimental study on bearing capacity of Q420 high-strength angle steel under axial compression
[J].DOI:10.19701/j.jzjg.2020.03.018 [本文引用: 1]
Q345GJ钢(中)厚板H形及箱形柱残余应力与轴压稳定承载力分析
[J].
Residual stress distribution and overall stability load-carrying capacities of H-shaped and box section columns welded by Q345GJ structural steel plates under axial compression
[J].
不锈钢压弯构件整体稳定性能有限元研究与承载力计算方法
[J].DOI:10.6052/j.issn.1000-4750.2018.12.0705
Fe research on the overall stability of stainless-steel beam-columns and calculation method of bearing capacity
[J].DOI:10.6052/j.issn.1000-4750.2018.12.0705
Study on stability and design guidelines for the combined system of scaffolds and shores
[J].
Effects of geometric imperfections on flexural buckling resistance of laterally braced columns
[J].DOI:10.1061/(ASCE)ST.1943-541X.0001508
Lateral bracing of columns and beams
[J].
Q420高强度等边角钢轴压构件整体稳定性能设计方法研究
[J].
Investigation on design method of overall bucking behavior for Q420 high strength steel equal-leg angle members under axial compression
[J].
剪切型支撑框架弹塑性失稳模式判定准则
[J].
Determination of buckling mode for elastic-plastic braced frames
[J].