盾构机凭借施工速度快、成型质量好、安全性高等优点广泛应用于隧道的开发建设中[1-3]. 在盾构施工过程中,滚刀失效严重,需要工作人员频繁在狭窄、高压、高湿的环境下进行换刀作业,换刀耗时较长且长时间处于高压环境会对人体造成极大伤害[4-6]. 随着对施工效率及安全要求的不断提高,实现换刀过程自动化已经成为一种必然趋势[7]. 自动换刀系统包括刀座系统和与之对应的换刀执行器,而传统刀座系统拆装动作复杂,对换刀执行器要求较高,不利于工程实际应用. 因此,适合机器换刀的一体式刀座系统应运而生. 刀座系统是滚刀与刀盘之间传递破岩载荷的关键连接件,若一体式刀座系统承载能力不足而频繁出现严重变形、开裂、压溃等失效问题,会使换刀执行器自动拆装滚刀的成功率大大降低. 因此,一体式刀座系统的承载性能是滚刀自动拆装成功与否的关键,基于承载性能分析对一体式刀座系统进行结构优化具有重要意义.
目前,国内外许多机构和学者针对自动更换滚刀进行了相关研究,研究主要集中在换刀执行器的构型设计方面. 张海东等[8]提出了一种6自由度串联式换刀机器人,并对其进行了换刀范围分析、关节轨迹规划与运动控制仿真. Chen[9]利用蛇形机器人和多轴机器人完成开挖仓的检查和滚刀的更换,并通过试验样机验证了该方案的可行性. Peng等[10]针对换刀机器人系统提出了一种单目视觉姿态测量方法,并通过数值模拟证明其具有更高的求解精度和鲁棒性. 同时,一些学者也提出了一体式刀座系统的构型设计方案. Meng等[11]提出了一种旋转楔块式刀座系统,并通过试验和数值模拟验证了该刀座的结构强度和防松性能. Yang等[12]提出了一种滑动楔块式刀座系统,通过螺栓带动两侧楔块横向滑动完成一体式刀座系统的锁紧和放松. Yuan等[13-14]提出了一种单自由度旋转式刀座系统,将多个锁紧零件组成共轴的圆柱状组件,通过共轴组件的旋转实现滚刀的锁紧. 中国铁建重工集团股份有限公司提出了一种用于更换盾构机滚刀的全流程换刀装置,其中包括一种只具有4个部件的双楔块转动式刀座系统[15]. 徐姣姣等[16]和杨冬建等[17]分别提出了一种连杆式刀座系统和滑动式刀座系统,并通过数值模拟对刀座结构强度进行验证. 以上针对一体式刀座系统的研究基本都局限在构型设计和结构强度验证方面,并没有对其各项性能进行深入分析. 而针对刀座系统性能的研究主要集中在传统刀座系统的焊接性能、振动特性和综合评价等方面. Zhu等[18]设计了一种新型的刀座系统焊接结构,并通过数值模拟验证了刀座的疲劳特性有显著提升. Huo等[19]分析了盾构机传统刀座系统的振动响应和载荷传递规律,并通过刀架振动试验对模型进行验证. Yang[20]等建立了传统刀座系统的性能评价指标体系,并给出了刀座系统各性能指标的权重. 目前还没有文献综合考虑一体式刀座系统滚刀拆装过程与承载性能要求,分析其内部尺寸联动关系,针对一体式刀座系统承载性能对其结构参数进行优化.
本研究针对双楔块转动式一体式刀座系统,根据其锁紧方式和受载工况建立数值模型,通过缩尺刀座模型静压试验验证数值模型结果的正确性. 考虑零部件装配关系与拆卸要求,分析各零部件结构参数间的尺寸联动关系. 利用单因素分析方法确定影响其承载性能的主要结构参数. 利用正交试验权矩阵分析法,对一体式刀座系统进行结构优化,以提高一体式刀座系统的承载能力.
1. 数值模型建立及有效性验证
1.1. 数值模型建立
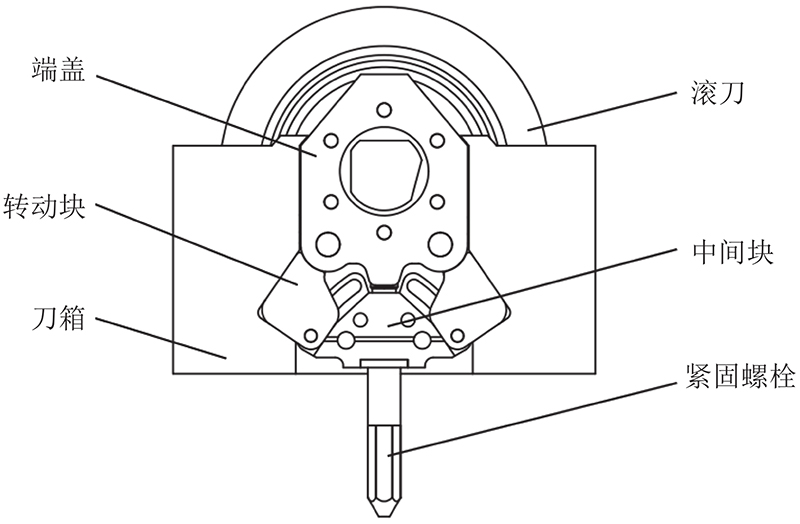
图 1
使用Solidworks软件建立刀座系统的三维模型,并对模型进行适当的简化处理,忽略模型非承载位置的倒角、圆角及其他细小结构以提高数值模型求解效率. 使用Ansys-Workbench建立刀座系统的静力学数值模型. 其中,各零件材料均选择Q345钢,材料的弹性模量为206 GPa,泊松比为0.28,密度为7 850 kg/m3. 螺栓与其连接的零件之间的接触类型设置为Bonded;其余零件之间的接触类型设置为Frictional,且摩擦系数设为0.2. 采用适应性更高的高阶四面体单元对刀座系统进行网格划分,对刀座系统零部件关键承载部位进行局部网格加密处理以提高计算精度,且网格增长速度设为1.15.
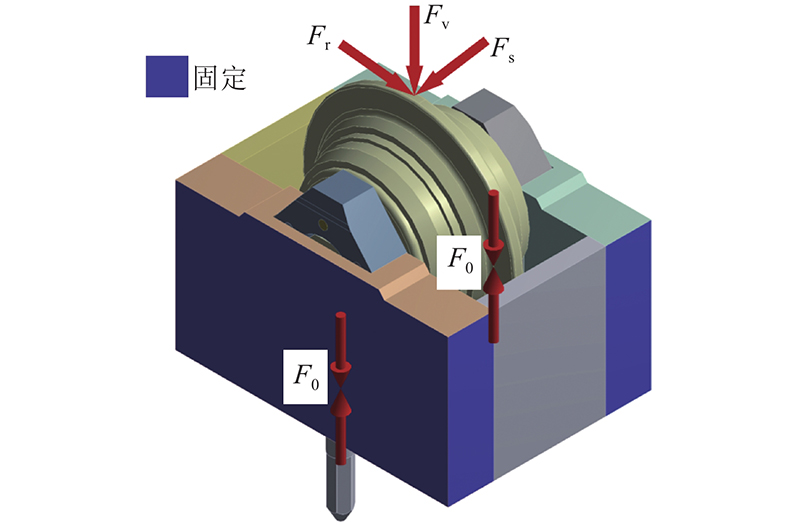
在一般工况下,对紧固螺栓施加预紧力,根据预紧力公式计算得出紧固螺栓预紧力F0=110 kN. 在滚刀顶部施加外载荷,其中包含垂直力Fv、侧向力Fs和滚动力Fr. 为了与实际情况保持一致,将数值模拟设置为2个载荷步,分别施加螺栓预紧力与滚刀破岩载荷. 第1个载荷步首先对紧固螺栓施加预紧力,在预紧力加载完成后,在第2个载荷步保持紧固螺栓预紧力不变,在滚刀顶部施加破岩载荷. 在刀箱四周施加Fixed固定约束. 刀座系统边界条件如图2所示.
图 2
1.2. 缩尺模型静压试验
为了验证刀座系统数值模型的正确性,在INSTRON1346型试验机上开展刀座系统静压试验. 该设备最大可施加载荷为2 000 kN,载荷测量精度能达到±0.5%. 考虑到刀座系统尺寸较大,加工、搬运不便以及试验台空间要求,使用0.4∶1的缩尺比例建立刀座系统的缩尺试验模型. 为了加载方便,使用等效压头代替滚刀承受静压载荷,等效压头顶端到刀轴的距离与滚刀半径相等. 缩尺刀座系统模型如图3所示.
图 3
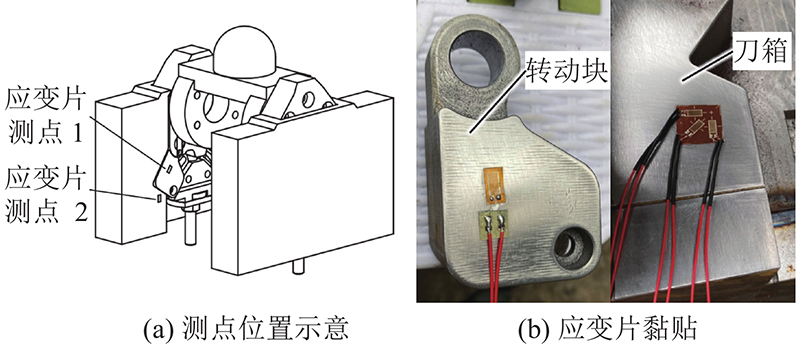
为了得到刀座系统受载条件下的应力情况,在转动块和刀箱表面黏贴应变片来采集应变,测点相对位置与应变片黏贴方向如图4所示. 其中刀箱应变片为竖直方向,与载荷加载方向一致,转动块应变片方向与转动块侧面平行.
图 4
对刀座系统缩尺模型进行垂直等效加载,等效载荷为125~250 kN,通过DH5925动态信号测试分析仪采集应变片的应变数据,刀座系统静压试验过程如图5所示.
图 5
1.3. 数值模型有效性验证
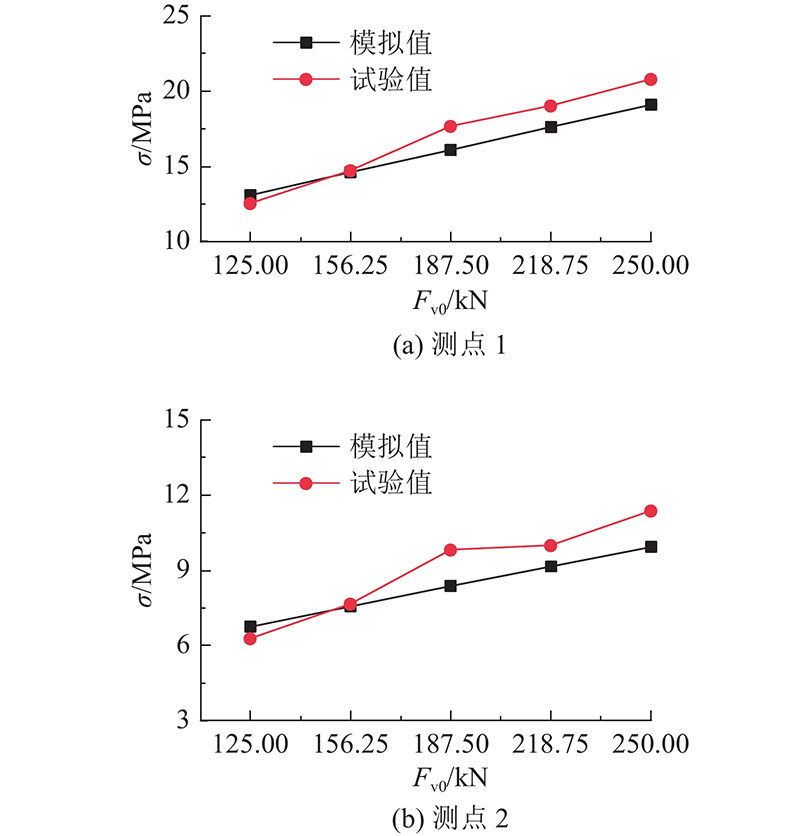
在刀座系统数值模型中施加与试验工况相同的外载荷,对刀座系统进行数值模拟,得到2个测点位置的应力. 将数值模拟结果与试验结果进行对比,结果如图6所示. 图中,σ为应力,Fv0为等效载荷. 测点1处应力模拟值较试验值最大误差为8.90%,测点2处应力模拟值较试验值最大误差为14.75%. 误差来源主要存在于以下方面:1)数值模型接触条件过于理想;2)数值模型几何体存在一定简化;3)由于试验条件限制,试验与数值模拟边界条件加载不一致,试验通过地脚螺栓将刀座系统固定在试验台上,数值模拟则为约束刀箱四周表面;4)取点位置误差,试验通过应变片测量刀座系统应力,而应变片黏贴需要覆盖一定的面积,且手工黏贴应变片存在一定位置误差与方向误差,数值模拟则为直接提取刀座系统对应点的应力;5)试验模型加工制造存在误差. 根据经验,认为模拟值相对试验值误差在20%内为合理. 测点1、2误差均在合理范围之内,验证了本研究数值模型的准确性.
图 6
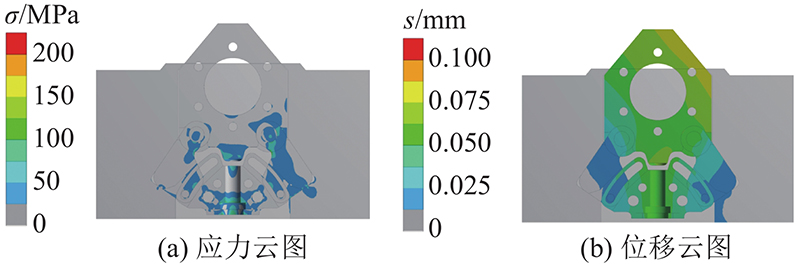
1.4. 承载性能分析
图 7
图 8
图 9
2. 结构参数对承载性能影响程度分析
2.1. 结构参数关系
图 10
图 11
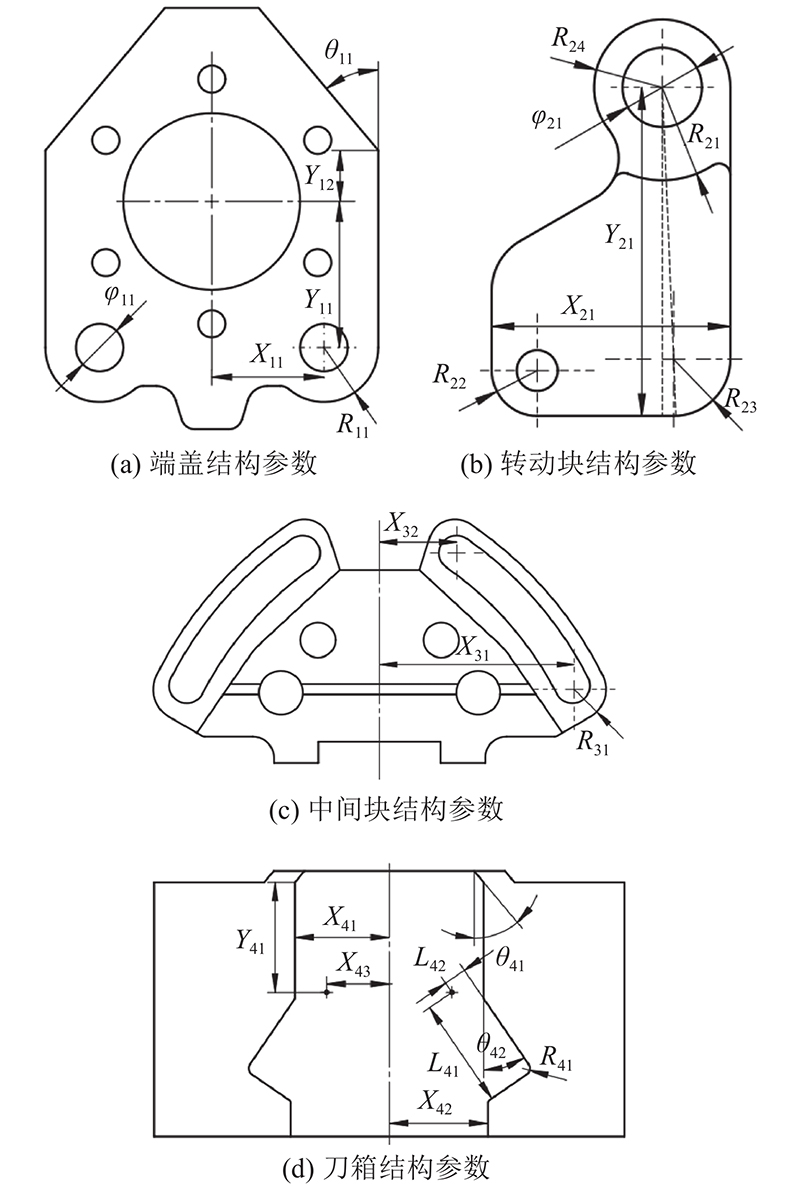
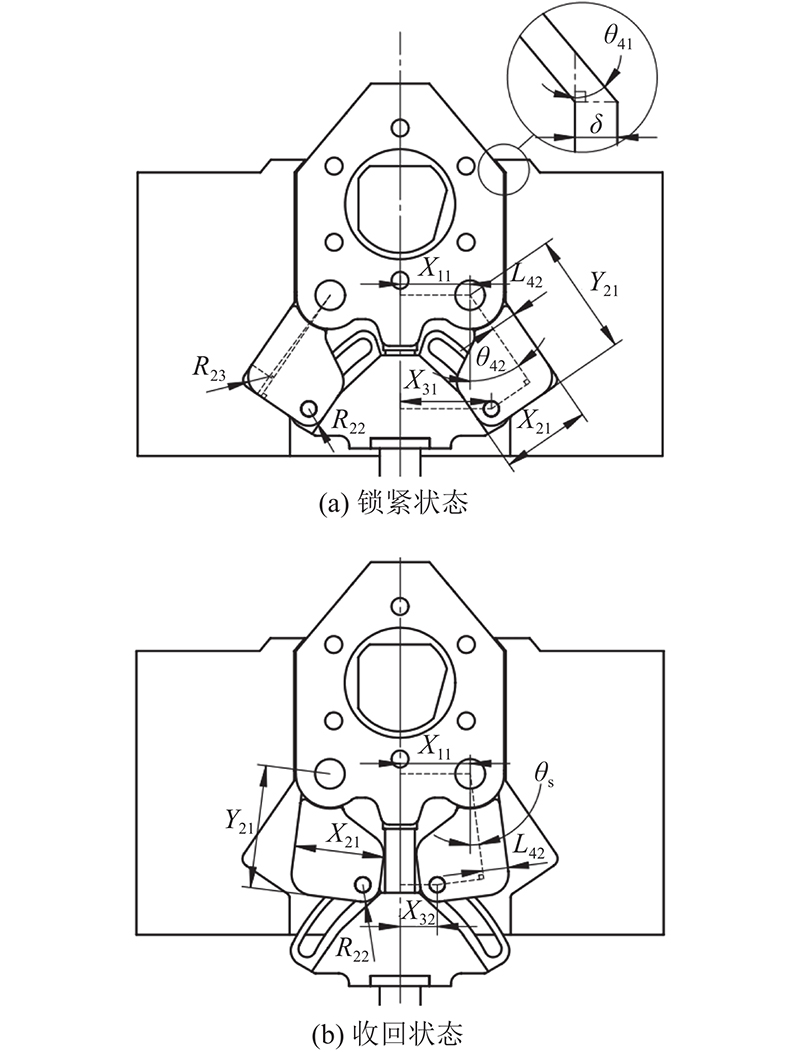
转动块安装在端盖两侧,须保证销轴安装孔直径相等,外侧配合圆弧面半径相等,即
式中:
端盖安装在刀箱内上半部分,并且端盖两侧和刀箱上半部分存在一定间隙,须保证端盖宽度与间隙之和与刀箱上部开口宽度相等,即
式中:X11为端盖销轴安装孔与其中轴线的水平距离,δ为锁紧状态下端盖与刀箱的水平间隙,X41为刀箱上方开口半宽.
刀箱顶部倾角对端盖安装时起限位作用,须保证两者上侧倾角相等,即
式中:θ11和θ41分别为端盖和刀箱的顶部倾角.
端盖与刀箱尺寸设计须提前确定转动块安装位置,须保证端盖与刀箱内部的转动块旋转中心位置一致,即
式中:X43为刀箱内部转动块旋转中心与中轴线的水平距离,Y11为端盖中心孔与销轴安装孔的竖直距离,Y12为端盖中心孔与端盖肩部的竖直距离,Y41为刀箱内部转动块旋转中心与刀箱顶部的竖直距离.
转动块位于锁紧状态时须锁紧在刀箱两侧的凹槽内,须保证刀箱两侧凹槽尺寸与转动块尺寸相等,即
式中:Y21为转动块旋转中心竖直高度,L41和L42为刀箱内部转动块旋转中心到凹槽两边的距离,R24为转动块头部外侧圆弧面半径.
中间块导向槽始末位置宽度须根据转动块旋转到锁紧状态与收回状态的极限位置确定. 当转动块位于锁紧状态时,由图11(a)可以得到中间块底部宽度与端盖宽度、转动块长度及锁紧状态转动块偏转角度之间的尺寸联动关系,即
式中:X31为中间块导向槽底部圆心与中轴线水平距离,X21为转动块宽度,R22为转动块底部左侧圆角半径,θ42为刀箱两侧凹槽偏转角度.
当转动块位于收回状态时,由图11(b)可以得到中间块顶部宽度与端盖宽度、转动块长度及收回状态转动块偏转角度之间的尺寸联动关系,即
式中:X32为中间块导向槽顶部圆心与中轴线水平距离,θs为转动块收回状态下的偏转角度.
刀座系统各零部件尺寸不仅须满足以上配合关系,还须保证在滚刀拆装过程中,各零部件之间不发生干涉,能顺利完成滚刀的锁紧与拆出.
在拆装过程中,滚刀、端盖、转动块及中间块组成的滚刀拆装结构从刀箱下方进出刀箱,为了保证上述零件能顺利拆装,须保证端盖总宽度、中间块底部总宽度和转动块在收回状态下的最大宽度均小于刀箱底部开口宽度,即
式中:X42为刀箱底部开口半宽,R31为中间块底部圆角半径,R23为转动块底部右侧圆角半径.
转动块的拆装与锁紧同样对其底部圆角R23有尺寸限制,若R23过小,其不仅会在锁紧状态下与刀箱两侧凹槽圆角R41发生干涉,还会在拆装过程中,与刀箱两侧凹槽承载面发生干涉. 为了避免转动块与刀箱干涉,须保证转动块底部圆角R23大于刀箱两侧凹槽圆角R41,以及转动块旋转过程中所覆盖的最大圆弧半径小于准许最大长度,即
式中:R41为刀箱两侧凹槽底部圆角半径.
2.2. 结构参数变量选取
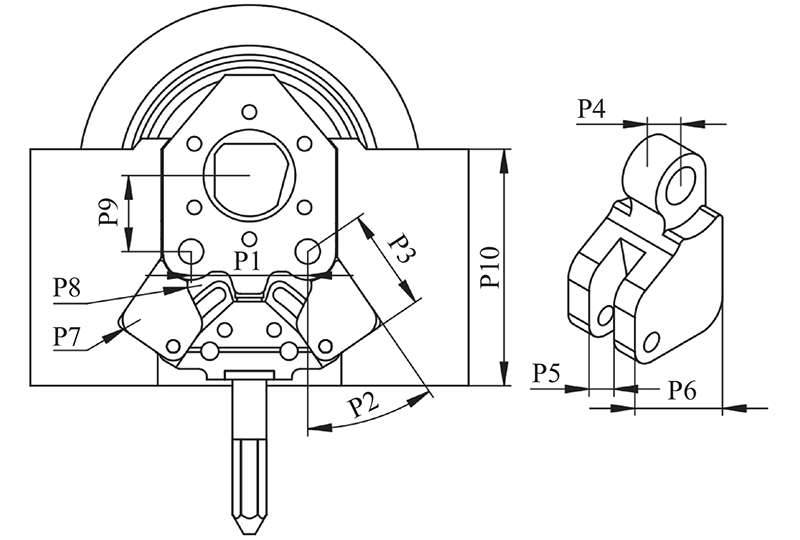
在刀座系统内部选取10组结构参数,分析刀座系统内部结构参数对其承载性能的影响. 参数具体位置如图12所示.
图 12
根据刀座系统零部件装配关系及拆卸空间要求计算确定各参数的取值范围,在取值范围内对每组参数取5组不同水平,如表1所示.
表 1 刀座系统参数水平表
Tab.1
| 参数名称 | 符号 | 水平 | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1)注:括号内的值为原始模型初始值 | ||||||
| 转动块轴间距/mm | P1 | 155.0 | 160.0 | (165.0)1) | 170.0 | 175.0 |
| 转动块偏转角/(°) | P2 | 30.4 | 32.4 | (34.4) | 36.4 | 38.4 |
| 转动块长度/mm | P3 | 125.0 | 135.0 | (145.0) | 155.0 | 165.0 |
| 转动块头部厚度/mm | P4 | 30.0 | 35.0 | (40.0) | 45.0 | 50.0 |
| 转动块槽宽/mm | P5 | 20.0 | 25.0 | (30.0) | 35.0 | 40.0 |
| 转动块宽度/mm | P6 | 102.50 | 103.75 | (105.00) | 106.25 | 107.50 |
| 转动块底部 圆角半径/mm | P7 | 10.0 | 15.0 | 20.0 | (25.0) | 30.0 |
| 转动块颈部 圆角半径/mm | P8 | (20.0) | 30.0 | 40.0 | 50.0 | 60.0 |
| 刀轴与转动块转轴 竖直距离/mm | P9 | 97.5 | (107.5) | 117.5 | 127.5 | 137.5 |
| 刀箱高度/mm | P10 | 315.0 | 325.0 | (335.0) | 345.0 | 355.0 |
2.3. 承载性能评价指标
刀座系统是滚刀与刀盘之间直接传递滚刀载荷的关键部件,其性能指标种类众多且相互关联. 综合考虑换刀需要及刀座系统工作要求,来确定刀座系统承载性能评价指标.
换刀要求:刀座系统拆装结构主要包括滚刀、端盖、转动块、中间块和紧固螺栓等结构. 在大范围换刀需求下,换刀执行器力臂较长,刀座系统拆装结构总质量越大,对换刀执行器的强度要求也就越高,换刀执行器的尺寸也就越大. 而盾构机内部空间狭窄,因此在合理范围内,刀座系统拆装结构总质量应越小越好.
工作要求:在盾构施工过程中,滚刀承受巨大的破岩载荷并将其传递给刀座系统,因此要求刀座系统具有较强的刚度和强度. 因此,用刀座系统受载条件下的整体最大变形作为其刚度指标,刀座系统变形应越小越好. 结合上文对刀座系统承载性能的分析,用端盖和转动块受载条件下应力的最大值作为刀座系统的强度指标,端盖应力以及转动块应力均应越小越好.
综上,确定刀座系统承载性能主要依靠拆装结构总质量m、整体最大变形smax、端盖应力σ1及转动块应力σ2以上4个指标进行评价.
2.4. 敏感结构参数确定
根据表1给出的结构参数变化范围及水平,只改变单一参数,控制其他参数不变,建立参数P1~P10的单因素变量数值模拟模型,数值模型共计50组. 在数值模拟模型中,除变量之外的其他尺寸参数、网格质量、边界条件等均与上文保持一致.
相对标准偏差能反映数据的相对离散程度. 数据的相对标准偏差越大,其相对离散程度越高,说明参数对指标的影响越明显. 相对标准偏差计算方法如下:
式中:
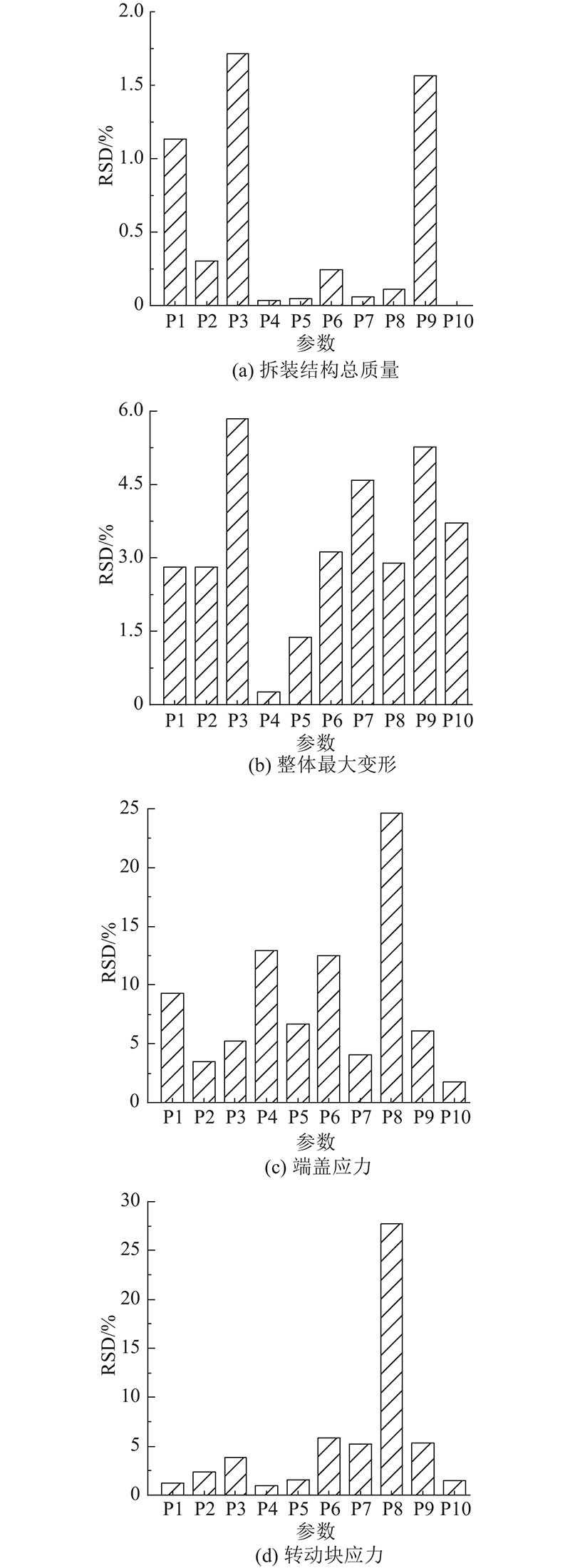
根据数值模拟结果分别计算每组参数不同指标的相对标准偏差,4组指标不同参数的相对标准偏差计算结果如图13所示. 由单一指标相对标准偏差计算结果可知,针对指标拆装结构总质量,P3对其影响最大,其后依次是P9和P1,其他参数对其几乎没有影响. 针对指标整体最大变形,对其影响最大的同样为P3,相对标准偏差为5.84%,其后P9、P7、P10对其影响依次减小,相对标准偏差值也略有减小. 针对指标端盖应力,对其影响最大的参数为P8,相对标准偏差为24.66%,其后分别为P4、P6,相对标准偏差分别为12.97%、12.51%. 针对指标转动块应力,对其影响最大的参数同样为P8,相对标准偏差为27.75%,其他参数与P8相比存在较大差距,相对标准偏差值均不足6%.
图 13
图 13 刀座系统参数相对标准偏差分析
Fig.13 Relative standard deviation analysis of cutter holder system parameters
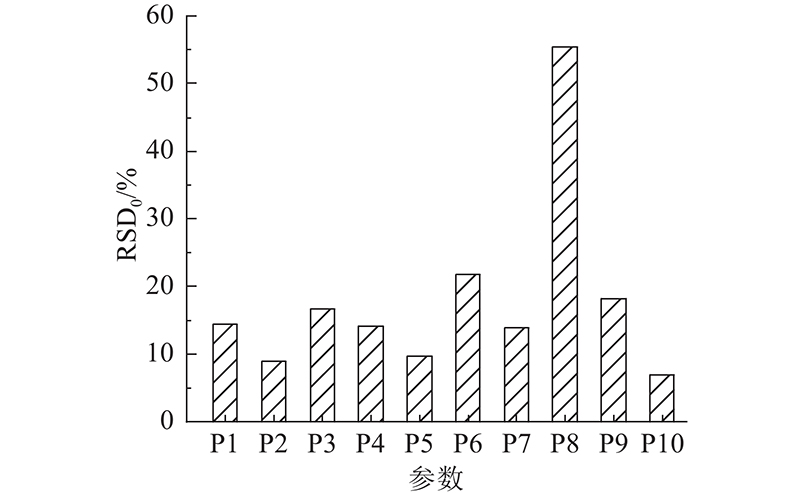
由于目前一体式刀座系统尚处于构型设计阶段,工程应用较少,对其各性能指标重要性程度要求尚不明晰,故默认其承载性能各项指标权系数相等. 对每个参数的各项指标相对标准偏差值求和,得到参数对所有指标的总相对标准偏差值,可以表示参数对所有指标的综合影响程度,总相对标准偏差计算结果如图14所示. 图中,RSD0为各项指标RSD之和. 由图14可知,P8对刀座系统承载性能指标的综合影响程度最大,总相对标准偏差为55.43%;其次是P6和P9,总相对标准偏差分别为21.72%和18.27%. P3、P1、P4、P7对承载性能指标的综合影响程度依次减小,总相对标准偏差分别为16.62%、14.45%、14.20%和13.90%. P5、P2、P10对承载性能指标的综合影响程度稍弱,总相对标准偏差均不足10%,与前述参数有一定差距. 综上,对刀座系统承载性能指标综合影响程度最大的3个参数为P6、P8和P9.
图 14
图 14 刀座系统参数综合影响程度
Fig.14 Comprehensive influence degree of cutter holder system parameters
3. 正交试验设计及参数优化
3.1. 正交试验设计
该试验为3因素5水平正交试验,故选用L25(56)正交表. 将A、B、C这3个参数分别放置于正交表的前3列. 正交试验方案共计25组,试验方案与数值模拟结果如表2所示. 在数值模拟模型中,除变量之外的其他尺寸参数、网格质量、边界条件等均与上文保持一致.
表 2 正交试验方案与数值模拟结果
Tab.2
| 试验号 | 因素 | 试验结果 | ||||||
| A | B | C | m/kg | smax/mm | σ1/MPa | σ2/MPa | ||
| 1 | 1(102.50) | 1(20.0) | 1(97.5) | 304.09 | 0.083 5 | 155.75 | 214.09 | |
| 2 | 1 | 2(30.0) | 2(107.5) | 307.39 | 0.083 1 | 153.60 | 167.22 | |
| 3 | 1 | 3(40.0) | 3(117.5) | 310.68 | 0.084 2 | 135.27 | 134.05 | |
| 4 | 1 | 4(50.0) | 4(127.5) | 313.97 | 0.086 2 | 105.58 | 140.04 | |
| 5 | 1 | 5(60.0) | 5(137.5) | 317.24 | 0.088 9 | 93.78 | 107.61 | |
| 6 | 2(103.75) | 1 | 2 | 307.63 | 0.084 3 | 148.78 | 215.16 | |
| 7 | 2 | 2 | 3 | 310.93 | 0.084 2 | 131.23 | 159.58 | |
| 8 | 2 | 3 | 4 | 314.24 | 0.085 5 | 96.11 | 126.65 | |
| 9 | 2 | 4 | 5 | 317.53 | 0.087 9 | 97.91 | 115.98 | |
| 10 | 2 | 5 | 1 | 305.42 | 0.076 0 | 91.73 | 108.50 | |
| 11 | 3(105.00) | 1 | 3 | 311.17 | 0.085 3 | 203.58 | 201.00 | |
| 12 | 3 | 2 | 4 | 314.48 | 0.085 9 | 109.39 | 153.94 | |
| 13 | 3 | 3 | 5 | 317.79 | 0.087 4 | 95.44 | 128.33 | |
| 14 | 3 | 4 | 1 | 305.70 | 0.075 2 | 92.70 | 110.01 | |
| 15 | 3 | 5 | 2 | 308.98 | 0.076 9 | 90.45 | 111.09 | |
| 16 | 4(106.25) | 1 | 4 | 314.72 | 0.086 5 | 136.96 | 192.04 | |
| 17 | 4 | 2 | 5 | 318.04 | 0.087 2 | 98.69 | 152.46 | |
| 18 | 4 | 3 | 1 | 305.96 | 0.074 9 | 94.97 | 123.98 | |
| 19 | 4 | 4 | 2 | 309.26 | 0.076 2 | 90.70 | 108.32 | |
| 20 | 4 | 5 | 3 | 312.54 | 0.078 3 | 88.01 | 108.10 | |
| 21 | 5(107.50) | 1 | 5 | 318.28 | 0.088 3 | 109.97 | 200.57 | |
| 22 | 5 | 2 | 1 | 306.21 | 0.075 2 | 110.75 | 140.04 | |
| 23 | 5 | 3 | 2 | 309.53 | 0.076 1 | 92.31 | 120.91 | |
| 24 | 5 | 4 | 3 | 312.83 | 0.078 0 | 89.73 | 109.20 | |
| 25 | 5 | 5 | 4 | 316.11 | 0.080 2 | 93.13 | 114.15 | |
3.2. 极差分析
采用极差分析法分别对正交试验结果的各项指标进行分析,计算结果如表3所示. 表中,kij表示正交试验中包含第i个因素第j个水平所有试验方案对应指标的算术平均值,Ri为kij的极差. kij的大小可以反映各因素水平的优劣,Ri的大小可以反映各因素对试验结果单一指标的影响程度.
表 3 正交试验极差分析结果
Tab.3
| 指标 | kij | |||
| i=A | i=B | i=C | ||
| m/kg | j=1 | 310.67 | 311.18 | 305.48 |
| j=2 | 311.15 | 311.41 | 308.56 | |
| j=3 | 311.62 | 311.64 | 311.63 | |
| j=4 | 312.11 | 311.86 | 314.70 | |
| j=5 | 312.59 | 312.06 | 317.77 | |
| Ri | 1.92 | 0.88 | 12.30 | |
| smax/mm | j=1 | 0.085 2 | 0.085 6 | 0.076 9 |
| j=2 | 0.083 6 | 0.083 1 | 0.079 3 | |
| j=3 | 0.082 2 | 0.081 6 | 0.082 0 | |
| j=4 | 0.080 6 | 0.080 7 | 0.084 9 | |
| j=5 | 0.079 5 | 0.080 1 | 0.088 0 | |
| Ri | 0.005 7 | 0.005 5 | 0.011 0 | |
| σ1/MPa | j=1 | 128.80 | 151.01 | 109.18 |
| j=2 | 113.15 | 120.73 | 115.17 | |
| j=3 | 118.31 | 102.82 | 129.56 | |
| j=4 | 101.87 | 95.32 | 108.23 | |
| j=5 | 99.18 | 91.42 | 99.16 | |
| Ri | 29.62 | 59.59 | 30.41 | |
| σ2/MPa | j=1 | 152.60 | 204.57 | 139.32 |
| j=2 | 145.17 | 154.65 | 144.54 | |
| j=3 | 140.87 | 126.78 | 142.39 | |
| j=4 | 136.98 | 116.71 | 145.36 | |
| j=5 | 136.97 | 109.89 | 140.99 | |
| Ri | 15.63 | 94.68 | 6.04 | |
由极差分析结果可知各因素对单一指标性能的影响. 其中,针对指标拆装结构总质量,对其影响最大的是因素C,因素A与因素B两者对其影响程度与因素C相比处于较低水平,且指标随着因素C的增大而增大. 各因素对其影响的主次顺序为C、A、B,最优结构参数组合为A1B1C1. 由于刀座系统拆卸结构主要包括滚刀、端盖、转动块和中间块,在这4种结构中,除了滚刀外端盖质量最大,因素C的变化会显著影响端盖的质量,而因素A、B变化只会小幅影响转动块质量,故因素C对指标拆装结构总质量影响最为显著,且两者呈正相关关系.
若仅以整体最大变形为指标,同样是因素C对其影响最大,因素A与因素B对其影响程度相当,仅为因素C的一半左右,且指标与因素A和因素B呈负相关,与因素C呈正相关. 各因素对其影响的主次顺序为C、A、B,最优结构参数组合为A5B5C1. 这是因为拆装结构通过其下方的转动块固定在刀箱内,滚动力和侧向力的作用会使拆装结构发生变形,由图7(b)可知,变形最大位置出现在拆装结构右上角. 因素A和因素B的增加,会增大转动块的刚度,而因素C的增加会导致拆装结构从锁紧位置向上伸出的距离增大,相当于减小拆装结构的刚度,故指标整体最大变形与因素A和因素B均呈负相关,与因素C呈正相关.
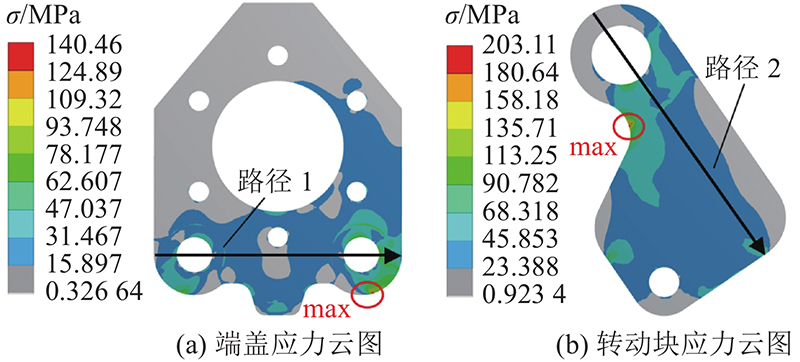
针对指标端盖应力,因素B对其影响程度最大,因素A与因素C对其影响程度差距不大,约为因素B的一半,且随着因素B的增加,指标呈减小趋势. 各因素对其影响的主次顺序为B、C、A,最优结构参数组合为A5B5C5. 由图8(a)可知,端盖应力最大值出现在销轴安装孔下侧边缘与转动块刚好接触处. 因素B的增加会增大转动块与端盖的接触面积,从而使端盖应力降低,故指标端盖应力与因素B呈负相关.
针对指标转动块应力,因素B对其影响程度最大,因素A与因素C对其影响处于较低水平,且指标随着因素B的增大而减小. 各因素对其影响的主次顺序为B、A、C,最优结构参数组合为A5B5C1. 由图8(b)可知,转动块应力最大值出现在其颈部几何结构过渡区域,该位置出现了应力集中现象. 因素B的增加使转动块几何结构过渡变得平滑,可以一定程度上降低该部位的应力集中. 故指标转动块应力与因素B呈负相关.
3.3. 结构参数优化
由于极差分析法主要用于单一指标最优因素组合方案的选取,无法进行多指标的综合优化分析,对于4种性能指标,得到的4组最优参数组合中仅有2组一致. 因此,采用权矩阵分析法对正交试验结果进行综合分析. 权矩阵分析法是一种对多指标试验数据进行处理的客观数据分析方法,该方法在默认各项指标权系数相等的前提下,通过矩阵运算的形式,对直观分析数据结果进行运算,得到各因素各水平对指标综合影响的权系数. 根据权矩阵分析结果,可以直接确定多指标下的综合最优方案以及因素对指标综合影响的主次顺序.
1)指标层矩阵M:正交试验中第i个因素第j个水平上的指标的平均值为kij,若试验指标越大越好,则令Kij=kij,若试验指标越小越好,则令Kij=1/kij,建立指标层矩阵M.
2)因素层矩阵T:令
3)水平层矩阵S:正交试验中第i个因素的极差为Ri,令
4)权矩阵W:根据式(20)、(21)计算总权矩阵W.
式中:Mi、Ti、Si和Wi分别为在u个指标中第i个指标所对应的指标层矩阵、因素层矩阵、水平层矩阵和权矩阵;u为指标个数,u=4.
通过计算,即可求解正交试验中各因素水平对所有指标的综合影响权重,根据权重大小即可得出因素水平的最优组合方案和因素对所有指标综合影响的主次顺序.
将刀座系统正交试验结果代入以上矩阵变量,可以得出刀座系统各因素水平的权矩阵计算结果ω,如表4所示.由矩阵分析结果可知,因素A和因素B的第5水平权重最大,因素C的第1水平权重最大,权重最大值分别为4.04、9.54和8.36. 因此,根据A5、B5、C1的权重大小可以判断出影响刀座系统承载性能的因素的主次顺序为B、C、A. 可以快速确定刀座系统最优水平组合为A5B5C1,即转动块宽度107.5 mm,转动块颈部圆角半径60.0 mm,刀轴与转动块转轴竖直距离97.5 mm.
表 4 权矩阵分析结果
Tab.4
| 水平 | ω | ||
| A | B | C | |
| 1 | 3.56 | 5.97 | 8.36 |
| 2 | 3.77 | 7.32 | 8.17 |
| 3 | 3.75 | 8.52 | 7.91 |
| 4 | 3.98 | 9.11 | 7.99 |
| 5 | 4.04 | 9.54 | 8.00 |
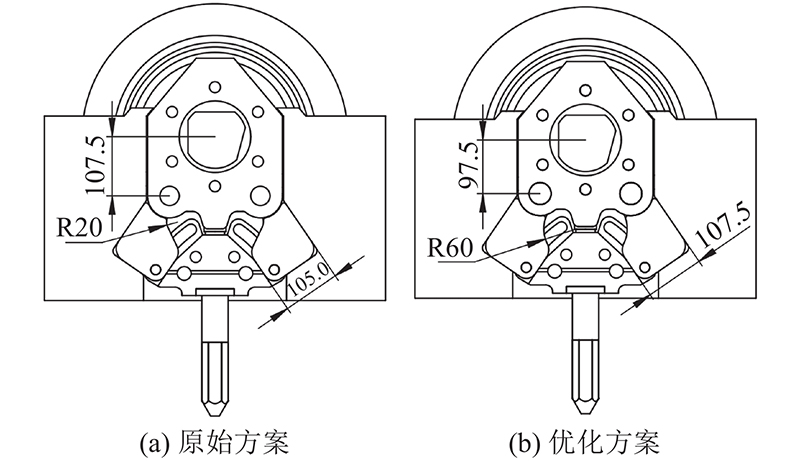
对刀座系统优化方案进行三维建模,刀座系统优化前、后结构对比如图15所示.
图 15
图 15 刀座系统优化前、后结构对比
Fig.15 Structural comparison before and after cutter holder system optimization
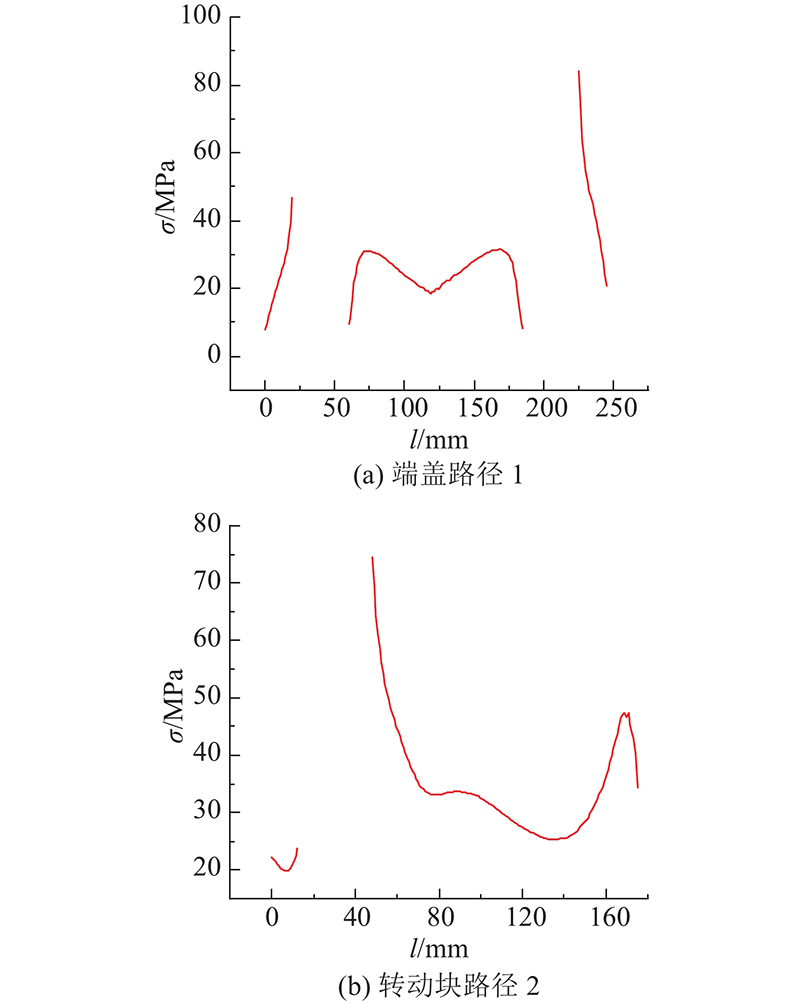
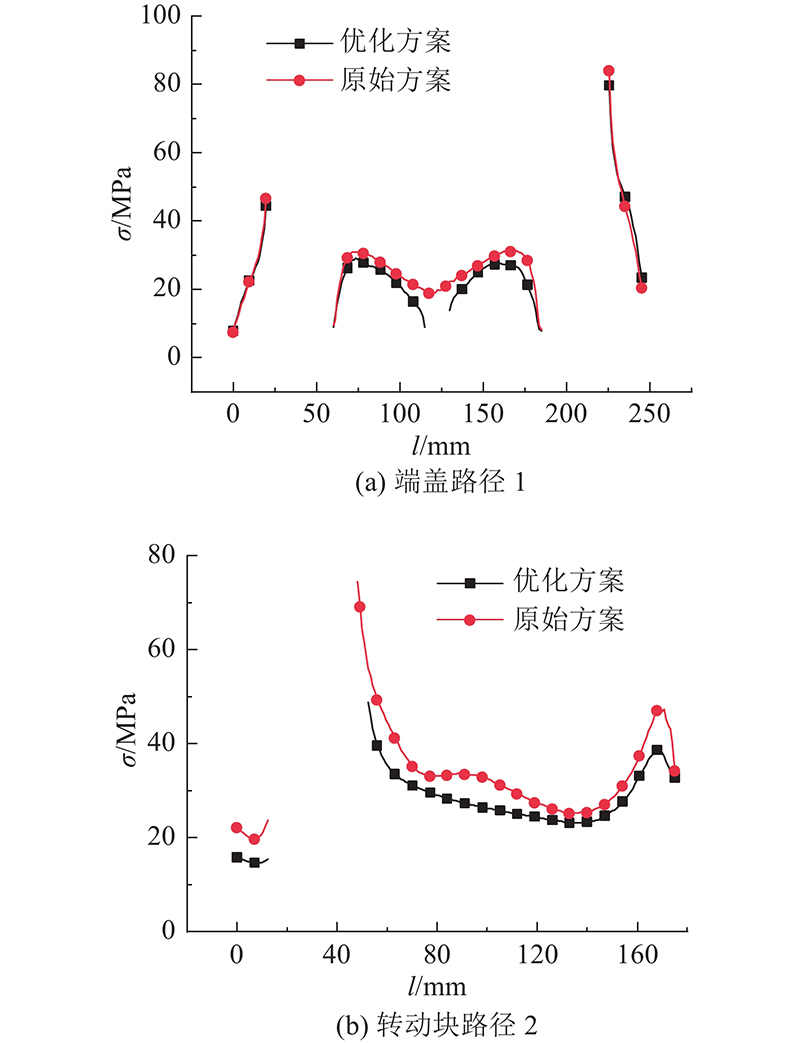
采用相同边界条件及网格质量对刀座系统优化方案进行数值模拟分析,并与原始方案数值模拟结果进行对比,验证刀座系统多指标优化方案的有效性. 刀座系统优化方案与原始方案的端盖及转动块路径应力对比曲线如图16所示.
图 16
图 16 刀座系统优化前、后路径应力对比
Fig.16 Comparison of path stress before and after cutter holder system optimization
针对端盖路径应力,刀座系统优化方案与原始方案整体趋势基本一致. 在端盖中间区域,优化方案路径应力较原始方案有一定降低,在端盖两侧销轴安装孔区域,优化前、后路径应力整体基本相同,优化方案路径最大应力略有降低. 针对转动块路径应力,刀座系统优化方案与原始方案整体趋势同样基本一致. 优化方案路径应力较原始方案整体有明显降低,其中转动块路径最大应力有显著降低.
将刀座系统优化方案各项指标与原始方案进行对比,如表5所示. 可以看出,优化方案各项指标与原始方案相比均有不同程度改善,其中,拆装结构总质量降低了0.44%,整体最大变形降低了11.31%,端盖最大应力降低了34.07%,转动块最大应力降低了41.01%.
表 5 刀座系统优化前、后指标对比
Tab.5
| 方案 | m/kg | smax/mm | σ1/MPa | σ2/MPa |
| 原始方案 | 308.22 | 0.081 9 | 140.46 | 203.11 |
| 优化方案 | 306.88 | 0.072 6 | 92.61 | 119.82 |
4. 结 论
综合考虑一体式刀座系统滚刀拆装过程与承载性能要求,采用正交试验与数值模拟相结合的方法,对一体式刀座系统结构参数进行优化,得到如下结论.
(1)综合一体式刀座系统内部零部件装配关系及拆卸要求,在避免干涉前提下,分析并确定了一体式刀座系统内部零部件各结构参数之间的联动关系及准许调整范围.
(2)影响一体式刀座系统综合性能的主要参数为转动块宽度、转动块颈部圆角半径和刀轴与转动块转轴竖直距离. 各参数对一体式刀座系统承载性能的影响程度由大到小依次为转动块颈部圆角半径、转动块宽度、刀轴与转动块转轴竖直距离.
(3)得到了一体式刀座系统综合性能最优的结构参数组合方案:转动块宽度107.5 mm,转动块颈部圆角半径60.0 mm,刀轴与转动块转轴竖直距离97.5 mm. 数值模拟结果对比分析表明,在一般工况下,优化方案的拆装结构总质量与原始方案基本持平,整体最大变形、端盖应力与转动块应力与原始方案相比均有显著降低.
本研究受限于试验条件,使用静态载荷对一体式刀座系统进行加载. 后续计划进行一体式刀座系统破岩实验和数值模拟研究,进一步验证一体式刀座系统在实际工况下的可靠性.
参考文献
基于HJC模型的盾构刀具切削混凝土数值模拟
[J].
Numerical simulation of shield tool cutting concrete based on HJC model
[J].
隧道掘进机大数据研究进展: 数据挖掘助推隧道挖掘
[J].
Research progress on big data of tunnel boring machine: how data mining can help tunnel boring
[J].
基于XGBoost的隧道掘进机操作参数智能决策系统设计
[J].
XGBoost based intelligent determination system design of tunnel boring machine operation parameters
[J].
TBM cutter wear under high-strength surrounding rock conditions: a case study from the second phase of the northern Xinjiang water supply project
[J].DOI:10.1007/s00603-021-02545-5 [本文引用: 1]
盾构隧道刀具更换技术综述
[J].DOI:10.3969/j.issn.1001-7372.2018.10.004
Technical review of cutter replacement in shield tunneling
[J].DOI:10.3969/j.issn.1001-7372.2018.10.004
Prediction of disc cutter life during shield tunneling with AI via the incorporation of a genetic algorithm into a GMDH-type neural network
[J].DOI:10.1016/j.eng.2020.02.016 [本文引用: 1]
中国隧道建设面临的若干挑战与技术突破
[J].DOI:10.3969/j.issn.1001-7372.2020.12.001 [本文引用: 1]
Challenges and technological breakthroughs in tunnel construction in China
[J].DOI:10.3969/j.issn.1001-7372.2020.12.001 [本文引用: 1]
TBM换刀机器人的设计分析与运动控制
[J].
Design and motion control of disc cutter changing robot for TBM
[J].
Pose determination of the disc cutter holder of shield machine based on monocular vision
[J].DOI:10.3390/s22020467 [本文引用: 1]
Development and performance evaluation of an integrated disc cutter system for TBMs
[J].DOI:10.3390/app11020644 [本文引用: 1]
A modular design method based on TRIZ and AD and its application to cutter changing robot
[J].
一种适用于机器人换刀的新型滚刀刀座设计与分析
[J].
Design and analysis of a new cutter holder of disc cutter suitable for robot change
[J].
基于机器操作的TBM一体化刀具系统设计及试验研究
[J].
Design and experimental research of TBM integrated cutter system based on robot operation
[J].
Finite element analysis of a new welding structure of cutter mount in TBM
[J].
Analyses of dynamic characteristics and structure optimization of tunnel boring machine cutter system with multi-joint surface
[J].DOI:10.1007/s11071-016-3038-0 [本文引用: 1]
A hybrid comprehensive performance evaluation approach of cutter holder for tunnel boring machine
[J].DOI:10.1016/j.aei.2022.101546 [本文引用: 1]
Comparisons between experimental and semi-theoretical cutting forces of CCS disc cutters
[J].DOI:10.1007/s00603-018-1400-x [本文引用: 1]
钢-超高性能混凝土组合板开裂荷载正交试验及计算方法
[J].
Orthogonal test and calculation method of cracking load of steel-ultra-high performance concrete composite specimen
[J].
基于正交试验的玻璃壳热应力影响因素分析
[J].DOI:10.3901/JME.2019.12.091 [本文引用: 1]
Analysis of glass shell’s thermal stress based on orthogonal experiment
[J].DOI:10.3901/JME.2019.12.091 [本文引用: 1]
正交试验设计的矩阵分析方法
[J].
A matrix analysis of orthogonal design
[J].