[1]
BRETON T, TASSIN A, JACQUES N Experimental investigation of the water entry and/or exit of axisymmetric bodies
[J]. Journal of Fluid Mechanics , 2020 , 901 : 37
DOI:10.1017/jfm.2020.559
[本文引用: 1]
[2]
DAYTON J W, POETTGEN B K, CETEGEN B M Non-isothermal mixing characteristics in the extreme near-field of turbulent jets in hot crossflow: effects of jet exit turbulence and velocity profile
[J]. Physics of Fluids , 2020 , 32 (11 ): 115114
[3]
KRISTENSEN H M, NORRIS R S Chinese nuclear forces, 2015
[J]. Bulletin of the Atomic Scientists , 2015 , 71 (4 ): 77 - 84
DOI:10.1177/0096340215591247
[4]
MA Z, HU J, FENG J, et al. A longitudinal air–water trans-media dynamic model for slender vehicles under low-speed condition. Nonlinear Dynamics , 2020, 99(2): 1195-1210.
[本文引用: 2]
[5]
NAIR V V, BHATTACHARYYA S K Water entry and exit of axisymmetric bodies by CFD approach
[J]. Journal of Ocean Engineering and Science , 2018 , 3 (2 ): 156 - 174
DOI:10.1016/j.joes.2018.05.002
[本文引用: 1]
[6]
KIM N, PARK H Water entry of rounded cylindrical bodies with different aspect ratios and surface conditions
[J]. Journal of Fluid Mechanics , 2019 , 863 : 757 - 788
DOI:10.1017/jfm.2018.1026
[本文引用: 1]
[7]
HAO H H, SONG Y P, YU J Y, et al Numerical analysis of water exit for a sphere with constant velocity using the lattice Boltzmann method
[J]. Applied Ocean Research , 2019 , 84 (12 ): 163 - 178
[本文引用: 1]
[8]
GUO C, LIU T, HAO H, et al Evolution of water column pulled by partially submerged spheres with different velocities and submergence depths
[J]. Ocean Engineering , 2019 , 187 (5 ): 106087
[本文引用: 1]
[9]
孙士丽, 孙义龙, 胡竞中, 等 圆柱体出水运动的自由面效应及水冢现象分析
[J]. 计算物理 , 2013 , 30 (2 ): 187 - 193
DOI:10.3969/j.issn.1001-246X.2013.02.004
[本文引用: 1]
SUN Shi-li, SUN Yi-long, HU Jing-zhong, et al Free surface effect and spike of a cylinder piercing water surface
[J]. Chinese Journal of Computational Physics , 2013 , 30 (2 ): 187 - 193
DOI:10.3969/j.issn.1001-246X.2013.02.004
[本文引用: 1]
[12]
赵蛟龙. 航行体出入水空泡载荷特性及缩比试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2016: 45-50.
[本文引用: 1]
ZHAO Jiao-long. Fluid dynamics and experimental investigation on the cavitation characteristics of the water-exit and -entry process of underwater vehicle [D]. Harbin: Harbin Engineering University, 2016: 45-50.
[本文引用: 1]
[13]
廖保全 附加质量变化率在航行体出水过程中的影响研究
[J]. 计算力学学报 , 2017 , 34 (1 ): 95 - 100
DOI:10.7511/jslx201701013
[本文引用: 1]
LIAO Bao-quan Influence on rate of change of added mass for an underwater vehicle during its water exit process
[J]. Chinese Journal of Computational Mechanics , 2017 , 34 (1 ): 95 - 100
DOI:10.7511/jslx201701013
[本文引用: 1]
[14]
张晓强, 冯金富, 吝科, 等 跨介质运动物体的附加质量
[J]. 北京航空航天大学学报 , 2016 , 42 (4 ): 821 - 828
DOI:10.13700/j.bh.1001-5965.2015.0478
[本文引用: 1]
ZHANG Xiao-qiang, FENG Jin-fu, LIN-Ke, et al Added mass of trans-media moving object
[J]. Journal of Beijing University of Aeronautics and Astronautics , 2016 , 42 (4 ): 821 - 828
DOI:10.13700/j.bh.1001-5965.2015.0478
[本文引用: 1]
[15]
陈林烽 基于 Navier-Stokes 方程残差的隐式大涡模拟有限元模型
[J]. 力学学报 , 2020 , 52 (5 ): 1314 - 1322
DOI:10.6052/0459-1879-20-055
[本文引用: 1]
CHEN Lin-feng A residual based unresolved-scale finite element modelling for implicit large eddy simulation
[J]. Chinese Journal of Theoretical and Applied Mechanics , 2020 , 52 (5 ): 1314 - 1322
DOI:10.6052/0459-1879-20-055
[本文引用: 1]
[16]
吴霆, 时北极, 王士召, 等 大涡模拟的壁模型及其应用
[J]. 力学学报 , 2018 , 50 (3 ): 453 - 466
DOI:10.6052/0459-1879-18-071
[本文引用: 1]
WU Ting, SHI Bei-ji, WANG Shi-zhao, et al Wall model for large-eddy simulation and its applications
[J]. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (3 ): 453 - 466
DOI:10.6052/0459-1879-18-071
[本文引用: 1]
[17]
王建丽, 张渭育. 统计学[M]. 北京: 清华大学出版社, 2010: 215-220.
[本文引用: 2]
[18]
李晓斌, 郭小威, 袁刚 基于逻辑靶场技术的导弹内外场联合试验训练系统
[J]. 兵工自动化 , 2019 , 38 (6 ): 9 - 13
DOI:10.7690/bgzdh.2019.06.002
[本文引用: 1]
LI Xiao-bin, GUO Xiao-wei, YUAN Gang Infield and airfield joint testing and training system of missile based on logical range technology
[J]. Ordnance Industry Automation , 2019 , 38 (6 ): 9 - 13
DOI:10.7690/bgzdh.2019.06.002
[本文引用: 1]
[19]
施红辉. 流体力学入门[M]. 杭州: 浙江大学出版社, 2013: 108-109.
[本文引用: 1]
[20]
刘志荣, 邹赫, 刘锦生, 等 开缝圆柱缝隙倾斜角对脱落涡的影响
[J]. 北京航空航天大学学报 , 2017 , 43 (1 ): 8
DOI:10.13700/j.bh.1001-5965.2016.0058
[本文引用: 1]
LIU Zhi-rong, ZOU He, LIU Jin-sheng, et al Effect of angle of slit on shedding vortex of slotted circular cylinder
[J]. Journal of Beijing University of Aeronautics and Astronautics , 2017 , 43 (1 ): 8
DOI:10.13700/j.bh.1001-5965.2016.0058
[本文引用: 1]
[21]
郑益华. 基于翠鸟界面润湿控制行为的跨介质航行器表面防浸润研究[D]. 吉林: 吉林大学, 2020: 129-130.
[本文引用: 1]
ZHENG Yi-hua. Research on the anti-wetting of aquatic UAV surface based on the wetting control behavior of kingfisher interface [D]. Jilin: Jilin University, 2020: 129-130.
[本文引用: 1]
Experimental investigation of the water entry and/or exit of axisymmetric bodies
1
2020
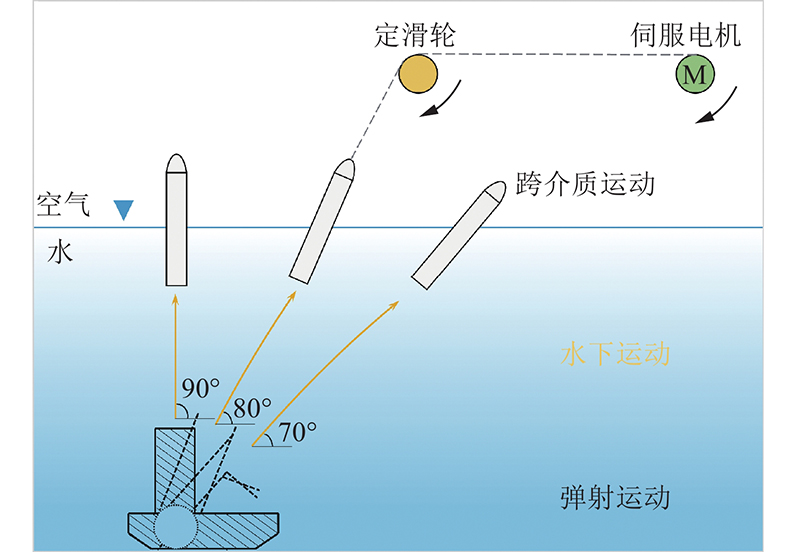
... 潜射航行器具备机动性高、隐蔽性好、射程远等优点. 典型作业区间包括水下运动段、跨介质段和空中飞行段. 其中,跨介质阶段涉及气/液多相耦合、介质突变与液面冲击等复合影响,造就了航行器跨介质运动时呈现非定常、非线性的特点,直接影响航行器的运动与作战效能[1 -4 ] . ...
Non-isothermal mixing characteristics in the extreme near-field of turbulent jets in hot crossflow: effects of jet exit turbulence and velocity profile
0
2020
Chinese nuclear forces, 2015
0
2015
2
... 潜射航行器具备机动性高、隐蔽性好、射程远等优点. 典型作业区间包括水下运动段、跨介质段和空中飞行段. 其中,跨介质阶段涉及气/液多相耦合、介质突变与液面冲击等复合影响,造就了航行器跨介质运动时呈现非定常、非线性的特点,直接影响航行器的运动与作战效能[1 -4 ] . ...
... 式中: $ x_i $ $ y_i $ $ i、j=x、y、z,{\boldsymbol{u}}_i、{\boldsymbol{u}}_j $ $ \bar {\boldsymbol{p}} $ $ \;\rho_ {\rm{w}} $ $ v $ $ {\boldsymbol{\tau}}_{ ij} $ [15 -16 ] . 动态网格重构技术采用弹簧扩散光顺与局部网格重构相结合的方式,可以提升计算效率. 使用C语言将潜射航行器运动学方程写入FLEUNT中的自定义函数中,通过高阶龙格库塔法求解瞬时速度与加速度,更新航行器运动姿态与位置至动态网格系统. 设置求解步长为1×10−5 s,循环迭代至完成算例[4 ] . ...
Water entry and exit of axisymmetric bodies by CFD approach
1
2018
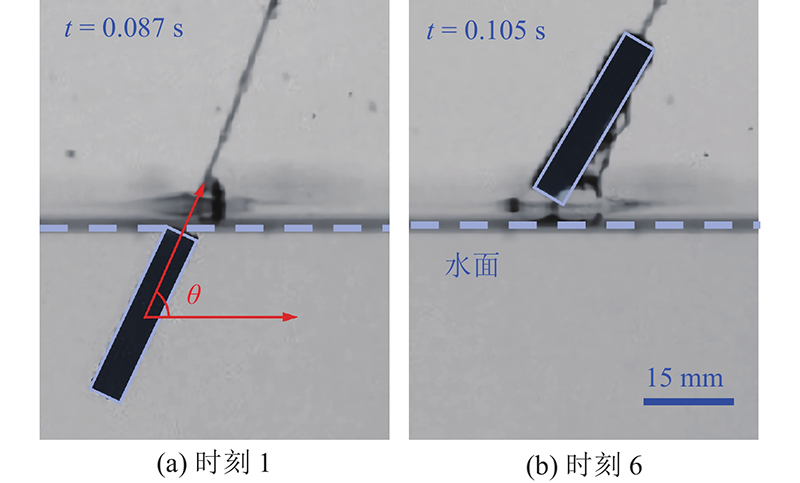
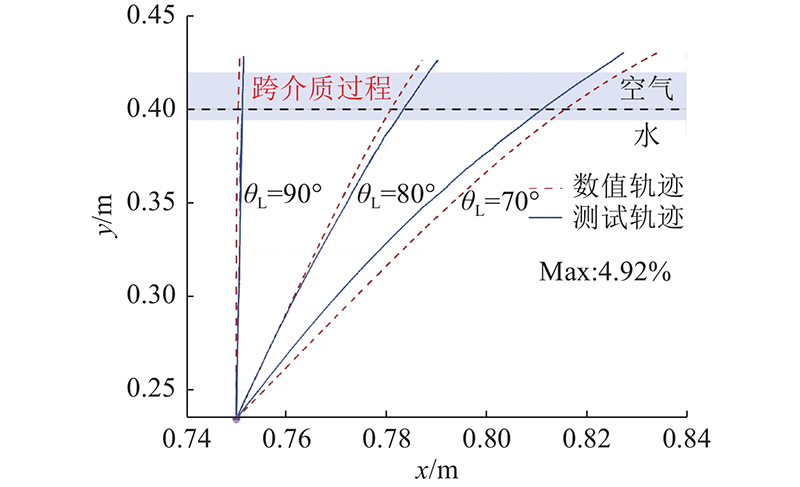
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
Water entry of rounded cylindrical bodies with different aspect ratios and surface conditions
1
2019
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
Numerical analysis of water exit for a sphere with constant velocity using the lattice Boltzmann method
1
2019
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
Evolution of water column pulled by partially submerged spheres with different velocities and submergence depths
1
2019
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
圆柱体出水运动的自由面效应及水冢现象分析
1
2013
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
圆柱体出水运动的自由面效应及水冢现象分析
1
2013
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
不同多相流模型在航行体出水流场数值模拟中的应用
1
2015
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
不同多相流模型在航行体出水流场数值模拟中的应用
1
2015
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
细长体倾斜出水的实验研究
1
2016
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
细长体倾斜出水的实验研究
1
2016
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
1
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
1
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
附加质量变化率在航行体出水过程中的影响研究
1
2017
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
附加质量变化率在航行体出水过程中的影响研究
1
2017
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
跨介质运动物体的附加质量
1
2016
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
跨介质运动物体的附加质量
1
2016
... 近年来,潜射航行器跨介质出水问题因具备良好的军事化应用前景,受到国内外众学者的关注. 目前,有关跨介质问题的数值模拟研究主要集中于以下2个方面. 1)针对简单回转结构体跨介质出水过程中的自由液面影响问题进行研究. Nair等[5 ] 证实VOF(volume of fluid)能够捕捉轴对称物体出水时的自由液面演化. Kim等[6 ] 对圆球、圆柱体入水自由液面变形进行试验研究,结果表明,结构物的运动速度对液面形态变化有明显的影响. Hao等[7 -8 ] 采用玻尔兹曼法,对不同垂直速度出水球体进行数值模拟发现,当弗劳德数Fr 为4.12~8.24时,自由液面高度明显受发射速度的影响. 孙士丽等[9 ] 考虑自由面效应,分析跨介质过程的水冢现象发现,柱体顶点压力在跨介质过程中会增至0.1 MPa. 2)针对简单结构物垂直出水相关运动特性的研究. 魏海鹏等[10 ] 证实VOF两相流模型较Mixture模型更能够反映柱体垂直出水的过程. 赵蛟龙[11 -12 ] 对细长体垂直出水运动规律进行数值研究,说明当构型参数比为0.4~2.0时计算误差小于11%. 廖保全[13 ] 在航行体垂直跨介质出水理论模型的基础上,引入附加质量变化率,验证其可以提升计算精度. 张晓强等[14 ] 研究柱体垂直出/入水附加质量的变化规律,证明垂直出/入水为不可逆过程. ...
基于 Navier-Stokes 方程残差的隐式大涡模拟有限元模型
1
2020
... 式中: $ x_i $ $ y_i $ $ i、j=x、y、z,{\boldsymbol{u}}_i、{\boldsymbol{u}}_j $ $ \bar {\boldsymbol{p}} $ $ \;\rho_ {\rm{w}} $ $ v $ $ {\boldsymbol{\tau}}_{ ij} $ [15 -16 ] . 动态网格重构技术采用弹簧扩散光顺与局部网格重构相结合的方式,可以提升计算效率. 使用C语言将潜射航行器运动学方程写入FLEUNT中的自定义函数中,通过高阶龙格库塔法求解瞬时速度与加速度,更新航行器运动姿态与位置至动态网格系统. 设置求解步长为1×10−5 s,循环迭代至完成算例[4 ] . ...
基于 Navier-Stokes 方程残差的隐式大涡模拟有限元模型
1
2020
... 式中: $ x_i $ $ y_i $ $ i、j=x、y、z,{\boldsymbol{u}}_i、{\boldsymbol{u}}_j $ $ \bar {\boldsymbol{p}} $ $ \;\rho_ {\rm{w}} $ $ v $ $ {\boldsymbol{\tau}}_{ ij} $ [15 -16 ] . 动态网格重构技术采用弹簧扩散光顺与局部网格重构相结合的方式,可以提升计算效率. 使用C语言将潜射航行器运动学方程写入FLEUNT中的自定义函数中,通过高阶龙格库塔法求解瞬时速度与加速度,更新航行器运动姿态与位置至动态网格系统. 设置求解步长为1×10−5 s,循环迭代至完成算例[4 ] . ...
大涡模拟的壁模型及其应用
1
2018
... 式中: $ x_i $ $ y_i $ $ i、j=x、y、z,{\boldsymbol{u}}_i、{\boldsymbol{u}}_j $ $ \bar {\boldsymbol{p}} $ $ \;\rho_ {\rm{w}} $ $ v $ $ {\boldsymbol{\tau}}_{ ij} $ [15 -16 ] . 动态网格重构技术采用弹簧扩散光顺与局部网格重构相结合的方式,可以提升计算效率. 使用C语言将潜射航行器运动学方程写入FLEUNT中的自定义函数中,通过高阶龙格库塔法求解瞬时速度与加速度,更新航行器运动姿态与位置至动态网格系统. 设置求解步长为1×10−5 s,循环迭代至完成算例[4 ] . ...
大涡模拟的壁模型及其应用
1
2018
... 式中: $ x_i $ $ y_i $ $ i、j=x、y、z,{\boldsymbol{u}}_i、{\boldsymbol{u}}_j $ $ \bar {\boldsymbol{p}} $ $ \;\rho_ {\rm{w}} $ $ v $ $ {\boldsymbol{\tau}}_{ ij} $ [15 -16 ] . 动态网格重构技术采用弹簧扩散光顺与局部网格重构相结合的方式,可以提升计算效率. 使用C语言将潜射航行器运动学方程写入FLEUNT中的自定义函数中,通过高阶龙格库塔法求解瞬时速度与加速度,更新航行器运动姿态与位置至动态网格系统. 设置求解步长为1×10−5 s,循环迭代至完成算例[4 ] . ...
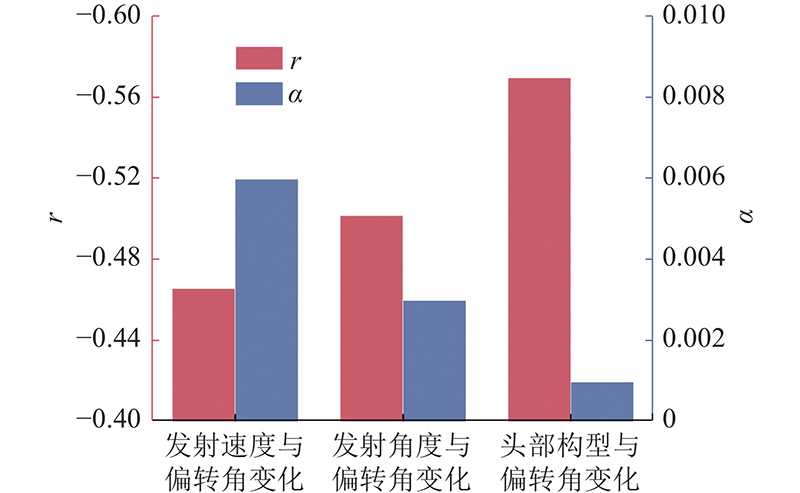
2
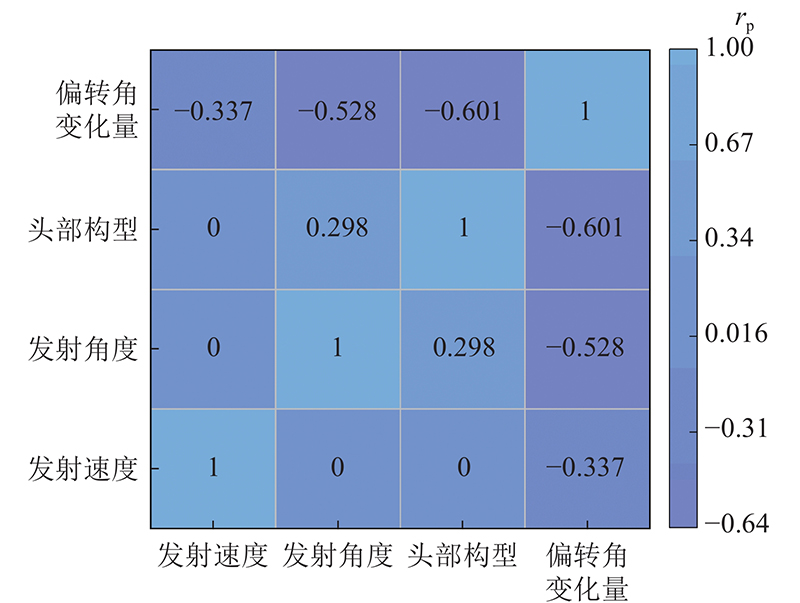
... 线性相关分析通过计算影响因素Pearson相关系数,呈现变量间的关联程度,相关系数为−1~1,系数越接近1,说明变量间关联强度越高. 该系数定义为两变量间协方差与标准差的商,如下式[17 ] 所示: ...
... 偏相关分析可以控制其他变量的影响,直接分析两变量间的实际相关性,偏相关分析的计算流程如下. 1)计算数据样本的偏相关系数. 2)计算样本检验统计量. 3)计算检验统计量与概率P . 若P < 0.05,则拒绝原假设,两变量存在偏相关;反之 P ≥ 0.05,则接受假设,两变量不存在偏相关. 相关计算公式[17 ] 如下所示: ...
基于逻辑靶场技术的导弹内外场联合试验训练系统
1
2019
... 式中: ${r_{{x_1}y}} $ ${r_{{x_2}y}} $ ${r_{{x_1}{x_2}}} $ x 1 与y 、x 2 与y 、x 1 与x 2 的线性相关系数,t ij n 为样本数量,c 为变量数量, $ n - c - 2 $ [18 ] . ...
基于逻辑靶场技术的导弹内外场联合试验训练系统
1
2019
... 式中: ${r_{{x_1}y}} $ ${r_{{x_2}y}} $ ${r_{{x_1}{x_2}}} $ x 1 与y 、x 2 与y 、x 1 与x 2 的线性相关系数,t ij n 为样本数量,c 为变量数量, $ n - c - 2 $ [18 ] . ...
1
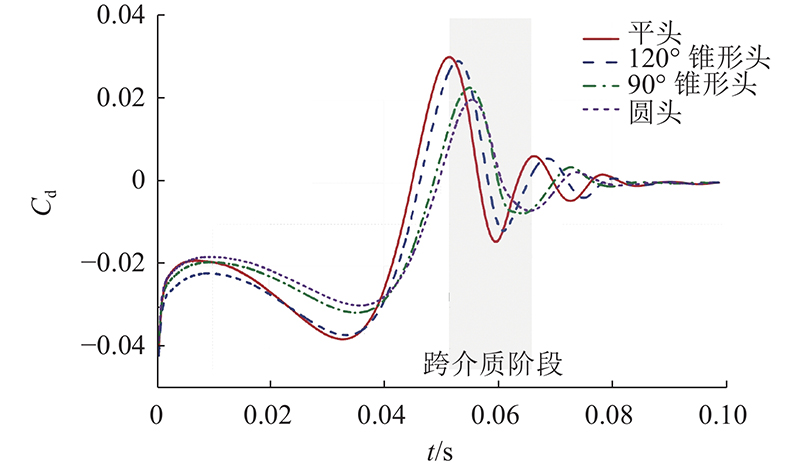
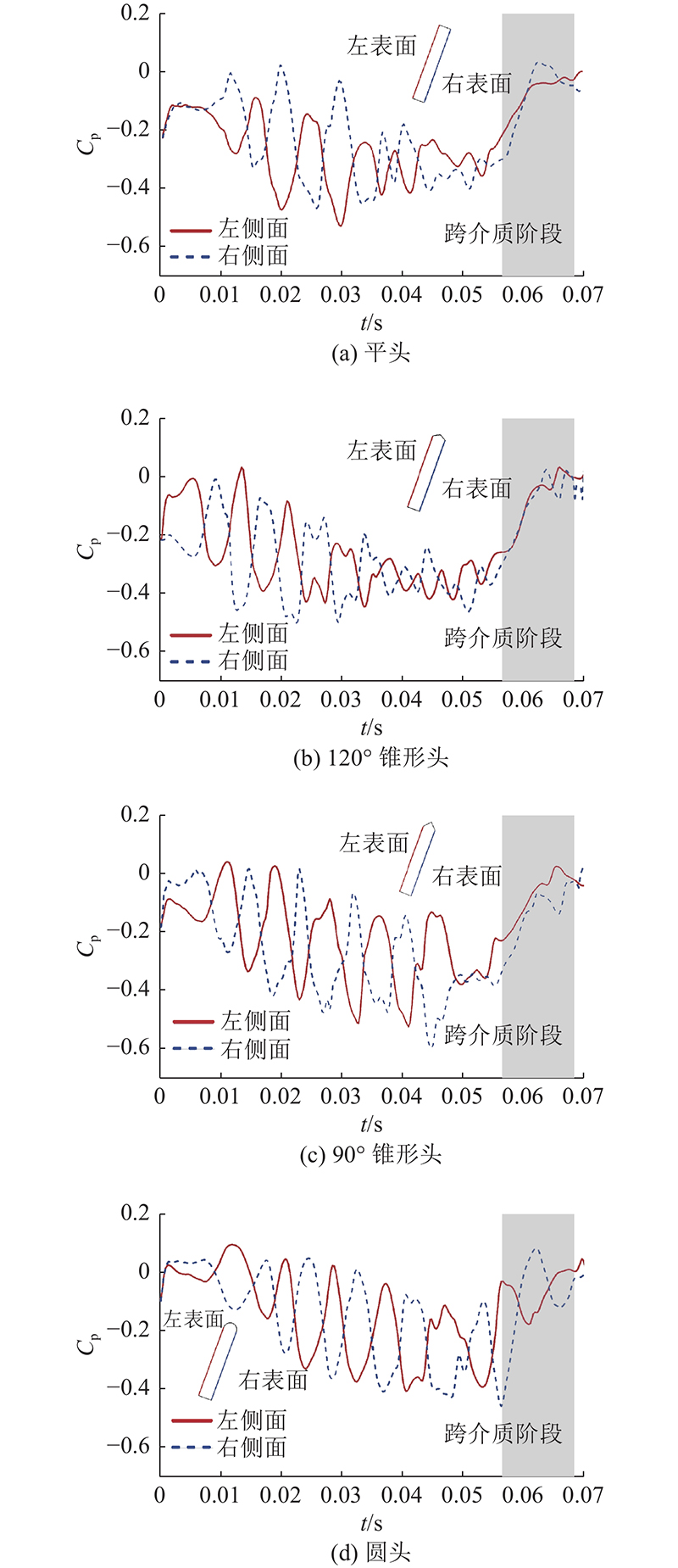
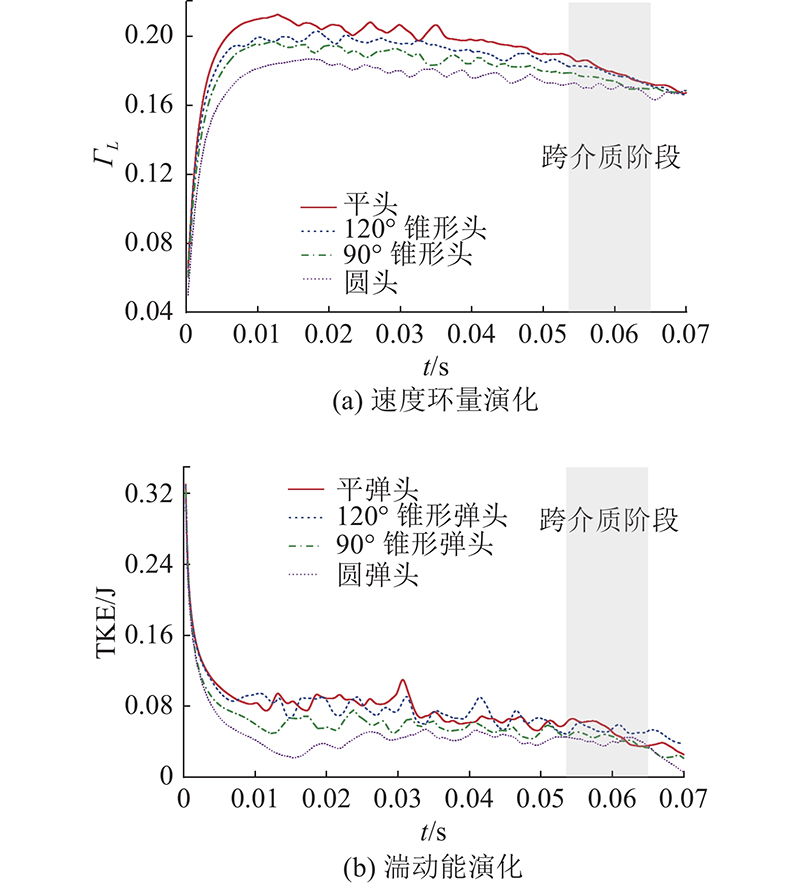
... 脱落涡频率与能量耗散是研究航行器表面流动分离演化的重要信息,基于航行器跨介质瞬时速度场,统计航行器周围在时间上的环量变化规律. 利用快速傅里叶变化(fast Fourier transform, FFT)得到脱落涡频率,环量Г L [19 -20 ] 为 ...
开缝圆柱缝隙倾斜角对脱落涡的影响
1
2017
... 脱落涡频率与能量耗散是研究航行器表面流动分离演化的重要信息,基于航行器跨介质瞬时速度场,统计航行器周围在时间上的环量变化规律. 利用快速傅里叶变化(fast Fourier transform, FFT)得到脱落涡频率,环量Г L [19 -20 ] 为 ...
开缝圆柱缝隙倾斜角对脱落涡的影响
1
2017
... 脱落涡频率与能量耗散是研究航行器表面流动分离演化的重要信息,基于航行器跨介质瞬时速度场,统计航行器周围在时间上的环量变化规律. 利用快速傅里叶变化(fast Fourier transform, FFT)得到脱落涡频率,环量Г L [19 -20 ] 为 ...
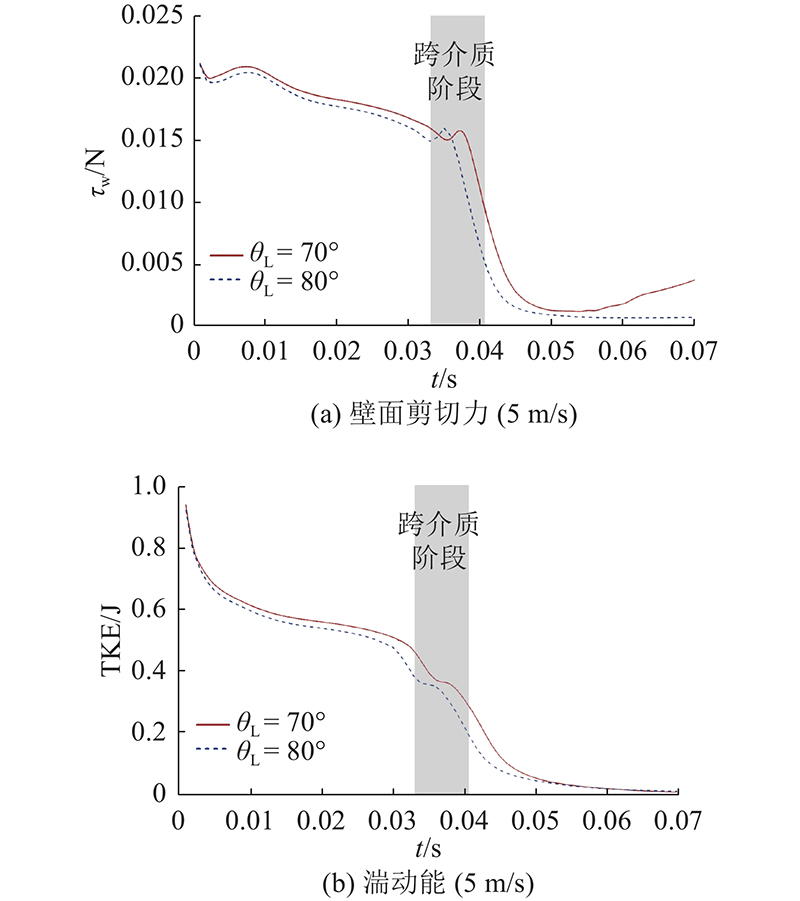
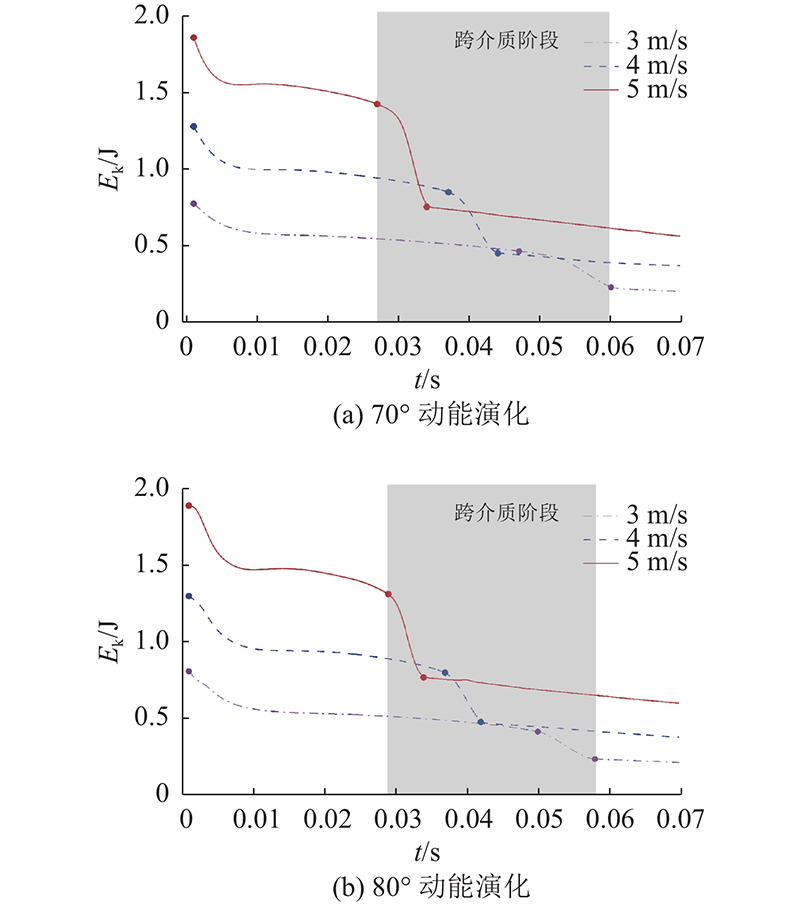
1
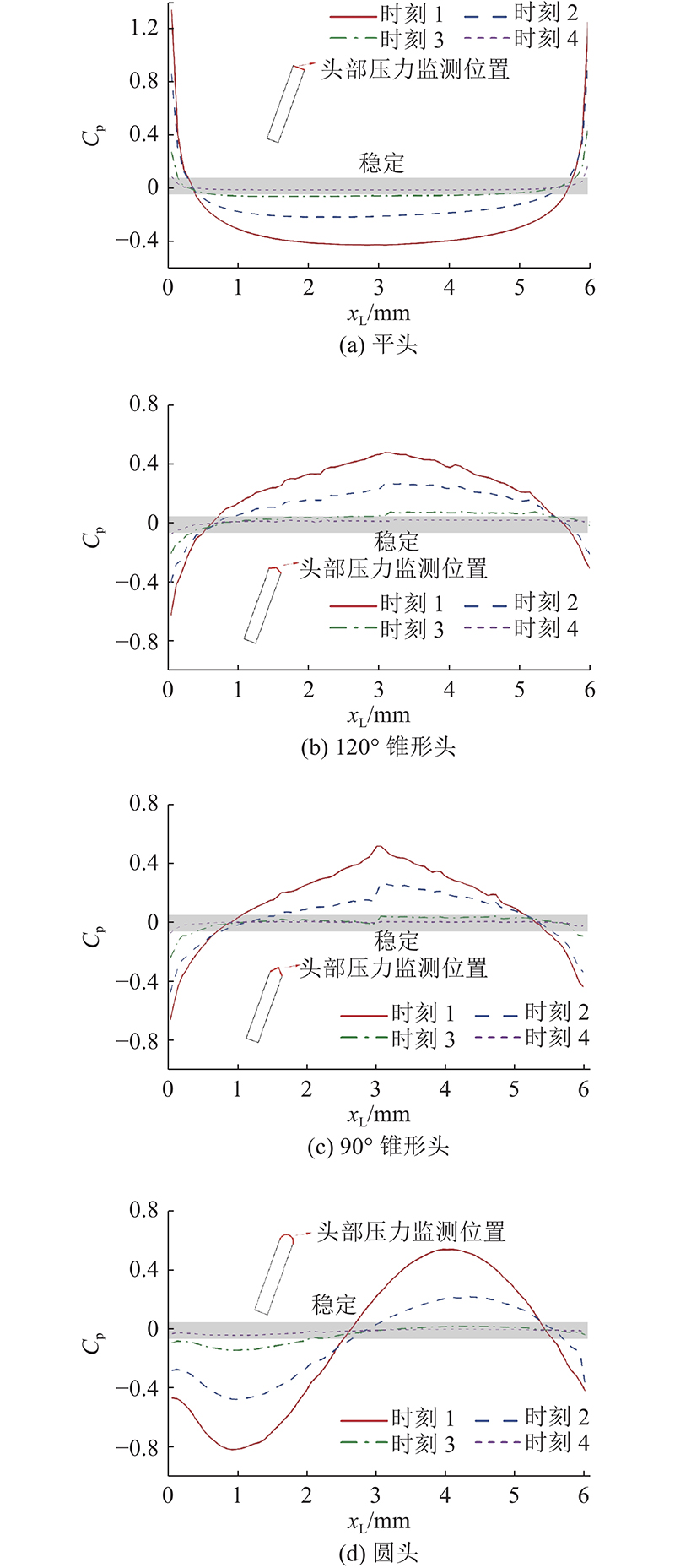
... 航行器发射角度影响航行器湍流动能的演化,导致运动阻力变化,跨介质阻力的改变会影响航行器的运动力学平衡,促使航行器流场演化稳定特性发生变化. 减小航行器跨介质所受的阻力,可以有效地提升航行器跨介质流场演化稳定性[21 ] . ...
1
... 航行器发射角度影响航行器湍流动能的演化,导致运动阻力变化,跨介质阻力的改变会影响航行器的运动力学平衡,促使航行器流场演化稳定特性发生变化. 减小航行器跨介质所受的阻力,可以有效地提升航行器跨介质流场演化稳定性[21 ] . ...