[1]
MONRAT A A, SCHELEN O, ANDERSSON K A survey of blockchain from the perspectives of applications, challenges, and opportunities
[J]. IEEE Access , 2019 , 7 : 117134 - 117151
DOI:10.1109/ACCESS.2019.2936094
[本文引用: 1]
[2]
BELOTTI M, BOZIC N, PUJOLLE G, et al A vademecum on blockchain technologies: when, which, and how
[J]. IEEE Communications Surveys and Tutorials , 2019 , 21 (4 ): 3796 - 3838
DOI:10.1109/COMST.2019.2928178
[3]
TRELEAVEN P, BROWN R G, YANG D Blockchain technology in finance
[J]. Computer , 2017 , 50 (9 ): 14 - 17
DOI:10.1109/MC.2017.3571047
[4]
BERTINO E, SANDHU R Database security-concepts, approaches, and challenges
[J]. IEEE Transactions on Dependable and Secure Computing , 2005 , 2 (1 ): 2 - 19
DOI:10.1109/TDSC.2005.9
[5]
EYAL I Blockchain technology: transforming libertarian cryptocurrency dreams to finance and banking realities
[J]. Computer , 2017 , 50 (9 ): 38 - 49
DOI:10.1109/MC.2017.3571042
[6]
SRIVASTAVA G, DHAR S, DWIVEDI A D, et al. Blockchain education [C]// IEEE Canadian Conference of Electrical and Computer Engineering . Edmonton: IEEE, 2019: 1-5.
[7]
METTLER M. Blockchain technology in healthcare: the revolution starts here [C]// 18th IEEE International Conference on e-Health Networking, Applications and Services . Munich: IEEE, 2016: 1-3.
[8]
CHANG S E, CHEN Y When blockchain meets supply chain: a systematic literature review on current development and potential applications
[J]. IEEE Access , 2020 , 8 : 62478 - 62494
DOI:10.1109/ACCESS.2020.2983601
[本文引用: 1]
[10]
CHAUHAN A, MALVIYA O P, VERMA M, et al. Blockchain and scalability [C]// IEEE International Conference on Software Quality, Reliability and Security Companion . Lisbon: IEEE, 2018: 122-128.
[本文引用: 1]
[11]
韩璇, 袁勇, 王飞跃 区块链安全问题: 研究现状与展望
[J]. 自动化学报 , 2019 , 45 (1 ): 206 - 225
[本文引用: 1]
HAN Xuan, YUAN Yong, WANG Fei-yue Blockchain security issues: research status and prospects
[J]. Acta Automatica Sinica , 2019 , 45 (1 ): 206 - 225
[本文引用: 1]
[12]
ZHENG Z, XIE S, DAI H, et al. An overview of blockchain technology: architecture, consensus, and future trends [C]// IEEE International Congress on Big Data . Boston: IEEE, 2017: 557-564.
[本文引用: 1]
[13]
NAKAMOTO S. Bitcoin: a peer-to-peer electronic cash system [EB/OL]. (2008-10-31)[2022-07-15]. https://bitcoin.org/bitcoin.pdf.
[本文引用: 3]
[14]
WOOD G Ethereum: a secure decentralised generalised transaction ledger
[J]. Ethereum Project Yellow Paper , 2014 , 151 (2014 ): 1 - 32
[本文引用: 3]
[15]
Unspent transaction output set [EB/OL]. [ 2022-07-15]. https://statoshi.info/d/000000009/unspent-transaction-output-set.
[本文引用: 2]
[16]
SAAD M, NJILLA L, KAMHOUA C, et al. Mempool optimization for defending against DDoS attacks in PoW-based blockchain systems [C]// IEEE International Conference on Blockchain and Cryptocurrency . Seoul: IEEE, 2019: 285-292.
[本文引用: 1]
[18]
XIONG Z, ZHANG Y, NIYATO D, et al When mobile blockchain meets edge computing
[J]. IEEE Communications Magazine , 2018 , 56 (8 ): 33 - 39
DOI:10.1109/MCOM.2018.1701095
[本文引用: 1]
[19]
XU C, ZHANG C, XU J, et al SlimChain: scaling blockchain transactions through off-chain storage and parallel processing
[J]. Proceedings of the VLDB Endowment , 2021 , 14 (11 ): 2314 - 2326
DOI:10.14778/3476249.3476283
[本文引用: 1]
[20]
GUO Z, GAO Z, MEI H, et al Design and optimization for storage mechanism of the public blockchain based on redundant residual number system
[J]. IEEE Access , 2019 , 7 : 98546 - 98554
DOI:10.1109/ACCESS.2019.2930125
[本文引用: 1]
[21]
TODD P. Making UTXO set growth irrelevant with low-latency delayed two-commitments [EB/OL]. (2016-05-17)[2022-07-15]. https://petertodd.org/2016/delayed-txo-commitments.
[本文引用: 3]
[22]
CHEPURNOY A, PAPAMANTHOU C, SRINIVASAN S, et al. Edrax: a cryptocurrency with stateless transaction validation [EB/OL]. (2018-10-14) [2022-07-15]. https://eprint.iacr.org/2018/968.
[本文引用: 3]
[23]
BAILEY B, SANKAGIRI S. Merkle trees optimized for stateless clients in bitcoin [C]// International Conference on Financial Cryptography and Data Security . Berlin: Springer, 2021: 451-466.
[本文引用: 1]
[24]
RAIKWAR M, GLIGOROSKI D. Aggregation in blockchain ecosystem [C]// 8th International Conference on Software Defined Systems . Gandia: IEEE, 2021: 1-6.
[本文引用: 1]
[25]
BONEH D, BUNZ B, FISCH B. Batching techniques for accumulators with applications to IOPs and stateless blockchains [C]// Annual International Cryptology Conference . Cham: Springer, 2019: 561-586.
[本文引用: 6]
[26]
CHEN H, WANG Y MiniChain: a lightweight protocol to combat the UTXO growth in public blockchain
[J]. Journal of Parallel and Distributed Computing , 2020 , 143 : 67 - 76
DOI:10.1016/j.jpdc.2020.05.001
[本文引用: 3]
[27]
OZCELIK I, MEDURY S, BROADDUS J, et al. An overview of cryptographic accumulators [EB/OL]. (2021-03-07) [2022-07-15]. https://arxiv.org/pdf/2103.04330.pdf.
[本文引用: 1]
[28]
BALDIMTSI F, CAMENISCH J, DUBOVITSKAYA M, et al. Accumulators with applications to anonymity-preserving revocation [C]// IEEE European Symposium on Security and Privacy . Paris: IEEE, 2017: 301-315.
[本文引用: 1]
[29]
ZHONG H, SANG Y, ZHANG Y, et al. Secure multi-party computation on blockchain: an overview [C]// International Symposium on Parallel Architectures, Algorithms and Programming . Singapore: Springer, 2019: 452-460.
[本文引用: 2]
[30]
RSA-2048 [EB/OL]. [2022-07-15]. https://community.rsa.com/community/labs.
[本文引用: 1]
[31]
LIN Y J, WU P W, HSU C H, et al. An evaluation of bitcoin address classification based on transaction history summarization [C]// IEEE International Conference on Blockchain and Cryptocurrency . Seoul: IEEE, 2019: 302-310.
[本文引用: 2]
[32]
PIERRE-ALAIN F, MEHDI T Close to uniform prime number generation with fewer random bits
[J]. IEEE Transactions on Information Theory , 2018 , 65 (2 ): 1307 - 1317
[本文引用: 1]
A survey of blockchain from the perspectives of applications, challenges, and opportunities
1
2019
... 区块链以其去中心化、防篡改、可追溯等特性,解决了中心化模式引起的数据可靠性差、维护困难、“数据孤岛”等问题,在金融、医疗、供应链等行业得到了广泛的应用[1 -8 ] . 目前,区块链已衍生出公有链、私有链、联盟链等多个分支[9 -10 ] ,通过与大数据、人工智能、安全多方计算等新兴技术的深度结合,区块链将深刻地改变社会的管理及运行方式[11 ] . ...
A vademecum on blockchain technologies: when, which, and how
0
2019
Blockchain technology in finance
0
2017
Database security-concepts, approaches, and challenges
0
2005
Blockchain technology: transforming libertarian cryptocurrency dreams to finance and banking realities
0
2017
When blockchain meets supply chain: a systematic literature review on current development and potential applications
1
2020
... 区块链以其去中心化、防篡改、可追溯等特性,解决了中心化模式引起的数据可靠性差、维护困难、“数据孤岛”等问题,在金融、医疗、供应链等行业得到了广泛的应用[1 -8 ] . 目前,区块链已衍生出公有链、私有链、联盟链等多个分支[9 -10 ] ,通过与大数据、人工智能、安全多方计算等新兴技术的深度结合,区块链将深刻地改变社会的管理及运行方式[11 ] . ...
Solutions to scalability of blockchain: a survey
1
2020
... 区块链以其去中心化、防篡改、可追溯等特性,解决了中心化模式引起的数据可靠性差、维护困难、“数据孤岛”等问题,在金融、医疗、供应链等行业得到了广泛的应用[1 -8 ] . 目前,区块链已衍生出公有链、私有链、联盟链等多个分支[9 -10 ] ,通过与大数据、人工智能、安全多方计算等新兴技术的深度结合,区块链将深刻地改变社会的管理及运行方式[11 ] . ...
1
... 区块链以其去中心化、防篡改、可追溯等特性,解决了中心化模式引起的数据可靠性差、维护困难、“数据孤岛”等问题,在金融、医疗、供应链等行业得到了广泛的应用[1 -8 ] . 目前,区块链已衍生出公有链、私有链、联盟链等多个分支[9 -10 ] ,通过与大数据、人工智能、安全多方计算等新兴技术的深度结合,区块链将深刻地改变社会的管理及运行方式[11 ] . ...
区块链安全问题: 研究现状与展望
1
2019
... 区块链以其去中心化、防篡改、可追溯等特性,解决了中心化模式引起的数据可靠性差、维护困难、“数据孤岛”等问题,在金融、医疗、供应链等行业得到了广泛的应用[1 -8 ] . 目前,区块链已衍生出公有链、私有链、联盟链等多个分支[9 -10 ] ,通过与大数据、人工智能、安全多方计算等新兴技术的深度结合,区块链将深刻地改变社会的管理及运行方式[11 ] . ...
区块链安全问题: 研究现状与展望
1
2019
... 区块链以其去中心化、防篡改、可追溯等特性,解决了中心化模式引起的数据可靠性差、维护困难、“数据孤岛”等问题,在金融、医疗、供应链等行业得到了广泛的应用[1 -8 ] . 目前,区块链已衍生出公有链、私有链、联盟链等多个分支[9 -10 ] ,通过与大数据、人工智能、安全多方计算等新兴技术的深度结合,区块链将深刻地改变社会的管理及运行方式[11 ] . ...
1
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
3
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
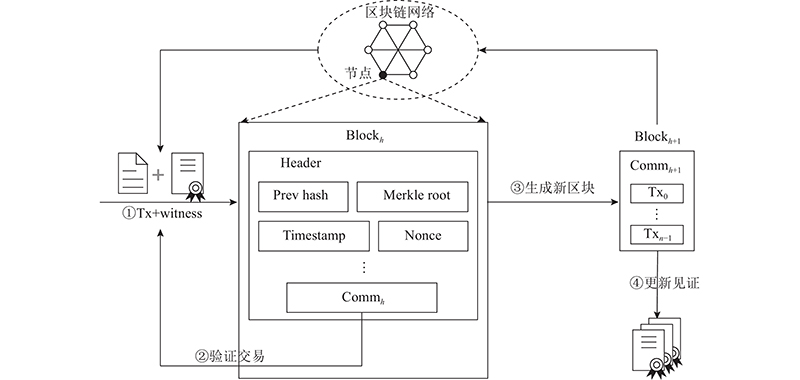
... 区块链是一系列区块通过加密算法连缀形成的反向链表. 区块由区块头和区块体组成. 区块头存储整个区块的元数据,主要包括父哈希、默克尔树根、难度值以及随机数等,可以实现区块链的大部分功能[14 ] . 父哈希是前一个区块的哈希值,凭借哈希函数的单向性及抗碰撞特性,保证了区块链的安全性[23 ] . 默克尔树根由包含在区块体内的全部交易哈希以二叉树的形式两两向上聚合得到,保证了交易的数据完整性. 难度值与随机数用来判定“记账权”,各节点争夺“记账权”的过程被称为共识. 目前,最常用也最安全的共识算法是工作量证明(proof of work, PoW),在该过程中,节点不断改变随机数的值,直到整个区块头的哈希小于预设难度[13 ] . ...
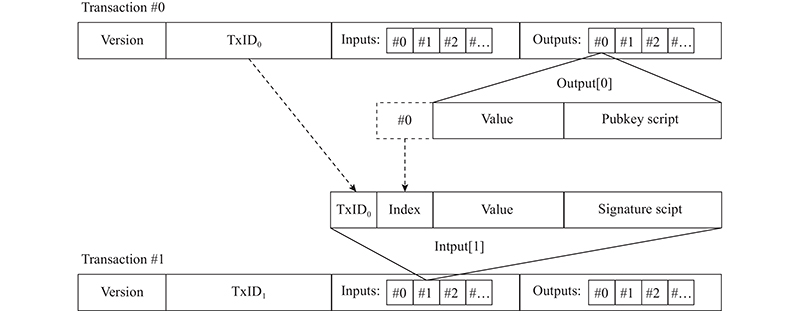
... 区块体维护全部的历史记录,即网络中发生过的每一笔交易,是区块链数据产生、状态变化的凭证. 交易是实现区块链功能的最小单位. 比特币中,一笔合法的交易由多个输入、输出组成,其中每个输入都必须引用之前某笔合法交易产生的未花费的输出(UTXO). 输入被称为已花费的交易输出(STXO). 最简单的交易只有单个输入和输出. 伴随着交易的执行,各节点添加每个UTXO至UTXO Set,从中移除每个STXO,在区块达成共识后,统一更新本地状态. 在节点本地,UTXO Set一般以键值对的形式存储,一个UTXO可以由键值对{TxID:(Index, Address, Value)}唯一表征. TxID是产生该UTXO的交易哈希,Index是该UTXO在输出集合中的索引,两者结合反映了UTXO 的存在性. Address和Value分别是交易接收者和锁定在该UTXO内的金额. UTXO模型区块链中交易的数据结构如图1 所示. 其中,第2笔交易(Tx1 )引用第1笔交易(Tx0 )产生的第1笔输出(Outputs[0])作为自己的第1笔输入(Inputs[0]). Version表示版本号,SignScript与PubScript分别表示解锁脚本与锁定脚本[13 ] . ...
Ethereum: a secure decentralised generalised transaction ledger
3
2014
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
... 区块链是一系列区块通过加密算法连缀形成的反向链表. 区块由区块头和区块体组成. 区块头存储整个区块的元数据,主要包括父哈希、默克尔树根、难度值以及随机数等,可以实现区块链的大部分功能[14 ] . 父哈希是前一个区块的哈希值,凭借哈希函数的单向性及抗碰撞特性,保证了区块链的安全性[23 ] . 默克尔树根由包含在区块体内的全部交易哈希以二叉树的形式两两向上聚合得到,保证了交易的数据完整性. 难度值与随机数用来判定“记账权”,各节点争夺“记账权”的过程被称为共识. 目前,最常用也最安全的共识算法是工作量证明(proof of work, PoW),在该过程中,节点不断改变随机数的值,直到整个区块头的哈希小于预设难度[13 ] . ...
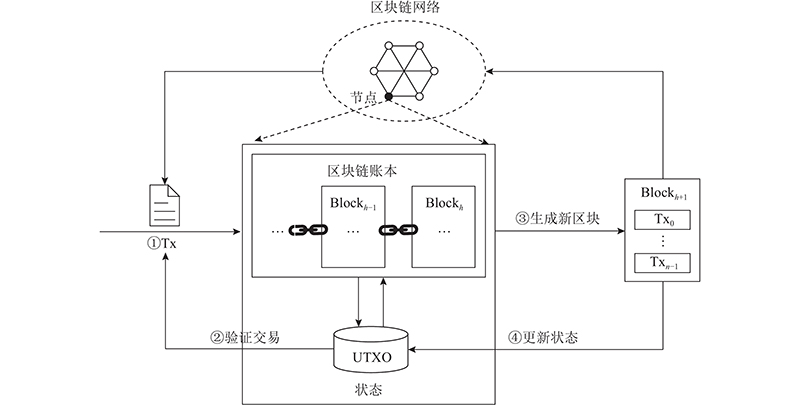
... 目前, UTXO模型区块链均采用状态化设计,即节点本地维护并更新UTXO Set,不需要追溯整个账本,即可高效验证交易合法性. 如图2 所示,状态区块链中,一笔交易从签发到最终确认,要经历以下步骤. 1)节点基于本地维护的UTXO Set,引用合法的UTXO作为输入,签发交易并发送给邻居节点. 2)接收到新交易的节点验证交易签名(SignScript),基于本地维护的UTXO Set验证交易输入是否引用合法的UTXO,锁定在该UTXO内的资产是否不小于转账金额. 若验证通过,则交易合法. 节点将交易缓存进本地交易池,转发给邻居节点. 3)节点从本地交易池挑选部分交易打包进区块,执行交易并更新本地UTXO Set,生成默克尔树根,寻找满足难度要求的随机数. 率先完成PoW过程的节点获得“记账权”,将新生成的区块广播至全网. 4)收到新区块的各节点停止本地PoW过程,校验新区块. 若校验成功,则同步新区块到本地区块链,更新本地UTXO Set (添加新的UTXO,移除STXO). 5)当包含该交易的区块接续足够数量的后续区块时,该交易可以被认为得以最终确认[14 ] . ...
2
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
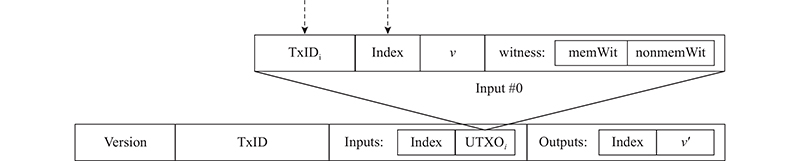
... 在应用无状态交易验证方案后,交易数据结构发生改变,新增的witness字段带来了额外的通信开销. 由于RSA累加器的性质,引用一笔UTXO,witness带来的额外开销是固定值,为3b . 其中,b 为所选系统参数N 的位宽. N 一般选用RSA-2048 (2 048 bits),则本文方案相应的通信开销为6 144 bits. Boneh等[25 ] 提出的方案为每笔UTXO引入固定的通信开销. 由于只采用一个RSA累加器,通信开销只有本文方案的1/3. 与基于RSA累加器的无状态交易验证方案相比,Todd[21 ] 采用的累加器为默克尔累加器,每笔UTXO对应的通信开销随着UTXO数量的增加呈对数增长. EDRAX[22 ] 采用默克尔累加器的变种,其中每一笔UTXO引入的额外通信开销为10 240 bits,远远超过本文方案. MiniChain[26 ] 的通信开销不仅会受到区块中输出数量的影响,而且会随着区块的增加而无限制地增大. 考虑到实际生产环境中UTXO数量超过1亿[15 ] ,基于双RSA累加器的无状态交易验证方案在通信开销表现上,虽然略逊于Boneh等[25 ] 提出的单RSA方案,但相对于基于默克尔体制的验证方案具有显著的优势. 如表1 所示为目前主流无状态交易验证方案体制及通信开销,与本文方案进行了对比. 表中,M 为预设的UTXO数量,且M $ > $ m $ \gg $ b ;n 为产生该UTXO的区块中交易输出的总数;h 为当前区块的高度. ...
1
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
Blockchain for the IoT and industrial IoT: a review
1
2020
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
When mobile blockchain meets edge computing
1
2018
... 持续增长的存储量已成为制约区块链可扩展性的关键瓶颈[12 ] . 在区块链中,存储主要分为链上数据和状态数据2部分. 网络中的全节点2部分数据都须存储,数量更多的轻节点通常只需要维护状态数据,即可实现交易合法性的高效验证. 根据状态数据存储方式的不同,区块链可以分为两大范式:以以太坊为代表的“账户-余额”模型(状态数据被存储为State Tries)和以比特币为代表的“未花费的交易输出(unspent transaction outputs, UTXO)”模型(状态数据被存储为UTXO Set)[13 -14 ] . 随着用户、交易数量的激增,节点需要存储的状态数据不断膨胀. 最近,比特币节点维护的UTXO Set已达到4.65 GB,并保持增长的趋势[15 ] . 一方面,状态数据的不断增长加剧了节点的存储负担;另一方面,超出节点内存容量的状态数据将不得不存放到访问速度缓慢的磁盘中,这不仅会拖慢交易验证效率,而且会增大遭受拒绝服务攻击的风险[16 ] . 上述“状态爆炸”问题阻碍了资源有限节点参与区块链系统的交易验证过程,在增大区块链中心化风险的同时,制约了其在供应量金融、工业物联网、边缘计算等场景中的应用[17 -18 ] . ...
SlimChain: scaling blockchain transactions through off-chain storage and parallel processing
1
2021
... 目前针对区块链“状态爆炸”问题,研究者提出一系列解决方案,具体可分为数据转移、分布式存储及无状态交易验证3类. 第1类方案中,Xu等[19 ] 提出状态信息线下存储方案SlimChain. 其中,完整的状态信息被转移到选定的全节点,轻节点只保留状态信息摘要,实现存储量的大幅削减. 轻节点验证交易必须依靠全节点,在增大系统中心化程度的同时,额外引入了数据泄露的风险. 第2类方法中,Guo等[20 ] 提出基于冗余余数系统的分布式存储模型,通过求模运算,将固定长度的余额映射为一系列截短的余数,分发至不同节点存储,削减了单个节点的存储量. 单个节点的存储负担会随着整体状态的增加而线性增长,无法从根本上解决问题,数据的分发、收集、恢复过程引入额外的安全风险. ...
Design and optimization for storage mechanism of the public blockchain based on redundant residual number system
1
2019
... 目前针对区块链“状态爆炸”问题,研究者提出一系列解决方案,具体可分为数据转移、分布式存储及无状态交易验证3类. 第1类方案中,Xu等[19 ] 提出状态信息线下存储方案SlimChain. 其中,完整的状态信息被转移到选定的全节点,轻节点只保留状态信息摘要,实现存储量的大幅削减. 轻节点验证交易必须依靠全节点,在增大系统中心化程度的同时,额外引入了数据泄露的风险. 第2类方法中,Guo等[20 ] 提出基于冗余余数系统的分布式存储模型,通过求模运算,将固定长度的余额映射为一系列截短的余数,分发至不同节点存储,削减了单个节点的存储量. 单个节点的存储负担会随着整体状态的增加而线性增长,无法从根本上解决问题,数据的分发、收集、恢复过程引入额外的安全风险. ...
3
... 基于密码学累加器的无状态交易验证是解决区块链“状态爆炸”问题的崭新思路,基本思想是利用密码学承诺取代状态信息,利用承诺更新来反映状态变化,利用成员证明来验证交易合法性. 节点只存储承诺就可以验证交易的前提是,交易发起者在原本的交易之上需要提供对应的成员证明,而这份证明会带来额外的通信开销. Todd[21 ] 通过默克尔树对UTXO Set进行聚合,记录默克尔树根并生成对应的见证,实现了UTXO模型区块链的无状态交易验证. 该方案的不足之处在于默克尔证明的数据大小随着UTXO Set的膨胀呈对数增长,这份证明带来的通信开销将远远大于交易本身. Chepurnoy等[22 -24 ] 提出的方案可以视为Todd方案的变种. Boneh等[25 ] 利用RSA累加器生成的定长证明来验证UTXO的存在性和未花费性,通过“批处理”技术进一步降低通信开销. 该方案的不足之处在于花掉的UTXO需要从累加器中删除,删除操作的复杂性极大地拖慢了平均出块时间,阻碍了方案的实际应用. 在Boneh等[25 ] 的基础上,Chen等[26 ] 利用RSA累加器证明UTXO的未花费性,利用默克尔山脉证明UTXO的存在性,回避了RSA累加器删除元素的问题,提高了交易验证效率,但默克尔证明导致了通信开销的增加. ...
... 在应用无状态交易验证方案后,交易数据结构发生改变,新增的witness字段带来了额外的通信开销. 由于RSA累加器的性质,引用一笔UTXO,witness带来的额外开销是固定值,为3b . 其中,b 为所选系统参数N 的位宽. N 一般选用RSA-2048 (2 048 bits),则本文方案相应的通信开销为6 144 bits. Boneh等[25 ] 提出的方案为每笔UTXO引入固定的通信开销. 由于只采用一个RSA累加器,通信开销只有本文方案的1/3. 与基于RSA累加器的无状态交易验证方案相比,Todd[21 ] 采用的累加器为默克尔累加器,每笔UTXO对应的通信开销随着UTXO数量的增加呈对数增长. EDRAX[22 ] 采用默克尔累加器的变种,其中每一笔UTXO引入的额外通信开销为10 240 bits,远远超过本文方案. MiniChain[26 ] 的通信开销不仅会受到区块中输出数量的影响,而且会随着区块的增加而无限制地增大. 考虑到实际生产环境中UTXO数量超过1亿[15 ] ,基于双RSA累加器的无状态交易验证方案在通信开销表现上,虽然略逊于Boneh等[25 ] 提出的单RSA方案,但相对于基于默克尔体制的验证方案具有显著的优势. 如表1 所示为目前主流无状态交易验证方案体制及通信开销,与本文方案进行了对比. 表中,M 为预设的UTXO数量,且M $ > $ m $ \gg $ b ;n 为产生该UTXO的区块中交易输出的总数;h 为当前区块的高度. ...
... Communication overheads brought by each UTXO
Tab.1 方案 累加器体制 额外开销(bits/UTXO) Todd[21 ] 默克尔树 256log2 m EDRAX[22 ] 默克尔树 256log2 M Boneh[25 ] 单RSA b MiniChain[26 ] RSA+默克尔树 2b +256log2 n +256log2 h 本文方案 双RSA 3b
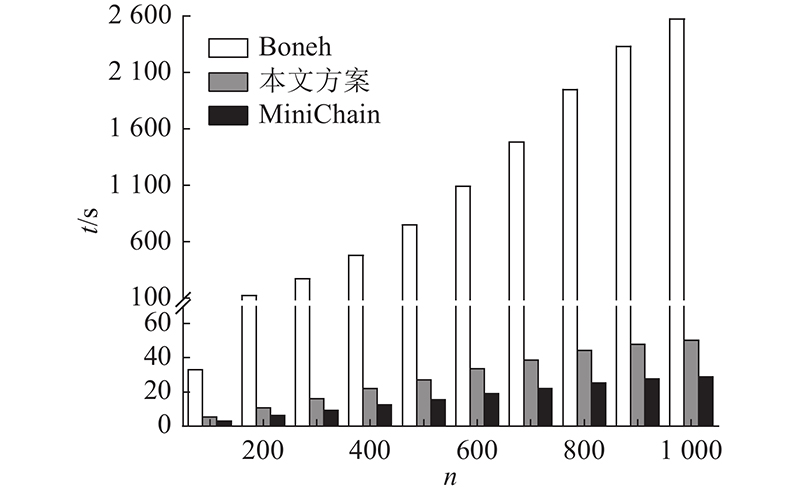
4.1.3. 计算复杂度分析 双RSA无状态交易验证方案在交易生命周期的不同阶段,分别执行累加器初始化、见证初始化、(非)成员验证以及承诺、见证更新. 不同的操作具有不同的时间复杂度. 基于通用累加器的性质可知,RSA初始化、添加元素、验证(非)成员见证均为O (1). 当矿工打包新区块时,要遍历全部交易花费及产生的UTXO,对应更新密码学承诺. 时间复杂度与区块体包含花费及产生UTXO的数量呈线性正相关. 与双RSA方案相比,Boneh的单RSA方案由于安全删除操作本身的复杂性,承诺更新的时间复杂度与花费的UTXO总量的平方呈正相关的关系. 尽管双RSA方案要同步更新2个承诺,计算开销仍远远小于单RSA方案. 与RSA体制相比,在基于默克尔累加器的验证方案中,初始化、承诺生成、更新以及见证生成、更新的复杂度均取决于默克尔树(或其变体)的高度,随着UTXO数量的增加呈对数增长的关系. 由于各个过程均实际执行高效的哈希计算,整体时间开销远小于基于RSA的无状态验证方案. ...
3
... 基于密码学累加器的无状态交易验证是解决区块链“状态爆炸”问题的崭新思路,基本思想是利用密码学承诺取代状态信息,利用承诺更新来反映状态变化,利用成员证明来验证交易合法性. 节点只存储承诺就可以验证交易的前提是,交易发起者在原本的交易之上需要提供对应的成员证明,而这份证明会带来额外的通信开销. Todd[21 ] 通过默克尔树对UTXO Set进行聚合,记录默克尔树根并生成对应的见证,实现了UTXO模型区块链的无状态交易验证. 该方案的不足之处在于默克尔证明的数据大小随着UTXO Set的膨胀呈对数增长,这份证明带来的通信开销将远远大于交易本身. Chepurnoy等[22 -24 ] 提出的方案可以视为Todd方案的变种. Boneh等[25 ] 利用RSA累加器生成的定长证明来验证UTXO的存在性和未花费性,通过“批处理”技术进一步降低通信开销. 该方案的不足之处在于花掉的UTXO需要从累加器中删除,删除操作的复杂性极大地拖慢了平均出块时间,阻碍了方案的实际应用. 在Boneh等[25 ] 的基础上,Chen等[26 ] 利用RSA累加器证明UTXO的未花费性,利用默克尔山脉证明UTXO的存在性,回避了RSA累加器删除元素的问题,提高了交易验证效率,但默克尔证明导致了通信开销的增加. ...
... 在应用无状态交易验证方案后,交易数据结构发生改变,新增的witness字段带来了额外的通信开销. 由于RSA累加器的性质,引用一笔UTXO,witness带来的额外开销是固定值,为3b . 其中,b 为所选系统参数N 的位宽. N 一般选用RSA-2048 (2 048 bits),则本文方案相应的通信开销为6 144 bits. Boneh等[25 ] 提出的方案为每笔UTXO引入固定的通信开销. 由于只采用一个RSA累加器,通信开销只有本文方案的1/3. 与基于RSA累加器的无状态交易验证方案相比,Todd[21 ] 采用的累加器为默克尔累加器,每笔UTXO对应的通信开销随着UTXO数量的增加呈对数增长. EDRAX[22 ] 采用默克尔累加器的变种,其中每一笔UTXO引入的额外通信开销为10 240 bits,远远超过本文方案. MiniChain[26 ] 的通信开销不仅会受到区块中输出数量的影响,而且会随着区块的增加而无限制地增大. 考虑到实际生产环境中UTXO数量超过1亿[15 ] ,基于双RSA累加器的无状态交易验证方案在通信开销表现上,虽然略逊于Boneh等[25 ] 提出的单RSA方案,但相对于基于默克尔体制的验证方案具有显著的优势. 如表1 所示为目前主流无状态交易验证方案体制及通信开销,与本文方案进行了对比. 表中,M 为预设的UTXO数量,且M $ > $ m $ \gg $ b ;n 为产生该UTXO的区块中交易输出的总数;h 为当前区块的高度. ...
... Communication overheads brought by each UTXO
Tab.1 方案 累加器体制 额外开销(bits/UTXO) Todd[21 ] 默克尔树 256log2 m EDRAX[22 ] 默克尔树 256log2 M Boneh[25 ] 单RSA b MiniChain[26 ] RSA+默克尔树 2b +256log2 n +256log2 h 本文方案 双RSA 3b
4.1.3. 计算复杂度分析 双RSA无状态交易验证方案在交易生命周期的不同阶段,分别执行累加器初始化、见证初始化、(非)成员验证以及承诺、见证更新. 不同的操作具有不同的时间复杂度. 基于通用累加器的性质可知,RSA初始化、添加元素、验证(非)成员见证均为O (1). 当矿工打包新区块时,要遍历全部交易花费及产生的UTXO,对应更新密码学承诺. 时间复杂度与区块体包含花费及产生UTXO的数量呈线性正相关. 与双RSA方案相比,Boneh的单RSA方案由于安全删除操作本身的复杂性,承诺更新的时间复杂度与花费的UTXO总量的平方呈正相关的关系. 尽管双RSA方案要同步更新2个承诺,计算开销仍远远小于单RSA方案. 与RSA体制相比,在基于默克尔累加器的验证方案中,初始化、承诺生成、更新以及见证生成、更新的复杂度均取决于默克尔树(或其变体)的高度,随着UTXO数量的增加呈对数增长的关系. 由于各个过程均实际执行高效的哈希计算,整体时间开销远小于基于RSA的无状态验证方案. ...
1
... 区块链是一系列区块通过加密算法连缀形成的反向链表. 区块由区块头和区块体组成. 区块头存储整个区块的元数据,主要包括父哈希、默克尔树根、难度值以及随机数等,可以实现区块链的大部分功能[14 ] . 父哈希是前一个区块的哈希值,凭借哈希函数的单向性及抗碰撞特性,保证了区块链的安全性[23 ] . 默克尔树根由包含在区块体内的全部交易哈希以二叉树的形式两两向上聚合得到,保证了交易的数据完整性. 难度值与随机数用来判定“记账权”,各节点争夺“记账权”的过程被称为共识. 目前,最常用也最安全的共识算法是工作量证明(proof of work, PoW),在该过程中,节点不断改变随机数的值,直到整个区块头的哈希小于预设难度[13 ] . ...
1
... 基于密码学累加器的无状态交易验证是解决区块链“状态爆炸”问题的崭新思路,基本思想是利用密码学承诺取代状态信息,利用承诺更新来反映状态变化,利用成员证明来验证交易合法性. 节点只存储承诺就可以验证交易的前提是,交易发起者在原本的交易之上需要提供对应的成员证明,而这份证明会带来额外的通信开销. Todd[21 ] 通过默克尔树对UTXO Set进行聚合,记录默克尔树根并生成对应的见证,实现了UTXO模型区块链的无状态交易验证. 该方案的不足之处在于默克尔证明的数据大小随着UTXO Set的膨胀呈对数增长,这份证明带来的通信开销将远远大于交易本身. Chepurnoy等[22 -24 ] 提出的方案可以视为Todd方案的变种. Boneh等[25 ] 利用RSA累加器生成的定长证明来验证UTXO的存在性和未花费性,通过“批处理”技术进一步降低通信开销. 该方案的不足之处在于花掉的UTXO需要从累加器中删除,删除操作的复杂性极大地拖慢了平均出块时间,阻碍了方案的实际应用. 在Boneh等[25 ] 的基础上,Chen等[26 ] 利用RSA累加器证明UTXO的未花费性,利用默克尔山脉证明UTXO的存在性,回避了RSA累加器删除元素的问题,提高了交易验证效率,但默克尔证明导致了通信开销的增加. ...
6
... 基于密码学累加器的无状态交易验证是解决区块链“状态爆炸”问题的崭新思路,基本思想是利用密码学承诺取代状态信息,利用承诺更新来反映状态变化,利用成员证明来验证交易合法性. 节点只存储承诺就可以验证交易的前提是,交易发起者在原本的交易之上需要提供对应的成员证明,而这份证明会带来额外的通信开销. Todd[21 ] 通过默克尔树对UTXO Set进行聚合,记录默克尔树根并生成对应的见证,实现了UTXO模型区块链的无状态交易验证. 该方案的不足之处在于默克尔证明的数据大小随着UTXO Set的膨胀呈对数增长,这份证明带来的通信开销将远远大于交易本身. Chepurnoy等[22 -24 ] 提出的方案可以视为Todd方案的变种. Boneh等[25 ] 利用RSA累加器生成的定长证明来验证UTXO的存在性和未花费性,通过“批处理”技术进一步降低通信开销. 该方案的不足之处在于花掉的UTXO需要从累加器中删除,删除操作的复杂性极大地拖慢了平均出块时间,阻碍了方案的实际应用. 在Boneh等[25 ] 的基础上,Chen等[26 ] 利用RSA累加器证明UTXO的未花费性,利用默克尔山脉证明UTXO的存在性,回避了RSA累加器删除元素的问题,提高了交易验证效率,但默克尔证明导致了通信开销的增加. ...
... [25 ]的基础上,Chen等[26 ] 利用RSA累加器证明UTXO的未花费性,利用默克尔山脉证明UTXO的存在性,回避了RSA累加器删除元素的问题,提高了交易验证效率,但默克尔证明导致了通信开销的增加. ...
... 2)通过系统预置的映射算法 $ {H}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}} $ [25 ,32 ] ,将 $ {\mathrm{U}\mathrm{T}\mathrm{X}\mathrm{O}}_{i} $ $ {H}_{i} $ $ {P}_{i} $ . 在UTXO Set处理完毕后,得到包含 $ n $ $ {S}_{\mathrm{U}} $ . ...
... 在应用无状态交易验证方案后,交易数据结构发生改变,新增的witness字段带来了额外的通信开销. 由于RSA累加器的性质,引用一笔UTXO,witness带来的额外开销是固定值,为3b . 其中,b 为所选系统参数N 的位宽. N 一般选用RSA-2048 (2 048 bits),则本文方案相应的通信开销为6 144 bits. Boneh等[25 ] 提出的方案为每笔UTXO引入固定的通信开销. 由于只采用一个RSA累加器,通信开销只有本文方案的1/3. 与基于RSA累加器的无状态交易验证方案相比,Todd[21 ] 采用的累加器为默克尔累加器,每笔UTXO对应的通信开销随着UTXO数量的增加呈对数增长. EDRAX[22 ] 采用默克尔累加器的变种,其中每一笔UTXO引入的额外通信开销为10 240 bits,远远超过本文方案. MiniChain[26 ] 的通信开销不仅会受到区块中输出数量的影响,而且会随着区块的增加而无限制地增大. 考虑到实际生产环境中UTXO数量超过1亿[15 ] ,基于双RSA累加器的无状态交易验证方案在通信开销表现上,虽然略逊于Boneh等[25 ] 提出的单RSA方案,但相对于基于默克尔体制的验证方案具有显著的优势. 如表1 所示为目前主流无状态交易验证方案体制及通信开销,与本文方案进行了对比. 表中,M 为预设的UTXO数量,且M $ > $ m $ \gg $ b ;n 为产生该UTXO的区块中交易输出的总数;h 为当前区块的高度. ...
... [25 ]提出的单RSA方案,但相对于基于默克尔体制的验证方案具有显著的优势. 如表1 所示为目前主流无状态交易验证方案体制及通信开销,与本文方案进行了对比. 表中,M 为预设的UTXO数量,且M $ > $ m $ \gg $ b ;n 为产生该UTXO的区块中交易输出的总数;h 为当前区块的高度. ...
... Communication overheads brought by each UTXO
Tab.1 方案 累加器体制 额外开销(bits/UTXO) Todd[21 ] 默克尔树 256log2 m EDRAX[22 ] 默克尔树 256log2 M Boneh[25 ] 单RSA b MiniChain[26 ] RSA+默克尔树 2b +256log2 n +256log2 h 本文方案 双RSA 3b
4.1.3. 计算复杂度分析 双RSA无状态交易验证方案在交易生命周期的不同阶段,分别执行累加器初始化、见证初始化、(非)成员验证以及承诺、见证更新. 不同的操作具有不同的时间复杂度. 基于通用累加器的性质可知,RSA初始化、添加元素、验证(非)成员见证均为O (1). 当矿工打包新区块时,要遍历全部交易花费及产生的UTXO,对应更新密码学承诺. 时间复杂度与区块体包含花费及产生UTXO的数量呈线性正相关. 与双RSA方案相比,Boneh的单RSA方案由于安全删除操作本身的复杂性,承诺更新的时间复杂度与花费的UTXO总量的平方呈正相关的关系. 尽管双RSA方案要同步更新2个承诺,计算开销仍远远小于单RSA方案. 与RSA体制相比,在基于默克尔累加器的验证方案中,初始化、承诺生成、更新以及见证生成、更新的复杂度均取决于默克尔树(或其变体)的高度,随着UTXO数量的增加呈对数增长的关系. 由于各个过程均实际执行高效的哈希计算,整体时间开销远小于基于RSA的无状态验证方案. ...
MiniChain: a lightweight protocol to combat the UTXO growth in public blockchain
3
2020
... 基于密码学累加器的无状态交易验证是解决区块链“状态爆炸”问题的崭新思路,基本思想是利用密码学承诺取代状态信息,利用承诺更新来反映状态变化,利用成员证明来验证交易合法性. 节点只存储承诺就可以验证交易的前提是,交易发起者在原本的交易之上需要提供对应的成员证明,而这份证明会带来额外的通信开销. Todd[21 ] 通过默克尔树对UTXO Set进行聚合,记录默克尔树根并生成对应的见证,实现了UTXO模型区块链的无状态交易验证. 该方案的不足之处在于默克尔证明的数据大小随着UTXO Set的膨胀呈对数增长,这份证明带来的通信开销将远远大于交易本身. Chepurnoy等[22 -24 ] 提出的方案可以视为Todd方案的变种. Boneh等[25 ] 利用RSA累加器生成的定长证明来验证UTXO的存在性和未花费性,通过“批处理”技术进一步降低通信开销. 该方案的不足之处在于花掉的UTXO需要从累加器中删除,删除操作的复杂性极大地拖慢了平均出块时间,阻碍了方案的实际应用. 在Boneh等[25 ] 的基础上,Chen等[26 ] 利用RSA累加器证明UTXO的未花费性,利用默克尔山脉证明UTXO的存在性,回避了RSA累加器删除元素的问题,提高了交易验证效率,但默克尔证明导致了通信开销的增加. ...
... 在应用无状态交易验证方案后,交易数据结构发生改变,新增的witness字段带来了额外的通信开销. 由于RSA累加器的性质,引用一笔UTXO,witness带来的额外开销是固定值,为3b . 其中,b 为所选系统参数N 的位宽. N 一般选用RSA-2048 (2 048 bits),则本文方案相应的通信开销为6 144 bits. Boneh等[25 ] 提出的方案为每笔UTXO引入固定的通信开销. 由于只采用一个RSA累加器,通信开销只有本文方案的1/3. 与基于RSA累加器的无状态交易验证方案相比,Todd[21 ] 采用的累加器为默克尔累加器,每笔UTXO对应的通信开销随着UTXO数量的增加呈对数增长. EDRAX[22 ] 采用默克尔累加器的变种,其中每一笔UTXO引入的额外通信开销为10 240 bits,远远超过本文方案. MiniChain[26 ] 的通信开销不仅会受到区块中输出数量的影响,而且会随着区块的增加而无限制地增大. 考虑到实际生产环境中UTXO数量超过1亿[15 ] ,基于双RSA累加器的无状态交易验证方案在通信开销表现上,虽然略逊于Boneh等[25 ] 提出的单RSA方案,但相对于基于默克尔体制的验证方案具有显著的优势. 如表1 所示为目前主流无状态交易验证方案体制及通信开销,与本文方案进行了对比. 表中,M 为预设的UTXO数量,且M $ > $ m $ \gg $ b ;n 为产生该UTXO的区块中交易输出的总数;h 为当前区块的高度. ...
... Communication overheads brought by each UTXO
Tab.1 方案 累加器体制 额外开销(bits/UTXO) Todd[21 ] 默克尔树 256log2 m EDRAX[22 ] 默克尔树 256log2 M Boneh[25 ] 单RSA b MiniChain[26 ] RSA+默克尔树 2b +256log2 n +256log2 h 本文方案 双RSA 3b
4.1.3. 计算复杂度分析 双RSA无状态交易验证方案在交易生命周期的不同阶段,分别执行累加器初始化、见证初始化、(非)成员验证以及承诺、见证更新. 不同的操作具有不同的时间复杂度. 基于通用累加器的性质可知,RSA初始化、添加元素、验证(非)成员见证均为O (1). 当矿工打包新区块时,要遍历全部交易花费及产生的UTXO,对应更新密码学承诺. 时间复杂度与区块体包含花费及产生UTXO的数量呈线性正相关. 与双RSA方案相比,Boneh的单RSA方案由于安全删除操作本身的复杂性,承诺更新的时间复杂度与花费的UTXO总量的平方呈正相关的关系. 尽管双RSA方案要同步更新2个承诺,计算开销仍远远小于单RSA方案. 与RSA体制相比,在基于默克尔累加器的验证方案中,初始化、承诺生成、更新以及见证生成、更新的复杂度均取决于默克尔树(或其变体)的高度,随着UTXO数量的增加呈对数增长的关系. 由于各个过程均实际执行高效的哈希计算,整体时间开销远小于基于RSA的无状态验证方案. ...
1
... 目前,构建无状态交易验证方案常用的密码学工具是RSA累加器. 作为通用累加器,RSA累加器可以通过模幂运算,生成动态变化集合的密码学承诺. 基于该承诺,分别为任何一个(不)属于集合的元素生成定长的(非)成员见证[27 ] . RSA累加器具有抗碰撞性与不可否认性,分别使得伪造非集合元素的成员见证、伪造集合元素的非成员见证在计算上不可行,具有极高的安全性. RSA累加器生成的密码学承诺同集合元素插入累加器的顺序无关,相对于密码学承诺与元素顺序深度绑定的默克尔累加器具有明显优势[28 ] . RSA累加器的构建过程如下. ...
1
... 目前,构建无状态交易验证方案常用的密码学工具是RSA累加器. 作为通用累加器,RSA累加器可以通过模幂运算,生成动态变化集合的密码学承诺. 基于该承诺,分别为任何一个(不)属于集合的元素生成定长的(非)成员见证[27 ] . RSA累加器具有抗碰撞性与不可否认性,分别使得伪造非集合元素的成员见证、伪造集合元素的非成员见证在计算上不可行,具有极高的安全性. RSA累加器生成的密码学承诺同集合元素插入累加器的顺序无关,相对于密码学承诺与元素顺序深度绑定的默克尔累加器具有明显优势[28 ] . RSA累加器的构建过程如下. ...
2
... 1)从未知阶数的有限循环群中选出一大数N 作为模幂运算的模数,该模数可以分解为2个强素数,即有N = $ p q $ . p 、q 由可信的第三方机构或安全多方计算秘密生成,计算得到N 后即行销毁[29 ] . 在实际中,N 一般选用RSA-Lab的RSA-2048或RSA-3072[30 ] . ...
... 当批量添加元素进S 时,将全部元素的乘积视为x n S 中删除元素时,用全部元素的累积成员见证替换密码学承诺[29 ] . 基于RSA累加器的性质,删除操作的复杂度远远超过添加元素. ...
1
... 1)从未知阶数的有限循环群中选出一大数N 作为模幂运算的模数,该模数可以分解为2个强素数,即有N = $ p q $ . p 、q 由可信的第三方机构或安全多方计算秘密生成,计算得到N 后即行销毁[29 ] . 在实际中,N 一般选用RSA-Lab的RSA-2048或RSA-3072[30 ] . ...
2
... 生成集合外元素 u 的非成员见证 :对于u ( $ u\notin S $ ) ,u 一定与x i $ 1 \leqslant i \leqslant n-1 $ ) 互质. 由裴蜀定理[31 ] 可知,必有整数a 、b , 满足ax +bu =1. 令d = G b t 时刻u 对应的非成员见证为 ...
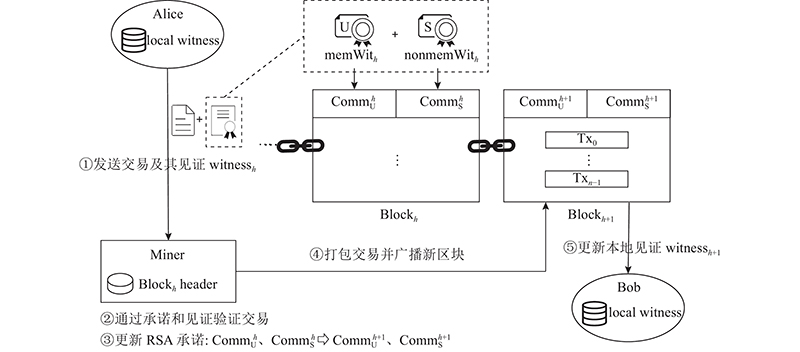
... 如2.3节所示,为了应用基于双RSA累加器的无状态交易验证方案,区块链系统应预置1组公共参数G 、N 充当模幂运算的生成元与模数. Alice与Bob可以在创世区块block0 (区块高度 $ h=0 $ ) 处对 $ {\mathrm{R}\mathrm{S}\mathrm{A}}_{\mathrm{U}} $ $ {\mathrm{R}\mathrm{S}\mathrm{A}}_{\mathrm{S}} $ [31 ] . 创世区块只包含铸币交易(如比特币的coinbase交易),特点是交易只有输出,没有输入. 为了简单起见,假设创世区块包含 $ n $ $ {v}_{i}(0 \leqslant i \leqslant n-1) $ $ n $
Close to uniform prime number generation with fewer random bits
1
2018
... 2)通过系统预置的映射算法 $ {H}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}} $ [25 ,32 ] ,将 $ {\mathrm{U}\mathrm{T}\mathrm{X}\mathrm{O}}_{i} $ $ {H}_{i} $ $ {P}_{i} $ . 在UTXO Set处理完毕后,得到包含 $ n $ $ {S}_{\mathrm{U}} $ . ...