随着人工智能的发展,机器学习技术成为解决这类问题的有效工具. 目前,很多学者开展了基于波动法和机器学习的结构损伤识别研究[11-12],尤其在神经网络领域取得较大进展. 神经网络结构的参数选择存在随机性,基于梯度下降的方法容易陷入局部最优的问题. 遗传算法(genetic algorithm,GA)的发展克服了这些缺陷[13],通过优化神经网络(back propagation neural network,BPNN)的初始权值和阈值,网络快速收敛至全局最优解. GA-BPNN以数据为核心,可以建立从损伤特征空间到损伤状态空间的非线性映射关系,对损伤特征的离散有较强的鲁棒性. 如何全方位提取结构损伤特征是实现模式识别的关键.
基于小波包的特征提取方法[14-16]是提取信号特征的有力工具. 小波包变换(wavelet packet transform,WPT)通过对信号进行逐层分解,聚焦宽频带中的子频带,实现在频域内多分辨率剖析信号的特征. 以子频带系数构建的时频矩阵的信息维度较大,需要对矩阵进行再处理,以提取多维矩阵中的主要信息. 矩阵奇异值有较好的稳定性[17],通过选择主要奇异值,可以用较小的奇异值表示较大的矩阵,同时不丢失矩阵的主要特征,这符合模式识别中对特征值的基本要求. 采用奇异值分解(singular value decomposition,SVD)对时频矩阵进行处理,可以有效地提取反映初始矩阵的本质特征,为模式识别方法提供更全面的损伤特征.
本文以预应力混凝土梁为研究对象,提出基于WPT-SVD和GA-BPNN的混凝土结构损伤识别方法. 利用该方法深度挖掘结构开裂损伤信号的时频域变化特征,构建损伤信号特征与损伤间的非线性关系,提高结构损伤识别的精度.
1. 混凝土结构损伤识别策略
针对静载作用下混凝土结构的开裂损伤情况,基于传感信号矩阵的奇异值向量和GA-BPNN,对混凝土结构的损伤位置和程度进行识别. 具体思路如下.
1)信号特征提取. 对信号进行小波包变换,构建时频矩阵,对时频矩阵进行奇异值分解,得到能够反映信号损伤特征信息的奇异值向量.
2)混凝土结构损伤识别. 采用模式识别方法,输入集为奇异值向量,输出集为损伤位置和程度的分类向量,建立能够映射两者关系的GA-BPNN模型,实现混凝土结构损伤位置和程度的识别.
1.1. 基于外贴式PS的损伤识别原理
混凝土结构损伤最直观的表现形式为裂缝,裂缝使得检测波产生衍射现象,造成检测波的传播路径发生改变,应力波的声压与损伤之前相比较小,导致传感器接收信号的能量衰减[20]. 由于各频带内信号能量受结构损伤的影响较大,单从扫频信号能量绝对值的变化对结构进行损伤分析是不够全面的. 基于WPT和SVD对信号进行分析,通过观察信号在多频带下的奇异值,针对性地选取信号中的有效损伤信息,降低噪声对信号的干扰,能够更全面地提取损伤信号特征.
1.2. 压电信号特征提取
应力波在通过损伤部位时,能量在时频域上的分布会发生变化. 对损伤前、后的压电信号在时频域内进行分析,可以获取更详细的损伤特征信息. WPT可以将较宽的信号频带划分为带宽相等且互不重叠的窄频带,具有较高的时频分辨率,适用于压电信号损伤特征的提取.
任意信号
式中:j、i、k分别为频带阶次、小波分解层数、变换参数,
利用小波包变换,构造时频矩阵:
式中:n为每个频带的小波包系数长度. 该矩阵能够反映压电信号频域上各频带阶次的混凝土损伤特征.
由于时频矩阵的维度较高,不适合直接反映结构损伤状态. 对时频矩阵进行奇异值分解降维,SVD能够在控制样本维度的情况下较完整地保留样本特征信息,减少细节信息的丢失,找到损伤信息中的主成分特征.
式中:
若令A的秩为k,则
带有混凝土结构损伤信息的时频矩阵经奇异值分解后,得到的奇异值向量为该矩阵的特征值向量. 由奇异值分解的性质可知,特征向量反映了矩阵的本质特征,也反映了信号的特征;因此,奇异值
1.3. 基于GA-BPNN的结构损伤识别
由于混凝土结构损伤的不确定性和损伤特征的离散性,传统方法,如理论计算、经验公式和数值模拟,难以在不同应用场景中构建统一的基准值[10]. BPNN具有较强的自适应学习能力,通过处理多维数据的非线性关系,以一维数据的形式输出结果,使得奇异值
在(0,1.0)区间随机选取网络各层的初始权值
式中:
BPNN的初始权值和阈值存在随机性,这会导致BPNN因连接层权值、阈值过度调整,出现学习过程收敛速度较慢、易陷入局部最小化的问题. 利用GA的全局优化能力,可以减少BPNN网络权值修正的盲目性,保证稳定的高精度识别. GA-BPNN可以有效提高混凝土结构损伤识别的稳定性[17].
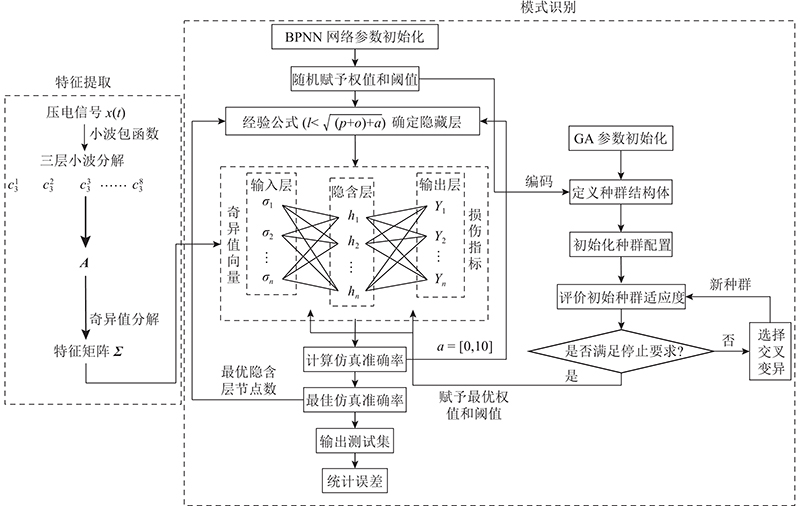
基于WPT-SVD和GA-BPNN的混凝土结构损伤识别的主要思路如图1所示. 数据集由训练集和测试集组成. 数据集中的样本为实测压电信号,经过小波包变换和奇异值分解所得到的带有结构损伤特征信息的奇异值向量作为输入,构建的损伤位置和程度的分类向量作为输出. 隐含层l根据图1的经验公式调试,BPNN网络训练输出结果后,与实际期望值进行比较,验证网络的准确性. 选取预测结果良好的网络,利用GA对权阈值进行编码,以定义种群结构. 通过适应度函数评价种群对网络的匹配度,经过选择、交叉和变异产生优质种群,实现迭代过程,得到当前网络下的最优初始权值和阈值,将最优初始权值和阈值赋予到BPNN中,开展权阈值优化后的网络训练与预测. 采用拟合优度R2和均方差值MSE进行模型评价. GA-BPNN可以根据有限样本反映信号奇异值向量和损伤状态之间的非线性关系,实现混凝土结构损伤的识别.
图 1
图 1 基于WPT-SVD和GA-BPNN的混凝土结构损伤识别框架
Fig.1 Damage identification frame of concrete structures based on WPT-SVD and GA-BPNN
2. 试验概况
2.1. 试验梁设计
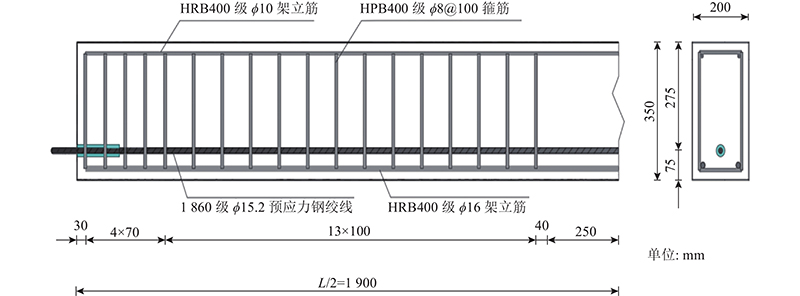
为了保证模型样本的泛化能力和稳定性,制作了3片尺寸相同的预应力混凝土梁,分别为B1、B2和B3. 试验梁尺寸及配筋如图2所示. 在梁底部75 mm处设置1根直径为15.2 mm、等级为1 860 MPa的钢绞线. 在梁底部设置2根直径为16 mm的受拉钢筋,在梁顶部设置2根直径为10 mm的架立筋. 试验梁采用的混凝土强度等级为C40,m(水泥)∶m(水)∶m(粗集料)∶m(细集料)=1∶0.54∶3.58∶2.49. 采用立方体试块测量混凝土抗压强度,28 d抗压强度平均值为41.7 MPa.
图 2
2.2. 试验梁加载及数据采集
采用四点弯曲加载法对试验梁进行加载,在单调荷载作用下加载至破坏. 加载试验时,试验梁从空载状态开始加载,在达到开裂荷载前,以5 kN的增量进行加载;在达到开裂荷载后,以10 kN的增量进行加载,直至混凝土受压区被压溃或预应力筋被拉断. 每个加载步骤的载荷保持时间约为8 min,用于采集压电信号、位移、裂纹和挠度等数据.
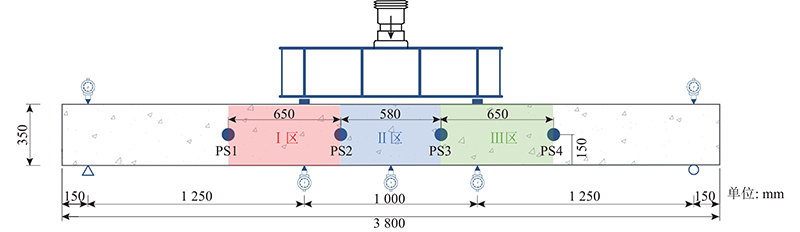
为了研究不同荷载作用下预应力混凝土梁弯剪区、纯弯曲区和整体区域的损伤过程,在试验梁混凝土表面布置4个PS传感器. 将PS1作为驱动器,PS2和PS4作为PS1的传感器,分别用于获取Ⅰ区和总长度Ⅳ区的损伤信息(总长度Ⅳ区为Ⅰ区、Ⅱ区和Ⅲ区之和). 将PS2(PS3)作为驱动器,PS3(PS4)作为传感器,用于获取Ⅱ(Ⅲ)区的损伤信息,如图3所示. 选用PZT-5H型压电陶瓷片制作压电传感器,压电陶瓷片的直径为10 mm,厚为0.3 mm,传感器的外包层为大理石,由上海市联能科技有限公司生产,传感器的主要性能参数如表1所示. 表中,ρ为密度,ε为介电常数,k为机电耦合系数,tan δ为介质损耗因子,tc为居里温度,Qm为机械品质因数. 采用位移测量计,获得梁跨中、加载点和支座位置处的垂直挠度.
图 3
图 3 混凝土梁加载及传感器布置
Fig.3 Loading diagram of concrete beams and arrangement of transducers
表 1 压电传感器的主要性能参数
Tab.1
| ρ/(g·cm−3) | ε | k | tan δ | tc/℃ | Qm |
| 7.6 | 3 400 | 0.76 | 1.3 | 250 | 75 |
2.3. 混凝土梁损伤的压电波动法检测
扫频信号有较宽的频带范围,能够满足对结构损伤的随机性和多样性的要求. 由于混凝土材料的离散性,应力波在混凝土中的传播时会出现绕射、衍射、反射等行为. 若激励信号频率不高,由于激励信号的波长较长,易产生重度绕射行为,致使实测的信号杂乱,影响试验结果;若激励信号频率太高,会加快信号衰减速率,这限制了传感器的信号传输范围. 孙威[24]通过压电波动测量理论和试验发现,当针对混凝土结构的检测系统工作频率为1~50 kHz时,效果较理想. Zhou等[18]认为100 Hz以下的频率易受低频噪声的干扰,采用0.1~100 kHz的正弦信号,对FRP筋混凝土梁的抗弯刚度进行实时监测. Laskar等[25]提出基于SA的方法来评估混凝土框架的健康状态,采用0.1~5 kHz的正弦信号作为激励源.
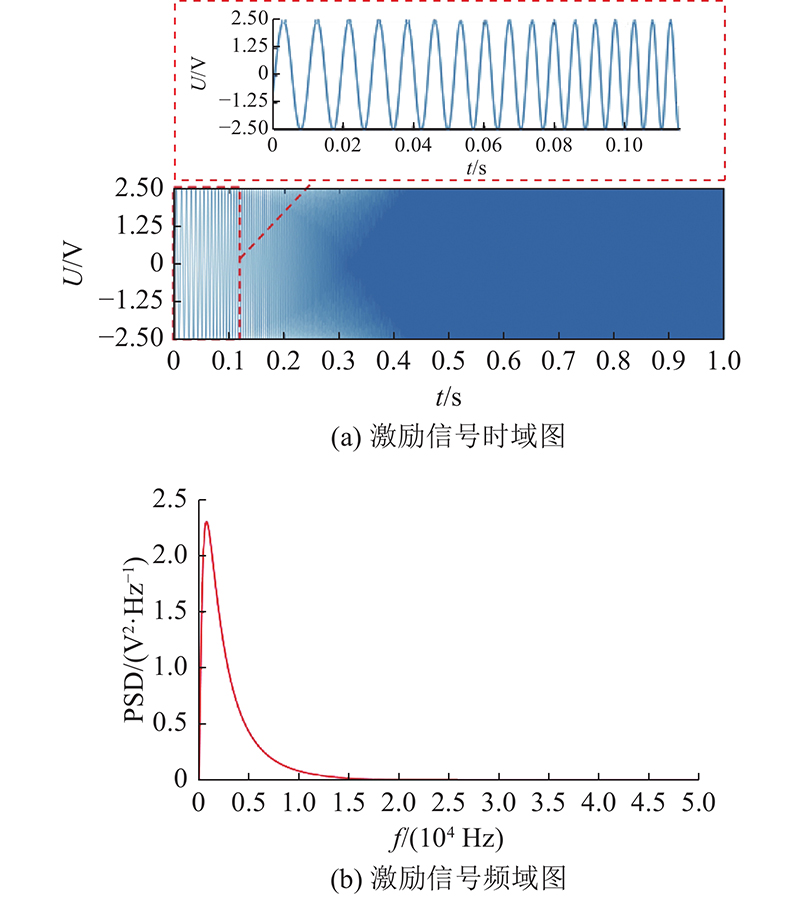
基于上述文献调研,结合试验前期选用不同频率的检测信号,采用扫频范围为0.1~50 kHz,幅值为2.5 V,长度为1 s的正弦扫频信号,由功率放大器放大50倍传输至驱动器,采样频率为2 MHz. PS传感器的测试装置包括数据采集设备(NI USB-6363)、功率放大器和笔记本电脑等. 正弦扫频激励信号的时域和频域图如图4所示. 图中,U为幅值,t为时间,PSD为功率谱密度,f为频率。
图 4
根据PS传感器的位置,将预应力混凝土梁分为4个区域. 对预应力混凝土梁在13个荷载等级下的损伤信号各采集8次(在加载后8 min内每隔1 min激励一次),共有1 248组信号.
3. 试验结果分析
3.1. 试验梁荷载-挠度曲线及裂缝扩展
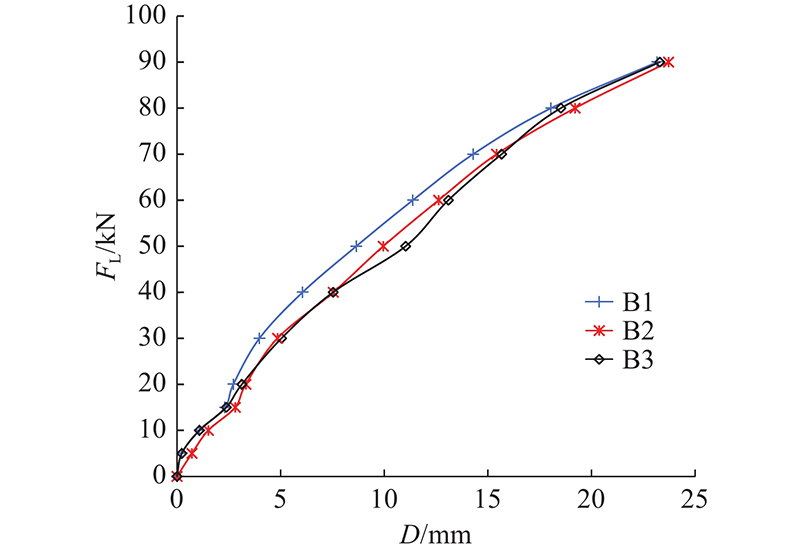
试验梁的荷载与挠度关系如图5所示. 图中,FL为荷载,D为挠度. B1、B2和B3的开裂荷载均为15 kN,极限承载力分别为105、100和98 kN. 由于梁体在临近破坏阶段的挠度变化较大,未能绘制90 kN以后的荷载-挠度曲线. 在出现裂缝前,试验梁的挠度随着荷载的增大而增大. 在超过开裂荷载(15 kN)后,试验梁挠度迅速增加,刚度显著退化,这意味着裂缝的出现导致了截面有效惯性矩的减小和结构性能的降低. 这表明裂缝的发展是造成混凝土梁损伤的主要原因,裂缝和挠度可以作为反映预应力混凝土梁损伤演化的典型特征.
图 5
如图6所示为B1处于极限状态时的裂缝分布情况. 当荷载为15 kN时,B1在跨中出现裂缝. 随着荷载的增加,裂缝数目和裂缝宽度逐渐增大. 在加载至一定荷载等级后,只有主裂缝附近处的裂缝往试验梁顶部扩展延伸,其余裂缝宽度和高度增速放缓. 最后B1受压区混凝土被压碎,构件失效. B2和B3的裂纹开展情况与B1相似,仅以B1为例,对裂缝发展情况进行分析.
图 6
3.2. 信号时频域分析
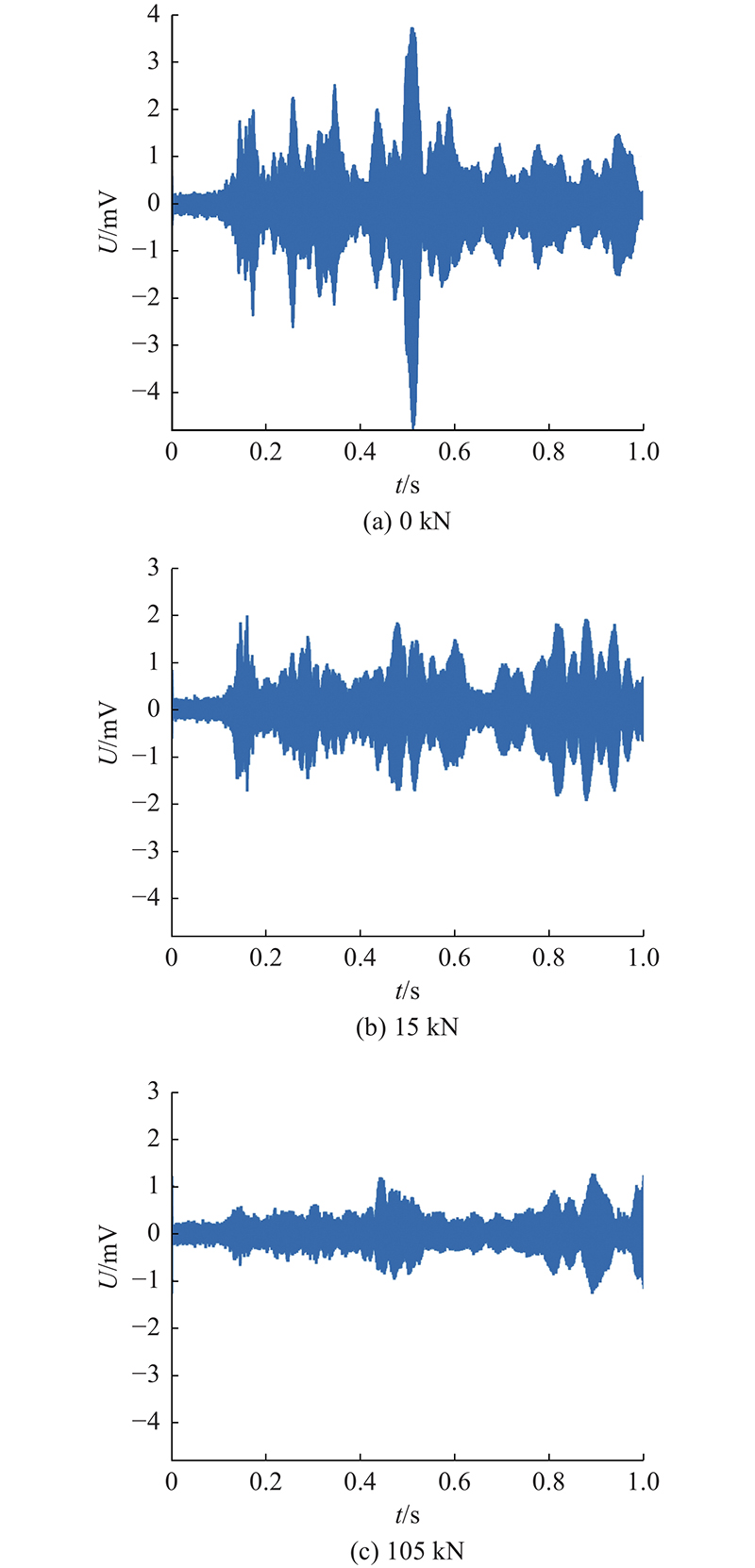
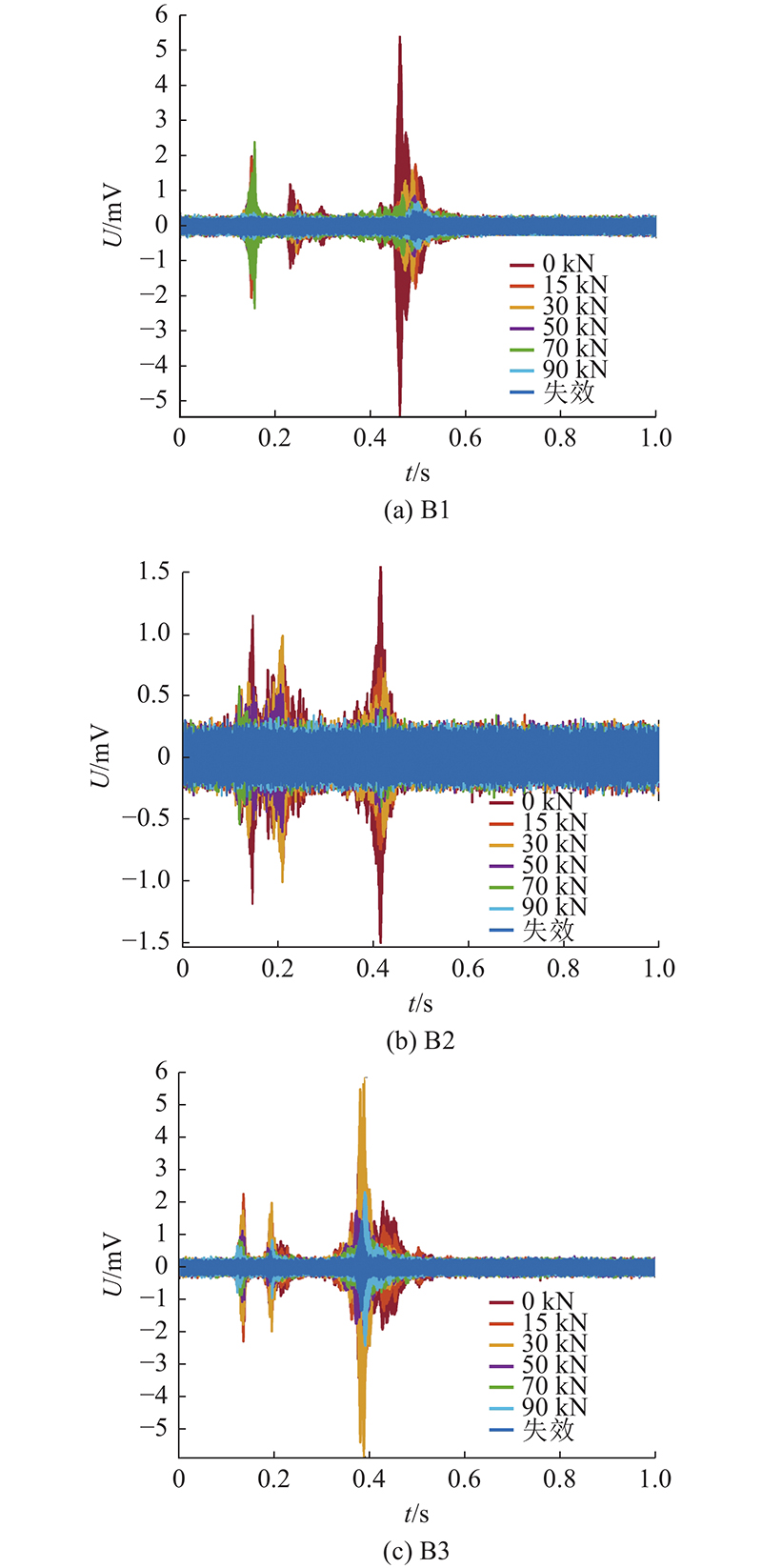
根据PS采集到的信号,可以得出相应时域图. 如图7(a)~(c)所示分别为B1在0 kN、15 kN(开裂荷载)和105 kN(极限荷载)时Ⅱ区段的时域信号. 随着荷载的增加,时域信号逐渐衰减. 15 kN下的能量衰减量为0 kN下的48.83%,105 kN下的能量衰减量为0 kN下的86.83%. 通过时域信号分析,可以初步判断出面波对于混凝土结构的损伤监测有较好的敏感性.
图 7
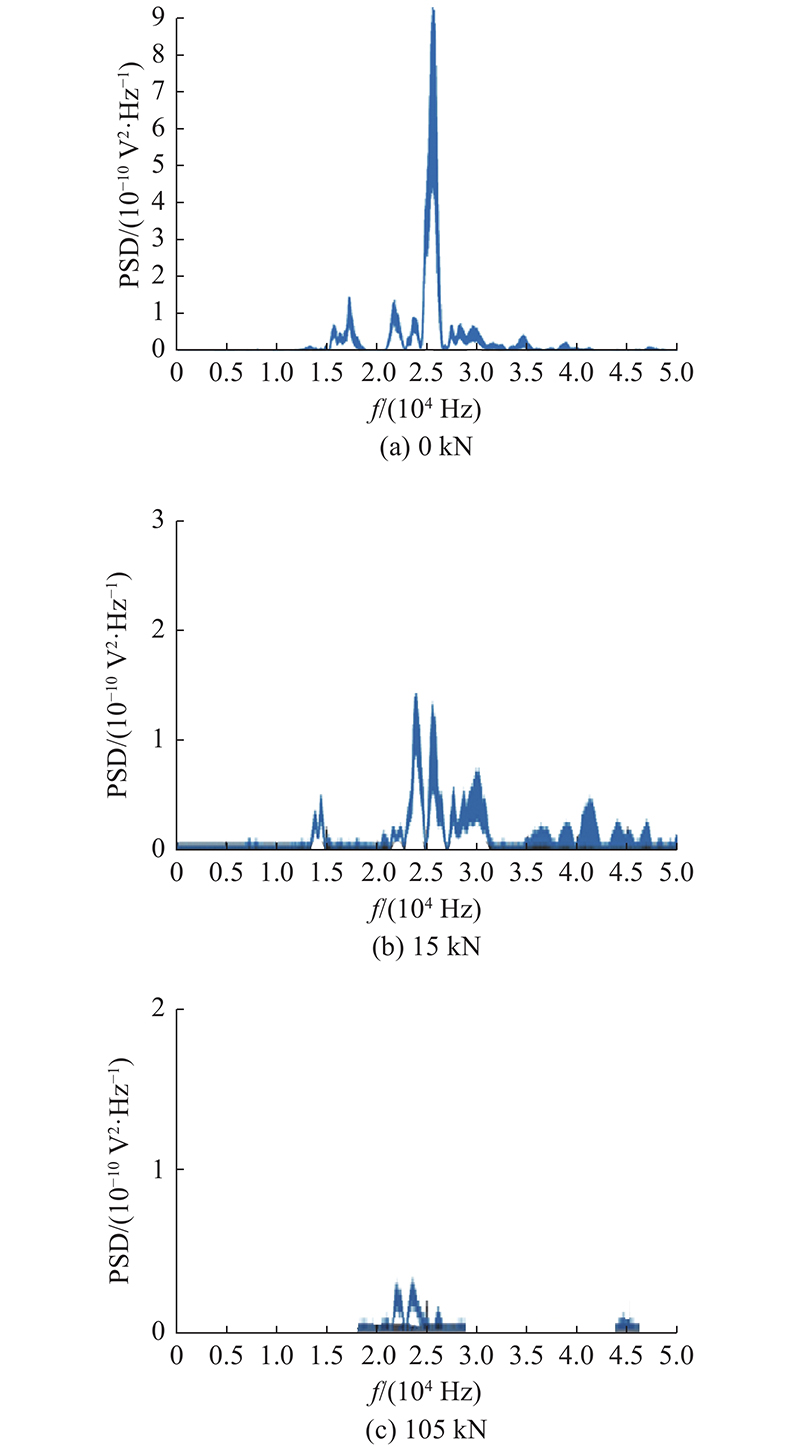
通过傅里叶变换分析信号的频域特征,得到不同荷载下PS接收到的频谱. 如图8所示为B1梁在0、15和105 kN荷载下Ⅱ区段信号的频域图. 可知,在不同损伤状态下频率分布一致,主频约为25 kHz. 随着荷载的增加,PS在Ⅱ区段接收到主频的峰值总体上呈现减小的趋势. 15 kN下的信号幅值衰减了85.01%,105 kN下的信号幅值衰减了99.66%.
图 8
图 9
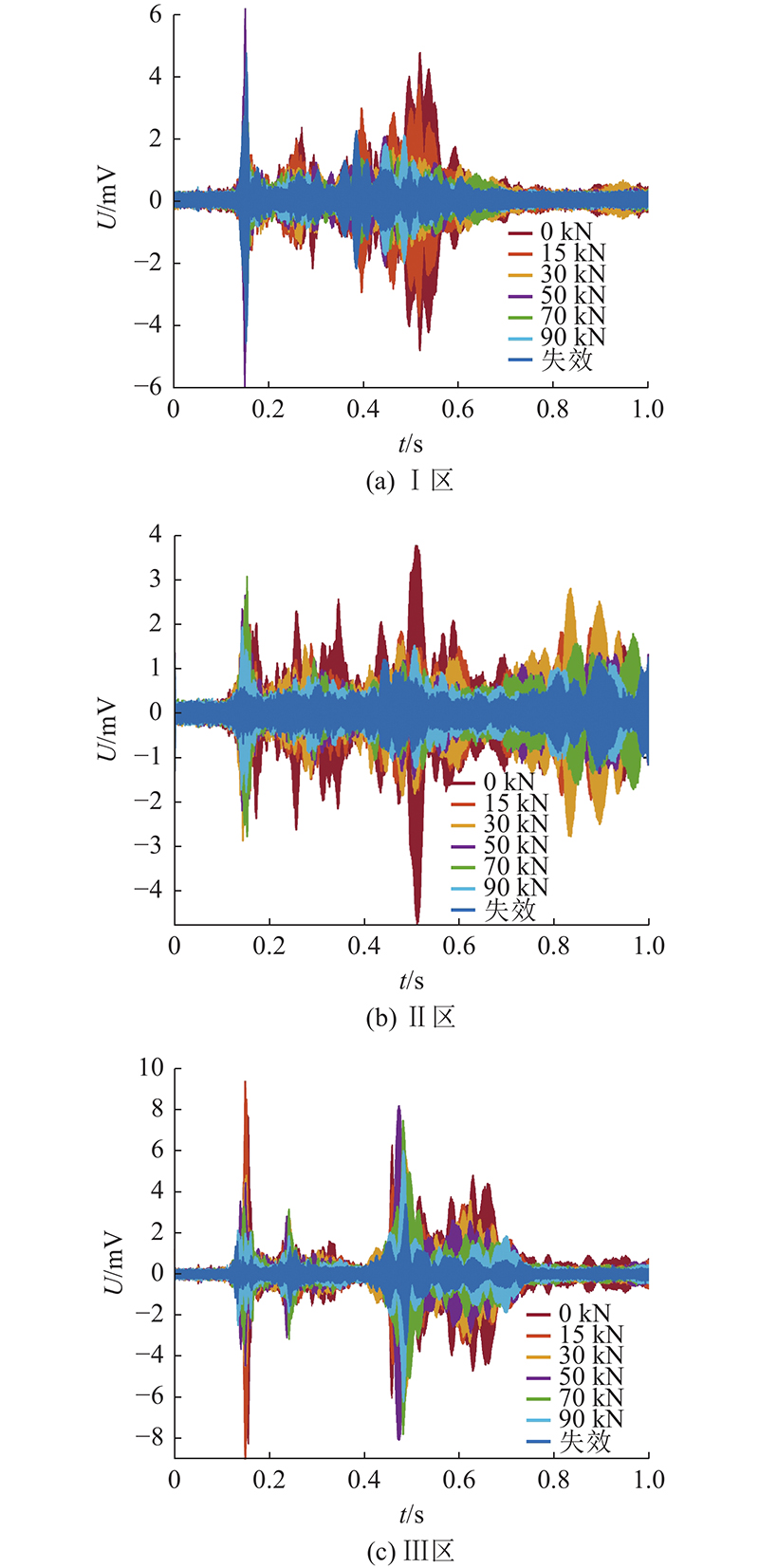
3片试验梁在Ⅳ区的信号幅值如图10所示. 信号幅值可以反映混凝土梁的能量减少情况和损伤程度. 当荷载为15 kN(即开裂荷载)时,混凝土的开裂导致信号幅值降低. 当混凝土梁接近破坏时,由于大裂纹的存在,传输能量受到严重阻碍,只接收到噪声,应力波能量在传播过程中完全被裂缝反射和耗散. 荷载的增加导致混凝土梁整体长度信号幅值的减小,通过Ⅳ区PS传感器接收到的信号变化,可以判断混凝土结构的损伤状况.
图 10
3.3. 奇异值向量与混凝土结构损伤的关系
通过对压电信号进行小波包变换,可以得到由不同频带小波域上的重构系数构成的时频矩阵. 由信息熵理论可知,信息熵越大,表示各个频带之间的信息差越大,更有利于找到最能反映压电信号和结构损伤程度相关性的敏感频带. 采用小波包能量熵作为不同小波包函数的评价指数.
压电信号x的第i层小波包分解序列为
根据信息熵的基本理论可知,第
通过对压电信号分别使用Daubechies函数和Coiflets函数进行3层小波包分解,计算得到各小波包函数的小波包能量熵. 随着函数阶次的增加,能量熵S下降显著. 其中,‘db1’的能量熵最高,为0.492 3,因此选取‘db1’小波包基函数对信号进行小波包变换,有利于获得更完整的特征信息.
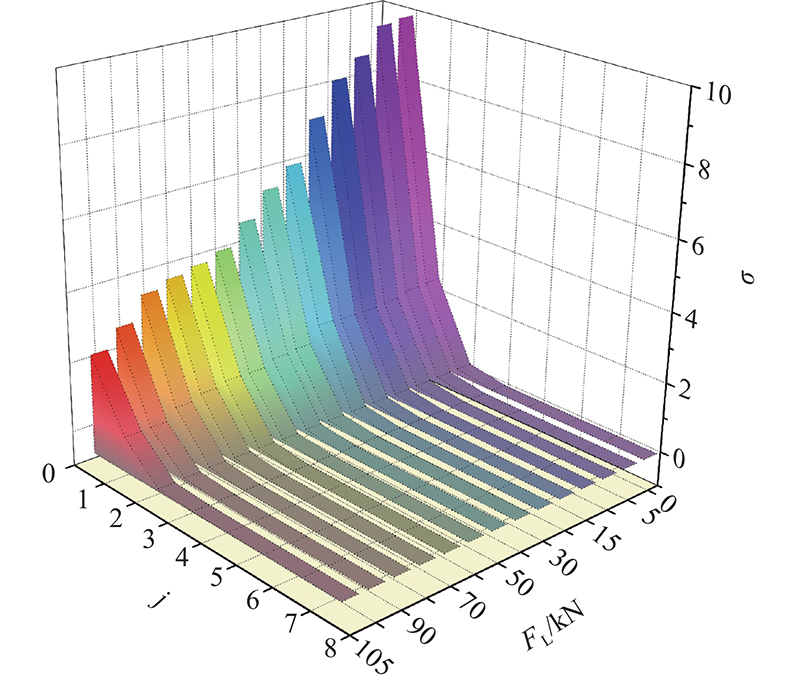
利用分解后得到的8个频带的小波包重构系数,根据式(3)构建时频矩阵. 将时频矩阵按式(4)进行奇异值分解,可得试验梁在不同荷载等级下的信号奇异值向量(以B1为例),如图11所示. 随着荷载的增加,奇异值逐渐减小,分解到第5频带时的奇异值趋近于0,这表明前4个频带的奇异值有效地保留了信号携带的损伤特征信息. 通过比较不同荷载对应的奇异值,能够定性地分析试验梁的荷载等级,结合挠度对奇异值向量与混凝土结构损伤的关系进行定量评价.
图 11
图 11 不同荷载等级的信号奇异值向量
Fig.11 Singular value vectors of signal at different load levels
提出将健康状态下混凝土结构的信号奇异值向量作为标准奇异值向量
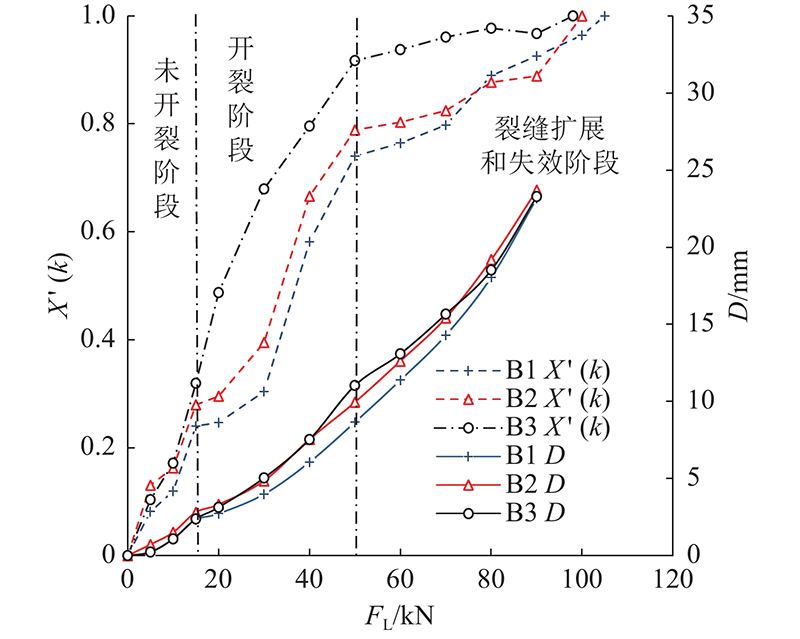
荷载、挠度及归一化奇异值向量距
图 12
图 12 荷载、挠度及归一化奇异值向量距的关系曲线
Fig.12 Relation curves among load, deflection and normalization singular value vector distance
以B1为例,在未开裂阶段,由于整体刚度的作用,混凝土梁的挠度较小,该阶段的
4. 基于GA-BPNN的结构损伤识别结果分析
奇异值向量与混凝土结构损伤间存在对应关系,通过建立具有学习能力的神经网络模型,可以有效地反映两者间的映射关系,实现混凝土的结构损伤识别. 基于WPT和SVD的方法,将试验得到的1 248组压电信号进行特征提取,为GA-BPNN提供特征向量. 在损伤位置(程度)识别中,选择B1和B2梁,即624(832)个压电信号的奇异值向量作为训练样本集,B3梁的312(416)个压电信号的奇异值向量作为测试样本集. 梁Ⅳ区无须进行位置识别,因此损伤位置的数据比损伤程度的数据少.
将训练集置于GA-BPNN进行训练,设定最大迭代次数为100,初始种群规模为30个,交叉概率为0.8,变异概率为0.1. 在损伤位置(程度)识别中,最优隐含层为10(22)层,迭代51(100)次后,得出最佳适应度为0.03675(0.053 45). 将得到的最优权值和阈值赋值给BPNN进行预测,模型评估结果如表2所示.
表 2 网络的评估指标
Tab.2
| 损伤情况 | 模型 | 数据集 | R2 | MSE |
| 损伤位置 | BPNN | 训练集 | 0.890 9 | 9.222×10−3 |
| BPNN | 测试集 | 0.860 5 | 1.209×10−2 | |
| GA-BPNN | 训练集 | 0.974 3 | 7.863×10−4 | |
| GA-BPNN | 测试集 | 0.950 6 | 2.938×10−3 | |
| 损伤程度 | BPNN | 训练集 | 0.501 4 | 0.101 2 |
| BPNN | 测试集 | 0.482 4 | 0.115 3 | |
| GA-BPNN | 训练集 | 0.792 6 | 0.041 5 | |
| GA-BPNN | 测试集 | 0.827 9 | 0.060 5 |
从表2可知,GA-BPNN的网络评估指标较BPNN而言均得到明显的改善,在损伤程度识别中,BPNN拟合优度较小. 这是因为程度识别对样本群体质量的要求更高,损伤指标的离散性严重影响损伤程度的识别结果;由于BPNN随机选取初始权值和阈值,导致网络结构参数调整过度,训练样本集的预测结果不理想. 经GA赋予最优初始权阈值后,显著加强了各神经元间的链接强度,GA-BPNN深入挖掘了奇异值向量中的特征,减弱了特征离散性对识别结果的干扰,使得识别结果更加稳定.
图 13
在损伤位置(程度)识别中,BPNN准确率为91.03%(89.66%),GA-BPNN模型的准确率为95.19%(94.47%). 两者均具有较高的准确性,但GA-BPNN的识别结果明显更优,能够基本修正BPNN中的失效识别. 综上所述,基于奇异值向量和GA-BPNN的混凝土结构损伤识别结果有较高的准确性和稳定性. 经过小波包变换和奇异值分解后,信号频域上的结构损伤本质特征能够较完整地被提取出来. 利用遗传算法,能够修复网络结构参数的随机性造成的局部最优问题,使得GA-BPNN能够从信号奇异值向量中更好地挖掘时频矩阵中的本质损伤特征,有效提升了结构损伤识别的准确率.
5. 结 论
(1) 本文提出基于WPT-SVD和GA-BPNN的混凝土结构损伤识别方法. WPT和SVD的耦合可以提取压电信号在多分辨率下反映时频矩阵的损伤本质特征,以奇异值向量作为信号损伤特征建立GA-BPNN,实现在役混凝土结构的损伤识别.
(2) 结合WPT和SVD构建的奇异值向量是混凝土结构损伤的有效特征参量. 随着荷载的逐步增加,时频矩阵的奇异值逐渐减小. 归一化奇异值向量距与损伤情况呈现三阶段对应关系.
(3) 利用基于GA-BPNN的方法,能够稳定识别混凝土结构损伤位置和程度,精确度可以达到95.19%和94.47%. 与BPNN相比,GA-BPNN更好地拟合了损伤信号特征与损伤情况间的关联性,对损伤位置和程度的识别精度分别提升了4.16%和4.81%.
(4) 本文试验主要通过结构开裂判别损伤的发展趋势,而服役结构在多病害作用下的损伤问题更加复杂,损伤(如锈蚀、疲劳荷载)的累积会影响结构的伤害评级和预测,如何综合考虑上述因素对结构损伤评定的影响有待进一步的研究.
参考文献
再生混凝土悬臂梁阻尼性能与损伤关系的试验研究
[J].DOI:10.15951/j.tmgcxb.2016.07.009 [本文引用: 1]
Experimental study on relationship between damping capacity and damage degree of recycled concrete cantilever beam
[J].DOI:10.15951/j.tmgcxb.2016.07.009 [本文引用: 1]
基于分级免疫萤火虫算法的桥梁振动传感器优化布置研究
[J].
Optimal vibration sensor placement for bridges using gradation-immune firefly algorithm
[J].
土木工程结构健康监测系统的研究状况与进展
[J].DOI:10.3321/j.issn:1000-0992.2008.02.002 [本文引用: 1]
Research status and progress of structural health monitoring system in civil engineering
[J].DOI:10.3321/j.issn:1000-0992.2008.02.002 [本文引用: 1]
Guided wave based structural health monitoring: a review
[J].DOI:10.1088/0964-1726/25/5/053001
Non-destructive concrete strength evaluation using smart piezoelectric transducer: a comparative study
[J].DOI:10.1088/0964-1726/25/8/085021 [本文引用: 1]
Online monitoring of cracking in concrete structures using embedded piezoelectric transducers
[J].DOI:10.1088/0964-1726/23/11/115016 [本文引用: 1]
Detection and monitoring of flexural cracks in reinforced concrete beams using mounted smart aggregate transducers
[J].DOI:10.1088/1361-665X/aa849a [本文引用: 1]
Smart-aggregate-based damage detection of fiber-reinforced-polymer-strengthened columns under reversed cyclic loading
[J].DOI:10.1088/0964-1726/20/7/075014 [本文引用: 1]
Detection of structural damage from the local temporal coherence of diffuse ultrasonic signals
[J].DOI:10.1109/TUFFC.2005.1561631 [本文引用: 1]
基于能量图谱和孪生网络的导波损伤诊断方法
[J].
Guided wave damage diagnosis method based on energy spectrum and twin network
[J].
Damage detection in a novel deep-learning framework: a robust method for feature extraction
[J].DOI:10.1177/1475921719846051 [本文引用: 1]
Smart crawfish: a concept of underwater multi-bolt looseness identification using entropy-enhanced active sensing and ensemble learning
[J].DOI:10.1016/j.ymssp.2020.107186 [本文引用: 1]
基于可靠度指标的桥梁安全评估分级方法
[J].DOI:10.11990/jheu.201507035 [本文引用: 1]
A method for bridge safety assessment based on reliability index
[J].DOI:10.11990/jheu.201507035 [本文引用: 1]
Structural damage identification through sensitivity-based finite element model updating and wavelet packet transform component energy
[J].DOI:10.1016/j.istruc.2021.07.030 [本文引用: 1]
基于导波多点散射的在役拱桥吊杆腐蚀损伤识别
[J].DOI:10.13465/j.cnki.jvs.2021.19.037
Corrosion damage identification of suspenders of arch bridges in service based on guided wave multi-point scattering
[J].DOI:10.13465/j.cnki.jvs.2021.19.037
基于双谱和奇异值分解的结构损伤试验
[J].DOI:10.3785/j.issn.1008-973X.2012.10.021 [本文引用: 2]
Experimental study of structural damage based on bispectral analysis and singular value decomposition
[J].DOI:10.3785/j.issn.1008-973X.2012.10.021 [本文引用: 2]
Monitoring of bending stiffness of BFRP reinforced concrete beams using piezoceramic transducer enabled active sensing
[J].DOI:10.1088/1361-665X/ab936d [本文引用: 2]
Identification of the structural damage mechanism of BFRP bars reinforced concrete beams using smart transducers based on time reversal method
[J].
基于压电波动法的混凝土裂缝损伤监测技术
[J].DOI:10.6052/j.issn.1000-4750.2012.04.S058 [本文引用: 1]
Monitoring technology for crack damage of concrete structure based on piezoelectric wave method
[J].DOI:10.6052/j.issn.1000-4750.2012.04.S058 [本文引用: 1]
基于导波能量谱的钢绞线腐蚀损伤识别研究
[J].DOI:10.13465/j.cnki.jvs.2018.20.018 [本文引用: 1]
Steel strands corrosion identification based on guide wave energy spectrum
[J].DOI:10.13465/j.cnki.jvs.2018.20.018 [本文引用: 1]
基于小波-奇异值分解差分谱的弱故障特征提取方法
[J].DOI:10.3901/JME.2012.07.037 [本文引用: 1]
Extraction method of faint fault feature based on wavelet-SVD difference spectrum
[J].DOI:10.3901/JME.2012.07.037 [本文引用: 1]
基于桥梁单元刚度损伤识别的新型间接量测方法研究
[J].DOI:10.3969/j.issn.1001-7372.2021.02.009 [本文引用: 1]
Bridge element bending stiffness damage identification based on new indirect measurement method
[J].DOI:10.3969/j.issn.1001-7372.2021.02.009 [本文引用: 1]
Progressive collapse of a two-story reinforced concrete frame with embedded smart aggregates
[J].





 表示实际试验中的损伤位置(期望位置),
表示实际试验中的损伤位置(期望位置),  和
和  分别表示BPNN和GA-BPNN的预测位置.
分别表示BPNN和GA-BPNN的预测位置. 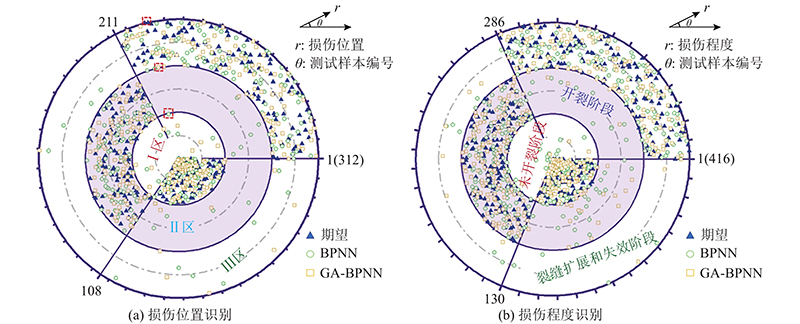
 标记点),在BPNN和GA-BPNN完成训练后,输入的奇异值向量为[6.700 4,3.931 0,0.808 2,0.175 2]T,期望输出为3(表示在实际试验中该奇异值向量代表的损伤位置为Ⅲ区,对应
标记点),在BPNN和GA-BPNN完成训练后,输入的奇异值向量为[6.700 4,3.931 0,0.808 2,0.175 2]T,期望输出为3(表示在实际试验中该奇异值向量代表的损伤位置为Ⅲ区,对应 