[21]
中国城镇供水排水协会, 北京市自来水集团有限责任公司. 城镇供水管网漏损控制及评定标准: CJJ 92-2016 (2018年修订) [S]. 北京: 中国建筑工业出版社, 2016.
[本文引用: 1]
[1]
周扬, 李云飞, 袁宏永, 等 基于听觉显著图的长输管道漏失检测算法
[J]. 吉林大学学报: 工学版 , 2020 , 50 (4 ): 1487 - 1494
[本文引用: 1]
ZHOU Yang, LI Yun-fei, YUAN Hong-yong, et al Identification method of long distance pipeline leakage based on auditory saliency map
[J]. Journal of Jilin University: Engineering and Technology Edition , 2020 , 50 (4 ): 1487 - 1494
[本文引用: 1]
[2]
国家统计局. 2017城市供水统计年鉴[Z/OL]. [2022-02-21]. https://www.yearbookchina.com/navibooklist-n3019080610-1.html.
[本文引用: 1]
State Statistical Bureau. 2017 urban water supply statistical yearbook [Z/OL]. [2022-02-21]. https://www.yearbookchina.com/navibooklist-n3019080610-1.html.
[本文引用: 1]
[3]
国家统计局. 2016城市供水统计年鉴[Z/OL]. [2022-02-21]. https://www.yearbookchina.com/navibooklist-n3019022704-1.html.
[本文引用: 1]
State Statistical Bureau. 2016 urban water supply statistical yearbook [Z/OL]. [2022-02-21]. https://www.yearbookchina.com/navibooklist-n3019022704-1.html.
[本文引用: 1]
[4]
FATHI-MOGHADAM M, KIANI S Simulation of transient flow in viscoelastic pipe networks
[J]. Journal of Hydraulic Research , 2020 , 58 (3 ): 531 - 540
DOI:10.1080/00221686.2019.1581669
[本文引用: 1]
[6]
郑成志, 赵焱, 孙国胜, 等 实测方法评估压力管理对漏失水量降低程度的适用性
[J]. 中国供水排水 , 2019 , 35 (19 ): 50 - 56
[本文引用: 1]
ZHENG Cheng-zhi, ZHAO Yan, SUN Guo-sheng, et al Applicability of measurement method in assessing extent of real losses reduction through pressure management
[J]. China Water and Wastewater , 2019 , 35 (19 ): 50 - 56
[本文引用: 1]
[7]
杨新兰 论银行监管的相机抉择
[J]. 金融研究 , 2004 , (9 ): 108 - 118
[本文引用: 2]
YANG Xin-lan On the discretionary choice of banking supervision
[J]. Journal of Financial Research , 2004 , (9 ): 108 - 118
[本文引用: 2]
[8]
CASSA A M, VAN ZYL J E. A numerical investigation into the behavior of cracks in uPVC pipes under pressure [D]. Johannesburg: University of Johannesburg, 2011.
[本文引用: 1]
[9]
DE M S, MOLARI L, SCALET G, et al A physically-based analytical relationship for practical prediction of leakage in longitudinally cracked pressurized pipes
[J]. Engineering Structures , 2014 , 79 : 142 - 148
DOI:10.1016/j.engstruct.2014.08.011
[本文引用: 1]
[10]
BRUNONE B, MENICONI S, CAPPONI C Numerical analysis of the transient pressure damping in a single polymeric pipe with a leak
[J]. Urban Water Journal , 2018 , 14 (8 ): 760 - 768
[本文引用: 1]
[11]
FERRANTE M, MASSARI C, BRUNONE B, et al Experimental evidence of hysteresis in the head-discharge relationship for a leak in a polyethylene pipe
[J]. Journal of Hydraulic Engineering , 2010 , 137 (7 ): 775 - 780
[本文引用: 2]
[12]
MASSARI C, FERRANTE M, BRUNONE B, et al Is the leak head-discharge relationship in polyethylene pipes a bijective function?
[J]. Journal of Hydraulic Research , 2012 , 50 (4 ): 409 - 417
DOI:10.1080/00221686.2012.696558
[本文引用: 1]
[13]
郑成志. 基于信号处理算法的供水管网物理漏失流量分析模型研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
[本文引用: 3]
ZHENG Cheng-zhi. Research on leakage discharge analysis model of water distribution network based on algorithm for signal processing [D]. Harbin: Harbin Institute of Technology, 2015.
[本文引用: 3]
[15]
PEARSON D. Standard definitions for water losses [M]. London: IWA Publishing, 2019: 40.
[本文引用: 1]
[16]
邵煜, 虞介泽, 俞亭超 埋地管线均匀腐蚀失效力学模型及随机分析
[J]. 浙江大学学报: 工学版 , 2010 , 44 (6 ): 1225 - 1230
[本文引用: 1]
SHAO Yu, YU Jie-ze, YU Ting-chao Mechanical model and probability analysis of buried pipelines failure under uniform corrosion
[J]. Journal of Zhejiang University: Engineering Science , 2010 , 44 (6 ): 1225 - 1230
[本文引用: 1]
[17]
范钦珊, 蔡新. 材料力学(土木水利类)[M]. 北京: 清华大学出版社, 2006: 246-248.
[本文引用: 1]
[18]
赵荣国, 李其棒, 刘亚风, 等. 几种典型黏弹性固体模型的松弛模量与蠕变柔量表达式比较研究[C]// 第十二届全国流变学学术会议论文集. 广州: 中国力学学会, 2014: 6.
[本文引用: 1]
ZHAO Rong-guo, LI Qi-bang, LIU Ya-feng, et al. Comparative research on expressions of relaxation modulus and creep compliance of several typical viscoelastic solid models [C]// Proceedings of the 12th National Conference on Rheology . Guangzhou: CSTAM, 2014: 6.
[本文引用: 1]
[19]
李茂东, 李彦, 杨波, 等 PE100燃气管材的非线性蠕变行为及其本构模型研究
[J]. 中国塑料 , 2021 , 35 (11 ): 91 - 96
DOI:10.19491/j.issn.1001-9278.2021.11.014
[本文引用: 1]
LI Mao-dong, LI Yan, YANG Bo, et al Characterization and constitutive modelling of nonlinear creep of PE100 grade gas pipe material
[J]. China Plastics , 2021 , 35 (11 ): 91 - 96
DOI:10.19491/j.issn.1001-9278.2021.11.014
[本文引用: 1]
[20]
于波, 王玥, 刘国富, 等 索膜结构的蠕变性能研究
[J]. 科学技术与工程 , 2006 , (15 ): 2301 - 2305
DOI:10.3969/j.issn.1671-1815.2006.15.019
[本文引用: 1]
索膜结构的蠕变性能研究
1
2006
... 李茂东等[19 ] 在常温条件下对DN100的PE管道进行蠕变测试,发现在应力不超过5.4 MPa的情况下,蠕变柔量不受受力的影响,为线黏弹性行为. 在城市供水管网的实际运行过程中,绝大部分管道的运行压力不会超过1.0 MPa,远小于线性黏弹性行为和非线性黏弹性行为的界限值5.4 MPa,因此认为供水塑料管道表现为线黏弹性行为. 对于线性黏弹性行为,可以使用Boltzmann叠加原理量化历史应力对应变的影响[20 ] : ...
1
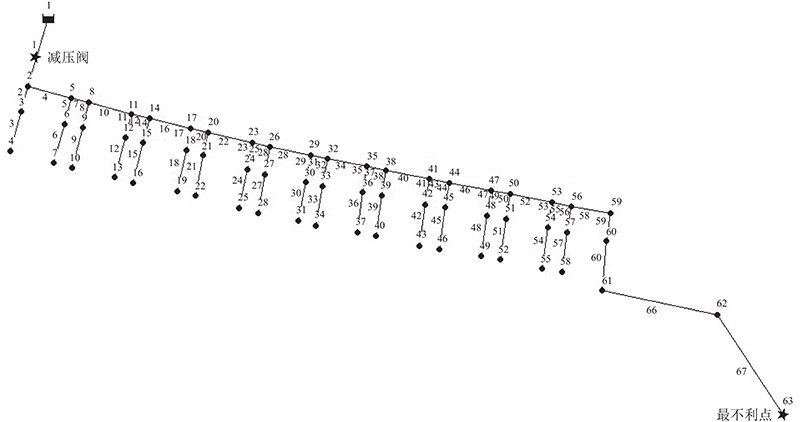
... A小区位于南方沿海地区,为20世纪初所修建的居民小区. A小区供水管网具有统一的铺设年代(20世纪),采用相同材质的供水管道(PE材质供水管道)、相同的施工质量(为同一施工队所铺设)、相同的探漏修复周期(水司每隔一段时间对该片区管网进行统一的漏点检测和修复工作). A小区拥有单一进水口,与其他分区供水分界线明显,供水管网的拓扑关系明确,面积约为25 000 m2 ,用户数为210,最高楼层数为5,A小区可以作为DMA[21 ] . 如图2 所示为A小区供水管网的拓扑结构. 图2 中,1号管段为A小区唯一入水口,在1号管段上安装智能减压阀,实现对A小区的压力管理. 在智能减压阀前、后各安装一块具有流量测量、压力测量与信号远传功能的电磁流量计,减压阀前的电磁流量计用于测量A小区入水口处的压力和流量,减压阀后的电磁流量计用于测量A小区减压阀后的压力和流量. ...
小区给水管网调压减漏技术研究
1
2016
... 根据该片区修复漏点的资料可知,由于该片区管网建立的年代较早,至今已连续运行近20年,管网老化较严重,漏点多,漏失水量大,背景漏损较大. 在第1周采用夜间最小流量法[22 ] 估计A小区漏损率,计算得到A小区漏损率高达38.2%,亟须对A小区进行压力管理. ...
小区给水管网调压减漏技术研究
1
2016
... 根据该片区修复漏点的资料可知,由于该片区管网建立的年代较早,至今已连续运行近20年,管网老化较严重,漏点多,漏失水量大,背景漏损较大. 在第1周采用夜间最小流量法[22 ] 估计A小区漏损率,计算得到A小区漏损率高达38.2%,亟须对A小区进行压力管理. ...
基于听觉显著图的长输管道漏失检测算法
1
2020
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
基于听觉显著图的长输管道漏失检测算法
1
2020
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
1
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
1
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
1
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
1
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
Simulation of transient flow in viscoelastic pipe networks
1
2020
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
城镇供水管网漏损原因及应对措施
1
2021
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
城镇供水管网漏损原因及应对措施
1
2021
... 城市供水管网为城市居民输送日常生活中不可或缺的用水,是城市生命线的重要组成部分之一. 据统计[1 ] 可知,我国各个城市供水管网漏损率平均值为15.7%,每年约有相当于太湖总水量的优质出厂水在配水过程中漏损, 加剧水资源欠缺的问题. 2017年全国新增供水管道中塑料管道占比为41.95%[2 -3 ] ,远超其他材质供水管道,供水管网中绝大部分漏损由塑料管道破损引起[4 -5 ] . 控制与降低城市供水塑料管道漏损率是解决水资源欠缺问题的有效途径. ...
实测方法评估压力管理对漏失水量降低程度的适用性
1
2019
... 压力管理相比于其他控漏降漏技术更经济有效,具有控制背景漏损的功能[6 ] ,受到研究人员的青睐. 在压力管理的应用过程中,研究人员逐渐意识到,分时段调压的传统压力管理方式对供水管网压力控制过于粗糙,不仅无法完全发挥压力管理控漏降漏的潜能,而且用水高峰时段的管道压力可能无法满足部分用户用水压力的需求. 为了改进传统的压力管理方法,本文模仿经济学领域的相机抉择策略[7 ] ,提出相机压力管理方法. ...
实测方法评估压力管理对漏失水量降低程度的适用性
1
2019
... 压力管理相比于其他控漏降漏技术更经济有效,具有控制背景漏损的功能[6 ] ,受到研究人员的青睐. 在压力管理的应用过程中,研究人员逐渐意识到,分时段调压的传统压力管理方式对供水管网压力控制过于粗糙,不仅无法完全发挥压力管理控漏降漏的潜能,而且用水高峰时段的管道压力可能无法满足部分用户用水压力的需求. 为了改进传统的压力管理方法,本文模仿经济学领域的相机抉择策略[7 ] ,提出相机压力管理方法. ...
论银行监管的相机抉择
2
2004
... 压力管理相比于其他控漏降漏技术更经济有效,具有控制背景漏损的功能[6 ] ,受到研究人员的青睐. 在压力管理的应用过程中,研究人员逐渐意识到,分时段调压的传统压力管理方式对供水管网压力控制过于粗糙,不仅无法完全发挥压力管理控漏降漏的潜能,而且用水高峰时段的管道压力可能无法满足部分用户用水压力的需求. 为了改进传统的压力管理方法,本文模仿经济学领域的相机抉择策略[7 ] ,提出相机压力管理方法. ...
... 李克强总理提出要“更加精准有效地实施定向调控和相机调控”[14 ] . 相机调控即相机抉择,是指政府根据市场情况和特点,灵活地采取某种或多种宏观调控措施,保证经济在合理范围内运行的方式[7 ] . 相机调控的核心为“相机”,即在一定的时间和场景下使用一种或多种最适合的调控方法,具体选用方法并非一成不变,可以根据时间和场景的不同,灵活地进行组合和变化.“精准”与“微调”是相机调控最主要的特征. ...
论银行监管的相机抉择
2
2004
... 压力管理相比于其他控漏降漏技术更经济有效,具有控制背景漏损的功能[6 ] ,受到研究人员的青睐. 在压力管理的应用过程中,研究人员逐渐意识到,分时段调压的传统压力管理方式对供水管网压力控制过于粗糙,不仅无法完全发挥压力管理控漏降漏的潜能,而且用水高峰时段的管道压力可能无法满足部分用户用水压力的需求. 为了改进传统的压力管理方法,本文模仿经济学领域的相机抉择策略[7 ] ,提出相机压力管理方法. ...
... 李克强总理提出要“更加精准有效地实施定向调控和相机调控”[14 ] . 相机调控即相机抉择,是指政府根据市场情况和特点,灵活地采取某种或多种宏观调控措施,保证经济在合理范围内运行的方式[7 ] . 相机调控的核心为“相机”,即在一定的时间和场景下使用一种或多种最适合的调控方法,具体选用方法并非一成不变,可以根据时间和场景的不同,灵活地进行组合和变化.“精准”与“微调”是相机调控最主要的特征. ...
1
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
A physically-based analytical relationship for practical prediction of leakage in longitudinally cracked pressurized pipes
1
2014
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
Numerical analysis of the transient pressure damping in a single polymeric pipe with a leak
1
2018
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
Experimental evidence of hysteresis in the head-discharge relationship for a leak in a polyethylene pipe
2
2010
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
... [11 ]发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
Is the leak head-discharge relationship in polyethylene pipes a bijective function?
1
2012
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
3
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
... [13 ]通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
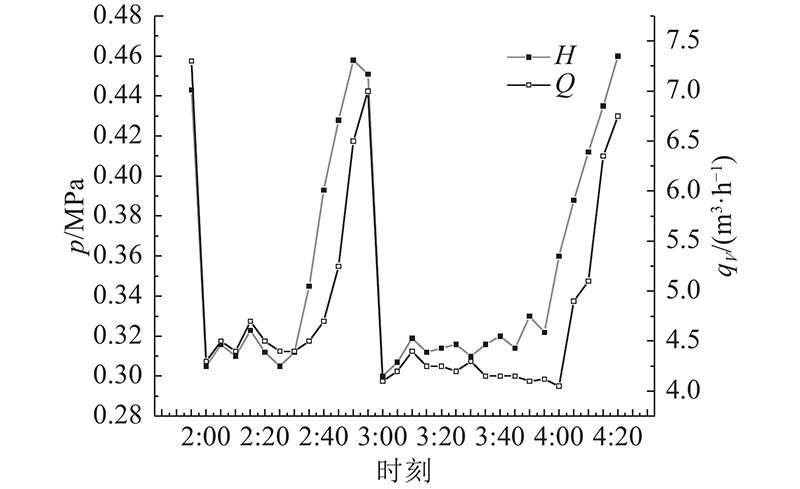
... 从表2 可知,在相机压力管理方案中,夜间2:00—4:20这个时段的调压策略经历了2次先迅速降低管道内压力,再缓慢升压的过程,这与降-复压调压策略[13 ] 相同,解决了降、复压的时段划分与压力设定值不确定的问题. 现场实验结果显示,第3周中每天2:00—4:20时段的p 与q V p -t 折线与q V t 折线如图4 所示. ...
3
... 为了模拟供水管道物理漏失流量(本文流量均指体积流量)与管道压力之间的关系,国内外常用模型主要有孔口出流模型、FAVAD模型[8 -9 ] 、指数模型[10 ] . 这3种漏失模型均难以解释供水塑料管道物理漏失流量会随着管道压力变化而产生滞后变化这一特性[11 -13 ] ,导致减压阀后最优压力设定值的模拟误差较大,制约相机的压力管理效果. Ferrante等[11 ] 发现,管道材质对管道压力p 和漏失流量q V q V p 曲线所在平面上,升压时段q V p 曲线和降压时段q V p 曲线并非2条重合的曲线,升压时段q V p 曲线在降压时段q V p 曲线的上方,因此猜想q V p 关系的滞后行为是由管道材料的黏弹性引起的. 在之后的研究中,Ferrante等[12 ] 采用聚乙烯(polyethylene,PE)管道验证黏弹性对q V p 关系的影响,证明在PE管道中p 、q V q V p 关系滞后行为这一猜想. 郑成志[13 ] 通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
... [13 ]通过实验证明PE管道黏弹性导致漏口面积变化滞后于压力变化,引起q V p 关系滞后行为,打破了压力管理中一味追求降低压力的传统观念,提出降-复压调压策略. ...
... 从表2 可知,在相机压力管理方案中,夜间2:00—4:20这个时段的调压策略经历了2次先迅速降低管道内压力,再缓慢升压的过程,这与降-复压调压策略[13 ] 相同,解决了降、复压的时段划分与压力设定值不确定的问题. 现场实验结果显示,第3周中每天2:00—4:20时段的p 与q V p -t 折线与q V t 折线如图4 所示. ...
习近平宏观调控重要论述的科学体系及原创性贡献
1
2020
... 李克强总理提出要“更加精准有效地实施定向调控和相机调控”[14 ] . 相机调控即相机抉择,是指政府根据市场情况和特点,灵活地采取某种或多种宏观调控措施,保证经济在合理范围内运行的方式[7 ] . 相机调控的核心为“相机”,即在一定的时间和场景下使用一种或多种最适合的调控方法,具体选用方法并非一成不变,可以根据时间和场景的不同,灵活地进行组合和变化.“精准”与“微调”是相机调控最主要的特征. ...
习近平宏观调控重要论述的科学体系及原创性贡献
1
2020
... 李克强总理提出要“更加精准有效地实施定向调控和相机调控”[14 ] . 相机调控即相机抉择,是指政府根据市场情况和特点,灵活地采取某种或多种宏观调控措施,保证经济在合理范围内运行的方式[7 ] . 相机调控的核心为“相机”,即在一定的时间和场景下使用一种或多种最适合的调控方法,具体选用方法并非一成不变,可以根据时间和场景的不同,灵活地进行组合和变化.“精准”与“微调”是相机调控最主要的特征. ...
1
... 与国民经济调节相同,压力管理可以采取的调控方法有很多. 国际水协会总结了4种使用减压阀进行压力管理的主要方法:固定出口压力、分时段调节、按流量调节和按最不利点调节[15 ] . 除此以外,压力管理可以通过安装减压罐或水泵控制装置来实现. 这些调控方法的适用范围不同,使用后对压力管理结果的影响也不同,对区域漏损控制结果有着巨大的影响,“相机”选取合适的压力管理方法极为重要. ...
埋地管线均匀腐蚀失效力学模型及随机分析
1
2010
... 引起埋设管段失效的主要原因有管道内压力、管道外部荷载及管道腐蚀等[16 ] . 由于本文的主要研究对象为管道内压力与物理漏失流量的关系,为了简化公式表达,仅考虑管道内压力对管道漏口面积变化的影响. 在管道内压力作用于管道内壁后,分别产生径向、纵向和环向应力. 径向应力非常小,与其他2种应力相比可以忽略不计;纵向应力主要存在于管段转弯的弯头处;环向应力是导致直管段破坏和漏口面积逐渐扩大的最主要原因. 考虑到供水管网中直管段占大部分,以下推导过程仅考虑环向应力[17 ] : ...
埋地管线均匀腐蚀失效力学模型及随机分析
1
2010
... 引起埋设管段失效的主要原因有管道内压力、管道外部荷载及管道腐蚀等[16 ] . 由于本文的主要研究对象为管道内压力与物理漏失流量的关系,为了简化公式表达,仅考虑管道内压力对管道漏口面积变化的影响. 在管道内压力作用于管道内壁后,分别产生径向、纵向和环向应力. 径向应力非常小,与其他2种应力相比可以忽略不计;纵向应力主要存在于管段转弯的弯头处;环向应力是导致直管段破坏和漏口面积逐渐扩大的最主要原因. 考虑到供水管网中直管段占大部分,以下推导过程仅考虑环向应力[17 ] : ...
1
... 引起埋设管段失效的主要原因有管道内压力、管道外部荷载及管道腐蚀等[16 ] . 由于本文的主要研究对象为管道内压力与物理漏失流量的关系,为了简化公式表达,仅考虑管道内压力对管道漏口面积变化的影响. 在管道内压力作用于管道内壁后,分别产生径向、纵向和环向应力. 径向应力非常小,与其他2种应力相比可以忽略不计;纵向应力主要存在于管段转弯的弯头处;环向应力是导致直管段破坏和漏口面积逐渐扩大的最主要原因. 考虑到供水管网中直管段占大部分,以下推导过程仅考虑环向应力[17 ] : ...
1
... 标准线性体模型是常用的蠕变函数[18 ] . 在塑料管道黏弹性模型中,标准线性体模型表达式的形式简单,能够很好地描述塑料材料黏弹性: ...
1
... 标准线性体模型是常用的蠕变函数[18 ] . 在塑料管道黏弹性模型中,标准线性体模型表达式的形式简单,能够很好地描述塑料材料黏弹性: ...
PE100燃气管材的非线性蠕变行为及其本构模型研究
1
2021
... 李茂东等[19 ] 在常温条件下对DN100的PE管道进行蠕变测试,发现在应力不超过5.4 MPa的情况下,蠕变柔量不受受力的影响,为线黏弹性行为. 在城市供水管网的实际运行过程中,绝大部分管道的运行压力不会超过1.0 MPa,远小于线性黏弹性行为和非线性黏弹性行为的界限值5.4 MPa,因此认为供水塑料管道表现为线黏弹性行为. 对于线性黏弹性行为,可以使用Boltzmann叠加原理量化历史应力对应变的影响[20 ] : ...
PE100燃气管材的非线性蠕变行为及其本构模型研究
1
2021
... 李茂东等[19 ] 在常温条件下对DN100的PE管道进行蠕变测试,发现在应力不超过5.4 MPa的情况下,蠕变柔量不受受力的影响,为线黏弹性行为. 在城市供水管网的实际运行过程中,绝大部分管道的运行压力不会超过1.0 MPa,远小于线性黏弹性行为和非线性黏弹性行为的界限值5.4 MPa,因此认为供水塑料管道表现为线黏弹性行为. 对于线性黏弹性行为,可以使用Boltzmann叠加原理量化历史应力对应变的影响[20 ] : ...
索膜结构的蠕变性能研究
1
2006
... 李茂东等[19 ] 在常温条件下对DN100的PE管道进行蠕变测试,发现在应力不超过5.4 MPa的情况下,蠕变柔量不受受力的影响,为线黏弹性行为. 在城市供水管网的实际运行过程中,绝大部分管道的运行压力不会超过1.0 MPa,远小于线性黏弹性行为和非线性黏弹性行为的界限值5.4 MPa,因此认为供水塑料管道表现为线黏弹性行为. 对于线性黏弹性行为,可以使用Boltzmann叠加原理量化历史应力对应变的影响[20 ] : ...