自Phillips[1]首次提出利用离心力模拟超重力以来,人类利用超重力不断探索自然界中的物质运动规律,离心试验技术广泛应用于岩土工程、材料制造、海洋科学等领域[2-4]的研究中. 随着离心机技术的高速发展,离心机的应用从准静态试验[5-6]逐渐发展到动态试验[7-8]中. 与地球重力相比,离心超重力不仅具有时空缩尺的特性,还能够增强固液间由于密度差产生的浮力效应[9]. 在大型岩土体受水力侵蚀后土颗粒细观运动描述[10]、深海矿物水力运输系统[11]研究、潜射导弹发射试验[12]设计、悬浮颗粒长历时沉降[13]机理研究、高性能合金材料凝固制备[14]等涉及固液两相物质的研究领域有很好的应用前景. 与理想超重力场相比,离心超重力场是离心机高速旋转产生的模拟超重力场,内部的固液两相间相对运动存在一定的差异. 为了保证试验的适用性和精度,揭示其差异的影响机理显得尤为重要.
上述研究主要针对物质在空气中的运动,未考虑流体的其他作用力,大多忽略了吊篮摆动遗留角的影响. 本文基于旋转非惯性系,提出考虑吊篮摆动遗留角的试验超重力势,严格推导了模型箱中流体压力及物体所受浮力的表达式,考虑地球重力和流体作用的外力作用,建立离心模型试验中静止流体内物体的运动控制方程. 以球形固体为例,揭示了小球的运动规律.
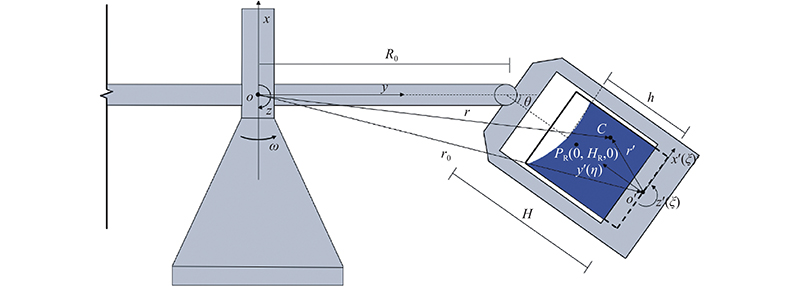
1. 试验模型与遗留角
图1给出采用双吊篮对称臂结构形式的离心机示意图,吊篮通过销轴与转臂联接,带动模型箱高速旋转营造超重力环境. 图中,R0为转臂长度,H为吊篮底板以上高度. 为了描述方便,以离心机主轴和转臂的交点为原点o,以天地向为x轴,转臂方向为y轴,建立随离心机旋转的右手笛卡尔坐标系o-xyz. 假定吊篮和模型箱均具有2个对称面,且对称面重合. 以吊篮底板面中心为原点o',如图1所示,建立笛卡尔坐标系o'-x'y'z'坐标系,o'-x'y'和o'-y'z'为吊篮的对称面. 坐标轴y'过转臂端点,与转臂的夹角记为遗留角θ (
图 1
为了简化起见,给定如下假设. 1)忽略转臂和吊篮变形,即假定转臂和吊篮是刚性的. 2)忽略吊篮和转臂间的转动摩擦. 3)运动物体为刚体,忽略刚体转动. 4)忽略固液间空泡的作用.
从图1可以推出坐标系o-xyz和o'-x'y'z'间的几何变换关系:
记由吊篮、模型箱和模型构成的系统的质心在坐标系o'-x'y'z'中的坐标为(0,HG,0). 当考虑地球重力作用时,自由液面不再关于坐标面o'-y'z'对称,这种不对称导致吊篮、模型箱和模型系统的重心不再位于y'轴上. 考虑到离心加速度远大于地球重力加速度,流体质量远小于吊篮质量,本文计算时忽略自由液面不对称性的影响,则可以由下式确定:
由于离心加速度场具有非均匀性,离心模型试验时通常在模型中选取一点作为参考点,以该点的离心加速度作为试验离心加速度. 在y'轴上,选取距离o'为HR的点PR作为参考点. 利用参考点,式(4)可以改写为
式中:
其中:
无量纲函数
式中:
一般来说,
式(5)采用如下迭代格式迭代求解:
从式(5)、(8)可得如下结论. 1)当
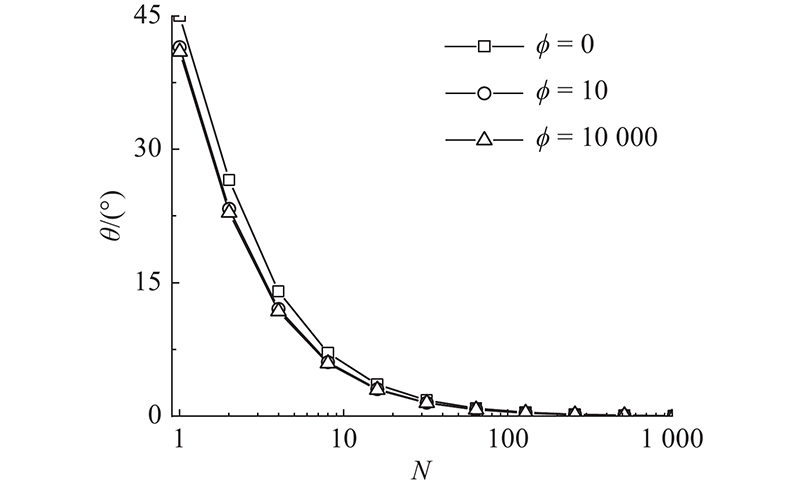
图2给出当
图 2
图 2
Fig.2
Change of θ with N for
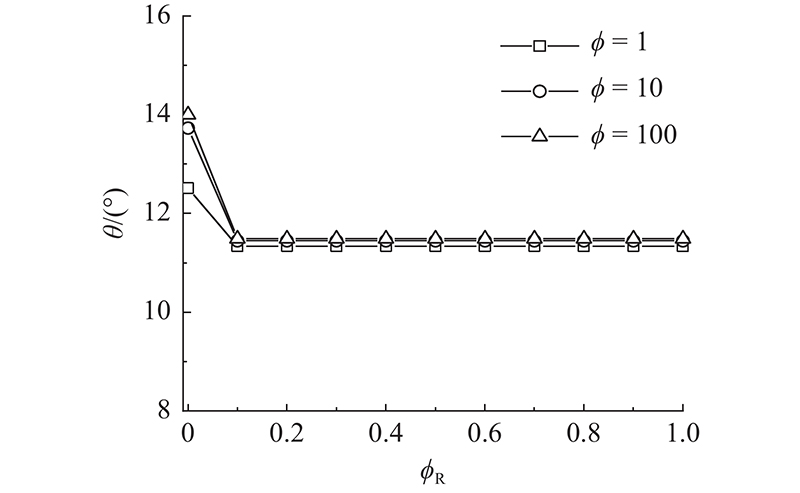
图3给出当N=5,
图 3
图 3
当N = 5,
Fig.3
Change of θ with
2. 非惯性系浮力作用
在超重力试验过程中,模型同时承受地球常重力场和离心超重力场的作用,流体内部压力和流体中物体承受的浮力有别于地球重力场和理想超重力场. 为了方便起见,用试验超重力场来替代地球常重力场和离心超重力场共同作用形成的超重力场.
2.1. 静止流体压力
旋转坐标系o-xyz中任意空间点的试验超重力加速度为
上述试验超重力场存在重力势,势函数G可以表示为
式中:
将式(1)、(13)改写为模型箱坐标系中的试验超重力势函数:
流体压力
式中:
利用流体液面压力为0,可以确定式(15)中的常数c:
将式(16)代入式(14),再代入式(15)可得
式中:
从式(13)可以看出,试验重力场中相对静止流体的等压面表现为中心轴为x轴、母线为抛物线的椭圆抛物面的一部分,流体等压面与水平面的交线为一段圆弧,与过离心机主轴和转臂形成竖直面的交线为抛物线. 为了定量反映模型箱中的流体压力分布与理想超重力场中存在的差异,令N0= 1,定义变量:
式中:
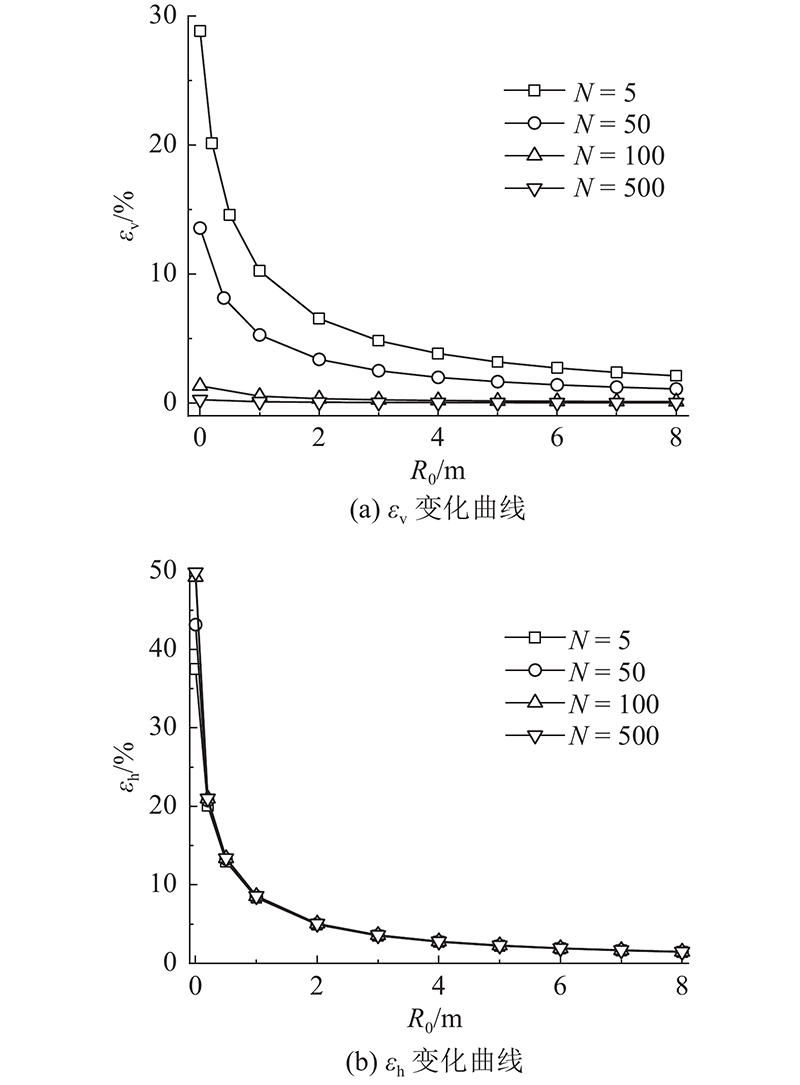
图4给出在H = 1.5 m,HR= 0.5 m,h = a = b = 1 m,N不同的情况下,静止流体自由液面的εv、εh随R0的变化曲线,可得如下结论. 1)地球重力作用下的自由液面在竖直方向上会发生明显倾斜,呈现随着N和R0增大(θ减小),倾斜程度减小的趋势. 2)随着R0的增大(θ减小),自由液面形态在水平方向越来越接近于理想超重力,当R0 ≥ 0.5 m时,N的不同(θ变化)不会引起自由液面水平方向的明显改变.
图 4
2.2. 流体浮力
假设静止流体中存在体积为V、质量为m的刚性物体,排开流体的质量为
物体所受的浮力
利用式(12)、(15)、(16),式(23)可以化简为
类似可得浮力沿y和z轴的分量
从式(24)、(25)、(26)可以看出,离心超重力引起的浮力为向心力,与物体质心位置有关,存在非均匀性. 当
利用坐标变换关系,可得坐标系o-x'y'z'中物体的浮力分量,
从式(27)~(29)可以看出,物体所受浮力可以分解为以下2个部分. 1)地球常重力和理想超重力引起与位置无关(但与参考点选取有关)的常量部分. 2)离心超重力非均匀性引起的与随动坐标x'y'z'线性相关的部分.
3. 运动控制方程及求解
由于超重力离心试验是在吊篮中完成的,通过试验观测的物质运动为以吊篮为参考系的相对运动. 建立并求解吊篮坐标系中的物体运动控制方程. 重点关注离心超重力对流体中物体运动规律的影响,为了简洁起见,假定物体的几何中心和质心重合.
3.1. 控制方程
根据文献[23]可知,非惯性系o'-x'y'z'中的物体运动控制方程可以写为
式中:r0和r' 分别为o到o'、o'到物体质心的位矢,F为外力.
将式(30)在o'-x'y'z'中展开,可得流体中物体的运动控制方程:
式中:
离心超重力环境下流体中物体承受的外荷载包括地球重力
式中:
式中:D为球型固体的直径,
当物体在流体中变速运动时,流体惯性反作用于物体一个附加质量力
将式(27)~(29)和(35)、(37)代入式(34),再代入式(31)~(33),并表示为矩阵形式,不考虑其他力
式中:
其中,
定义无量纲量:
式(38)可以改写成如下的无量纲形式:
式中:
表 1 不同Re下CD的表达式
Tab.1
| Re | CD的表达式 |
| Re < 0.01 | |
| 0.01< Re ≤20 | |
| 20 ≤ Re ≤ 260 | |
| 260 ≤ Re ≤ 1500 | |
| 1.5×103<Re≤1.2×104 | |
| 1.2×104<Re≤4.4×104 | |
| 4.4×104<Re≤3.38×105 | |
| 3.38×105<Re≤4×105 | |
| 4×105<Re≤106 | |
| Re > 10 6 | |
将式(39)~(41)代入式(36),利用定义的无量纲数,将Re表示为
当
3.2. 数值求解与验证
式(44)是非线性常微分方程,很难得到解析解. 采取数值求解方法,采用4阶-5阶Runge-Kutta算法进行求解. 为了描述方便,记无量纲位置矢量
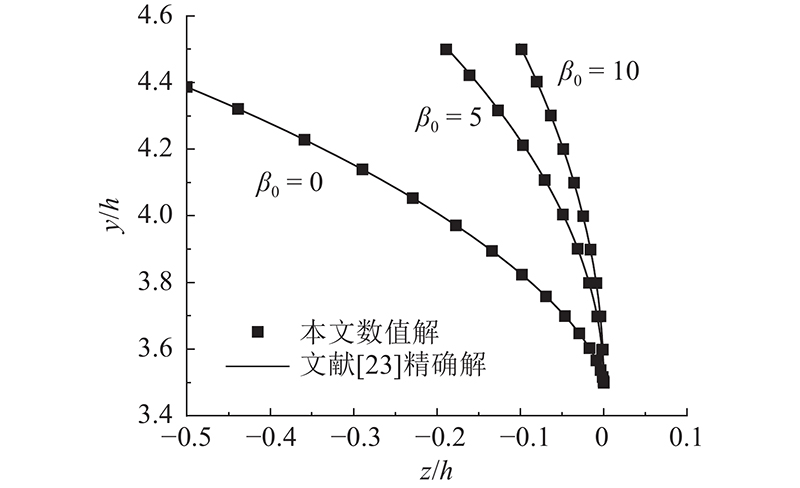
为了验证数值解的正确性,令ε= 0,即忽略流体作用. 此时,式(44)退化为真空中物体的运动控制方程,与文献[23]的情况相同,但后者没有考虑遗留角θ的影响. 图5给出在坐标系
图 5
图 5
N = 10时,不同
Fig.5
Solid falling trajectory with different
式中:
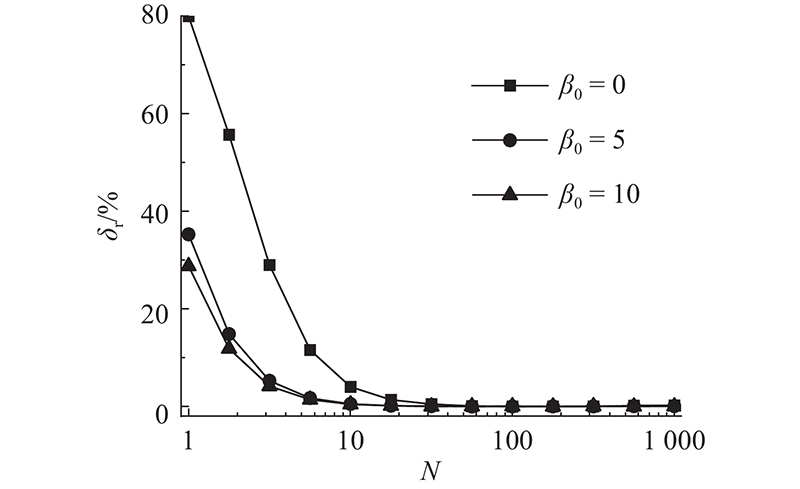
图6给出当
图 6
图 6
不同
Fig.6
Change of
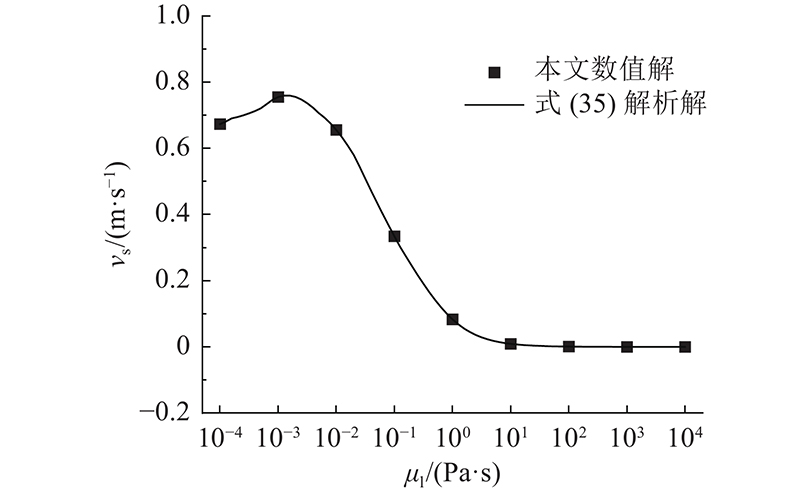
令ω = 0,即忽略非惯性系的作用. 式(44)退化为常重力下流体中自由下落物体运动控制方程. Brown等[28]给出流体中自由下落颗粒的极限沉降速度
式中:ρ为物体密度. 图7给出当D = 10−2 m,
图 7
图 7 沉降速度随流体黏度的变化曲线
Fig.7 Change of sedimentation velocity with viscosity coefficient
4. 流体中的物体运动
影响离心超重力环境下流体中物体运动的因素有很多,为了简化起见,令
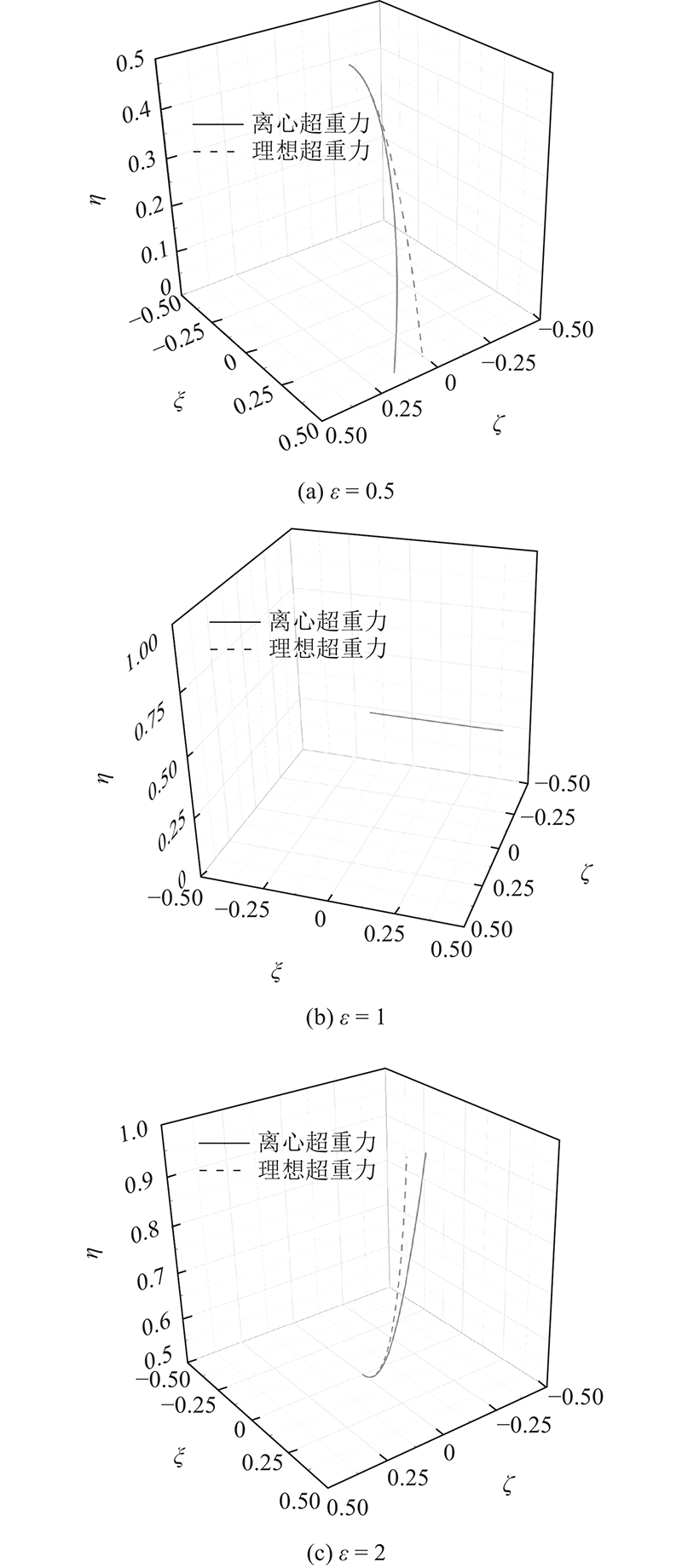
图8给出当ε = 0.5、1、2,
图 8
图 8
Fig.8
Sphere trajectory for
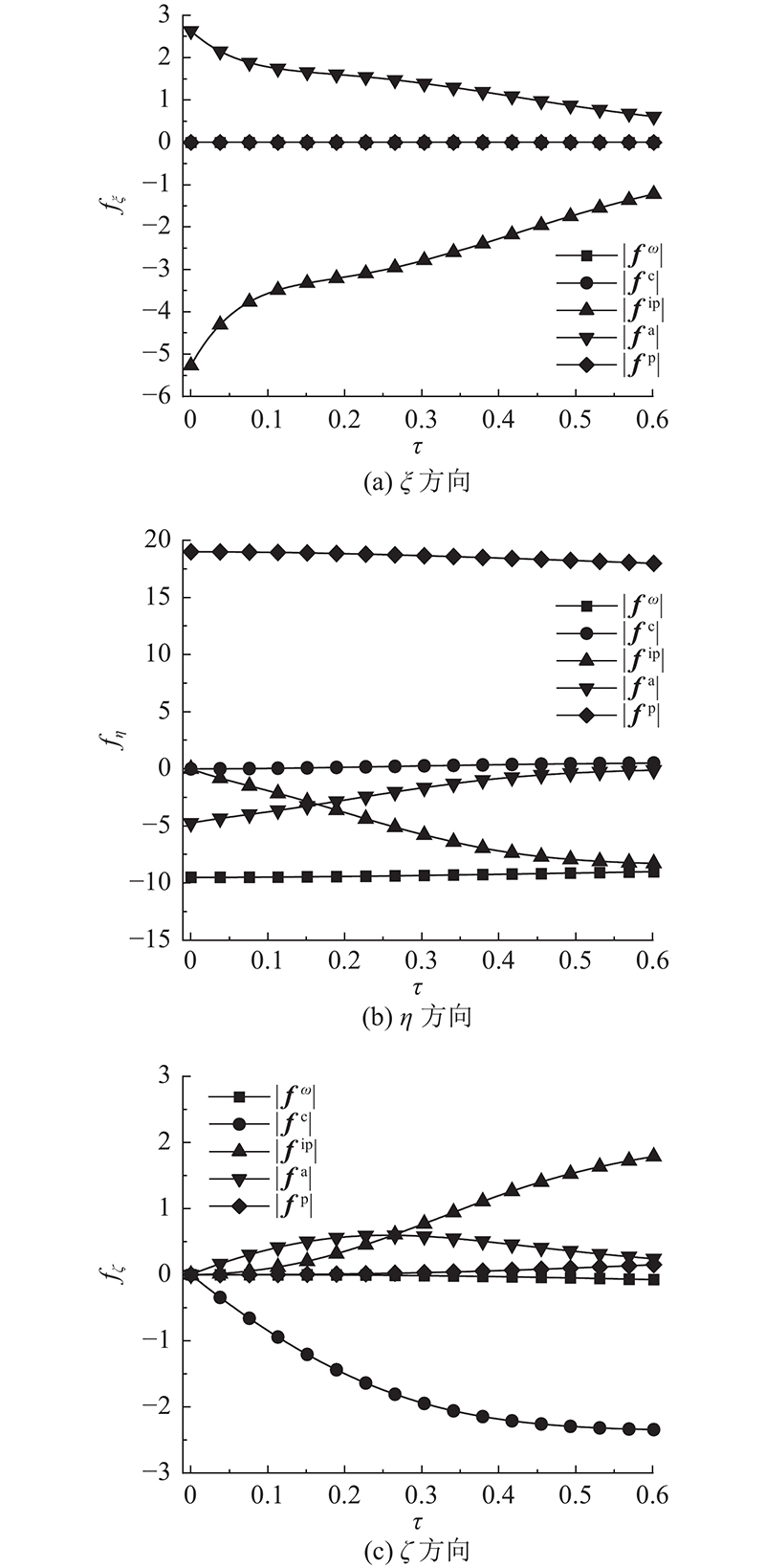
为了反映圆球在运移过程中受力的相对大小,根据式(43)定义:
图9给出当ε= 2,
图 9
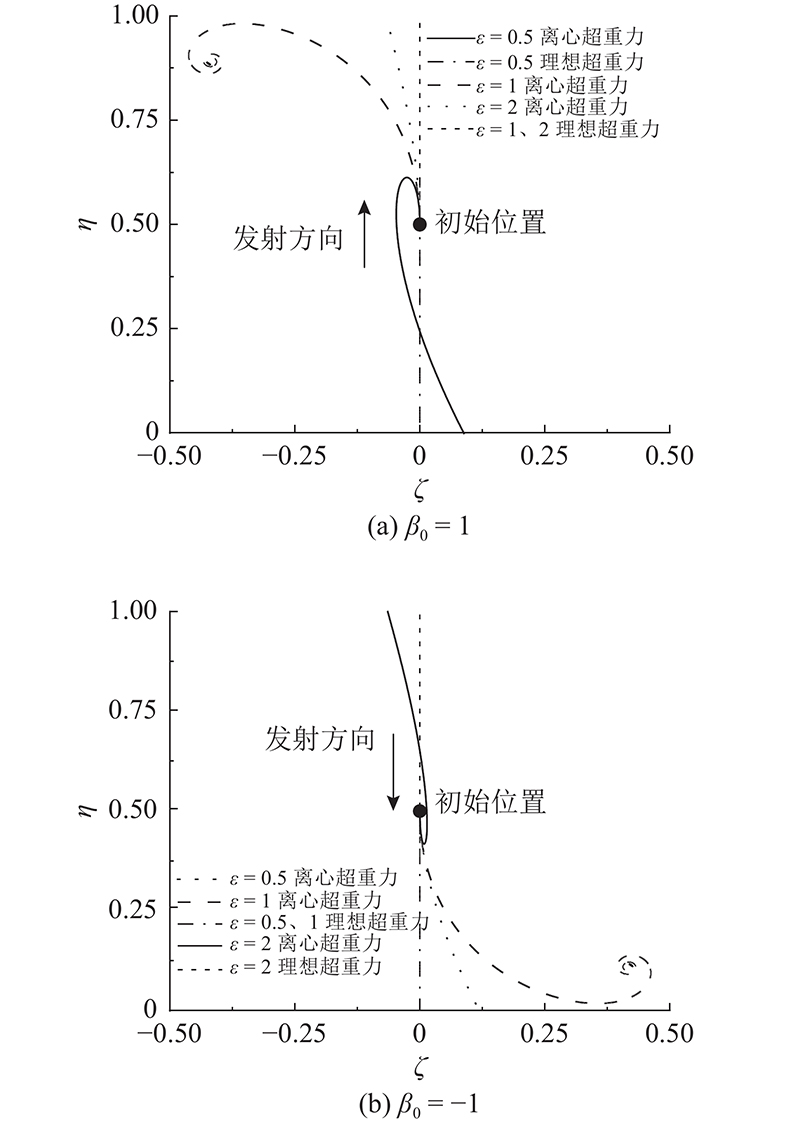
图10给出当ε= 0.5、1、2,
图 10
图 10
Fig.10
Sphere trajectory for
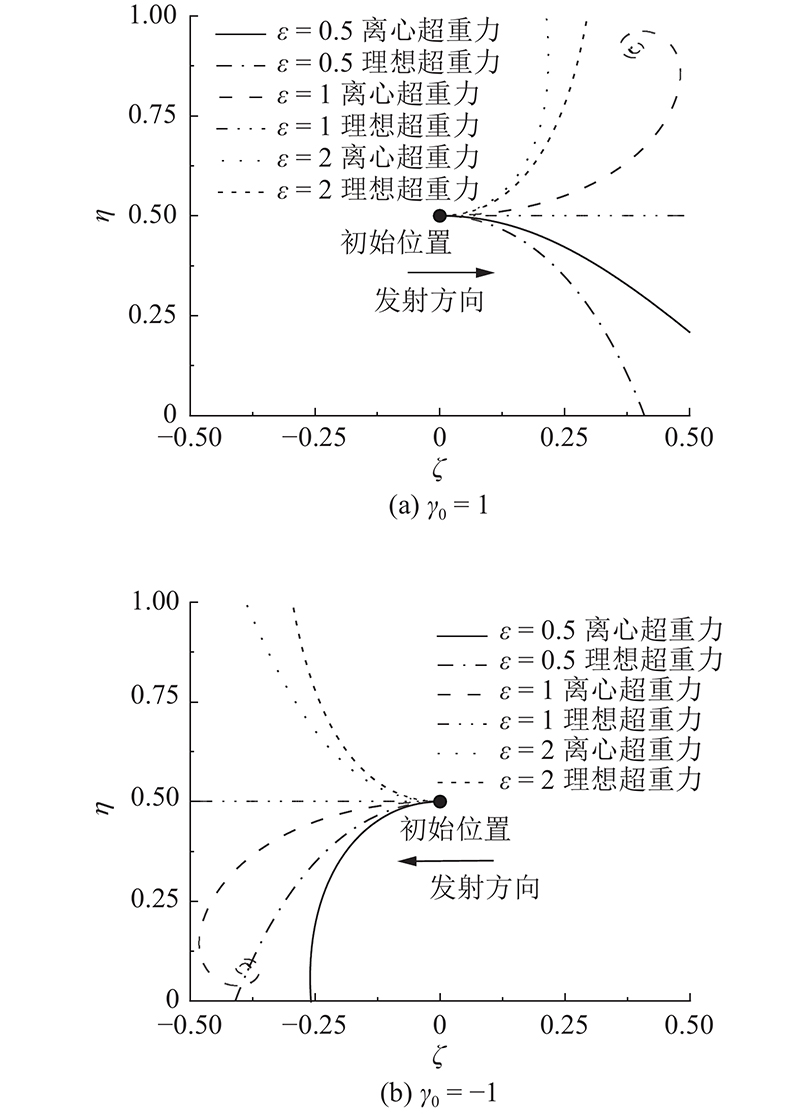
图11分别给出当ε=0.5、1、2,
图 11
图 11
Fig.11
Sphere trajectory for
5. 结 论
(1)当离心加速度较大时,吊篮摆动遗留角接近为0,可以忽略不计.
(2)离心模型试验中的试验超重力等势面和模型箱中静止流体的等压面是以离心机主轴为轴线的旋转抛物面,随着离心加速度的增大,等势面和等压面形态受地球重力的影响而逐渐减小,趋于圆柱面. 物体在流体中所受的浮力具有向心性和非均匀性.
(3)在离心模型试验中,流体内圆球在不同方向受各作用力的影响有较大的差异,沿离心机转臂方向和切向运动时所受的科氏力影响不可忽略,不会产生天地向的运动.
本文只针对简单形状的物体运动规律进行分析,忽略了自身旋转. 在未来工作中,将重点针对物体运动的影响因素进行分析,定量反映非惯性系效应的影响,研究复杂形状的物体运动,为有关试验的开展提供指导依据.
参考文献
Seismic response of retaining walls with cohesive backfill: centrifuge model studies
[J].DOI:10.1016/j.soildyn.2016.09.013 [本文引用: 1]
A model for the viscosity of rhyolite as a function of H2O-content and pressure: a calibration based on centrifuge piston cylinder experiments
[J].
Wave-induced liquefaction of beds of sand in a centrifuge
[J].DOI:10.1680/geot.1999.49.5.621 [本文引用: 1]
含水率对非饱和土质覆盖层塌陷模式的影响
[J].
Effect of water content on failure modes of evapotranspiration landfill cover
[J].
竖向荷载对黏土地基中单桩水平受荷性能的影响
[J].
Effect of vertical load on lateral behavior of single pile in clay
[J].
Effects of gravity level on bubble formation and rise in low-viscosity liquids
[J].DOI:10.1103/PhysRevE.91.053009 [本文引用: 1]
爆炸离心模型试验研究进展与展望
[J].DOI:10.16285/j.rsm.2011.09.004 [本文引用: 1]
Development and prospect for centrifugal blasting modeling
[J].DOI:10.16285/j.rsm.2011.09.004 [本文引用: 1]
离心超重力实验: 探索多相介质演变的革命性手段
[J].
Centrifugal hypergravity experiment: revolutionary means to explore the evolution of multiphase media
[J].
Mathematical modelling of shallow flows: closure models drawn from grain-scale mechanics of sediment transport and flow hydrodynamics
[J].
深海采矿提升系统研究综述
[J].DOI:10.3901/JME.2021.20.232 [本文引用: 1]
Summary of research on lifting system of deep sea mining
[J].DOI:10.3901/JME.2021.20.232 [本文引用: 1]
全尺寸模型弹水下发射试验的有关问题
[J].DOI:10.3969/j.issn.1004-7182.2000.04.001 [本文引用: 1]
Problems on the underwater launching test of full scale model missile
[J].DOI:10.3969/j.issn.1004-7182.2000.04.001 [本文引用: 1]
Influences of super-gravity field on aluminum grain refining
[J].
Uniform representation of the gravitational potential and its derivatives
[J].
利用地球重力位模型计算重力和重力梯度
[J].
Computing earth’s gravity and gravity gradient using geopotential model
[J].
Gravitational field of the earth
[J].DOI:10.1016/S0076-6895(07)41003-4 [本文引用: 1]
土工离心模型的试验原理
[J].
Principle of the geotechnical centrifuge model test
[J].
Physical meanings of kinematics in centrifuge modeling technique
[J].
离心模型试验物质运动非惯性系效应
[J].
Non-inertial effects on matter motion in centrifugal model test
[J].
离心模拟超重力场下的雨滴运动轨迹分析
[J].
Analysis of raindrop trajectory in centrifuge-simulated hypergravity field
[J].
Mathematical and physical modelling of rainfall in centrifuge
[J].DOI:10.1680/jphmg.14.00023 [本文引用: 1]
That's a drag: the effects of drag forces
[J].
Sphere drag and settling velocity revisited
[J].DOI:10.1061/(ASCE)0733-9372(2003)129:3(222) [本文引用: 1]