浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(1): 63-70 doi: 10.3785/j.issn.1008-973X.2023.01.007

机械与能源工程

太阳电池工程简化模型参数确定及模型应用

虞效益,, 饶大千, 胡长兴, 徐美娟,

1. 浙大宁波理工学院 机电与能源工程学院，浙江 宁波 315100

2. 浙江大学 制冷与低温研究所，浙江 杭州 310027

3. 浙江大学宁波研究院，浙江 宁波 315100

Parameter estimation of solar cell engineering model and model application

YU Xiao-yi,, RAO Da-qian, HU Chang-xing, XU Mei-juan,

1. School of Mechatronics and Energy Engineering, NingboTech University, Ningbo 315100, China

2. Institute of Refrigeration and Cryogenics, Zhejiang University, Hangzhou 310027, China

3. Ningbo Research Institute, Zhejiang University, Ningbo 315100, China

通讯作者: 徐美娟，女，副教授，博士. orcid.org/0000-0003-3864-9203. E-mail： 03nyhjyxy@zju.edu.cn

收稿日期: 2022-02-5  

基金资助: 国家自然科学基金资助项目（51406180）；宁波市自然科学基金资助项目（202003N4312）

Received: 2022-02-5  

Fund supported: 国家自然科学基金资助项目（51406180）；宁波市自然科学基金资助项目（202003N4312）

作者简介 About authors

虞效益（1984—），男，副教授，博士，从事太阳能利用的研究.orcid.org/0000-0003-1404-7216.E-mail：yuxiaoyi@nbt.edu.cn , E-mail：yuxiaoyi@nbt.edu.cn

摘要

针对现有文献中太阳电池工程简化模型的模型系数值不适用于当今光伏组件的问题，提出简单的仅需利用光伏组件出厂数据的模型系数确定方法.系数b通过拟合25 ℃下不同辐照度对应的开路电压数据得到，系数a和c分别取短路电流和开路电压的温度系数. 不同厂家生产的光伏组件系数b不同，同一厂家生产的不同型号的光伏组件系数b可以取相同值.综合改进后的太阳电池工程简化模型、分段函数形式的太阳电池温度模型和考虑安装条件的入射光强度模型，开展光伏组件电气输出特性的动态仿真. 当组件倾角小于最佳倾角时，角度变化对最大输出功率的影响很小；当倾角大于最佳倾角时，角度变化对最大输出功率的影响较大，影响程度随着角度的增大而增大.

关键词： 太阳电池工程简化模型 ; 模型参数估计 ; 电池温度模型 ; 辐照度模型

Abstract

A simple method for estimating model parameters that only uses the available information in the manufacturer datasheet was proposed aiming at the problem that the parameter values of the simplified solar cell engineering model in the existing literature were not suitable for current PV modules. The parameter b was obtained by fitting the open-circuit voltage data corresponding to different irradiance at 25 ℃. The parameters a and c were treated equal to the temperature coefficients of the short-circuit current and the open-circuit voltage, respectively. The value of parameter b for PV modules produced by different manufacturers is different, while it can take the same value for the same manufacturer’s different type of PV modules. The electrical output characteristics of PV modules were dynamically simulated by integrating the improved solar cell engineering model, the cell temperature model in piecewise function form and the solar irradiance model considering the installation conditions of the PV module. The angle change has little effect on the maximum output power when the module inclination angle is less than the optimal one. The angle change has a great influence on the maximum output power when the inclination angle is greater than the optimum one, and the influence degree increases with the increase of the angle.

Keywords： simplified solar cell engineering model ; model parameter estimation ; cell temperature model ; irradiance model

PDF (864KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

虞效益, 饶大千, 胡长兴, 徐美娟. 太阳电池工程简化模型参数确定及模型应用. 浙江大学学报(工学版)[J], 2023, 57(1): 63-70 doi:10.3785/j.issn.1008-973X.2023.01.007

YU Xiao-yi, RAO Da-qian, HU Chang-xing, XU Mei-juan. Parameter estimation of solar cell engineering model and model application. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(1): 63-70 doi:10.3785/j.issn.1008-973X.2023.01.007

太阳能是世界公认的清洁能源，将太阳能转换成电能的光伏组件是太阳能转化利用的典型器件. 光伏组件由单体太阳电池串联封装后得到，是光伏发电系统的核心组成部分. 光伏组件的实际运行条件变化多端，使得实际性能与出厂参数的差别较大，研究光伏组件在不同工况下的电学性能对光伏系统的设计、控制、评估和优化等具有重要意义[1-2]. 建模仿真是研究这一问题的有效手段，到目前为止，研究者已开展了大量工作. Chin等[3]对太阳电池的数学模型进行了较系统而全面的综述，其中最常用的是等效电路模型. 依据未知参量个数的不同，等效电路模型包括单二极管三参数模型、单二极管四参数模型、单二极管五参数模型和双二极管七参数模型等[3-5]，其中以单二极管五参数模型的应用最广泛[2-3]. 模型参数的确定方法有利用出厂参数的解析法、I-V曲线拟合法和软计算法（如遗传算法、差分进化、粒子群优化等）[3].

工程应用强调实用性和精确性的统一，因而基于各种假设的太阳电池工程简化模型被提出[6-8]. 其中最典型的一种是通过模型参量降级法，将五参数模型降级为二参数模型，仅利用标准测试条件（STC）下的出厂参数（短路电流、开路电压、最大功率点电流和电压）计算得到模型参数值，无须进行迭代，计算简便又具有工程上足够的精度，被较多研究者采用[9-13]. 笔者发现在现有文献中存在模型公式[9, 13]和系数取值[13]错误的情况，对模型的应用产生了一定的误导和干扰. 随着光伏技术的发展，应用现有文献中的模型系数值计算当今光伏组件电气输出特性的适用性以及模型系数采用统一的固定值的合理性，均值得商榷. 本文在比对该类太阳电池工程简化模型正确形式的基础上，对应用现有文献中的模型系数值计算当今主要厂家生产的光伏组件的电气输出特性的适用性进行检验，提出简单且更加精确的确定模型系数值的方法. 结合太阳电池温度模型和入射光辐照度模型，对模型的应用进行举例分析，为光伏发电系统的研究和设计提供一定的参考.

1. 太阳电池工程简化模型

太阳电池的工程用简化数学模型[9-13]如下：

$ I = {I_{{\text{sc}}}} - {C_1}{I_{{\text{sc}}}}\left[ {\exp \left( {\frac{V}{{{C_2}{V_{{\text{oc}}}}}}} \right) - 1} \right]. $

式中：I 和Isc分别为太阳电池的输出电流和短路电流，V和Voc分别为输出电压和开路电压，C1和C2为待定系数. C1和C2的表达式如下：

$ {C_1} = \left( {1 - \frac{{{I_{\text{m}}}}}{{{I_{{\text{sc}}}}}}} \right)\exp \left( {\frac{{ - {V_{\text{m}}}}}{{{C_2}{V_{{\text{oc}}}}}}} \right), $

$ {C_2} = \left( {\frac{{{V_{\text{m}}}}}{{{V_{{\text{oc}}}}}} - 1} \right){\left[ {\ln \left( {1 - \frac{{{I_{\text{m}}}}}{{{I_{{\text{sc}}}}}}} \right)} \right]^{ - 1}}. $

式中：Im为太阳电池的最大功率点电流，Vm为最大功率点电压. 太阳电池的电学性能与电池接收到的入射光辐照度和电池自身的温度有关. 将STC下的入射光辐照度和温度，即1 000 W/m2和25 ℃，作为参考入射光辐照度和参考电池温度，则任意入射光辐照度和电池温度下的太阳电池参数可以通过下式计算：

$ {I_{{\text{sc}}}} = {I_{{\text{sc,ref}}}}\left( {\frac{{{E_{\text{c}}}}}{{{E_{{\text{ref}}}}}}} \right)\left( {1+a\Delta t} \right), $

$ {V_{{\text{oc}}}} = {V_{{\text{oc,ref}}}}\left( {1 - c\Delta t} \right)\ln\; \left( {{\rm{e}}+b\Delta E} \right), $

$ {I_{\text{m}}} = {I_{{\text{m,ref}}}}\left( {\frac{{{E_{\text{c}}}}}{{{E_{{\text{ref}}}}}}} \right)\left( {1+a\Delta t} \right), $

$ {V_{\text{m}}} = {V_{{\text{m,ref}}}}\left( {1 - c\Delta t} \right)\ln\; \left( {{\rm{e}}+b\Delta E} \right), $

$ \Delta t = {t_{\text{c}}} - {t_{{\text{ref}}}}, $

$ \Delta E = {E_{\text{c}}} - {E_{{\text{ref}}}}. $

式中：Ec和Eref分别为电池接收到的入射光辐照度和参考入射光辐照度；tc和tref分别为电池温度和参考电池温度；Isc,ref、Voc,ref、Im,ref和Vm,ref分别为STC下太阳电池的短路电流、开路电压、最大功率点电流和电压；e为自然对数底数（近似取为2.718 28）；a、b和c为待定系数. ΔE也可以表达成ΔE = E/Eref −1的形式 [9-10, 12-13]，此时系数b的取值随之改变.

最大输出功率可以由下式[14]计算：

$ {P_{\text{m}}} = {V_{\text{m}}} {I_{\text{m}}}, $

$ {P_{\text{m}}} = {P_{{\text{ref}}}}\frac{{{E_{\text{c}}}}}{{{E_{{\text{ref}}}}}}\left[ {1+d\left( {{t_{\text{c}}} - {t_{{\text{ref}}}}} \right)} \right]. $

式中：Pm为最大功率，Pref为STC条件下的最大功率，d为最大功率温度系数.

2. 模型系数确定

在已有文献中，系数a、b、c的取值分别为[9-12]：a = 0.0025 ℃−1、b = 0.000 5 m2/W（当ΔE = E/Eref —1时，b = 0.5）、c = 0.002 88 ℃−1. 比较采用这些值的模型计算结果与当今国内主要厂家生产的光伏组件的电学性能发现，两者存在较大偏差. 采用新的方式对a、b和c进行取值. 系数b利用25 ℃下不同入射光辐照度对应的开路电压数据拟合公式Voc = Voc,ref ln (e+bΔE)得到，拟合所需的数据利用图像数字化软件GetData从产品技术文档的I-V特性曲线中获取. 光伏组件的技术文档可以方便地从生产厂家网站获得. 在拟合过程中发现，对于不同厂家生产的光伏组件，系数b不同. 表1给出国内3个主要厂家生产的光伏组件的系数b以及采用新旧b计算得到的开路电压. 表中，组件型号与技术文档来源分别为：晶科(JKM395M-6RL3) ( http://www.jinkosolar.com/uploads/JKM390-410M-6RL3-(V)-F2-CN.pdf)、晶澳(JAM60S10-335/MR) ( https://www.jasolar.com//uploadfile/2020/0528/20200528103954335.pdf)、天合(TSM-DE17M(II)-445) ( https://static.trinasolar.com//sites/default/files/CN_Datasheet_DE17M(II)_20200202.PDF)；Voc,exp为开路电压实验测量值，Voc,cal为开路电压计算值；拟合优度R2 = 0.953 (晶科)，R2 = 0.930 (晶澳)，R2 = 0.972 (天合)；相对偏差RE = (Voc,cal − Voc,exp)/Voc,exp. 从表1可以看出，采用拟合b值计算得到的开路电压明显比采用文献b值准确. 对于同一厂家生产的不同型号的光伏组件，系数b可以取同一值. 表2给出厂家晶澳生产的3种不同型号光伏组件采用同一系数b的开路电压计算结果. 表中，组件的技术文档来源分别为：JAM60S10-335/MR ( https://www.jasolar.com//uploadfile/2020/0528/20200528103954335.pdf)、JAM54S30-405/MR ( https://www.jasolar.com/uploadfile/2022/0224/20220224052404814.pdf)、JAM72S20-455/MR ( https://www.jasolar.com//uploadfile/2021/0601/20210601042312362.pdf). 系数a、c直接从光伏组件的技术文档中获取，即a取短路电流温度系数，c取开路电压温度系数.

表 1   采用新旧b值的开路电压计算结果的比较

Tab.1  Comparison of calculation results of open-circuit voltage using old and new b values

厂家 Ec/(W∙m−2) Voc,exp/V b/(m2∙W−1) Voc,cal/V RE/%
文献值 拟合值 采用文献b值 采用拟合b值 采用文献b值 采用拟合b值
晶科 1000 43.53 0.0005 0.00028 43.93 43.93 0.92 0.92
晶科 800 42.98 0.0005 0.00028 42.28 43.02 −1.62 0.08
晶科 600 42.33 0.0005 0.00028 40.57 42.08 −4.15 −0.59
晶科 400 41.40 0.0005 0.00028 38.79 41.13 −6.30 −0.66
晶科 200 39.83 0.0005 0.00028 36.94 40.15 −7.26 0.81
晶澳 1000 41.35 0.0005 0.00018 41.32 41.32 −0.07 −0.07
晶澳 800 40.95 0.0005 0.00018 39.77 40.77 −2.88 −0.44
晶澳 600 40.56 0.0005 0.00018 38.16 40.21 −5.91 −0.85
晶澳 400 39.87 0.0005 0.00018 36.49 39.64 −8.48 −0.56
晶澳 200 38.78 0.0005 0.00018 34.74 39.07 −10.41 0.75
天合 1000 49.55 0.0005 0.00016 49.40 49.40 −0.30 −0.30
天合 800 49.01 0.0005 0.00016 47.55 48.81 −2.98 −0.40
天合 600 48.38 0.0005 0.00016 45.62 48.22 −5.70 −0.32
天合 400 47.76 0.0005 0.00016 43.62 47.62 −8.66 −0.29
天合 200 46.86 0.0005 0.00016 41.54 47.02 −11.36 0.34

新窗口打开| 下载CSV


表 2   同一厂家不同型号组件采用同一b值的开路电压计算结果

Tab.2  Calculation results of open-circuit voltage using same b value for different modules of same manufacturer

型号 Ec /(W∙m−2) Voc,exp /V b /(m2∙W−1) Voc,cal /V RE /%
晶澳
JAM60S10-335/MR 		1000 41.35 0.00018 41.32 −0.07
800 40.95 0.00018 40.77 −0.44
600 40.56 0.00018 40.21 −0.85
400 39.87 0.00018 39.64 −0.56
200 38.78 0.00018 39.07 0.75
晶澳
JAM54S30-405/MR 		1000 37.22 0.00018 37.23 0.03
800 36.87 0.00018 36.73 −0.37
600 36.43 0.00018 36.23 −0.55
400 35.91 0.00018 35.72 −0.53
200 34.96 0.00018 35.20 0.70
晶澳
JAM72S20-455/MR 		1000 49.50 0.00018 49.85 0.71
800 49.01 0.00018 49.19 0.36
600 48.52 0.00018 48.51 −0.02
400 47.79 0.00018 47.83 0.08
200 46.57 0.00018 47.14 1.22

新窗口打开| 下载CSV


3. 模型验证

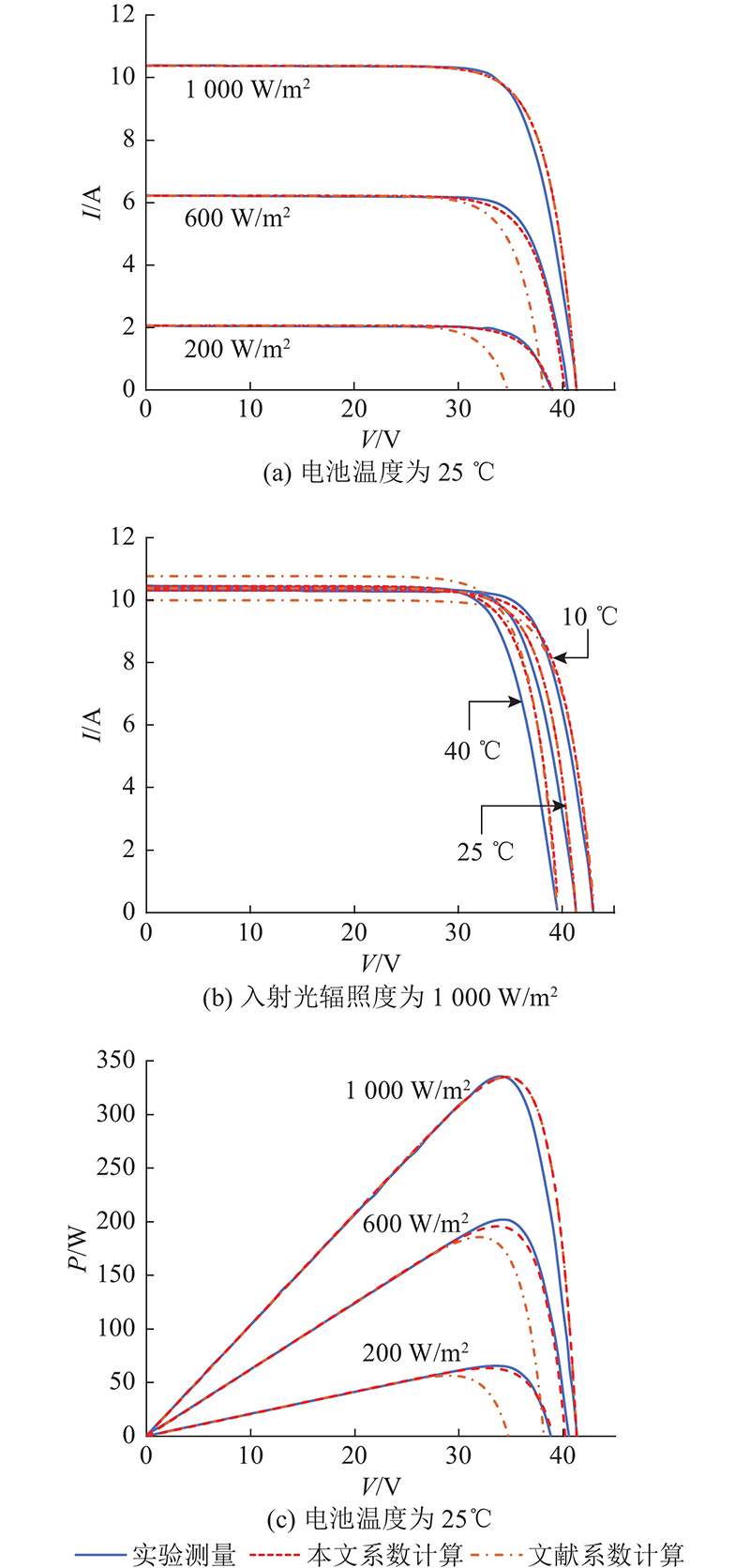
以晶澳JAM60S10-335/MR组件为例，STC下的组件参数如表3所示. 如图1所示为分别采用本文方法得到的a、b、c值（a = 0.000 44 ℃−1，b = 0.000 18 m2/W，c = 0.002 72 ℃−1）和文献[9~12]的a、b、c值计算得到的该组件的I-V曲线和P-V曲线与技术文档中给出的I-V曲线和P-V曲线（利用图像数字化软件GetData获取）的比较. 可以看出，采用本文a、b、c值计算得到的I-V曲线和P-V曲线与技术文档中的I-V曲线和P-V曲线均具有较好的吻合度，采用文献a、b、c值计算得到的I-V曲线和P-V曲线均出现了较大偏差（STC条件下的除外）. 这种偏差主要是由文献a、b取值均偏大所致的. 如图1(a)所示的曲线偏差主要是由b偏大导致Voc偏小所致，以入射光辐照度1 000 W/m2为基准，偏差随着入射光辐照度的减小而增大. 如图1(b)所示的曲线偏差主要由a偏大引起，以电池温度25 ℃为基准，Isc随着温度的升高而增大，随着温度的降低而减小. 如图1(c)所示，P-V曲线偏差由a、b偏大共同所致. 表4给出最大功率计算值与测量值的比较. 表中，Pm,exp为最大功率实验测量值（利用软件GetData从晶澳JAM60S10-335/MR技术文档中获取），Pm,cal为最大功率计算值，均方根误差为

表 3   晶澳JAM60S10-335/MR组件在STC下的参数

Tab.3  PV module (JAM60S10-335/MR) parameters at STC

参数 参数值
开路电压 41.32 V
短路电流 10.38 A
最大功率点电压 34.48 V
最大功率点电流 9.72 A
最大功率 335 W
短路电流温度系数 +0.044%/℃
开路电压温度系数 −0.272%/℃
最大功率温度系数 −0.350%/℃

新窗口打开| 下载CSV


图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   不同入射光辐照度和电池温度下的I-V和P-V曲线

Fig.1   I-V and P-V curves under different solar irradiance and cell temperatures


表 4   最大功率计算值与测量值比较（tc= 25 ℃）

Tab.4  Comparison of calculated maximum power values and measured ones (tc = 25 ℃)

Ec /(W∙m−2) Pm,exp /W 式（10）+文献[9~12]系数 式（10）+本文系数 式（11）
Pm,cal /W RE /% RMSE /% Pm,cal /W RE /% RMSE /% Pm,cal /W RE /% RMSE /%
1000 335.7 335.1 −0.18 9.07 335.1 −0.18 2.81 335 −0.21 1.11
800 269.1 258.1 −4.09 264.5 −1.71 268 −0.41
600 202.5 185.7 −8.31 195.7 −3.37 201 −0.75
400 133.7 118.4 −11.46 128.6 −3.84 134 0.20
200 65.5 56.4 −13.94 63.4 −3.22 67 2.31

新窗口打开| 下载CSV


$ {\text{RMSE}} = \sqrt {n^{-1}\sum\limits_{i = 1}^n {{{\left[ {{{\left( {{P_{{\text{m,cal}},i}} - {P_{{\text{m,exp}},i}}} \right)} \mathord{\left/ {\vphantom {{\left( {{P_{{\text{m,cal}},i}} - {P_{{\text{m,exp}},i}}} \right)} {{P_{{\text{m,exp}},i}}}}} \right. } {{P_{{\text{m,exp}},i}}}}} \right]}^2}} } . $

从表4可以看出，采用本文a、b、c值时，利用式（10）计算最大功率的精度与式（11）相当，准确度大大高于采用文献a、b、c值，特别是在入射光辐照度较低时.

4. 模型应用分析

太阳电池工程简化模型中的tc为电池的温度，较难直接测量，常见的测定温度多为环境温度. 太阳电池接收到的入射光辐照度除了与当时的光照条件有关外，还受到组件安装的地理位置、倾斜角、方位角等多种因素的影响. 建立光伏组件的电池温度模型和入射光辐照度模型，对开展光伏组件电气输出特性的动态仿真以及系统分析各种因素对电池性能的影响具有重要意义.

4.1. 太阳电池温度模型

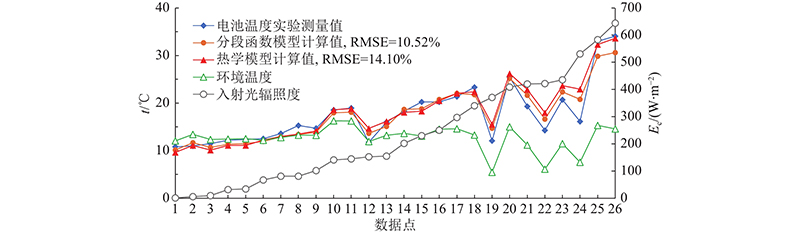
计算太阳电池温度的数学模型主要有2类：一类是考虑热传导、对流和辐射换热的热学模型，另一类是经验公式模型[1]. 热学模型的计算精度高，但较复杂；经验公式模型较简单，计算精度依公式不同而不同. 在经验公式模型中，最常用的有太阳电池标称工作温度模型（NOCT模型）和Sandia模型[1, 14-15]. NOCT模型的形式简单，只考虑环境温度和入射光辐照度对电池温度的影响. Sandia模型除了包含环境温度和入射光辐照度之外，还考虑风速以及组件的类型和安装方式等因素. Sandia模型在入射光辐照度较低时计算误差较大[1]. Coskun等[16]评估了17个计算太阳电池温度的经验公式并进行了修正，指出修正的Chenni公式总体上适用性较强. 综合考虑模型复杂度和计算精度，采用分段函数的形式计算太阳电池的温度. 当入射光辐照度较低时，采用修正的Chenni公式；反之，采用Sandia模型，

$ {t_{\rm{c}}} = \left\{ {\begin{array}{l} \begin{array}{l} {t_{\rm{a}}} - 1.936\;66 + 0.013\;8{E_{\rm{c}}}(1 + \\ \left. {0.031{t_{\rm{a}}}} \right)\left( {1 - 0.042{V_{\rm{w}}}} \right) + \\ 0.007\;882{E_{\rm{c}}} - 0.000\;013\;464\;7E_{\rm{c}}^2,\;\;{E_{\rm{c}}} \leqslant 160\;{\rm{W}}/{{\rm{m}}^2}; \end{array}\\ {{t_{\rm{a}}} + {E_{\rm{c}}} \exp \left( {{k_1} + {k_2} {V_{\rm{w}}}} \right),\;\;\;\;\;\;\;\;\;\;\;\;\quad{E_{\rm{c}}} > 160\;{\rm{W}}/{{\rm{m}}^2}}. \end{array}} \right.$

式中：ta为环境温度；Vw为风速；k1和k2为模型系数，取值与组件类型和安装方式有关[15]，如表5所示.

表 5   不同组件类型和安装方式的k1、k2取值

Tab.5  k1 and k2 coefficients for different modules and installations

组件类型 安装方式 k1 k2
玻璃/硅电池/玻璃 敞开支架 −0.35 −0.0594
玻璃/硅电池/玻璃 靠近屋顶 −2.98 −0.0471
玻璃/硅电池/聚合物层 敞开支架 −3.56 −0.0750
玻璃/硅电池/聚合物层 绝热背面 −2.81 −0.0455
聚合物层/薄膜/不锈钢 敞开支架 −3.58 −0.1130

新窗口打开| 下载CSV


图2给出分别由分段函数模型和热学模型[1]计算得到的太阳电池温度与实验测量值[17]的比较（计算时k1和k2分别取−3.56和−0.075 0）. 可以看出，分段函数模型显示了与热学模型相当的计算精度，两者的均方根误差分别为10.52%和14.10%.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   太阳电池温度计算模型的比较（风速Vw= 1 m/s）

Fig.2   Comparison of different cell temperature models (wind speed Vw = 1 m/s)


4.2. 入射光辐照度模型

光伏组件通常以一定的角度倾斜放置，表面能够接收太阳直射辐射、太阳散射辐射以及太阳辐射投射到地面上以后的反射辐射[18-19]. 太阳电池封装在组件内，太阳辐射须穿过光伏玻璃盖板和乙烯-醋酸乙烯酯共聚物（EVA）层到达电池表面. 倾斜放置的光伏组件内太阳电池表面接收到的总入射光辐照度为

$ {E_{\text{c}}} = {\tau _{{\text{g-EVA}}}}\left( {{E_{{\text{BT}}}}+{E_{{\text{DT}}}}+{E_{{\text{RT}}}}} \right) . $

式中：τg-EVA为光伏玻璃和EVA层压件的透光率，EBT、EDT和ERT分别为倾斜光伏组件表面上的太阳直射辐照度、太阳散射辐照度和反射辐照度. 太阳电池不能把所有太阳辐射都转换成电，晶硅太阳电池的光谱波长为380~1 100 nm，超出范围的辐射不起作用[20-21]，故此处的τg-EVA为该波段内的透光率. EBT、EDT和ERT可以分别由水平面上的太阳辐照度转换得到[19, 22-23]：

$ {E_{{\text{BT}}}} = {E_{\text{B}}}\frac{{\cos\; \theta }}{{\sin \;\alpha }} , $

$ {E_{{\text{DT}}}} = {E_{\text{D}}}{\cos ^2}\;\frac{\beta }{2} , $

$ {E_{{\text{RT}}}} = \rho \left( {{E_{\text{B}}}+{E_{\text{D}}}} \right)\left( {1 - {{\cos }^2}\;\frac{\beta }{2}} \right) ,$

式中：EB和ED分别为水平面上的太阳直射辐照度和散射辐照度；θ为光伏组件表面的太阳入射角；α为太阳高度角；β为光伏组件的倾斜角；ρ为地面反射率，一般情况下可取0.2 [19, 22]. 太阳入射角和高度角可以分别按下式[22-23]计算：

$ \begin{split} \mathrm{cos}\;\theta = &\left(\mathrm{sin}\;\varphi \mathrm{cos}\;\beta -\mathrm{cos}\;\varphi \mathrm{cos}\;\gamma \mathrm{sin}\;\beta \right)\mathrm{sin}\;\delta +\\ &\left(\mathrm{cos}\;\varphi \mathrm{cos}\;\beta +\mathrm{sin}\;\varphi \mathrm{cos}\;\gamma \mathrm{sin}\;\beta \right)\mathrm{cos}\;\delta \mathrm{cos}\;\omega +\\ &\mathrm{sin}\;\gamma \mathrm{sin}\;\beta \mathrm{cos}\;\delta \mathrm{sin}\;\omega \text{ }\text{，}\end{split} $

$ \sin \alpha = \sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega . $

式中：δ为太阳赤纬角，指地球中心和太阳中心连线与地球赤道平面的夹角；ω为太阳时角，指用角度表示的太阳时，每小时相当于15°；γ为光伏组件方位角，面向正南时γ = 0°，面向偏东时γ为负值，面向偏西时γ为正值；φ为当地地理纬度. 太阳赤纬角和时角可以分别按下式[19, 22- 23]计算：

$ \delta = 23.45\sin \left[ {\frac{{360^\circ (284+n)}}{{365}}} \right] , $

$ \omega = 15^\circ {{H}} . $

式中：n为一年中某一天的顺序数，1月1日为1，12月31日为365，以此类推，2月通常按28 d计算；H表示中午12时后第几小时，上午为负，下午为正.

由上述入射光辐照度的计算模型可知，在光伏组件的光伏玻璃和EVA层压件的透光率、安装的地理位置、倾斜角、方位角及日期等因素均为已知的条件下，只要拥有当天的逐时太阳辐射气象数据（水平面太阳直射辐照度和散射辐照度），就能得到太阳电池表面在该日期内不同时刻接收到的太阳辐照度.

4.3. 模型应用举例

综合上述太阳电池工程简化模型、电池温度模型和入射光辐照度计算模型，可以开展光伏组件电气输出特性的动态仿真，系统分析各种因素对输出特性的影响规律，包括气象参数（环境温度、风速、水平面太阳直射辐照度和散射辐照度）及安装参数（组件地理位置、倾斜角、方位角）. 以光伏建筑一体化（BIPV）为对象进行举例分析.

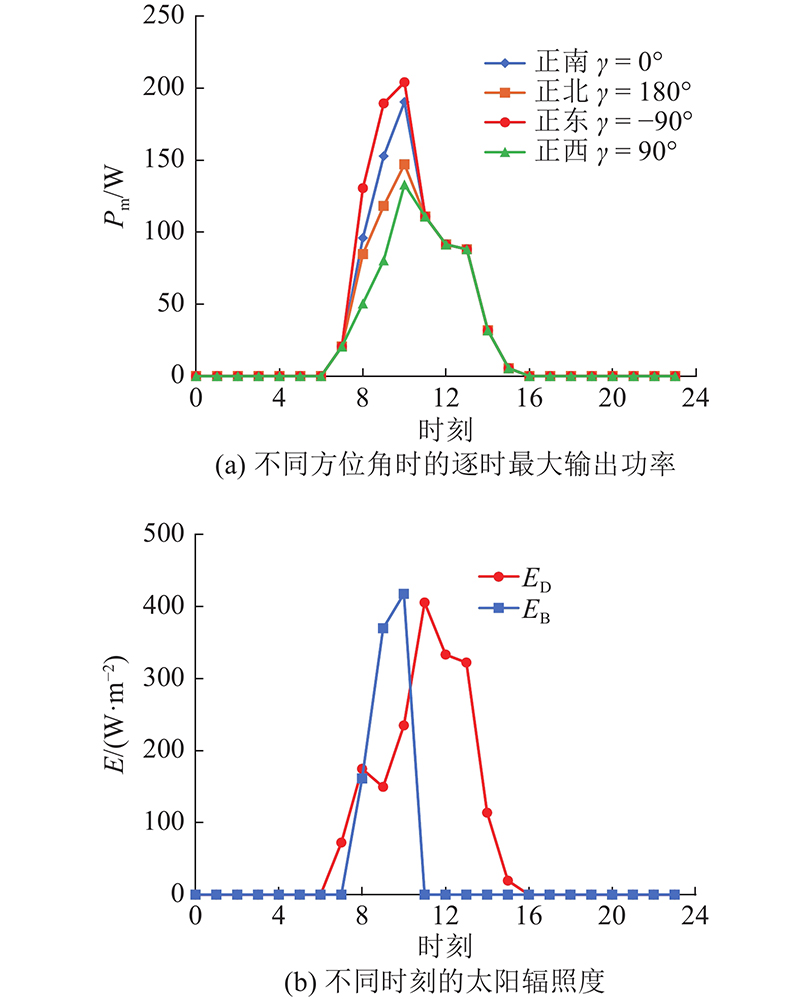
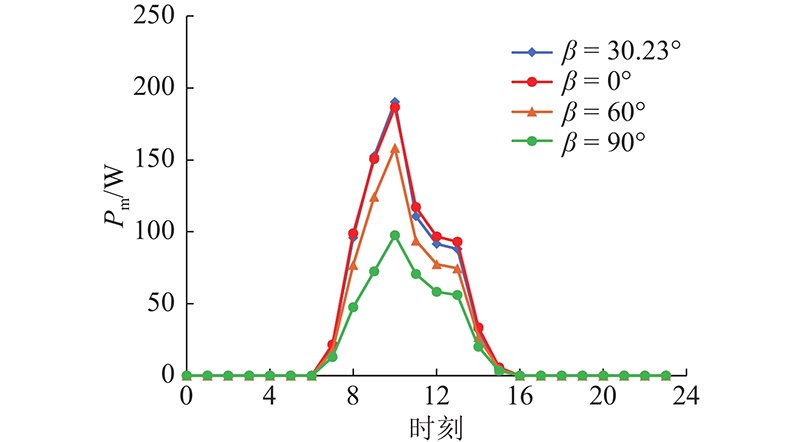
光伏组件的最佳安装方式以全年收集的太阳能最多为原则而确定. 对于固定式光伏组件，一般情况下最佳倾角β取φ，最佳方位角γ取0°（北半球），即面向正南[22]. 随着双碳目标的提出，BIPV因可以充分利用建筑屋顶、墙面、窗户等闲置面积的优势，将成为未来光伏的主流形式. 到2025年，我国BIPV可安装容量预估达到35 GW [24]. BIPV组件作为建筑物外部结构的一部分，安装方式主要是依建筑而定. 有必要分析倾角和方位角的不同对光伏组件输出特性的影响，为评估BIPV的实际发电效果提供一定的参考.

以杭州市，典型气象年4月7日，光伏组件晶澳JAM60S10-335/MR为例，图3(a)给出组件在4个不同方位角时的逐时最大输出功率（倾角均取杭州的地理纬度30.23°），计算所需的气象参数来自文献[25]，τg-EVA近似取0.93[26]. 从图3(a)可以看出，在上午8、9、10点这3个时刻，光伏组件的最大输出功率排序依次为正东＞正南＞正北＞正西，其他时刻的最大输出功率均相等. 导致该结果的原因如下：该日只有上午8、9、10点这3个时刻有水平太阳直射辐射（见图3(b)），对于上午而言，显然是面向正东方向的光伏组件能够接收到最多的太阳直射辐射（见式（15））. 光伏组件能够接收到的太阳散射辐射只与安装倾角有关，与方位角无关（见式（16）），即面向4个不同方位的光伏组件接收到的太阳散射辐射相等. 图4给出该光伏组件在4个不同倾角时的逐时最大输出功率（方位角均取0°）. 可以看出，当倾角小于最佳倾角时，角度的变化对最大输出功率的影响很小；当倾角大于最佳倾角时，角度的变化对最大输出功率的影响较大，且影响程度随着角度的增大而增大.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   光伏组件方位角对最大输出功率的影响

Fig.3   Influence of azimuth angle on maximum power of photovoltaic module


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   光伏组件倾角对最大输出功率的影响

Fig.4   Influence of inclination angle on maximum power of photovoltaic module


5. 结　论

(1) 采用现有文献中统一固定的模型系数值时，利用太阳电池工程简化模型计算得到的光伏组件电学性能曲线与当今主要光伏厂家提供的出厂数据存在较大的偏差.

(2) 基于光伏组件出厂数据，拟合25 ℃下不同辐照度对应的开路电压数据得到系数b，系数a和c分别取短路电流和开路电压温度系数，由此可得更加精确的模型系数值.

(3) 不同厂家生产的光伏组件系数b不同，同一厂家生产的不同型号的光伏组件系数b可取相同值.

参考文献

GU W, MA T, SHEN L, et al

Coupled electrical-thermal modelling of photovoltaic modules under dynamic conditions

[J]. Energy, 2019, 188 (23): 1- 15

[本文引用: 5]

申璐. 光伏器件能量分布的综合建模和实验研究[D]. 上海: 上海交通大学, 2020.

[本文引用: 2]

SHEN Lu. Modeling and experimental study of energy distribution of solar photovoltaic devices [D]. Shanghai: Shanghai Jiao Tong University, 2020.

[本文引用: 2]

CHIN V J, SALAM Z, ISHAQUE K

Cell modelling and model parameters estimation techniques for photovoltaic simulator application: a review

[J]. Applied Energy, 2015, 154 (18): 500- 519

[本文引用: 4]

孙航, 肖海伟, 李晓辉, 等

光伏电池模型综述

[J]. 电源技术, 2016, 40 (3): 743- 745

DOI:10.3969/j.issn.1002-087X.2016.03.078     

SUN Hang, XIAO Hai-wei, LI Xiao-hui, et al

Review in photovoltaic cell model

[J]. Chinese Journal of Power Sources, 2016, 40 (3): 743- 745

DOI:10.3969/j.issn.1002-087X.2016.03.078     

易施光, 张文杰, 罗志荣, 等

太阳电池各等效电路模型的对比分析

[J]. 玉林师范学院学报:自然科学, 2020, 41 (3): 20- 25

[本文引用: 1]

YI Shi-guang, ZHANG Wen-jie, LUO Zhi-rong, et al

Comparative analysis of various equivalent circuit models of solar cells

[J]. Journal of Yulin Normal University: Natural Science, 2020, 41 (3): 20- 25

[本文引用: 1]

BELLINI A, BIFARETTI S, IACOVONE V, et al. Simplified model of a photovoltaic module [C]// 2009 Applied Electronics. Pilsen: IEEE, 2009: 47-51.

[本文引用: 1]

LIAO Z L, XU Y J, XU D

An improved engineering model of silicon solar cell

[J]. Advanced Materials Research, 2011, 204-210 (1): 1669- 1672

肖文波, 胡方雨, 戴锦, 等

太阳电池工程数学模型精确度对比分析研究

[J]. 太阳能学报, 2016, 37 (3): 703- 708

DOI:10.3969/j.issn.0254-0096.2016.03.027      [本文引用: 1]

XIAO Wen-bo, HU Fang-yu, DAI Jin, et al

Comparison and investigation on the accuracy of the photovoltaic cells engineering mathematical model

[J]. Acta Energiae Solaris Sinica, 2016, 37 (3): 703- 708

DOI:10.3969/j.issn.0254-0096.2016.03.027      [本文引用: 1]

苏建徽, 余世杰, 赵为, 等

硅太阳电池工程用数学模型

[J]. 太阳能学报, 2001, 22 (4): 409- 412

DOI:10.3321/j.issn:0254-0096.2001.04.009      [本文引用: 7]

SU Jian-hui, YU Shi-jie, ZHAO Wei, et al

Investigation on engineering analytical model of silicon solar cells

[J]. Acta Energiae Solaris Sinica, 2001, 22 (4): 409- 412

DOI:10.3321/j.issn:0254-0096.2001.04.009      [本文引用: 7]

戴聿雯. 光伏阵列输出特性研究及预估分析[D]. 合肥: 合肥工业大学, 2007.

[本文引用: 1]

DAI Yu-wen. Research and evaluation on solar array’s output characteristics [D]. Hefei: Hefei University of Technology, 2007.

[本文引用: 1]

廖志凌, 阮新波

任意光强和温度下的硅太阳电池非线性工程简化数学模型

[J]. 太阳能学报, 2009, 30 (4): 430- 435

DOI:10.3321/j.issn:0254-0096.2009.04.005     

LIAO Zhi-ling, RUAN Xin-bo

Nonlinear engineering simplification model of silicon solar cells in arbitrary solar radiation and temperature

[J]. Acta Energiae Solaris Sinica, 2009, 30 (4): 430- 435

DOI:10.3321/j.issn:0254-0096.2009.04.005     

杨文杰. 光伏发电并网与微网运行控制仿真研究[D]. 成都: 西南交通大学, 2010.

[本文引用: 4]

YANG Wen-jie. Simulation and research of grid connected photovoltaic generation and microgrid operation control [D]. Chengdu: Southwest Jiaotong University, 2010.

[本文引用: 4]

许玉贞, 詹红霞, 张瑞冬, 等

基于仿真模型的光伏电池输出功率的分析

[J]. 半导体光电, 2014, 35 (6): 1115- 1118

DOI:10.16818/j.issn1001-5868.2014.06.039      [本文引用: 5]

XU Yu-zhen, ZHAN Hong-xia, ZHANG Rui-dong, et al

Analysis on the output power of photovoltaic cells based on simulation model

[J]. Semiconductor Optoelectronics, 2014, 35 (6): 1115- 1118

DOI:10.16818/j.issn1001-5868.2014.06.039      [本文引用: 5]

LI C X, SPATARU S V, ZHANG K J, et al

A multi-state dynamic thermal model for accurate photovoltaic cell temperature estimation

[J]. IEEE Journal of Photovoltaics, 2020, 10 (5): 1465- 1473

DOI:10.1109/JPHOTOV.2020.2987401      [本文引用: 2]

DOLARA A, LEVA S, MANZOLINI G

Comparison of different physical models for PV power output prediction

[J]. Solar Energy, 2015, 119 (9): 83- 99

[本文引用: 2]

COSKUN C, TOYGAR U, SARPDAG O, et al

Sensitivity analysis of implicit correlations for photovoltaic module temperature: a review

[J]. Journal of Cleaner Production, 2017, 164 (1): 1474- 1485

[本文引用: 1]

MATTEI M, NOTTON G, CRISTOFARI C, et al

Calculation of the polycrystalline PV module temperature using a simple method of energy balance

[J]. Renewable Energy, 2006, 31 (4): 553- 567

DOI:10.1016/j.renene.2005.03.010      [本文引用: 1]

李梦. 装配式建筑光伏一体化预制构件的电热性能及其对建筑能耗影响的研究[D]. 上海: 上海交通大学, 2020.

[本文引用: 1]

LI Meng. Experimental and numerical investigation of precast concrete façade integrated with photovoltaic panels and its effects on buildings energy consumption [D]. Shanghai: Shanghai Jiao Tong University, 2020.

[本文引用: 1]

肖泽成. 太阳电池组件的水冷冷却流动传热特性及方法研究[D]. 广州: 广东工业大学, 2012.

[本文引用: 4]

XIAO Ze-cheng. Research on the water-cooled solar photovoltaic module’s heat transfer characteristics and methods [D]. Guangzhou: Guangdong University of Technology, 2012.

[本文引用: 4]

龚皓, 朱晓岗

光伏玻璃透光率测量方法简析

[J]. 太阳能, 2012, 33 (19): 19- 22

DOI:10.3969/j.issn.1003-0417.2012.19.005      [本文引用: 1]

GONG Hao, ZHU Xiao-gang

Brief analysis of measurement method of photovoltaic glass transmittance

[J]. Solar Energy, 2012, 33 (19): 19- 22

DOI:10.3969/j.issn.1003-0417.2012.19.005      [本文引用: 1]

韩延刚, 陈洪波, 江敏芳, 等

光伏玻璃透光性能评价方法及影响因素研究

[J]. 化工新材料, 2014, 42 (11): 154- 155

[本文引用: 1]

HAN Yan-gang, CHEN Hong-bo, JIANG Min-fang, et al

Transmission property and influencing factor pf solar glass

[J]. New Chemical Materials, 2014, 42 (11): 154- 155

[本文引用: 1]

刘鉴民. 太阳能利用: 原理∙技术∙工程[M]. 北京: 电子工业出版社, 2010.

[本文引用: 5]

张鹤飞. 太阳能热利用原理与计算机模拟[M]. 2版. 西安: 西北工业大学出版社, 2004.

[本文引用: 3]

曾泽荣, 李进, 罗多, 等

中国建筑分布式光伏利用现状及未来趋势分析

[J]. 建设科技, 2020, 19 (20): 10- 14

DOI:10.16116/j.cnki.jskj.2020.20.001      [本文引用: 1]

ZENG Ze-rong, LI Jin, LUO Duo, et al

Analysis of current situation and future trend of distributed photovoltaic utilization in Chinese buildings

[J]. Construction Science and Technology, 2020, 19 (20): 10- 14

DOI:10.16116/j.cnki.jskj.2020.20.001      [本文引用: 1]

中国气象局气象信息中心气象资料室, 清华大学建筑技术科学系. 中国建筑热环境分析专用气象数据集[M]. 北京: 中国建筑工业出版社, 2005.

[本文引用: 1]

何宝华, 王慧, 赵邦桂, 等

太阳电池组件中玻璃与EVA透光率测试方法研究

[J]. 上海航天, 2014, 31 (Supple.1): 86- 87

DOI:10.19328/j.cnki.1006-1630.2014.s1.024      [本文引用: 1]

HE Bao-hua, WANG Hui, ZAHO Bang-gui, et al

Study on transmittance test method of glass and EVA used in solar modules

[J]. Aerospace Shanghai, 2014, 31 (Supple.1): 86- 87

DOI:10.19328/j.cnki.1006-1630.2014.s1.024      [本文引用: 1]

/

〈 〉