在换刀机器人运动过程中,为了避免机器人振动、延长关节使用寿命和提高轨迹跟踪精度,对换刀机器人进行轨迹规划. 机器人的运动学分析是进行轨迹规划的基础,王明斗等[4]提出新型的管片拼装机器人逆运动学解析解的求解方法,极大地提高了逆运动学求解的效率. 赵京等[5]利用肘部的自运动理论解耦了7自由度拟人臂的冗余度,验证了该解的仿人性和连续性. 轨迹在进行优化前,通常需要经过规划插值得到基本轨迹曲线,曲线需要满足速度、加速度约束,保证轨迹的连续与平滑. 传统的插值函数主要是多项式插值,包括经典的3次多项式与5次多项式插值法[6]以及Boscariol等[7]提出的‘5455’混合多项式插值法. 秦超等[8]采用5次多项式插值法,得到7自由度番茄采摘机械手从复位点到采摘点的连续平滑轨迹. 多项式插值法计算量小,但是容易出现失真现象. 参数化表达的样条函数可以更加灵活地控制曲线的阶次,Xu等[9]应用贝塞尔曲线拟合关节轨迹,得到连续光滑的曲线,然而节点的改变会导致贝塞尔曲线的整体重构. 经过轨迹插值后得到的运动轨迹,往往不符合预期,需要进一步进行轨迹优化. 轨迹优化的优化目标主要包括时间、能量和冲击等[10]. Xidias[11]提出超冗余度机械臂时间最优轨迹规划的方法,采用多种群遗传算法求解优化问题,寻找执行所需任务的最小时间轨迹. Lu等[12]提出基于序列二次规划算法冲击最优的轨迹规划方法,将轨迹规划问题转化为约束非线性多变量优化问题,显著提高了轨迹的连续性和平滑性. 随着研究的深入,单一的优化目标已难以满足实际作业任务的要求,越来越多的研究着手考虑多目标综合优化[13]. Liu等[14]采用多目标粒子群优化算法来优化柔性机械手的残余振动与运行时间,通过假设模态法建立机械手运动方程,利用分段多项式进行插值得到平滑轨迹,但是该方法的轨迹高阶连续性可以进一步改善. 为了满足轨迹的时间冲击综合最优,Huang等[15]采用精英非支配排序遗传算法,得到满足运动学约束的帕累托最优解集,决策者在选择最优解时需要进一步权衡. Lan等[16]提出改进的多目标粒子群算法,针对时间、能量、冲击3个指标同时进行优化,虽然得到了满足目标的优化轨迹,但是算法的收敛需要一定的时间.
针对TBM换刀机器人的轨迹规划问题,本文建立新型冗余换刀机器人的Denavit-Hartenberg(DH)模型,采用位姿分离算法与关节变量最小策略得到换刀机器人逆运动学的解析解. 在运动学分析的基础上,利用NURBS曲线保证关节空间轨迹的冲击连续,采用改进型PSO算法进行时间-冲击最优轨迹规划. 通过轨迹优化的仿真,验证了该算法的适用性与有效性.
1. 换刀机器人的运动学建模与分析
1.1. 运动学建模
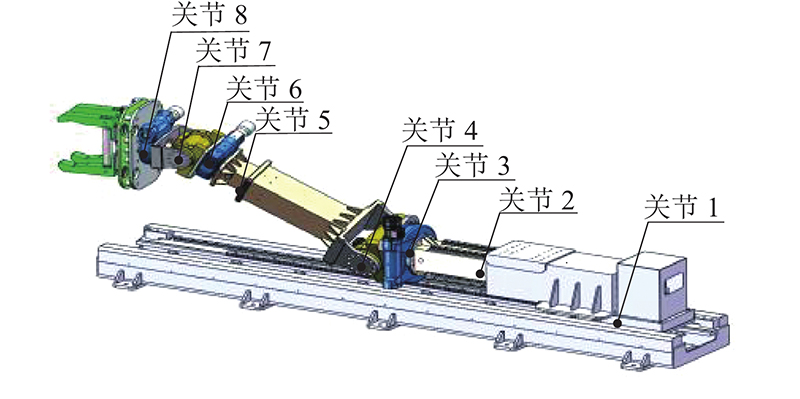
图 1
图 1 换刀机器人的关节示意图
Fig.1 Schematic diagram of joint of disc cutter changing robot
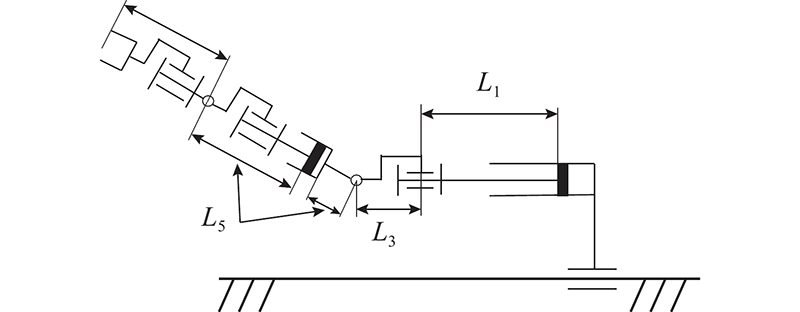
换刀机器人的机构简图如图2所示. 图中,
图 2
采用修正的DH建模方法,得到如图3所示的换刀机器人运动学模型.
图 3
换刀机器人的DH参数如表1所示. 表中,
表 1 换刀机器人的DH表
Tab.1
| i | | | | | |
| 1 | 0 | 0 | 0~3480 | 0 | 0 |
| 2 | 0 | 0 | 0~390 | 1147 | 0 |
| 3 | 0 | 0 | 364 | 0 | −90~90 |
| 4 | 0 | −90 | 0 | 0 | −30~90 |
| 5 | 0 | 90 | 0~460 | 1204 | 0 |
| 6 | 0 | 0 | 0 | 0 | −45~45 |
| 7 | 0 | −90 | 0 | 0 | −90~75 |
| 8 | 0 | 90 | 764 | 0 | −90~90 |
在建立DH模型后,根据
可以得到换刀机器人正运动学的位姿矩阵:
式中:
1.2. 逆运动学分析
换刀机器人通过增加冗余自由度,增强了自身的工作能力,但增加了机器人逆运动学的求解难度. 采用位姿分离法,初步得到换刀机器人逆解的解析解. 换刀机器人最后3个关节轴相交于腕点,根据坐标变换,对于每一个给定末端位姿矩阵,可以得到腕点的位置坐标:
根据换刀机器人的正解连杆矩阵,得到腕点在基坐标系中的位置坐标为
联立式(3)、(4),将
利用式(5)得到2个
令
求解得到
对于每一组
式中:
2. 5次NURBS曲线构造
2.1. NURBS基函数
非均匀有理B样条(non-uniform rational B-splines, NURBS)是参数化的曲线表达,便于工程数据库的存取与应用. NURBS曲线具有良好的局部支撑特性,改变一个路径点只会引起相邻的曲线发生变化,不会影响整个轨迹曲线的形状. 利用节点向量非均匀分布的NURBS基函数,可以处理轨迹点的突变现象. 5次NURBS曲线可以保证C4连续,满足关节轨迹的脉动约束与连续. NURBS是由分段有理B样条多项式基函数定义的,形式是:
式中:
式中:
2.2. 反求控制顶点
NURBS曲线通常不通过除首末点之外的其他控制点,保证曲线可以通过规划要求的轨迹型值点,在k次NURBS曲线中,给定
式中:
联立式(17)~(21),得到由轨迹型值点反求控制点的矩阵方程:
式中:
3. 基于时间冲击最优的轨迹优化
在通过NURBS曲线构造出光滑连续的曲线后,应在实际应用过程中考虑机器人运动学和动力学约束、工作效率和平稳性等因素,找到每种工况下的最优轨迹来指导机器人的作业[14].
3.1. 提出优化目标
在人工换刀作业效率低下的情况下,采用换刀机器人代替传统的人工换刀,要保证换刀作业时间最优,得到优化目标
式中:
考虑到换刀机器人的工作空间狭小、末端承载大、具有微动特性等问题,对换刀机器人运行轨迹的冲击变化与平稳性提出进一步的要求,提出冲击最优目标,包括冲击最大绝对值
式中:
3.2. 构造多目标优化函数
对于多目标轨迹优化的问题,利用加权系数法,将多目标函数转化为单目标函数. 采用单目标优化的方法,达到对多目标函数的求解. 最终的轨迹优化目标函数如下:
式中:
3.3. 基于GL-PSO算法的轨迹优化流程
粒子群优化算法(particle swarm optimization, PSO)由于参数较少、寻优效率高,目前被广泛应用于工业领域. 经典PSO中,所有粒子每次都基于个体最优与群体最优进行学习,这可能导致早熟收敛. 为了避免陷入局部最优解,提出改进PSO算法. 在经典PSO算法中引入遗传算法(genetic algorithm, GA)的思想,利用遗传进化技术为粒子群优化算法培育出多样性样本,称为genetic learning PSO (GL-PSO). 不同于传统的PSO-GA并行式混合算法,GL-PSO将遗传算法和粒子群优化算法以级联方式进行融合,利用遗传技术为粒子群优化算法提供优质基因. 根据粒子历史信息为基因进化提供指导,提高了粒子群优化算法的全局搜索能力和搜索效率[18].
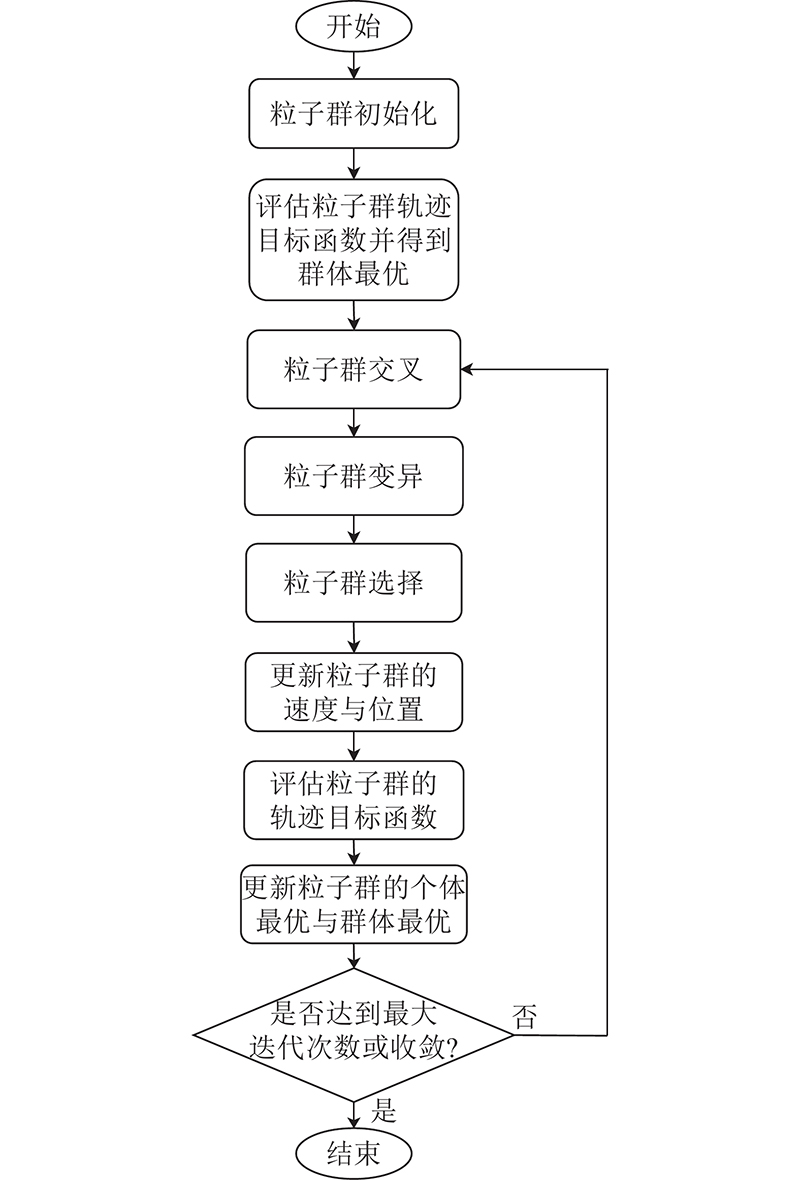
综合轨迹优化目标函数与优化算法,可以得到如图4所示的轨迹优化流程.
图 4
1)初始化一群随机粒子,评估粒子群轨迹优化目标函数,寻找个体最优与群体最优,通过迭代找到最优解. 在每一次的迭代中,粒子通过跟踪个体最优与群体最优,更新自己的速度和位置.
假设粒子维度为
式中:
为了防止
2)利用遗传算子构建粒子的样本. 其中,交叉、变异和选择构成了遗传算法的遗传操作.
对于每个粒子
式中:
对后代
式中:
对交叉与变异创造的后代进行选择:
随机选择多个样本加入竞争,选取具有最佳适应度的样本替换粒子的当前样本,使得粒子产生突变,改变搜索方向,跳出局部最优解.
3)对更新后的粒子群评估个体最优与群体最优,进行收敛性判断. 若满足条件,则跳出循环,程序结束运行.
4. 数值验证
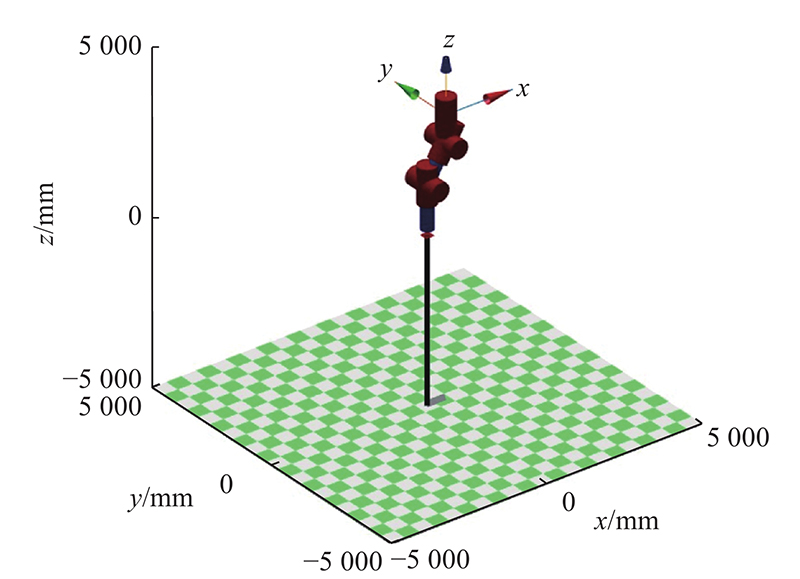
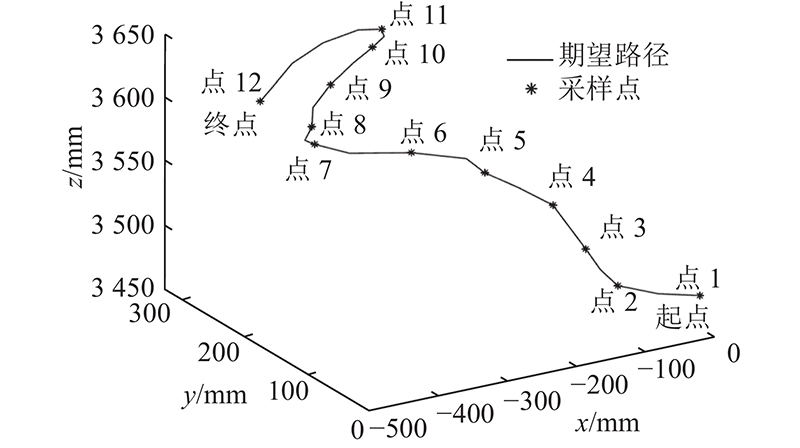
为了验证提出的轨迹规划方法的有效性,以8自由度换刀机器人为研究对象,根据实际换刀作业的需求,规划如图5所示的期望路径. 对路径进行采样,得到一系列三维空间路径点.
图 5
利用提出的逆运动学求解方法,将笛卡尔空间路径点映射到关节空间,得到如表2所示的各关节经过的位置点.
表 2 各关节位置列表
Tab.2
| 位置点 | d/mm | θ/(°) | |||||||
| 关节1 | 关节2 | 关节5 | 关节3 | 关节4 | 关节6 | 关节7 | 关节8 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 14.38 | 2.57 | 103.18 | −29.01 | −5.42 | 17.01 | 5.42 | 3.01 | |
| 3 | 81.67 | 14.58 | 217.03 | −25.23 | −6.28 | 33.03 | 6.28 | 10.23 | |
| 4 | 225.76 | 40.31 | 365.02 | −18.77 | −8.12 | 49.05 | 8.11 | 15.77 | |
| 5 | 378.41 | 67.57 | 428.21 | −18.78 | −8.57 | 65.06 | 8.56 | 18.78 | |
| 6 | 538.07 | 96.08 | 460.00 | −16.90 | −11.21 | 81.08 | 11.20 | 19.07 | |
| 7 | 686.70 | 122.62 | 460.00 | −25.12 | −12.87 | 76.79 | 12.86 | 13.12 | |
| 8 | 830.28 | 148.26 | 460.00 | −30.61 | −13.65 | 62.07 | 13.65 | 10.61 | |
| 9 | 967.20 | 172.71 | 460.00 | −30.61 | −13.65 | 47.35 | 13.65 | 11.61 | |
| 10 | 1125.65 | 201.00 | 460.00 | −25.60 | −16.14 | 32.63 | 16.14 | 10.60 | |
| 11 | 1291.57 | 230.63 | 460.00 | −20.02 | −20.54 | 17.91 | 20.54 | 6.02 | |
| 12 | 1472.53 | 263.34 | 460.00 | −16.89 | −24.43 | 4.85 | 24.42 | 6.21 | |
表 3 各关节运动学约束
Tab.3
| | | | |
| 1 | 400 | 500 | 500 |
| 2 | 120 | 350 | 400 |
| 5 | 120 | 300 | 400 |
| i | vr/((°)·s−1) | ar/((°)·s−2) | jr/((°)·s−3) |
| 3 | 75 | 45 | 45 |
| 4 | 60 | 30 | 40 |
| 6 | 80 | 50 | 45 |
| 7 | 70 | 45 | 30 |
| 8 | 90 | 50 | 45 |
图 6
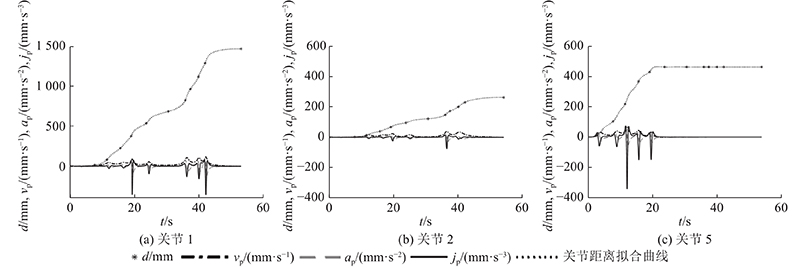
图 6 换刀机器人的移动关节运动曲线
Fig.6 Translation joints motion curve of disc cutter changing robot
图 7
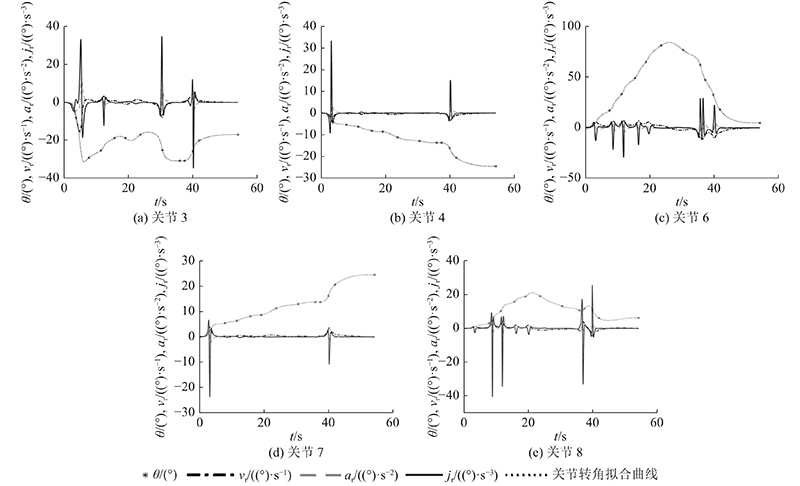
图 7 换刀机器人的转动关节运动曲线
Fig.7 Rotation joints motion curve of disc cutter changing robot
在换刀机器人的运动过程中,各关节速度、加速度最大值均满足如表3所示的运动学约束. 8个关节中的移动关节冲击最大绝对值分别为359.84、73.43、338.92
采用GL-PSO轨迹优化算法得到最优时间序列后,利用NURBS曲线规划出给定采样点轨迹的平均规划时间为50.37
图 8
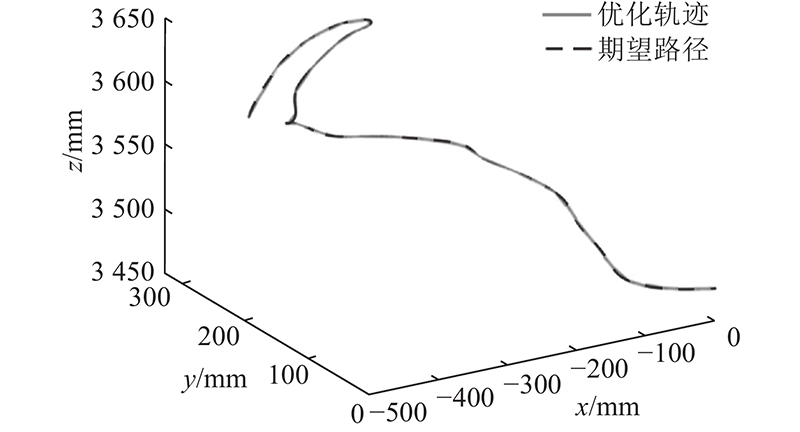
利用换刀机器人正运动学,将关节空间的轨迹映射到笛卡尔空间,得到如图9所示的三维优化轨迹. 可以看出,利用本文方法对采样点进行轨迹优化后,可以与换刀机器人笛卡尔空间的期望路径具有良好的重合度. 受益于NURBS曲线良好的局部支撑性,采样点数的增加仅对它附近的一段曲线产生影响,保证提出的轨迹规划方法对高精度轨迹跟踪的换刀作业需求具有很好的延展性与适应性.
图 9
5. 结 论
(1)以8自由度换刀机器人为研究对象,提出基于位姿分离法与关节变量最小策略的逆运动学解析解求解方法. 通过仿真验证了该逆解求解方法的有效性与正确性,运算速度与求解精度满足机器人轨迹规划的要求.
(2)基于5次NURBS曲线基函数构造的轨迹满足位置、速度、加速度与冲击的光滑连续,可以有效地提高换刀机器人运行的平稳性. 仿真结果表明,与多项式插值算法相比,采用NURBS曲线对复杂轨迹进行规划,可以更好地控制轨迹曲线平滑度和曲率连续性.
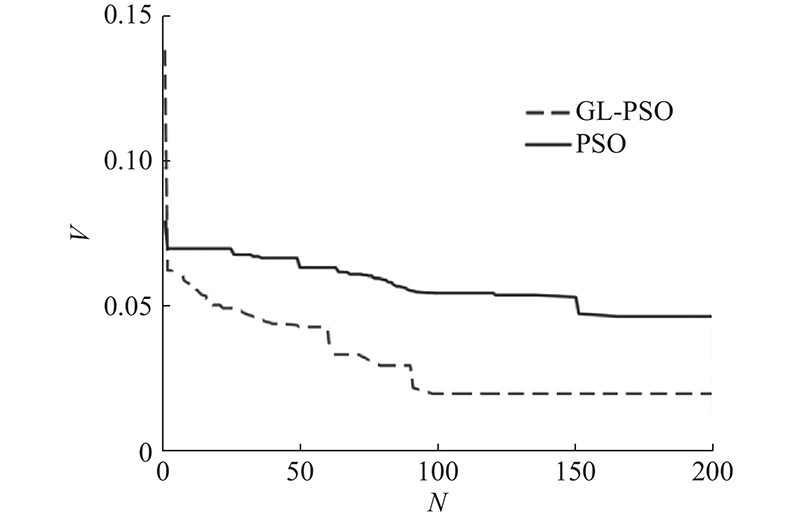
(3)考虑到换刀机器人运动的时间最优与冲击最优,提出多目标轨迹优化轨模型. 将多目标进行归一化处理,基于GL-PSO算法完成轨迹的时间冲击最优规划. 结果表明,GL-PSO算法在全局搜索能力、求解精度、搜索速度上较传统PSO算法具有更好的表现.
参考文献
Intelligent assistant driving method for tunnel boring machine based on big data
[J].DOI:10.1007/s11440-021-01327-1 [本文引用: 1]
变刚度条件下隧道掘进机撑靴液压缸的动态特性
[J].
Vibration performance analysis for the gripper cylinder of tunnel boring machine with variable stiffness
[J].
一种适用于机器人换刀的新型滚刀刀座设计与分析
[J].
Design and analysis of a new cutter holder of disc cutter suitable for robot change
[J].
空间余量最优的拼装机轨迹规划
[J].
Trajectory planning for segment erector based on optimal space allowance
[J].
7自由度拟人臂仿人运动的逆运动学解析解
[J].DOI:10.3901/JME.2018.21.025 [本文引用: 1]
Analytical inverse kinematics of anthropomorphic movements for 7-DOF humanoid manipulators
[J].DOI:10.3901/JME.2018.21.025 [本文引用: 1]
七自由度番茄收获机械手的轨迹规划与仿真
[J].
Trajectory planning and simulation for 7-DOF tomato harvesting manipulator
[J].
Self-adaptive MRPBIL-DE for 6D robot multiobjective trajectory planning
[J].DOI:10.1016/j.eswa.2019.06.033 [本文引用: 1]
Time-optimal trajectory planning for hyper-redundant manipulators in 3D workspaces
[J].DOI:10.1016/j.rcim.2017.10.005 [本文引用: 1]
Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation
[J].
工业机器人关节空间轨迹规划及优化研究综述
[J].
Review of joint space trajectory planning and optimization for industrial robot
[J].
Optimal time-jerk trajectory planning for industrial robots
[J].DOI:10.1016/j.mechmachtheory.2017.11.006 [本文引用: 1]
A multi-objective trajectory planning method for collaborative robot
[J].DOI:10.3390/electronics9050859 [本文引用: 1]
Genetic learning particle swarm optimization
[J].