在各种波能转换装置(wave energy conversion, WEC)中,振荡水柱(oscillating water column, OWC)波能装置因结构简单、易布置于不同海域而得到广泛应用[1]. OWC装置由2个关键部分组成:1)气室,用于收集波能并传输至空气;2)能量输出(power take-off, PTO)系统,用于转换气动能为电能[1]. OWC的技术原理是气室内水柱在波诱导下作垂荡运动,使水柱上方气体被迫压缩或膨胀,进而驱动PTO系统. Evans[2]利用船舶水动力理论,通过简化OWC装置内部液面,理论研究了OWC装置的水动力特性. 随后,Evans[3]又提出表面气压分布理论,并推导出OWC装置最佳能量转换效率的表达式.为了提升OWC装置的水动力特性,相关研究多关注优化单气室OWC装置的结构配置. Deng等[4]采用匹配特征函数展开法研究对称OWC装置的结构优化. Deng等[5]理论证明V形通道可以显著提高OWC装置转换效率. Ashlin等[6]发现底部轮廓为圆形曲线的 OWC装置具有更好的性能. Vyzikas等[7]实验比较OWC和U-OWC装置性能,提出传统OWC装置优化方案. Ning等[8]发现前壁厚度增加将提升U-OWC装置的效率.
将OWC装置嵌入海洋结构中能够降低施工和维护成本. 由于防波堤与OWC装置在适宜水深、断面尺寸和承波能力等方面的相似性,OWC耦合防波堤的集成装置逐渐流行. Ning等[9]采用完全非线性高阶边界元法(higher-order boundary element method,HOBEM)模型预测OWC装置在阶梯式底部上的水动力响应. Deng等[10]总结出在矩形防波堤上构建OWC装置的相对最优结构配置. Zheng等[11]采用匹配特征函数展开法,解决了OWC集成垂直管状结构在有限水深下的波散射和辐射问题. Qu等[12]对集成OWC的桩基防波堤开展试验研究,得到兼具良好发电效果和消浪特性的结构方案. Trivedi等[13]研究了耦合进梯形防波堤的OWC装置在不规则入射波下的波能转换效率. 动网格技术的应用使可运动OWC装置的水动力特性研究取得进展. Wang等[14-16]应用6自由度求解器进行相关研究,包括垂直约束力、可转动前板及其他几何参数对OWC装置水动力性能影响. Guo等[17]对前板可作俯仰运动的OWC装置展开理论研究,发现前板运动与气压振荡的相互作用能够显著拓宽高效频率带宽.
相较传统直墙或斜堤式防波堤,透空式防波堤具有造价低、施工快、易于维护等优点,对不同海况有更高适应性.将OWC波能装置嵌入已成型的透空式防波堤,不仅能维持防波堤原有的消浪性能,还能大幅提升波能利用效率. 在海洋环境中,OWC波能装置耦合透空式防波堤系统会发生垂荡、俯仰和旋转,由OWC技术原理可知,耦合系统在波浪作用下的垂荡运动相当关键.基于Deng等[18]的固定装置相对最优结构尺寸,本研究针对垂荡式OWC波能装置耦合透空式防波堤的集成系统开展水动力特性的数值研究,以期阐明集成系统在垂荡运动下对不同入射波频波能的利用效率及反透射动力响应规律.
1. 数值模型
1.1. 控制方程
基于开源计算流体力学软件包OpenFOAM建立二维非线性数值波浪水槽,利用其自带求解器interFoam求解RANS方程. 对于小尺度模型,气室内的空气可压缩性可以忽略不计[19]. 不可压缩两相流运动的控制方程包括质量守恒方程和动量守恒方程,在笛卡尔坐标系下的表达式为
式中:
式中:
式中:
1.2. 边界条件
确保控制方程有唯一解的条件是对数值波浪水槽定义合理的边界条件. 在OpenFOAM中有众多经典的边界条件,其中无滑移边界条件用于定义结构物刚体表面和海床边界,压力边界条件用于定义大气边界. 对于二维数值波浪水槽,前后边界定义为空边界. 采用OpenFOAM中的工具箱waves2foam[24]定义进口边界,模拟规则波的产生. 选用二阶斯托克斯波作为测试规则波,在进口边界处的自由表面高程和速度分量分别表示为
式中:
式中:
1.3. 数值计算方法
采用有限体积法(FVM)求解控制方程. 将计算域离散成一系列不重复的控制体单元格,在每个控制体单元格中存在1个中心节点,中心节点储存着控制体单元格的流场信息. 采用PIMPLE算法解决不可压缩N-S方程组中压力与速度的耦合问题. PIMPLE算法包含PISO和SIMPLE算法,主要继承了PISO的算法规则. 对于数值离散,采用Euler处理时间域,采用Gauss limitedLinearV 1处理对流项,采用Gauss linear corrected处理拉普拉斯项.
1.4. 水动力参数计算
固定式OWC装置通常在单个波周期内提取波能的时均值
式中:
式中:
式中:
根据Goda两点法[25]分离得到入射波和反射波. 反射系数
式中:
式中:
2. 模型建立与验证
2.1. 数值波浪水槽
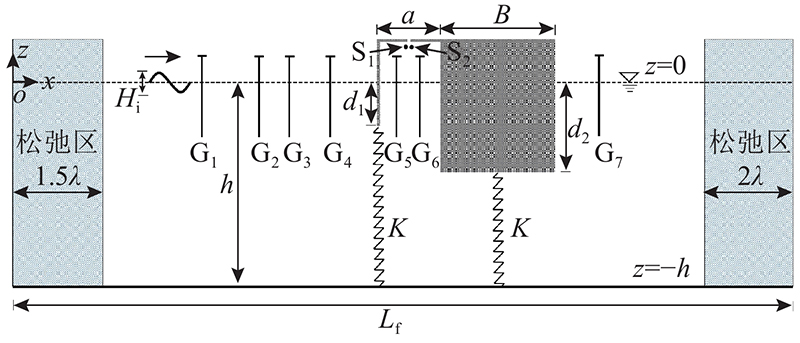
如图1所示为垂荡式OWC装置耦合方箱式防波堤系统的数值波浪水槽模型示意图. 图中,计算域长度
图 1
图 1 垂荡式振荡水柱装置数值波浪水槽示意图
Fig.1 Sketch of numerical wave tank for heave-only oscillating water column device
式中:
2.2. 网格收敛性验证
基于FVM的离散方式,数值模型验证的第一步是确认空水槽的网格设置已达到收敛状态. 在单位波长和单位波高内各选取5种网格尺寸进行测试,
图 2
图 3
图 3 不同网格下气室内液面高度与压强的数值收敛性结果
Fig.3 Numerical convergence results of water surface elevation and pressure in chamber under different grids different grids
2.3. 动网格求解器的验证
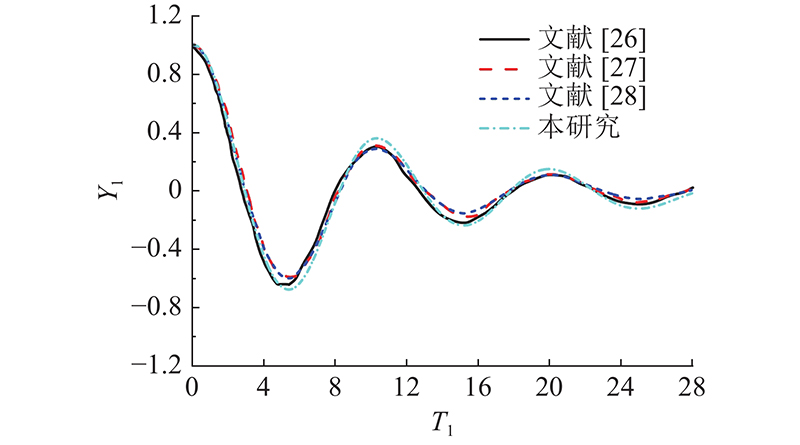
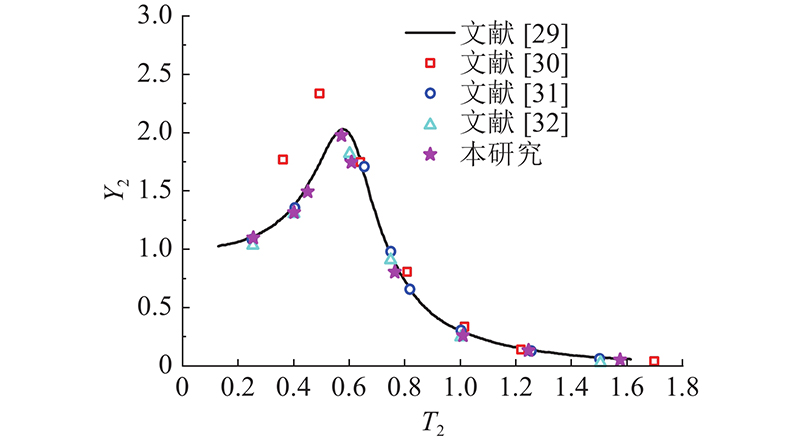
采用rigid-body dynamic (RBD) waveDyMFoam求解器求解描述垂荡运动所需的动网格. 为了确保RBD waveDyMFoam求解器的可靠性,模拟二维圆柱体自由释放及波浪诱导下的方箱垂荡运动,将结果分别与文献[26]~[32]的结果进行对比. 直径为D的圆柱体自由入水过程中的运动位移与质心高度的比值Y1随无量纲时间参数T1的变化如图4所示,其中T1=t(g/D)1/2. 可以看出,除了在峰、谷处的微小差异,本研究数值结果与其他研究结果总体吻合良好. 边长为w的方箱在波浪作用下发生垂直位移,振荡幅度与入射波幅之比Y2随无量纲频率参数T2的变化过程如图5所示,其中T2=2π2 W/gT2. 可以看出,本研究数值结果与其他理论、实验及数值结果验证良好. 验证结果表明,采取的RBD waveDyMFoam求解器在处理波浪诱导下的结构物垂荡运动具有良好的准确性和可靠性.
图 4
图 4 圆柱体运动位移与质心高度的比值随无量纲时间参数的变化
Fig.4 Ratio of displacement of cylinder to centroid height versus non-dimensional time parameter
图 5
图 5 方箱振荡幅度与入射波幅的比值随无量纲频率参数的变化
Fig.5 Ratio of oscillation amplitude of box to incident wave amplitude versue non-dimensional frequency parameter
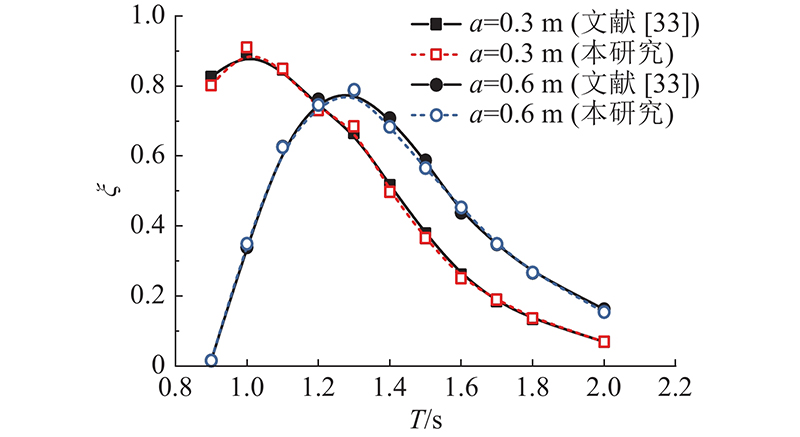
2.4. 效率计算方法的验证
图 6
图 6 不同求解器下的波能转换效率对比
Fig.6 Comparison of wave energy conversion efficiency under different solvers
3. 结果分析
针对嵌入方箱式防波堤的单气室OWC波能装置,选取文献[18]中经过实验和数值测试得到的较优越的尺寸结构,即防波堤宽度为0.5 m、防波堤吃水为0.3 m、气室前吃水为0.04 m、气室宽度为0.2 m、气室开口率为1%. 在水深为0.5 m、波高为0.05 m、波浪周期为1.0~2.4 s的条件下,对安装不同弹簧刚度
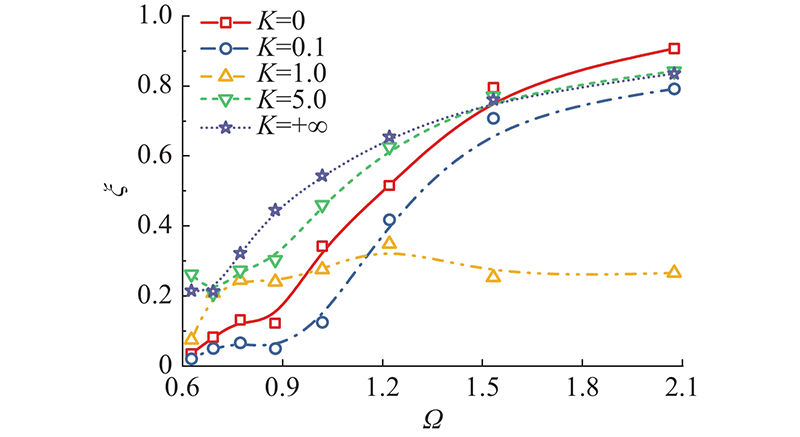
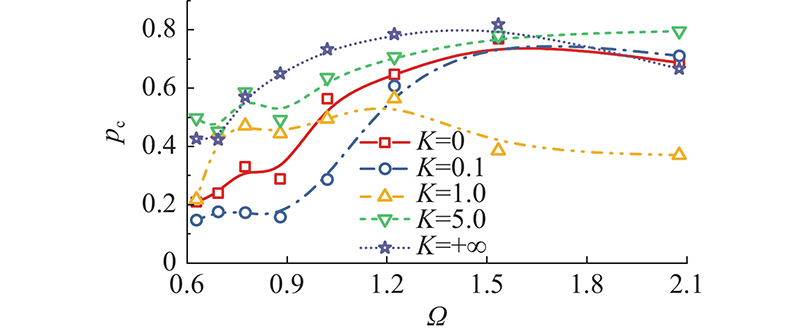
如图7所示为不同弹簧刚度条件下,OWC装置的波能转换效率随无量纲入射波频
图 7
图 7 无量纲弹簧刚度对能量转换效率的影响
Fig.7 Effects of non-dimensional spring coefficients on energy conversion efficiency
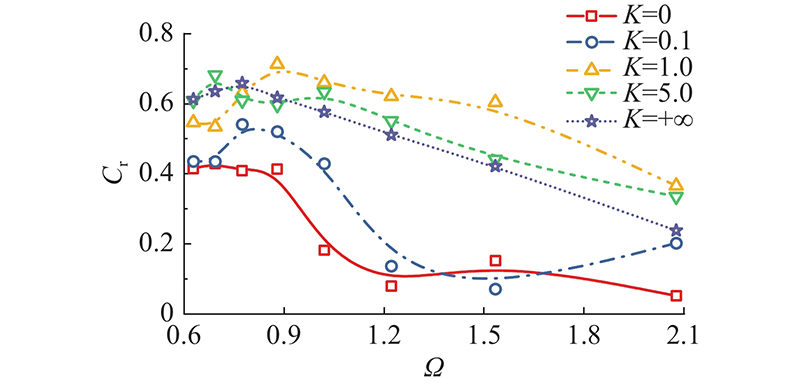
如图8、9所示为不同弹簧刚度条件下,OWC装置耦合防波堤结构的反射及透射系数随
图 8
图 8 无量纲弹簧刚度对反射系数的影响
Fig.8 Effects of non-dimensional spring coefficients on reflection coefficient
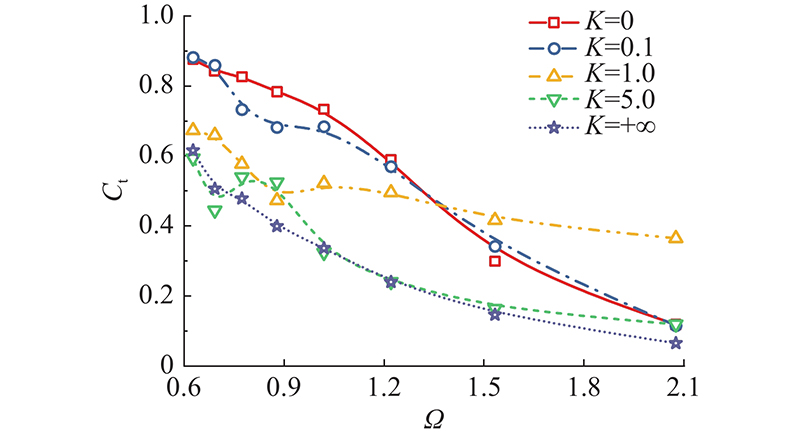
图 9
图 9 无量纲弹簧刚度对透射系数的影响
Fig.9 Effects of non-dimensional spring coefficients on transmission coefficient
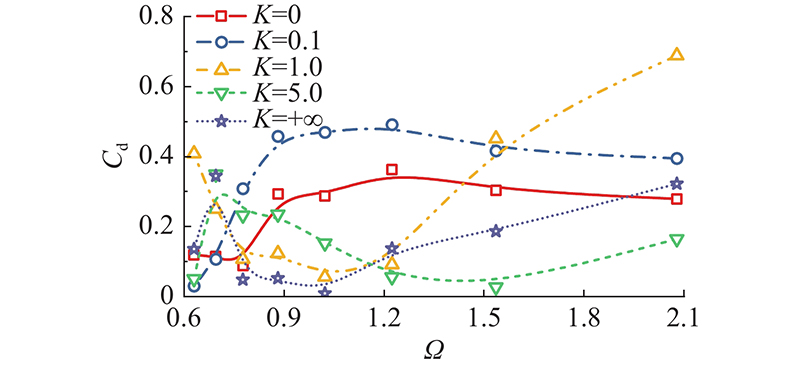
垂荡式OWC装置耦合方箱式防波堤系统的能量耗散情况如图10所示. 当
图 10
图 10 无量纲弹簧刚度对能量耗散系数的影响
Fig.10 Effects of non-dimensional spring coefficients on energy dissipation coefficient
绘制气室内外的无量纲相对压降
图 11
图 11 无量纲弹簧刚度对压降的影响
Fig.11 Effects of non-dimensional spring coefficients on relative pressure drop
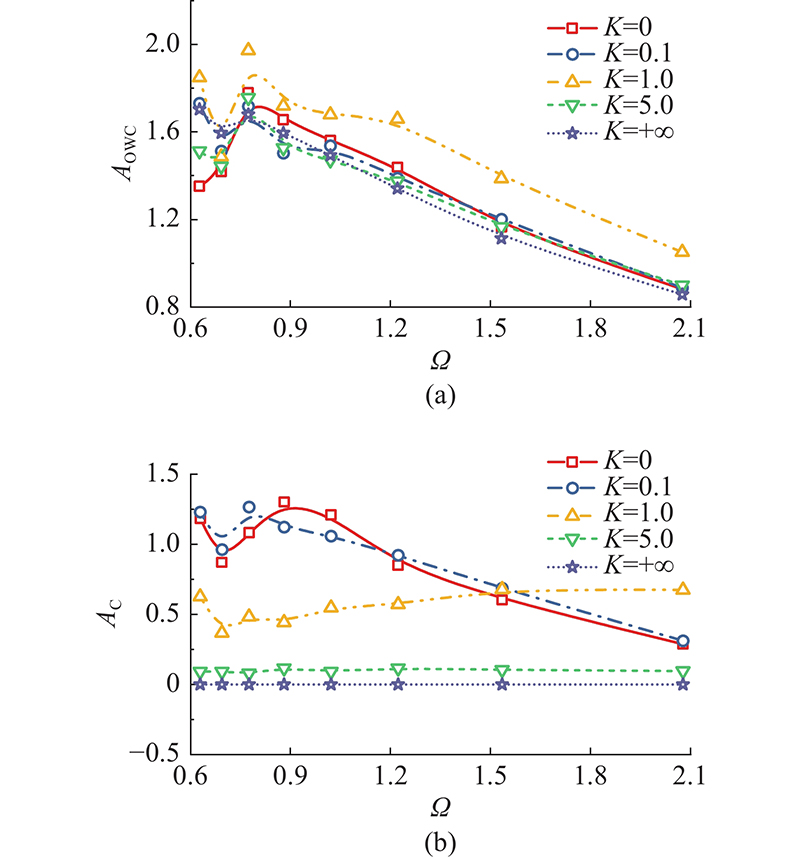
对于垂荡式OWC装置而言,由于结构物自身存在上下垂荡运动,计算波能转换效率时的OWC的实际振荡为OWC自身振荡与结构物振荡之差. 如图12所示为OWC相对振幅(OWC振幅与入射波幅之比)
图 12
图 12 无量纲弹簧刚度对不同相对振幅的影响
Fig.12 Effects of non-dimensional spring coefficients on different relative oscillation amplitude
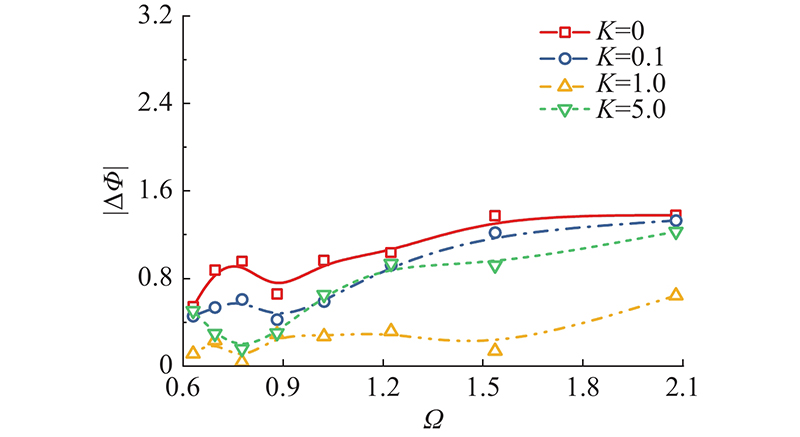
对于垂荡式的OWC耦合防波堤结构,不论是振荡水柱还是作垂荡运动的结构物,它们的运动位移曲线都可以拟合成弦函数. 在相同的入射波频条件下,振荡水柱和结构物位移弦函数的相位差对OWC装置的波能转换效率来说意义重大. 在入射波频不变的条件下,当相位差的绝对值
图 13
图 13 无量纲弹簧刚度对相位差绝对值的影响
Fig.13 Effects of non-dimensional spring coefficients on absolute value of phase difference
4. 结 论
(1)固定式OWC波能装置的能量转换效率并不一定在全频域始终最高,结构物适当的垂荡运动有利于提升OWC装置吸收特定频率波能的效率.
(2)对于垂荡式OWC波能装置,振荡水柱和结构物的运动相位差是决定能量转换效率的关键因素之一,相位差越接近0,装置的波能转换性能越低,相位差越接近
(3)对于垂荡式OWC波能装置,弹簧结构的存在对气室内水柱本身的振荡情况影响较小,通过弹簧控制结构物的垂荡运动来调节相位差,从而提升能量转换效率的措施是可行的.
(4)垂荡式OWC装置耦合透空式方箱型防波堤的系统在实现高效率获取波能的状态下,依然能够维持可观的消浪性能.
(5)受限于弹簧等机械装置的实验条件约束,本研究尚未开展垂荡式OWC装置的物理模型试验. 未来计划通过物理试验进一步验证数值模型的可靠性,并进行物理试验探究.
参考文献
A review of oscillating water columns
[J].
A theory for wave-power absorption by oscillating bodies
[J].
Wave-power absorption by systems of oscillating surface pressure distributions
[J].
Wave power extraction by an axisymmetric oscillating-water-column converter supported by a coaxial tube-sector-shaped structure
[J].
Wave power extraction from a bottom-mounted oscillating water column converter with a V-shaped channel
[J].DOI:10.1098/rspa.2014.0074 [本文引用: 1]
Effects of bottom profile of an oscillating water column device on its hydrodynamic characteristics
[J].DOI:10.1016/j.renene.2016.04.091 [本文引用: 1]
Experimental investigation of different geometries of fixed oscillating water column devices
[J].DOI:10.1016/j.renene.2016.11.061 [本文引用: 1]
Geometrical investigation of a U-shaped oscillating water column wave energy device
[J].DOI:10.1016/j.apor.2020.102105 [本文引用: 1]
Numerical investigation on hydrodynamic performance of an OWC wave energy device in the stepped bottom
[J].DOI:10.3389/fenrg.2019.00152 [本文引用: 1]
Numerical simulation of an oscillating water column device installed over a submerged breakwater
[J].
Wave power extraction from a tubular structure integrated oscillating water column
[J].DOI:10.1016/j.renene.2020.01.008 [本文引用: 1]
Design and experimental study of a pile-based breakwater integrated with OWC chamber
[J].DOI:10.1007/s13344-021-0041-0 [本文引用: 1]
Mathematical modeling of breakwater-integrated oscillating water column wave energy converter devices under irregular incident waves
[J].
Wave power extraction from a dual oscillating-water-column system composed of heave-only and onshore units
[J].
垂荡双气室振荡水柱波能装置水动力特性研究
[J].
Hydrodynamics of a dual-chamber OWC wave energy converter in heaving motion
[J].
带纵摇前墙的新型振荡水柱式波浪能装置转换效率以及水动力性能数值研究
[J].DOI:10.16483/j.issn.1005-9865.2021.05.007 [本文引用: 1]
Numerical simulation on the extraction efficiency and hydrodynamic performance of an OWC device with a pitching front-wall
[J].DOI:10.16483/j.issn.1005-9865.2021.05.007 [本文引用: 1]
Hydrodynamics of an oscillating water column WEC-breakwater integrated system with a pitching front-wall
[J].
Hydrodynamic performance of an asymmetry OWC device mounted on a box-type breakwater
[J].DOI:10.3389/fmars.2021.677030 [本文引用: 3]
Hydrodynamic performance of an offshore-stationary OWC device with a horizontal bottom plate: experimental and numerical study
[J].DOI:10.1016/j.energy.2019.115941 [本文引用: 1]
Volume of fluid (VOF) method for the dynamics of free boundaries
[J].DOI:10.1016/0021-9991(81)90145-5 [本文引用: 1]
Evaluating the performance of the two-phase flow solver interFoam
[J].DOI:10.1088/1749-4699/5/1/014016 [本文引用: 1]
A tensorial approach to computational continuum mechanics using object-oriented techniques
[J].DOI:10.1063/1.168744 [本文引用: 1]
A wave generation toolbox for the open-source CFD library: OpenFoam®
[J].
Estimation of incident and reflected waves in random wave experiments
[J].
The transient motion of a floating body
[J].
Validation and application of a fully nonlinear numerical wave tank for simulating floating offshore wind turbines
[J].
On the increase of the resistance of a ship in rough seas
[J].
A study on the drift force on two-dimensional floating body in regular waves
[J].
Freely floating-body simulation by a 2D fully nonlinear numerical wave tank
[J].
Numerical simulation of a heave-only floating OWC (oscillating water column) device
[J].
Hydrodynamic performance of single–chamber and dual–chamber offshore–stationary oscillating water column devices using CFD
[J].