压实作为路基施工的重要工序,是路基施工质量的重要评价指标. 随着智能压实的快速发展[1],亟需从新的角度探索用于评价现场压实质量的新指标. 研究级配碎石在旋转压实过程中的颗粒运动特征,对从颗粒运动角度揭示级配碎石的压实机理和促进智能压实的发展均具有重要意义.
已有研究结果表明,与其他压实方法相比,旋转压实能够从实验室角度获得最接近现场压实质量的试样[2–8]. 旋转压实可以较好表征级配碎石的压实过程[9-10]. Masad等[11]使用X射线断层扫描技术记录试样在旋转压实过程中的内部结构变化,发现在旋转次数较高的情况下,能够获得与现场取芯试样较为接近的密实度. 可见,较高的旋转压实次数是保证压实质量的前提. 王萌等[12]使用智能颗粒传感器研究旋转压实的不同阶段,发现在旋转次数为80~100次时的试样压实效果较重型击实的好. 针对旋转压实次数的定量研究较少,原因可能是研究者对旋转压实过程中颗粒的自组织行为认识不够深入. 为了探讨旋转压实过程中颗粒的自组织行为,Wang等[13-14]使用智能颗粒传感器研究混合料在旋转压实过程中的颗粒运动特性,在一定程度上揭示了旋转压实过程中颗粒的运动学行为. 由于智能颗粒的尺寸通常与粒径为19.0~26.5 mm的骨料尺寸接近,且形状为规则的立方体,导致表征颗粒的接触特性和运动行为存在不足. 虽然研究者在部分室内试验中通过传感器发现了压实过程中颗粒的运动规律,但是旋转压实过程中颗粒运动与压实特性关联机制的研究成果较少. 离散元方法(discrete element method,DEM)[15–23]为弥补智能颗粒在反映颗粒真实接触状态方面存在的缺陷提供了可行的解决方案. 在旋转压实的DEM研究方面,Chen等[15]使用DEM分析了级配、旋转次数、回旋角度和接触模型参数对沥青混合料压实效果的影响,并优化了沥青混合料的压实参数设计;Gong等[16]使用DEM方法研究了不同颗粒形状的沥青混合料在压实过程中的运动特征,并分析了骨料形状对压实效果的影响. Chen等[17–19]研究了旋转压实过程中的细观特性. 可见,DEM提供了颗粒运动和旋转压实关联机制的解决方案,且DEM中的骨料间接触状态与实况接近. 本研究基于DEM,构建考虑真实骨料形状的旋转压实模型,研究级配碎石在旋转压实过程中的颗粒运动特征,揭示颗粒运动与旋转压实特性的关联机制.
1. 离散元数值模型构建
1.1. 级配碎石骨料获取
图 1
1.2. 旋转压实数值模型构建
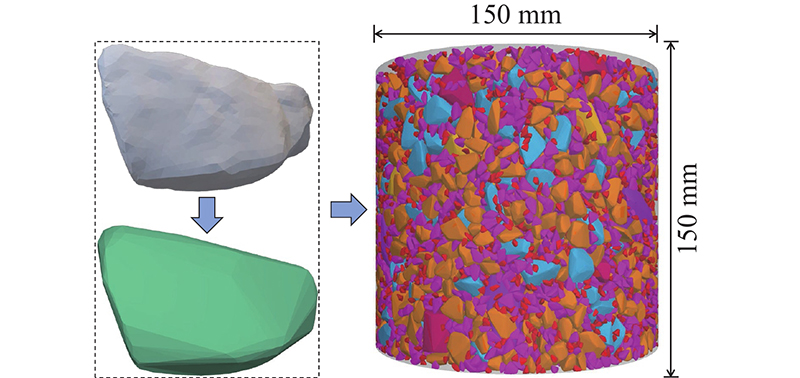
如表1所示为本研究使用的试样颗粒级配. 表中,d为骨料的粒径,P为累计过筛率. 可以看出,d<2.36 mm的骨料较少,为了提高离散元数值模拟的计算效率,将d<2.36 mm的骨料统一使用d=2.36 mm的替代. 在该级配中随机投放如图1所示的集料,构建DEM模型用于旋转压实的数值模拟. 颗粒形状影响颗粒的运动响应,若不考虑骨料的真实形状将引起颗粒运动信息失真[15],进而无法探讨颗粒运动与级配碎石压实机理的联系. 本研究基于凸多面体颗粒表征骨料的形状,以反映真实颗粒的主要形状:1)通过三维激光扫描仪获得骨料的真实颗粒形状,将文件保存为stl格式;2)随机选择图1中的不同类型骨料各30个,共计90个,用于构建凸多面体的模板;3)根据表1所示的级配以随机投放的方式,在高度比设计试样略大的容器中随机投放,使骨料充分弹开并处于几乎无接触的状态.
表 1 虚拟多面体试样颗粒级配
Tab.1
| d/mm | P/% | d/mm | P/% | d/mm | P/% | d/mm | P/% | |||
| 22.40 | 100 | 16.00 | 83.0 | 9.50 | 50.0 | 2.36 | 0.5 | |||
| 19.00 | 92.0 | 13.20 | 75.0 | 4.75 | 12.0 | 1.60 | 0 |
图 2
图 2 多面体骨料生成与虚拟模型构建
Fig.2 Polyhedral aggregate generation and virtual model construction
图 3
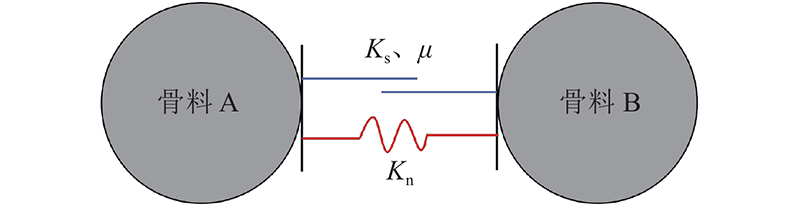
1.3. 接触模型与细观参数
虽然DEM细观强度参数与骨料的宏观强度参数没有线性相关性[24],但细观强度参数对试样的宏观性能有重要影响. 骨料间的宏观强度无法直接应用于DEM模型中,采用参数标定的方法可以校准骨料间的细观强度参数. 常用的参数标定方法为试错法[25-26],即通过离散元虚拟试验多次试算来匹配骨料的宏细观参数. 本研究采用线性接触模型模拟骨料间的刚度和摩擦行为,在该细观接触模型中,须校准的参数主要有法向刚度
图 4
1.4. 压实过程描述
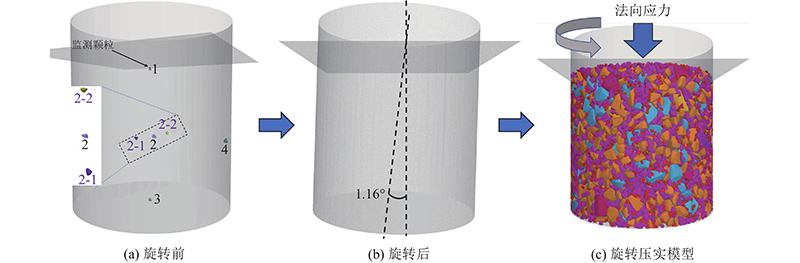
构建离散元数值模型后,进行如图5所示的级配碎石试样的旋转压实虚拟试验,步骤如下. 1)选取试样中不同位置的颗粒作为监测颗粒运动信息的监测点. 监测点共6个,分别布设在试样上、中、下、中部侧边以及试样中部附近的2个测点位置,编号分别为1、2、3、4、2-1、2-2. 2)通过试样顶部墙体伺服的方式,在试样顶部施加固定荷载800 kPa,直至其压力和颗粒系统平衡. 3)使装有骨料的容器旋转1.16°. 4)设定旋转压实速率为30 r/min,进行虚拟试样的旋转压实数值模拟研究. 数值模拟所用计算机配置情况:I9-9900K(8核16线程)-32G(运行内存)-RX560(4 GB)显卡,其中100次旋转压实计算时间为650 h.
图 5
图 5 颗粒运动监测点及旋转压实流程图
Fig.5 Particle movement monitoring points and gyratory compaction flow chart
2. 数值模拟结果
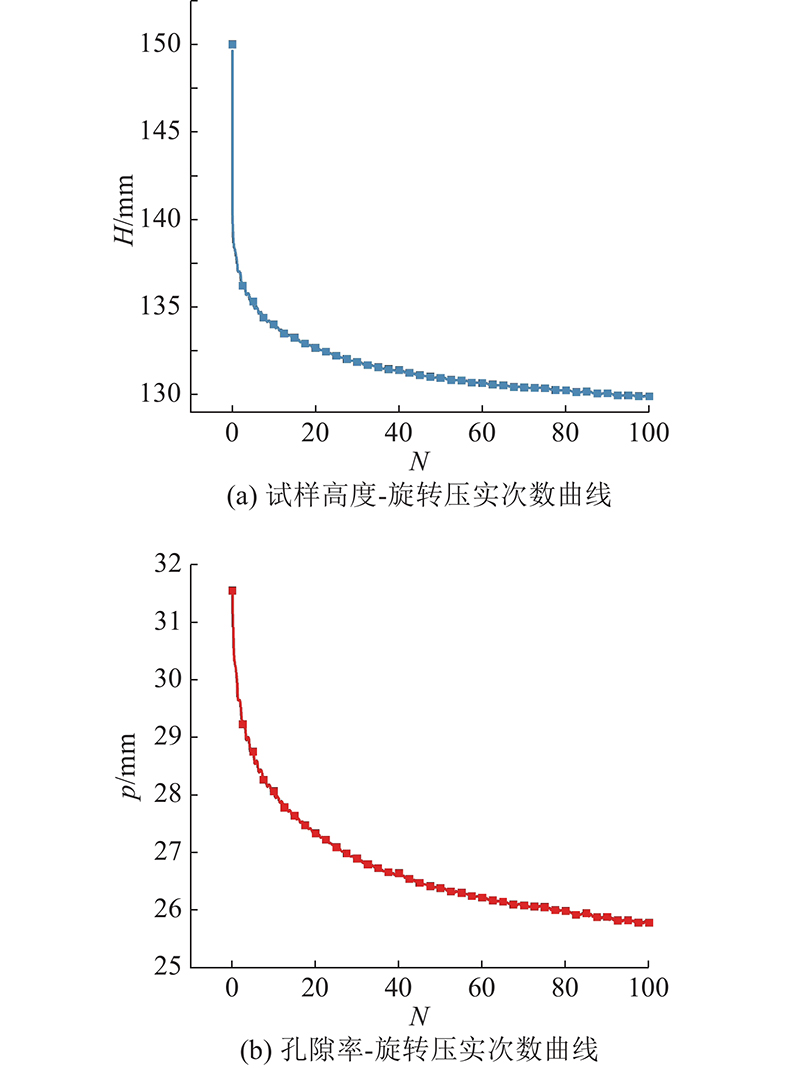
2.1. 试样高度和孔隙率变化
图 6
图 6 压实高度和孔隙率随旋转压实次数的变化曲线
Fig.6 Variation curve of compaction height and porosity with gyratory compaction times
2.2. 不同位置颗粒相对转角
图 7
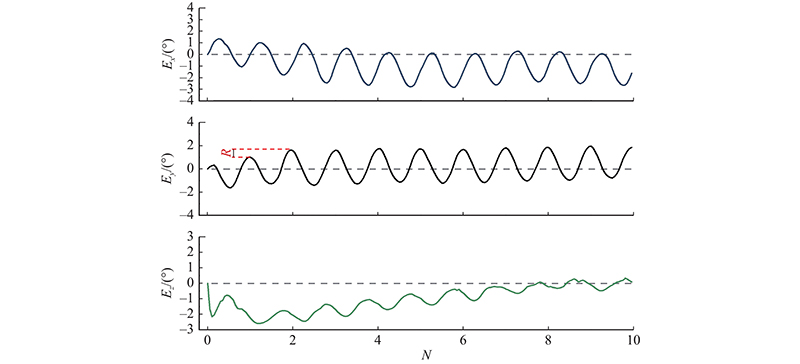
图 7 监测点2欧拉角随旋转压实次数的变化曲线
Fig.7 Variation curve of euler angle with gyratory compaction times at monitoring point 2
式中:
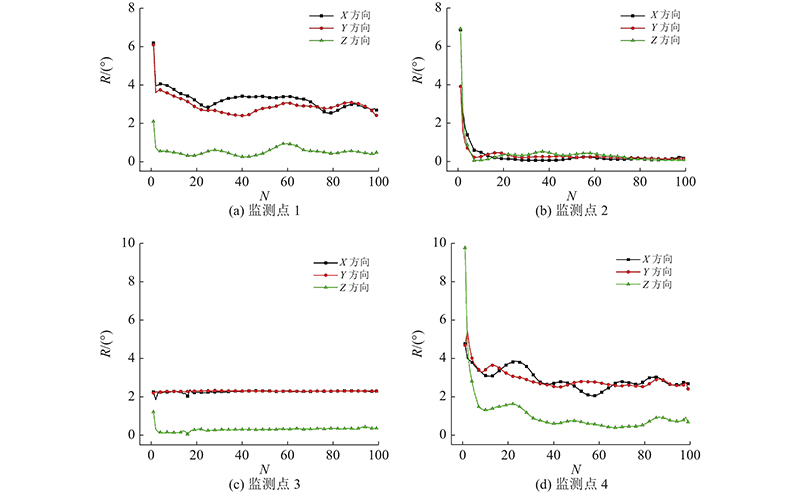
在旋转压实过程中不同监测点的相对转角如图8所示. 在旋转压实初期(N∈(0, 20]),试样中的骨料较为松散,在旋转压实的触发下,颗粒的姿态调整较大,因此试样的不监测点均出现较大的初始相对转角. 在旋转压实中期(N∈(20, 80]),各监测点的相对转角变化相对初始时较小,说明在旋转压实过程中,颗粒运动逐渐被限制,也说明试样内部骨料正在逐渐向密实状态发展,这是骨料自由度减少的结果. 在旋转压实后期(N∈(80, 100]),仅监测点2的相对转角随旋转次数的变化率接近0. 因此,可以考虑将试样中部位置颗粒的运动作为压实效果评价的标准. 不同监测点的相对转角在旋转压实过程中的变化规律值得关注. 监测点1的颗粒在旋转压实初始阶段的姿态有较大幅度的调整,即具有较大的相对转角;在后续的旋转压实过程中,相对转角的较大起伏是骨料接触状态不断变化的结果. 对于监测点2的颗粒,整个压实过程中的相对转角周期性强,且相对转角呈现逐渐减小的趋势,变化曲线的规律性较强,且在压实次数超过80次后的相对转角接近0°。说明这个位置的骨料具有稳健的接触状态,颗粒间的咬合作用较强. 监测点3的颗粒相对转角的变化幅度较小. 原因可能是该颗粒距离加载板较远,旋转压实的压缩力和剪切力传递至此处时被大幅削弱,导致颗粒的姿态在经过短暂的初始扰动后保持稳定. 监测点4的颗粒相对转角的变化规律与监测点1的相似,压实旋转次数-相对转角曲线都是在经过较大的初始扰动后呈波浪式,无稳定阶段. 原因是旋转桶边界对骨料具有较大的约束扰动作用. 综上所述,监测点2对应的试样中心位置具有最佳的压实效果,可以使用试样中心位置的监测点对不同的压实阶段进行进一步划分.
图 8
图 8 各监测点颗粒的相对转角随旋转压实次数的变化曲线
Fig.8 Variation curve of particles’ relative rotation angle with gyratory compaction times at each monitoring position
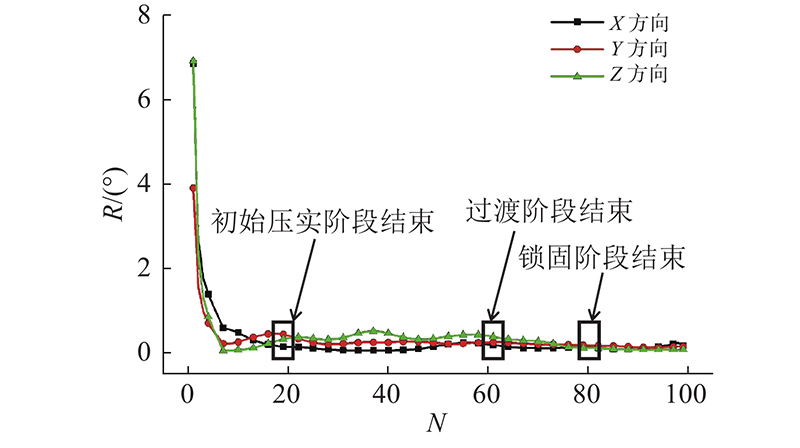
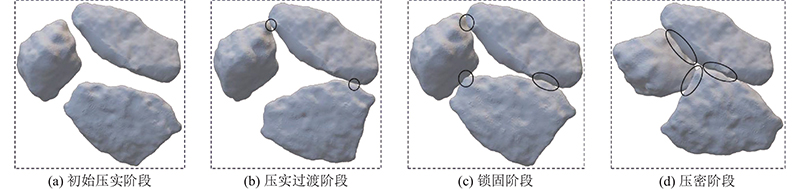
如图9所示,根据颗粒运动信息,将旋转压实分为初始压实、过渡压实、锁固和压密4个阶段. 初始压实阶段的旋转压实次数约为0~20次,由于初始阶段的颗粒较为松散,在压实时颗粒运动较为剧烈,导致相对转角的变化较大. 过渡压实阶段对应的压实次数约为20~60次,颗粒间通过自身姿态调整与周围颗粒相互接触,且在旋转压实过程中不断优化自身姿态,以获得更好的接触状态. 此阶段的颗粒表现出波动的相对转动特征,说明颗粒的稳定骨架开始形成,并在不断压实作用下被强化. 锁固阶段的旋转次数约为60~80次,颗粒稳定骨架基本形成,颗粒间的相对运动较弱,骨料通过姿态调整达到锁固状态,从而形成稳定的颗粒骨架. 锁固阶段结束后,颗粒基本处于压密状态,颗粒间存在锁固效应,很难发生较大的相对运动,因此骨料的相对转角几乎为0°,表明试样被压密. 由此可见,颗粒运动与试样的压实状态息息相关,在旋转压实过程中,松散状态时的颗粒相对运动最剧烈,相对转角的变化最大,当骨料间由于嵌挤、摩擦作用发生锁固效应时,颗粒间的相对运动较弱,试样被压密.
图 9
图 9 根据相对转角变化特征对压实阶段进行划分
Fig.9 Division of compaction stages according to relative angle variation characteristics
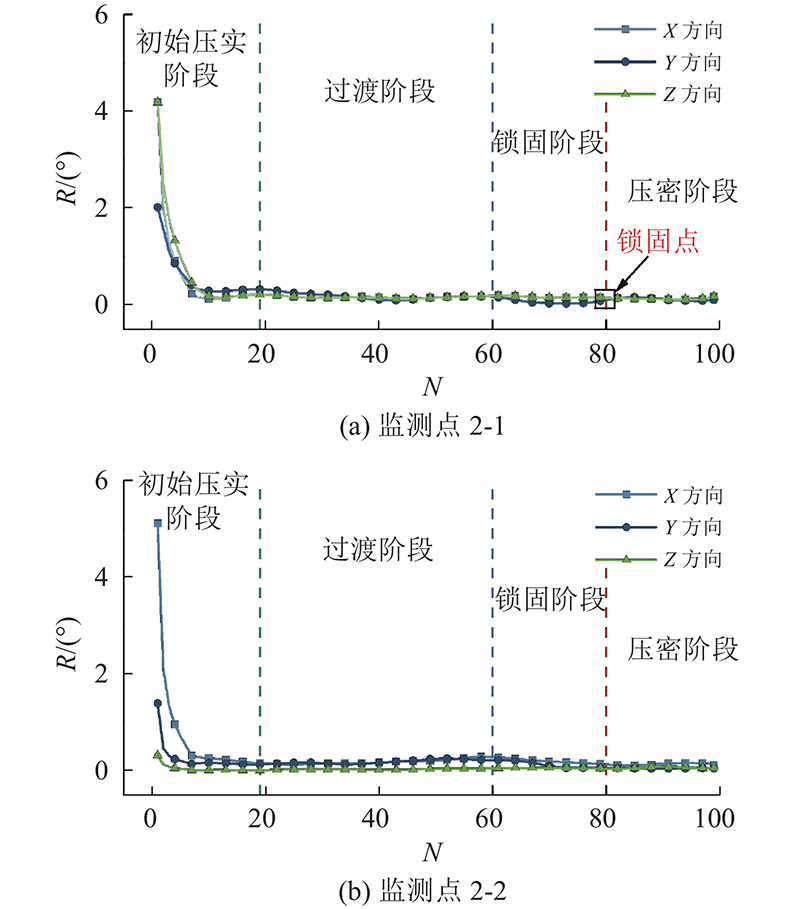
如图10所示,为了增强说明试样中心位置在旋转压实过程中的颗粒运动特征,在中心位置附近选取监测点2-1、2-2,记录监测点在旋转压实过程中相对转角的计算结果,并根据图9中所示转角特征划分监测点的旋转压实的阶段. 与其他监测点相比,试样中心位置的骨料运动不受试样边界条件的影响,具有高度相似的特征和更加合理的接触状态. 在初始压实阶段,骨料从静止状态被扰动,进行了较大幅度的姿态调整,这是在外界扰动情况下的颗粒自组织行为,目的是寻求稳定的接触状态. 在过渡阶段,骨料根据外部扰动,不断调整自身姿态,以获得更加稳固的接触状态. 进入锁固阶段,骨料间保持着稳定的接触状态,直至颗粒间形成紧密的咬合,即形成稳健的锁固点. 锁固点的出现是试样被压密的颗粒运动学标志,在随后的旋转压实过程中,颗粒的姿态不会继续发生大幅度的调整,这与试样在压密阶段的特征相互对应.
图 10
图 10 试样中部监测点颗粒的相对转角随旋转压实次数的变化曲线
Fig.10 Variation curve of particles ’ relative rotation angle with gyratory compaction times at central monitoring position
2.3. 压实机理分析
在级配碎石旋转压实的不同阶段,内部骨料间的接触状态是不同的,这与试样内部骨料的运动状态息息相关,也反映了骨料的压实状态. 如图11所示为级配碎石的旋转压实过程. 在初始压实阶段,试样内部骨料接触较为松散,试样中多存在悬浮颗粒,此时颗粒运动剧烈,相对转角较大. 在压实过渡阶段,大部分颗粒间已发生接触. 此时骨料的稳定骨架基本形成,但是骨架效应较弱,骨料仍然具有较大的运动空间. 在锁固阶段,颗粒相互嵌挤、摩擦的运动使颗粒间接触进一步增强,形成了较为紧密的骨架结构. 在锁固阶段结束后,试样进入压密阶段,颗粒间发生锁固效应,已无太大的运动空间. 此时的试样已经压实完成,后续的持续旋转压实对试样的压实状态影响不大. 分析结果表明,可以通过试样中部的颗粒运动特征反映试样的压实状态,以判识试样的压实效果.
图 11
图 11 级配碎石压实过程中颗粒姿态调整示意图
Fig.11 Schematic diagram of particle attitude adjustment during compaction of graded aggregates
3. 结 论
(1)在旋转压实过程中,试样各部位颗粒运动状态有所差别,边界效应对颗粒运动具有重要影响. 试样中部颗粒运动与骨料压实状态的关联强烈.
(2)从颗粒运动角度,将旋转压实分为初始压实、过渡压实、锁固和压实4个阶段. 锁固阶段结束时,颗粒间接触紧密,试样被压实.
(3)在过渡压实阶段,骨料的受力骨架基本形成,颗粒运动相较于初始压实阶段明显减弱. 在锁固阶段,骨料被进一步压密,颗粒运动进一步减弱,直至颗粒间运动被锁止. 由此可见,骨料在压实过程中的运动特征可以作为评价试样压实状态的关键指标.
(4)本研究通过DEM研究了级配碎石在旋转压实过程中的颗粒运动特征,揭示了骨料压实和内部颗粒运动的关联机制. 未来计划从颗粒运动的角度提出级配碎石的压实指标,开发相应的智能压实传感器,应用于现场实时智能压实监测.
参考文献
高速铁路路基振动压实理论与智能压实技术综述
[J].DOI:10.3969/j.issn.1001-4632.2021.05.01 [本文引用: 1]
Review of vibration compaction theory and intelligent compaction technology of high-speed railway subgrade
[J].DOI:10.3969/j.issn.1001-4632.2021.05.01 [本文引用: 1]
Estimating mechanistic parameters for subgrade using gyratory compaction with pressure distribution analyzer
[J].DOI:10.1061/(ASCE)MT.1943-5533.0002028
Comparing superpave gyratory compactor data to field cores
[J].DOI:10.1061/(ASCE)0899-1561(2004)16:1(78)
Lab assessment and discrete element modeling of asphalt mixture during compaction with elongated and flat coarse aggregates
[J].DOI:10.1016/j.conbuildmat.2018.06.059
Comparative analysis of gyratory and proctor compaction processes of unbound granular materials
[J].DOI:10.1080/14680629.2011.9695251
Evaluating laboratory compaction techniques of reclaimed asphalt pavement
[J].DOI:10.3141/2335-10
Evaluation of effect of compaction method on the macrostructure of asphalt mixtures through digital image processing under Brazilian conditions
[J].DOI:10.1016/j.conbuildmat.2019.116821 [本文引用: 1]
振动旋转压实级配碎石制样方法及力学性能试验
[J].
Sample preparation method and mechanical property test of graded crushed stone under gyrator and vibration compaction
[J].
旋转压实成型水泥稳定类基层材料试验
[J].
Experiment on gyratory compaction of cement stabilized base course materials
[J].
Internal structure characterization of asphalt concrete using image analysis
[J].DOI:10.1061/(ASCE)0887-3801(1999)13:2(88) [本文引用: 1]
道砟压实质量与颗粒运动关联特征及内在机制研究
[J].DOI:10.19713/j.cnki.43-1423/u.t20210240 [本文引用: 1]
Investigating correlation characteristics and intrinsic mechanism between compaction quality and particle movement of railway ballasts
[J].DOI:10.19713/j.cnki.43-1423/u.t20210240 [本文引用: 1]
Characterization of particle movement in Superpave gyratory compactor at meso-scale using SmartRock sensors
[J].DOI:10.1016/j.conbuildmat.2018.04.146 [本文引用: 2]
Evaluating gyratory compaction characteristics of unbound permeable aggregate base materials from meso-scale particle movement measured by smart sensing technology
[J].DOI:10.3390/ma14154287 [本文引用: 3]
Application of discrete element method to Superpave gyratory compaction
[J].DOI:10.1080/14680629.2012.694160 [本文引用: 3]
Using discrete element models to track movement of coarse aggregates during compaction of asphalt mixture
[J].DOI:10.1016/j.conbuildmat.2018.08.133 [本文引用: 1]
Air-void distribution analysis of asphalt mixture using discrete element method
[J].
DEM simulation of laboratory compaction of asphalt mixtures using an open source code
[J].DOI:10.1061/(ASCE)MT.1943-5533.0001069 [本文引用: 1]
Investigation of asphalt mixture internal structure consistency in accelerated discrete element models
[J].DOI:10.1016/j.conbuildmat.2020.118272 [本文引用: 1]
The bonded-particle model as a tool for rock mechanics research and application: current trends and future directions
[J].DOI:10.1080/12269328.2014.998346
Material model for simulation of progressive damage of composite materials using 3D Puck failure criterion
[J].DOI:10.1016/j.compstruct.2020.113435
A discrete numerical model for granular assemblies
[J].
Research on meso-scale deformation and failure mechanism of fractured rock mass subject to biaxial compression
[J].DOI:10.1007/s12517-021-07769-x [本文引用: 1]
Calibration of micro-scaled mechanical parameters of granite based on a bonded-particle model with 2D particle flow code
[J].DOI:10.1007/s10035-019-0889-3 [本文引用: 1]
平行黏结模型宏细观力学参数相关性研究
[J].
Relationship between particle micro and macro mechanical parameters of parallel-bond model
[J].
Forensic analysis and numerical simulation of a catastrophic landslide of dissolved and fractured rock slope subject to underground mining
[J].DOI:10.1007/s10346-021-01842-y [本文引用: 1]
Micromechanical simulation of porous asphalt mixture compaction using discrete element method (DEM)
[J].DOI:10.1016/j.conbuildmat.2021.124305 [本文引用: 1]