乌鸦搜索算法（crow search algorithm, CSA）是Askarzadeh^[1]于2016 年受乌鸦觅食行为启发而提出的群智能优化算法. CSA只模拟了乌鸦觅食过程中追踪和隐藏食物2个智能行为，具有易于理解实现、控制参数少、通用性好、全局搜索能力强等优点. CSA自提出以来，已在数值优化^[2-3]、特征选择^[4-5]、图像处理^[6-7]、最优潮流^[8-9]、经济负荷分配^[10-11]、云计算^[12-13]、控制工程^[14]、化学工程^[15]等领域获得了广泛的应用.

与其他智能优化算法相比，CSA算法在寻优过程中能保持较高的种群多样性，具有良好的全局搜索能力和鲁棒性. 但是，CSA只使用随机选择的个体来引导搜索，缺乏优秀个体或者精英个体的引导，极易造成算法在进化后期仍处于搜索发散的状态，种群陷入大量的局部最优区域（尤其是在求解高维度问题时），最终导致算法收敛速度慢，收敛精度低. 为此，大量学者提出许多策略和方法来改进原始CSA，主要包括以下3个方面. 1）控制参数改进策略. CSA中感知概率AP和飞行长度fl是控制算法性能的2个重要参数. 在赵世杰等^[16]提出的改进CSA中，AP、fl随迭代进程自适应动态改变以调控算法全局搜索性能和局部开采能力. Necira等^[17]基于广义帕累托概率密度函数，提出fl动态变化的改进CSA. 2）搜索方式改进策略. Zamani等^[3]提出基于邻域意识的CSA（conscious neighborhood-based crow search algorithm, CCSA），该算法包含3种策略，即基于邻域的局部搜索、基于非邻域的搜索和徘徊搜索.为了使原始 CSA 能够完成高维优化任务，Jain等^[2]通过添加莱维飞行、经验因子和适应调整因子来平衡算法勘探和开发间的关系. Moghaddam等^[18]在CSA中使用交叉和变异算子来提高算法性能，防止其陷入次最优区域. 3）混合其他优化算法. 这类型的改进 CSA通过混合其他算法的优势来弥补CSA的不足，如混合灰狼乌鸦搜索算法（hybrid grey wolf optimizer with crow search algorithm, GWOCSA）^[19]，混合蝙蝠乌鸦搜索算法（hybrid bat-crow search algorithm, BCSA）^[20]，混合海豚回声定位乌鸦搜索算法（hybrid dolphin echolocation and crow search optimization, DECSA） ^[21]，混合粒子群乌鸦搜索算法（crow search algorithm auto-drive particle swarm optimization, CSA-PSO）^[22]等.

虽然当前大多数的改进措施都能够一定程度地改善CSA 的性能，但算法种群多样性控制不足、全局勘探和局部开发平衡不够造成的，如算法收敛速度慢、收敛精度不高的问题仍然存在，即CSA仍具有改进空间. 本研究从种群多样性动态控制、搜索引导个体自适应选择和多种搜索方式随机执行3个角度出发，提出基于种群多样性的自适应乌鸦搜索算法（adaptive crow search algorithm based on population diversity, ACSA）. 新算法旨在通过种群多样性和多个搜索引导个体的自适应相互作用，实现算法全局勘探和局部开发的平衡，提高算法搜索精度和速度.

在CSA中，每只乌鸦代表优化问题的一个解. 假设优化问题解空间的维度为d，乌鸦群的规模为N，则第i只乌鸦在第t次迭代时的位置表示为 ${\boldsymbol{X}}_i^t = [x_{i,1}^t,\,x_{i,2}^t,\, \cdots,x_{i,d}^t]$ ； $i{{= 1,2,}}\cdots{\text{,}}\,N$ ； $t = 1, 2,\cdots{\text{,}}\,T$. 其中 $T$为最大迭代次数. 每只乌鸦都有记忆且能记住当前自己找到的最优食物源（即食物的隐藏地），假设乌鸦i在第t次迭代时的食物源为 ${\boldsymbol{m}}_i^t$. CSA的主要步骤如下.

1）随机初始化d维乌鸦种群C，并以C作为乌鸦群的初始记忆M（食物源集合）.

2）乌鸦i通过随机选择另一只乌鸦j并跟随实现其位置更新，位置更新方式为

(1) $ {{\boldsymbol{X}}}_{i}^{t+1}=\left\{\begin{array}{l}{{\boldsymbol{X}}}_{i}^{t}+{r}_{i}\times {\text{fl}}_{i}^{t}\times ({{\boldsymbol{m}}}_{j}^{t}-{{\boldsymbol{X}}}_{i}^{t}),\,\;\;\;\;\;\;\;\;{r}_{j}\geqslant {\text{AP}}_{j}^{t}\text{；} \\ {{\boldsymbol{X}}}_{r}^{t}{,} \;\,\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r}_{j} < {\text{AP}}_{j}^{t}\text{.} \end{array}\right. $

式中： ${r_i}$为[0,1]的随机数， ${\text{fl}}_i^t$为乌鸦i在第t次迭代时的飞行长度， ${\text{AP}}_j^t$为乌鸦j在第t次迭代时被跟随的感知概率， $ {\boldsymbol{X}}_r^t $为随机生成的新个体（位置）.

3）根据新位置的适应度值，更新乌鸦记忆，表达式为

(2) $ {\boldsymbol{m}}_i^{t+1} = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{X}}_i^{t{\text+}1},\;\;f({\boldsymbol{X}}_i^{t{\text+}1})\;{\text{ < }}f({\boldsymbol{m}}_i^t)\;;\;} \\ {{\boldsymbol{m}}_i^t,\;\;\;\;\;f({\boldsymbol{X}}_i^{t{\text+}1})\; \geqslant {\text{ }}f({\boldsymbol{m}}_i^t){\text{.}}} \end{array}} \right. $

式中： $ f(.) $为求得的函数值（适应度）. 对于最小化问题， $ f(.) $越小越优；对于最大化问题， $ f(.) $越大越优. 本研究以最小化问题为例.

使用欧几里得距离来度量2个个体的差异程度. 整个种群多样性的计算式为

(3) $ {d_{\rm{v}}} = \frac{{d_{\rm{f}}^{\rm{c}}}}{{d_{\rm{f}}^{\rm{o}}}}\;, $

(4) $ d_{\rm{f}}^{\rm{c}}{\text{ = }}\frac{1}{N}\sum\limits_{i = 1}^N {\left\| {{\boldsymbol{X}}_i^t - {{\boldsymbol{a}}^t}} \right\|} \;. $

式中： $d_{\rm{f}}^{\rm{c}}$为当前种群的差异程度， $d_{\rm{f}}^{\rm{o}}$为初始种群的差异程度， ${{\boldsymbol{a}}^t}$为第t代种群的均值个体（整个种群的中心）. 整个种群的差异程度可以通过每个个体与种群中心的距离来度量.

从CSA的位置更新式（1）可以看出，乌鸦种群主要通过向单个个体学习的方式来更新自身位置，因此随着种群的进化，乌鸦种群会逐渐集群化，种群多样性逐渐降低. 还可以看出，每个乌鸦个体实际上通过随机选择的个体来引导搜索，即整个种群未使用同一个个体（如最优个体）来引导. 这种方式虽然能减缓种群多样性的减小速度，使得整个种群在进化中后期仍能保持较好的多样性，但容易造成种群搜索方向发散，形成过多的局部最优，不利于算法在后期进行小范围的精细搜索，使得算法的求解精度和速度降低.为了解决这个问题，本研究构建多种引导个体，并结合种群多样性在进化不同阶段的变化，提出基于种群多样性的引导个体自适应选择策略，实现方法表述为

(5) $ {\boldsymbol{G}}_i^t = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{m}}_b^t,\;\;\,{d_{\rm{v}}} > \alpha ;} \\ {{\boldsymbol{m}}_e^t,\;\;\;\beta < {d_{\rm{v}}} \leqslant \alpha ;} \\ {{\boldsymbol{X}}_r^t,\;\;\;{d_{\rm{v}}} \leqslant \beta .\;\;\;} \end{array}} \right. $

式中： ${\boldsymbol{G}}_i^t$为当前代用于引导个体 ${\boldsymbol{X}}_i^t$进行搜索的个体（引导个体）； ${\boldsymbol{m}}_b^t$为从食物源集合中随机选择，且适应度优于 ${\boldsymbol{X}}_i^t$的食物源（优秀个体）； ${\boldsymbol{m}}_e^t$为当前食物源集合中最优的食物源（精英个体）； ${\boldsymbol{X}}_r^t$为随机生成的位置（随机个体）； $\alpha $、 $\;\beta $分别为选择优秀个体和精英个体引导的多样性阈值.所提策略的设计遵循了种群多样性和搜索引导方式在进化过程中的变化规律. 在进化初期，种群的多样性 ${d_{\rm{v}}}$较大，选择优秀个体作为种群进化的引导，既可以避免个体的盲目搜索，又可以避免种群多样性的过快衰减，符合算法在迭代初期应尽可能进行大范围勘探的要求. 在进化的中后期，种群的多样性 ${d_{\rm{v}}}$逐渐减小，这时选择精英个体作为种群进化的引导，可以促成算法从全局勘探向局部开发转变，避免算法搜索方向的发散. 当种群的多样性变得过小（小于 $\;\beta $）时，使用随机生成的个体作为搜索的引导，可以有效增加种群的多样性，跳出局部最优，使种群回到精英个体引导的搜索方式. 因此，所提策略体现了种群多样性和多种搜索引导个体的自适应相互作用，即种群的多样性变化体现了进化的不同阶段，可以自适应选择不同的搜索引导方式，而不同的引导方式又可以反过来改变种群的多样性，扩大算法的搜索范围和加强算法的搜索精细度，实现算法全局勘探和局部开发的平衡.

CSA的搜索方式（个体位置更新方式）单一，既不利于算法全局勘探，也不利于算法局部开发，这也是造成CSA收敛精度不高、收敛速度慢的主要原因. 本研究借鉴正余弦算法（sine cosine algorithm, SCA）^[23]搜索方式的特性，构建基于线性递减、混合正余弦震荡递减的多种飞行长度控制参数及相应的多种搜索方式为

(6) $ {\boldsymbol{X}}_i^{t+1} = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{X}}_i^t+k \sin \;(2{\text{π }} {r_1}) \times {\rm{fl}} \left| {{\boldsymbol{G}}_i^t - {\boldsymbol{X}}_i^t} \right|,\;{r_{\rm{c}}} = 1;} \\ {{\boldsymbol{X}}_i^t+k \cos \;(2{\text{π }} {r_1}) \times {\rm{fl}} \left| {{\boldsymbol{G}}_i^t - {\boldsymbol{X}}_i^t} \right|,{r_{\rm{c}}} = 2;} \\ \begin{gathered} {\boldsymbol{X}}_i^t+k \times {\rm{fl}} ({\boldsymbol{G}}_i^t - {\boldsymbol{X}}_i^t),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_{\rm{c}}} = 3; \\ k \times {\rm{fl}}\times {r_2} {\boldsymbol{G}}_i^t,\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_{\rm{c}}} = 4. \\ \end{gathered} \end{array}} \right. $

式中： ${r_1}$、 ${r_2}$为[0,1]的随机变量； $\;{r_c}$为{1, 2, 3, 4}的随机整数变量；按照CSA，取fl=2；k、 $ k \sin\; (2{\text{π }} {r_1}) $和 $ k \cos \;(2{\text{π }} {r_1}) $均为乌鸦飞行长度的控制参数，k随进化代数线性减小，

(7) $ k{\text{ = }}2\left(1 - \frac{t}{T}\right)\;. $

使用等概率的方式随机选择某种搜索方式的主要原因如下. 1）尽可能保持算法结构简单，避免引入过多的选择控制参数或复杂的选择机制. 这种思想也体现在SCA中（正弦、余弦搜索方式也采用等概率选择方法）. 2）尽可能保持种群的多样性，避免某种搜索方式过多或过少使用，以期产生多种不同的高质量解. 3）虽然本研究采用等概率的搜索方式选择方法，但实质上式（6）中的4种搜索方式各具优点（擅长求解不同类型的函数），可以形成优势互补.

比较本研究所提搜索方式与SCA的搜索方式，可以发现：本研究只是借鉴了SCA的搜索理念，即使用正余弦函数构造乌鸦飞行长度的控制参数，以期产生高质量的多样性解. 2种搜索方式的本质区别是ACSA根据种群的多样性自适应选择不同的引导个体 $ {\boldsymbol{G}}_i^t $来指导当前的搜索，而SCA在搜索过程中只使用最优个体来指导搜索，因此ACSA能够比SCA搜索到更广阔的范围. 进一步比较ACSA与CSA的异同，可以发现：1）ACSA的前3种搜索方式与CSA的第1种搜索方式在计算结构上一致，ACSA的第4种搜索方式对应CSA的第2种搜索方式，其计算结构也一致；2）两者的根本区别一方面在于ACSA在乌鸦飞行长度的控制上使用线性减小（k）和震荡减小（ $k \sin \;(2{\text{π }} {r_1})$、 $k \cos \;(2{\text{π }} {r_1})$）控制参数，而CSA只使用随机变量控制参数 ${r_i}$；另一方面ACSA根据种群的多样性自适应选择不同的引导个体 $ {\boldsymbol{G}}_i^t $来指导当前的搜索，而CSA只使用随机选择个体 ${\boldsymbol{m}}_j^t$（第1种搜索方式）和随机生成的个体（第2种搜索方式）来引导搜索. 鉴此，ACSA仍然遵循乌鸦觅食寻优的基本原理，但与CSA相比，ACSA更兼顾算法早期注重全局勘探、中后期逐渐过渡到局部开发的均衡，且具备跳出局部最优的能力.

ACSA算法的伪代码如算法1所示.

算法1　　基于种群多样性的自适应乌鸦搜索算法

输入：目标函数，种群规模N，最大迭代次数 $T$输出：当前全局最优解1. 　初始化乌鸦群位置，初始化乌鸦群记忆2. 　计算每只乌鸦的适应度值3. 　 $t \leftarrow 0$4. 　while $t \leqslant T$5. 　根据式（3）计算种群的多样性6. 　根据式（5）选择搜索引导个体 ${\boldsymbol{G}}_i^t$7. 　根据式（6）计算新一代个体 ${\boldsymbol{X}}_i^{t+1}$8. 　检查新个体的可行性9. 　评估新个体的适应度函数10.　更新记忆11.　 $t \leftarrow t+1$12.　end while

以ACSA中最耗时操作的时间复杂度总和来计算算法的时间复杂度. 设种群规模为N，问题空间维度为D，算法最大迭代次数（种群进化代数）为T，适应度（函数）计算复杂度为 $O(f)$，2个个体间欧式距离的计算复杂度为 $O(d)$. 则种群在一次迭代过程中，种群多样性的计算复杂度为 $O(Nd)$，种群更新的计算复杂度为 $O(ND)$，计算种群适应度（函数评估）的复杂度为 $O(Nf)$，ACSA的计算复杂度为

(8) $ \begin{split} {O_{{\text{ACSA}}}} =& O(T(Nd+ND+Nf)) =\\ & O(TNd+TND+TNf)\;. \\ \end{split} $

使用同样的方法，得到CSA的计算复杂度为

(9) $ {O_{{\text{CSA}}}} = O(TND+TNf))\;. $

显然，ACSA的时间复杂度比CSA多出了种群多样性的计算部分 $O(TNd)$.

为了验证ACSA 的有效性，选取文献[24]中使用的23个基准测试函数F₁~F₂₃进行实验，包括单峰测试函数、多峰测试函数和固定维数多峰测试函数. 将ACSA与CSA^[1]、SCA^[23]、SCCSA^[25]、ICSA^[26]、MTDE^[27]、BLPSO^[28]、HHO^[29]和EO^[30]等8个优秀的智能优化算法进行比较. 所有实验如无特别说明，比较算法的种群规模都设置为20，使用函数评价次数（function evaluations, FEs）作为算法终止的判断条件，FEs_max为最大函数评价次数，设置FEs_max=20 000. ACSA的多样性阈值参数设置为 $\alpha {\text{ = 0}}{\text{.7}}$， $\;\beta {\text{ = 0}}{\text{.3}}$. 比较算法的其余参数都按照相应文献中的方式设置. 使用Matlab 2018b编程实现各算法，测试机CPU为I7 2.2 GHz，内存为16 GB，操作系统为Windows10. 每种实验、每个算法都独立执行30次，通过最优函数值的均值、标准差、Wilcoxon符号秩检验和Friedman检验来衡量算法的优劣.

$\alpha $用于控制使用随机选择的优秀个体引导搜索的强度，其值须反映出算法处于迭代的初期，以便于使用随机优秀个体进行全局搜索，因此须设置 $\alpha $∈[0.5,1.0]，本研究设置 $\alpha $的取值范围为 $ \left\{ {0.5,\;0.6,\;0.7,\;0.8,\;0.9,\;1.0} \right\} $. $\;\;\beta $用于控制使用随机生成的新个体引导搜索的强度，在算法迭代后期，加入少量随机生成的新个体，就能明显提高种群的多样性，其作用类似于进化算法的“变异”操作，因此须设置 $\;\beta $为较小的数值，本研究设置 $\;\beta $的取值范围为 $ \left\{ {0.1,\;0.2,\;0.3} \right\} $. 在基准测试函数中选择4个极难求得最优解的函数作为每种函数类型的代表，分别为F₅、F₁₂、F₁₅和F₂₀. 通过这些函数来测试不同 $\alpha $、 $\;\beta $组合下ACSA的收敛性能（函数均值avg），并使用Friedman检验来确定最优的阈值组合，如表1所示. 表中，R为均秩. 可以看出，当 $\alpha {\text{ = 0}}{\text{.7}}$、 $\;\beta {\text{ = 0}}{\text{.3}}$时，函数的均秩最小，因此ACSA的种群多样性阈值分别设置为 $\alpha $=0.7、 $\;\beta $=0.3.

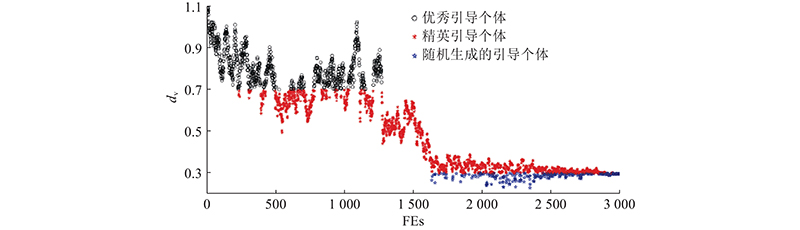
使用F₅作为该实验的测试函数，设置FEs_max=3 000，作ACSA在不同进化时期使用各种搜索引导个体的分布图，如图1所示. 可以看出：1）通过控制种群多样性阈值，种群的多样性能够很好地反映出算法的不同迭代时期，且多样性总体变化趋势是收敛的. 在算法迭代的初期（FEs<1 300），种群多样性 $d_{\rm{v}}$的数值存在大大超过阈值 $\alpha $（0.7）的情况，这样可以保证算法进行充足的全局搜索（通过随机选择的优秀个体引导）. 在算法迭代的中期（1 300<FEs<2 000）， $d_v$的数值绝大部分都大于 $\;\beta $（0.3）的，这时使用精英个体引导算法搜索，可以使种群逐渐向高质量区域靠拢，提高算法的收敛精度和速度. 此外，该阶段存在少量使用随机生成个体引导搜索的情况，这样可以避免算法过早陷入局部最优. 在算法迭代的后期（FEs>2 000）， ${d_{\rm{v}}}$∈(0.2, 0.4)，并逐渐收敛于0.3. 该阶段算法根据种群的多样性动态选择精英个体或随机生成的个体来引导搜索，使得算法可以在当前的最优解附近进行充分的精细化搜索，当种群多样性的数值小于 $\;\beta $的时，又通过引入随机生成个体来改善种群的多样性，增加算法跳出局部最优、继续探索有潜质新区域的概率. 2）不同引导个体的使用可以反作用于种群多样性，使得种群多样性呈动态变化的过程.

总之，基于种群多样性的引导个体自适应选择策略使种群在进化过程中维持了良好的多样性，兼顾了算法的全局探测和局部开发.

为了验证每种搜索方式的求解性能，选择8个代表性函数测试各搜索方式，并与融合使用多搜索方式的ACSA进行比较，结果均值如表2所示. 可以看出，搜索方式各具优势，擅长求解不同类型的函数. 正、余弦搜索方式（r_c=1、2）擅长求解最优解不在原点且位于复杂区域的函数，如F₅、F₁₂、F₁₅和F₂₀，主要原因是这2种方式使用震荡递减的飞行控制参数，有利于算法跳出局部最优. r_c=4的搜索方式擅长求解最优解位于原点的函数，如F₁、F₇和F₉，原因是这种搜索方式通过对引导个体 ${\boldsymbol{G}}_i^t$的随机伸缩操作来产生新个体，有利于算法在 ${\boldsymbol{G}}_i^t$和原点间的区域进行高强度搜索. 虽然r_c=3的搜索方式在大部分情况下不是最优的搜索方式，但也能有效求解复杂函数和最优解在原点的函数，特别是求解固定低维的多峰函数F₁₅、F₂₀和F₂₃，因此当组合使用多种搜索方式时，该搜索方式仍然可以在优化过程中发挥重要作用，提供一些高质量的解. 测试结果表明，在大多数情况下，使用等概率搜索方式组合的ACSA优于任一单一的搜方式. 主要原因如下：1）各搜索方式具有不同的特征，形成优势互补，使得ACSA在求解各类基准函数时，表现出优良的性能；2）等概率使用多种搜索方式，提高了种群的多样性，增加了ACSA找到优秀解的概率.

为了验证ACSA的整体性能，将ACSA与CSA、SCCSA、ICSA、SCA、MTDE、BLPSO、EO和HHO在23个测试函数下进行对比，对比内容包括均值avg、标准差std、和总平均运行时间t，实验结果如表3、4所示. 表中，所有算法中最好的结果用粗体表示. 在大多数情况下，ACSA的性能都优于其他算法，具有最小的函数均值和标准差. 在23个测试函数中，ACSA能求得15个函数的理论最优值，分别为F₁~F₄、F₈~F₉、F₁₁、F₁₄、F₁₆~F₁₈、F₁₉和F₂₁~F₂₃. 其中F₁~F₄为最优解在原点的单峰函数，ACSA都能找到理论最优值. 对于最优解不在原点而位于狭长峡谷中的单峰函数F₅，只有ACSA的收敛精度可达到10⁻⁴数量级，说明ACSA具有良好的局部搜索能力. 对于多峰函数F₈、F₉、F₁₁，ACSA找到了理论最优解，其中F₈为最优解不在原点的复杂函数，其在远离理论最优解的地方, 存在大深度的局部值，极易造成算法陷入局部最优. 对于其余多峰函数，相较于其他算法，ACSA求得了最小的函数值，说明ACSA具有良好的全局搜索能力. 对于10个维度固定的多峰函数，ACSA在8个函数上获得了最优解. 在F₁₅上，ACSA稍劣于MTDE；对于F₂₀，ACSA虽未求得最优解，但其求解精度在所有算法中最高，说明ACSA在求解固定维度函数时，具有良好的性能. 综上所述，本研究提出的基于种群多样性的引导个体自适应选择策略和混合正余弦的多搜索方式的组合是有效的. ACSA很好地兼顾了全局搜索的覆盖性和局部搜索的精细性，既增强了种群的多样性，又避免了搜索的发散性，在一定程度上解决了CSA收敛精度不足、收敛速度慢的缺点. 在运行时间方面，ACSA的耗时稍长于CSA，因为每次迭代时，ACSA都须计算种群的多样性，这也符合本研究的时间复杂度分析. 在平均总运行时间上，SCA耗时最少，MTDE耗时最多，ACSA在所有算法中排名第6，稍多于CSA和ICSA，因此ACSA的运行时间是完全可接受的.

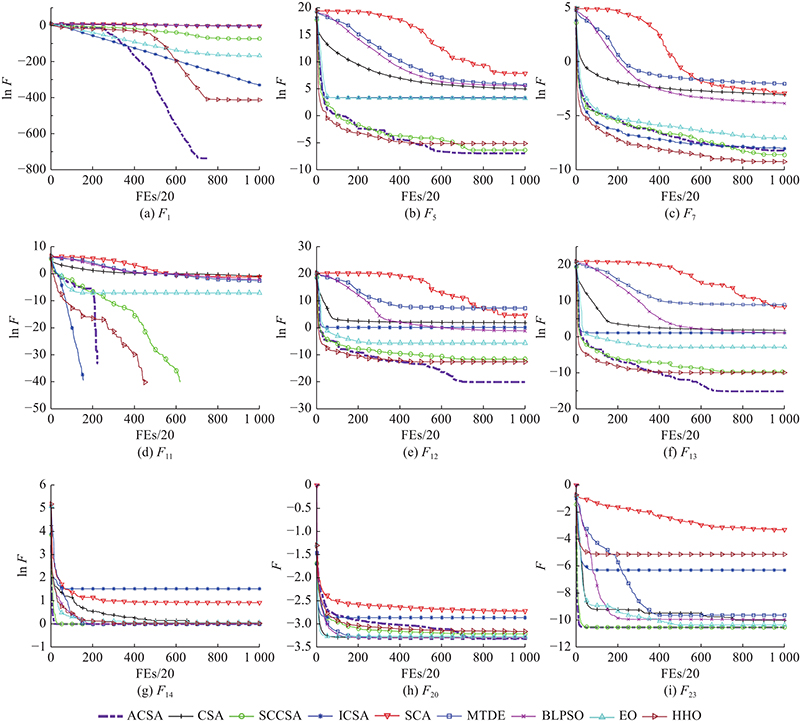
进一步分析各算法的收敛速度和进化过程，选择9个函数为代表绘制各算法的收敛曲线，如图2所示. 图中，为了清晰地观察和识别不同算法的收敛曲线，除函数值为负数的函数外，对每个函数值求自然对数ln F. 对于最优解在原点的单峰函数F₁，ACSA的收敛速度最快，且明显快于对比算法；对于最优解也在原点的多峰函数F₁₁，ACSA的收敛稍慢于SCCSA，但快于其余算法. 对于最优解不在原点且极难求解的函数F₅（单峰）、F₁₂（多峰）、F₁₃（多峰）和F₂₀（固定维度多峰），ACSA在进化的后期仍能保持搜索能力，求得了最好的收敛精度，而其他算法陷入停滞. 对于函数F₇，ACSA的收敛精度虽然劣于HHO、SCCSA，但在进化后期，收敛曲线仍保持下降趋势. 对于极值同样难求得的函数F₁₄、F₂₃，ACSA的收敛曲线几乎与SCCSA的重合，都在产生极少EFs时求得最优值. 由此可见，ACSA很好地兼顾了算法的收敛精度和收敛速度.

如表5所示，使用Wilcoxon符号秩检验和Friedman检验^[31]从非参数统计分析的角度进一步验证ACSA的有效性和优越性，设置显著性水平为0.05，均秩由Friedman检验求得. 表中，+/=/−分别为在Wilcoxon符号秩检验中，ACSA优于、相当于或劣于对比算法的测试函数数量. 根据Wilcoxon符号秩检验，ACSA在绝大多数情况下优于或相当于对比算法，仅有1个函数劣于SCCSA、MTDE和HHO. 在Friedman检验中，ACSA获得了最小的均秩. 检验结果证明，ACSA在统计上相较于其他算法具有一定优势.

本研究依据种群在进化不同阶段的多样性变化，提出基于种群多样性的搜索引导个体自适应选择策略. 结合正余弦搜索理念，提出混合正余弦的多种飞行长度控制参数和相应的个体位置更新方式；将自适应选择策略和位置更新方式融入CSA，提出基于种群多样性的自适应乌鸦搜索算法（ACSA）. 通过单峰、多峰和固定维度多峰3种类型共23个测试函数进行试验验证，并从收敛精度、收敛速度、非参数统计等角度对算法进行比较分析. 试验结果表明，相较于对比算法，ACSA的性能更好，优势较明显，不但实现了算法全局勘探和局部开发的平衡，也实现了算法收敛精度和收敛速度的平衡. 后续的研究工作将进一步改进ACSA，使其适用于求解多峰优化的多极值点问题；此外还将结合算法对工程实践中的高维优化问题、多目标优化问题和排列组合的离散优化问题进行应用研究.