随着科技和经济的快速发展,人类社会面临的决策问题及评估情境越来越复杂,大量充满多样性、不确定性和复杂性的信息对科学决策的水平要求越来越高[1]. 多属性决策问题作为现代决策科学的重要组成部分,在政治、经济、管理、设计、投资等专业领域都有重要的应用价值[2]. 由于产品造型设计属性信息存在不完全性和差异性,设计决策专家存在自身偏好、知识结构、科研经验以及教育水平等方面的差异,使得决策结果在很大程度上也存在不确定性和模糊性[3]. 如何选择具有针对性且客观高效的多属性决策方法,避免产品造型设计存在的信息模糊、数据缺失和真实数值偏差等不确定性问题,对于提高最佳备选方案决策的准确性具有重要的现实意义.
产品设计方案多属性决策研究存在部分不足之处. 1)缺乏综合考虑决策专家在多属性决策中存在的犹豫程度、情绪状态或主观偏好等心理行为特征因素. 大多数决策方法基于期望效用理论进行多属性决策,即假设获得的定量信息均为决策专家在完全理性的理想状态下得出。在实际多属性决策过程中,决策专家个体存在局限性,难以给出确切的实际属性值,且存在非理性地表达决策信息以获得期待备选方案排名的策略操控问题. 2)现有研究对存在相似决策观点的专家权重分配过程考虑不足,忽略了少数决策专家持积极意见、多数持消极意见的情况,导致多数决策专家不满意的备选方案获得较好排序. 3)缺乏能够融合多维数据可视化识别的多属性决策方法. 针对产品造型设计方案的多属性决策多基于公式推导和数据计算的虚拟模型方法,无法对备选方案的决策结果进行立体空间展示. 针对上述不足,本研究提出基于单值中智集(single-valued neutrosophic sets,SVNS)和云模型聚类的产品造型设计多属性决策方法,利用云模型聚类对相似决策专家进行集群划分的优点,得到有效的决策专家权重,通过将SVNS的3个隶属度值映射为单值中智立方体(single-valued neutrosophic cube,SVNC),决策产品造型设计方案,解决多属性决策问题中决策专家心理行为特征考虑不足的弊端,构建更加客观与科学的汽车造型设计评价体系.
1. 基本概念
1.1. SVNS理论
令X为对象空间,x为空间内任一元素. 集合
其中TA(x)、FA(x)、IA(x)满足
对任意
设X为给定论域,x为空间内任一元素. 集合
式中:
1.2. 云模型聚类理论
云的数字特征表示为
式中:
对于任意2朵云
2. 产品造型设计多属性决策
2.1. 基于SVNS的产品造型设计多属性决策
2.1.1. 决策系统框架
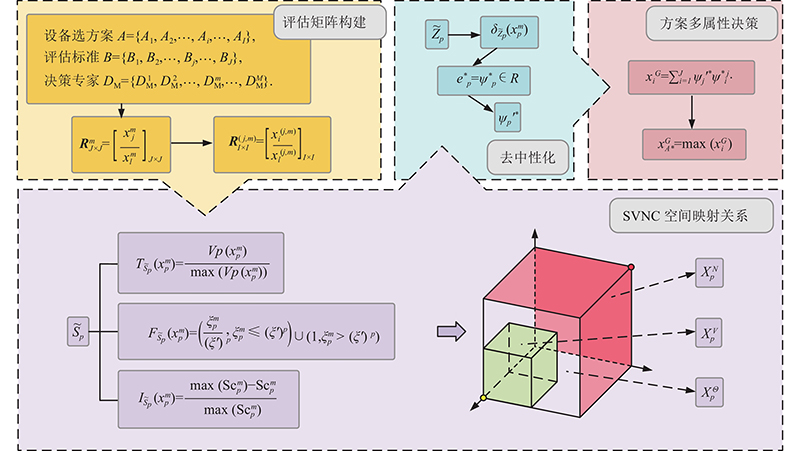
如图1所示为基于SVNS的产品造型设计多属性决策框架,共分为4个部分.
图 1
图 1 基于单值中智集(SVNS)的产品造型设计多属性决策框架
Fig.1 Multi-attribute decision-making framework for product styling design based on single-valued neutrosophic sets (SVNS)
1)评估矩阵构建. 设评估过程有I个备选方案A,J个标准属性B,M位决策专家D. 决策专家分别构造标准属性集和备选方案集的成对比较比率平方矩阵. 2)SVNC空间映射关系. 每个离散SVNS的3个独立隶属度转换为在SVNC三维空间中的映射,分为不可接受区域
2.1.2. 评估矩阵构建
SVNS采用的附加符号分别为第m位专家在评估第p个标准或备选方案时的可信度或投票权
每位专家为标准集和备选方案集分别构造成对比较比率的平方矩阵
使用
应用相对测量法,导出有序元素
检查每个比较矩阵的一致性,确保数据的传递性和互易性[19]. 由文献[20]可知,一致性比率
式中:
2.1.3. SVNC空间映射关系
将SVNS的3个独立隶属度映射在三维空间中形成SVNC,如图2所示. 图中,V、N为点. 不可接受的SVNC区域为面
图 2
图 2 单值中智集(SVNC)空间划分
Fig.2 Space division of single-valued neutrosophic sets (SVNC)
此区域所有元素应提前排除,最大不可忍受点为
此区域所有元素能够做出重大贡献. 理想SVNS可靠区域点为
此区域所有元素能够做出轻微贡献.
2.1.4. 去中性化
1)将
式中:
2)重心法(center of gravity,COG)反模糊化
每个标准的折中清晰值
须保留备选方案的差异性,对各标准优先级权重
2.1.5. 方案多属性决策
由总体加权和计算方案的总体优先级得分
式中:
所提出方法通过Matlab实现.
2.2. 基于云模型聚类的决策专家权重分配
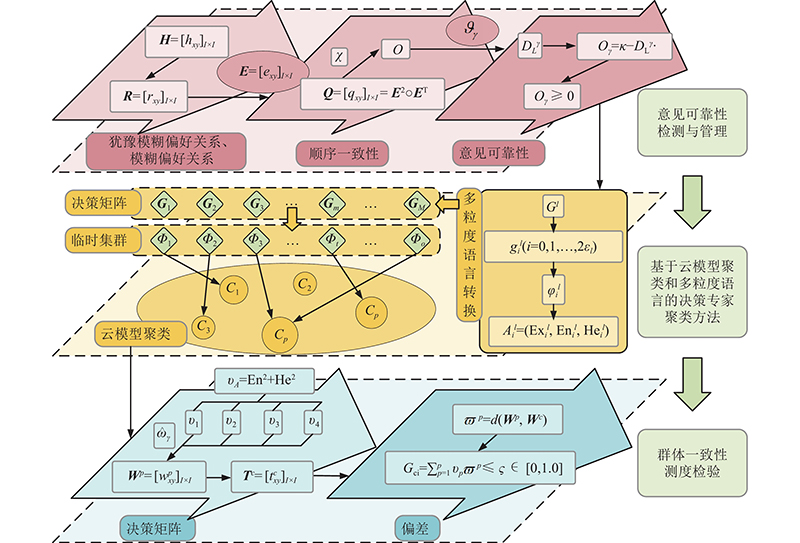
2.2.1. 决策专家权重分配框架
如图3所示,建立基于云模型聚类的决策专家权重分配框架。决策框架分为以下3个部分. 1)意见可靠性检测与管理. 给出备选方案集和决策专家集后,获得备选方案矩阵的犹豫模糊偏好关系(hesitant fuzzy reciprocal preference relations,HFPR )和模糊偏好关系(fuzzy preference relation,FPR);由邻接矩阵获得哈达玛乘积,引入长度为3的循环数,获得顺序一致性指数(ordinal consistency index,OCI);计算个人意见和集体意见的偏差,获得意见可靠性指数(opinionreliability index,ORI). 2)基于云模型聚类和多粒度语言的决策专家聚类方法. 将自然语言评估集合中的任一元素转换为对应的云模型,通过计算获得云;将上个阶段筛选后合格决策专家的每个单独的决策矩阵分配到临时集群,根据聚类的阈值,形成
图 3
图 3 基于云模型聚类的决策专家权重分配框架
Fig.3 Framework for weight allocation of decision-making experts based on cloud model clustering
2.2.2. 意见可靠性检测与管理
使用犹豫模糊偏好关系
若
设节点集
式中:
式中:
式中:
由于决策专家的意见须进行矛盾检测,引入可接受的可靠性水平,意见可靠性指数定义为
式中:
2.2.3. 基于云模型聚类和多粒度语言的决策专家聚类方法
由于决策专家数量多且存在差异性,很难使用同一标准的语言评估集准确表达其评估意见,因此,决策专家根据需求选择不同语言短语数目的多粒度语言评估集,更能发挥决策专家的主观能动性.
自然语言评估集合
式中:
式中:设
算法1 云模型聚类算法
输入:云模型决策矩阵
输出:集群数量
1. 将每个单独的决策矩阵分配到临时集群
2. 计算相似性矩阵
3. 最大相似性集群
4. while
5. 将集群
若
6. 计算新集群和其余每个集群之间的相似性,获得相似性矩阵
7. 最大相似性集群
8. return
2.2.4. 群体一致性测度检验
设云
子集群
式中:
获得
同理,获得群决策矩阵
式中:
若
3. 应用案例
3.1. 案例分析与决策过程
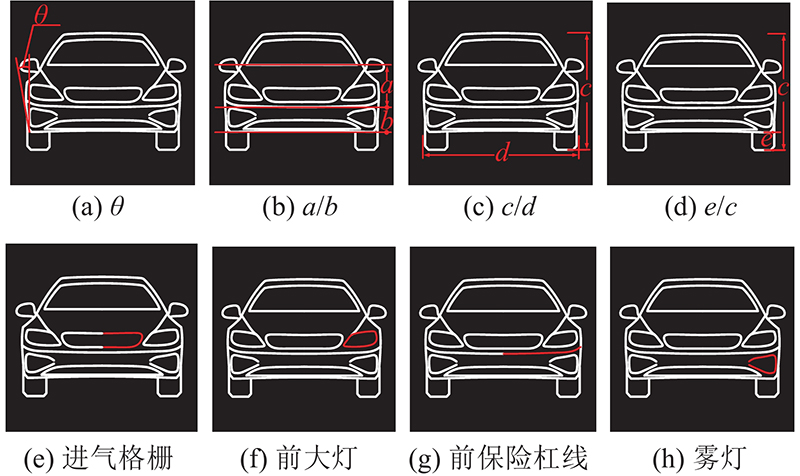
如图4所示,以6个家用汽车前视图造型设计方案
图 4
图 5
图 5 汽车前视图造型设计方案的评估标准图例
Fig.5 Legend of evaluation criteria for car front view styling design scheme
表 1 备选方案成对比较比率平方矩阵
Tab.1
| A | | |||||
| A1 | A2 | A3 | A4 | A5 | A6 | |
| A1 | 1 | 1/5 | 3 | 1/2 | 1/3 | 4 |
| A2 | 5 | 1 | 7 | 3 | 2 | 9 |
| A3 | 1/3 | 1/7 | 1 | 1/3 | 1/5 | 1/2 |
| A4 | 2 | 1/3 | 3 | 1 | 1/2 | 5 |
| A5 | 3 | 1/2 | 5 | 2 | 1 | 6 |
| A6 | 1/4 | 1/9 | 2 | 1/5 | 1/6 | 1 |
表 2 各决策专家对各标准的权重、一致性比率和置信度得分
Tab.2
| | | | | | | | | | |
| | 0.028 3, 90 | 0.158 8, 85 | 0.041 8, 100 | 0.020 4, 80 | 0.330 6, 100 | 0.250 9, 95 | 0.070 4, 85 | 0.098 9, 90 | 3.46 |
| | 0.067 7, 100 | 0.153 1, 85 | 0.030 7, 80 | 0.022 2, 95 | 0.345 9, 100 | 0.231 8, 90 | 0.045 6, 100 | 0.103 0, 85 | 2.49 |
| | 0.066 7, 85 | 0.173 8, 75 | 0.029 9, 80 | 0.022 3, 70 | 0.358 8, 85 | 0.218 3, 70 | 0.043 4, 90 | 0.086 8, 75 | 5.61 |
| | 0.067 1, 85 | 0.108 3, 90 | 0.019 7, 80 | 0.027 8, 90 | 0.349 2, 85 | 0.230 2, 75 | 0.047 1, 95 | 0.150 6, 95 | 4.10 |
| | 0.063 8, 75 | 0.106 7, 80 | 0.018 9, 70 | 0.028 9, 85 | 0.359 5, 80 | 0.225 8, 70 | 0.048 7, 90 | 0.147 6, 90 | 5.20 |
| | | | | | | | | | |
| | 0.068 5, 100 | 0.148 1, 80 | 0.030 6, 75 | 0.021 0, 95 | 0.367 1, 90 | 0.221 9, 85 | 0.044 5, 100 | 0.098 4, 90 | 3.15 |
表 3
决策专家
Tab.3
| | | | | | | | |
| B1 | 0.102 5, 100 | 0.413 2, 95 | 0.050 6, 80 | 0.152 8, 85 | 0.247 9, 100 | 0.032 9, 90 | 1.99 |
| B2 | 0.095 5, 85 | 0.410 6, 65 | 0.049 1, 45 | 0.150 5, 60 | 0.254 6, 75 | 0.039 6, 75 | 5.13 |
| B3 | 0.087 8, 85 | 0.424 0, 80 | 0.051 7, 85 | 0.143 8, 95 | 0.255 4, 65 | 0.037 3, 100 | 3.28 |
| B4 | 0.096 4, 80 | 0.411 9, 85 | 0.049 6, 75 | 0.145 1, 80 | 0.255 9, 70 | 0.041 1, 75 | 4.96 |
| B5 | 0.100 8, 95 | 0.425 6, 100 | 0.039 1, 90 | 0.138 4, 85 | 0.253 7, 95 | 0.042 5, 70 | 3.46 |
| B6 | 0.090 8, 60 | 0.432 0, 65 | 0.047 0, 85 | 0.136 2, 75 | 0.255 6, 50 | 0.038 5, 45 | 7.32 |
| B7 | 0.096 1, 65 | 0.424 6, 70 | 0.049 4, 65 | 0.142 2, 60 | 0.255 5, 75 | 0.032 3, 80 | 2.76 |
| B8 | 0.096 3, 85 | 0.418 4, 100 | 0.049 4, 80 | 0.151 5, 90 | 0.251 2, 60 | 0.033 2, 85 | 1.54 |
图 6
根据各点位置,对点的可靠性估计值进行分类. 1)必须排除的不可接受SVNC区域的点. 存在100%假特征:
存在100%假和100%不确定度特征:
2)对最终决策结果有重大影响的点:
3)对最终决策结果有轻微贡献的点:
表 4 所有备选方案在各标准下的总体优先级得分
Tab.4
| B | | |||||
| A1 | A2 | A3 | A4 | A5 | A6 | |
| B1 | 0.101 2 | 0.370 5 | 0.034 5 | 0.173 6 | 0.264 9 | 0.069 5 |
| B2 | 0.100 3 | 0.367 3 | 0.034 9 | 0.175 5 | 0.264 7 | 0.069 9 |
| B3 | 0.100 7 | 0.364 0 | 0.036 0 | 0.178 0 | 0.268 3 | 0.068 6 |
| B4 | 0.111 0 | 0.357 5 | 0.035 0 | 0.166 4 | 0.268 6 | 0.064 5 |
| B5 | 0.106 1 | 0.364 2 | 0.034 4 | 0.138 4 | 0.261 2 | 0.071 6 |
| B6 | 0.103 4 | 0.355 7 | 0.033 9 | 0.175 1 | 0.274 9 | 0.071 9 |
| B7 | 0.105 6 | 0.367 3 | 0.034 1 | 0.166 9 | 0.264 0 | 0.070 6 |
| B8 | 0.105 7 | 0.365 4 | 0.035 3 | 0.171 3 | 0.263 2 | 0.069 4 |
| | 0.104 3 | 0.363 2 | 0.034 5 | 0.161 4 | 0.265 9 | 0.070 7 |
3.2. 决策专家权重分配过程
根据计算决策专家的权重分配,20位决策专家使用HFPR对6个备选方案进行评估,获得原始HFPR数据
表 5
决策专家
Tab.5
| A | hxy | ||
| | | | |
| A1 | 0.5 | 0.4, 0.3, 0.5 | 0.5, 0.6, 0.7 |
| A2 | 0.6, 0.7, 0.5 | 0.5 | 0.7, 0.8, 0.9 |
| A3 | 0.5, 0.4, 0.3 | 0.3, 0.2, 0.1 | 0.5 |
| A4 | 0.5, 0.6, 0.7 | 0.2, 0.3, 0.4 | 0.5, 0.8, 0.7 |
| A5 | 0.6, 0.8, 0.5 | 0.3, 0.4, 0.5 | 0.7, 0.8, 0.9 |
| A6 | 0.3, 0.2, 0.4 | 0.1, 0.3, 0.2 | 0.4, 0.2, 0.3 |
表 6 决策专家的意见可靠性推导值
Tab.6
| | | | | | | |
| | 0 | −0.333 | 0 | 1 | 0.049 | 0.071 |
| | 0 | 0 | 0 | 0 | 0.052 | 0.068 |
| | 0 | 0 | −1 | 1 | 0.056 | 0.064 |
| | 0 | −1.333 | 0 | 1 | 0.071 | 0.049 |
| | | | | | | |
| | 0 | 0 | −0.667 | 1 | 0.042 | 0.078 |
表 7 决策专家对各备选方案在各标准下决策专家的云模型数据
Tab.7
| B | | |||||
| A1 | A2 | A3 | A4 | A5 | A6 | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
| | | | | | | |
表 8 3个模糊偏好关系下的群决策矩阵
Tab.8
| A | | | |||||
| | | | | | | ||
| | R1 | 0.128 0 | 0.162 7 | 0.097 2 | 0.139 2 | 0.170 1 | 0.093 2 |
| R2 | 0 | 0.181 4 | 0.075 2 | 0.150 1 | 0.160 4 | 0.086 3 | |
| R3 | 0 | 0.164 2 | 0.092 5 | 0.151 5 | 0.171 3 | 0.096 1 | |
| | |||||||
| | R1 | 0.162 8 | 0.184 6 | 0.109 4 | 0.156 2 | 0.174 0 | 0.128 0 |
| R2 | 0.169 6 | 0.187 0 | 0.116 1 | 0.148 7 | 0.156 4 | 0 | |
| R3 | 0.159 9 | 0.189 2 | 0.111 0 | 0.146 3 | 0.172 1 | 0 | |
3.3. 决策方法比较
3.3.1. 准确性对比
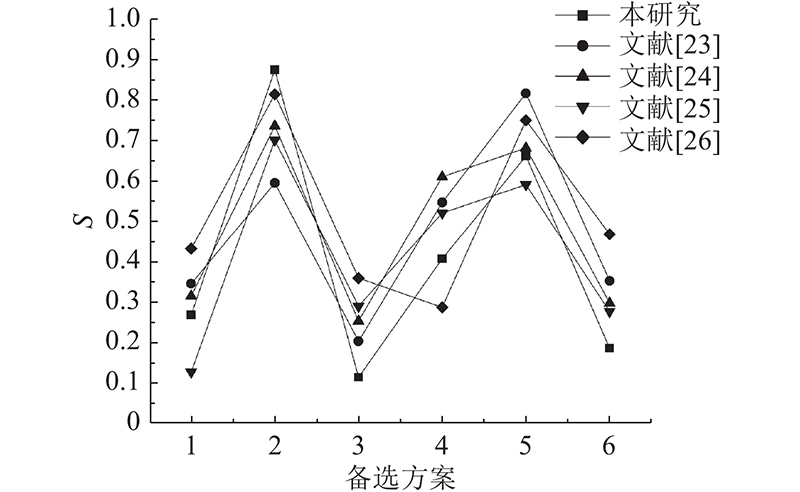
图 7
图 7 不同决策方法的总体得分结果对比图
Fig.7 Comparison chart of overall score results of different decision methods
1)本研究所提方法中SVNS理论由3个独立的隶属度共同构建,具备一定的容错范围,相较对比方法更具有实际的应用意义. 不确定性隶属度充分考虑决策专家的态度偏好,避免了不一致性较高或置信度低的备选方案获得较高评分的情况. 文献[23]仅考虑决策专家对备选方案的不确定性偏好,导致备选方案5比2获得更高得分. 2)通过意见可靠性检验对专家权重分配进行优化,排除自身存在较大矛盾值的专家个体,能够避免决策专家评估异常值对后期评估结果造成的不利影响. 文献[23]未将与群体评估结果相差甚远的决策专家排除,导致最终排序结果出现偏差. 3)由于其他方法均出现得分相似的情况(如文献[23]中的备选方案1与6、2与4,文献[24]、[26]中的备选方案1、3和6,文献[23]中的备选方案3、6),导致无法判断两个方案的绝对更优选择. 相比之下,本研究所提方法可以追溯SVNC空间映射关系进行比较,更具差异性和辨识度.
3.3.2. 性能对比
将本研究所提方法与SVNS、扩展多准则妥协解(VIKOR)、BWM方法进行决策性能比较,分别对4个和6个备选方案进行多轮决策,结果如表9所示. 表中,e为决策误差,t为运算时间. 在决策误差方面,本研究所提方法获得最小决策误差为4.82%;VIKOR、BWM决策误差均超过10%。推测产生原因,可能是未综合考虑专家主观随意性对整体方案总体优先级得分的影响. 在6个备选方案情况下,本研究所提方法的决策误差增加最低为2.09%,即对决策专家使用多粒度语言方法和云模型聚类进行权重分配有助于保持SVNS决策模型的稳定性. 在运算时间方面,VIKOR、BWM均不超过60 s;本研究所提方法与SVNS的运算时间较长,且前者大于后者。推测产生原因,可能是本研究所提方法须对决策专家进行筛选和聚类后获得权重,运算过程和公式较为烦琐. 虽然运算时间略有增加,但较大幅度地降低了决策误差,保证了决策结果的准确性和可实施性.
表 9 决策性能结果对比
Tab.9
| 决策方法 | e/% | t/min | |||
| 4个备选方案 | 6个备选方案 | 4个备选方案 | 6个备选方案 | ||
| 本研究 | 4.82 | 6.91 | 1.37 | 1.91 | |
| SVNS | 5.07 | 9.30 | 1.19 | 1.75 | |
| VIKOR | 11.13 | 18.62 | 0.53 | 0.84 | |
| BWM | 12.29 | 20.46 | 0.78 | 0.95 | |
4. 结 论
(1)SVNS中的不确定性隶属度能够充分反映决策专家的真实心理感知特征,避免策略操控问题,相比于其他决策方法具有较强的可操作性,更符合客观实际环境.
(2)SVNS的真、假、不确定3个隶属度可映射形成SVNC,区别于传统的虚拟数字评分排序方法,能够通过可视化的方式对评估结果进行筛选.
(3)采用云模型聚类方法能够有效衡量决策专家的差异程度,进行科学性和针对性的聚类划分,获得的权重分配具有区分度高、稳定性强的特点.
(4)由于产品造型设计属性存在不一致性,决策专家倾向于随机使用不同标准的模糊语言变量表达评估决策。使用多粒度语言可以有效解决该问题.
(5)通过意见可靠性检测对决策专家个体进行筛选,聚类后通过群体一致性测度检验对集群进行管理,同时兼顾个体顺序一致性并提高群体满意度.
(6)在后续的研究中可以考虑进一步优化改进基于云模型聚类的决策专家权重分配过程,简化决策专家筛选与管理步骤,缩减运算时间,为产品造型设计提供更加科学、高效的多属性决策方法.
参考文献
基于策略权重的模糊多属性决策方法
[J].DOI:10.13195/j.kzyjc.2019.0542 [本文引用: 1]
Strategic weight manipulation in fuzzy multiple attribute decision making
[J].DOI:10.13195/j.kzyjc.2019.0542 [本文引用: 1]
Integrated multiphase sustainable product design with a hybrid quality function deployment-multi-attribute decision-making (QFD-MADM) framework
[J].DOI:10.1016/j.spc.2020.06.013 [本文引用: 1]
基于前景理论的勾股模糊多属性决策
[J].DOI:10.12011/1000-6788-2018-2422-10 [本文引用: 1]
Pythagorean fuzzy multi-criteria decision-making based on prospect theory
[J].DOI:10.12011/1000-6788-2018-2422-10 [本文引用: 1]
考虑客户需求偏好的产品创新设计方案多属性决策评价
[J].DOI:10.13196/j.cims.2015.02.014 [本文引用: 1]
Multi-attribute decision-making evaluation method for product innovation design scheme with demand preferences of customers
[J].DOI:10.13196/j.cims.2015.02.014 [本文引用: 1]
Power-average-operator-based hybrid multiattribute online product recommendation model for consumer decision-making
[J].DOI:10.1002/int.22394 [本文引用: 1]
New approach for quality function deployment using linguistic Z-numbers and EDAS method
[J].
A novel multi-attribute decision making approach for selection of appropriate product conforming ergonomic considerations
[J].DOI:10.1016/j.orp.2018.01.004 [本文引用: 1]
Preliminary design for assembling and manufacturing sports equipment: a study case on aerobic walker
[J].
Fuzzy sets
[J].DOI:10.1016/S0019-9958(65)90241-X [本文引用: 1]
Intuitionistic fuzzy sets
[J].DOI:10.1016/S0165-0114(86)80034-3 [本文引用: 1]
Hesitant fuzzy sets
[J].
Q-single valued neutrosophic soft sets
[J].
Sustainable supplier selection based on SSCM practices: a rough cloud TOPSIS approach
[J].DOI:10.1016/j.jclepro.2019.03.070 [本文引用: 1]
Dual linguistic term set and its application based on the normal cloud model
[J].DOI:10.1109/TFUZZ.2020.2994994 [本文引用: 1]
Risk-based multi-attribute decision-making for normal cloud model considering pre-evaluation information
[J].DOI:10.1109/ACCESS.2020.3018153 [本文引用: 1]
A linguistic large group decision making method based on the cloud model
[J].DOI:10.1109/TFUZZ.2018.2822242 [本文引用: 1]
Note on a new optimization based approach for estimating priority weights and related consistency index
[J].DOI:10.1016/j.eswa.2012.04.051 [本文引用: 1]
An alternative consensus model of additive preference relations for group decision making based on the ordinal consistency
[J].DOI:10.1007/s40815-019-00696-w [本文引用: 1]
An uncertain Z-number multicriteria group decision-making method with cloud models
[J].DOI:10.1016/j.ins.2019.05.090 [本文引用: 2]
An integrated fuzzy QFD and grey decision-making approach for supply chain collaborative quality design of large complex products
[J].DOI:10.1016/j.cie.2019.106212 [本文引用: 5]
A combined thermal power plant investment decision-making model based on intelligent fuzzy grey model and ito stochastic process and its application
[J].DOI:10.1016/j.energy.2018.06.184 [本文引用: 3]
Decision-making model for sustainable supply chain finance under uncertainties
[J].DOI:10.1016/j.ijpe.2018.08.024 [本文引用: 1]
On multicriteria decision-making method based on a fuzzy rough set model with fuzzy alpha-neighborhoods
[J].DOI:10.1109/TFUZZ.2020.3001670 [本文引用: 3]