随着制造自动化水平的提高和智能制造技术的发展,数控加工企业对加工效益的要求也更高,提高机床效能和加工效率是企业利用数控加工技术的有效途径. 加工参数的多目标优化是实现最佳加工效益的有效方法之一. 目前,针对机床效能和加工效率的优化方法已经产生了许多成果,成果展示的优化过程总结是通过理论模型或者数据驱动方法构建目标变量与决策变量的优化函数,再利用优化方法来获得优化解. 在复杂的加工过程中,影响因素较多导致不容易建立理论模型,比较容易获得依赖试验数据的数据驱动模型,并且该模型不需要分析目标函数的构建机理. 常用的数据建模方法主要有响应面法[1-2]、反向传播神经网络(back propagation neural network,BPNN)[3-4]、支持向量回归[5-6]和渐进梯度回归树[7]. 在4种方法中,响应面法通常使用二次多项式模型构建决策变量与目标变量之间的关联关系模型,若在模型中存在对响应影响不显著的项,需要通过人为剔除以提高模型的预测精度,这样的方式需要耗费些许时间且难以获得最优精度. 相比响应面建模法,其他3种方法均通过调整自身少量内部参数来提高模型精度,且对非线性数据具有较高的拟合效果. 相较于支持向量回归(惩罚系数、不敏感损失区域半径和核函数系数)和渐进梯度回归树(弱学习器个数、学习率和子采样系数),反向传播神经网络(神经元数量和学习率)仅需调整2种参数便能快速完成建模.
优化方法的选择是实现加工参数优化的重要环节,主要是以启发式优化算法为主. CHENG等[8]以侧铣加工效率、切削力和表面粗糙度为优化目标,通过非线性回归建立了优化目标与工艺参数的优化函数,并且提出一种基于非支配排序遗传算法的模型求解方法. GHOSH等[9]通过贝叶斯正则化神经网络建立铣削加工中材料去除率、切削力及表面粗糙度的预测模型,采用天牛须搜索算法求解多目标优化模型得到最优的刀具直径、主轴转速、进给速度和切削深度. HE等[10]同时考虑碳钢铣削过程中的切削力、加工时间和能耗,通过理论分析和经验公式建立了各个目标与加工参数的关联关系模型,并采用基于分解的多目标进化算法进行寻优求解得到了该问题的Pareto前沿. Osorio-Pinzon等[11]针对铝6063加工过程中切削力、微观结构细化度及材料去除率的多目标优化问题,利用响应面法和人工神经网络构建目标与加工参数的优化函数,并采用粒子群算法进行优化求解. VAN[12]采用BPNN构建加工参数与切削力、振动及能耗的优化模型,利用多目标粒子群算法执行多目标优化,为高速铣削的参数优化提供了有效的解. LI等[13]通过响应面法建立数控铣削加工切削力与铣削参数之间的关系模型,在此基础上,构建了考虑切削力、R和表面粗糙度的多目标优化模型,并提出了一种基于改进教学优化算法的模型求解方法. 翁剑等[14]研究插铣过程中加工参数对切削力和材料去除率的影响,在此基础上以最小切削力和最大材料去除率为目标建立加工参数优化模型,并通过多目标遗传算法得到最优的加工参数组合.
上述提出的方法虽然在相应问题中表现出良好的优化效果,但是启发式算法只擅长搜索而不擅长学习,并且只是根据当前样本来求解,得到的结果不一定是期望的最优解. 此外,由于实际加工过程的复杂性,加工条件稍有变化都有可能会对此类算法的性能产生影响,因此探求优化算法的改进、算法组合以及其他的智能算法应用于加工参数的多目标优化问题是必要的. 强化学习(RL)是一种基于马尔可夫决策过程[15]的机器学习方法,通过利用历史样本更新网络参数来获得最优策略. 该学习方法眼光长远,考虑长期回报,对很多问题找到最优解非常关键. 深度强化学习(DRL)是深度学习(DL)与强化学习(RL)相结合而产生的,近年来已成为人工智能领域的研究热点. 它可以解决现实中经典RL无法处理的具有大型甚至连续状态空间和动作空间的复杂任务,还可以将训练好的模型直接扩展到新的问题上,而无需重新进行训练. 因此它已被广泛应用于组合优化问题、机器人运动控制和计算机视觉等领域[16-18]. 深度Q网络(deep q network,DQN)[19]是DRL中的经典代表,它将状态输入神经网络,选择动作价值最大的作为输出,通过不断迭代获得最优策略. 但是由于DQN需要计算每个动作的价值函数,包括一些对学习环境没有任何影响的动作,导致学习效率降低,影响学习效果. 为提高学习效率,Wang等[20]提出竞争网络架构算法(dueling DQN),将每个动作的Q值函数分解为状态价值函数和优势函数的和,大幅提高了学习效果. Dueling DQN凭借较强的寻优能力和感知能力,在蜂窝网络能耗优化[21]和通信网络传输[22]等领域已有突出表现,但在如何利用深度强化学习,研究合适的动作搜索策略来解决加工领域的工艺参数多目标优化问题方面还鲜有研究.
为充分发挥机床效能和提高加工效率,以及探究深度强化学习在加工参数多目标优化中的适用性及优化效果,本研究采用反向传播神经网络进行建模,并提出了一种基于深度强化学习的加工参数优化方法. 为了提高BPNN构建目标变量与决策变量优化函数的准确性,利用GA优化的BPNN 构建优化模型,采用Dueling DQN执行多目标优化. 为从优化解集中获得决策解,利用优劣解距离法结合熵值法从解集中得到决策解,并通过加工试验验证提出的方法的有效性.
1. 优化模型和建模方法
1.1. 优化模型
以铣削加工为例,研究Dueling DQN在解决加工参数多目标优化问题中的应用. 选取主轴转速
在实际加工过程中,为提高加工效率,材料去除率越大越好,而考虑到切削刀具损耗和加工系统稳定性,切削力合力越小越好,故多目标优化模型可表示:
式中:
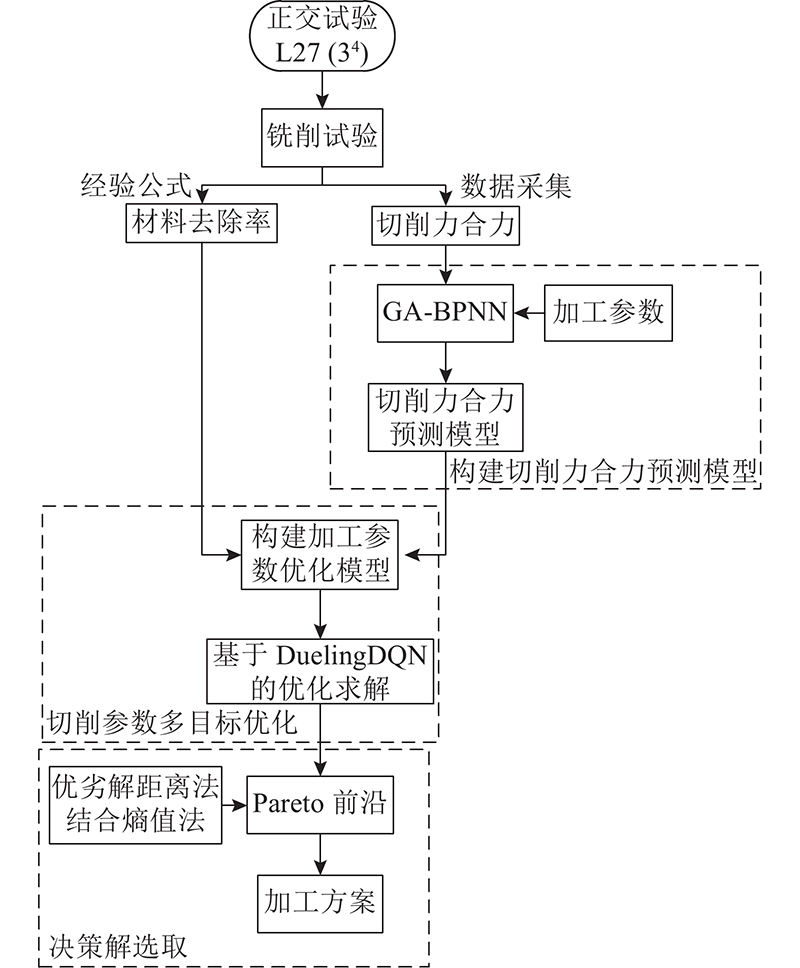
为了获得多目标优化模型(式(1))的决策解,给出求解流程,如图1所示. 通过铣削试验获取切削力合力数据,材料去除率可通过式(2)计算获取. 利用遗传算法优化反向传播神经网络构建切削力合力与切削参数的关联关系模型,以切削力合力最小和材料去除率最大为目标,确定切削参数多目标优化模型,并采用Dueling DQN进行优化求解. 最后,利用优劣解距离法结合熵值法从Pareto前沿中获取决策解.
图 1
图 1 工艺参数(主轴转速、进给量、切削宽度和深度)优化求解框架
Fig.1 Framework of machining parameters (spindle speed、feed rate、cutting width、cutting depth) optimization
1.2. GA-BPNN模型
神经网络是一种模仿生物结构和功能的计算模型,具有很强的非线性映射能力和学习速度. BPNN的网络架构由输入层、隐藏层和输出层组成. 在学习过程中,隐藏层和输出层的神经元将输入的信号与相应权重相乘,并通过传递函数处理相乘结果获得输出值,最终实现输入与输出之间的非线性映射. 神经元的数学模型如下式表示[3]:
式中:
BPNN的建模思想是将样本数据输入到神经网络中进行学习得到期望输出,接着根据实际输出与期望输出之间的误差
式中:
在BPNN的建模过程中,学习率和隐藏层的神经元个数
2. 优化方法
2.1. Dueling DQN优化原理及流程
Dueling DQN是基于值的深度强化学习算法,在算法中需要找出对学习环境具有重大影响的动作,并根据这些动作所对应的
式中:
在Dueling DQN中,为降低学习样本间的相关性,提高学习效果,在每次训练时,将当前时刻t下的状态st、动作at、奖励Rt以及下一时刻状态st+1存储在经验回放池中,并在之后的学习中随机抽取经验回放池中的一些样本给当前网络进行训练. 另外为解决算法易出现训练不收敛的问题,引入当前估计网络结构一样的目标网络,每隔一段时间将当前估计网络的参数拷贝并赋予目标网络,得到目标网络的输出
式中:
根据最优策略
式中:
但在算法的学习过程中,若给定一个
基于Dueling DQN的优化原理,结合优化目标(最小的Fc和最大的R)及优化变量
输入:铣削工艺参数
1) 初始化经验回放容量上限
2) 初始化当前估计网络的参数
3) 以4个工艺参数作为状态空间,确定状态空间s的搜索范围和动作空间a的搜索机制.
4) 在状态空间中随机选择状态s作为初始状态.
5) For
6) 将状态
7) 将状态
8) 根据
9) 将
10) 采用均方差损失函数
11) 经验回放池容量达到
12) End for
13) 记录算法学习过程中获得最高奖励Rt的工艺参数组合.
输出:Dueling DQN优化的铣削工艺参数组合.
2.2. 面向工艺参数优化的强化学习环境构建
在实现Fc和R基于工艺参数的优化过程中,需要对Dueling DQN算法的状态空间、动作空间和奖励函数进行设计.
2.2.1. 状态空间设计
在工艺参数多目标优化问题中,状态
2.2.2. 动作空间设计
动作空间主要依据为优化变量的变化方式进行设计,工艺参数
2.2.3. 奖励函数构造
奖励函数主要通过依据优化目标性质和优化形式进行构建. 多目标优化模型是以1/R和Fc最小为目标,在奖励函数中应包含这两个目标. 另外,为了减小Fc和R之间数值差异过大带来的影响,在奖励函数中将2个目标进行归一化处理,其结果分别用
3. 试 验
为了验证铣削工艺参数优化模型和优化方法的有效性,采用VDL-600A立式加工中心进行铣削试验. 利用YDCB-III05压电式三向切削测力仪采集X、Y、Z 3个方向上切削力,基于采集的数据计算切削力合力,得到机床效能评价指标Fc的数据. 铣削试验的加工和测量设备图如图2所示. 铣削刀具为直径10.0 mm的硬质合金立铣刀,切削刃数为4,工件材料为45钢,尺寸为100 mm×80 mm×60 mm.
图 2
表 1 试验因素及其水平
Tab.1
| 水平 | 加工参数 | |||
| n /( | f /( | ae /mm | ap /mm | |
| 1 | 1 500 | 0.08 | 2.00 | 0.20 |
| 2 | 1 900 | 0.10 | 4.00 | 0.40 |
| 3 | 2 300 | 0.12 | 6.00 | 0.60 |
表 2 27组Taguchi试验数据的切削力合力和材料去除率
Tab.2
| 序号 | n/ ( | f/ ( | ae/ mm | ap/ mm | Fc/ N | R/ ( |
| 1 | 1 500 | 0.08 | 2 | 0.2 | 17.241 | 48.0 |
| 2 | 1 500 | 0.08 | 4 | 0.4 | 33.117 | 192.0 |
| 3 | 1 500 | 0.08 | 6 | 0.6 | 44.120 | 432.0 |
| 4 | 1 500 | 0.10 | 2 | 0.6 | 44.246 | 180.0 |
| 5 | 1 500 | 0.10 | 4 | 0.2 | 23.873 | 120.0 |
| 6 | 1 500 | 0.10 | 6 | 0.4 | 33.256 | 360.0 |
| 7 | 1 500 | 0.12 | 2 | 0.4 | 35.638 | 144.0 |
| 8 | 1 500 | 0.12 | 4 | 0.6 | 53.547 | 432.0 |
| 9 | 1 500 | 0.12 | 6 | 0.2 | 25.398 | 216.0 |
| 10 | 1 900 | 0.08 | 2 | 0.6 | 38.787 | 182.4 |
| 11 | 1 900 | 0.08 | 4 | 0.2 | 21.276 | 121.6 |
| 12 | 1 900 | 0.08 | 6 | 0.4 | 27.223 | 364.8 |
| 13 | 1 900 | 0.10 | 2 | 0.4 | 29.856 | 152.0 |
| 14 | 1 900 | 0.10 | 4 | 0.6 | 49.820 | 456.0 |
| 15 | 1 900 | 0.10 | 6 | 0.2 | 19.837 | 228.0 |
| 16 | 1 900 | 0.12 | 2 | 0.2 | 22.726 | 91.2 |
| 17 | 1 900 | 0.12 | 4 | 0.4 | 37.849 | 364.8 |
| 18 | 1 900 | 0.12 | 6 | 0.6 | 45.732 | 820.8 |
| 19 | 2 300 | 0.08 | 2 | 0.4 | 42.285 | 147.2 |
| 20 | 2 300 | 0.08 | 4 | 0.6 | 65.958 | 441.6 |
| 21 | 2 300 | 0.08 | 6 | 0.2 | 32.286 | 220.8 |
| 22 | 2 300 | 0.10 | 2 | 0.2 | 26.537 | 92.00 |
| 23 | 2 300 | 0.10 | 4 | 0.4 | 52.899 | 368.0 |
| 24 | 2 300 | 0.10 | 6 | 0.6 | 70.342 | 828.0 |
| 25 | 2 300 | 0.12 | 2 | 0.6 | 62.847 | 331.2 |
| 26 | 2 300 | 0.12 | 4 | 0.2 | 44.824 | 220.8 |
| 27 | 2 300 | 0.12 | 6 | 0.4 | 50.243 | 662.4 |
4. 结果与讨论
4.1. 基于GA-BPNN的Fc预测模型精度评估
建模和优化程序均采用Python 3.6进行实现,计算机配置为i5-10400F CPU,RAM16GB,显卡型号GTX1650. 将试验得到的27组Fc和工艺参数数据作为GA-BPNN模型的训练样本,为了检验所构建的Fc预测模型的精度,在给定优化变量水平范围内与范围外,随机选取8组工艺参数数据作为测试样本(如表3所示). 在建模过程中,根据文献[26]的参数设定,并结合所用样本总数较少的特点,设置GA算法中的种群数为
表 3 测试集样本数据
Tab.3
| 组数 | n/( | f/( | ae/ | ap / | |
| 1 | 1 500 | 0.12 | 5 | 0.60 | 56.809 |
| 2 | 1 800 | 0.10 | 3 | 0.60 | 61.264 |
| 3 | 2 000 | 0.08 | 3 | 0.20 | 27.541 |
| 4 | 1 600 | 0.10 | 5 | 0.20 | 22.172 |
| 5 | 2 000 | 0.09 | 4 | 0.20 | 31.305 |
| 6 | 1 600 | 0.08 | 3 | 0.21 | 15.546 |
| 7 | 1 400 | 0.10 | 4 | 0.21 | 14.013 |
| 8 | 1 800 | 0.08 | 3 | 0.21 | 18.663 |
图 3
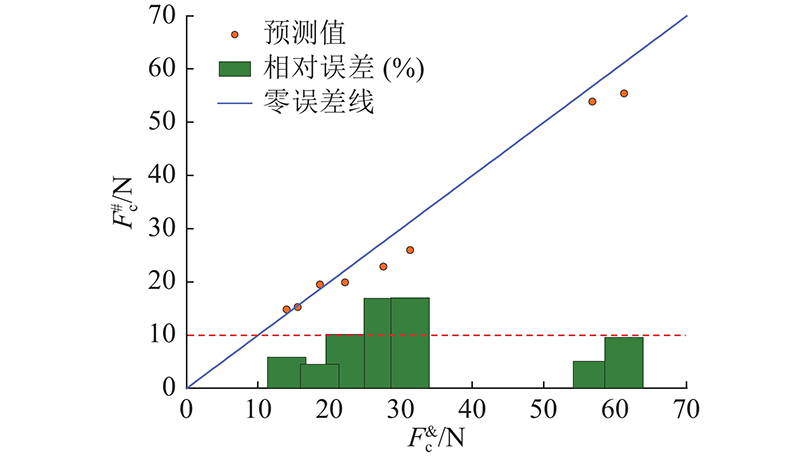
图 3 切削力合力预测值与测量值比较
Fig.3 Comparison of predicted and measured values of combined cutting force
为进一步评价GA-BPNN模型的预测精度,与支持向量回归(SVR)模型和渐进梯度回归树(gradient boosting regression tree,GBRT)对Fc的预测结果进行对比. 采用均方误差MSE、平均绝对百分比误差MAPE和决定系数R2作为预测精度评价指标. MSE和MAPE的值越小,说明预测值越接近真实值,R2越接近1.0,说明模型的输入变量能较好解释输出变量的能力越强,3个指标的表达式为
式中:
表 4 三个模型的预测指标
Tab.4
| 模型 | MSE | MAPE/% | R2 |
| GA-BPNN | 12.417 | 8.854 | 0.932 |
| SVR | 33.903 | 16.129 | 0.884 |
| GBRT | 44.887 | 21.249 | 0.847 |
4.2. 工艺参数优化结果及验证
4.2.1. Pareto前沿和决策解选取
参考文献[6]中关于强化学习参数的选择,并通过网格搜索确定Dueling DQN算法的内部参数为学习率
图 4
图 4 Dueling DQN优化4个工艺参数的过程
Fig.4 Dueling DQN process for optimizing four machining parameters
为从优化解集中选择出满足要求的决策解,采用优劣解距离法(technique for order preference by similarity to ideal solution,TOPSIS)结合熵值法(entropy weight method,EWM)从Pareto前沿解的中心区域
采用式(21)计算各个理想解的贴近系数Ci,并选择最大Ci值对应的铣削工艺参数组合作为决策解.
表 5 工艺参数组合决策结果
Tab.5
| 组数 | n/ (r·min−1) | f/ (mm·r−1) | ae/ mm | ap/ mm | Fc/ N | R/ (mm3·min−1) | Ci |
| 1 | 1 700.000 | 0.103 | 6.000 | 0.411 | 30.120 | 431.797 | 0.591 |
| 2 | 1 725.455 | 0.100 | 6.000 | 0.411 | 29.975 | 427.337 | 0.585 |
| 3 | 1 830.909 | 0.098 | 6.000 | 0.404 | 30.568 | 434.142 | 0.581 |
| 4 | 1 801.818 | 0.101 | 5.964 | 0.415 | 31.512 | 449.089 | 0.580 |
| 5 | 1 674.545 | 0.107 | 6.000 | 0.367 | 27.372 | 394.839 | 0.576 |
4.2.2. 优化结果验证
将Dueling DQN和决策解选择方法得到的最优铣削工艺参数组合输入机床中进行验证试验. 为避免试验数据的偶然性及减少测量误差的影响,对这组工艺参数重复5次加工试验,结果如表6所示. Fc的测量值Fc&与优化值Fc*的最大相对误差
表 6 切削力合力优化值与测量值的比较结果
Tab.6
| 序号 | Fc&/N | Fc*/N | | |
| 1 | 28.033 | — | 6.929 | — |
| 2 | 29.194 | — | 3.074 | — |
| 3 | 28.667 | 30.120 | 4.824 | 4.802 |
| 4 | 28.753 | — | 4.538 | — |
| 5 | 28.721 | — | 4.645 | — |
4.3. Dueling DQN优化性能对比及评估
为分析深度强化学习算法和元启发式算法在铣削工艺参数多目标优化问题上的优化性能,针对Fc和R的优化模型,对比了Dueling DQN、DQN、深度确定性策略梯度(DDPG)和非支配排序遗传算法(NSGA-II)的优化结果. DQN的内部结构设置与Dueling DQN相同,DDPG的策略网络学习率为0.001,评价网络的学习率为0.002,其他参数设置均与Dueling DQN一致. NSGA-II的种群数设为150,交叉概率为0.8,变异概率为0.2,最大迭代次数为200.
选择算法运行时间U、平均理想距离(MID)和完成目标比率(RAS)作为评价指标[32],其中MID的值越小,Pareto前沿到理想点的平均距离越小,解集的效果越好;RAS越小,Pareto前沿离2个目标的最小值越近,解集的效果越好,见式(22)和(23).
式中:
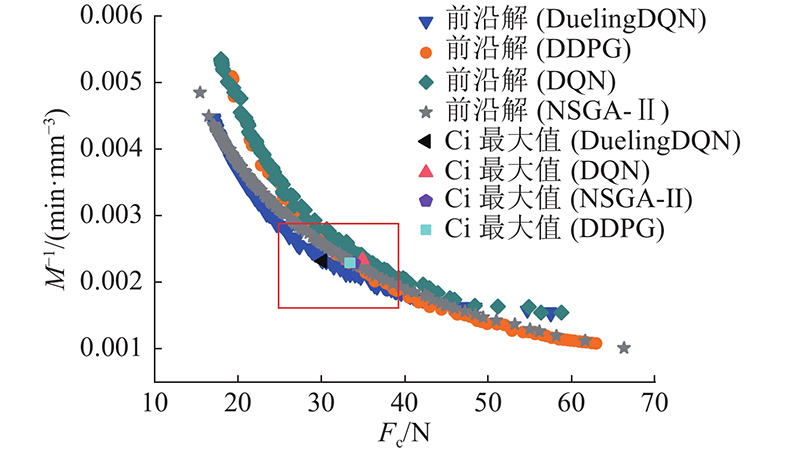
图5为4个优化算法的Pareto前沿解及最大Ci值对应的解. 4个算法的Pareto前沿曲线趋势是一致的,在折中选取最优解的区间
图 5
表 7 不同算法在铣削工艺参数多目标优化问题上的优化性能比较
Tab.7
| 方法 | N | MID | RAS | U/s |
| Dueling DQN | 173 | 26.014 | 0.013 | 1 063 |
| DDPG | 92 | 39.161 | 0.025 | 1 052 |
| DQN | 123 | 29.589 | 0.018 | 1 065 |
| NSGA-II | 140 | 28.713 | 0.018 | 501 |
采用TOPSIS-EWM决策法选出DQN、DDPG和NSGA-II的最优工艺参数组合进行验证试验,并与Dueling DQN的实际加工效果进行对比,得到表8的结果,Fc*为优化得到的切削力合力. 4个优化算法获得的Fc*与测量值Fc&都较接近,表明了优化算法的有效性,其中,Dueling DQN优化获得的Fc*最小,R仅略低于DQN,而DQN得到的Fc*值最大. 因此,基于Dueling DQN获得的优化解优化效果最好,验证了Dueling DQN优的优化性能.
表 8 各方法优化下的切削力合力和材料去除率结果对比
Tab.8
| 方法 | n/(r·min−1) | f/(mm·r−1) | ae/mm | ap/mm |
| Dueling DQN | 1 700.000 | 0.103 | 6.000 | 0.411 |
| DDPG | 1 808.154 | 0.116 | 5.972 | 0.349 |
| DQN | 1 809.091 | 0.098 | 6.000 | 0.404 |
| NSGA-II | 1 720.582 | 0.119 | 5.984 | 0.357 |
| 方法 | Fc&/N | Fc*/N | R/(mm3·min−1) | |
| Dueling DQN | 29.194 | 30.120 | 431.797 | |
| DDPG | 32.847 | 33.463 | 437.158 | |
| DQN | 33.211 | 34.327 | 429.753 | |
| NSGA-II | 33.117 | 33.728 | 437.403 |
表 9 Dueling DQN优化结果与经验结果对比
Tab.9
| 方法 | n/(r·min−1) | f/(mm·r−1) | ae/mm | ap/mm |
| Dueling DQN | 1 700 | 0.103 | 6 | 0.411 |
| 经验铣削参数 | 1 900 | 0.080 | 6 | 0.450 |
| 方法 | Fc&/N | R/(mm3·min−1) | | |
| Dueling DQN | 29.194 | 431.797 | 8.29 | 4.95 |
| 经验铣削参数 | 31.614 | 410.400 | ||
5. 结 论
为提高机床效能和加工效率,提出了一种基于Dueling DQN的加工参数多目标优化方法. 基于45钢的铣削试验,验证了该方法应用于加工参数优化领域的有效性和优异性,为加工过程优化方法的选择提供了有利的选择依据,主要结论如下:
(1)采用GA优化的BPNN模型构建切削力合力Fc与工艺参数的优化模型,模型的R2为 93.2%,与SVR和GBRT模型进行对比,发现GA-BPNN的建模精度更高.
(2)利用Dueling DQN获得最小Fc和最大R的多目标优化问题进的Pareto前沿,并采用TOPSIS-EWM得到决策解. 基于得到的决策解进行加工,优化得到Fc与测量值的误差均值仅为4.802%,并与经验选择的工艺参数对比,发现通过Dueling DQN得到的加工方案使Fc降低了8.29%,加工效率提高了4.95%.
(3)对比了3种深度强化学习方法(Dueling DQN、DQN、DDPG)和启发式优化方法(NSGA-II)解决机床效能和加工效率多目标优化问题的优化性能发现,Dueling DQN求解得到的Pareto前沿在解集数、平均理想距离和完成目标比率上均优于DQN、DDPG和NSGA-II,获得的优化解实际优化效果最好. 考虑更多影响因素和优化目标来构建多目标模型,设计更高效的Dueling DQN探索策略,实现复杂加工的工艺参数选择,提高模型优化效率将是下一步研究的方向.
参考文献
Multi-objective optimization for improving machinability of Ti-6Al-4V using RSM and advanced algorithms
[J].DOI:10.1016/j.jcde.2018.04.004 [本文引用: 1]
Experimental investigation of surface integrity and multi-objective optimization of end milling for hybrid Al7075 matrix composites
[J].
Study of cutting forces using FE, ANOVA, and BPNN in elliptical vibration cutting of titanium alloy Ti-6Al-4V
[J].DOI:10.1007/s00170-019-04537-w [本文引用: 2]
Online monitoring and multi-objective optimization of technological parameters in high-speed milling process
[J].DOI:10.1007/s00170-020-06444-x [本文引用: 1]
基于局部线性嵌入和支持向量机回归的TBM施工参数预测
[J].
TBM tunneling parameters prediction based on locally linear embedding and support vector regression
[J].
车削表面粗糙度解析模型与DDQN-SVR预测模型研究
[J].DOI:10.3901/JME.2021.13.262 [本文引用: 2]
Research on analytical model and DDQN-SVR prediction model of turning surface roughness
[J].DOI:10.3901/JME.2021.13.262 [本文引用: 2]
基于数字孪生的铣削参数动态多目标优化策略
[J].DOI:10.13196/j.cims.2021.02.015 [本文引用: 1]
Dynamic multi-objective optimization strategy of milling parameters based on digital twin
[J].DOI:10.13196/j.cims.2021.02.015 [本文引用: 1]
Tool design and cutting parameter optimization for side milling blisk
[J].DOI:10.1007/s00170-018-2846-4 [本文引用: 1]
A surrogate-assisted optimization approach for multi-response end milling of aluminum alloy AA3105
[J].DOI:10.1007/s00170-020-06209-6 [本文引用: 1]
Pareto fronts of machining parameters for trade-off among energy consumption, cutting force and processing time
[J].DOI:10.1016/j.ijpe.2016.12.012 [本文引用: 1]
Cutting parameter optimization of Al-6063-O using numerical simulations and particle swarm optimization
[J].DOI:10.1007/s00170-020-06200-1 [本文引用: 1]
Application of singularity vibration for minimum energy consumption in high-speed milling
[J].DOI:10.1142/S0217979221400087 [本文引用: 1]
Modeling and multi-objective optimization of cutting parameters in the high-speed milling using RSM and improved TLBO algorithm
[J].DOI:10.1007/s00170-020-06284-9 [本文引用: 1]
基于机器学习和多目标算法的钛合金插铣优化
[J].DOI:10.3969/j.issn.1004-132X.2021.07.002 [本文引用: 1]
Plunge milling of tianium alloys based on machine learning and multi-objective optimization
[J].DOI:10.3969/j.issn.1004-132X.2021.07.002 [本文引用: 1]
Structural estimation of markov decision processes
[J].
Deep reinforcement learning for multi-objective optimization
[J].DOI:10.1109/TCYB.2020.2977661 [本文引用: 1]
可变环境下仿人机器人智能姿态控制
[J].
Intelligent posture control of humanoid robot in variable environment
[J].
Human level control through deep reinforcement learning
[J].DOI:10.1038/nature14236 [本文引用: 1]
End-to-end CNN-based dueling deep Q-Network for autonomous cell activation in Cloud-RANs
[J].DOI:10.1016/j.jnca.2020.102757 [本文引用: 2]
An autonomous transmission scheme using dueling DQN for D2D communication networks
[J].
Cutting forces in micro-end-milling processes
[J].
Parameters optimization considering the trade-off between cutting power and R based on linear decreasing particle swarm algorithm in milling
[J].DOI:10.1016/j.jclepro.2020.121388 [本文引用: 1]
Energy-efficient machining process analysis and optimization based on BS EN24T alloy steel as case studies
[J].DOI:10.1016/j.rcim.2019.01.011 [本文引用: 1]
Multi-objective optimization in face milling process with cryogenic cooling using grey fuzzy analysis and BPNN-GA methods
[J].
Playing atari with deep reinforcement learning
[J].
Estimation of tool wear and optimization of cutting parameters based on novel ANFIS-PSO method toward intelligent machining
[J].
Autonomous cell activation for energy saving in cloud-RANs based on dueling deep q-network
[J].
Multi-objective optimization using different methods of assigning weights to energy consumption responses, surface roughness and material removal rate during rough turning operation
[J].DOI:10.1016/j.jclepro.2017.06.077 [本文引用: 1]
Multi-objective optimization for MQL-assisted end milling operation: an intelligent hybrid strategy combining GEP and NTOPSIS
[J].DOI:10.1007/s00521-019-04450-z [本文引用: 1]
A multi-phase covering pareto-optimal front method to multi-objective parallel machine scheduling
[J].
Resource slicing and customization in RAN with dueling deep Q-network
[J].