现阶段,装配式混凝土结构竖向构件的钢筋连接方式应用最广泛的有灌浆套筒连接和浆锚搭接等. 灌浆套筒连接构件常常因为施工不当或套筒堵塞的原因造成灌浆缺陷,影响承载力、变形性能和刚度等,随着缺陷数量和厚度的增大,套筒灌浆连接失效[9-10]. 对于约束浆锚搭接连接,现有预留孔的成孔制作方法不适用于工厂大批量试件生产,带螺纹的钢管在浇筑时存在固定困难的问题. 《装配式混凝土结构技术规程》(JGJ1-2014)要求直径大于20 mm的钢筋和直接承受动力荷载的纵向钢筋不宜(或应)采用浆锚搭接,因此浆锚搭接在工程应用中具有局限性. 超高性能混凝土(ultra-high performance concrete,UHPC)具有优异的力学性能和耐久性[11-13],在受拉时呈多裂缝开展和应变硬化特征,不需额外胶结剂,即可与混凝土形成良好的黏结[14],因此仅需较小的搭接长度即可实现力的可靠传递[15].
基于上述研究,本文在课题组前期进行的UHPC钢筋搭接材性试验研究[16]基础上,采用具有高强度、高黏结性的UHPC作为预制构件连接材料代替套筒灌浆连接和约束浆锚搭接,考虑实际工程中最不利的情况,将钢筋搭接段设置在柱弯矩最大且易出现塑性铰的根部区域,以改善装配式结构中构件连接部位的抗震性能. 根据试验结果,结合本构方程与截面分析,提出UHPC装配式柱试件正截面受弯承载力的计算公式,为工程设计提供参考.
1. 试验概况
1.1. 试件设计与制作
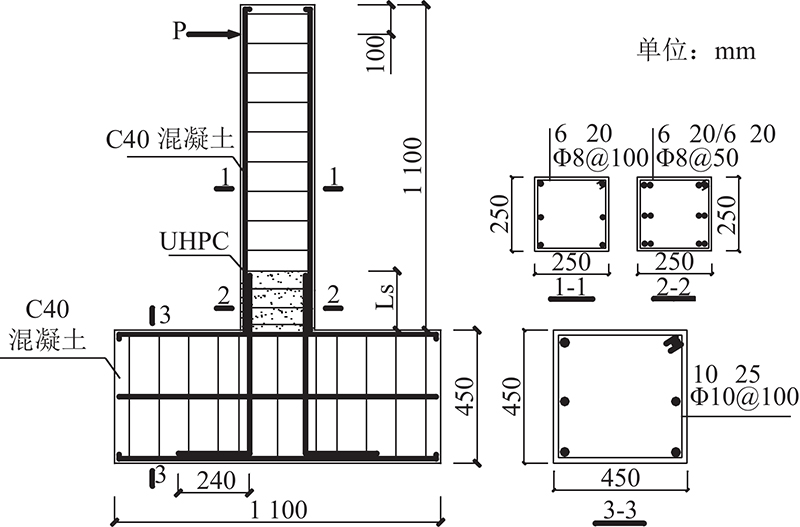
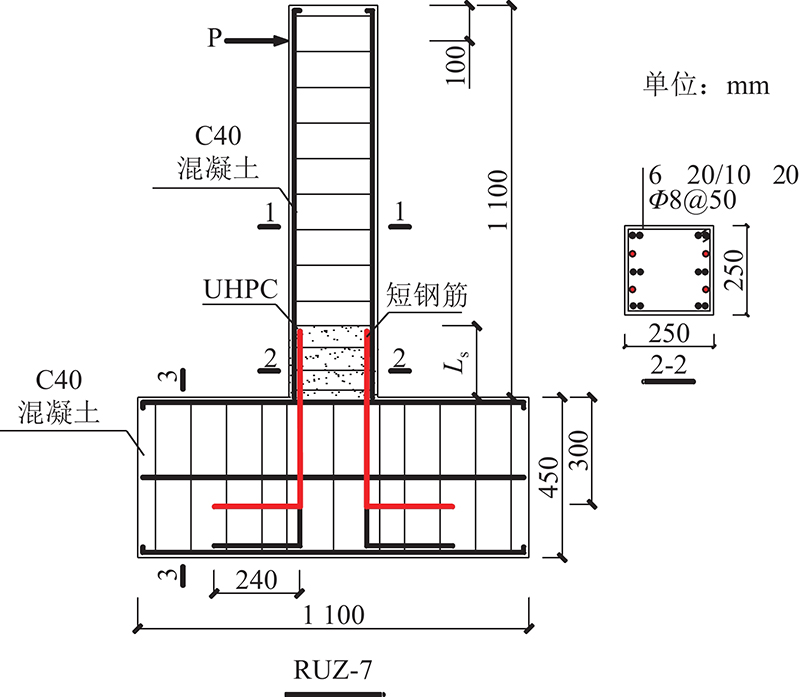
设计制作了7个“倒T形”悬臂构件,柱截面尺寸均为250 mm×250 mm,柱高度取1 100 mm,剪跨比为4.0,底梁截面尺寸取450 mm×450 mm,柱纵筋采用直径为20 mm的HRB400级钢筋,箍筋采用直径为8 mm的HPB300级钢筋. UHPC后浇高度为搭接长度,试件的几何尺寸及配筋如图1所示.
图 1
图 1 普通混凝土柱/超高性能混凝土装配式柱的尺寸及配筋
Fig.1 Dimensions and reinforcement arrangement of normal concrete column/ultra high performance concrete assembled column
表 1 NC柱/UHPC装配式柱的设计参数
Tab.1
| 编号 | S/mm2 | λt/λd | 纵筋 | Ls | 箍筋 |
| RCZ-1 | 250×250 | 0.33/0.75 | 6ϕ20 mm | — | 8@100 mm/50 mm |
| RUZ-2 | 250×250 | 0.33/0.75 | 6ϕ20 mm/6ϕ20 mm | 8d | 8@100 mm/50 mm |
| RUZ-3 | 250×250 | 0.17/0.40 | 6ϕ20 mm/6ϕ20 mm | 8d | 8@100 mm/50 mm |
| RUZ-4 | 250×250 | 0.33/0.75 | 6ϕ20 mm/6ϕ20 mm | 8d | 8@100 mm/160 mm |
| RUZ-5 | 250×250 | 0.33/0.75 | 6ϕ20 mm/6ϕ20 mm | 6d | 8@100 mm/50 mm |
| RUZ-6 | 250×250 | 0.33/0.75 | 6ϕ20 mm/6ϕ20 mm | 12d | 8@100 mm/50 mm |
| RUZ-7 | 250×250 | 0.33/0.75 | 6ϕ20 mm/10ϕ20 mm | 8d | 8@100 mm/50 mm |
图 2
装配式柱的浇筑过程分为以下2个部分. 1)采用C40混凝土浇筑上部混凝土柱与下部底梁部分,用隔板与泡沫胶分隔,待该部分硬化后,拆掉隔板,用高压水枪清洗封堵的泡沫胶,将预留搭接段两侧的混凝土表面凿毛,清洗干净后安装侧模. 2)在该区段进行后浇UHPC,收面抹平后覆盖保鲜膜,防止产生干缩裂缝. 在养护期间,将毡布包裹于试件表面,每天定时浇水养护,以防止UHPC水化反应不充分. 60 d后开始加载,以提高黏结强度.
1.2. 材料的力学性能
试验采用的超高性能混凝土(UHPC)由42.5级普通硅酸盐水泥、Ⅰ级粉煤灰、粒径为0.16~1.25 mm的石英砂、矿粉、无定型超细(非晶体)粉末状硅灰、聚羧酸系高效减水剂和带钩镀铜钢纤维组成. 采用100 mm×100 mm×100 mm的立方体试块测得立方体抗压强度、100 mm×100 mm×300 mm的棱柱体试块测得轴心抗压强度,采用“狗骨形”试块测得单轴抗拉强度,UHPC的力学性能如表2所示. 表中,Vt为钢纤维体积掺量,
表 2 UHPC的力学性能
Tab.2
| Vt/% | fcu /MPa | fc /MPa | ft /MPa |
| 2 | 108.13 | 102.35 | 5.21 |
表 3 钢筋的力学性能
Tab.3
| 钢筋级别 | d/mm | fy /MPa | fu /MPa | δ/% |
| HPB300 | 8 | 360 | 525 | 27 |
| HRB400 | 20 | 470 | 660 | 16.3 |
1.3. 加载方案和测试内容
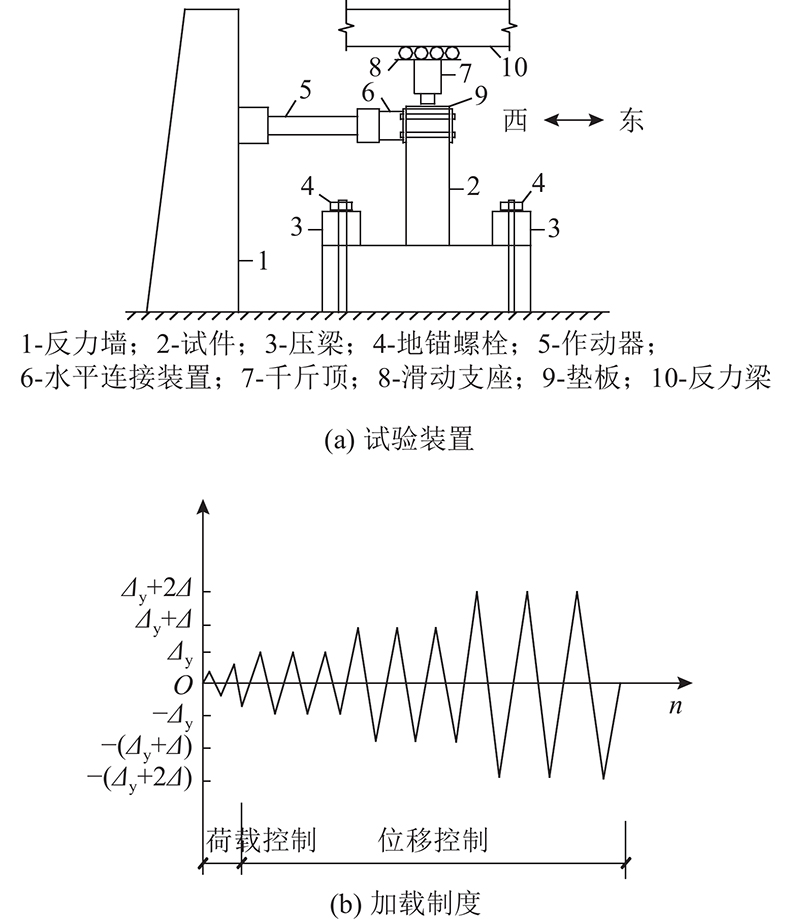
本次试验在美国MTS公司生产的拟静力试验反力架装置上进行,试验装置如图3(a)所示. 采用低周反复加载的方式,通过液压千斤顶对柱顶施加恒定竖向荷载,由固定在反力墙上的MTS100作动器施加水平荷载. 为了防止试件倾覆,将试件通过钢制压梁和螺栓固定在地面.
图 3
试验采用荷载-位移混合控制方式加载,加载制度如图3(b)所示. 图中,Δy为屈服位移,Δ为位移级差. 在试件屈服前,按荷载控制,每级荷载增量为10 kN,循环1次. 以荷载-位移曲线出现明显弯折判定试件的屈服,在试件屈服后,采用位移控制加载,以Δy的倍数为极差进行加载,每级位移循环3次,直至试件破坏或荷载下降至峰值荷载的85%以下时停止加载.
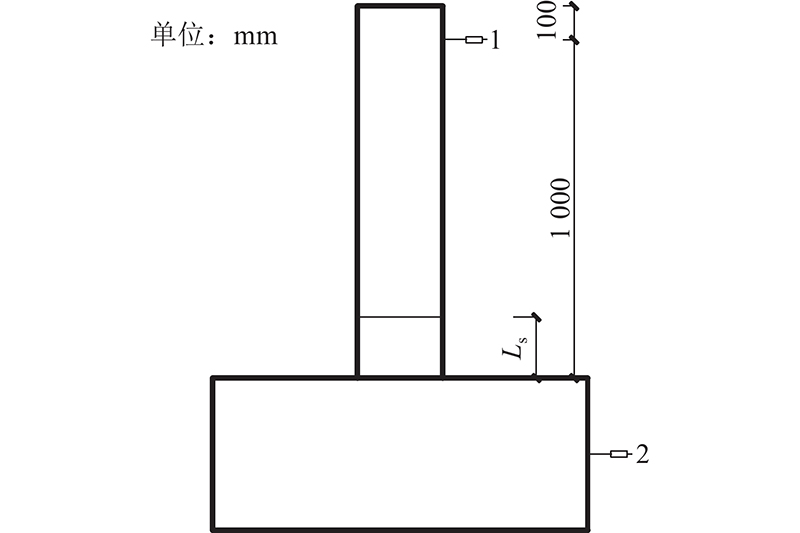
在柱顶加载点处安装线性位移计LVDT-1,于测量柱顶的水平位移;在底梁一侧安装小量程位移计LVDT-2,以测量试件的整体水平滑移. 位移计的布置如图4所示.
图 4
图 4 NC柱/UHPC装配式柱的位移计布置
Fig.4 Displacement meter arrangement of NC column/UHPC assembled column
2. 试验现象及破坏形态
为了便于描述试验现象,规定MTS作动器推为正向,拉为负向,各试件的裂缝分布及破坏形态如图5所示.
图 5
图 5 NC柱/UHPC装配式柱的破坏形态
Fig.5 Failure patterns of NC column/UHPC assembled column
1)对比试件. 对于试件RCZ-1,当试件加载至60 kN时,柱西侧距底部高16 cm处出现1条长约为3 cm的水平细微裂缝. 随着水平荷载的增加,柱身不断出现水平弯曲裂缝,柱脚出现剪切斜裂缝. 当加载至100 kN时,荷载-位移曲线的斜率开始变缓,构件屈服,此时改为位移加载方式.
当加载至2Δy时,柱脚与底梁界面处的裂缝贯通. 当加载至4Δy时,柱中部出现多条斜裂缝,水平弯曲裂缝不断延伸、变宽. 当加载至6Δy时,柱身东、西两侧出现竖向裂缝并逐渐向柱头延伸,柱脚混凝土压碎、纵筋轻微外鼓. 当加载至7Δy时,柱脚混凝土压溃,纵筋外鼓成“灯笼”状,承载力彻底丧失,试件破坏.
2)UHPC装配试件. 对于试件RUZ-2,当试件加载至64 kN时,柱西侧底梁与UHPC的界面处出现1条长约为3 cm的水平裂缝. 随着水平荷载的继续增加,柱身出现多条水平裂缝,其中NC与UHPC界面、UHPC与底梁处界面裂缝加宽. 当加载至120 kN时,构件屈服,改用位移加载. 当加载至Δy时,柱身西侧高40 cm处出现3条沿右下方45°的斜裂缝. 随着位移的增大,裂缝不断延伸、加宽. 当加载至5Δy时,UHPC与底梁界面处完全脱开,形成宽约为1 cm的裂缝. 当加载至6Δy时,荷载下降至峰值荷载的85%,此时构件破坏.
其他UHPC后浇装配试件的加载过程与试件RUZ-2基本相似. 与试件RUZ-2相比,试件RUZ-3的开裂荷载明显减小,塑性铰区UHPC段裂缝开展迅速、数量增加、宽度更细小,最终破坏时柱表面混凝土压碎脱落的面积减小. 这主要是因为轴压比的降低,在一定程度上减小了试件的抗剪承载力,加速了斜裂缝的产生和发展.
对于RUZ-4,试件在UHPC搭接段产生的劈裂裂缝宽,裂缝开展更严重. 这是由于配箍率的减小,减弱了纵筋对核心UHPC的约束,降低了核心UHPC的抗剪强度,促使了劈裂裂缝的产生与发展.
与试件RUZ-2相比,RUZ-5裂缝数量较多,柱与底梁交界的混凝土表皮鼓起,柱底倾斜加剧. RUZ-6较试件RUZ-2裂缝开展缓慢且数量减少,搭接段UHPC表面较完整,无劈裂裂缝. 随着搭接长度的增加,钢筋肋会使包裹在周围的UHPC挤压力减小,即挤压力的径向分量使得UHPC受到的环向拉应力减小,因而试件产生的劈裂裂缝减少,最终破坏时试件状态更完整.
试件RUZ-7的UHPC搭接段配置了短钢筋,导致配筋率增大. UHPC表面的开裂情况得到明显的改善,裂缝多集中于UHPC段上部普通混凝土部分,达到极限荷载时UHPC段上部的普通混凝土出现酥碎现象,表明在搭接截面配置短钢筋,可以改变装配式柱的破坏形态,使得塑性铰区上移.
试件RCZ-1为整浇柱,最终破坏时柱脚混凝土被压溃. UHPC后浇试件RUZ-2~RUZ-7的初始裂缝均出现在柱根部的接缝处,柱最终破坏时塑性铰区的破坏程度较轻.
3. 试验结果及分析
3.1. 滞回曲线
图 6
1)各试件的滞回性能相似,均表现为试件开裂前,荷载-位移曲线近似呈线性变化,卸载后无残余变形. 开裂后,随着柱顶水平荷载的增大,滞回环面积逐渐增大,卸载后出现残余变形. 在试件屈服后,随着柱顶水平位移的增加,滞回环面积继续增大,残余变形增大,加卸载刚度降低,滞回环出现一定程度的捏缩. 在达到峰值荷载后,随着柱顶水平位移的继续增加,加卸载刚度及滞回环面积均迅速降低.
2)试件RUZ-2的峰值荷载和极限位移均略高于整浇试件RCZ-1,滞回曲线的饱满程度高于试件RCZ-1. 可知,装配柱试件RUZ-2的抗震效果与整浇试件相当.
3)与RUZ-2相比,试件RUZ-5的滞回曲线饱满程度降低,试件RUZ-6的峰值荷载和极限位移均提高,滞回环面积明显增大,试件变形能力大幅提高,承载力退化速率缓慢. 增大搭接段长度,可以显著地提高试件的抗震性能.
4)与试件RUZ-2相比,试件RUZ-4的滞回环出现捏缩现象,残余变形减小,承载力退化较快,最终破坏时滞回曲线包围的总面积减小. 减小搭接段体积配箍率,使得试件的耗能能力减弱.
5)在相同的柱顶水平位移下,试件RUZ-3较试件RUZ-2滞回环的饱满程度及卸载后的残余变形和峰值荷载均减小. 这主要是因为试件在低轴压比下,塑性铰区受复合应力作用,此时竖向轴力降低,水平力导致的切应力占比提高,削弱了UHPC与搭接段钢筋的握裹,导致低轴压比不利于钢筋搭接,会削弱柱的耗能能力.
6)与试件RUZ-2相比,试件RUZ-7的峰值荷载明显提高,但达到峰值点后,滞回曲线的承载力退化较快,滞回环饱满程度和变形能力降低. 在后浇UHPC搭接段配置短钢筋,增大了搭接区的配筋率,提高了试件的承载力,但降低了耗能能力.
3.2. 骨架曲线
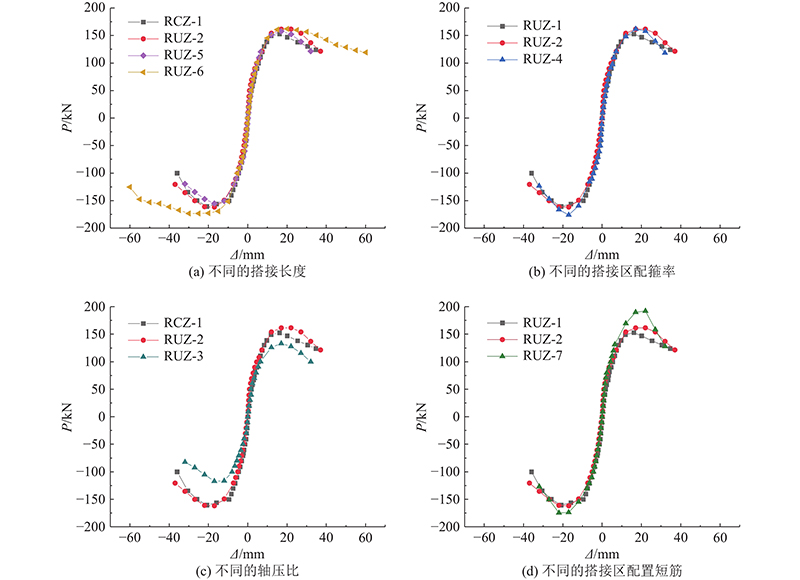
图 7
图 7 不同参数下的柱骨架曲线对比
Fig.7 Comparison of skeleton curves of column under different parameters
表 4 NC柱与UHPC装配式柱的特征点试验结果
Tab.4
| 试件编号 | Pcr /kN | Δcr /mm | Py /kN | Δy /mm | Pm /kN | Δm /mm | Pu /kN | Δu /mm | μ |
| RCZ-1 | 60.23 | 2.14 | 132.22 | 8.14 | 154.41 | 16.05 | 131.25 | 31.01 | 3.81 |
| RUZ-2 | 70.11 | 2.51 | 134.08 | 9.29 | 161.63 | 17.03 | 137.39 | 31.70 | 3.41 |
| RUZ-3 | 49.81 | 2.01 | 105.49 | 8.42 | 125.12 | 17.03 | 106.35 | 25.88 | 3.07 |
| RUZ-4 | 59.98 | 1.93 | 139.52 | 9.91 | 168.90 | 17.05 | 143.57 | 27.03 | 2.73 |
| RUZ-5 | 70.25 | 2.48 | 130.68 | 8.54 | 156.48 | 17.04 | 133.01 | 27.97 | 3.28 |
| RUZ-6 | 70.00 | 2.75 | 144.36 | 9.62 | 167.42 | 20.03 | 142.31 | 47.28 | 4.91 |
| RUZ-7 | 90.03 | 3.71 | 152.41 | 10.51 | 183.37 | 22.02 | 155.86 | 26.95 | 2.56 |
1)与试件RUZ-2相比,试件RUZ-3的承载力、极限位移、延性系数分别降低了22.6%、18.4%、10.0%. 降低轴压比,会减弱UHPC与钢筋间的黏结作用,减小极限位移,减弱试件塑性变形能力,降低延性.
2)与试件RUZ-2相比,试件RUZ-4的极限位移、延性系数分别降低了14.7%、19.9%. 减小搭接段配箍率,会减弱UHPC对搭接钢筋的环向约束作用和试件塑性变形能力,降低延性.
3)试件RUZ-2、RUZ-6较试件RUZ-5的极限位移分别提高了13.3%、69.0%,延性系数分别提高了4.0%、49.7%. 搭接长度越长,搭接段浇筑的UHPC高性能混凝土越多,钢筋与UHPC的黏结作用越强,使得试件变形能力增强,延性提高.
4)在其他参数相同的条件下,试件RUZ-7的承载力比试件RUZ-2高,极限位移和延性系数分别降低了15.0%、24.9%. 搭接区设置短钢筋,会使得钢筋周围包裹的UHPC减少,肋间混凝土咬合齿易被挤碎、切断,试件的塑形变形能力减弱,延性降低.
3.3. 强度衰减
强度衰减是描述承载能力退化的宏观物理量之一,退化速率越快,表明在低周反复荷载作用下,装配式柱抵抗外荷载作用的能力丧失越快. 从试验结果分析得到各试件强度衰减关系的曲线,如图8所示. 图中,
图 8
图 8 不同参数下柱的强度衰减对比
Fig.8 Structural strength reduction comparison of column under different parameters
从图8可得如下结论.
1)不同设计参数下各试件的强度衰减曲线具有一定的相似性. 当水平位移为1倍屈服位移时,装配式柱的强度衰减幅度较小. 随着屈服位移倍数的增加,柱截面受压区混凝土的破碎面积增大,截面有效高度减小,导致试件强度衰减幅度增大.
2)试件RUZ-4的强度衰减速率较试件RUZ-2加快,这是由于配箍率减小会使UHPC对搭接钢筋的环向约束减弱,试件易发生劈裂破坏.
3)在同级加载位移下,装配式柱的强度衰减速率较整浇柱变缓. 试件RUZ-2、RUZ-6的强度衰减速率较试件RUZ-5变缓,试件RUZ-6随着位移的增加具有良好的持荷能力,这是因为增大搭接长度,可以增强UHPC与钢筋的锚固性能,有效避免了UHPC发生劈裂或钢筋拔出破坏.
4)在搭接段设置短钢筋的试件RUZ-7强度退化系数先减小,后增大. 原因主要是当柱顶位移较小时,短钢筋可以增强界面性能;当柱顶位移较大时,搭接段配置了较多的钢筋,减弱了UHPC的黏结性能.
3.4. 刚度退化
采用实测的割线刚度Ki来反映试件的刚度退化情况,计算式为
式中:+Pi和−Pi为正、负向加载时,第i次循环加载的峰值荷载;+Δi和−Δi表示第i级循环加载下正、负向最大荷载对应的位移.
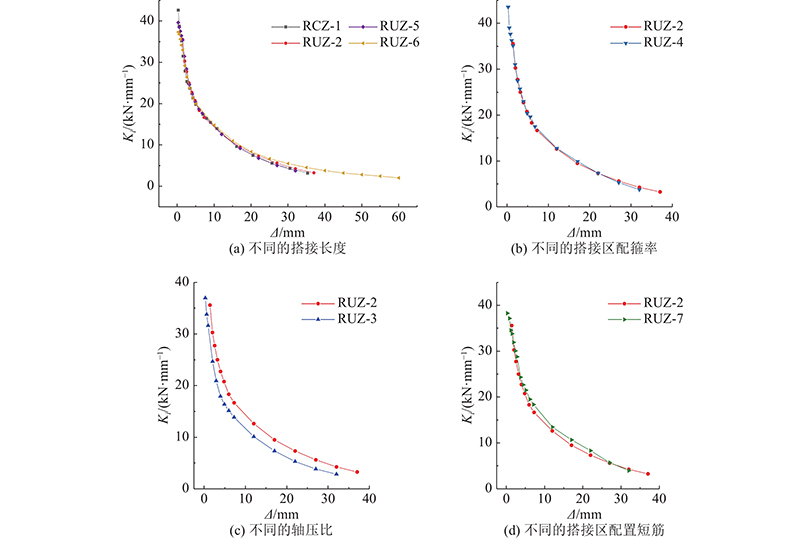
图 9
图 9 不同参数下的柱刚度退化曲线对比
Fig.9 Comparison of column stiffness degradation curves under different parameters
1)在加载初期,各试件均处于弹性工作阶段,刚度较大. 随着加载位移的不断增大,各柱的刚度退化加快,屈服后刚度退化速率降低,峰值后试件刚度退化,趋于稳定.
2)在相同的加载位移下,试件RUZ-3的刚度小于试件RUZ-2,但两者的刚度退化速率基本相同,表明轴压比对试件的刚度退化影响不大.
3)试件RUZ-2与试件RUZ-4的初期刚度退化速率相同,2个试件的刚度退化曲线几乎一致,说明搭接段配箍率对UHPC装配式柱的刚度退化影响较小.
3.5. 累积耗能
表 5 NC柱与UHPC装配式柱的累积耗能
Tab.5
| 试件编号 | E/ (kN·m) | ||
| P=Py | P=Pm | Δ=Δu | |
| RCZ-1 | 2.204 | 5.398 | 32.424 |
| RUZ-2 | 1.952 | 6.591 | 33.474 |
| RUZ-3 | 1.518 | 6.059 | 19.872 |
| RUZ-4 | 2.174 | 6.780 | 22.813 |
| RUZ-5 | 1.989 | 7.128 | 24.529 |
| RUZ-6 | 1.596 | 11.061 | 112.539 |
| RUZ-7 | 2.149 | 13.031 | 22.316 |
1)不同设计参数下各试件的累积耗能均表现如下. 在加载初期,试件处于线弹性加卸载阶段,累积耗能几乎为零;随着加载循环次数的增加,试件内部损伤累积,耗能近似呈指数增长.
2)试件RUZ-2达到峰值荷载和极限位移时对应的累积耗能均高于整浇试件RCZ-1,可以认为试件RUZ-2的抗震效果与整浇试件相当. 试件RCZ-6达到峰值荷载和极限位移对应的累积耗能分别为试件RUZ-2的1.69倍和3.47倍,表明UHPC装配式柱的耗能能力明显大于整浇柱,增大搭接长度可以显著地提高装配式柱的耗能能力.
3)在其他条件相同的情况下,试件RUZ-3达到极限位移时的累积耗能较试件RUZ-2降低了68.4%. 轴压比较低的试件产生一定位移所需消耗的能量较少,未能充分发挥塑性耗能能力,累积耗能随着试件轴压比的减小,呈下降趋势.
4. 承载力计算
为了简化计算,给出以下假定. 1)UHPC装配式柱的正截面符合平截面假定. 2)在UHPC拉应变小于峰值拉应变
4.1. UHPC材料的本构关系
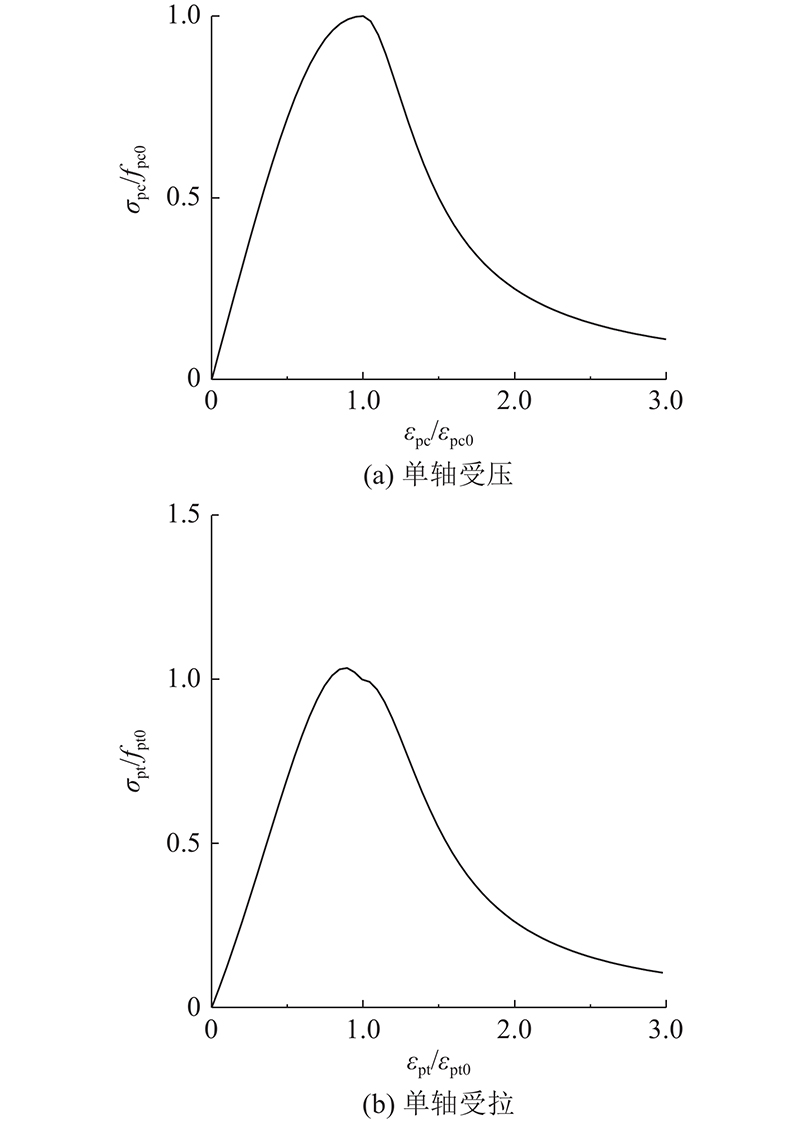
图 10
1)单轴受压本构:
式中:
2)单轴受拉本构:
式中:
4.2. 柱截面压弯承载力
1)NC与UHPC连接处的截面. 由于普通混凝土抗拉强度较低且为脆性破坏,截面受拉区拉力主要由钢筋承担,截面受弯承载力可以参考我国《混凝土结构设计规范》[18]给出的混凝土柱受弯承载力计算公式:
式中:
对应柱顶水平承载力为
式中:M为受压区UHPC承担弯矩;
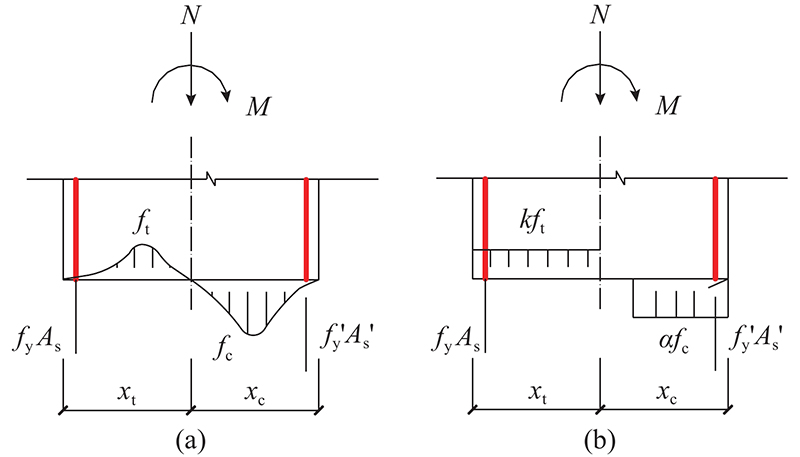
根据假定可得如图11(a)所示的截面破坏时的应力分布图. 对于UHPC装配式柱,对称配筋且受拉区钢筋先屈服,由力的平衡条件可得柱顶压力和截面拉应力合力之和为压应力合力.
图 11
受压区合力
式中:xc为中和轴高度,即受压区理论计算高度;σc为压应力;εc为压应变.
由平截面假定可知,距离中性轴y处的截面压应变为
将式(7)、(8)代入式(6),可得
式中:
令
根据式(11),可得
令
为了简化计算,假定力的大小和作用点不变,将截面受拉区UHPC应力分布图等效为矩形,如图11(b)所示. 由应力平衡方程与试验结果进行反推,得到受拉区等效应力值
利用求根公式解得
3)控制截面的判定. 以RUZ-2为例,由式(13)可得试件RUZ-2的受弯承载力MUk2c,根据式(5)计算柱的水平荷载VUk2c. 按VUk2c在柱顶施加力,得到NC与UHPC连接截面处的弯矩Mv,与普通混凝土的受弯承载力MNk2c进行对比.
若Mv>MNk2c,则破坏截面发生在搭接段上部普通混凝土部分;若Mv<MNk2c,则破坏截面发生在UHPC搭接段.
表6中,
表 6 柱截面压弯承载力的计算值与试验值对比
Tab.6
| 试件编号 | MUt/(kN·m) | 考虑UHPC抗拉 | 不考虑UHPC抗拉 | |||
| MUkc/(kN·m) | MUkc/MUt | MUbc/(kN·m) | MUbc/MUt | |||
| RCZ-1 | 154.41 | — | — | 141.85 | 0.92 | |
| RUZ-2 | 161.63 | 155.74 | 0.96 | 136.12 | 0.84 | |
| RUZ-3 | 125.12 | 117.45 | 0.94 | 99.90 | 0.80 | |
| RUZ-4 | 168.90 | 155.74 | 0.92 | 136.12 | 0.81 | |
| RUZ-5 | 156.48 | 155.74 | 1.00 | 136.12 | 0.87 | |
| RUZ-6 | 167.42 | 155.74 | 0.93 | 136.12 | 0.81 | |
| RUZ-7 | 183.37 | 180.53 | 0.98 | 160.91 | 0.88 | |
4.3. 计算结果分析
1)采用考虑UHPC受拉作用的装配柱的MUkc/MUt平均值为0.95,标准差为0.03,变异系数为0.03. 可知,上述推导所得公式的计算值与试验值吻合较好.
2)采用不考虑UHPC受拉作用的装配柱的MUbc/MUt平均值为0.85,标准差为0.04,变异系数为0.05,计算结果偏小,不能准确计算塑性铰区采用UHPC装配式柱的承载力. 设计时,须考虑截面受拉区UHPC的作用.
5. 结 论
(1)普通混凝土整浇柱最终破坏时发生弯曲破坏,混凝土的受损程度严重,丧失竖向承载力. 装配式柱破坏时相对完整,受压区混凝土压碎剥离面积较小,具有较好的耐损伤能力,可以减少震后修复费用.
(2)当搭接长度为8 d时,装配式柱的各项性能指标均高于普通混凝土整浇柱,可以实现与现浇整体柱相同的效果. 当搭接长度为12 d时,试件的累积耗能、变形能力、承载力等均有大幅提高,承载力退化速率缓慢,显著提高了试件的抗震性能.
(3)对于UHPC连接的装配式柱,降低轴压比或减小搭接段配箍率均无法充分发挥UHPC的黏结性能,不利于钢筋搭接. 在搭接段配置短钢筋的装配式柱,由于搭接区配筋率增大,承载力相应增大,但在一定程度上会降低试件的变形能力、延性和耗能能力,应谨慎考虑.
(4)在水平及竖向荷载的共同作用下,UHPC的受拉作用可以使得装配柱承载力提高约10%~20%,故设计时须考虑截面受拉区UHPC的作用.
本文将UHPC材料用于装配式柱构件连接部位,与已有的UHPC连接预制桥梁立柱、UHPC连接预制桥面板形成有效延伸,可以充分发挥UHPC材料优异的力学性能,使UHPC在装配式建筑领域推广发展. 限于试验量的原因,本文只考虑最方便、简单的直接搭接形式,未能考虑其他搭接形式. 采用UHPC材料连接的装配式构件只需较短的搭接长度,即可实现等同现浇的效果. 考虑UHPC受拉作用计算所得的装配式柱正截面受弯承载力与试验值吻合较好,可以为工程设计提供参考.
参考文献
基于螺栓连接的新型钢筋混凝土框架装配式节点抗震性能研究
[J].DOI:10.13204/j.gyjz201908016 [本文引用: 1]
Experimental research on seismic behavior of new RC frame assembly joints based on bolted connection
[J].DOI:10.13204/j.gyjz201908016 [本文引用: 1]
现浇柱叠合梁框架节点抗震性能试验研究
[J].DOI:10.3321/j.issn:1000-6869.2008.06.002 [本文引用: 1]
Experimental study on seismic behavior of different type of frame connections with composite beams and cast-in-place columns
[J].DOI:10.3321/j.issn:1000-6869.2008.06.002 [本文引用: 1]
钢筋混凝土分体柱框架梁柱中节点抗震性能的研究
[J].DOI:10.3321/j.issn:1000-6869.2001.04.010
Study on seismic behavior of beam column joints in RC frame with split columns
[J].DOI:10.3321/j.issn:1000-6869.2001.04.010
Performance of precast/prestressed concrete building structure during northridge earthquake
[J].
装配式混凝土框架节点基本性能研究进展
[J].DOI:10.14006/j.jzjgxb.2018.02.001 [本文引用: 1]
Research progress on fundamental performance of precast concrete frame beam-to-column connections
[J].DOI:10.14006/j.jzjgxb.2018.02.001 [本文引用: 1]
Grouted sleeve connections used in precast reinforced concrete construction: experimental investigation of a column-to-column joint
[J].
Experimental investigation of precast concrete based dry mechanical column–column joints for precast concrete frames
[J].
套筒灌浆缺陷对装配式混凝土柱抗震性能影响的试验研究
[J].DOI:10.15951/j.tmgcxb.2018.05.009 [本文引用: 1]
Experimental study on effects of grout defects on seismic performance of assembled concrete columns
[J].DOI:10.15951/j.tmgcxb.2018.05.009 [本文引用: 1]
Experimental test methods to determine the uniaxial tensile and compressive behaviour of ultra high performance fibre reinforced concrete (UHPFRC)
[J].DOI:10.1016/j.conbuildmat.2012.04.030 [本文引用: 1]
Influence of fibre geometry and matrix maturity on the mechanical performance of ultra high-performance cement-based composites
[J].DOI:10.1016/j.cemconcomp.2012.08.005
Mechanical, durability and microstructural characteristics of ultra-high-strength self-compacting concrete incorporating steel fibers
[J].DOI:10.1016/j.matdes.2009.04.024 [本文引用: 1]
基于超高性能混凝土的钢筋锚固性能研究
[J].
Study on anchorage behavior of steel bar in ultra-high performance concrete
[J].
变形钢筋/超高性能混凝土搭接黏结性能
[J].DOI:10.13801/j.cnki.fhclxb.20201229.006 [本文引用: 2]
Bonding properties of deformed steel bar/ultra high performance concrete
[J].DOI:10.13801/j.cnki.fhclxb.20201229.006 [本文引用: 2]
局部采用纤维增强混凝土柱的抗震性能试验与分析
[J].DOI:10.6052/j.issn.1000-4750.2012.06.0394
Experiments and analyses of seismic behavior of columns with fiber-reinforced concrete in bottom region
[J].DOI:10.6052/j.issn.1000-4750.2012.06.0394
钢筋UHPC梁正截面抗弯承载力计算方法
[J].DOI:10.15951/j.tmgcxb.2021.03.008
Calculation method of flexural capacity of normal section of reinforced UHPC beam
[J].DOI:10.15951/j.tmgcxb.2021.03.008
碱镁混凝土大偏心受压柱的试验研究
[J].DOI:10.11990/jheu.201603105 [本文引用: 1]
Study on large eccentric compression column of basic magnesium sulfate cement concrete
[J].DOI:10.11990/jheu.201603105 [本文引用: 1]