近年来,随着越来越多的大型三维模型数据集变得可用,虚拟现实、地质勘探、三维打印等应用领域对三维模型的分析与处理需求呈井喷式增长. 其中,三维模型对应关系计算是对三维模型进行分析与处理的一项基本任务,如何快速、准确地构建三维模型之间的对应关系是相关研究领域亟待解决的研究热点及难点问题[1].
联合分析与优化集合中的模型间对应关系可以改善单独计算成对模型间对应关系的准确率. 本文提出无监督三维模型簇对应关系协同计算的方法,结合三维点云模型所包含的特征信息,优化函数映射矩阵,协同计算三维模型簇对应关系,提高近似等距的非刚性变换的三维模型簇对应关系计算的准确率. 本文的主要创新点和贡献如下.
1)提出共享权重的三维点云特征提取网络,以获取更具鉴别力的特征.
2)在优化函数映射矩阵时,通过添加无监督加权正则化约束项获得更高质量的函数映射矩阵,计算出更准确的近似等距的非刚性变换的模型间对应关系.
3)结合函数映射理论与循环一致性约束,协同分析三维模型簇,提高对应关系计算的准确率.
1. 相关研究工作
目前,专注于解决2个模型间对应关系计算的研究日渐成熟. 在函数映射框架的基础上,Ren等[13]提出利用函数映射框架计算非刚性变换模型间对应关系的方法,通过添加连续性和方向性约束,获得高质量的函数映射关系. 杨军等[14]提出校准三维几何模型之间基矩阵的对应关系计算方法,将模型间对应关系的构建转化为由模型特征函数构建的基矩阵之间的校准运算. Wu等[15]针对非刚性三维残缺模型的对应关系问题,提出基于全频谱特征值对齐和上采样细化的三维模型部分函数映射新方法. Eisenberger等[16]提出计算非等距三维模型对应关系的新方法,将输入模型嵌入到内在光谱和外在几何坐标的乘积空间中,结合内在和外在特征信息并不断迭代,以得到精细化映射. Litany等[17]结合深度学习技术与函数映射理论,提出深度函数映射网络,将对应关系计算直接作为学习过程的一部分,通过任务驱动的特征描述符学习方式得到更准确、涵盖信息更全面的模型特征描述符. Halimi等[18]提出无监督深度函数映射网络,该方法用模型的几何约束代替模型间的真实对应关系,定义无监督损失函数,评估对应关系的准确性,减少对带标签数据的依赖. Donati等[19]提出新的基于学习的非刚性变换三维模型对应关系计算方法,该方法直接从原始模型中学习几何特征,显著提高了网络的泛化能力.
随着三维模型数据量的不断增多,如何利用大规模数据集合提供的多个模型的信息准确地计算三维模型簇的对应关系,是国内外相关研究领域的关键瓶颈问题. Huang等[20]提出新的凸优化框架,将循环一致性约束表示为半正定的解,但半正定规划对于映射关系的优化有所受限,无法得到准确的映射结果. Kim等[21]将模型联合划分为具有相似结构的簇,学习每个模型簇内基于部分可变形模型的形变方式,为具有相似模板的所有模型提供语义等价点之间的对应关系,但该方法依赖于初始模板的质量且当不同模型部件非常相似时会产生错误对应. Cosmo等[22]将模型簇对应关系的计算问题建模为计算整个模型集合的最小失真对应,该方法不需要模型对之间的初始映射作为输入,但依赖于模型对之间的测地距离,导致算法的计算复杂度偏高;该方法对带有孔洞的模型十分敏感,无法有效构建出模型簇准确的对应关系. 杨军等[23]提出基于迪杰斯特拉最远点采样、函数映射理论与循环一致性约束的计算三维模型簇的新方法,但该方法在计算函数映射矩阵时需要人工调参进行优化,导致算法的鲁棒性不佳. Bernard等[24]提出用于多模型对应关系计算的高阶投影幂迭代法,该算法将多模型匹配问题描述为同时解决具有二阶匹配分数的成对模型匹配问题,在计算复杂度和确保稳定的循环一致性约束方面都具有良好的表现,但该方法依赖于模型间初始映射的质量,导致算法的泛化能力不佳.
以上的传统算法往往需要良好的初始映射作为输入条件,若加入新的模型,则整个算法须重新计算. 随着深度学习技术的快速发展,研究者们提出基于深度学习的方法,解决模型簇对应关系的计算问题. Huang等[25]提出多标签半监督学习算法,用来计算模型簇的对应关系. 该算法将给定类别的大型模型集合作为输入,联合学习每个类的距离度量,以捕获类内潜在的几何相似性,但该方法要求输入模型皆为带标签的数据,且集合内的模型都属于同一类别. Fish等[26]建立对应关系网络,分析大型模型集合的对应关系. 该方法从模型集合中提取相似的模型对,估计模型的相似性和对应性,构建模型簇的对应关系,但该方法须对模型进行二维投影与分割,仅适用于具有铰接关节的人体模型. Huang 等[27]提出多映射同步方法,以异构三维模型簇为输入,输出一致的稠密成对模型间的映射关系. 该方法的关键是用基于张量的表示方法显式编码相关模型集合之间的映射,但该方法对非刚性变换的三维模型簇对应关系计算结果的准确率不高. Groueix等[28]提出深度表面变形的自监督方法,计算三维模型簇的稠密对应关系. 该方法利用参数预测网络来预测2个模型间的变形参数,利用循环一致性约束作为监督信号,预测有意义的对应,但该方法对应关系结果的准确性依赖于初始带标签的数据,构建的循环一致性损失可能会求解出次最优的模型簇对应关系.
为了提高三维模型簇对应关系准确率及算法的普适性,本文以实现高精度三维模型簇对应关系计算为主要研究目标,结合深度学习技术、循环一致性约束及函数映射理论,对三维模型簇的对应关系计算展开探索.
2. 理论基础
将模型建模为嵌入在
2.1. 模型簇对应关系表示及循环一致性约束
给定用三角网格表示的三维模型簇数据集
式中:P为由0、1构成的矩阵,s、t为任意2个非负整数,
设
图 1
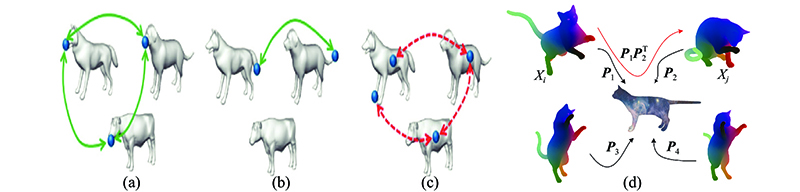
对于不满足双射映射的情况,Bernard等[24]使用模型到虚拟全局模型的对应,表示模型簇的对应关系. k个模型上所有不同点的并集称为虚拟全局点,用d表示虚拟全局点的总数,则k个模型上的每个点都与虚拟全局模型中的一个点相对应. k个模型上与同一虚拟全局点对应的所有点都是彼此对应的. 用
如图1(d)所示,从模型
将所有的
式中:
2.2. 函数映射
函数映射将模型间对应关系的求解问题转换为在模型
式中:
式中:
设C具有所有
为了对成对的函数映射
式中:
将所有
定义矩阵块
2.3. 深度函数映射
深度函数映射由Litany等[17]提出,该方法通过训练神经网络对描述符进行优化,解决谱域中的模型间对应关系问题. 具体来讲,通过神经网络学习每个点的新的局部特征来改进模型之间的函数映射矩阵C,使得全局映射更加准确. 该体系结构定义了模糊矩阵
式中:
3. 无监督动态图卷积循环一致函数映射网络
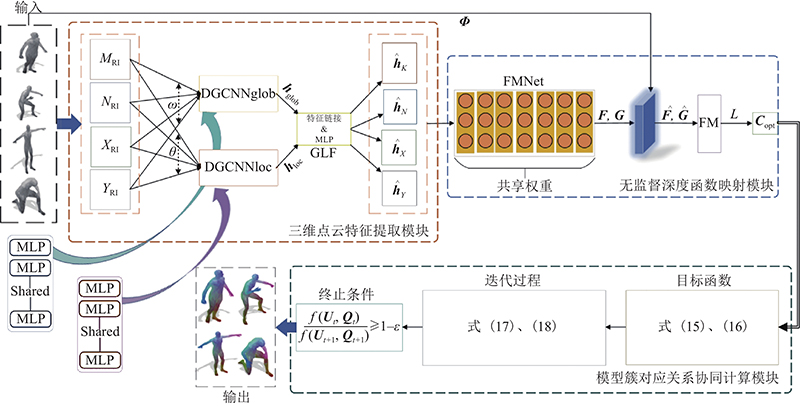
针对现有三维模型簇对应关系计算方法的不足,结合数据驱动技术、经典函数映射理论与循环一致性约束,构建无监督动态图卷积循环一致函数映射网络,计算三维模型簇的一致对应关系. 总体的网络框架如图2所示,主要由三维点云特征提取模块、无监督深度函数映射模块、模型簇对应关系协同计算模块3部分组成.
图 2
图 2 无监督动态图卷积循环一致函数映射网络框架
Fig.2 Unsupervised DGCNN cycle-consistency functional map network framework
无监督三维模型簇对应关系协同计算方法的具体实现步骤如下.
1)在点云特征提取模块中完成对输入模型的特征提取. 将一组三维点云模型输入到特征提取模块中,提取模型的旋转不变特征描述符. 将该特征描述符输入共享网络参数的动态图卷积全局与局部特征提取网络中,分别提取模型的全局与局部特征. 将局部特征与全局特征融合,以获取信息量更丰富的模型特征.
2)在无监督深度函数映射模块中,获得模型对之间的最优函数映射矩阵Copt. 将获得的特征输入无监督深度函数映射模块中,经过残差网络处理得到模型对的空间域描述符F、G,将它们投影至各自的拉普拉斯特征基上,获得谱描述符
3)计算出最终的模型簇对应关系. 将得到的各模型对之间的最优函数映射矩阵Copt输入到模型簇对应关系协同计算模块中,求解出每个模型与虚拟全局模型的最优函数映射矩阵Ci,将其堆叠记为矩阵
3.1. 三维点云特征的提取模块
1)从输入点云的欧氏坐标中提取旋转不变特征描述符. 对于三维点云模型
式中:
聚合后的RI特征表示为
2)通过局部特征提取模块和全局特征提取模块,将模型的旋转不变特征描述符嵌入到高维的特征空间中. 对于具有N个点的模型
3)对生成的全局和局部特征进行融合(global-local fusion, GLF). 将局部特征与全局特征进行拼接,生成特征
3.2. 无监督深度函数映射模块
构建无监督深度函数映射模块的目的是获得最优的模型间函数映射矩阵Copt. 将提取到的特征输入到具有7个完全相同残差块的孪生残差网络中进行学习,得到增强后的空间域描述符. 将空间域描述符分别投影至各自拉普拉斯-贝尔特拉米特征基上,获得相应的谱描述符,利用式(6)计算成对模型间函数映射矩阵C.
Donati等[19]指出,当满足
式中:ci为矩阵C的行向量,bi为矩阵B的行向量.
为了解决先验知识不足和人工标注成本过高的问题,研究者们探究对模型自身的结构属性进行约束,以代替计算损失函数
因已将正交性作为先验条件,该模块的最后一步操作通过对模型间函数映射矩阵C施加无监督加权正则化约束项,获取优化后的函数映射矩阵Copt. 无监督加权正则化约束项为
约束项E1的权重
无监督深度函数映射模块中所构建的网络利用模型的几何性质来代替标签,使用加权正则化约束项优化目标函数,以无监督的学习方式代替有监督的学习方式,在节省成本的同时,提高了网络模型的泛化能力.
3.3. 模型簇对应关系协同计算模块
模型簇对应关系协同计算模块将循环一致性约束融入函数映射理论中,构建模型簇对应关系协同计算目标函数,通过对目标函数进行求解,得到最优的模型簇对应关系.
目标函数定义为
式中:
所有成对的i与j对应的基函数
为了计算最大化的目标函数,需要不断地迭代优化矩阵
式中:
定义
式中:
当满足
4. 实验结果与分析
4.1. 实验环境和实验数据集
该算法的实验环境基于Linux Ubuntu 16.04操作系统,硬件支撑为Intel i9-9900k CPU和NVIDIA GeForce RTX2080Ti GPU(11 GB的显存),内存为32 GB,运算平台为CUDA-Toolkit 9.0版本. 采用Cudnn7.6.5作为网络的GPU加速器,深度学习框架为TensorFlow-GPU,版本号为1.13,编程语言为Python 3.7.
4.2. 参数设置与评估标准
在实验中,设置Batch Size为8,初始学习率为0.001,使用自适应矩估计优化器(adaptive moment estimation, Adam),学习率衰减指数为0.5,衰减速度为300 000,网络训练过程迭代5 000次.
根据普林斯顿基准协议(Princeton benchmark protocol, PBP)[36]和循环误差(cycle error),对模型簇的对应关系质量进行评估.
假设计算出一对模型的对应关系为
式中:DY表示模型Y计算出的对应关系与真实对应关系间的测地距离,area (Y)为模型Y的表面积. 测地误差越小,对应关系的准确率越高.
对于模型簇协同计算迭代停止条件,根据目前主流算法的最优测地误差,将FAUST、SCAPE和TOSCA数据集人体模型上的
利用循环误差来量化算法的循环一致性约束,循环误差定义为在总循环次数中违背循环一致性约束的次数除以总循环的次数. 在3种不同数据集中,均以4个模型为一组,总循环次数为在测试集10个模型中任选4个的组合,共
4.3. 实验结果与分析
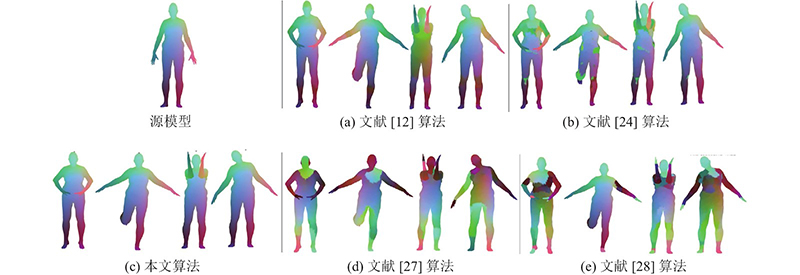
图 3
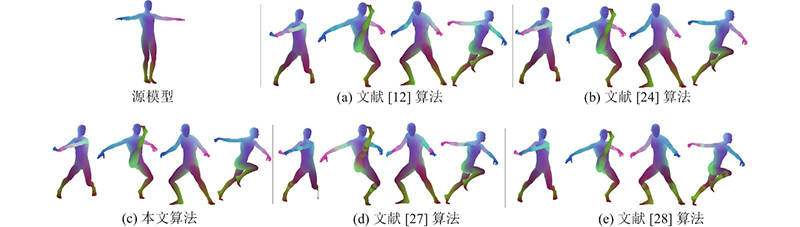
图 3 FAUST数据集上不同方法构建的人体模型簇一致对应关系结果的对比
Fig.3 Comparison of consistent correspondences of human shape collections constructed by different methods on FAUST dataset
图 4
图 4 SCAPE数据集上不同方法构建的人体模型簇一致对应关系结果的对比
Fig.4 Comparison of consistent correspondences of human shape collections constructed by different methods on SCAPE dataset
图 5
图 5 TOSCA数据集上不同方法构建的人体模型簇一致对应关系结果的对比
Fig.5 Comparison of consistent correspondences of human shape collections constructed by different methods on TOSCA dataset
图 6
图 6 TOSCA数据集上不同方法构建的猫模型簇一致对应关系结果的对比
Fig.6 Comparison of consistent correspondences of cat shape collections constructed by different methods on TOSCA dataset
图 7
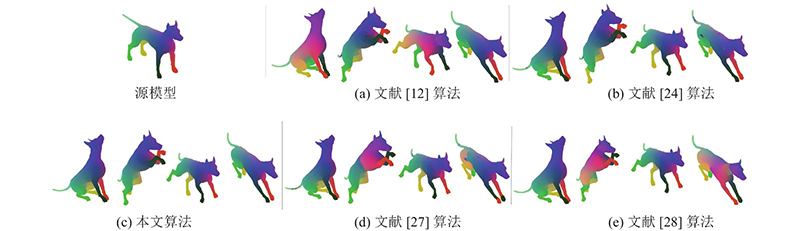
图 7 TOSCA数据集上不同方法构建的狗模型簇一致对应关系结果的对比
Fig.7 Comparison of consistent correspondences of dog shape collections constructed by different methods on TOSCA dataset
图 8
图 8 TOSCA数据集上不同方法构建的马模型簇一致对应关系结果的对比
Fig.8 Comparison of consistent correspondences of horse shape collections constructed by different methods on TOSCA dataset
图 9
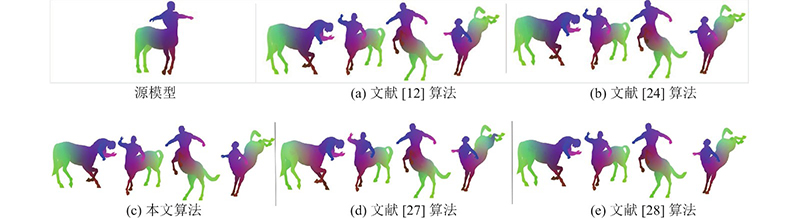
图 9 TOSCA数据集上不同方法构建的半人马模型簇一致对应关系结果对比
Fig.9 Comparison of consistent correspondences of centaur shape collections constructed by different methods on TOSCA dataset
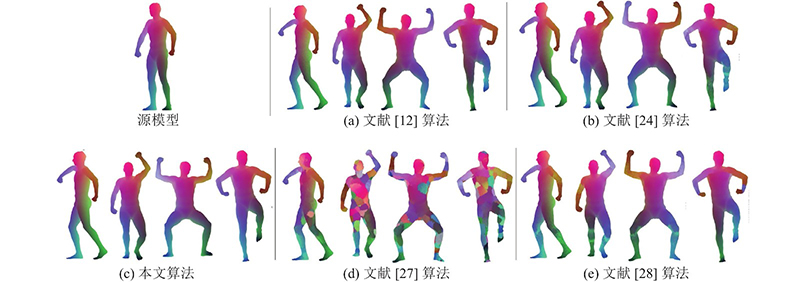
从图3(a)、4(a)、5(a)可以看出,文献[12]算法的整体映射连续性较好,但在不同数据集上人体模型的手部和腿部均产生了错误对应. 主要原因是该算法依赖于输入模型的初始映射,当初始映射准确率不高时,容易产生错误对应,利用该算法无法有效地解决模型因自身对称性影响而产生的错误对应. 从图3(b)、4(b)和5(b)可以看出,文献[24]算法在不同数据集上人体模型的局部位置均出现了错误对应,如手臂、腿部、腹部、胸部,这是由于该算法在初始映射不满足双射条件时,很容易产生离群值,导致发生错误对应. 文献[24]算法采用与本文算法相同的虚拟全局模型思想,有效克服了因模型自身对称性影响对应关系计算的问题. 从图3(d)、4(d)、5(d)可以看出,文献[27]算法在不同数据集人体模型上的一致映射结果最差,在人体模型胸部、腹部、手臂和小腿出现了大量的错误对应,这是由于该算法适用于刚性变换的等距模型,对于产生非刚性形变的近似等距模型的对应关系计算效果不佳,无法消除模型自身对称性的影响. 从图3(e)、4(e)、5(e)可以看出,文献[28]算法在人体模型腹部、胸部、腿部产生了局部错误对应,这是由于该算法依赖用初始带标签的数据预测模型变形过程,使得该算法对拓扑结构改变敏感,无法消除模型因自身对称性影响而产生的错误对应. 从图3(c)、4(c)、5(c)可以看出,利用本文算法可以计算近似等距的非刚性变换的模型簇对应关系,得出的对应关系质量最高,不仅能够消除模型自身对称性的影响,而且所得结果在语义上更加平滑、自然.
综上所述,定性结果表明,本文算法所构建的对应关系准确性更高,模型簇映射分布均匀一致且连续性更好,有效解决了模型因自身对称性影响对应关系计算的问题,证明了本文算法的优越性.
表 1 不同算法的平均测地误差
Tab.1
| 模型 | | ||||
| 文献[12]算法 | 文献[24]算法 | 文献[27]算法 | 文献[28]算法 | 本文算法 | |
| 人体模型簇(FAUST) | 0.039 | 0.058 | 0.124 | 0.097 | 0.026 |
| 人体模型簇(SCAPE) | 0.107 | 0.174 | 0.449 | 0.217 | 0.046 |
| 人体模型簇(TOSCA) | 0.046 | 0.036 | 0.168 | 0.157 | 0.025 |
| 猫模型 | 0.087 | 0.139 | 0.329 | 0.131 | 0.023 |
| 狗模型 | 0.334 | 0.169 | 0.393 | 0.244 | 0.034 |
| 马模型 | 0.375 | 0.258 | 0.284 | 0.129 | 0.037 |
| 半人马模型簇 | 0.069 | 0.053 | 0.171 | 0.065 | 0.028 |
从表1可以看出,与文献[12]算法相比,本文算法所构建的人体模型簇对应关系测地误差在FAUST、SCAPE和TOSCA数据集上分别减小了0.013、0.061和0.021,猫模型、狗模型、马模型和半人马模型簇的对应关系测地误差分别减小了0.064、0.300、0.338和0.041. 与文献[24]算法相比,本文算法所构建的人体模型簇对应关系测地误差在FAUST、SCAPE和TOSCA数据集上分别减小了0.032、0.128和0.011,猫模型、狗模型、马模型和半人马模型簇的对应关系测地误差分别减小了0.116、0.135、0.221和0.025. 与文献[27]算法相比,本文算法所构建的人体模型簇对应关系测地误差在FAUST、SCAPE和TOSCA数据集上分别减小了0.098、0.403和0.143,猫模型、狗模型、马模型和半人马模型簇的对应关系测地误差分别减小了0.306、0.359、0.247和0.143. 与文献[28]算法相比,本文算法所构建的人体模型簇对应关系测地误差在FAUST、SCAPE和TOSCA数据集上分别减小了0.071、0.171和0.132,猫模型、狗模型、马模型和半人马模型簇的对应关系测地误差分别减小了0.108、0.210、0.092和0.037. 综上所述,本文算法在计算近似等距的非刚性变换的三维模型对应关系的能力上,比其他4种对比算法更优异,准确率更高.
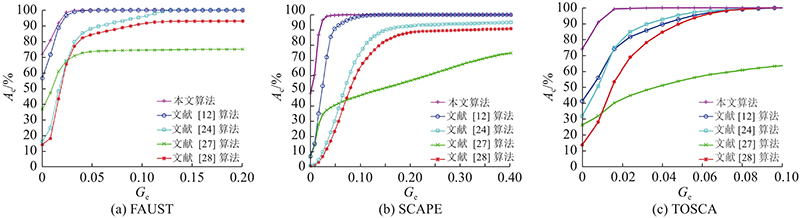
通过绘制测地误差曲线,进一步展示定量结果. 本文算法与其他算法在FAUST、SCAPE和TOSCA数据集上人体模型的测地误差对比曲线如图10所示. 图中,Ge为测地误差,Ac为对应关系准确率. 在FAUST数据集上,本文算法有71.4%的对应关系没有测地误差,有98.3%的对应关系的Ge小于0.02,当Ge接近0.03时,本文算法的Ac达到100%. 在SCAPE数据集上,本文算法有48.6%的对应关系没有测地误差,有96.2%的对应关系的Ge小于0.02,当Ge接近0.04时,本文算法的Ac达到100%. 在TOSCA数据集上,本文算法有74.5%的对应关系没有测地误差,有90%的对应关系的Ge小于0.01,当Ge达到0.02时,本文算法的Ac达到100%.
图 10
图 10 不同算法在FAUST、SCAPE和TOSCA数据集上的测地误差曲线
Fig.10 Geodesic error curves of different algorithms on FAUST, SCAPE and TOSCA datasets
表 2 不同算法的模型簇对应关系的循环误差
Tab.2
如表3所示为本文算法与文献[27,28]算法在FAUST数据集上计算模型簇对应关系所需的运行时间对比结果. 表中,tp为数据预处理时间,tr为训练和测试时间,tt为总运行时间,‘—’表示不包含该部分时间. 总体运行时间主要由以下2个阶段构成. a)在数据预处理(pre-processing)阶段,文献[27]算法需要计算每个模型的初始函数空间及初始映射,本文算法需要计算每个模型的拉普拉斯算子的特征值和特征向量. b)在训练和测试(train and test)阶段,文献[27]算法通过显示映射编码并不断迭代进行张量恢复,得到最终的模型簇对应关系. 文献[28]算法的整个网络框架分为参数预测网络和变形网络,网络参数量较大,所以需要耗费较长时间. 本文算法分为3个模块,算法计算过程需要多次迭代优化,总运行时间是3种算法中最长的,但模型簇对应关系计算的准确率得到了有效提升,所以本文算法在运行时间和模型簇对应关系计算的准确率之间达到较佳的平衡状态.
表 3 不同方法的运行时间比较
Tab.3
3)消融实验. 为了验证本文算法各模块的有效性,如表4所示为在计算模型簇对应关系时,不包含三维点云特征提取模块、不包含无监督深度函数映射模块、不包含模型簇对应关系协同计算模块以及同时包含3种模块时在FAUST、SCAPE和TOSCA数据集上构建的人体模型族对应关系测地误差消融实验的对比结果. 表中,‘√’表示包含该模块,‘—’表示移除该模块. 可以看出,本文构建的网络各组件是有效的,能够相互促进,以达到最佳性能. 对网络性能影响最大的是模型簇对应关系协同计算模块,该模块融合循环一致性约束与函数映射理论,显著提高了模型簇对应关系计算的准确率.
表 4 验证各模块有效性的消融实验对比
Tab.4
| 三维点云 特征提取模块 | 无监督深度 函数映射模块 | 模型簇对应关系 协同计算模块 | Ge | ||
| FAUST | SCAPE | TOSCA | |||
| — | √ | √ | 0.059 | 0.127 | 0.103 |
| √ | — | √ | 0.103 | 0.205 | 0.086 |
| √ | √ | — | 0.185 | 0.288 | 0.176 |
| √ | √ | √ | 0.026 | 0.046 | 0.025 |
5. 结 语
本文提出无监督三维模型簇对应关系协同计算方法,解决近似等距的非刚性变换的三维模型簇对应关系计算准确率不高的问题. 对输入的原始三维点云模型进行特征提取,在共享权重的全局、局部特征提取网络中分别提取模型的全局与局部特征,并将其融合. 在无监督深度函数映射网络中,对融合后的特征进行转换,以获取所需的谱描述符. 利用函数映射理论和加权正则化约束,构建模型间的最优函数映射矩阵. 在模型簇对应关系协同计算模块中,通过优化模型簇对应关系协同计算的目标函数,获得最终的模型簇对应关系. 本文算法在FAUST、SCAPE和TOSCA数据集上开展的实验结果表明,在不需要真实对应关系作为监督的情况下,本文算法均取得优于目前主流算法的对应关系计算结果. 如何提高算法的时间效率以及如何解决更普遍的模型间对应关系问题,如非等距三维模型簇对应关系计算问题与残缺三维模型簇对应关系计算问题,是今后需要继续研究的方向.
参考文献
Recent advances in shape correspondence
[J].DOI:10.1007/s00371-019-01760-0 [本文引用: 1]
Method for registration of 3D shapes
[J].DOI:10.1109/34.121791 [本文引用: 1]
Functional maps: a flexible representation of maps between shapes
[J].
Jointly learning shape descriptors and their correspondence via deep triplet CNNs
[J].
Exploring collections of 3D models using fuzzy correspondences
[J].
An optimization approach for extracting and encoding consistent maps in a shape collection
[J].
Functional map networks for analyzing and exploring large shape collections
[J].
Consistent zoomout: efficient spectral map synchronization
[J].DOI:10.1111/cgf.14084 [本文引用: 9]
Continuous and orientation-preserving correspondences via functional maps
[J].
校准三维模型基矩阵的函数映射的对应关系计算
[J].
Correspondence calculation of functional maps for calibrating the base matrix of 3D model
[J].
Partial 3D shape functional correspondence via fully spectral eigenvalue alignment and upsampling refinement
[J].DOI:10.1016/j.cag.2020.09.004 [本文引用: 1]
Consistent shape maps via semidefinite programming
[J].DOI:10.1111/cgf.12184 [本文引用: 1]
Learning part-based templates from large collections of 3D shapes
[J].
Consistent partial matching of shape collections via sparse modeling
[J].DOI:10.1111/cgf.12796 [本文引用: 1]
结合函数映射与循环一致性约束的模型簇对应关系计算
[J].
Correspondence calculation of shape collections by functional maps combined with cycle-consistency constraints
[J].
Fine-grained semi-supervised labeling of large shape collections
[J].
Structure-oriented networks of shape collections
[J].
Tensor maps for synchronizing heterogeneous shape collections
[J].
Unsupervised cycle-consistent deformation for shape matching
[J].DOI:10.1111/cgf.13794 [本文引用: 12]
Dynamic graph CNN for learning on point clouds
[J].
Structured regularization of functional map computations
[J].DOI:10.1111/cgf.13788 [本文引用: 1]
SCAPE: shape completion and animation of people
[J].DOI:10.1145/1073204.1073207 [本文引用: 1]
Blended intrinsic maps
[J].