在全球范围内，心脏疾病的死亡率高居首位，心电图 (electrocardiograph, ECG) 辅助诊疗是目前诊断心脏疾病最直接、最有效的方法^[1]. 以往的研究主要集中在以下方面. 1）利用心电RR间隔变化和波形形态特征检测^[2]，该类方法较简单，但针对动态心电的普适性不强. 2）利用支持向量机(support vector machine, SVM)、决策树的传统机器学习算法^[3]，在特定样本训练和测试集下，由于特征提取的针对性，能够发挥较好的作用，但面对大量未知测试数据时，存在需要人工提取特征和泛化能力差的问题.

近年来，深度神经网络凭借强大的特征提取能力，在医疗保健领域中得到了广泛应用. 卷积神经网络 (convolutional neural network, CNN)具有局部连通性和参数共享性，是有效的特征提取方法. Fan等^[4] 使用多尺度融合CNN进行ECG信号特征提取，检测心房颤动，取得了96.99%的分类准确率. Hannun等^[5] 设计4层CNN模型，在识别12类律失常时取得了较高的识别性能. 长短期记忆 (long short-term memory, LSTM) 和门控循环单元(gated recurrent cell, GRU) 是用于处理时间序列信号的神经网络，可以应用于心律失常检测^[6]. Saadatnejad等^[7] 提出基于小波变换和多重LSTM的连续实时的特定患者心电图分类算法. Lynn等^[8] 提出基于深度双向GRU网络的生物特征心电图分类方法，在测试集上的总体分类准确率为98.55%. Yao等^[9] 提出用于心律失常分类的模型，该模型集成了基于VGG-Net的CNN和LSTM层，该模型在9分类心电信号测试集上取得总体分类F₁为77.3%. He等^[10] 提出由残差卷积网络和双向LSTM层组成的模型，该模型在9种心律失常分类中取得的总体F₁为80.6%. Yao 等^[11] 提出在CNN层后引入注意力模块，该模型是检测阵发性心律失常的有效方法. Wang 等^[12] 提出使用GAN和残差网络对ECG心律失常检测，在解决了数据集不平衡问题的同时，提高了分类准确率. Hou等^[13] 提出基于LSTM自动编码器的网络，利用SVM对这些信号进行分类，该模型的总体准确率较高，但是对于数据量较少的心率失常类别，分类准确率较低.

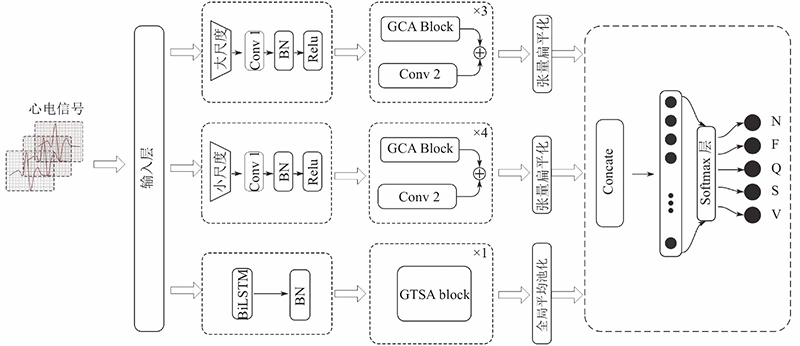
相较于现有的神经网络模型，本文提出的神经网络模型是并行架构，采用2种尺度卷积对心电信号进行局部空间特征提取，分为2路特征向量分别处理. 另设一路为增强特征向量，该特征向量是心电信号经过长短时记忆网络提取的时序特征，结合设计的GCA Block (gate channel attention block)和GTSA Block (gate time step attention block) 模块，实现时空注意力机制，使得提取到心电信号的特征损失最小，实现对不同心电信号的精确分类.

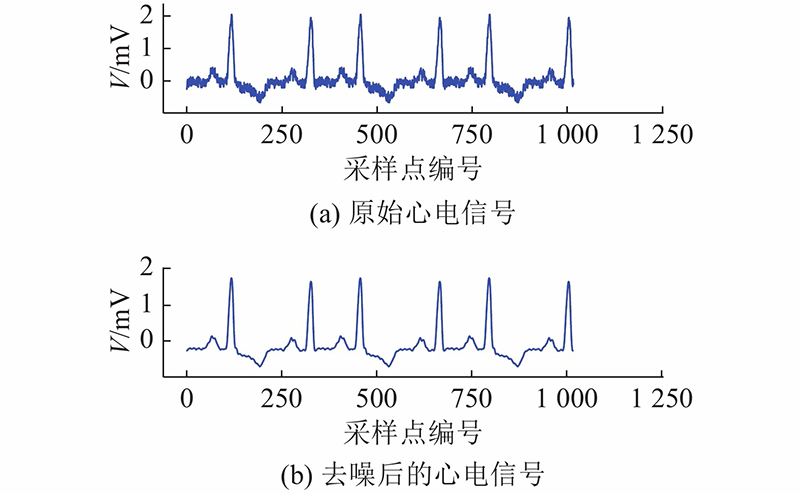
采用的数据来自于 MIT-BIH 心率失常数据库^[14]. 该数据库是目前在心电信号分类研究领域使用最广泛的心电信号数据库，由麻省理工学院和波士顿贝丝以色列医院共同记录完成. 在 MIT-BIH心率失常数据库中，包含来自47名受试者（编号201与编号202来自同一受试者个体）的心电信号数据，每条记录30 min，共计48条记录数据. 在原始心电信号中常会夹杂基线漂移、工频干扰、肌电干扰等噪声，这会在一定程度上影响心电分类的准确率. 为了抑制噪声，采取小波软阈值去噪算法^[15]. 在对小波进行多尺度分解后，通过对每层的高频系数进行阈值设定和消噪处理，利用小波逆变换将各层依次进行小波重构，得到去噪后的信号. 图1中，V为心电信号电压. 如图1所示，对比原始心电信号与去噪后的信号可以看出，利用小波软阈值去噪算法可以较好地消除噪声，去噪后的信号更平滑，保留了有用信号.

由于本文分类方法是针对心拍数据的，在心电信号去噪后须完成心电信号心拍分割. 根据MIT-BIH心率失常数据库中对QRS波位置的标记，可以将连续的心电信号分割成单个的心拍数据. 由心电信号的特性可知，R波峰的位置偏向于P波，不位于心拍的中心位置. 以R波峰为基准点，前、后分别取160和180个数据点，分割出完整的心拍.

按照AAMI标准^[16]将心拍分为5种类型：正常心拍(N)、室上性早搏(S)、室性早搏(V)、融合心拍(F) 和未知心拍(Q). 将MIT-BIH心律失常数据库48条心电记录分割并按照AAMI标准分类后，分别得到N类型心拍90 519个、V类型心拍7 140个、S类型心拍2 757个、F类型心拍800个和Q类型心拍8 034个，共计109 250个心拍. 从每种类型的心拍中选取一个形态，如图2所示.

深度学习模型具有强大的自动提取特征和表达能力，在训练和优化过程中，需要一定数量的训练数据才能达到模型最优点. 当数据量不足时，容易出现过拟合和局部最优解的现象，严重影响模型的性能. 从1.1节可知，心电信号分类存在数据不平衡的问题，S、V、F、Q 、N这5种心拍类型，在心拍数量上相差较大，数量比例严重失衡. 利用自适应合成采样 (adaptive synthetic sampling, ADASYN)算法^[17]，合成少数类型的心拍样本，以获得更多少数类的训练数据，提升模型的分类性能. 具体算法的流程如下.

1）计算需要合成的样本数量：

(1) $ G=\left(S_{\mathrm{maj}}-S_{\min }\right) \beta . $

式中： $ S_{\mathrm{maj}} $为多数类样本数量； $ S_{\min } $为少数类样本数量；β为系数， $\;\beta \in [0,1.0]$； $ G $为总共需要合成的少数类样本数量.

2）对于每个少数类样本 $ x_{i} $，找出 $ K $近邻点，计算：

(2) $ \varGamma_{i}=\frac{\varDelta_i / K}{Z} .$

式中： $ \varDelta_{{i}} $为 $ K $近邻点中多数类样本的数量； $ {Z} $为规范化因子，以确保 $ \varGamma $构成一个密度分布.

3）针对每个少数类样本，计算需要合成的样本数量：

(3) $ g_{i}=\varGamma_{i} G . $

4）从 $ x_{i} $近邻点中随机选取 $ \hat{x}_{i} $，利用下式计算合成新样本：

(4) $ x_{\text {new }}=\left(\hat{x}_{{i}}-x_{{i}}\right) \eta+x_{{i}} .$

式中： $ x_{\text {new }} $为合成的新样本；η为随机数， $ \eta $ $ \in [0,1.0] $.

该算法利用分布 $ \varGamma $自动决定每个少数类样本需要合成的样本数量，给每个少数类样本施加权重. 周围的多数类样本越多，则权重越高.

参考训练集划分规则^[18]，将心拍数据集按照如图3所示的方式划分为训练集和测试集. 利用ADASYN算法对训练集进行数据增强，得到后续实验所需要的训练集.

如表1所示为数据增强前训练集和测试集的心拍数量N_b对比，如表2所示为数据增强后训练集的心拍数量对比. 为了保证测试集数据的真实性，只针对已划分好的训练集中的4种少数类心拍数据进行数据增强. 从表1可知，心电信号数据集按照8∶2的比例划分后，训练集共87 400个心拍样本，测试集共21 850个心拍样本. 从表2可知，在对训练集的少数类心拍数据增强后，N类心拍数量不变，S、V、F、Q 4种类型心拍数量的生成比例分别为1.43、1.28、4.16、1.34.

目前，在心电信号分类领域中，CNN和LSTM 是应用最多的分类模型. 相关的研究人员大多将CNN和LSTM分开训练或者采用串行的方式将CNN层的输出作为 LSTM的输入^[19-20]. 使用联合训练的方式，规避串行方式增加模型深度所带来的问题；融合时空注意力机制，达到降低训练复杂度和提升模型性能的目的. 设计并行架构模型，以CNN和Bi-LSTM为基特征提取模型，分为3条并行支路，分别提取ECG信号特征. 利用Concate层和Softmax层，对心电信号进行特征融合和自动分类. 整体模型结构如图4所示，具体参数的设置如表3所示.

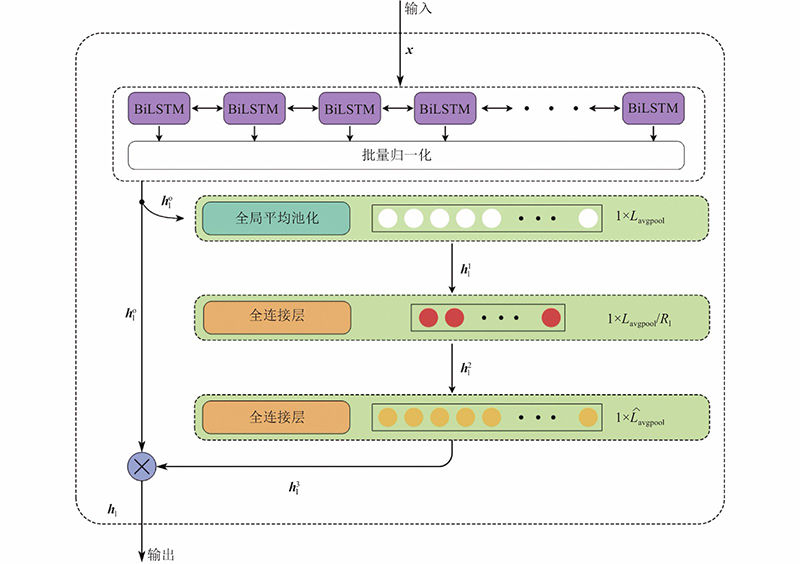
表3中，输入层大小为340，大尺度和小尺度输入分别由大小为7和5的卷积窗口处理得到. 最大池化层用于数据降维，分别根据不同卷积层的输出尺寸设置相应尺寸和步长. Bi-LSTM层将隐藏单元设置为170个，采用全输出模式，且在Bi-LSTM层后加全局平均池化层(global average pooling, GAP)用于数据降维. 将来自不同支路的特征融合，作为全连接分类器输入，为了防止过拟合，将Dropout Rate设置为0.5，最后Softmax的输出为分类结果.

在该模型中，CNN通过卷积核来捕捉输入序列的局部相关特征，其中的不同尺度表示对输入序列采用不同的滑动窗口进行处理. 卷积核的结构使得 CNN难以提取到序列数据中的前后依赖关系， Bi-LSTM通过引入记忆单元能够弥补这一缺陷^[21-24]，如图5所示为Bi-LSTM的整体结构. 从图4可以看出，该模型中的时空注意力机制是通过GCA Block和GTSA Block 2个模块实现的，具体的实现方式在1.4节介绍. 在GCA Block模块中，为了降低网络深度和保留CNN原始输出信息，采用残差的方式融合通道注意力机制. 在GTSA Block模块中，由于Bi-LSTM的输出具有前后相关的连续性，采用直连的方式，融合Bi-LSTM的输出与时间步注意力机制.

提出的时空注意力机制由2部分组成：1）基于门控机制和通道注意力机制的GCA Block (gate channel attention Block)，关注不同特征通道间的依赖关系；2)基于门控机制和时间步注意力机制的GTSA (gate time step attention) Block，关注输入序列的特征在不同时间点上的依赖关系. 时空注意力机制的引入，不但提高了该模型在ECG分类方面的性能，而且该机制的可扩展性强.

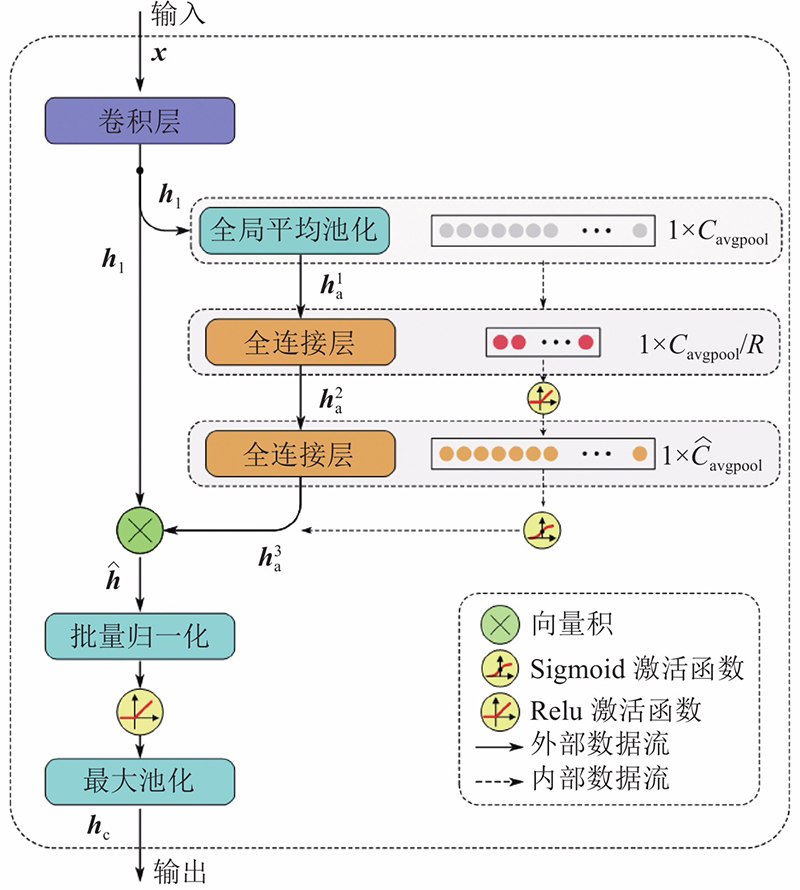
在传统方法中，对于不同CNN层的输入输出操作，是将上一层特征图传到下一层，不考虑不同通道特征图之间的关系. 提出的GCA Block根据网络全局损失函数的优化过程，利用门控机制自适应地调整不同通道之间的权重，建模通道之间的相互依赖关系^[24]. 门控机制采用双层全连接的方式，对不同特征通道间的相关性进行建模，得到代表相关性的特征向量. 利用Sigmoid函数，将特征向量映射到[0,1]空间，将特征向量与原始特征通道的内积作为输出. GCA Block的具体结构如图6所示. 可以看出，该模块主要分为压缩和还原2个步骤. 压缩操作通过在 $ \boldsymbol{h}_{1} $（ $ \boldsymbol{h}_{1} $表示不同通道特征向量的集合）上执行全局平均池化操作，得到每个通道的全局压缩特征向量 $ {\boldsymbol{h}}_{{\rm{a}}}^{1} $. 还原操作使用2层全连接构成门控机制，利用Relu和Sigmoid激活函数，得到每个通道的权值向量 $ \boldsymbol{h}_{{\rm{a}}}^{3} $. 将原始特征通道特征向量 $ \boldsymbol{h}_{1} $与权值向量 $ \boldsymbol{h}_{{\rm{a}}}^{3} $进行内积，得到加权后的特征向量 $ \hat{\boldsymbol{h}} $. 对 $ \hat{\boldsymbol{h}} $进行批量归一化和最大池化操作，得到最终的输出 $ {\boldsymbol{h}}_{{\rm{c}}} $，作为下一层网络的输入.

$ {\boldsymbol{h}}_{{\rm{a}}}^{1} $由下式得出：

(5) $ {\boldsymbol{h}}_{{\rm{a}}}^{1}={\rm{GAP}}\left({h}_{1}\right)=\frac{1}{W} \sum_{i=1}^{W} {\boldsymbol{h}}_{1}(i, j) .$

式中： $ \boldsymbol{x} $为输入向量； $ {\boldsymbol{h}}_{1} $为 $ \boldsymbol{x} $经过卷积操作输出的特征向量集； $ W $为 $ {\boldsymbol{h}}_{1} $的长度； $ {\boldsymbol{h}}_{{\rm{a}}}^{1} $向量大小为 $ 1 \times C_{\text {avgpool }} $，其中 $ C_{\text {avgpool }} $为 $ {\boldsymbol{h}}_{1} $中的通道数. $ \boldsymbol{h}_{{\rm{a}}}^{2} $由下式得出：

(6) $ {\boldsymbol{h}}_{{\rm{a}}}^{2}={\boldsymbol{W}}_{1} \cdot \delta\left({\boldsymbol{h}}_{{\rm{a}}}^{1}\right). $

式中： $ \delta $为Relu激活函数； $ \boldsymbol{h}_{{\rm{a}}}^{2} $向量大小为 $ 1 \times C_{\rm {avgpool }} / R $，其中 $ R $为门限宽度，本文设置为16. $ \boldsymbol{h}_{{\rm{a}}}^{3} $计算如下：

(7) $ {\boldsymbol{h}}_{{\rm{a}}}^{3}={\boldsymbol{W}}_{2} \cdot \sigma\left({\boldsymbol{h}}_{{\rm{a}}}^{2}\right) .$

式中： $ \sigma $为Sigmoid激活函数； $ {\boldsymbol{W}}_{1} $、 $ {\boldsymbol{W}}_{2} $分别为2个全连接层的权值矩阵，经过还原操作得到与 $ {\boldsymbol{h}}_{{\rm{a}}}^{1} $大小相同但值不同的 $ \boldsymbol{h}_{{\rm{a}}}^{3} $. 经过加权、批量归一化和最大池化操作，得到最终输出 $ {\boldsymbol{h}}_{{\rm{c}}} $.

为了学习特征图中不同时间片段的依赖关系，设计基于时间步注意力机制的TSA Block. 如图7所示，采用门控机制为不同时间片段自适应分配权重.

在 $ {\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}} $（ $ {\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}} $表示不同时间片段的特征）上执行全局平均池化操作 (global average pooling) ，得到 $ {\boldsymbol{h}}_{{\rm{l}}}^{1} $. 用2层全连接构成门机制，利用Relu和Sigmoid激活函数，得到每个时间片特征的权值向量 $ \boldsymbol{h}_{{\rm{l}}}^{3} $. 对 ${\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}}$进行加权，作为下一层网络的输入. 图7中， ${\boldsymbol{x}} $为输入向量， $ {\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}} $为 $ {\boldsymbol{x}} $经过Bi-LSTM和批量归一化操作输出的特征图. $ {\boldsymbol{h}}_{{\rm{l}}}^{1} $由下式得出：

(8) $ {\boldsymbol{h}}_{{\rm{l}}}^{1}={\rm{GAP}}\left({\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}}\right)=\frac{1}{H} \sum_{i=1}^{H} {\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}}(i, j). $

式中： $ H $为 $ {\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}} $的长度； $ {\boldsymbol{h}}_{{\rm{l}}}^{1} $向量大小为 $ 1 \times L_{\text {avgpool }} $，其中 $ L_{\text {avgpool }} $为 $ {\boldsymbol{h}}_{{\rm{l}}}^{{\rm{o}}} $中的时间片特征数量. $ \boldsymbol{h}_{{\rm{l}}}^{2} $由下式得出：

(9) $ \boldsymbol{h}_{{\rm{l}}}^{2}={\boldsymbol{H}}_{1} \cdot \delta\left(\boldsymbol{h}_{{\rm{l}}}^{1}\right) .$

式中： $ \boldsymbol{h}_{{\rm{l}}}^{2} $向量大小为 $ 1 \times L_{\text {avgpool }} / R_{1} $. $ \boldsymbol{h}_{{\rm{l}}}^{3} $计算如下：

(10) $ {\boldsymbol{h}}_{{\rm{l}}}^{3}={\boldsymbol{H}}_{2} \cdot \sigma\left({\boldsymbol{h}}_{{\rm{l}}}^{2}\right) .$

式中： $ \boldsymbol{H}_{1} $、 $ {\boldsymbol{H}}_{2} $分别为2个全连接层的权值矩阵，经过加权操作得到最终输出 $ {\boldsymbol{h}}_{{\rm{l}}} $.

实验所用服务器基于 64 位的 Window10 系统，显卡是NVIDIA 2080Ti，驱动版本为 456.71，CUDA 版本为 11.1.96. 本文算法基于Python下的Keras和TensorFlow框架实现.

MIT-BIH心率失常数据库中存在严重的数据不平衡问题，为了在模型训练过程中增大少数类型心拍的关注度，用Focal Loss作为损失函数^[25-26]. 与传统交叉熵损失函数相比，Focal Loss作出了改进. 优势在于按照一定的比例因子，对于预测准确率低的样本，保留大部分交叉熵损失；对于预测准确率高的样本，减小交叉熵损失. 在模型训练的过程中，预测准确率较低的少数类样本的交叉熵损失在总体中的比例会逐渐增加，模型会更专注于优化由少数类样本带来的损失.

为了更真实、客观地验证分类器结果，采取数据集上的5折交叉验证算法^[24]. 将数据集D均匀划分为5个互斥子集，划分过程中采用分层随机采样，保持数据集本身的分布特性. 每次使用4个子集作为训练集，剩余1个子集作为测试集，总共进行5次训练和性能测试，保证单个模型内每次训练的训练集均不同，避免了数据划分随机性所造成的影响. 对于所有的实验结果，用总体分类准确率(overall accuracy, OA)、特异性 (specificity, Spe)、敏感度 (sensitivity, Sen)、精确度 (precision, Pre) 和Macro-F₁作为评价标准进行评估. 具体的计算方法^[27-29]如下.

(11) $ {\rm{O}} {\rm{A}}=\frac{{\rm{T}} {\rm{N}}+{\rm{T}} {\rm{P}}}{{\rm{T}} {\rm{N}}+{\rm{F}} {\rm{P}}+{\rm{F}} {\rm{N}}+{\rm{T}} {\rm{P}}} \times 100 {\text{%}} , $

(12) $ {\rm{Spe}}=\frac{{\rm{TN}}}{{\rm{TN}}+{\rm{FP}}} \times 100 {\text{%}}, $

(13) $ {\rm{Pre}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FP}}} \times 100 {\text{%}}, $

(14) $ {\rm{Sen}}=\frac{{\rm{TP}}}{{\rm{TP}}+{\rm{FN}}} \times 100 {\text{%}} ,$

(15) $ { F_1 }=2 \times \frac{ { {\rm{Sen}} } \times {\rm{Pre}}}{{{\rm{Sen}}}+{\rm{Pre}}} \times 100 {\text{%}}, $

(16) $ {\rm{Macro}}{\text{-}} F_1 = K^{-1}{{\displaystyle\sum_{i = 1}^K {F_1 } }} \times 100 {\text{%}}. $

式中： $ {{\rm{ Pre }}} $为精确度， $ { {\rm{Sen}} } $为敏感度，两者用来计算 $ F_1 $； $ {\rm{TP}} $为正确分类的正例样本数量； $ {\rm{TN}}$为正确分类的负例样本数量； $ {\rm{FP}} $为负例样本被错误地分类为正例样本的数量； $ {\rm{FN}} $为正例样本被错误地分类为负例样本的数量. 在所有的测试实验中， $ {\rm{OA}} $表示被正确分类的心拍在所有测试样本中所占的比例； $ {\rm{Spe}} $表示所有负例中被正确分类的比例，衡量了模型对负例的分类能力； $ { {\rm{Macro}}-F_1 } $中 $ K $取5，对5种类型的心拍分别计算 $ F_1 $，取均值得到，不受数据不平衡的影响，适合作为提出模型的评价指标.

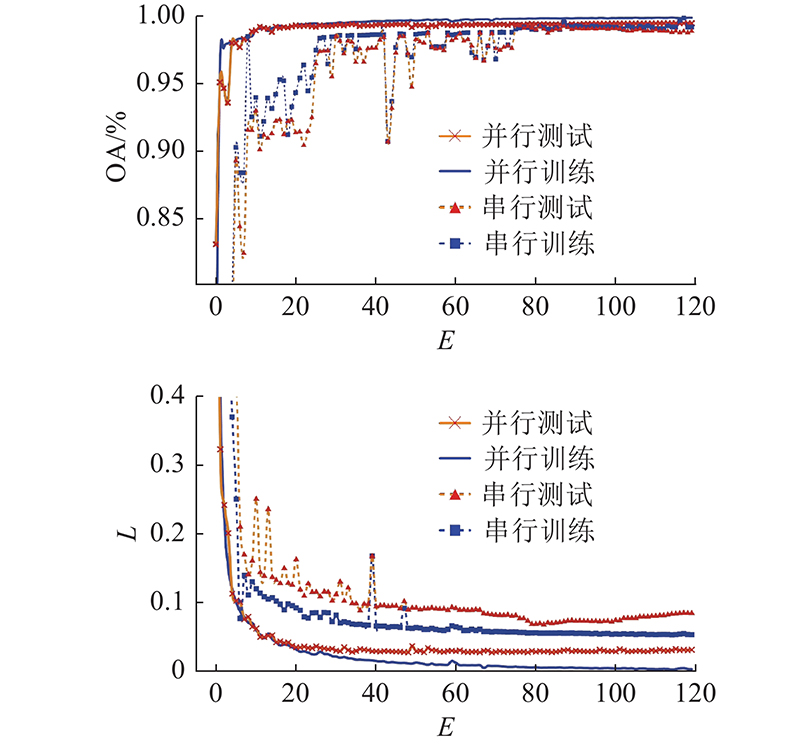
在串行架构模型中，不需要对数据集进行特殊处理，GCA Block和GSTA Block采用前后相接的方式. 在训练过程中需要不同阶段的输入输出相互依赖，增加了模型网络的深度. 在并行架构模型中，存在3个子模型. 将数据集分成独立同分布的3份，对于每个子模型，采取并行预训练的方式，获得子模型收敛的权重矩阵. 基于预训练的权重矩阵和完整数据集，采取特征融合的方式进行联合训练，获得最终模型的权重矩阵. 实验表明，在相同的硬件条件下，相较于串行架构模型，并行架构模型的训练效率和测试效率平均提升了6.3和2.4倍. 在利用5折交叉校验法进行验证后，所得数据表明可以实现对5种不同类型心拍的准确分类. 图8中，L为损失值. 对于串行架构模型，当训练迭代次数E < 80时，分类准确率和损失值曲线都出现不同程度的上下波动，这是由于在训练过程中模型参数需要不断优化，以寻找使得损失函数值最小的参数组合. 当训练迭代次数超过100时，从 图8可以看出，串行测试集的损失值逐渐增大，串行训练损失值逐渐减小，此时串行架构模型出现过拟合问题. 相较于串行架构模型，当训练迭代次数为60时，并行架构模型的准确率曲线图已经收敛，曲线波动程度极小，训练过程平稳. 在迭代次数超过80后，并行训练的准确率接近于100%，并行训练损失值接近于0，曲线相对平坦. 对于测试集，分类准确率为99.45%~99.55%，损失值接近于0.01且数据波动极小，没有出现过拟合的现象.

对于训练和测试验证过程而言，并行架构模型具有训练过程平稳、模型收敛较快、更易于达到全局最优点的特点，在训练过程中不会出现过拟合的现象，这对于进一步提高模型的准确率和泛化能力具有重要意义.

在训练好的模型上，对共计21 850个心拍进行测试. 如图9所示为测试结果的混淆矩阵，如表4所示为在不同评价指标下的分类效果. 由于不同类别样本的数量不平衡，模型对 N、V、Q 类都有较好的分类能力，但是对 S、F 类的分类能力较差. 若本文不作数据不平衡处理，则对S、F类的分类效果会更差. 从图9可以看出，N 类和S类相互之间的误判率较高，这是由于2种类型心拍的相似度较高. 从图9可以看出，心拍分类的OA为99.50%. 如表4所示，分别对每种类型心拍计算F₁，取均值得到Macro-F₁为97.08%.

在多分类任务中，数据增强是处理数据不平衡和提升分类效果的有效方式. 采用ADASYN算法对原始心电信号进行数据增强处理，对心电信号分类效果的影响如图10所示，分类效果提升值P_i取数据增强前、后差值的相反数.

图10表明，数据增强对4种少数类型的心电数据的分类效果提升明显. 在4种数据指标中，Sen和Macro-F₁提升最明显，原因是这2种指标关注的是该类型的真阳性率，属于局部关注度，因此单个类型心电数据的变化对这2种指标的影响较大. F类型的分类效果提升值最高，Sen和Macro-F₁分别提升了2.37%和2.26%. N类型的分类效果提升值最低，由于其属于多数类型数据，未进行数据增强，提升值只受其他4种类型心电分类效果提升所带来的隐性影响.

如表5所示为本文方法与其他方法的分类效果对比. 可知，本文方法在总体分类准确率和特异性上均高于其他方法，在敏感度和Macro-F₁上高于大多数其他方法. Gao等^[31]的方法与本文一样，都用Focal Loss作为损失函数，但只用LSTM进行特征提取，准确率和特异性较低. Chen等^[21]将MITDB数据集分为病人间和病人内，因为同一类型ECG信号在不同个体间的差异性较大，在病人内测试中准确率高达99.56%，在病人间测试中只有96.77%. Luo等^[27]与本文一样，均设计新模型对心拍分类，但是Luo等^[27]采用加权平均法计算敏感度和Macro-F₁，本文采用取均值法. 与表5的其他文献相比，本文方法在心电信号分类方面的总体准确率最高.

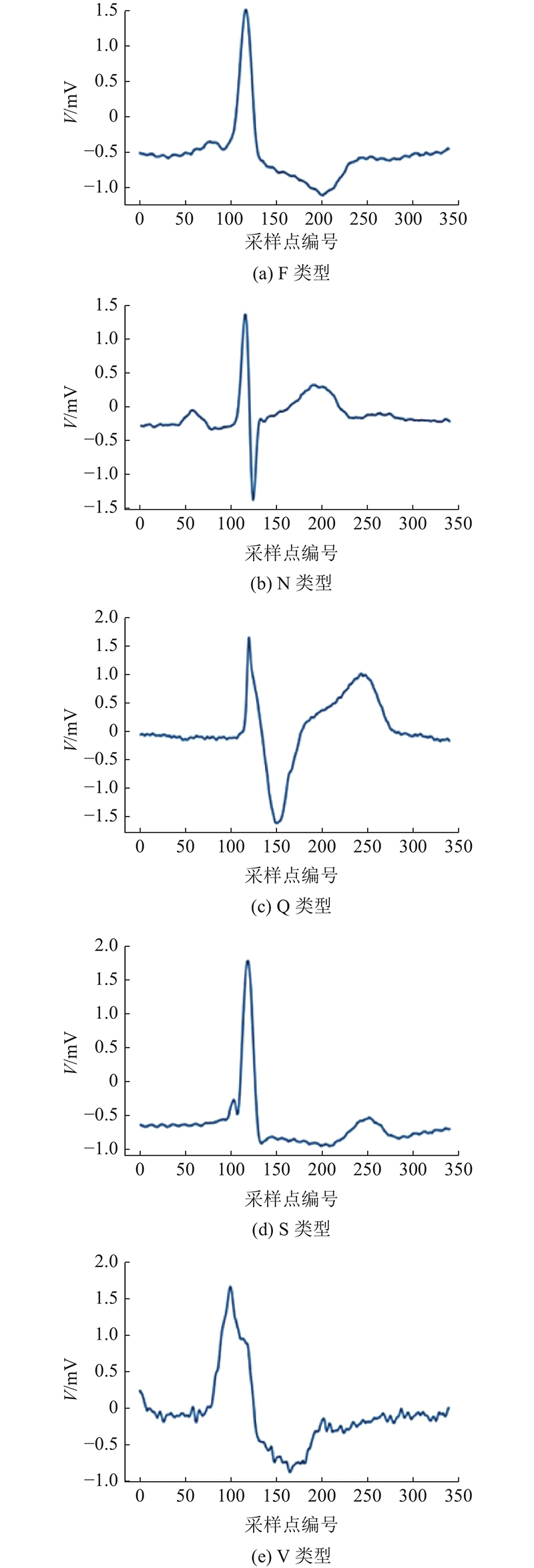
影响心电分类性能的因素除了心电数据不平衡之外，还与不同类型心电信号的相似度有关. 在MIT-BIH心律失常数据库中，5种类型心电信号的形态相似度具有一定程度的差异，这种差异包括心电信号在同种类型间的差异和不同类型间的差异. 如图11所示为5种类型心电信号的热度图，其中的颜色由亮到暗代表相似度从高到低.

从图11可以看出，对于同种类型的心电信号，N和S类型热度图中的亮点相对集中且连续，说明N和S类型心电信号的类内相似度高. F、Q和V类型热度图中的亮点相对分散且呈片段式，说明这3种类型心电信号的类内相似度较低. 对于不同类型的心电信号，N和S类型热度图之间的形态相似度较高，结合上述类内相似度高的特点，说明这2种类型信号间的特征相似度高，对精确分类造成一定的困难. F、Q和V类型热度图之间的形态相似度较低，结合上述类内相似度较低的特点，说明这3种类型信号间的特征相似度较低，不会成为精确分类的瓶颈（数据不平衡是对应的瓶颈，在数据预处理部分已采用ADASYN算法进行相应的处理）.

为了实现对5种不同类型心电信号的准确分类，提高N和S类型的分类精确度，采用不同尺度的窗口处理和时空注意力机制方法.

采用小尺度和大尺度2种方法，开展相关实验和结果比对，通过并行架构进行多尺度特征融合. 如表6所示为小尺度方法下的心拍分类结果，在Spe、Sen、Pre、F₁评价指标下的均值分别为98.61%、94.16%、96.90%、95.48%.

如表7所示为大尺度方法的心拍分类结果，在Spe、Sen、Pre、F₁评价指标下的均值分别为99.09%、94.72%、97.11%、95.86%.

如表8所示为多尺度特征融合的心拍分类结果，在Spe、Sen、Pre、F₁ 、OA评价指标下的均值分别为99.33%、95.06%、97.63%、96.29%、99.27%. 在对应的评价指标上，较表6分别提升了0.71%、0.89%、0.73%、0.81%，较表7分别提升了0.25%、0.34%、0.52%、0.43%. 数据表明，在单一尺度下对5种类型心拍的分类效果较差. 其中，对N和S类型心拍分类效果的影响最大，相较于小尺度和大尺度方法，采用多尺度融合分类后，N类型心拍的Sen、Pre、F₁提升比例分别为0.62%、0.25%、0.43%，S类型心拍的Sen、Pre、F₁提升比例分别为1.35%、1.70%、1.52%.

在经过多尺度窗口处理后，对于所有类型心拍的分类效果更好. 在多尺度特征融合的基础上，引入本文设计的时空注意力机制，得到的心拍分类效果如表4所示. 与表8相比，在引入时空注意力机制后，5种评价指标分别提升了0.28%、1.14%、0.39%、0.79%、0.23%，增强了心拍的分类效果.

采用5折交叉校验法验证模型的性能，利用5个互斥的数据集进行5次独立的实验，可以在最大程度上减少数据集对心拍分类结果的影响. 如表9所示为经过5折交叉验证的5次分类结果. 分别利用特异性、敏感度和F₁指标，对5种类型的心拍分类结果进行对比. 在5次独立实验中，敏感度曲线较其他2个指标的波动最小，说明设计模型的鲁棒性较好. 在5种类型的心拍中，N和F类心拍的分类效果变化相对较大，这是由于数据不平衡引起的. 尽管本文利用自适应合成采样算法合成了一定的少数类型心拍样本，但只能起到一定程度的作用，这一点需要改进. 3个指标均保持在1%的波动范围内，5种类型心拍的分类效果明显，说明设计模型的性能较好.

与其他方法相比，该方法采用并行架构，在减小网络深度的同时，采用GCA Block和GSTA Block 2个模块实现时空注意力机制，融合不同的心电信号特征，实现了对心电信号的准确分类. 通过多尺度窗口和基于通道注意力机制的卷积操作，不仅能够发挥卷积操作提取深层次波形特征的能力，而且加强了心电信号不同特征通道间的联系. 在一维数据上使用的卷积操作属于局部空间共享参数，无法充分提取心电信号的时序相关信息，因此通过基于时间步注意力机制的TSA Block提取心电信号的时序特征. 将不同的心电信号特征按一定的方式融合，实现了更多层次的心电信号特征提取，提升了分类效果.

本文根据心电信号的特性和深度学习的特点，提出基于并行架构模型和时空注意力机制的心电信号分类方法. 该方法能够自动提取心电信号的局部相关特征和时序特征，融合时空注意力机制，实现对卷积通道和时间步的自适应关注度. 与其他心电分类算法相比，本文模型不仅准确率高，而且鲁棒性和泛化能力都较好，不容易出现过拟合. 在MIT-BIH心率失常数据库的21 850个样本中，经过5折交叉验证可知，测试结果的准确率为 99.50%，特异性为99.61%，Macro-F₁为97.08%. 在ECG数据增强的过程中，自适应合成采样法与Focal Loss损失函数的效果优于其他数据不平衡处理算法. 考虑采用不同数据集，利用多导联心电数据及相关性进行数据增强和分类优化，提高心电信号分类的准确性，为临床心电图诊断提供了有效的辅助手段和途径.