自适应采样是以经典采样与全空间采样为基础发展出来的采样方法，可用于灵敏度分析、不确定性分析及全局优化等方面. 学者已提出的自适应采样模型近似方法很多，举例如下. Böttcher等^[1]提出利用人工神经网络集合进行预测方差的自适应采样策略，Beck等^[2]通过最大化设计空间来增加采样点，Gratiet等^[3]提出基于Kriging的自适应采样方法，Liu等^[4]提出自适应最大熵（AME）采样方法，Kucherenko等^[5]提出基于概率图的自适应采样方法，郭述臻等^[6]提出利用设计空间稀疏性来新增采样点的方法. Ajdari等^[7]提出随机仿真模型自适应序列采样算法，Eason等^[8]提出的方法将基于人工神经网络的全空间填充与自适应采样相混合. Liu等^[9]提出基于径向基函数的最优加权点集自适应采样策略，Jiang等^[10]针对输出空间的特性提出自适应采样策略，Steiner等^[11]提出基于特定响应面模型的自适应采样方法，Wen等^[12]提出避免在概率密度很低的区域选择样本的自适应采样策略，谢雨珩等^[13]提出基于稀疏度和最邻近期望的自适应采样算法. Van等^[14]提出的基于模糊逻辑的采样策略，适用于高维模型的近似处理，具有计算快及鲁棒性强的特点； Pan等^[15]利用响应面模型的极值点和密度函数的最小点来自适应采样；Shahsavani等^[16]提出的基于粗糙度的自适应采样方法能够利用插值方式实现多项式近似模型. 在将自适应采样方法运用于全局优化方面，Diez等^[17]提出的方法将动态径向基函数响应面模型与顺序多准则自适应采样技术相结合，能够在优化目标过程中不断提高近似模型的精度；Serani等^[18]提出基于随机径向基函数的自适应采样方法；Li等^[19]提出基于多级自适应采样策略的改进SAO算法以逐步提高模型精度.

根据实际预测误差的表示方式，可以将上述自适应采样方法分为4类：1）基于方差自适应采样（Böttcher等^[1-6]提出的方法），2）基于委员会查询的自适应采样（Ajdarj等^[7-8,17-19]提出的方法），3）基于交叉验证的自适应采样（Liu等^[9-13]提出的方法），4）基于梯度自适应采样（Van等^[14-16]提出的方法）. 自适应采样方法可以利用自身的采样技术完成对相关函数模型或者复杂产品模型的近似处理. 然而上述方法1）只能构造特定响应面模型；2）没有考虑曲面曲率的几何特性，即没有从几何角度利用曲面曲率进行自适应采样研究；3）对设计域的范围有限定，不适合大的设计域. 针对上述问题，本研究提出自适应采样结合曲面曲率的全局近似方法(adaptive sampling combined with surface curvature global approximation, ASCGA)，并将其用于函数源模型及复杂电动车模型的近似处理测试，以证明ASCGA的实用性和有效性.

构造响应面（response surface，RS）模型是响应面方法的主要功能. RS的常用模型包括多项式响应面（polynomial response surface，PRS）模型、Kriging插值模型、径向基函数（radial basis functions，RBF）模型等. 鉴于PRS模型具有较高的计算效率，为了降低计算复杂度，本研究将主要考虑该模型.

PRS模型的计算式为

(1) $\begin{split} \hat y =& {\beta _0} + \displaystyle\sum\limits_{i = 1}^p {{\beta _i}{x_i}} + \sum\limits_{{i_1} = 1}^p {\displaystyle\sum\limits_{{i_2} = 1}^p {{\beta _{{i_1}{i_2}}}{x_{i_1}}{x_{{i_2}}}} } + \cdots + \displaystyle\sum\limits_{{i_1} = 1}^p \displaystyle\sum\limits_{{i_2} = 1}^p \cdots \\ & \displaystyle\sum\limits_{{i_{(m - 1)}} = 1}^p {{\beta _{{i_1}{i_2}\cdots{i_{(m - 1)}}}}{x_{i_1}}{x_{{i_2}}}} \cdots{x_{{i_{(m - 1}}_)}} + \displaystyle\sum\limits_{{i_1} = 1}^p \displaystyle\sum\limits_{{i_2} = 1}^p \cdots \\ & \displaystyle\sum\limits_{{i_m} = 1}^p {{\beta _{{i_1}{i_2}\cdots{i_m}}}{x_{{i_1}}}{x_{i_2}}} \cdots{x_{{i_m}}}.\\[-16pt] \end{split} $

使用二次多项式函数近似，得到

(2) $ \hat y = {\beta _0}+\sum\limits_{i = 1}^p {{\beta _i}{x_i}} +\sum\limits_{i = 1}^p {\sum\limits_{j = 1,j \geqslant i}^p {{\beta _{ij}}{x_i}{x_j}} } .$

式中： $\hat y$为多项式近似模型，p为数据维度， $\;\beta $为多项式相关系数.

ASCGA采用中心点加全部端点的部分因子采样法获取初始采样集S. 设 $ {N_0} $为初始采样点数， $ {N_0} \geqslant {2^d}+1 $，其中d为设计变量数. 利用S在初始设计域构造初始PRS模型. 此后，ASCGA转向迭代循环. 在第1次迭代过程中，初始设计域根据PRS模型曲面曲率相关特性不断进行自适应分割以获取新增采样点. 初始设计域被均分为2个子设计域. 在这2个子设计域上分别利用部分因子采样法进行采样，利用采样获得的新增采样点在这2个子设计域内分别构造新的PRS模型. 用新构造的PRS模型代替初始PRS模型，判定是否满足精度条件，若不满足，则进入第2次迭代. 由于第1次迭代过程中产生了2个子设计域，此时须确认哪些子设计域需要进一步分割. 若有子设计域满足分割条件，则在待分割的子设计域内继续分割以获得子子设计域，并使用部分因子采样法获得新增采样点. 此时，在子子设计域内分别利用域内新增采样点再次构造2个新的PRS模型，使用新的PRS模型代替已分割的子设计域构造PRS模型. 该迭代过程一直持续，直至满足退出迭代条件为止.

上述过程涉及2个问题：1）如何确定设计域最佳分割位置，2）如何确定哪个子设计域需要进一步分割. 对于问题1），ASCGA将启发式直接搜索算法DIRECT^[20]与曲面曲率几何计算法结合，迭代搜寻沿某个维度上的最大曲率点. DIRECT是全局优化算法，其搜寻准则为

(3) $ \left.\begin{array}{l}{\rm{find}}\;{x},\\ {\rm{max}} \;{{L}_{i}{}^{p}}\cdot {C}_{i}(x);\\ {\rm{s}}.{\rm{t}}.\;1 \leqslant i \leqslant p. \end{array}\right\} $

式中：x为曲面上所求的某点，L为沿第i个维度上设计域的边长， $ {C_i} $为第i个曲面上某个采样点的曲率近似值，计算式为

(4) $ \begin{split} {C_i} = \frac{{{{({a_i} + {b_i})}^2} - c_i^2}}{{4{a_i}{b_i}}} \end{split} .$

式中： $ a_i $、 $ b_i $、 $ c_i $分别表示曲面上针对某采样点构造的三角形三条边，其中 $ a_i $、 $ b_i $与采样点相连. $ C_i $∈[0, 1]，值越大，表示该点在该维度上的曲面弯曲程度越大，非线性越强，即PRS模型与真实数据背离最大；值越小，表示该点在该维度上曲面弯曲程度越小，非线性越弱. 根据设计域的维度分别计算不同维度的最大曲率点，

(5) $ {j_s} = \mathop {\arg \max }\limits_{1 \leqslant i \leqslant p} \left({L_i}^p \cdot {C_i}\left(p\right)\right). $

对不同维度的最大曲率进行排序及筛选，选择最大j_s所在的维度为该设计域的分割维度方向，同时最大j_s对应的最大曲率点位置也是设计域最佳分割位置.

对于问题2），ASCGA引入判定PRS模型精度的方法，通过判定各PRS模型域内已有采样点的最大源模型值与最小源模型值之差确定PRS模型的精度. 该值越大，说明PRS模型非线性越强. 在每次迭代过程中，ASCGA选择若干PRS模型作为最大误差单元. 上述判定PRS模型精度的方法区别于通过在子设计域内采样来判定RS模型精度的方法，可以大幅降低计算复杂度.

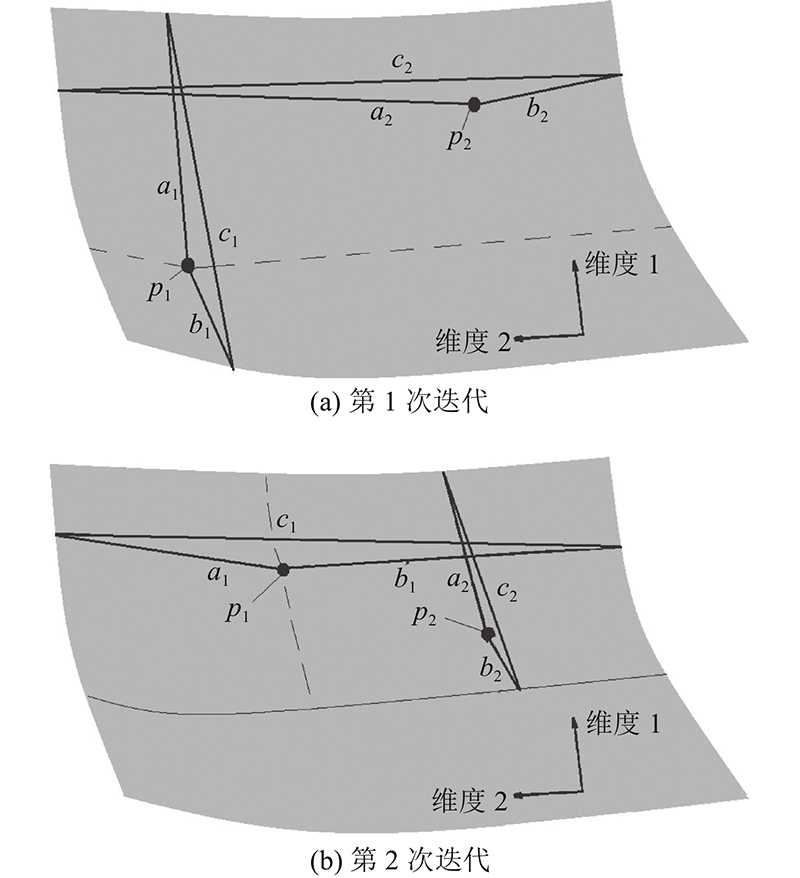
如图1所示，以某二维设计域内的曲面为例. 图中，阴影表示某二维PRS模型曲面，点p₁、p₂分别为利用DIRECT在曲面上找到的沿维度1、2方向上的最大曲率点. 比较L_i²C (p)以确定非线性最大的维度并进行分割. 若L₁²C (p₁)＞L₂²C (p₂)，则表示维度1方向上曲面的非线性强于维度2方向的，因此在维度1上按最佳分割位置p₁对设计域进行分割，如图1（a）中虚线所示，分割后得到上下2个子设计域. 在进行第2次迭代时，将判定的需要进一步分割的子设计域分割成左右2个部分，如图1（b）所示. 后续迭代以此类推.

采用ASCGA对现有设计域分割，每次都会获得2个子设计域，并会在子设计域内构造新的PRS模型. 因此随着迭代进行，原设计域被不断分割，子设计域及PRS模型越来越多，这些PRS模型的集合称为响应面集（response surface set，RSS）. DIRECT在PRS模型内进行全局搜索时，若最大曲率点与设计域边界十分接近，将使DIRECT进行局部搜索，引起较大误差. 为了避免这种情况，应适当增加曲率最大点与设计域边界的距离. 分割不同源模型的原设计域得到的子设计域数量不同，ASCGA中子设计域数量主要取决于源模型特性和参数设置. 若源模型存在非线性较强的区域，则在该区域一般需要较多的子设计域来满足总体近似模型在该区域的精度要求. ASCGA设置了多个参数作为迭代计算退出准则. 若在自适应设计域分割过程中满足某退出准则，则退出迭代计算，并在获得一定精度的总体近似模型情况下得到一定数量的子设计域. 为了使不同的源模型的设计域分割成合理数量的子设计域，并兼顾计算效率和总体近似模型精度，须根据实际需求确定源模型的总体近似模型精度要求δ₃. 若δ₃设置过小，则子设计域数量增加，计算效率降低. 根据源模型的原设计域设置参数：δ₁为子设计域最小边长、δ₂为子设计域构造的PRS模型误差. 若原设计域具有较大的尺寸，则δ₁应适当增大，避免原设计域在非线性较强的区域过度划分，以降低计算复杂度，提高计算效率. 也应注意到，这样做适度降低了近似模型精度. 设置δ₂为合理值，可以避免由于δ₂过小使原设计域划分过密，从而导致计算效率降低. 总之，为了使原设计域在自适应分割过程中能够平衡计算效率及总体近似模型精度，应该在确定δ₃的情况下，选择合适的δ₁、δ₂，使得ASCGA在计算过程中能够保证总体近似模型具有较好的精度和计算效率.

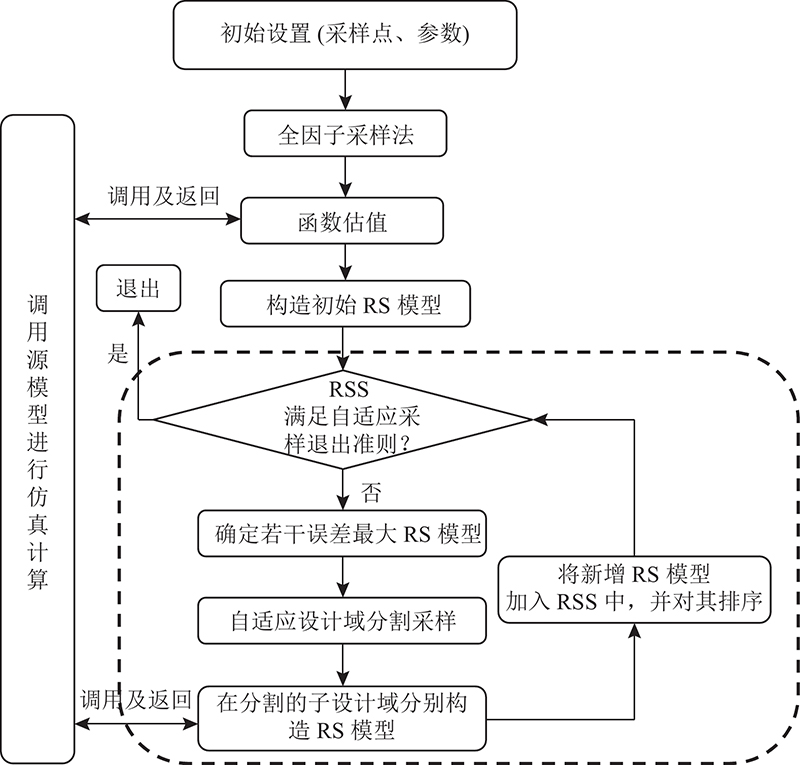
ASCGA实现源模型全局近似的流程如图2所示.

1 ）初始采样点及参数设置. 采样点采用端点加中心点的全因子采样法获取. 参数包括设计域最大分割次数N、δ₁、δ₂、δ₃.

2） 构建初始RS模型. 在整个设计域内，利用初始采样点调用源模型进行仿真计算，获得相应的源模型值，结合初始采样点及源模型值构造初始RS模型.

设计域自适应采样过程步骤如下. 3）迭代计算，若方法满足退出准则，则退出. 迭代准则主要涉及：迭代过程达到设计域最大分割次数、子设计域边长小于δ₁、RSS中每个RS模型误差都小于δ₂、RSS总体近似模型误差小于δ₃. 4）获取RSS中每个RS模型的绝对误差，选择最大误差的RS模型的设计域作为后续分割对象. 5）利用DIRECT结合曲面曲率计算方法迭代搜寻RS模型曲面上沿某个维度的最大曲率点（设计域最佳分割位置），获得非线性最强的维度方向，在该维度上按最佳分割位置分割子设计域. 在分割的2个子设计域内分别利用已有采样点集构建新的RS模型. 6）更新RSS模型，返回步骤3）. 在构造新的RS模型添加到原有RSS时，重新对原有RSS内的各个RS模型进行删减、排序.

7）计算结束.

使用标准无约束测试函数源模型测试ASCGA. 测试函数源模型为generalized polynomial function (GF)函数、Schaffer’s函数、Apline函数及Hartmann函数. 如表1所示，δ₁根据算例的不同设计域尺寸进行设定；δ₂、δ₃均设置为10⁻³，若数值设置较大，则可能导致近似处理过早结束.

算例1）: 二维GF函数为

(6) $ \begin{split} y =& {(0.5 - {x_1}(1 - {x_2}))^2}+{(2.25 - {x_1}(1 - {x_2}^2))^2}+ \\ &{(2.625 - {x_1}(1 - {x_2}^3))^2} . \end{split} $

式中：x₁、x₂∈[−2, 2].

算例2）: 二维Schaffer’s 函数为

(7) $ y = 12 \times \left( {0.5+\frac{{{{\sin }^2}(\sqrt {{x_1}^2+{x_2}^2} - 0.5)}}{{1+0.000\;1({x_1}^2+{x_2}^2)}}} \right). $

式中：x₁、x₂∈[−2, 2].

算例3）: 三维Apline函数为

(8) $ y = \sqrt {\left| {{x_1}{x_2}{x_3}} \right|}\sin {x_1}\sin {x_2}\sin {x_3}. $

式中：x₁、x₂、x₃∈[0,10].

算例4）: 三维Hartmann函数为

(9) $\left.\begin{split} &y = { - }\sum\limits_{i = 1}^4 {{a_i}{\exp\;{\left( - \displaystyle\sum\limits_{j = 1}^3 {{A_{ij}}{{({x_j} - {P_{ij}})}^2}} \right)}}}; \\ &{\boldsymbol{a}} = {[1.0,1.2,3.0,3.2]^{\rm{T}}},\\ &{\boldsymbol{A}} = \left[ \begin{array}{*{20}l} 3.0 & 10 & 30 \\ 0.1 & 10 & 35 \\ 3.0 & 10 & 30 \\ 0.1 & 10 & 35 \end{array} \right], \,\, \\ &{\boldsymbol{P}} = {10^{ - 4}}\left[ \begin{array}{*{20}l} 3\;689 & 1\;170 & 2\;673 \\ 4\;699 & 4\;387 & 7\;470 \\ 1\;091 & 8\;732 & 5\;547 \\ \;\;\;381 & 5\;743 & 8\;828 \end{array} \right]. \end{split} \right\} $

式中：x₁、x₂、x₃∈[0,1].

采用增量拉丁超立方采样（Latin hypercube sampling，LHCS）及基于粗糙度的自适应采样（adaptive sampling based on roughness sampling，ASRS）^[16]近似处理函数源模型. LHCS为全空间采样方法，是在全空间内随机但不重叠的采样. ASRS作为自适应采样方法，可以对设计域进行自适应分割采样. 利用LHCS、ASRS采样评估ASCGA的采样效率及近似模型构造精度，并在LHCS及ASRS采样后均利用RBF构造近似模型. 在测试最终获得的近似模型时，为了克服LHCS采样的随机性，进行多次数值试验并取均方根误差（root mean square error，RMSE）的平均值.

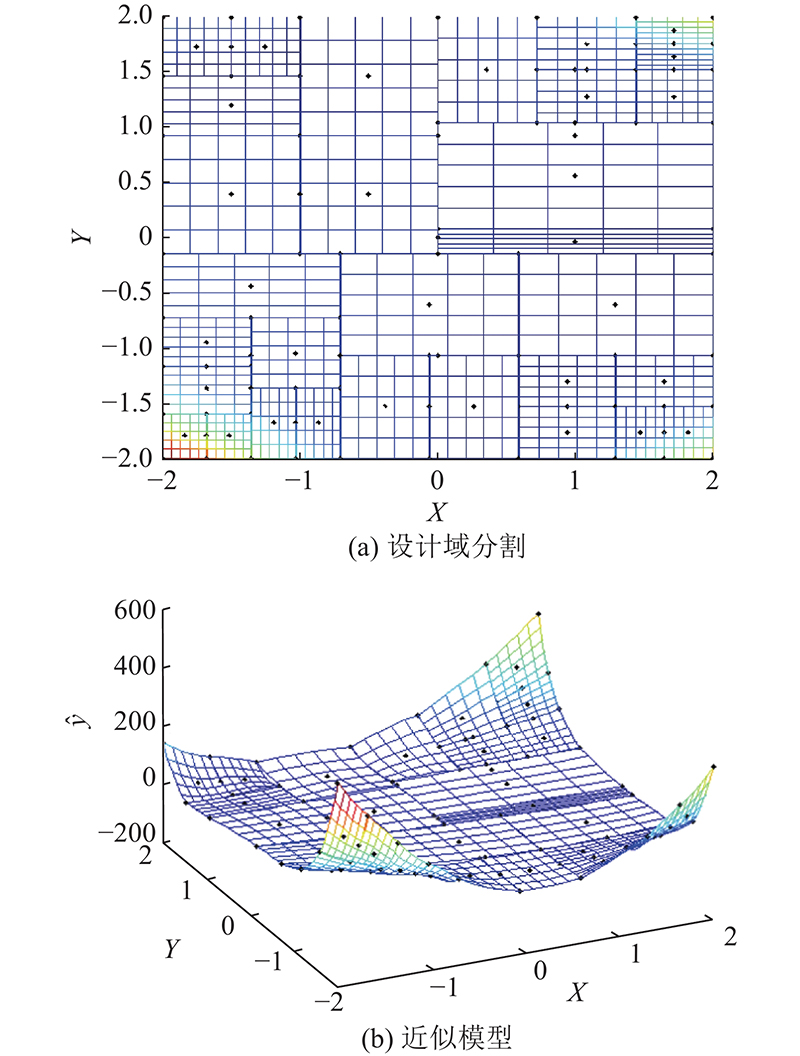
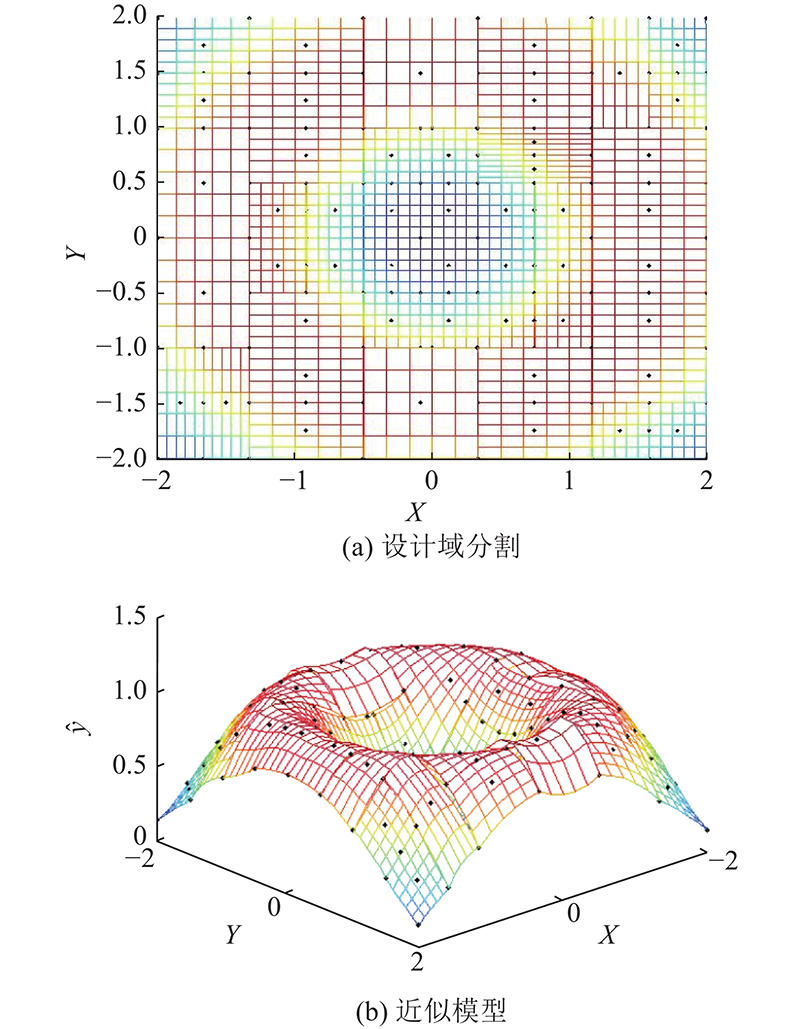
利用3种采样方法构造的函数源模型的近似模型测试结果如表2、3所示. 表中，R₁、R₂、R₃及R₄表示利用ASCGA分别构造算例1）~4）近似模型的均方根误差. T₁、T₂、T₃及T₄分别构造算例1）~4）近似模型的估值次数. 可知，与LHCS、ASRS相比，ASCGA能够在二维情况下使用有限个采样点构造较高精度的近似模型. 不同采样方法的效率高低由函数源模型的估值次数多少来判断. 函数源模型越复杂，估值次数越多，耗时越长，相应方法的效率越低. 可知，在相同精度条件下，ASCGA比LHCS、ASRS的效率更高. 如图3、4所示分别为采用ASCGA对二维函数源模型的设计域分割情况和近似模型三维视图. 在三维情况下， ASCGA需要较多数量的采样点才能获得一定精度的近似模型. 由表可知，ASCGA对源模型进行近似处理的初期效果略逊于LHCS，但是随着采样点的增多，ASCGA的精度、效率都有明显提升. ASRS的三维源模型近似处理效果不佳，即使增加采样点，也不能提高该方法的近似模型精度.

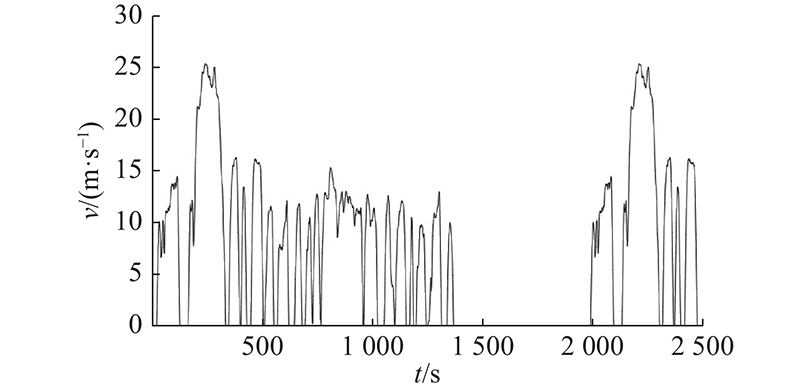
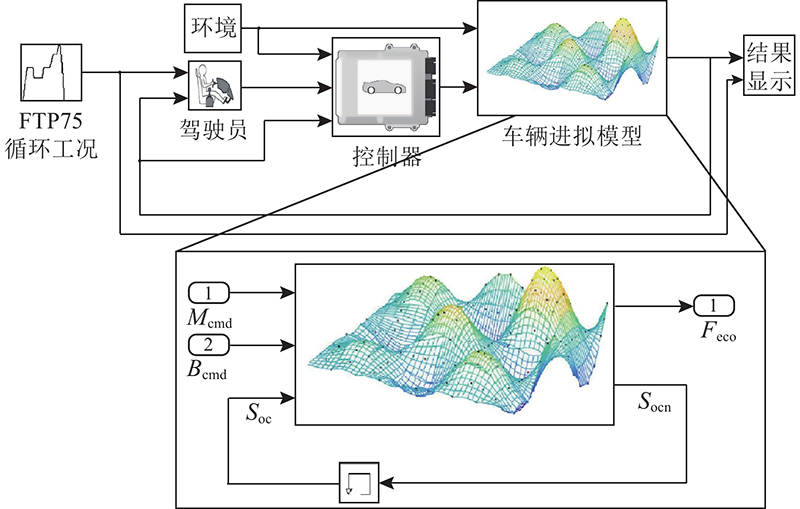
将ASCGA应用于电动车模型的近似处理. 如图5所示，Matlab电动车模型主要包含电机发动机、电池、传动系统及控制器等部件. 电动车模型主要用于动力总成匹配分析，控制与诊断算法设计及硬件在环（hardware in the loop，HIL）测试. HIL测试要求电动车模型仿真无延迟，因此须简化电动车模型. 车辆模型的复杂度最高，对整车模型计算复杂度有直接影响. 为了加快模型仿真计算速度，降低计算复杂度并保证实时性，采用响应面近似模型代替车辆模型，利用足够精度的近似模型进行快速计算. 如图6所示，电动车模型仿真采用FTP75循环工况作为车辆公路行驶的驱动循环. 图中，t为时间，v为车辆行驶速度.

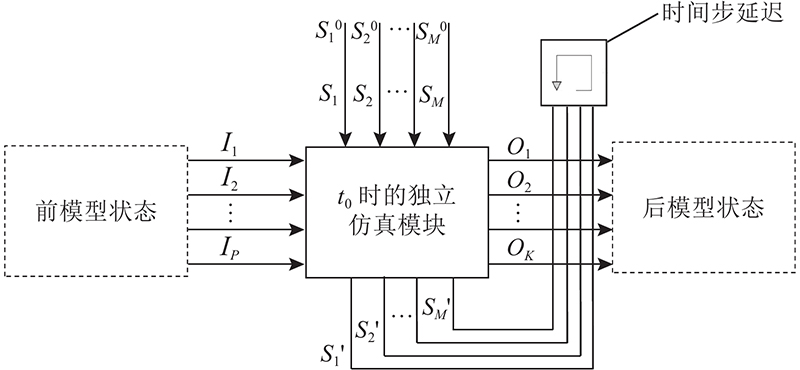
提出基于固定步长且带有反馈的模型处理方法. 如图7所示，模型在运行时存在3个状态：前模型状态、当前模型状态及后模型状态. 图中，I_p为模型的第p个输入，O_K为模型的第K个输出. 忽略前后模型状态，对当前状态进行如下处理.

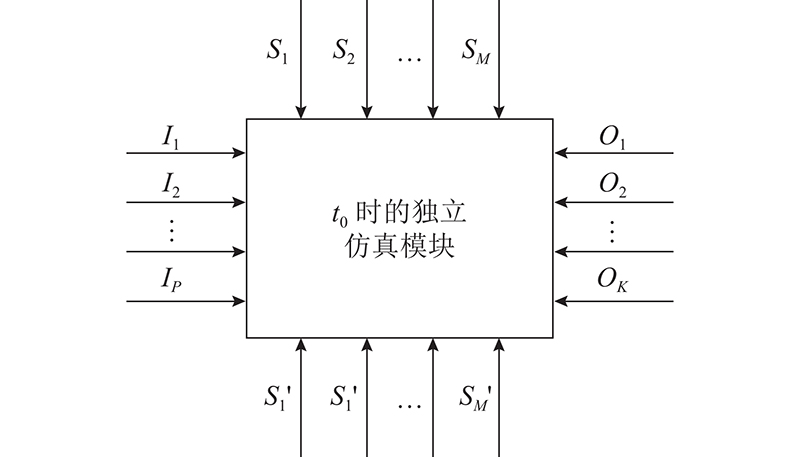
1）建立独立仿真模块（independent simulation module，ISM）. 给ISM添加输入端口和输出端口，包括状态变量的输入及输出端口；由完整电动车模型的历史仿真数据，获得ISM输入变量的取值范围；确定时间步长t₀. 不同t₀的ISM输出不同结果. 考虑模型的实时环境，设定t₀=0.1 s. 如图8所示，处理后的ISM包含状态变量的输入和输出端口及t₀. ISM的表达式为

(10) $\begin{split} &\left\{ O_1,O_2,\cdots,O_K,S_1',S_2',\cdots,S_M'\right\} = \\ & \qquad {\text{ISM}}\_{{t} _0}\left\{ I_1,I_2,\cdots,I_P,S_1^{},S_2,\cdots,S_M\right\}. \end{split} $

式中：S_M为第M个状态变量输入. $S_M' $为第M个状态变量输出. ${\rm{ISM}}_{t_0}$表示基于t₀的独立仿真模块.

2）利用ASCGA对ISM进行近似处理.

3）验证近似模型精度Acc. Acc的计算式为

(11) $ {{\rm{Acc}}} = 1 - \frac{{\displaystyle\sum\limits_{k = 1}^n {{{\left( {f({x_{k}}) - {f_{{\rm{a}}}}({x_k})} \right)}^2}} }}{{\displaystyle\sum\limits_{k = 1}^n {{{\left( {f({x_k}) - {{\overline f }_{{\rm{a}}}}} \right)}^2}} }}. $

式中：x_k表示第k个测试点，f(x_k)为在点x_k在源模型上的真实值，f_a(x_k)为点x_k在近似模型上的估值， ${\overline f _{_{{\rm{a}}}}}$为所有测试点在近似模型上估值的平均值. Acc∈（0，1），Acc越接近1，近似模型越精确. 将该近似模型代替整体模型的相应组件，并对包含近似模型组件的整体模型进行仿真，对比相关输出变量曲线.

4）若近似模型精度满足要求，则完成对当前状态的处理. 若近似模型精度不能满足要求，则需返回步骤2），继续使用ASCGA处理ISM，进一步提高近似模型精度.

模型状态变量的表达式为

(12) $\begin{split} f({{\boldsymbol{u}}},{{\boldsymbol{s}}},{{\boldsymbol{\dot s}}},t) = 0 ,\; {{\boldsymbol{y}}} = g({{\boldsymbol{s}}},{{\boldsymbol{\dot s}}},{{\boldsymbol{u}}},t) . \end{split} $

式中：t、u、s、y分别为时间、输入、状态和输出变量. 验证近似模型精度，须处理M个状态变量（S₁、S₂，···，S_M），使其能自循环，并能在仿真过程中自动更新，如图9所示. 此时，ISM的输入端口为P个输入加上M个状态变量输入，输出端口为P个输出加上M个状态变量输出. 状态变量输出与输入相差时间步长t₀.

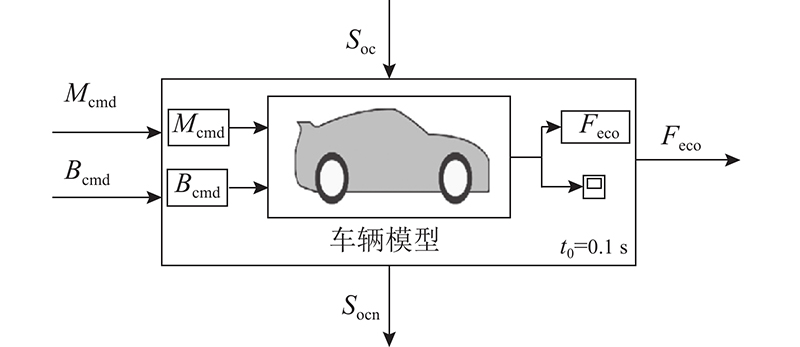
如图10所示，建立车辆模型的ISM，添加3个输入端口（加速指令M_cmd、刹车指令B_cmd及当前电池状态S_OC）. 添加2个输出端口（燃料经济性F_eco，下个时间步长的放电状态S_OCn），t₀=0.1 s.

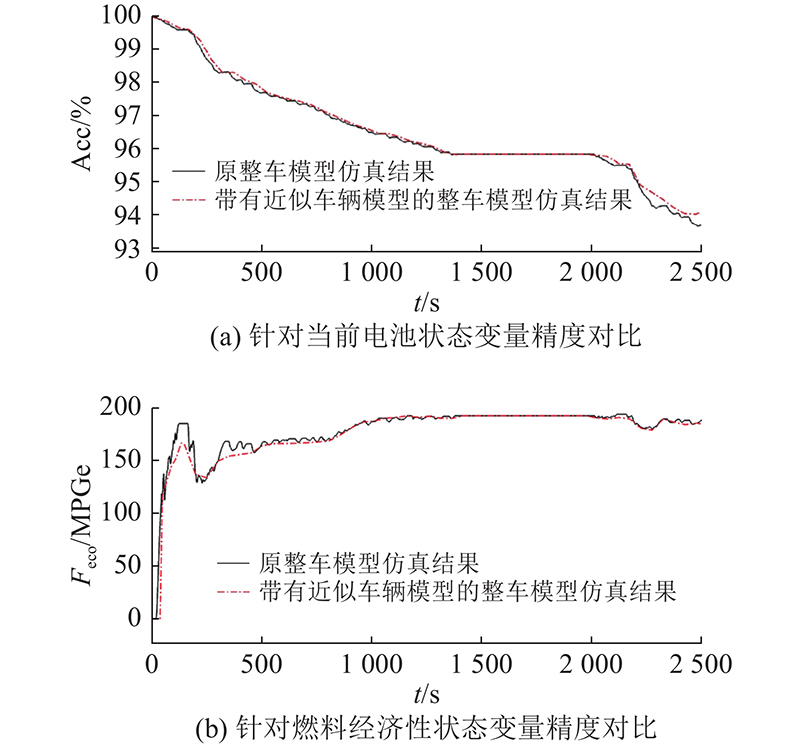
建立车辆模型的ISM，利用ASCGA对ISM进行近似处理，针对2个输出端口的变量分别建立3输入1输出的F_eco近似模型和S_OC近似模型. 近似过程中M_cmd∈[0,1]，B_cmd∈[0,1]，S_OC∈[93,100]. M_cmd的δ₁=0.1, δ₂、δ₃=10⁻³. B_cmd的δ₁=0.5, δ₂、δ₃=10⁻³. S_OC的δ₁=0.5, δ₂、δ₃=10⁻³. 为了验证近似车辆模型精度，使用近似车辆模型代替原车辆模型，如图11所示. 在相同工况下，带有近似车辆模型的整车模型与原整车模型的仿真结果对比如图12所示. 该图纵坐标采用每加仑汽油等同燃料计算整车在特定工况下的经济燃油性，可根据图示曲线计算得到等效百公里耗油. 可知，带有近似车辆模型的整车模型与原整车模型相关仿真曲线基本一致. 带有近似车辆模型的整车模型其S_OC的Acc=0.9358，F_eco的Acc=0.8977，表明近似车辆模型具有较好的精度. 在一台4 GHz，8 GB内存的计算机上仿真运行原整车模型和带有近似车辆模型的整车模型，前者运行近15 min，后者约为1 min，表明近似模型的仿真计算效率明显高于原有模型.

由上述案例可知，通过近似模型代替原有模型，可以大大加速仿真计算效率. 因此，后续可以将带有近似模型的整车模型进行代码生成，导入相应目标机，利用相应电动车控制器实物控制整车模型并测试其实时性，最终实现半物理仿真实验（hardware-in-loop，HIL）.

（1）针对复杂模型近似处理问题，提出自适应采样结合曲面曲率的全局近似方法. 该方法1）具有一定的灵活性，可以运用于其他响应面模型；2）引入新的判定响应面模型精度的方法；3）提出利用几何方法计算曲面曲率，并结合启发式的直接搜索算法DIRECT搜索响应面模型上的最大曲率点及最佳分割位置；4）对于大设计域、大数据量的源模型可以进行有效的近似处理.

（2）本研究所提方法采用设计域自适应分割的采样策略，并在分割后的设计域上进行采样并构造子响应面模型，避免了在大设计域上构造单一的、简单的近似模型，有效提高了大设计域模型的整体近似模型精度. 在分割的子设计域上采用PRS模型构造的近似模型具有计算效率高、占用空间少的优点. 该方法在分割后的众多子设计域上进行采样，仍能高效地实现近似模型构造，避免了在大设计域上采样过多导致近似模型构造缓慢，甚至构造失败的问题.

（3）本研究所提方法存在如下不足之处. 1）ASCGA从几何角度计算曲面曲率. 由于几何方法有自身的缺陷，超过四维的问题，待进一步研究并解决. 2）未能解决设计域分割后子域边界的连续性问题. 即使关键点连续，也不能保障所有边界连续. 3）ASCGA只能构造单个目标的近似模型，因此拓展该方法，使其同时构造多个目标的响应面集近似模型是需要考虑的问题. 4）ASCGA对约束函数的近似处理能力有限，获得的近似模型精度较差；后续可以以此为研究点，并进一步探索非连续区域的约束函数近似问题.