超薄罩面与传统沥青磨耗层相比更容易发生剪切破坏，出现层间失效行为^[1]. 揭示沥青超薄罩面层间剪切行为的形成和发展机制，对预防沥青超薄罩面层间失效行为，指导沥青超薄罩面设计、建设和养护具有积极意义. Mohammad等^[2]通过室内剪切试验，研究沥青超薄罩面层间界面抗剪强度与黏层材料洒布量间的关系. West等^[3]借助沥青路面层间剪切试验，分析影响沥青层间抗剪强度的主要因素. 毛昱^[4]基于弹性层状体系力学、接触力学及分形理论，理论推导沥青路面层间机械摩阻强度，结合黏弹性理论研究加载速度、加载温度和加载角度对沥青路面层间抗剪强度的影响. 李彦伟等^[5-6]基于分层失效理论，分析沥青路面层间连接层的破坏形态，研究固定的静态荷载对沥青路面结构的影响. 马玉钦等^[7]基于HyperWorks有限元分析软件，研究不同铺装材料组成的结构层间抗剪特性. 周秀丽^[8]借用Midas数值分析软件模拟分析在温度与荷载耦合作用下，温度梯度对沥青路面层间剪切破坏的影响机制.

内聚力模型由Dugdale等^[9-10]提出，已被广泛应用于研究各种材料的断裂损伤问题^[11-14]. 沥青超薄罩面的层间失效行为的本质是沥青混合料层间发生断裂破坏^[15-16]. Gong等^[17]利用内聚力模型定义沥青混合料的层间黏着力，以层间界面产生位移裂缝为失效指标，研究在双层连续摊铺沥青混合料过程中影响层间黏着力的因素，在用内聚力模型定义层间黏着力的基础上引入层间摩擦作用. 张敏江等^[18]引入含有Cohesive单元的双线性内聚力本构模型，表征路面罩面层与面层间的连接层，研究移动荷载大小、连接层初始损伤状态对路面结构层间抗剪性能的影响，结果表明内聚力模型适用于表征路面罩面层与面层间的连接层特性. 周晓和等^[19]基于内聚力模型建立路面层间结合数值模型，研究在荷载作用下层间界面的剪切破坏，结果表明利用内聚力模型定义材料的初始损伤能够较好地表现材料的力学特性，数值模拟结果与试验结果较为接近. 黄宝涛等^[20-21]在建立层间接触模型时，定义法向、切向弹簧用以表征层间接触面上的力学行为.

上述研究证明，内聚力模型在沥青层间问题研究中具有适用性. 沥青超薄罩面的实际受力为压剪体系，因此罩面层间抗剪能力由层间黏结力与正向压力产生的层间摩擦力共同提供. 已有研究大多将沥青超薄罩面的层间抗剪行为归结于层间摩擦力或层间黏结力，而忽略二者的耦合作用，这与沥青超薄罩面层间的实际受力情况有所差别. 本研究将层间摩擦力和黏结力耦合，推导改进内聚力模型本构参数，确定改进内聚力模型的层间材料连接本构参数；将该模型用于沥青超薄罩面直剪试验的数值计算，并通过试验结果验证模型的有效性；基于改进内聚力模型，分析沥青超薄罩面层间的失效行为.

参考已有直剪试验方法^[22]，原路面选用密级配AC-16沥青混合料，超薄罩面选用SMA-5小粒径沥青混合料，层间黏结材料选用确定的SBS改性乳化沥青，洒布量为1.8 kg/m²，成型并击实复合型试件，其中超薄罩面厚度为2 cm，原沥青面层厚度为8 cm. 将复合型试件切割成边长为10 cm的正方体试件，试件及加载示意图如图1所示.

本试验设计的思路：通过改变法向应力的大小，记录不同水平应力作用下沥青超薄罩面层间剪切强度，获得层间剪切强度与剪切位移的关系曲线，进一步获得法向应力与层间剪切强度的关系曲线，通过摩尔−库伦理论拟合该关系曲线，得到沥青超薄罩面层间黏结应力与层间摩擦系数.

基于沥青超薄罩面层间的抗剪行为来源于层间摩擦力和层间黏结力的耦合作用，列平衡方程为

(1) $ \tau = {\mu _{\text{f}}}{\sigma _{\text{i}}}+c . $

式中： $ \tau $为层间切应力， $ {\mu _{\text{f}}} $为层间摩擦系数， $ {\sigma _{\text{i}}} $为层间法向应力， $ c $为层间黏结应力. 试验中，将复合型试件施加的法向应力记为 $ \sigma $，水平应力记为 $ {\sigma _{\text{r}}} $. 当法向应力 $ \sigma $不变，施加水平应力 $ {\sigma _{\text{r}}} $得到的切应力达到层间抗剪强度 $ {\tau _{{\text{max}}}} $时，水平应力记为 $ {\sigma _{\text{r}}}' $，此时的层间法向应力 $ {\sigma _{\text{i}}} $与层间抗剪强度 $ {\tau _{{\rm{max}}}} $表达式^[22]分别为

(2) $ {\sigma _{\text{i}}} = \frac{{\sigma {S_{\text{v}}}+W}}{{{S_{\text{i}}}}} ， $

(3) $ {\tau _{{\rm{max}}}} = {\sigma _{\text{r}}}' .\quad\;\; $

式中： $ {S_{\text{v}}} $为法向荷载竖向施加面面积， $ W $为超薄罩面混合料试件重量， $ {S_{\text{i}}} $为层间剪切面面积. 如表1所示，通过改变法向应力 $ \sigma $的大小对试件进行直剪试验，结合试验结果，由式（2）、（3）分别得到 $ {\sigma _{\text{i}}} $、 $ {\tau _{{\rm{max}}}} $. 最小二乘法曲线拟合表1中的数据，得到法向应力与试件抗剪强度的拟合曲线方程为 $ {\tau _{{\text{max}}}} $=0.364 1 $ {\sigma _{\text{i}}} $+0.089 1，拟合优度R²=0.968 8. 由式（1）得到层间黏结应力 $ c $=0.089 1 MPa，层间摩擦系数 $ {\mu _{\text{f}}} $=0.364 1. 当法向应力 $ \sigma $=0 、0.2 MPa时，由直剪试验得到层间剪切强度与剪切位移 $ x $的关系曲线如图2所示.

双线性内聚力模型^[23]未将摩擦力与层间材料固有内力（黏结力）同时设置为层间抗力，导致材料在线性软化阶段表现出的特性与实际情况有所差别. 对双线性内聚力模型进行如下改进：引入热力学位中的势能函数，统一控制层间固有内力和线性刚度，耦合层间黏结力、层间摩擦力抵抗层间剪切作用. 以此为基础，开发更符合沥青超薄罩面界面实际断裂特性的改进内聚力模型.

沥青超薄罩面层间剪切破坏的实质是黏性断裂破坏，本构关系由“势”推导而得，“势”代表材料表面断裂张开时断裂能量分布，结合电势的物理性质，势能函数的一阶导数提供断裂表面上的牵引力（黏性相互作用即内聚力），二阶导数提供本构关系（材料切向刚度即层间材料雅克比矩阵）. 将沥青超薄罩面与道路面层间的层间黏结力、线性刚度进行统一调控，模型的法向、切向牵引分离关系分别通过对法向和切向张开位移求导得出，改进内聚力模型的势能函数为

(4) $ \left. \begin{aligned} \varphi \left({\mathit{\Delta} }_{\text{n}},{\mathit{\Delta} }_{\text{t}}\right) =& {\text{min} {（ E_{\rm{n}}},{E_{\rm{t}} ）} + \left( {G_{\rm{n}}}\displaystyle{\left( {1 - \frac{{{\mathit{\Delta} _{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}} \right)^\alpha } \displaystyle{\left( {\frac{m}{\alpha } + \frac{{{\mathit{\Delta} _{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}} \right)^m} + \right.}\\ &\Biggr.{\left( {{E_{\rm{n}}} - {E_{\rm{t}}}} \right)\Biggr) \left( {{G_{\rm{t}}}\displaystyle{{\left( {1 - \frac{{\left| {{\mathit{\Delta} _{\rm{t}}}} \right|}}{{{\mathit{\Delta} _{\rm{t}}}^{\rm{f}}}}} \right)}^\beta }\displaystyle{{\left( {\frac{n}{\beta } + \frac{{{\mathit{\Delta} _{\rm{t}}}}}{{{\mathit{\Delta} _{\rm{t}}}^{\rm{f}}}}} \right)}^n} + } \right.}\\ &{\Biggr.\langle {E_{\rm{t}}} - {E_{\rm{n}}}\rangle \Biggr)；}\\ \langle {E_{\rm{t}}} - {E_{\rm{n}}}\rangle =& \left\{ \begin{aligned} &{{E_{\rm{t}}} - {E_{\rm{n}}}， {E_{\rm{t}}} - {E_{\rm{n}}} \geqslant 0；}\\ &{0， \;\;\;\;\;\;\;\;\;\;\,{E_{\rm{t}}} - {E_{\rm{n}}} <\, 0.} \end{aligned} \right. \end{aligned} \right\}\\[-40pt] $

式中： $\langle \rangle $为McAulay公式； ${\mathit{\Delta} _{\text{n}}}$、 ${\mathit{\Delta} _{\text{t}}}$分别为法向和切向的剪切张开位移； $ {E_{\text{n}}} $、 $ {E_{\text{t}}} $分别为法向和切向的内聚能，当内聚能达到极限值时为断裂能； $ {G_{\text{n}}} $、 $ {G_{\text{t}}} $分别为法向和切向的内聚能常数； $ m $、 $ n $为无量纲常数； ${\mathit{\Delta} _{\text{n}}}^{\text{f}}$、 ${\mathit{\Delta} _{\text{t}}}^{\text{f}}$分别为法向和切向的最终剪切张开位移； $ \alpha $、 $\,\beta$分别为调控模型达到界面剪切强度之后，法向和切向内聚力软化形式的参数. 当 $ \alpha $、 $\,\beta$=2时，内聚力软化阶段的下降曲线为直线；当 $ \alpha $、 $\,\beta$＞2时，内聚力软化阶段的下降曲线为凹曲线；当 $ \alpha $、 $\,\beta$＜2时，内聚力软化阶段的下降曲线为凸曲线. 内聚力分量 $ {t_{\text{n}}} $、 $ {t_{\text{t}}} $随界面剪切张开位移变化的梯度关系分别为

(5) $ \begin{split} {t_{\rm{n}}}\left( {{\mathit{\Delta} _{\rm{n}}},{\mathit{\Delta} _{\rm{t}}}} \right) = &\frac{{\partial \varphi }}{{\partial {\mathit{\Delta} _{\rm{n}}}^{}}} = \frac{{{G_{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}\left( {m{{\left( {1 - \frac{{{\mathit{\Delta} _{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}} \right)}^\alpha }{{\left( {\frac{m}{\alpha } + \frac{{{\mathit{\Delta} _{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}} \right)}^{m - 1}} - } \right.\\ & \left. {\alpha {{\left( {1 - \frac{{{\mathit{\Delta} _{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}} \right)}^{\alpha - 1}}{{\left( {\frac{m}{\alpha } + \frac{{{\mathit{\Delta} _{\rm{n}}}}}{{{\mathit{\Delta} _{\rm{n}}}^{\rm{f}}}}} \right)}^m}} \right) \times\\ & \left( {{G_{\rm{t}}}{{\left( {1 - \frac{{\left| {{\mathit{\Delta} _{\rm{t}}}} \right|}}{{{\mathit{\Delta} _{\rm{t}}}^{\rm{f}}}}} \right)}^\beta } } {{{\left( {\frac{n}{\beta } + \frac{{\left| {{\mathit{\Delta} _{\rm{t}}}} \right|}}{{{\mathit{\Delta} _{\rm{t}}}^{\rm{f}}}}} \right)}^n} + \left\langle {{E_{\rm{t}}} - {E_{\rm{n}}}} \right\rangle } \right), \\[-18pt] \end{split} $

(6) $ \begin{split} {t_{\text{t}}}\left( {{\mathit{\Delta} _{\text{n}}},{\mathit{\Delta} _{\text{t}}}} \right) = &\frac{{\partial \varphi }}{{\partial {\mathit{\Delta} _{\rm{t}}}^{}}} = \frac{{{G_{\text{t}}}}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}\left( n{{\left( {1{-}\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^\beta }{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^{n{-}1}}-\right.\\ &\left.\beta {{\left( {1{-}\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^{\beta {-}1}}{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^n} \right) \left( {{G_{\text{n}}}{{\left( {1{-}\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^\alpha }}\right. \times \\ &\left.{{{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^n}+\left\langle {{E_{\text{n}}} - {E_{\text{t}}}} \right\rangle } \right)\frac{{{\mathit{\Delta} _{\text{t}}}}}{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}. \\[-18pt] \end{split} $

当法向与切向的断裂能不相同时，法向和切向的内聚能常数 $ {G_{\text{n}}} $、 $ {G_{\text{t}}} $的表达式为

(7) $ {G_{\text{n}}} = {\left( {{ - }{E_{\text{n}}}} \right)^{\frac{{\left\langle {{E_{\text{n}}} - {E_{\text{t}}}} \right\rangle }}{{\left( {{E_{\text{n}}} - {E_{\text{t}}}} \right)}}}}{\left( {\dfrac{\alpha }{\;m\;}} \right)^m} \text{，} $

(8) $ {G_{\text{t}}} = {\left( {{ - }{E_{\text{t}}}} \right)^{\frac{{\left\langle {{E_{\text{t}}} - {E_{\text{n}}}} \right\rangle }}{{\left( {{E_{\text{t}}} - {E_{\text{n}}}} \right)}}}}{\left( {\frac{\beta }{\;n\;}} \right)^n} . \quad$

当法向与切向断裂能相同时， $ {G_{\text{n}}} $、 $ {G_{\text{t}}} $的表达式为

(9) $ {G_{\text{n}}} = \left( {{-}{E_{\text{n}}}} \right){\left( {\frac{\alpha }{\;m\;}} \right)^m} \text{，} $

(10) $ {G_{\text{t}}} = {\left( {{-}{E_{\text{t}}}} \right)^{}}{\left( {\frac{\beta }{\;n\;}} \right)^n} . \;\quad$

无量纲常数 $ m $、 $ n $的计算式分别为

(11) $ m = \frac{{\alpha \left( {\alpha {-}1} \right){\lambda _{\text{n}}}^2}}{{1{-}\alpha {\lambda _{\text{n}}}^2}} \text{，} $

(12) $ n = \frac{{\beta \left( {\beta {-}1} \right){\lambda _{\text{t}}}^2}}{{1{-}\beta {\lambda _{\text{t}}}^2}} . \quad$

定义层间黏结材料初始刚度指标 $ \lambda $，即内聚力与位移关系曲线的斜率，为剪切张开的初始位移与最终位移的比值. 法向、切向的刚度指标的表达式分别为

(13) $ {\lambda _{\text{n}}} = \frac{{{\mathit{\Delta} _{\text{n}}}^0}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}} \text{，} $

(14) $ {\lambda _{\text{t}}} = \frac{{{\mathit{\Delta} _{\text{t}}}^0}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}} . \quad$

式中： ${\mathit{\Delta} _{\text{n}}}^0$、 ${\mathit{\Delta} _{\text{t}}}^0$分别为法向和切向的初始张开位移. 由以上算式推导出法向、切向最终张开位移量分别为

(15) $ {\mathit{\Delta} _{\text{n}}}^{\text{f}} = \frac{{{E_{\text{n}}}}}{{{\sigma _{{\text{max}}}}}}\alpha {\lambda _{\text{n}}}{\left( {1{-}{\lambda _{\text{n}}}} \right)^{\alpha {-}1}}\left( {\frac{\alpha }{m}+1} \right){\left( {\frac{\alpha }{m}{\lambda _{\text{n}}}+1} \right)^{m{-}1}} , $

(16) $ {\mathit{\Delta} _{\text{t}}}^{\text{f}} = \frac{{{E_{\text{t}}}}}{{{\tau _{{\text{max}}}}}}\beta {\lambda _{\text{t}}}{\left( {1{-}{\lambda _{\text{t}}}} \right)^{\beta {-}1}}\left( {\frac{\beta }{n}+1} \right){\left( {\frac{\beta }{n}{\lambda _{\text{t}}}+1} \right)^{n{-}1}} . \quad$

式中： ${\sigma _{{\text{max}}}}$、 ${\tau _{{\text{max}}}}$分别为法向和切向的内聚力强度.

超薄罩面的界面断裂能为层间法向力、切向力分别沿层间法向、切向变形所做的功，即应力−变形曲线与坐标轴所包围的面积，可以通过对应力−应变拟合曲线积分求得，计算式分别为

(17) $ {E_{\text{n}}} = \int_0^{{\mathit{\Delta} _{\text{n}}}^{\text{f}}} {{t_{\text{n}}}} {\text{d}}{\mathit{\Delta} _{\text{n}}} \text{，} $

(18) $ {E_{\text{t}}} = \int_0^{{\mathit{\Delta} _{\text{t}}}^{\text{f}}} {{t_{\text{t}}}} {\text{d}}{\mathit{\Delta} _{\text{t}}} .\quad $

常规的内聚力模型对内聚力和摩擦力抵抗剪切作用的关系模型大致有2种：1）内聚力与摩擦力无法同时存在，当内聚力下降为0时，摩擦力开始发挥作用，由于内聚力与摩擦力间的过渡不平滑，导致计算难以收敛，影响模拟效率；2）假设材料内聚力达到峰值时出现层间摩擦力. 模型2）考虑了摩擦力和内聚力对抗剪强度的影响，但当抗剪强度较大时，会出现剪切应力峰值滞后的现象，原因是在该模型中摩擦力峰值与内聚力峰值对应的剪切位移不相等. 模型2）无法真实模拟材料内聚力与层间摩擦力共同提供的整体抗剪强度. 改进常规的内聚力模型，使得材料的内聚力、层间摩擦力达到峰值时拥有相同的剪切位移.

当界面单元变形向两侧单元侵入时，挤压面产生抵抗力，挤压力的大小与侵入深度和接触刚度有关。 受压时的接触刚度始终与受拉状态时张开位移为0时的接触刚度相等. 改进的内聚力模型将材料内聚力与层间摩擦力耦合，假设层间摩擦力出现在界面受压且层间产生位移时. 摩擦力随着层间位移的增加而变大，接触面摩擦力计算式为

(19) $ {t_{\text{f}}} = {\mu _{\text{f}}}k\left( {{\mathit{\Delta} _{\text{t}}}} \right)\left|{{t_{\text{n}}}} \right| ; \;\; {t_{\text{n}}} < 0,\; {\mathit{\Delta} _{\text{t}}} > 0 . $

式中： $ \;{\mu _{\text{f}}} $由试验得到； $ k $∈[0,1]为破坏形态参数，随剪切位移 ${\mathit{\Delta} _{\text{t}}}$的增大而单调增大，计算式为

(20) $ k\left( {{\mathit{\Delta} _{\text{t}}}} \right) = {\left( {1 - \frac{{{t_{\text{t}}}\left( {0,{\mathit{\Delta} _{\text{t}}}} \right)}}{{{D_0}{\mathit{\Delta} _{\text{t}}}}}} \right)^s} . $

式中： $ s $为调节模型内聚力与摩擦力关系的转换关系参数，其对破坏形态参数 $ k $的影响如图3所示； $ {D_0} $为初始破坏时的接触刚度，计算式为

(21) $ \begin{split} {D_0} =& \frac{{{G_{\text{t}}}}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}\left( {n{{\left( {1{-}{\lambda _{\text{t}}}} \right)}^\beta } {{\left( {\frac{n}{\beta }+{\lambda _{\text{t}}}} \right)}^{n{-}1}} {-}\beta {{\left( {1{-}{\lambda _{\text{t}}}} \right)}^{\beta {-}1}}{{\left( {\frac{n}{\beta }+{\lambda _{\text{t}}}} \right)}^n}} \right) \times \\ & \left( {{G_{\text{n}}}{{\left( {\frac{m}{\alpha }} \right)}^n}+\left\langle {{E_{\text{n}}} - {E_{\text{t}}}} \right\rangle } \right)\frac{1}{{{\lambda _{\text{t}}}{\mathit{\Delta} _{\text{t}}}}}. \\[-18pt] \end{split} $

${t_{\text{t}}}(0,{\mathit{\Delta} _{\text{t}}}))$为法向张开位移量为0时的切向内聚力，计算式为

(22) $\begin{split} {t_{\text{t}}}\left( {0,{\mathit{\Delta} _t}} \right) =& \frac{{{G_{\text{t}}}}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}\left( {n{{\left( {1{-}\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^\beta } {{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^{n{-}1}}{-}\beta {{\left( {1{-}\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^{\beta {-}1}}}\times\right.\\ &\left.{{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^n}} \right) \left( {{G_{\text{n}}}{{\left( {\frac{m}{\alpha }} \right)}^n} +\left\langle {{E_{\text{n}}} - {E_{\text{t}}}} \right\rangle } \right)\frac{{{\mathit{\Delta} _{\text{t}}}}}{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}. \\[-18pt] \end{split} $

耦合材料内聚力和层间摩擦力，得到各个方向的内聚力为

(23) $ {\boldsymbol{t}} = \left[ {\begin{array}{*{20}{c}} {{t_{\text{n}}}} \\ {{t_{\text{t}}}\dfrac{{{\mathit{\Delta} _2}}}{{{\mathit{\Delta} _{\text{t}}}}}+{t_{\text{f}}}\left( {\dfrac{{\left| {{\mathit{\Delta} _2}} \right|}}{{{\mathit{\Delta} _1}}}} \right)\dfrac{{\mathop {{\mathit{\Delta} _2}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _2}} \right|}\limits^ \bullet }}} \\ {{t_{\text{t}}}\dfrac{{{\mathit{\Delta} _3}}}{{{\mathit{\Delta} _{\text{t}}}}}+{t_{\text{f}}}\left( {\dfrac{{\left| {{\mathit{\Delta} _3}} \right|}}{{{\mathit{\Delta} _1}}}} \right)\dfrac{{\mathop {{\mathit{\Delta} _3}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _3}} \right|}\limits^ \bullet }}} \end{array}} \right] . $

式中： ${\mathit{\Delta} _2}$、 ${\mathit{\Delta} _3}$为破坏面中间剪切方向的张开量， ${{\mathop {\mathit{\Delta}} \limits^ \bullet} _2}$、 ${{\mathop {\mathit{\Delta}} \limits^ \bullet} _3}$为剪切方向的张开量的变化， ${\mathit{\Delta} _{\text{t}}} = {({\mathit{\Delta} _2}^2+{\mathit{\Delta} _3}^2)^{0.5}}$

将改进后的内聚力模型引入Abaqus，进行扩展有限元子程序的编写. 在定义改进内聚力层间摩擦作用后须给出材料的刚度. 根据势能函数改进内聚力模型的刚度矩阵（雅克比矩阵）为

(24) $ {\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{J_{11}}}&{{J_{12}}}&{{J_{13}}} \\ {{J_{21}}}&{{J_{2{\text{2}}}}}&{{J_{2{\text{3}}}}} \\ {{J_{31}}}&{{J_{32}}}&{{J_{3{\text{3}}}}} \end{array}} \right] . $

式中：

$ \begin{array}{l} {J_{11}} = \dfrac{{\partial {t_{\text{n}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}} \text{，} {J_{12}} = \dfrac{{\partial {t_{\text{n}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\dfrac{{{\mathit{\Delta} _2}}}{{{\mathit{\Delta} _{\text{t}}}}} \text{，} {J_{13}} = \dfrac{{\partial {t_{\text{n}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\dfrac{{{\mathit{\Delta} _3}}}{{{\mathit{\Delta} _{\text{t}}}}} \text{，} \\ {J_{21}} = \dfrac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}\dfrac{{{\mathit{\Delta} _2}}}{{{\mathit{\Delta} _{\text{t}}}}}+\dfrac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}\dfrac{{\left| {{\mathit{\Delta} _2}} \right|}}{{{\mathit{\Delta} _{\text{t}}}}}\dfrac{{\mathop {{\mathit{\Delta} _2}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _2}} \right|}\limits^ \bullet }} \text{，} \end{array}$

$ {J_{22}} = \left( {\frac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}{\mathit{\Delta} _2} + \frac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\left| {{\mathit{\Delta} _2}} \right|\frac{{\mathop {{\mathit{\Delta} _2}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _2}} \right|}\limits^ \bullet }}} \right) \frac{{{\mathit{\Delta} _2}}}{{{\mathit{\Delta} _{\text{t}}}^2}} {-} \left( {{t_{\text{t}}} + {t_{\text{f}}}\frac{{{\mathit{\Delta} _2}}}{{{{\left| {{\mathit{\Delta} _{\text{2}}}} \right|}^{}}}}\frac{{\mathop {{\mathit{\Delta} _2}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _2}} \right|}\limits^ \bullet }}} \right) \frac{{{\mathit{\Delta} _3}^2}}{{{\mathit{\Delta} _{\text{t}}}^3}} \text{，} $

$ \begin{array}{l} {J_{23}} = \left( {\dfrac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}{\mathit{\Delta} _2} + \dfrac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\left| {{\mathit{\Delta} _2}} \right|\dfrac{{\mathop {{\mathit{\Delta} _2}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _2}} \right|}\limits^ \bullet }}} \right) \dfrac{{{\mathit{\Delta} _3}}}{{{\mathit{\Delta} _{\text{t}}}^2}} - \left( {{t_{\text{t}}}{\mathit{\Delta} _2} + {t_{\text{f}}}\left| {{\mathit{\Delta} _{\text{2}}}} \right|\dfrac{{\mathop {{\mathit{\Delta} _2}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _2}} \right|}\limits^ \bullet }}} \right) \dfrac{{{\mathit{\Delta} _3}^{}}}{{{\mathit{\Delta} _{\text{t}}}^3}} \text{，} \\ {J_{31}} = \left( {\dfrac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}\dfrac{{{\mathit{\Delta} _3}}}{{{\mathit{\Delta} _{\text{t}}}}}+\dfrac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}\dfrac{{\left| {{\mathit{\Delta} _3}} \right|}}{{{\mathit{\Delta} _{\text{t}}}}}\dfrac{{\mathop {{\mathit{\Delta} _3}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _3}} \right|}\limits^ \bullet }}} \right) \text{，} \end{array} $

$ {J_{32}} = \left( {\frac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}{\mathit{\Delta} _3} + \frac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\left| {{\mathit{\Delta} _3}} \right|\frac{{\mathop {{\mathit{\Delta} _3}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _3}} \right|}\limits^ \bullet }}} \right)\frac{{{\mathit{\Delta} _2}}}{{{\mathit{\Delta} _{\text{t}}}^2}} {-} \left( {{t_{\text{t}}}{\mathit{\Delta} _3}+{t_{\text{f}}}\left| {{\mathit{\Delta} _{\text{3}}}} \right|\frac{{\mathop {{\mathit{\Delta} _3}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _3}} \right|}\limits^ \bullet }}} \right) \frac{{{\mathit{\Delta} _3}^{}}}{{{\mathit{\Delta} _{\text{t}}}^3}} \text{，} $

$ {J_{33}} = \left( {\frac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}{\mathit{\Delta} _3} + \frac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\left| {{\mathit{\Delta} _3}} \right|\frac{{\mathop {{\mathit{\Delta} _3}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _3}} \right|}\limits^ \bullet }}} \right)\frac{{{\mathit{\Delta} _3}}}{{{\mathit{\Delta} _{\text{t}}}^2}} {-} \left( {{t_{\text{t}}} + {t_{\text{f}}}\frac{{{\mathit{\Delta} _{\text{3}}}}}{{\left| {{\mathit{\Delta} _{\text{3}}}} \right|}}\frac{{\mathop {{\mathit{\Delta} _3}}\limits^ \bullet }}{{\mathop {\left| {{\mathit{\Delta} _3}} \right|}\limits^ \bullet }}} \right)\frac{{{\mathit{\Delta} _2}^{}}}{{{\mathit{\Delta} _{\text{t}}}^3}} \text{，} $

其中 $\partial {t_{\rm{n}}}/\partial {\mathit{\Delta} _{\rm{t}}} = \partial {t_{\rm{t}}}/\partial {\mathit{\Delta} _{\rm{n}}}$， $\partial {t_{\rm{n}}}/\partial {\mathit{\Delta} _{\rm{n}}}$、 $\partial {t_{\rm{n}}}/\partial {\mathit{\Delta} _{\rm{t}}}$、 $\partial {t_{\rm{t}}}/\partial {\mathit{\Delta}_{\rm{t}}}$的计算式分别为

(25) $ \begin{split} \frac{{\partial {t_{\text{n}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}=& \frac{{{G_{\text{n}}}}}{{{{\left( {{\mathit{\Delta} _{\text{n}}}^{\text{f}}} \right)}^2}}}\left( {\left( {{m^2} - m} \right){{\left( {1 - \frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^\alpha }{{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^{m - 2}}} \right.+ \\ &\left( {{\alpha ^2} - \alpha } \right){\left( {1 - \frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)^{\alpha - 2}}{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)^m}{-} \\ &2\alpha m{\left( {1 - \frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)^{\alpha - 1}}\left. {{{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^{m - 1}}} \right) \times \\ &\left( {{G_{\text{t}}}{{\left( {1{-}\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^\beta }{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _t}^{\text{f}}}}} \right)}^n}+\left\langle {{E_{\text{t}}} - {E_{\text{n}}}} \right\rangle } \right)，\\[-18pt] \end{split} $

(26) $ \begin{split} \frac{{\partial {t_{\text{n}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}} = & \frac{{{G_{\text{t}}}{G_{\text{n}}}}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}\left( {m{{\left( {1 - \frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^\alpha }{{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^{m - 2}}} \right. - \\ &\alpha {\left( {1 - \frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)^{\alpha - 1}}\left. {{{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^m}} \right) \times \\ &\left( {n{{\left( {1 - \frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^\beta }{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^{n - 1}}} \right. - \\ &\beta {\left( {1 - \frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)^{\beta - 1}}\left. {{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^n}} \right)\frac{{{\mathit{\Delta} _{\text{t}}}}}{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}， \end{split} $

(27) $ \begin{split} \frac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}=& \frac{{{G_{\text{t}}}}}{{{{\left( {{\mathit{\Delta} _{\text{t}}}^{\text{f}}} \right)}^2}}}\left( {\left( {{n^2} - n} \right){{\left( {1 - \frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^\beta }{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)}^{n - 2}}} \right.+ \\ &\left( {{\beta ^2} - \beta } \right){\left( {1 - \frac{{{\mathit{\Delta} _{\text{n}}}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)^{\beta - 2}}{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)^n} - \\ &2\beta n{\left( {1 - \frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{t}}}^{\text{f}}}}} \right)^{\beta - 1}}\left. {{{\left( {\frac{n}{\beta }+\frac{{\left| {{\mathit{\Delta} _{\text{t}}}} \right|}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^{n - 1}}} \right) \times \\ &\left( {{G_{\text{n}}}{{\left( {1{-}\frac{{\left| {{\mathit{\Delta} _{\text{n}}}} \right|}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^\alpha }{{\left( {\frac{m}{\alpha }+\frac{{{\mathit{\Delta} _{\text{n}}}^{}}}{{{\mathit{\Delta} _{\text{n}}}^{\text{f}}}}} \right)}^n}+\left\langle {{E_{\text{n}}} - {E_{\text{t}}}} \right\rangle } \right). \end{split} $

改进内聚力模型摩擦力部分法向和切向的刚度计算式分别为

(28) $ \frac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}} = s{\mu _{\text{f}}}{\left( {\frac{{{t_{\text{t}}}\left( {0,{\mathit{\Delta} _{\text{t}}}} \right)}}{{{\tau _{\max }}}}} \right)^{s - 1}}\frac{{\partial {t_{\text{t}}}}}{{\partial {\mathit{\Delta} _{\text{t}}}}}\left| {{t_{\text{n}}}} \right| ， $

(29) $ \frac{{\partial {t_{\text{f}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}} = {\mu _{\text{f}}}{\left( {\frac{{{t_{}}\left( {0,{\mathit{\Delta} _{\text{t}}}} \right)}}{{{\tau _{\max }}}}} \right)^s}\left| {\frac{{\partial {t_{\text{n}}}}}{{\partial {\mathit{\Delta} _{\text{n}}}}}} \right|\frac{{{t_{\text{n}}}}}{{\left| {{t_{\text{n}}}} \right|}} . $

将改进的内聚力模型编入Abaqus，对沥青超薄罩面结构进行建模分析，模型尺寸同图1. 沥青超薄罩面层的弹性模量为1 200 MPa，泊松比为0.3，道路面层的弹性模量为1 600 MPa，泊松比为0.25；用改进内聚力模型定义沥青超薄罩面和道路面层间的黏层应力和层间摩擦系数. 分2步对模型施加荷载和约束：1）在模型顶部施加法向应力 $ \sigma $，在模型底部施加竖向约束；2）在超薄罩面层的左侧施加水平应力 $ {\sigma _{\text{r}}} $，在道路面层的右侧施加水平约束，使得模型试件能够产生剪切破坏. 结合直剪试验结果计算出层间材料的力学参数，如表2所示.

在直剪试验中，试件底部被加以竖向约束且竖向位移基本为0，同个工况加载下，正向应力始终不变，直至试件发生剪切破坏，加载停止. 因此，正向力学系数取值与切向相应系数取值相同，即 $ {E_{\text{n}}} $= $ {E_{\text{t}}} $、 $ {\sigma _{{\text{max}}}} $= $ {\tau _{{\text{max}}}} $、 $ \alpha $= $ \beta $、 $ {\lambda _{\text{n}}} $= $ {\lambda _{\text{t}}} $. 初始断裂能均取为在正向应力荷载为0时，直剪试验中剪切位移曲线与剪切应力曲线围成的面积；层间材料的切向与法向强度即内聚力强度均取直剪试验中的切应力峰值；软化形式参数 $ \alpha $、 $ \beta $与转换形式参数 $ s $根据图3，由直剪试验得到的剪切位移与剪切应力曲线图估测. 初始刚度 $ {\lambda _{\text{n}}} $、 $ {\lambda _{\text{t}}} $均取为直剪试验中剪切破坏的最大应力峰值与层间材料剪切破坏初始应力值之比；层间的摩擦系数 $ {\mu _{\text{f}}} $由摩尔−库伦理论拟合计算直剪试验结果得到.

对数值模拟结果进行最小二乘法曲线拟合，得到法向应力与抗剪强度的关系曲线图，将其与试验数据的拟合图对比如图4所示. 可以看出，2条拟合曲线的重合度较高，说明改进内聚力模型能够较好地反映直剪试验中抗剪强度随法向应力的变化关系.

本研究所建模型的计算结果如图5所示. 可以看出，在剪切刚开始时，切应力随剪切位移呈线性快速增大，此时沥青超薄罩面层间内聚力以及摩擦力不断增大，在接近剪切强度即最大切应力时，切应力增加的速度逐渐降低，当切应力达到剪切强度时，切应力随剪切位移的增加而减小，最终趋于定值，此时切应力完全由层间的摩擦力提供. 摩擦力由正向荷载间接提供，因此在正向荷载为0的工况下，切应力最终降为0.

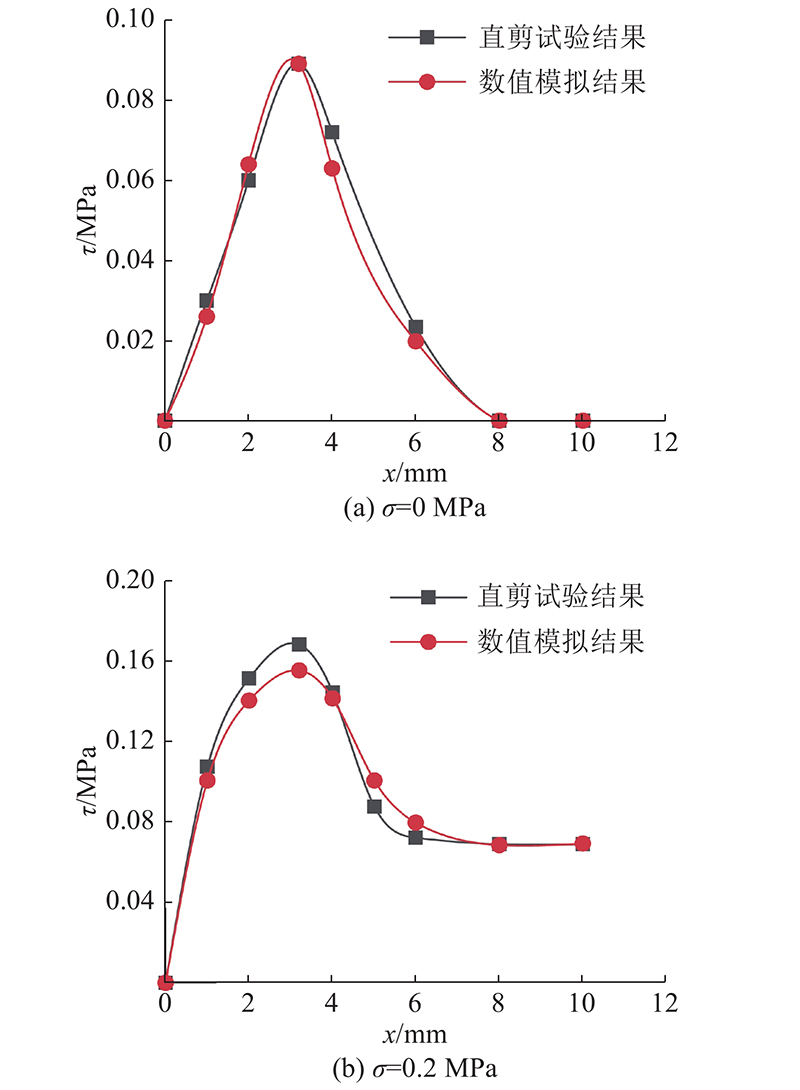
绘制正向荷载为0、0.2 MPa的剪切位移−切应力曲线，并分别与对应的试验结果进行比较，如图6所示. 1）数值模拟所得的剪切位移−切应力曲线与试验所得的曲线基本一致，说明本研究所采用的改进内聚力模型可用于沥青超薄罩面直剪试验的数值模拟. 2）数值模拟计算的应力强化阶段与试验结果的几乎一致，应力软化阶段的数值模拟结果与试验结果误差较小. 原因是改进内聚力模型在应力软化下降阶段利用软化形式参数 $ \alpha $、 $ \beta $控制内聚力，改变了应力软化的下降模式，同时转换形式参数 $ s $调节了内聚力与摩擦力的关系，这2种参数共同确定了在剪切软化阶段切应力随剪切位移的变化情况. 3）当正向荷载为0.2 MPa时，数值模拟计算的最大剪切应力略小于试验值. 原因是在选取改进内聚力模型层间材料力学参数时，层间材料的切向、法向强度及断裂能均由正向荷载为0的情况下切应力−剪切位移曲线计算所得. 4）在不受正向荷载的情况下（0 MPa），比较分析直剪试验与数值模拟所得的切应力−剪切位移曲线. 试验所得最大切应力为0.089 6，数值模拟所得的最大切应力为0.092，相对误差为2.68%. 在受正向荷载的情况下（0.2 MPa），试验所得最大切应力为0.176 2，数值模拟所得的最大切应力为0.159 7，相对误差为−9.37%. 在对受与不受正向荷载的2种情况下，直剪工况试验结果与数值模拟结果的相对误差均未超过10%，在工程应用中，试验结果与数值模拟结果误差不超过±20%均认为数值模拟结果比较合理^[24]. 因此本研究的数值模拟结果是合理可靠的，即采用的改进内聚力模型是有效的.

利用改进内聚力模型进行数值模拟，使层间材料的内聚力、层间摩擦力达到峰值时拥有相同的剪切位移，该阶段材料的抗切应力达到最大，即当内聚力达到最大时，摩擦力达到峰值. 最大切应力对应的剪切位移就是材料破坏临界位移，材料所能提供的最大内聚力就是破坏临界内聚力，此时达到材料的临界断裂能. 本研究选择临界断裂能作为判断沥青超薄罩面层间抗剪行为是否失效的指标.

深入分析直剪试验数值模拟结果，利用多项式拟合切应力达到峰值时层间切应力和层间剪切变形关系曲线，如图7所示. 由式（18）对图7中的拟合曲线进行积分，得到不同正向应力作用下沥青超薄罩面构件层间切应力达到极值时的临界断裂能，结果如表3所示. 1）在残余应力应变阶段之前，拟合曲线与数值模拟结果曲线贴切度良好，切应力与剪切位移的拟合相关系数均接近1，表明拟合有效，即对拟合曲线进行积分计算能够获得相应工况下试件破坏时的临界断裂能. 2）当正向应力从0 MPa增加至1.0 MPa时，层间破坏的临界断裂能从11.6 J增加至81.6 J，临界剪切位移在3.3~3.4 mm波动，说明临界剪切位移受正向应力影响较小，临界断裂能随正向应力增大而增大。即施加的正向应力越大，构件发生剪切破坏时的临界断裂能越大，相应的层间剪切位移须克服更大的外力进行做功，使施加较大正向应力的构件具有更好的层间抗剪性能.

（1）基于直剪试验获得法向应力与层间剪切强度的关系曲线，并通过摩尔−库伦理论进行拟合，得到沥青超薄罩面层间黏结应力为0.089 1，层间摩擦系数为0.364 1.

（2）从理论上改进现有内聚力模型不足，基于“沥青超薄罩面层间抗剪行为是由层间摩擦力和层间黏结力耦合作用而得的”，推导改进内聚力模型及其关键参数表达式.

（3）施加正向应力的沥青超薄罩面界面的切应力与剪切位移的关系可分为3个阶段：1）切应力应变弹性强化阶段，此阶段切应力随切位移增加而增大，切应力由内聚力及摩擦力共同提供；2）切应力应变软化阶段，此阶段切应力随剪切位移增大而减小，减小的是内聚力，摩擦力始终保持不变；3）残余应力应变阶段，此阶段切应力不随剪切位移变化，内聚力为0，切应力完全由层间摩擦力提供.

（4）选择临界断裂能作为评价沥青超薄罩面层间失效行为的指标. 对于施加正向应力的构件，在发生剪切破坏时，临界断裂能大小与施加的正向应力大小有关. 随着正向应力的增大，构件的临界断裂能不断增加，层间抗剪强度越大. 当正向应力分别为0、0.2、0.4、0.6、0.8和1.0 MPa时，对应的临界断裂能分别为11.6、32.9、43.9、46.3、63.7和81.6 J.

（5）数值模拟获得的法向应力与抗剪强度的关系曲线以及剪切位移与切应力的关系曲线与试验结果基本相一致，最大应力峰值相差较小，最大误差绝对为9.37%. 改进内聚力模型能够表征界面接触特性，较好地反应沥青超薄罩面层间抗剪过程中各阶段的力学响应，可以用于研究相类似结构的层间剪切破坏行为.

（6）本研究引入改进内聚力模型表征界面接触特性，对沥青超薄罩面直剪试验进行数值模拟，提出利用临界断裂能分析评价沥青超薄罩面层间抗剪失效行为. 在实际工程中，水、荷载作用频率对罩面层间抗剪失效可能有较大的影响，因此“临界断裂能”的工程应用有待进一步研究完善.