我国寒区( 冬季最低气温低于273.15 K (0 ℃)或冻融深度小于30 cm的地区^[1]) 面积约占国土总面积的75%^[2]. 由结构面劣化引起的危岩体失稳是寒区主要的地质灾害之一，如新疆天山危岩长期受冻融作用影响，结构面持续劣化引起失稳倾覆破坏^[3]. 开展冻融循环作用下的岩体劣化机理研究对危岩体稳定性意义重大.

冻融循环作用对寒区危岩体的影响主要有岩体力学性能的劣化和冻结深度的演进. 开展危岩体稳定性分析的关键是建立表征岩体抗拉强度劣化及冻结深度演化的理论模型. 学者针对冻融作用下岩石力学性能弱化及冻结深度开展了大量研究. 刘慧等^[4]从细观尺度分析冻融作用对砂岩劣化的影响，通过冻融试验发现砂岩抗拉强度呈指数型函数下降；周元辅等^[5]依托单向冻结深度试验比较4种冻结深度计算方法的结果表明，Stephan公式和鲁基杨诺夫公式对冻结深度的预测结果相对合理. 在危岩体工程方面，Chen等^[6]在对天山危岩体的研究中发现，冻融作用对岩块的劣化主要由赋存于岩石内部的宏细观缺陷引起，在反复冻融中缺陷持续发展，导致岩石载荷能力降低进而引起危岩体失稳；Chen等^[7]计算模拟分析边坡危岩材料的结果表明，冻结软岩的强度呈指数下降趋势.

寒区倾倒式危岩体的稳定性与岩石抗拉强度的劣化、冻结深度的演化关系密切. 对危岩体未贯通段岩石抗拉强度随冻融循环次数的演化关系研究主要是拟合室内试验结果，对力学作用机理方面的研究多集中在岩石强度劣化方面，鲜有针对影响危岩体稳定性多种影响参数耦合作用的研究. 本研究基于极限平衡理论和岩石冻胀理论，构建冻融循环作用下倾倒式危岩体稳定性劣化的分析模型.

在长期地质作用下，自然界危岩体内部存在不同尺度的宏细观缺陷：弱结构面（宏观尺度缺陷），微裂隙、微孔洞（细观尺度缺陷）等. 这些缺陷间存在机制复杂的相互作用，当不同缺陷共同作用时，将使危岩体力学性能劣化. 对危岩体稳定起控制作用的往往是力学强度低的软弱结构面，即主控结构面^[8-9]，本研究忽略缺陷间的相互作用，把倾倒式危岩体中的结构面作为研究对象. 考虑宏观结构面贯通段冻胀力，延伸非贯通段一定冻结深度范围内的岩石抗拉强度弱化，基于极限平衡理论，建立长期冻融循环作用下倾倒式危岩体稳定性劣化模型.

由极限平衡分析理论^[10]可知，位于寒区的倾倒式危岩体长期受冻融作用影响， 致使危岩体倾覆点处的倾覆力矩增大、抗倾覆力矩减小，引起危岩体失稳破坏. 因此，判断该类危岩体是否出现倾覆破坏的关键是基于倾覆点建立极限平衡方程.

如图1所示为倾倒式危岩体计算模型. 图中，P为危岩体贯通段冻胀力，G、Q分别为危岩体所受重力和水平力. AC为危岩体主控面，包括贯通段和未贯通段. 其中OA为危岩体结构面，属于贯通段，OC为结构面沿倾角方向的延长部分，属于未贯通段；CD为后缘岩石在主控面上的投影. H、h、h^d、h^w分别为结构面高度、结构面贯通段高度、冻结区深度和未冻区深度. l^d、l^w分别为冻结岩石长度和未冻岩石长度. c、d分别为重心至倾覆点的水平距离和竖直距离，e为后缘岩体至倾覆点的距离，E为危岩体倾覆点，α为后缘岩体与水平轴线夹角，β为危岩体倾角. 实际上，裸露在危岩体表面、与外界接触的岩石均存在冻结区，倾倒式危岩体稳定性主要由主控结构面控制，本研究仅在主控结构面处考虑冻结区深度对危岩体稳定性的影响.

倾覆点处倾覆力矩M_q和由重力、岩石抗拉强度引起的抗倾覆力矩M_k的计算式为

(1) $ \left. \begin{split} &{M_{\text{q}}} = P\frac{h}{{\sin \beta }}\left( {\frac{{2H - h}}{{2\sin \beta }}+\frac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right)+Qd, \\ &{M_{\text{k}}} = {f_{{\text{k}}n}}{l^{\text{d}}}\left( {\frac{{{l^{\text{d}}}}}{2}+{l^{\text{w}}}+\frac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right)+ \\ &\qquad\,\,\,{f_{\text{c}}}{l^{\text{w}}}\left( {\frac{{{l^{\text{w}}}}}{2}+\frac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right)+Gc. \\ \end{split} \right\} $

式中：f_kn、f_c分别为冻结区内和未冻区内岩石抗拉强度. 冻结岩石长度l^d、未冻岩石长度l^w和冻结区深度h^d间存在几何关系，表达式为

(2) $ \begin{gathered} {l^{\text{d}}}{\text{ = }}\frac{{{h^{\text{d}}}}}{{\sin \beta }},\; {l^{\text{w}}}{\text{ = }}\frac{{H - h}}{{\sin \beta }} - \frac{{{h^{\text{d}}}}}{{\sin \beta }} \\ \end{gathered} . $

冻融循环对未贯通段的作用表现在冻结岩石长度和抗拉强度的弱化上，即f_kn、l^d均与冻融循环作用次数有关. 危岩体未贯通段由冻结岩石和未冻岩石组成，冻结岩石长度变化必然引起未冻岩石长度变化，须研究不同冻融循环次数对危岩体稳定性的影响. n次冻融循环作用后，倾倒式危岩体稳定系数F_n的计算式为

(3) $ {F_n}{{ = }}\dfrac{{{f_{{\text{k}}n}}l_n^{\text{d}}\left( {\dfrac{{l_n^{\text{d}}}}{2} + l_n^{\text{w}} + \dfrac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right) + {f_{\text{c}}}l_n^{\text{w}}\left( {\dfrac{{l_n^{\text{w}}}}{2} + \dfrac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right) + Gc}}{{P\dfrac{h}{{\sin \beta }}\left( {\dfrac{{2H - h}}{{2\sin \beta }}+\dfrac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right)+Qd}}. $

由式（3）可知，冻融循环作用下的冻胀力P、岩石抗拉强度f_kn、冻结岩石长度l_n ^d等均会改变倾覆点处的力矩并影响危岩体的稳定性.

危岩体结构面多为贯通的软弱夹层，由于结构面的冻胀通常发生在宏观尺度上，可以将结构面贯通段视为赋存于危岩体中的宏观缺陷开展研究^[11]. 宏观尺度缺陷岩石冻胀力的计算方法较多^[12-13]，其中利用水分迁移引起的分离压力计算冻胀力的方法被广泛认可. Vlahou等^[14-15]在开展岩石冻胀试验时发现，大部分的结构面裂隙被冰透镜覆盖，冰透镜界面存在未冻水膜，水膜两端的压力差驱使水分迁移，岩石界面产生冻胀力. Derjaguin等^[16]研究了石英岩的冻胀力与温度变化的关系，提出未冻水膜两端压力差为分离压力，并采用分离压力解释结构面软弱夹层间的冻胀力. Rempel等^[17]得出分离压力与未冻水膜厚度间的函数关系为

(4) $ P{\text{ = }}\frac{{ - A}}{{6{\text{π }} {\delta ^3}}}. $

式中：A为水的Hamaker常数，通常取A=−10⁻¹⁸ J；δ为未冻水的水膜厚度. ${{{\rm{D\ddot oppenschmidt}}}}$等^[18]研究冻结冰体表面上的未冻水膜厚度，考虑水−冰系统和冰−岩系统自由能变化过程，通过理论分析和室内试验得到计算水膜厚度的经验式为

(5) $ \delta {\text{ = }}\left( {35 - 22\lg \Delta T} \right) \times {10^{ - 9}}, \;\Delta T = {T_0} - T. $

式中：T ₀为水冻结温度，T为环境温度. 将式（5）代入式（4），得到分离压力与温度的函数关系式为

(6) $ P{\text{ = }}\frac{{ - A \times {{10}^{27}}}}{{6{\text{π }}{{\left( {35 - 22\lg \left( {{T_0} - T} \right)} \right)}^3}}}. $

由式（6）可知，利用分离压力计算得到的结构面贯通段冻胀力仅与冻结温度有关. 若危岩体在受到冻融作用时采用平均温度计算，则认为结构面冻胀力仅受平均温度影响，不受循环次数影响.

危岩体未贯通段岩石冻结深度、抗拉强度对抗倾覆力矩的影响是同步的. 原因为在冻融循环作用下，岩石微裂隙不断发生细观冻胀破坏，累积效应在宏观上表现为岩石抗拉强度弱化，而抗拉强度的弱化区域全部作用在一定深度的冻结岩石中. 本研究从细观尺度分析冻融循环作用对岩石微裂隙的影响. 借鉴刘红岩等^[19-20]对冻结岩石微裂隙的变形与扩展研究，提出以下2个假定条件. 1）将细观微裂隙和外包岩石等效为扁平状椭圆形裂隙，椭圆的长轴远大于短轴. 冻融作用不改变椭圆的形状和几何中心位置. 2）岩块由无数个细观微裂隙和外包围岩石组成.

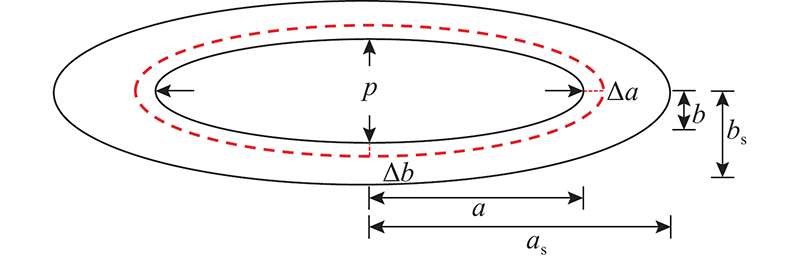
如图2所示为微裂隙冻胀扩径示意图. a、b分别为初始微裂隙等效椭圆的长半轴和短半轴，a_s、b_s分别为裂隙外包围岩石等效椭圆的长半轴和短半轴_s，Δa、Δb分别为单次冻融作用下微裂隙长半轴和短半轴的增量，p为微裂隙冻胀力. 冻融作用完成后微裂隙体积增大，体积增量由微裂隙半轴增量计算得到. 微裂隙扩展由裂隙间未冻水迁移产生的冻胀力引起，因此须计算分析细观微裂隙中的冻胀力. Walder等^[21]在对多孔岩石的冻胀研究中提出考虑冻胀时间、冻胀温度、水流阻以及材料比容等因素的微裂隙冻胀力计算模型，根据该模型可得微裂隙冻胀力的计算式为

(7) $ \left. \begin{gathered} {p_i}\left( t \right){\text{ = }}\frac{{ - LT}}{{{v_{\text{s}}}{T_0}}}\left( {1 - {{\rm{exp}}\;({ - t/\tau })}} \right)+{p_0}{{\rm{exp}}\;({ - t/\tau })}, \\ \tau {\text{ = }}\frac{{8{R_f}}}{{3{\text{π}} }}\left( {\frac{{1 - \nu }}{{{G_{\text{r}}}}}} \right)\left( {\frac{{ga{v_{\text{L}}}}}{{v_{\text{s}}^2}}} \right). \\ \end{gathered} \right\} $

式中：p_i (t)为冻结时刻为t时的微裂隙冻胀力；L为温度T下的水冰相变潜热；τ为冻结压力增量的特征时间参数；ν_s、ν_L分别为冰和水的比容；υ、G_r分别为岩石的泊松比和剪切模量；R_f为裂隙冻结缘对迁移水的阻力，计算方法见文献[21]. 由式（7）可知，裂隙冻胀力p_i(t)随冻结时刻变化，考虑到寒区工程中岩石冻结时间较长，用等效冻胀力p代替p_i (t)进行计算. 由于能量守恒，完成单次冻融循环作用时等效冻胀力p和p_i (t)产生的能量是相等的，裂隙内壁冻胀力在法向作功，其扩展能为

(8) $ E = 4pa\Delta b .$

在冻结时间内短半轴位移速度为 $ \Delta b/t $，据此得到

(9) $ E = 4a\Delta b\frac{{\displaystyle\int_0^t {{p_i}\left( t \right){\text{d}}t} }}{t} .$

根据式（8）、（9）得到微裂隙等效冻胀力为 $ p = \displaystyle\int_0^t {{p_i}\left( t \right){\text{d}}t} /t $. Muskhelishvili^[22]根据弹性力学和复变函数理论得到微裂隙半轴增量计算式为

(10) $ \begin{gathered} \Delta a = \frac{{pR}}{{2{G_{\text{r}}}}}\left( {1 - \frac{{3 - v}}{{v+1}}r} \right), \; \Delta b = \frac{{pR}}{{2{G_{\text{r}}}}}\left( {1+\frac{{3 - v}}{{v+1}}r} \right). \\ \end{gathered} $

式中：R、r为椭圆形状参数，R= (a+b)/2，r= (a−b)/(a+b). 当椭圆形微裂隙长轴远大于短轴时，有R=a / 2，r=1，此时式（10）简化为

(11) $ \begin{gathered} \Delta a = \frac{{pa\left( {v - 1} \right)}}{{2{G_{\text{r}}}\left( {v+1} \right)}}, \; \Delta b = \frac{{pa}}{{{G_{\text{r}}}\left( {v+1} \right)}}. \\ \end{gathered} $

在冻融过程中，未冻水不能充满整个微裂隙，微裂隙中的岩石碎屑占据了一定空间，单次冻融所增加的水体积为排除碎屑所占体积后的融化水体积. 残留的岩石碎屑在冻融过程中被冻结冰包裹，不产生冻胀效应. 实际上，微裂隙冻胀扩径小于未考虑岩石碎屑存在的情况，因此在计算微裂隙长、短半轴的扩展时须考虑岩石碎屑残留的影响.

假定单次冻融循环作用后流失的碎屑厚度与新产生石屑厚度比为碎屑流失比q，有

(12) $ \left. \begin{gathered} \Delta a' = q\left( {{a_n} - {a_{n - 1}}} \right) = q\Delta a, \\ \Delta b' = q\left( {{b_n} - {b_{n - 1}}} \right) = q\Delta b . \\ \end{gathered} \right\} $

式中：Δa'、Δb'分别为不考虑岩石碎屑流失比时的裂隙长半轴增量和短半轴增量. a_n为历经n次冻融循环作用后的微裂隙长半轴长度，b_n为历经n次冻融循环作用后的微裂隙短半轴长度. 考虑碎屑流失比时，微裂隙半轴增量变化较未考虑时更小，增量的减小将使得微裂隙劣化面积比未考虑时更小. 裂隙面积的劣化通常会引起岩石质量的变化，引入岩石质量损失来分析碎屑流失比. 在平面状态中，初始未冻融阶段的微裂隙断面面积为πa₀b₀，历经n次冻融循环作用后，断面面积为π(a_n−1+qΔa_n−1)(b_n-1+qΔa_n−1). 建立岩石面积劣化与质量流失的关系式为

(13) $\begin{split} \text{π} \sum\limits_1^i & \left( \left( {a_{n - 1}^i+q\Delta a_{n - 1}^i} \right)\left( {b_{n - 1}^i+q\Delta b_{n - 1}^i} \right) -a_{n - 1}^ib_{n - 1}^i \right) {\text{ = }}\\ & \frac{{\left( {{M_{n - 1}} - {M_n}} \right)}}{{{\rho _{\text{m}}}}}. \\[-11pt] \end{split}$

式中：aⁱ_n−1、bⁱ_n−1分别为第i个微裂隙n−1次冻融循环后的长、短半轴，M_n为冻融循环n次后的岩石单位长度质量，ρ_m为岩石密度. 由式（13）可知，碎屑流失比与每次冻融作用后损失的岩石质量相关. 由于假定条件中采用的是微裂隙等效长度，式（13）中的碎屑流失比可以通过等效岩体方法计算，表达式为

(14) $ \begin{split} \text{π} {\rho _{\text{m}}} & \sum\limits_1^i {\text{(}}qa_{n - 1}^i\Delta b_{n - 1}^i+qb_{n - 1}^i\Delta a_{n - 1}^i+\\ &{q^2}\Delta a_{n - 1}^i\Delta b_{n - 1}^i{\text{)}} {\text{ = }}\left( {{M_{n - 1}} - {M_n}} \right). \end{split} $

微裂隙半轴远大于其增量，且增量相对半轴长度为极小值，即 $ \Delta a \ll a $， $ \Delta b \ll b $， $ \Delta a \cdot \Delta b \approx 0 $，适当简化式（14）中半轴增量的乘积，有

(15) $ \text{π} {\rho _{\text{m}}}\sum\limits_1^i {\left( {qa_{n - 1}^i\Delta b_{n - 1}^i+qb_{n - 1}^i\Delta a_{n - 1}^i} \right)} {\text{ = }}\left( {{M_{n - 1}} - {M_n}} \right). $

微裂隙的扩径作用在细观尺度上会导致缺陷面积变化，在宏观尺度上会引起岩石质量损失，根据式（15）可以得到

(16) $ \frac{{\left( {a_{n - 1}^i+q\Delta a_{n - 1}^i} \right)\left( {b_{n - 1}^i+q\Delta b_{n - 1}^i} \right) - a_{n - 1}^ib_{n - 1}^i}}{{a_{\text{s}}^ib_{\text{s}}^i - a_{n - 1}^ib_{n - 1}^i}} = \frac{{{M_{n - 1}} - {M_n}}}{{{M_{n - 1}}}}. $

化简式（16），得到碎屑流失比q的计算式为

(17) $ q = \frac{{\left( {{M_{n - 1}} - {M_n}} \right)/{M_{n - 1}}}}{{\left( {b_{n - 1}^i\Delta a_{n - 1}^i+a_{n - 1}^i\Delta b_{n - 1}^i} \right)/\left( {a_{\text{s}}^ib_{\text{s}}^i - a_{n - 1}^ib_{n - 1}^i} \right)}}. $

将岩石碎屑流失比与其质量损失关联，并将式（17）中的分子视为质量损失率λ_M，分母视为微裂隙面积损失率λ_S，以便应用于寒区工程中. 利用闻磊等^[23]对标准岩样的冻融循环试验所得岩石质量损伤数据结果，并结合式（17）拟合碎屑流失比q. 拟合中的参数参照文献[23]，选取张向东等^[24]在岩石损伤试验中测得的微裂隙等效长度和面积作为计算参数. 微裂隙尺寸和微裂隙中的水分活动空间均随冻融循环次数增加而增加，碎屑随水分迁移被带出裂隙的比例保持不变，即假定碎屑流失比为仅与岩石类型有关的常数. 拟合碎屑流失比，结果如图3所示. 可知，利用线性拟合所得结果与闻磊等^[23]的试验结果拟合效果较好.

碎屑流失条件下历经n次冻融循环后的裂隙半轴分别为

(18) $ \left. \begin{split} & {a_n} = {a_{n - 1}}+\frac{{q{a_{n - 1}}\left( {v - 1} \right)\displaystyle\int_0^t {{p_i}\left( t \right){\text{d}}t} }}{{2{G_{\text{r}}}\left( {v+1} \right)t}}, \\ & {b_n} = {b_{n - 1}}+\frac{{q{a_{n - 1}}\displaystyle\int_0^t {{p_i}\left( t \right){\text{d}}t} }}{{{G_{\text{r}}}\left( {v+1} \right)t}} . \\ \end{split} \right\} $

式中：a_n、b_n可以通过裂隙初始半轴长度a₀、b₀渐进求解获取. 冻融循环作用使裂隙等效半轴增大并引起裂隙体积增大，导致宏观上岩石孔隙率增大，意味着岩石受破坏和变形不可恢复的区域范围增大. 从细观角度考虑，视为在冻融循环作用下岩石内部劣化效果不断累积，使岩石抗拉强度随之持续弱化. 在平面内岩石的初始孔隙率ω₀和历经n次冻融作用后的岩石孔隙率ω_n的计算式分别为

(19) $ \left. \begin{gathered} {\omega _0}{\text{ = }}\left( {\text{π} \sum\limits_1^i {a_0^ib_0^i} } \right)/\left( {\text{π} \sum\limits_1^i {a_{\text{s}}^ib_{\text{s}}^i} } \right), \\ {\omega _n}{\text{ = }}\left( {\text{π} \sum\limits_1^i {a_n^ib_n^i} } \right)/\left( {\text{π}\sum\limits_1^i {a_{\text{s}}^ib_{\text{s}}^i} } \right) . \\ \end{gathered} \right\} $

通过等效岩体方法，将平面孔隙率变化转换为岩石内部缺陷面积的劣化，得到冻融循环n次后的岩石劣化D_n的计算式为

(20) $ {D_n} = 1 - \frac{{1 - {\omega _n}}}{{1 - {\omega _0}}}{\text{ = }}1 - \frac{{1 - {{a_n}{b_n}} {{\left( {{a_0}{b_0}} \right)}^{ - 1}}{\omega _0}}}{{1 - {\omega _0}}}. $

岩石内部缺陷的劣化与其抗拉强度的弱化密切相关，由式（20）得到n次冻融循环后的未贯通段冻结岩石抗拉强度f_kn的计算式为

(21) $ {f_{{\text{k}}n}} = \frac{{1 - \left( {{a_n}{b_n}} \right){{\left( {{a_0}{b_0}} \right)}^{ - 1}}{\omega _0}}}{{1 - {\omega _0}}}{f_{{\text{k0}}}}. $

微裂隙倾角会改变岩石的劣化程度^[25-26]，须在受荷方向等效转换不同倾角的裂隙.

假设微裂隙与受荷方向的夹角θ为随机值，且数值随机分布在直角扇形( $ 0 \leqslant \theta \leqslant \pi /2 $)中的不同区间，将直角扇形区域m等份，集中在第k个区间( $ 0 \leqslant k \leqslant m $)的夹角数为ψ_k个. 各区间的夹角频度χ_k和分布概率密度函数 $ {f_k}\left( \theta \right) $的计算式分别为

(22) $ {\chi _{k}}{\text{ = }}\frac{{{\psi _k}}}{{\displaystyle\sum\nolimits_{k = 1}^m {{\psi _k}} }}, \; {f_k}\left( \theta \right){\text{ = }}\frac{{2m}}{{\text{π} {\chi _k}}} . \\ $

利用混合Von Mises分布，即圆周正态分布将直角扇形等效为1/4个圆周^[27]，夹角分布概率密度函数为

(23) $ {f_k}\left( \theta \right){\text{ = }}\frac{{2\exp \,\left( {\upsilon \cos \left( {\theta - \phi } \right)} \right)}}{{\text{π} {B_0}\left( \upsilon \right)}}. $

式中：υ、φ为单一Von Mises分布的比例系数^[28]；B₀ (υ)为关于υ的0阶修正Bessel函数，计算式为

(24) $ {B_0}\left( \upsilon \right){\text{ = }}2{\text{π}^{ - 1}}\int_0^{\text{π} /2} {\exp \, \left( {\upsilon \cos \left( {\theta - \phi } \right)} \right){\text{d}}\theta } . $

对第i个区间的夹角分布概率密度函数进行积分，得到该区间夹角的频度计算式为

(25) $ {\chi _i} = {\text{2}}\int_{\tfrac{{\text{π} \left( {k - 1} \right)}}{{2m}}}^{\tfrac{{\text{π} i}}{{2m}}} {\frac{{\exp\, \left( {\upsilon \cos \left( {\theta - \phi } \right)} \right)}}{{\text{π} {B_0}\left( \upsilon \right)}}{\text{d}}\theta } . $

将不同区间内夹角值转换为受荷方向上的等效值，并将各区间所得等效值累加，得到转换系数η的计算式为

(26) $ \eta {\text{ = }}\sum\limits_{k = 1}^m {\left( {{\chi _k} \cos \left( {\frac{{\text{π} k}}{{2m}}} \right)} \right)} . $

联立式（18）、（21）、（26），得到在不同裂隙倾角和碎屑流失条件下，寒区危岩体未贯通段冻结岩石抗拉强度劣化的计算式为

(27) $ \begin{split} {f_{{\text{k}}n}} =& \sum\limits_{k = 1}^m {\left( {{\chi _k} \cos \left( {\frac{{\text{π} k}}{{2m}}} \right)} \right)} \times \\ & \frac{{1 - \left( {1+\displaystyle\sum\limits_1^i {q\Delta b_n^i} /b_0^i+\sum\limits_1^i {q\Delta a_n^i} /a_0^i} \right){\omega _0}}}{{1 - {\omega _0}}}{f_{{\text{k0}}}}. \end{split} $

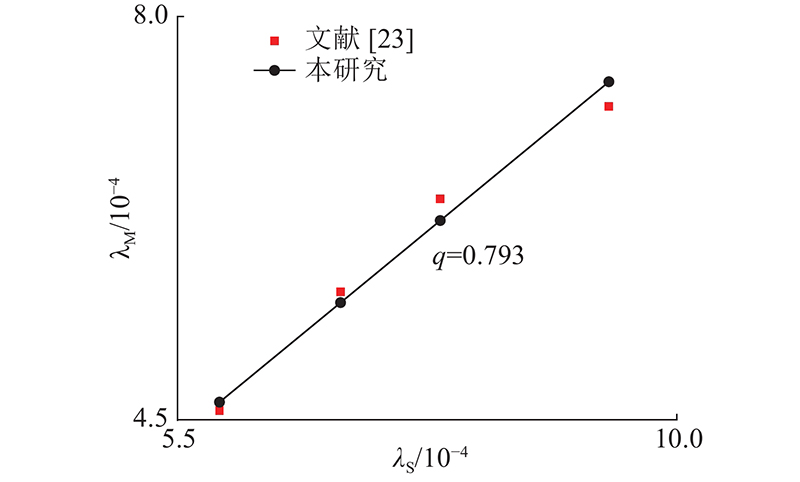
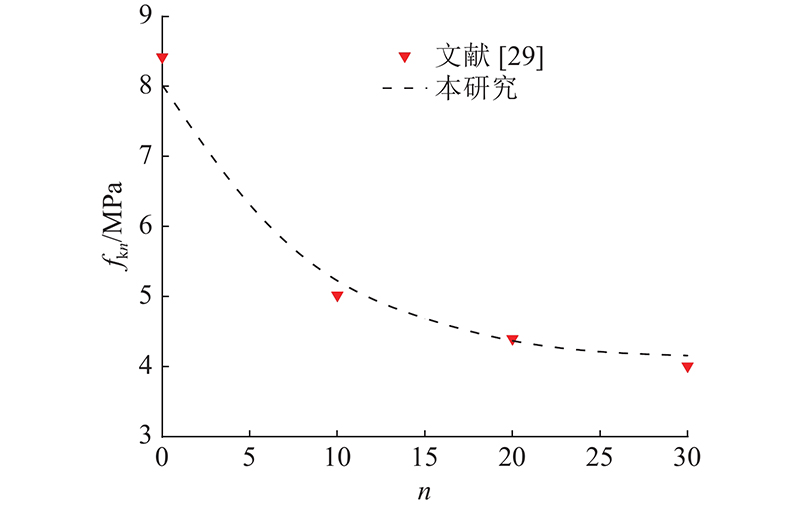
采用闻磊等^[23,29]对花岗斑岩的冻融循环试验结果比较验证本研究理论计算所得结果. 试验温度区间为253.15~293.15 K (−20~20 ℃)，单次冻融周期为24 h，岩石冻结和融化时间均为12 h，分别对岩石试样进行10、20、30次冻融循环，冻融作用结束后，利用万能试验机对岩样进行巴西劈裂试验，以获得不同冻融次数下的岩样抗拉强度值. 理论计算中的岩石物理力学参数取自文献[29]，岩石碎屑流失比通过文献[23]的质量损失率计算获得，微裂隙等效半轴长度取自文献[24]. 计算参数如表1所示. 将表中参数值代入式（27），得到不同冻融循环次数下岩石的抗拉强度，再将计算结果与文献[29]的试验结果对比，结果如图4所示. 可知，理论计算结果与试验结果在数值上整体吻合程度较好，且随冻融循环次数的变化趋势一致. 表明利用式（27）表征寒区危岩体抗拉强度的劣化是合理的.

应用较广的单一岩层冻结区深度计算式为Stephan经验公式^[30-31]，Nelson等^[32] 修正Stephan公式，得到岩石冻结深度h^d的表达式为

(28) $ {h^{\text{d}}} = \sqrt {\frac{{2SKD\left| {T_{\text{w}}} \right|}}{{L{\rho _{\rm{d}}}{\kappa _{{\rm{w}}}}\left( {1 - {\kappa _{\rm{n}}}} \right)}}} . $

式中：K为岩石导热系数；S为计算比例因子，取S=86 400，D为冻融循环周期内冬季持续天数. T_w为冬季冻结期平均温度，ρ_d为岩石干密度，κ_w、κ_n分别为岩石中水的质量分数和冻融时岩石未冻水的质量分数. 在低温作用下，与危岩体贯通段接触的岩石最先冻结，冻结过程中冷端要为岩石提供足够的负温才能使裂隙水冻结成冰. 岩石裂隙空间内水冰相变使未冻水向深处迁移，导致未贯通段冻结深度不断加大. 裴万胜^[33]在研究冻土水−热−力相互作用时，发现在水分迁移过程中，未冻水质量分数与岩石孔隙率和冻结温度存在关联，并通过室内试验得到未冻水质量分数的拟合式，同时联立式（19）中的孔隙劣化模式，得到

(29) $ {\kappa _n} = {\omega _n}\exp \left( {1.2\left( {T - {T_0}+{T_0}\frac{{{\rho _{\text{w}}} - {\rho _{\text{i}}}}}{{{\rho _{\text{w}}}{\rho _{\text{i}}}L}}\left( {p - u} \right)} \right)} \right). $

式中：ρ_w、ρ_i分别为水和冰的密度，u为孔隙水压力. 由于风化、侵蚀作用，靠近表面的岩石相较于埋深处孔隙率存在显著差异^[34]，岩石内部裂隙分布不均会影响冻结深度的分布范围. 在研究冻结深度的变化时，须分析不同深度下的岩石初始孔隙率. 孙利辉等^[35]在探究弱胶结地层中拟合得到岩石孔隙率与埋深呈线性变化规律. 埋深较浅的岩石采用密度变化表征孔隙率的变化^[36]，岩石孔隙率与埋置深度呈明显的线性关系. 岩石初始孔隙率与埋深的关系表达式为

(30) $ {\omega _h} = 1 - \frac{{{\rho _h}}}{{{\rho _{\text{r}}}}} = 1 - \frac{{{A_{\text{r}}}{h^{\rm{d}}}+{B_{\text{r}}}}}{{{\rho _{\text{r}}}}}. $

式中：ρ_h为埋深处岩石密度；ρ_r为致密岩石密度；A_r、B_r为计算埋深处岩石密度的线性回归系数，取值与岩石类型有关. 当深度取值为零时，可以求得岩石表面孔隙率，将式（30）转换为与ω₀有关的表达式为

(31) $ {\omega _h} = {\omega _0}\left( {1 - \frac{{{A_{\text{r}}}{h^{\rm{d}}}}}{{{\rho _{\text{r}}} - {B_{\text{r}}}}}} \right){\text{ = }}{\omega _0}\left( {1 - \mu {h^{\rm{d}}}} \right). $

将式中的A_r / (ρ_r − B_r)定义为裂隙分布不均匀系数μ，可以看出，不均匀系数越大，埋深处岩石孔隙率越低. 把式（19）、（29）、（31）代入式（28）可得考虑裂隙分布不均时的岩石冻结深度表达式为

(32) $ h_n^{\rm{d}} = \sqrt {\frac{{2SKD\left| {{T_{\text{w}}}} \right|}}{{L{\rho _{\rm{d}}}{\kappa _{\text{w}}}}}} {\left( {1 - {\omega _0}\frac{{{a_n}{b_n}}}{{{a_0}{b_0}}}\left( {1 - \eta h_{n - 1}^{\rm{d}}} \right)\exp {T_\kappa }} \right)^{ - 0.5}}. $

(33) $ {T_\kappa } = \exp \left( {1.2\left( {T - {T_0}+{T_0}\frac{{{\rho _{\text{w}}} - {\rho _{\text{i}}}}}{{{\rho _{\text{w}}}{\rho _{\text{i}}}L}}\left( {p - u} \right)} \right)} \right). $

由式（32）可以得到考虑岩石裂隙分布不均性的冻结岩石长度l_n ^d为

(34) $ l_n^{\text{d}} = \sqrt {\frac{{2SKD\left| {{T_{\text{w}}}} \right|}}{{L{\rho _{\rm{d}}}{\kappa _{\text{w}}}{{\sin }^2}\beta }}} {\left( {1 - {\omega _0}\frac{{{a_n}{b_n}}}{{{a_0}{b_0}}}\left( {1 - \eta h_{n - 1}^{\rm{d}}} \right)\exp {T_\kappa }} \right)^{ - 0.5}}. $

将式（6）、（27）和（34）代入式（3）得到冻融循环作用下倾倒式危岩体稳定性系数F_n的计算式为

(35) $ \begin{split} {F_n} =& {{\Bigg(}} {f_{{\text{k0}}}}\displaystyle\sum\limits_{k = 1}^m { \left({{\chi _k} \cos \left( {\frac{{\text{π} k}}{{2m}}} \right)} \right)} \frac{{1 - \left( {1+\displaystyle\sum\limits_1^i {q\Delta b_n^i} /b_0^i+\displaystyle\sum\limits_1^i {q\Delta a_n^i} /a_0^i} \right){\omega _0}}}{{1 - {\omega _0}}}\left( {\frac{{H - h}}{{\sin \beta }} - \sqrt {\frac{{SKD\left| {{T_{\text{w}}}} \right|{{\sin }^{ - 2}}\beta }}{{2L{\rho _{\rm{d}}}{\kappa _{\text{w}}}\left( {1 - {\kappa _n}} \right)}}} +\frac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right) \times \\ & \sqrt {\frac{{2SKD\left| {{T_{\text{w}}}} \right|{{\sin }^{ - 2}}\beta }}{{L{\rho _{\rm{d}}}{\kappa _{\text{w}}}\left( {1 - {\kappa _n}} \right)}}} +{f_{\text{c}}}\left( {\frac{{H - h}}{{\sin \beta }} - \sqrt {\frac{{2SKD\left| {{T_{\text{w}}}} \right|{{\sin }^{ - 2}}\beta }}{{L{\rho _d}{\kappa _{\text{w}}}\left( {1 - {\kappa _n}} \right)}}} } \right)\left( {\frac{{H - h}}{{2\sin \beta }} - \sqrt {\frac{{SKD\left| {{T_{\text{w}}}} \right|{{\sin }^{ - 2}}\beta }}{{2L{\rho _{\rm{d}}}{\kappa _{\text{w}}}\left( {1 - {\kappa _n}} \right)}}} +\frac{{e\sin \alpha }}{{\sin \left( {\beta - \alpha } \right)}}} \right)+Gc {{\Bigg)}} \times \\ & {{{\Bigg(}} \frac{{ - A \times {{10}^{27}}}}{{6{\text{π }}{{\left( {35 - 22\lg \left( {{T_0} - T} \right)} \right)}^3}}}\frac{h}{{\sin \beta }}\left( {\frac{{2H - h}}{{2\sin \beta }}+\frac{{e\sin \beta }}{{\sin \left( {\beta - \alpha } \right)}}} \right)+Qd {{\Bigg)}}^{ - 1}}. \\[-20pt] \end{split} $

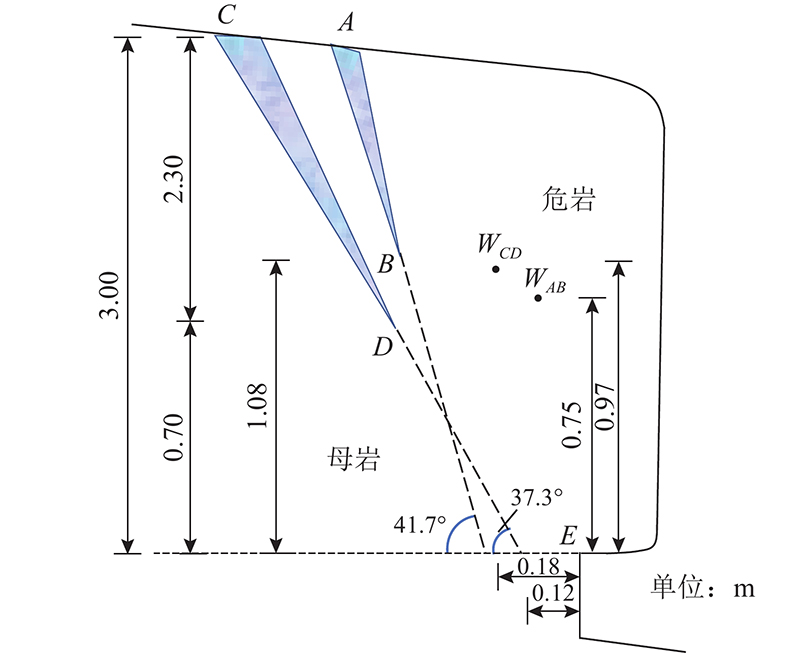
如图5所示为甘肃某倾倒式危岩体工程. 该危岩体所处地区冬季平均气温为263.55 K(−9.6 ℃)，抗震设防烈度为7度，设计基本地震加速度为0.15g，考虑岩土体覆盖、结构反应的放大系数，该地区水平地震力影响系数ξ=0.337 5. 该倾倒式危岩体离地4 m，自身高3 m，宽4.5 m，厚1.5 m，后缘岩体近似水平，整体呈板状，由厚层状砂砾岩组成，其中裂隙发育严重节理面平整，从危岩体顶部往下切割并形成贯通段. 如图6所示，该危岩体的稳定性主要由2条长度及倾角不一致的贯通裂隙控制. 分别计算并比较由结构面AB、CD控制的危岩体稳定性系数，判断危岩体是否出现倾覆破坏. 危岩体工程算例参数如表2所示. 岩石抗拉强度、弹性模量、泊松比、孔隙率、密度等岩石物理力学参数通过工程岩石试验获得，如气温、地震加速度的环境参数取自当地气象资料，岩石碎屑流失比根据岩石冻融质量损失试验获得.

将表2中参数值代入式（35），分别得到由结构面AB、CD控制的危岩体稳定性系数与冻融循环次数的演化曲线，如图7所示. 可以看出，2种结构面控制下的危岩体稳定性系数整体劣化趋势均为先快后缓. 根据文献[10]对不同类型危岩体的稳定性评价标准得出危岩体初始处于稳定态，经过50次冻融循环后二者的稳定性系数均低于临界值，危岩体从稳定状态进入失稳态. 在前20次冻融循环作用区间，由结构面AB控制的危岩体稳定性系数始终大于CD，随着冻融循环次数的增加，基于CD的稳定性系数大于AB. 在长期冻融循环作用下，影响危岩体稳定性的优势结构面会相互转化，须有针对性地采取危岩体加固措施.

改变上述倾倒式危岩体工程算例单一参数的控制变量法，分别讨论岩石初始孔隙率ω₀、冻结温度T以及碎屑流失比q对危岩体稳定性的影响. 本研究对由结构面AB控制的危岩体稳定性开展分析.

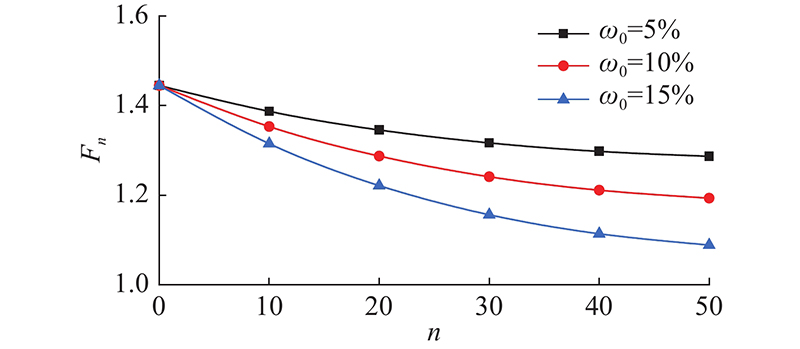
如图8所示为不同初始孔隙率对危岩体稳定性系数劣化的影响. 可以看出，随着冻融循环次数的增加，不同初始孔隙率的危岩体稳定性系数均减小，且初始孔隙率越大的曲线劣化幅度越大. 50次冻融循环后，初始孔隙率为5%、10%以及15%的危岩体稳定性系数分别下降10.96%、17.41%和24.66%. 这是由于岩石孔隙率越大，内部细观微裂隙等效尺寸越大，发生冻融时其半轴增量越大，导致危岩体劣化幅度显著.

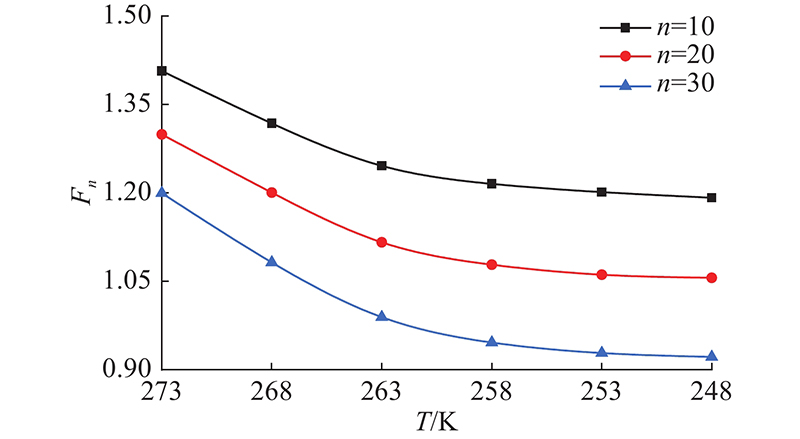
如图9所示为不同温度对危岩体稳定性系数的影响规律. 可以看出，危岩体稳定性系数随着温度的降低呈下降趋势. 当温度降至263 K时，不同冻融循环次数下的稳定性系数减小速率均明显放缓. 以冻融循环30次为例，当温度由268 K降至263 K时，稳定性系数下降8.6%，由263 K降至248 K时，下降6.8 %. 可见初期温度的降低对危岩体稳定性的影响更大. 因此，当环境温度处于[0，263] K时，在对寒区危岩体工程采取保温措施的效果显著.

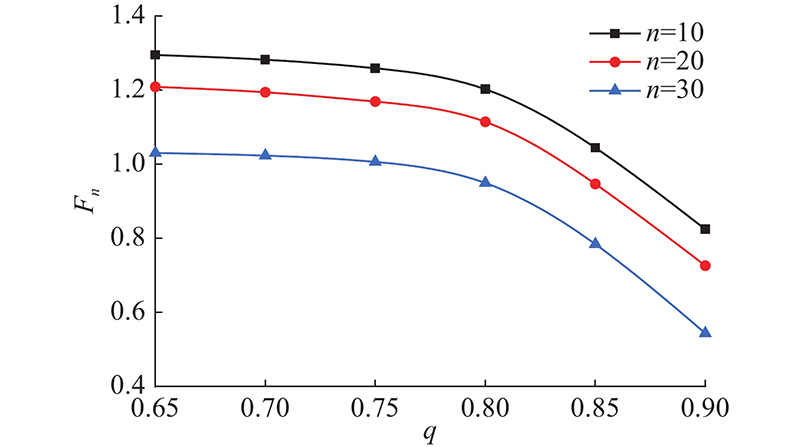
如图10所示为不同岩石碎屑流失比对危岩体稳定性系数的影响. 可以看出，当碎屑流失比低于0.8时，危岩体稳定性系数下降缓慢，当碎屑流失比超过0.8时，稳定性系数下降趋势显著. 当冻融循环为30次，碎屑流失比从0.65增至0.8时，稳定性系数下降0.02；从0.8增至0.9时，稳定性系数下降0.25. 冻融次数从10增加至20的危岩体稳定性减小幅度远小于冻融次数从20增至30的，这说明保持碎屑流失比至0.8能够提高寒区危岩体的长期冻融稳定性. 因此，在寒区工程中可以采用如注浆、封堵的措施来控制岩石碎屑流失比至合理值，以期满足工程的安全性和经济性.

（1）考虑岩石碎屑流失比和裂隙倾角影响，基于细观椭圆裂隙扩径模型推导的岩石抗拉强度劣化表达式，能够较好地预测冻融循环作用对抗拉强度的影响效果.

（2）利用线性回归后的岩石初始孔隙率修正传统Stephan冻结深度经验公式，能够有效地反映冻融循环作用下裂隙分布不均对危岩体冻结深度演化特性的影响.

（3）寒区倾倒式危岩体稳定性系数与温度和初始抗拉强度正相关，与碎屑流失比和初始孔隙率负相关. 当温度高于263.15 K (−10 ℃)、碎屑流失比低于0.8时，危岩体稳定性系数变化速率相较于其他工况更缓慢.

（4）寒区采取保温层、加固岩体、注浆充填、表面封堵等措施可以提高寒区危岩体的长期稳定性. 由于水−冰−岩相互作用机理较为复杂，寒区岩土工程存在尺寸效应，本研究对危岩体倾倒破坏的分析仍有局限性，后续将不断完善.