浙江大学学报(工学版)

浙江大学学报(工学版), 2022, 56(9): 1693-1703 doi: 10.3785/j.issn.1008-973X.2022.09.002

土木工程、交通工程

纤维织物增强高延性混凝土加固RC梁的受弯性能

张敏,, 邓明科,, 智奥龙, 宋诗飞, 陈晖

西安建筑科技大学 土木工程学院，陕西 西安 710055

Flexural behavior of RC beams strengthened by textile-reinforced highly ductile concrete

ZHANG Min,, DENG Ming-ke,, ZHI Ao-long, SONG Shi-fei, CHEN Hui

School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China

通讯作者: 邓明科, 男, 教授. orcid.org/0000-0002-9117-4625. E-mail: dengmingke@126.com

收稿日期: 2021-08-27  

基金资助: 国家自然科学基金资助项目(51878545); 西安市科技创新计划项目(20191522415KYPT015JC017)

Received: 2021-08-27  

Fund supported: 国家自然科学基金资助项目(51878545);西安市科技创新计划项目(20191522415KYPT015JC017)

作者简介 About authors

张敏（1992―），女，博士生，从事土木工程新材料研究.orcid.org/0000-0002-2460-3493.E-mail：zhang_miner@126.com , E-mail：zhang_miner@126.com

摘要

为了提高钢筋混凝土（RC）梁的受弯承载力，采用纤维织物增强高延性混凝土（TRHDC）对RC梁进行受弯加固，设计2个对比试件和8个TRHDC加固试件. 通过四点弯曲试验，研究纵筋配筋率、织物层数和持载水平对RC梁受弯性能的影响. 试验结果表明：TRHDC加固梁均发生纵筋屈服、织物被拉断、受压区混凝土被压碎的弯曲破坏；纵筋配筋率为0.93%的TRHDC加固梁在纵筋与混凝土界面出现脱黏裂缝. 与RC梁相比，TRHDC加固使梁的开裂荷载、屈服荷载和峰值荷载显著提高，最大提高幅度分别为1.61倍、65.9%和39.2%，裂缝发展被有效限制，但RC梁的位移延性系数降低2.6%~74.5%. 增加织物层数将使加固梁的屈服荷载和峰值荷载的提高幅度非线性增加，该变化与纵筋配筋率有关；当持载水平由对比梁屈服荷载的50%升至80%时，加固梁的屈服荷载减小8.6%，峰值荷载及相应挠度分别增大3.2%和13.9%. 提出TRHDC加固层滞后应变和TRHDC加固梁受弯承载力的计算方法，所得计算结果与试验结果吻合良好.

关键词： 纤维织物增强高延性混凝土(TRHDC) ; 钢筋混凝土(RC)梁 ; 受弯加固 ; 二次受力 ; 受弯承载力

Abstract

Textile-reinforced highly ductile concrete (TRHDC) was used to strengthen the reinforced concrete (RC) beams, to improve the flexural capacity of RC beams. Two control beams and eight TRHDC-strengthened beams were designed. And the effect of the longitudinal reinforcement ratio, the number of textile layers, and the level of sustained load on the flexural behavior of RC beams were investigated using the four-point bending test. Experimental results showed that TRHDC-strengthened beams failed in flexural with the longitudinal reinforcement yielding, textile fracturing, and compressive concrete crushing. The debonding cracks at the surface between the longitudinal rebar and the concrete were observed in TRHDC-strengthened beams with a longitudinal reinforcement ratio of 0.93%. Compared with RC beams, TRHDC strengthening method significantly improved the cracking load, yielding load, and peak load of beams, with the highest increase rates reaching 1.61 times, 65.9%, and 39.2%, respectively. Furthermore, this method effectively limited the development of cracks while decreasing the displacement ductility index of RC beams in the range of 2.6%-74.5%. The improvement in the yielding load and peak load of the strengthened beam nonlinearly increased with the number of textile layers, which depends on the longitudinal reinforcement ratio. When the sustained load level increased from 50% to 80% of the yielding load of the control beam, the yielding load of the strengthened beam was decreased by 8.6%, and the peak load and the corresponding deflection were increased by 3.2% and 13.9%, respectively. The calculation method for the lag strain of the TRHDC strengthening layer and the flexural capacity of TRHDC-strengthened beams was proposed, and the results was in good agreement with the experimental results.

Keywords： textile-reinforced highly ductile concrete(TRHDC) ; reinforced concrete (RC) beam ; flexural strengthening ; secondary load ; flexural capacity

PDF (2049KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张敏, 邓明科, 智奥龙, 宋诗飞, 陈晖. 纤维织物增强高延性混凝土加固RC梁的受弯性能. 浙江大学学报(工学版)[J], 2022, 56(9): 1693-1703 doi:10.3785/j.issn.1008-973X.2022.09.002

ZHANG Min, DENG Ming-ke, ZHI Ao-long, SONG Shi-fei, CHEN Hui. Flexural behavior of RC beams strengthened by textile-reinforced highly ductile concrete. Journal of Zhejiang University(Engineering Science)[J], 2022, 56(9): 1693-1703 doi:10.3785/j.issn.1008-973X.2022.09.002

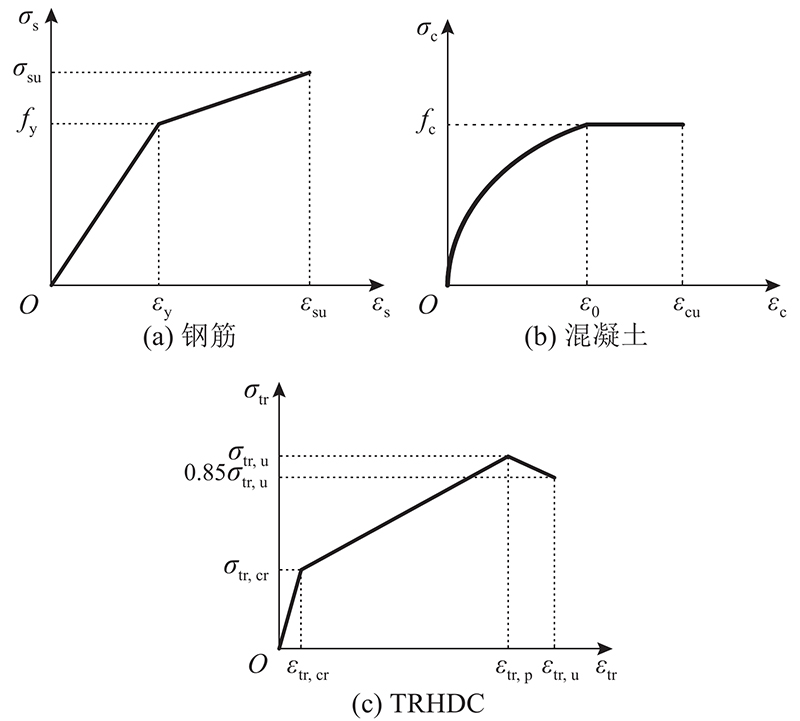
建筑材料老化、结构服役时间增长和环境侵蚀等引起的性能退化，使用功能改变和使用荷载增加，使钢筋混凝土结构（reinforced concrete, RC）加固与修复的需求日益增长. 纤维织物增强砂浆（textile reinforced mortar, TRM）加固技术受到学术界越来越多的关注. TRM是将多向纤维织物嵌入精细混凝土中的新型复合材料[1-2]，具有高强、限裂及耐腐蚀性能[3-5]. TRM薄层加固技术不仅可以改善由传统加固方式（如钢筋混凝土增大截面法、粘钢法）带来的自重较大、施工复杂的问题[6-7]，还可以克服外贴纤维增强复合材料（fiber-reinforced polymer, FRP）技术的抗火性能差、在高温或者潮湿环境下的脱黏问题、有机胶的有毒性等不足[8-9].

D'ambrisi等[10]采用不同织物种类和不同砂浆类型的TRM加固RC梁，结果表明：TRM可以有效提高梁的受弯性能，同时织物种类和砂浆类型对加固梁的弯曲破坏模式有很大影响. Escrig等[11]对TRM加固RC梁受弯性能的研究结果表明：加固梁受弯承载力的提高幅度取决于砂浆类型、织物几何形状和织物层数. Raoof等[12]研究了织物表面处理情况、TRM层数、织物种类和端部锚固措施对TRM加固RC梁受弯性能的影响. Yin等[13-16]研究了不同形式加固方式、不同损伤程度[14]以及织物不同表面处理情况对纤维织物增强混凝土（textile reinforced concrete, TRC）加固RC梁受弯性能的影响，还研究了TRC加固受弯构件的正截面承载性能.

上述研究均表明TRM是有效的受弯加固RC梁的复合材料，但织物利用率低、裂缝宽度大以及受拉脆性破坏等问题仍需改进方法以解决[17]. 目前，Wei等[18-19]研究了在基体中掺加短纤维以改善TRM的受力性能. Hinzen等[20]的研究表明：掺入芳纶、聚乙烯醇(polyvinyl alcohol, PVA)短纤维能显著提高TRC的开裂强度和抗拉强度. Barhum等[21]的研究表明：掺加短玻璃纤维和短碳纤维能显著提高织物与基体的界面性能，从而提高TRC的拉伸性能. 沈玲华等[22]的研究表明：掺入短碳纤维和钢纤维能有效改善TRC的裂缝分布，使裂缝宽度和间距显著减小. 可见，短纤维的掺入是有效改善TRM拉伸与弯曲性能的方式.

高延性混凝土（highly ductile concrete, HDC）是具有受拉应变硬化和多裂缝开展特性的纤维增强水泥基复合材料[23-25]. 本研究提出将碳纤维织物嵌入HDC中的新型复合材料，即纤维织物增强高延性混凝土(textile reinforced highly ductile concrete, TRHDC)[17,26]，用于RC梁的受弯加固. 在实际工程中，作用在RC梁上的荷载通常难以完全卸载，导致加固层应变滞后，即存在二次受力问题. 关于持载水平对加固效果影响的研究开展较少. 本研究通过不同纵筋配筋率、织物层数和持载水平的TRHDC加固RC梁受弯性能试验，分析加固梁的受弯性能，提出TRHDC加固层滞后应变及受弯承载力计算方法，为TRHDC的加固应用提供理论依据.

1. 受弯试验概况

1.1. 试件设计及制作

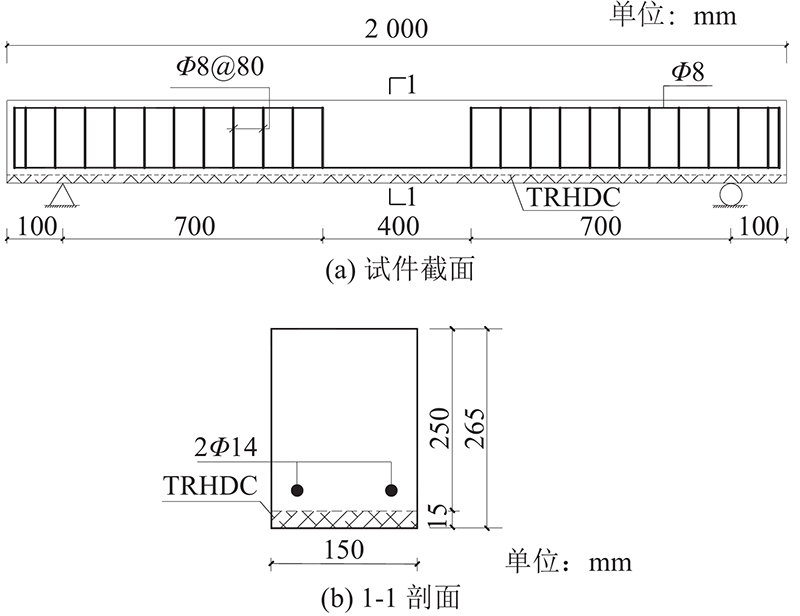
为了研究纵筋配筋率、织物层数和持载水平对TRHDC加固RC梁受弯性能的影响，试验设计并制作10个梁试件. 对比试件的截面尺寸为150 mm×250 mm，加固试件均为受拉区薄层加固，加固面层厚度为15 mm，纤维织物分为1、2和3层. 混凝土设计强度等级为C35；纵筋、架立筋和箍筋均采用HRB400级钢筋；纵筋配筋率共2种，分别为0.93%和1.55%；对应的纵向受拉钢筋为2Φ14 mm和2Φ18 mm. 箍筋和架立筋仅配置在剪跨区段，分别为Φ8@80 mm和2Φ8 mm. 各试件设计参数见表1。表中，ρs为纵筋配筋率；L为织物层数；SL表示持载水平，其为对比试件B5屈服荷载的50%或80%. 以试件B2为例，试件截面尺寸及配筋如图1所示.

表 1   梁试件设计参数

Tab.1  Parameters of beam specimens

试件编号 纵向受拉钢筋/mm ρs/% 加固材料 SL/%
L 基体
B1 2Φ14 0.93 — — —
B2 2Φ14 0.93 1 HDC —
B3 2Φ14 0.93 2 HDC —
B4 2Φ14 0.93 3 HDC —
B5 2Φ18 1.55 — — —
B6 2Φ18 1.55 1 HDC —
B7 2Φ18 1.55 2 HDC —
B8 2Φ18 1.55 3 HDC —
B9 2Φ18 1.55 2 HDC 50
B10 2Φ18 1.55 2 HDC 80

新窗口打开| 下载CSV


图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   纤维织物增强高延性混凝土加固试件截面尺寸及配筋图

Fig.1   Dimension and reinforcement of textile reinforced highly ductile concrete strengthened specimen


加固梁分为无初始受力加固梁和持载加固梁. 原梁养护28 d后，对其受拉区进行凿毛、冲刷，再进行抹面加固，步骤如下. 1）在梁的两侧放置木板，使用夹具固定，保持木板边缘和梁齐平. 2）在混凝土表面按压式均匀涂抹第1层HDC面层为6~7 mm（1层纤维织物）或4~5 mm（2或3层纤维织物）；铺设纤维织物，使用6 mm（1层纤维织物）或4 mm（2或3层纤维织物）木条将纤维织物固定在两侧木板上. 3）在1层的纤维织物上涂抹第2层面层为6~7 mm的HDC，控制总面层厚度为15 mm. 4）在多层的纤维织物上涂抹第2层面层为2~3 mm的HDC；铺设纤维织物，使用2 mm木条将纤维织物固定在两侧木板上. 5）对于3层的纤维织物，重复步骤4）. 6）在纤维织物上涂抹面层为4~5 mm的HDC，控制总面层厚度为15 mm. 7）将加固层表面均匀抹平. 通过以上步骤得到无初始受力加固梁. 将原梁加载至对比试件B5屈服荷载的50%或80%，再进行持载加固得到持载加固梁，界面处理及加固步骤与一次加固梁相同. 在养护过程中，对持载加固梁实时监测荷载和挠度.

1.2. 材料性能

1.2.1. 纤维织物

如图2所示，试验采用的纤维织物为正交的双向碳纤维织物，织物的网格尺寸为20 mm×20 mm. 为了得到较好的整体受力性能，碳纤维织物表面采用环氧浸渍织物力学性能见表2.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   碳纤维织物

Fig.2   Carbon textile


表 2   碳纤维织物力学性能指标

Tab.2  Mechanical characteristics of carbon textile

参数 数值 参数 数值
网格间距sct/mm 20 密度ρct/(g·cm−3) 1.74
抗拉强度fct,t/MPa 3600 束截面积Act,0/mm2 0.94
弹性模量Ect/GPa 230 伸长率λct/% 1.5
单束承载力Fct,0/N 3200 — —

新窗口打开| 下载CSV


1.2.2. HDC

试验采用的HDC主要由水泥、粉煤灰、矿粉、硅灰、砂子、高效减水剂、水和PVA短纤维组成. PVA短纤维的体积分数为1.5%，其各项力学性能指标见表3. 采用100 mm×100 mm×300 mm的棱柱体试块测得HDC的轴心抗压强度平均值为54.1 MPa. 采用350 mm×50 mm×15 mm的狗骨形试件测得HDC的开裂强度为4.16 MPa，抗拉强度和拉伸应变分别为4.24 MPa、0.6%。采用40 mm×40 mm×160 mm的棱柱体试块测得HDC的抗折强度为12.04 MPa，等效弯曲强度和等效弯曲韧性分别为8.32 MPa、80 kJ/m3.

表 3   PVA短纤维各项力学性能指标

Tab.3  Performance indicators of short PVA fibers

参数 数值 参数 数值
纤维类型 PVA 弹性模量Ef/GPa 40
直径Df/μm 39 密度ρf/(g·cm−3) 1.3
长度Lf/mm 12 伸长率λf/% 7
抗拉强度ff,t/MPa 1600 — —

新窗口打开| 下载CSV


1.2.3. TRHDC

为了减小试件尺寸对TRHDC单轴拉伸性能的影响，根据文献[27]、[28]对TRM拉伸试件尺寸的要求，采用尺寸为350 mm×50 mm×15 mm的狗骨形试件，其中标距段长为150 mm，如图3所示. 为了防止发生标距段以外的过早破坏，试件两端均采用100 mm×50 mm的碳纤维布双面加固.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

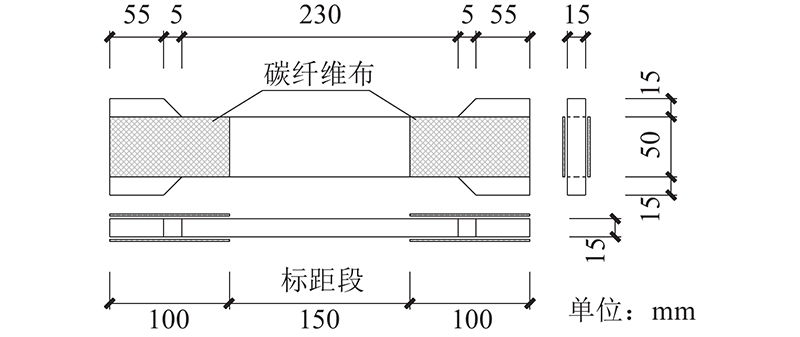
图 3   纤维织物增强高延性混凝土拉伸试件尺寸

Fig.3   Dimensions of textile reinforced highly ductile concrete tensile specimen


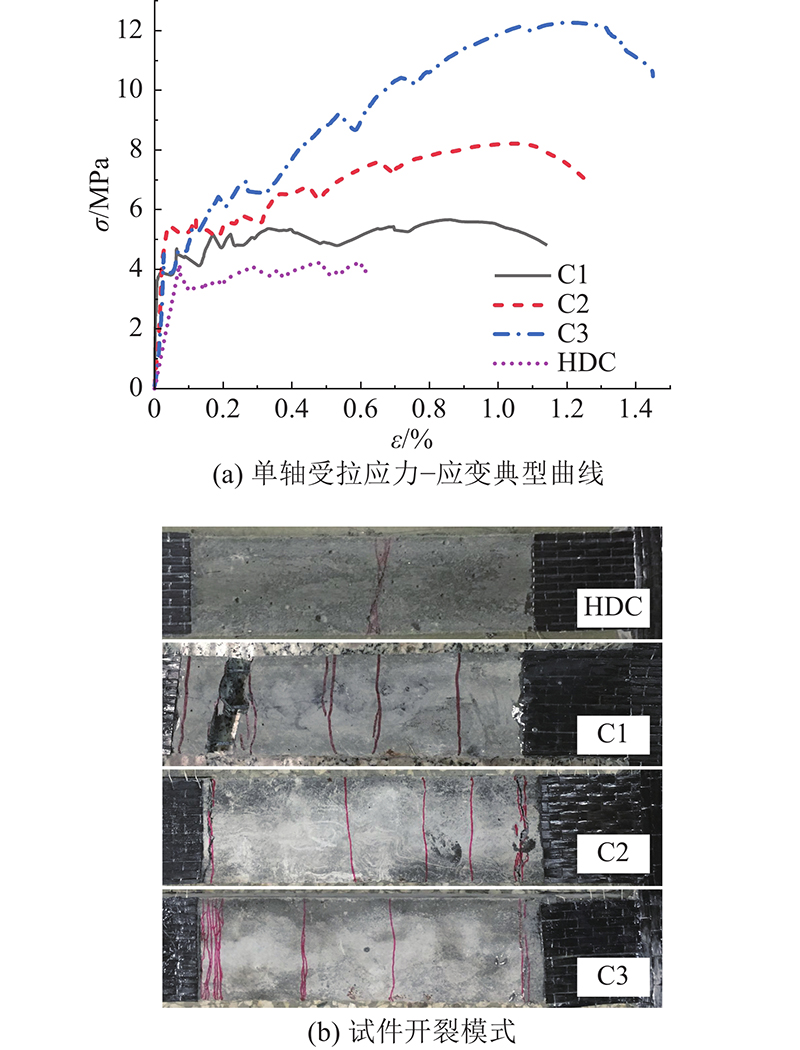
10 t万能试验机按位移控制加载，加载速率为0.2 mm/min，测得1层织物TRHDC的抗拉强度平均值为5.67 MPa，2、3层织物TRHDC的抗拉强度平均值分别为8.21 MPa和12.27 MPa，其单轴受拉应力−应变曲线和开裂模式如图4所示. 图中， $ \varepsilon $为应变， $ \sigma $为应力，C1、C2和C3分别表示1、2和3层织物的TRHDC. 可以看出，TRHDC的破坏呈现多裂缝开展模式.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   高延性混凝土与纤维织物增强高延性混凝土单轴受拉应力−应变典型曲线和开裂模式

Fig.4   Stress-strain curves and crack pattern of highly ductile concrete and textile reinforced highly ductile concrete specimen


1.2.4. 混凝土和钢筋

100 mm×100 mm×100 mm试块测得混凝土立方体抗压强度平均值fcu,m= 49.8 MPa，混凝土轴心抗压强度平均值fc,m= ${0.76{f_{\text{cu,m}}}}/ {1.05}$=35.8 MPa. 试验测得钢筋的力学性能指标见表4。表中，D为钢筋直径，fy为钢筋屈服强度，σsu为钢筋极限强度.

表 4   钢筋的力学性能

Tab.4  Mechanical properties of reinforcement

钢筋类型 D/mm fy/MPa σsu/MPa
HRB400 8 432 612
HRB400 14 430 592
HRB400 18 430 605

新窗口打开| 下载CSV


1.3. 加载装置与量测

试验在100 t电液伺服万能试验机上完成，采用两点对称加载方式，按位移控制加载，加载速率为0.2 mm/min. 如图5所示为受弯试验加载装置与量测详图. 为了量测混凝土应变，在梁跨水平居中位置沿高度方向均匀布置混凝土应变片；为了量测纵向受拉钢筋的应变，在梁跨中和加载点处布置钢筋应变片；为了量测纤维织物拉应变，在梁跨水平居中位置及距梁跨中水平居中位置40、80 mm处布置应变片；为了量测梁的挠度，在跨中、加载点以及支座处布置位移传感器. 采用梁式构件持载加固用试验装置[29]对原梁进行持载加固. 该装置利用螺杆的张拉变形以及力传感器在荷载作用下的数值变化，实现二次受力试验中构件的持载加固. 试验过程中，梁表面裂缝的出现和发展情况由人工观测得到.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   受弯试验加载装置与量测

Fig.5   Loading device and measurement of flexural tests


2. 试验结果及分析

2.1. 试验现象及破坏形态

2.1.1. 试验现象

引入参数Pm，表示试件的峰值荷载. 各试件的裂缝分布及破坏形态如图6所示，破坏过程如下.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   梁试件裂缝分布及破坏形态

Fig.6   Cracks distribution and failure pattern of beam specimens


1）对比试件. 在加载初期，试件B1处于弹性阶段. 当荷载增加至17.15 kN（17.84%Pm）时，B1的跨中受拉区出现第1条竖向裂缝. 随着荷载增大，竖向裂缝数量逐渐增多，裂缝宽度不断变大，并向上延伸. 当加载至73.14 kN（76.07%Pm）时，纵向受拉钢筋屈服. 继续加载，裂缝宽度和试件挠度快速增大. 当加载至96.15 kN时，B1达到峰值荷载，受压区混凝土压碎，梁失去承载能力. 与B1相比，B5的纵筋配筋率较大，其裂缝数量较少、裂缝宽度较小.

2）TRHDC加固试件. 当荷载加至37.74 kN（34.40%Pm）时，加固B2的纯弯段TRHDC层出现第1条竖向裂缝. 随着荷载增大，B2加固层的裂缝数量逐渐增多，裂缝分布细密，部分加固层裂缝向上延伸至混凝土，并不断扩展. 当加载至96.57 kN（88.01%Pm）时，纵筋达到屈服荷载. 继续加载，裂缝数量基本不变，裂缝发展和挠度增长较B1缓慢. 主要原因是碳纤维织物的弹性模量较大，同时TRHDC承担部分弯矩. 当加载至109.72 kN时，试件达到峰值荷载，织物被拉断，荷载突降至97.82 kN（89.15%Pm），之后荷载基本不变，挠度快速增大，纵筋与混凝土间出现脱黏裂缝，受压区混凝土被压碎并不断剥落，试件破坏. 加固试件B3、B4和B6的破坏过程与B2基本一致，纵筋与混凝土间均出现纵向脱黏裂缝，在混凝土与HDC、HDC与织物界面处均未出现脱黏裂缝. 与B2不同，B7、B8、B9和B10在接近峰值荷载时，织物被拉断；达到峰值荷载时，受压区混凝土被压碎，试件破坏；在纵筋与混凝土、混凝土与HDC、HDC与织物的界面处均未出现脱黏现象.

2.1.2. 破坏形态

对比试件B1、B5均发生典型的适筋破坏. 加固试件B2、B3、B4和B6发生纵筋屈服、织物拉断且受压区混凝土压碎破坏，受拉区混凝土沿纵筋位置出现脱黏裂缝，HDC与混凝土、HDC与织物的界面均未出现脱黏裂缝. 加固试件B7、B8、B9和B10发生纵筋屈服、织物拉断且受压区混凝土压碎破坏，未出现剥离现象.

与对比试件相比，加固试件的裂缝发展缓慢、裂缝数量增多、裂缝宽度和间距减小，且加固层裂缝较原梁细密. 可见，TRHDC受拉区加固可以有效限制梁裂缝的扩展. 随着织物层数增加，纯弯段裂缝数量逐渐增多，裂缝宽度和间距不断减小，加固层裂缝开展更为细密. 对于较小纵筋配筋率的加固试件，裂缝开展较充分，裂缝数量较多，裂缝宽度较小，破坏具有较好的可预见性. 与加固试件B7相比，持载加固试件B9、B10的加固层裂缝发展较不充分，裂缝数量较少，主要原因是受到应变（应力）滞后的影响.

2.2. 荷载−挠度曲线

所有试件的加载过程均可分为弹性阶段、裂缝开展阶段和破坏阶段. 在试件开裂前，荷载−挠度曲线呈直线. 随着荷载增大，受拉区混凝土或TRHDC开裂，荷载−跨中挠度曲线出现第1次转折，试件进入裂缝开展阶段；随着裂缝不断出现和发展，试件的刚度逐渐降低. 对于对比试件，继续加载，受压区混凝土被压碎，试件进入破坏阶段，荷载快速下降至低于85%Pm. 对于配筋率为0.93%的加固试件，随着荷载增大，织物被拉断，荷载陡降至峰值荷载的82%~92%，试件进入破坏阶段；继续加载，荷载基本不变，挠度快速增大；最终，受压区混凝土被压碎，试件破坏. 对于配筋率为1.55%的加固试件，临近峰值荷载时，织物被拉断；达到峰值荷载时，受压区混凝土被压碎，试件进入破坏阶段. 如图7所示为各试件的荷载−跨中挠度曲线. 图中，F为荷载，Δ为跨中挠度.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   梁试件的荷载−挠度曲线

Fig.7   Load-deflection curves of beam specimens


与对比试件相比，加固试件的屈服荷载提高，且随织物层数的增加而增大. 主要原因是TRHDC加固层有效地延缓了主裂缝的扩展，提高了梁的整体刚度；随着织物层数增加，织物承担的拉应力逐渐增大，梁屈服荷载不断提高. 在相同纵筋配筋率下，随着织物层数增加，加固试件的峰值荷载逐渐增大，峰值荷载对应的跨中挠度不断减小. 随着纵筋配筋率增大，相同织物层数的加固试件峰值荷载的提高幅度减小.

对于持载加固试件B9、B10，先将原梁加载至屈服荷载的50%（60 kN）和80%（96 kN），再进行持载加固. 因此，在相应荷载之前，B9、B10与对比试件B5的荷载−挠度曲线重合，其刚度较B5的大. 主要原因是TRHDC加固层限制了裂缝的扩展，并承担了一部分拉力. 随着持载水平提高，持载加固试件的刚度比无初始受力的加固试件B7低，且挠度均大于B7. 可见，持载水平越高，刚度越低，挠度越大. 持载加固试件的屈服荷载随着持载水平的提高而降低，原因是较大的初始受力水平使原梁受拉纵筋的初始拉应变（应力）较大，导致加固层较高的应变（应力）滞后，使得加固层在峰值荷载之前的利用率偏低. 持载水平对发生织物拉断的受弯破坏加固梁峰值荷载的影响较小. 主要原因是在达到峰值荷载时，织物均被拉断，即加固层利用率相同.

2.3. 承载力分析

将各试件的开裂荷载 $ {P_{{\text{cr}}}} $，纵筋屈服荷载 $ {P_{\text{y}}} $，峰值荷载 $ {P_{\text{m}}} $，极限荷载 $ {P_{\text{u}}} $及相应的跨中挠度Δcr、Δy、Δm、Δu的试验值汇总于表5. 表中，极限点为荷载下降至85%Pm所对应的点； $ {P}_{\text{m},\text{0}} $代表对比试件B1、B5的峰值荷载； ${\rm{\mu}} $为位移延性系数；破坏形态A表示典型的适筋破坏，破坏形态B表示织物拉断、受压区混凝土压碎、受拉区混凝土沿纵筋剥离，破坏形态C表示织物拉断且受压区混凝土压碎.

表 5   梁试件受弯试验的主要结果

Tab.5  Major results of flexural tests of beam specimens

试件编号 开裂点 纵筋屈服点 峰值点 极限点 $\dfrac{ { {P_{\text{m} } } }}{ { {P_{ {\text{m,0} } } } } }$ $ \mu $ 破坏形态
$ {P_{{\text{cr}}}} $/ kN Δcr/ mm $ {P_{\text{y}}} $/ kN Δy/ mm $ {P_{\text{m}}} $/ kN Δm/ mm $ {P_{\text{u}}} $/ kN Δu/ mm
B1 17.15 1.13 73.14 6.11 96.15 41.40 81.73 41.98 — 6.87 A
B2 37.74 1.79 96.57 5.74 109.72 12.17 93.26 38.41 1.141 6.69 B
B3 37.83 1.70 111.38 7.22 118.79 11.60 100.97 39.80 1.235 5.51 B
B4 36.05 1.54 121.31 7.29 133.87 11.46 113.79 12.73 1.392 1.75 B
B5 18.75 0.94 145.64 7.77 164.10 31.39 139.49 36.29 — 4.67 A
B6 40.61 1.37 160.89 7.80 175.52 13.48 149.19 33.00 1.070 4.23 B
B7 43.97 1.37 174.82 8.62 183.64 13.26 156.09 25.64 1.119 2.97 C
B8 48.97 1.67 177.94 8.67 194.30 12.64 165.16 20.47 1.184 2.36 C
B9 — — 160.92 7.32 187.66 14.13 159.51 23.36 1.143 3.19 C
B10 — — 147.14 6.79 193.72 16.09 164.66 19.41 1.180 2.86 C

新窗口打开| 下载CSV


与B1、B5相比，相应加固试件的开裂荷载提高1.17~1.61倍. 主要原因是1）加固试件的截面高度较大；2）TRHDC与原梁协同受力，分担部分截面弯矩；3）TRHDC的开裂强度较普通混凝土高，且TRHDC限制了受拉区混凝土开裂.

与试件B1相比，加固试件B2、B3和B4的屈服荷载分别提高32.0%、52.3%和65.9%；与试件B5相比，加固试件B6、B7和B8的屈服荷载分别提高10.5%、20.0%和22.2%. 可见，随着织物层数增加，加固试件的屈服荷载提高幅度非线性增大，提高幅度与纵筋配筋率有关.

与试件B1相比，加固试件B2、B3和B4的峰值荷载分别提高14.1%、23.5%和39.2%；与试件B5相比，加固试件B6、B7和B8的峰值荷载分别提高7.0%、11.9%和18.4%. 由于织物均被拉断，随着织物层数增加，相同纵筋配筋率加固试件的峰值荷载提高幅度非线性增大. 相同织物层数下，随着纵筋配筋率增大，加固试件峰值荷载的提高幅度减小. 主要原因是适筋梁的受弯承载力由混凝土强度和纵筋配筋率控制，纵筋配筋率越大，受拉区加固后，受弯承载力提高幅度越小.

与试件B5相比，无初始受力加固试件B6、持载加固试件B9和B10的屈服荷载分别提高20.0%、10.5%和1.0%，峰值荷载分别提高11.9%、14.4%和18.0%. 可见，随着持载水平提高，加固梁屈服荷载的提高幅度减小. 主要原因是初始受力水平提高导致滞后应变（应力）程度增大，使加固层作用减小. 持载水平对发生织物拉断的受弯破坏加固梁峰值荷载的影响较小，原因是在达到峰值荷载时，织物均被拉断，即加固层利用率相同.

2.4. 变形分析

位移延性系数为极限位移与屈服位移之比，表征梁试件的延性. 对比试件B1、B5具有良好的塑性变形能力，位移延性系数分别为6.87、4.67. 采用TRHDC薄层加固试件受拉区，试件的峰值挠度和延性均降低.

与试件B1相比，加固试件B2、B3和B4的峰值挠度分别降低70.6%、72.0%和72.3%，位移延性系数分别降低2.6%、19.8%和74.5%；与试件B5相比，加固试件B6、B7和B8的峰值挠度分别降低57.1%、57.8%和59.7%，位移延性系数分别降低9.4%、36.4%和49.5%. 可见，随着织物层数增加，相同纵筋配筋率加固试件的峰值挠度变化不大，位移延性系数不断减小. 在竖向荷载作用下，TRHDC面层和纵向受拉钢筋共同提供拉应力，即TRHDC的作用与纵向受拉钢筋类似. 随着织物层数增加，梁的塑性变形能力越来越差，因此位移延性系数不断减小.

持载加固试件B9、B10的峰值挠度分别为对比试件B5的45.0%和51.3%. 可见，随着持载水平提高，加固试件的峰值挠度增大. 这主要是由于较大的滞后应变（应力）导致在峰值荷载以前的加固层利用率较低.

3. 受弯承载力计算

3.1. 基本假定

1）正截面的应变分布符合平截面假定；2）不考虑普通混凝土的抗拉作用；3）TRHDC与混凝土间黏结良好，即不考虑两者间的滑移.

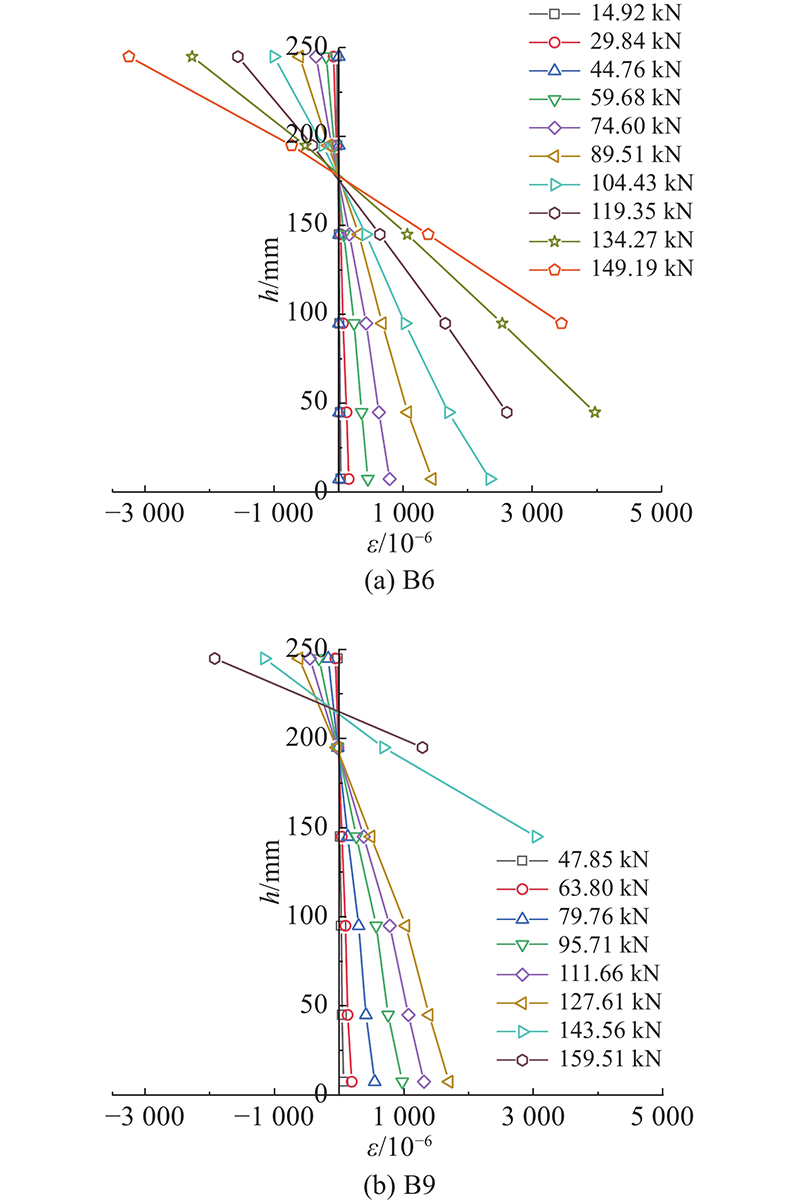
3.2. 平截面假定的验证

如图8所示，以B6、B9为例的截面应变沿梁高呈线性分布，符合平截面假定. 图中，h为截面高度， $ \varepsilon $为混凝土应变，缺失的点是部分应变片在混凝土开裂后失效导致的. 可知，TRHDC与混凝土间的应变连续，即无需考虑两者间的滑移.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   纤维织物增强高延性混凝土加固梁截面应变沿梁高分布

Fig.8   Strain distribution of cross-section along beam depth in textile reinforced highly ductile concrete-strengthened beams


3.3. 材料本构模型的选取

3.3.1. 钢筋

如图9（a）所示，钢筋的拉伸本构模型采用双线性强化应力−应变关系[30-31]，表达式为

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   钢筋、混凝土和纤维织物增强高延性混凝土的应力−应变曲线

Fig.9   Tensile stress-strain curves of rebar, concrete and textile  reinforced  highlyductile concrete


$ {\sigma _{\text{s}}} = \left\{ \begin{gathered} {E_{\text{1}}}{\varepsilon _{\text{s}}},\quad\qquad\qquad 0 < {\varepsilon _{\text{s}}} \leqslant {\varepsilon _{\text{y}}}; \\ {f_{\text{y}}}+{E_2}\left( {{\varepsilon _{\text{s}}} - {\varepsilon _{\text{y}}}} \right),{\text{ }}{\varepsilon _{\text{y}}} < {\varepsilon _{\text{s}}} \leqslant {\varepsilon _{{\text{su}}}}. \\ \end{gathered} \right. $

式中：σs为钢筋拉应力，εs为钢筋拉应变， $ {E_{\text{1}}} $为钢筋弹性段的弹性模量， $ {E_2} $为钢筋强化段的弹性模量， $ {\varepsilon _{\text{y}}} $为钢筋屈服应变， $ {\varepsilon _{{\text{su}}}} $为钢筋极限应变， $ {f_{\text{y}}} $为钢筋屈服强度， $ {\sigma _{{\text{su}}}} $为钢筋极限强度.

3.3.2. 混凝土

如图9（b）所示，在单轴受压时，混凝土的应力−应变曲线由二次抛物线和水平线组成[32]，表达式为

$ {\sigma }_{\mathrm{c}}=\left\{\begin{array}{l}{f}_{\text{c}}\left(2\left({{\varepsilon }_{\text{c}}}/{{\varepsilon }_{0}}\right)-{\left({{\varepsilon }_{\text{c}}}/{{\varepsilon }_{0}}\right)}^{2}\right)\text{，}0 \leqslant {\varepsilon }_{c}\leqslant {\varepsilon }_{0}\text{；}\\ {f}_{\text{c}}\text{，}\;\;\qquad\qquad\qquad\qquad{\varepsilon }_{0} < {\varepsilon }_{c}\leqslant {\varepsilon }_{\mathrm{cu}}.\end{array} \right.$

式中：σc为混凝土压应力，εc为混凝土压应变， $ {f_{\text{c}}} $为混凝土抗压强度， $ {\varepsilon _0} $为混凝土峰值压应变， $ {\varepsilon _{{\text{cu}}}} $为混凝土极限压应变.

3.3.3. TRHDC

如图9（c）所示，TRHDC的单轴受拉本构模型采用理想三线型模型[26]，表达式为

$ {\sigma _{{\text{tr}}}} = \left\{ \begin{array}{l} {E_{{\text{tr,1}}}}{\varepsilon _{{\text{tr}}}},\;\;0 < {\varepsilon _{{\text{tr}}}} \leqslant {\varepsilon _{{\text{tr,cr}}}}, \;\;{E_{{\text{tr,1}}}} = {{{\sigma _{{\text{tr,cr}}}}}/{\varepsilon _{{\text{tr,cr}}}}}; \\ {E_{{\text{tr,2}}}}\left( {{\varepsilon _{{\text{tr}}}} - {\varepsilon _{{\text{tr,cr}}}}} \right) + {\sigma _{{\text{tr,cr}}}},\;\;{\varepsilon _{{\text{tr,cr}}}} <{\varepsilon _{{\text{tr}}}} \leqslant {\varepsilon _{{\text{tr,p}}}},\\ \qquad{E_{{\text{tr,2}}}} = \dfrac{{{\sigma _{{\text{tr,u}}}} - {\sigma _{{\text{tr,cr}}}}}}{{{\varepsilon _{{\text{tr,p}}}} - {\varepsilon _{{\text{tr,cr}}}}}}; \\ {E_{{\text{tr,3}}}}\left( {{\varepsilon _{{\text{tr}}}} - {\varepsilon _{{\text{tr,p}}}}} \right) + {\sigma _{{\text{tr,u}}}}{\text{ }},\;\;{\varepsilon _{{\text{tr,p}}}} < {\varepsilon _{{\text{tr}}}} \leqslant {\varepsilon _{{\text{tr,u}}}},\\ \qquad{E_{{\text{tr,3}}}} = \dfrac{{{\sigma _{{\text{tr,u}}}} - 0.85{\sigma _{{\text{tr,u}}}}}}{{{\varepsilon _{{\text{tr,p}}}} - {\varepsilon _{{\text{tr,u}}}}}}. \end{array} \right.$

式中： ${\varepsilon _{{\text{tr}},{\text{cr}}}}$为TRHDC的开裂应变， ${\sigma _{{\text{tr}},{\text{cr}}}}$为TRHDC的开裂应力， ${\varepsilon _{{\text{tr}},\text{p}}}$为TRHDC的峰值拉应变， ${\varepsilon _{{\text{tr}},\text{u}}}$为TRHDC的极限拉应变， ${\sigma _{{\text{tr}},\text{u}}}$为TRHDC的抗拉强度， ${E_{{\text{tr}},1}}$为弹性阶段的斜率， ${E_{{\text{tr}},2}}$为硬化阶段的斜率， ${E_{{\text{tr}},3}}$为软化阶段的斜率.

3.4. TRHDC加固层滞后应变计算

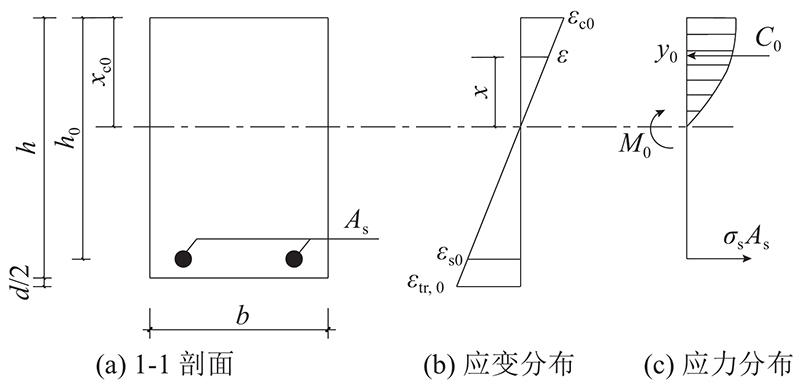
如图10所示为TRHDC加固层滞后应变计算简图. 由平截面假定，得到纵筋应变 $ {\varepsilon _{{\text{s}}0}} $的表达式为

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   纤维织物增强高延性混凝土加固层滞后应变计算简图

Fig.10   Calculation diagram of lag strain of  textile  reinforced  highlyductile concrete strengthened beams


$ {\varepsilon _{{\text{s0}}}} = \frac{{\left( {{h_0} - {x_{{\text{c0}}}}} \right){\varepsilon _{{\text{c0}}}}}}{{{x_{{\text{c0}}}}}}. $

式中： $ {h_0} $为原梁的截面有效高度， $ {x_{{\text{c0}}}} $为原梁的受压区高度， $ {\varepsilon _{{\text{c0}}}} $为原梁受压区外边缘混凝土压应变.

受压区混凝土合力C0的表达式为

$ {C_0}{\text{ = }}\int_0^{{x_{{\text{c0}}}}} {b{\sigma _{\text{c}}}{\text{d}}x = {f_{\text{c}}}b{x_{{\text{c0}}}}\left( {1 - \frac{{3{\varepsilon _{{\text{c0}}}}}}{{{\varepsilon _0}}}} \right)} {\text{.}} $

式中：b为截面宽度.

受压区混凝土合力作用点与受压区混凝土外边缘距离 $ {y_0} $的表达式为

$ {y_0} = {h_0} - \dfrac{{\displaystyle\int_0^{{x_{{\text{c0}}}}} {{\sigma _{\text{c}}}\left( {{h_0} - {x_{{\text{c0}}}}+y} \right){\text{d}}y} }}{{\int_0^{{x_{{\text{c0}}}}} {{\sigma _{\text{c}}}{\text{d}}y} }}. $

式中： $ {\sigma _{\text{c}}} $为混凝土压应力， $ y $为受压区任意一点距中和轴的距离.

由力与弯矩的平衡方程可以得到

$\left. \begin{array}{l}b{f}_{\text{c}}{x}_{\text{c0}}\dfrac{{\varepsilon }_{\text{c0}}}{{\varepsilon }_{0}}\left(1-\dfrac{3{\varepsilon }_{\text{c0}}}{{\varepsilon }_{0}}\right)={E}_{\text{s}}{\varepsilon }_{\text{s0}}{A}_{\text{s}},\\ {M}_{0}\text=b{f}_{\text{c}}{x}_{\text{c0}}\dfrac{{\varepsilon }_{\text{c0}}}{{\varepsilon }_{0}}\left(1-\dfrac{3{\varepsilon }_{\text{c0}}}{{\varepsilon }_{0}}\right)\left({h}_{0}-{y}_{0}\right).\end{array}\right\} $

式中： $ {E_{\text{s}}} $为钢筋的弹性模量， $ {A_{\text{s}}} $为纵筋的截面面积， $ {M_0} $为梁截面弯矩. 联立式（4）~（7），得到受压区外边缘混凝土压应变 $ {\varepsilon _{{\text{c}}0}} $和受压区高度 $ {x_{{\text{c}}0}} $.

由平截面假定可知，在M0作用下，TRHDC加固层滞后应变 $ {\varepsilon _{{\text{tr,0}}}} $的表达式为

$ {\varepsilon _{{\text{tr,0}}}} = \frac{{\left( {h+{d \mathord{\left/ {\vphantom {d {2 - {x_{{\text{c0}}}}}}} \right. } {2 - {x_{{\text{c0}}}}}}} \right){\varepsilon _{{\text{c0}}}}}}{{{x_{{\text{c0}}}}}}. $

式中：h为加固梁的截面高度，d为加固层厚度.

在二次受力状态下，定义TRHDC的名义拉应变 $ {\varepsilon _{{\text{tr,1}}}} $为TRHDC实际拉应变 $ {\varepsilon _{{\text{tr}}}} $与TRHDC滞后应变 $ {\varepsilon _{{\text{tr,0}}}} $之和，即：

$ {\varepsilon _{{\text{tr}}}} = {\varepsilon _{{\text{tr,1}}}} - {\varepsilon _{{\text{tr,0}}}}. $

式中： $ {\varepsilon _{{\text{tr,1}}}} $可以基于加固梁的平截面假定计算得到.

3.5. 受弯承载力计算模型

按承载能力极限状态计算TRHDC加固试件的受弯承载力. 对于加固试件B2、B3和B4，其峰值状态为纵筋屈服、织物被拉断、受压区混凝土未被压碎. 对于加固试件B6、B7、B8、B9和B10，其峰值状态为纵筋屈服、织物被拉断、受压区混凝土被压碎. 因此，受弯承载力计算可以分为以下2种情况.

3.5.1. 纵筋屈服、织物被拉断、受压区混凝土未被压碎

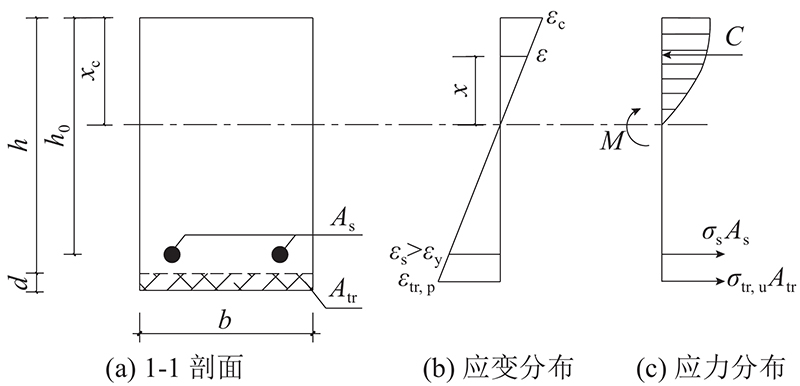
如图11所示为发生纵筋屈服、织物被拉断、受压区混凝土未被压碎破坏的TRHDC加固试件的正截面应力与应变分布图. 受压区边缘混凝土未达到极限压应变 $ {\varepsilon _{{\text{cu}}}} $，因此受压区混凝土合力C的表达式为

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   第1种破坏模式梁1-1剖面的应力与应变分布

Fig.11   Stress and strain distribution at section 1-1 of beams with first failure mode


$ C{\text{ = }}\int_0^x {b{\sigma _{\text{c}}}{\text{d}}x = \frac{{{x_{\text{c}}}}}{{{\varepsilon _{\text{c}}}}}} \int_0^\varepsilon {b{\sigma _{\text{c}}}{\text{d}}\varepsilon } . $

式中： $ {\varepsilon _{\text{c}}} $为受压区混凝土外边缘的应变， $ {x_{\text{c}}} $为加固梁受压区高度. 由力的平衡得到

$ \frac{{{x_{\text{c}}}}}{{{\varepsilon _{\text{c}}}}}\int_0^\varepsilon {b{\sigma _{\text{c}}}{\text{d}}\varepsilon } = {\sigma _{\text{s}}}{A_{\text{s}}}+{\sigma_{{\text{tr}},{\rm{u}}}}{A_{{\text{tr}}}}. $

式中： $ {\sigma _{\text{s}}} $为纵向受拉钢筋的应力， $ {A_{\text{s}}} $为纵筋截面面积， $ {A_{{\text{tr}}}} $为TRHDC面层的截面面积. 中和轴取矩的表达式为

$\begin{split} {M_{\text{u}}} =& {\sigma _{\text{s}}}{A_{\text{s}}}\left( {{h_0} - {x_{\text{c}}}} \right)+{\sigma_{{\text{tr}},{\rm{u}}}}{A_{{\text{tr}}}}\left( {h+0.5d - {x_{\text{c}}}} \right)+ \\ &{\left( {{{{x_{\text{c}}}}}/{{{\varepsilon _{\text{c}}}}}} \right)^2}\int_0^\varepsilon {b{\sigma _{\text{c}}}\varepsilon {\text{d}}\varepsilon } . \end{split} $

由平截面假定得到

$ {\sigma _{\text{s}}} = {f_{\text{y}}}+{E_2}\left( {{{\varepsilon _{\text{c}}}}}\left( {{h_0} - {x_{\text{c}}}} \right)/{{{x_{\text{c}}}}} - {\varepsilon _{\text{y}}} \right), $

$ {x_{\text{c}}} = \frac{{{\varepsilon _{\text{c}}}}}{{{\varepsilon _{\text{c}}}+{\varepsilon _{{\text{tr,p}}}}}}\left( {h+0.5d} \right). $

联立式（10）~（14），得到加固试件的受弯承载力.

3.5.2. 纵筋屈服、织物被拉断、受压区混凝土被压碎

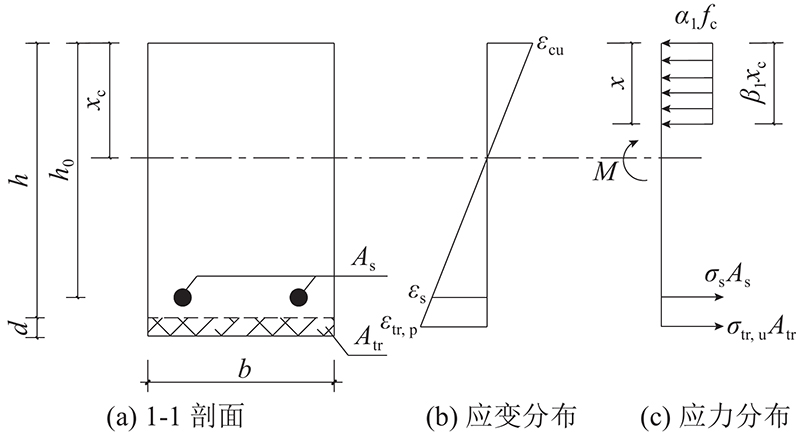
如图12所示，发生纵筋屈服、织物被拉断、受压区混凝土被压碎破坏加固试件的正截面应力与应变分布图. 由力与弯矩的平衡方程得到

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   第2种破坏模式梁1-1剖面的应力与应变分布

Fig.12   Stress and strain distribution at section 1-1 of beams with second failure mode


$\left. \begin{array}{l}{\alpha }_{1}{\beta }_{1}{f}_{\text{c}}b{x}_{\text{c}}={\sigma }_{\text{s}}{A}_{\text{s}}+{\sigma}_{\text{tr,u}}{A}_{\text{tr}},\\ M \leqslant {M}_{\text{u}}={\sigma }_{\text{s}}{A}_{\text{s}}\left({h}_{0}-\dfrac{{\beta }_{1}{x}_{\text{c}}}{2}\right)+{\sigma}_{\text{tr,u}}{A}_{\text{tr}}\left(h+\dfrac{d}{2}-\dfrac{{\beta }_{1}{x}_{\text{c}}}{2}\right).\end{array}\right\} $

式中： $ {\alpha _1} $、 $ {\;\beta _1} $为受压区混凝土等效矩形系数， $ {\alpha _1}= 1.0 $、 $ {\;\beta _1}{\text{ = }}0.8 $[32].

3.5.3. 计算结果与试验结果比较

所有试件受弯承载力计算结果与试验结果的比较见表6. 表中，Pu,t为试验值，Pu,cal为计算值. 可知，受弯承载力计算值与试验值吻合较好，平均值为0.96，标准差为0.08，变异系数为0.08. 通过本研究所提计算方法得到的受弯承载力计算结果在整体上偏于安全，对持载加固试件尤为明显。主要原因是未考虑持载作用的影响. 可见，采用本研究所提计算模型可以较好地预测TRHDC加固RC梁发生织物拉断破坏时的受弯承载力. 结合加固层滞后应变计算方法，将承载力计算模型中的TRHDC抗拉强度替换成加固梁峰值荷载对应的TRHDC实际应力，可以得到发生织物未拉断破坏时加固梁的受弯承载力.

表 6   梁试件受弯承载力计算结果与试验结果比较

Tab.6  Comparison for calculation values and test results of flexural capacity of beam specimens

试件编号 $ {P_{{\text{u,t}}}} $/ kN $ {P_{{\text{u,cal}}}} $/ kN ${ {P_{ {\text{u,cal} } } } } /{ {P_{ {\text{u,t} } } } }$
B1 96.15 107.32 1.12
B2 109.72 115.43 1.05
B3 118.79 119.12 1.00
B4 133.87 124.76 0.93
B5 164.10 158.89 0.97
B6 175.52 164.46 0.94
B7 183.64 167.03 0.91
B8 194.30 170.99 0.88
B9 187.66 167.03 0.89
B10 193.72 167.03 0.86

新窗口打开| 下载CSV


4. 结　论

（1）加固梁均发生纵筋屈服、织物被拉断，且受压区混凝土被压碎破坏. 配筋率为0.93%的加固梁在纵筋与混凝土界面出现脱黏裂缝，所有加固梁均未出现混凝土与HDC、HDC与织物的剥离现象.

（2）与相应的对比试件相比，无初始受力加固试件的开裂荷载提高1.17~1.61倍，屈服荷载提高10.5%~65.9%，峰值荷载提高7.0%~39.2%；持载加固试件的屈服荷载分别提高1.0%和10.5%，峰值荷载分别提高18.0%和14.4%. 无初始受力加固试件和持载加固试件裂缝的出现和发展缓慢，裂缝间距和宽度均减小.

（3）在试验中，增大织物层数将使加固梁的屈服荷载、峰值荷载的提高幅度非线性增大，该变化与纵筋配筋率有关；相同纵筋配筋率的加固梁峰值挠度变化不大，位移延性系数不断减小.

（4）当持载水平由对比梁屈服荷载的50%提高至80%时，加固梁的屈服荷载减小8.6%，峰值荷载及相应挠度分别增大3.2%、13.9%.

（5）本研究提出的TRHDC加固层滞后应变和TRHDC加固RC梁受弯承载力计算方法，所得计算结果与试验结果吻合良好，表明该计算方法可行，且偏于安全.

（6）本研究仅对缩尺梁进行两点受弯性能试验，未考虑损伤程度对TRHDC加固效果的影响。后续计划进行TRHDC加固足尺损伤梁受弯性能试验研究，为TRHDC在实际工程中的加固应用提供依据.

参考文献

AWANI O, EL-MAADDAWY T, ISMAIL N

Fabric-reinforced cementitious matrix: a promising strengthening technique for concrete structures

[J]. Construction and Building Materials, 2017, 132: 94- 111

DOI:10.1016/j.conbuildmat.2016.11.125      [本文引用: 1]

BOURNAS D A

Concurrent seismic and energy retrofitting of RC and masonry building envelopes using inorganic textile-based composites combined with insulation materials: a new concept

[J]. Composite Part B: Engineering, 2018, 148: 166- 179

DOI:10.1016/j.compositesb.2018.04.002      [本文引用: 1]

李赫, 徐世烺

纤维编织网增强混凝土薄板力学性能的研究

[J]. 建筑结构学报, 2007, 28 (4): 117- 122

DOI:10.3321/j.issn:1000-6869.2007.04.016      [本文引用: 1]

LI He, XU Shi-lang

A study on thin concrete plate reinforced with textile

[J]. Journal of Building Structures, 2007, 28 (4): 117- 122

DOI:10.3321/j.issn:1000-6869.2007.04.016      [本文引用: 1]

徐世烺, 阎轶群

低配网率纤维编织网增强混凝土轴拉力学性能

[J]. 复合材料学报, 2011, 28 (5): 206- 213

XU Shi-lang, YAN Yi-qun

Mechanical properties of textile reinforced concrete plate at low textile ratios

[J]. Acta Materiae Compositae Sinica, 2011, 28 (5): 206- 213

D'ANTINO T, PAPANICOLAOU C

Mechanical characterization of textile reinforced inorganic-matrix composites

[J]. Composite Part B: Engineering, 2017, 127 (15): 78- 91

[本文引用: 1]

BRUCKNER A, ORTHLEPP R, CURBACH M

Textile reinforced concrete for strengthening in bending and shear

[J]. Materials and Structures, 2006, 39 (8): 741- 748

DOI:10.1617/s11527-005-9027-2      [本文引用: 1]

LARBI A S, AGBOSSOU A, HAMELIN P

Experimental and numerical investigations about textile-reinforced concrete and hybrid solutions for repairing and/or strengthening reinforced concrete beams

[J]. Composite Structures, 2013, 99: 152- 162

DOI:10.1016/j.compstruct.2012.12.005      [本文引用: 1]

ELSANADEDY H M, ABBAS H, ALMUSALLAM T H, et al

Organic versus inorganic matrix composites for bond-critical strengthening applications of RC structures: state-of-the-art review

[J]. Composite Part B: Engineering, 2019, 174: 106947

DOI:10.1016/j.compositesb.2019.106947      [本文引用: 1]

RAOOF S M, BOURNAS D A

TRM versus FRP in flexural strengthening of RC beams: behaviour at high temperatures

[J]. Construction and Building Materials, 2017, 154: 424- 437

DOI:10.1016/j.conbuildmat.2017.07.195      [本文引用: 1]

D'AMBRISI A, FOCACCI F

Flexural strengthening of RC beams with cement-based composites

[J]. Journal of Composite Construction, 2011, 15: 707- 20

DOI:10.1061/(ASCE)CC.1943-5614.0000218      [本文引用: 1]

ESCRIG C, GIL L, BERNAT-MASO E

Experimental comparison of reinforced concrete beams strengthened against bending with different types of cementitious-matrix composite materials

[J]. Construction and Building Materials, 2017, 137: 317- 29

DOI:10.1016/j.conbuildmat.2017.01.106      [本文引用: 1]

RAOOF S M, KOUTAS L N, BOURNAS D A

Textile-reinforced mortar (TRM) versus fibre-reinforced polymers (FRP) in flexural strengthening of RC beams

[J]. Construction and Building Materials, 2017, 151: 279- 91

DOI:10.1016/j.conbuildmat.2017.05.023      [本文引用: 1]

YIN S P, CONG X, WANG C Y, et al

Research on flexural performance of composited RC beams with different forms of TRC permanent formwork

[J]. Structures, 2021, 29: 1424- 1434

DOI:10.1016/j.istruc.2020.12.034      [本文引用: 1]

YU Y L, YIN S P, NA M W

Bending performance of TRC-strengthened RC beams with secondary load under chloride erosion

[J]. Journal of Central South University, 2019, 26 (1): 196- 206

DOI:10.1007/s11771-019-3993-y      [本文引用: 1]

徐世烺, 尹世平, 蔡新华

纤维编织网增强混凝土加固钢筋混凝土梁受弯性能研究

[J]. 土木工程学报, 2011, 44 (4): 23- 34

XU Shi-lang, YIN Shi-ping, CAI Xin-hua

Investigation on the flexural behavior of reinforced concrete beam strengthened with textile-reinforced concrete

[J]. China Civil Engineering Journal, 2011, 44 (4): 23- 34

徐世烺, 尹世平

纤维编织网增强细粒混凝土加固RC受弯构件的正截面承载性能研究

[J]. 土木工程学报, 2012, 45 (1): 1- 7

[本文引用: 1]

XU Shi-lang, YIN Shi-ping

Investigation on the bearing capacity of the normal section of RC flexural component strengthened with textile-reinforced concrete

[J]. China Civil Engineering Journal, 2012, 45 (1): 1- 7

[本文引用: 1]

董志芳, 邓明科, 张聪

纤维织物增强高延性混凝土单轴拉伸性能试验研究

[J]. 土木工程学报, 2020, 53 (10): 13- 25

[本文引用: 2]

DONG Zhi-fang, DENG Ming-ke, ZHANG Cong

Experimental investigation on uniaxial tension behavior of textile-reinforced highly ductile concrete

[J]. China Civil Engineering Journal, 2020, 53 (10): 13- 25

[本文引用: 2]

WEI L Z, WANG Y C, YU J T, et al

Feasibility study of strain hardening magnesium oxychloride cement-based composites

[J]. Construction and Building Materials, 2018, 165: 750- 760

DOI:10.1016/j.conbuildmat.2018.01.041      [本文引用: 1]

LI B B, XIONG H, JIANG J F, et al

Tensile behavior of basalt textile grid reinforced engineering cementitious composite

[J]. Composites Part B: Engineering, 2019, 156: 185- 200

DOI:10.1016/j.compositesb.2018.08.059      [本文引用: 1]

HINZEN M, BRAMESHUBER W. Improvement of serviceability and strength of textile reinforced concrete by using short fibres [C]// 4th Colloquium on Textile Reinforced Structures. Dresden: [s. n.], 2009: 261–272.

[本文引用: 1]

BARHUM R, MECHTCHERINE V

Effect of short, dispersed glass and carbon fibres on the behaviour of textile-reinforced concrete under tensile loading

[J]. Engineering Fracture Mechanics, 2012, 92: 56- 71

DOI:10.1016/j.engfracmech.2012.06.001      [本文引用: 1]

沈玲华, 王激扬, 徐世烺

掺入短切纤维的纤维编织网增强混凝土薄板弯曲力学性能试验研究

[J]. 建筑结构学报, 2016, 37 (10): 98- 107

[本文引用: 1]

SHEN Ling-hua, WANG Ji-yang, XU Shi-lang

Experimental study on bending mechanical behavior of textile reinforced concrete thin-plates with short dispersed fibers

[J]. Journal of Building Structures, 2016, 37 (10): 98- 107

[本文引用: 1]

LI V C, LEUNG C K Y

Steady-state and multiple cracking of short random fiber composites

[J]. Journal of Engineering Mechanics, 1992, 188 (11): 2246- 2264

[本文引用: 1]

寇佳亮, 邓明科, 梁兴文

延性纤维增强混凝土单轴拉伸性能试验研究

[J]. 建筑结构, 2013, 43 (1): 59- 64

KOU Jia-liang, DENG Ming-ke, LIANG Xing-wen

Experimental study of uniaxial tensile properties of ductile fiber reinforced concrete

[J]. Building Structure, 2013, 43 (1): 59- 64

代洁, 邓明科, 陈佳莉

基于材料延性的高延性混凝土无腹筋梁受剪性能试验研究

[J]. 工程力学, 2018, 35 (2): 124- 132

[本文引用: 1]

DAI Jie, DENG Ming-ke, CHEN Jia-li

Influence of matrix ductility on shear behavior of high ductile fiber reinforced concrete beams

[J]. Engineering Mechanics, 2018, 35 (2): 124- 132

[本文引用: 1]

DENG M K, DONG Z F, ZHANG C

Experimental investigation on tensile behavior of carbon textile reinforced mortar (TRM) added with short polyvinyl alcohol (PVA) fibers

[J]. Construction and Building Materials, 2020, 235: 117801

DOI:10.1016/j.conbuildmat.2019.117801      [本文引用: 2]

ICC-Evaluation Service. Acceptance criteria for masonry and concrete strengthening using fiber-reinforced cementitious matrix (FRCM) composite systems: AC434 [S]. Whittier: [s. n.], 2013: 14–15.

[本文引用: 1]

KOUTAS L N, TETTA Z, BOURNAS D A, et al

Strengthening of concrete structures with textile reinforced mortars: state-of-the-art review

[J]. Journal of Composites for Construction, 2019, 23 (1): 03118001

DOI:10.1061/(ASCE)CC.1943-5614.0000882      [本文引用: 1]

邓明科, 马向琨. 一种梁式构件持载加固用试验装置: CN202021687914.7 [P]. 2021-04-20.

[本文引用: 1]

过镇海. 钢筋混凝土原理 [M]. 北京: 清华大学出版社, 2013: 122.

[本文引用: 1]

郑宇宙, 王文炜

复材网格-UHTCC复合增强钢筋混凝土梁抗弯性能试验研究

[J]. 土木工程学报, 2017, 50 (6): 23- 32

[本文引用: 1]

ZHENG Yu-zhou, WANG Wen-wei

Experimental research on flexural behavior of RC beams strengthened with FRP grid-UHTCC composite

[J]. China Civil Engineering Journal, 2017, 50 (6): 23- 32

[本文引用: 1]

中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010 [S]. 北京: 中国建筑工业出版社, 2010: 35-37.

[本文引用: 2]

/

〈 〉