[1]
路甬祥 仿生学的科学意义与前沿: 仿生学的意义与发展
[J]. 科学中国人 , 2004 , (4 ): 22 - 24
[本文引用: 1]
LU Yong-xiang The scientific significance and frontier of bionics: the significance and development of bionics
[J]. Scientific Chinese , 2004 , (4 ): 22 - 24
[本文引用: 1]
[2]
MANDELBROT B B. The fractal geometry of nature [M]. New York: WH freeman, 1982.
[本文引用: 1]
[3]
FERKO K, LACHENDRO D, CHIAPPAZZI N, et al. Interaction of side-by-side fluidic harvesters in fractal grid-generated turbulence [C]// Active and Passive Smart Structures and Integrated Systems XII . Denver: International Society for Optics and Photonics, 2018: 105951E.
[本文引用: 1]
[4]
STEIROS K, BRUCE P J K, BUXTON O R H, et al Power consumption and form drag of regular and fractal-shaped turbines in a stirred tank
[J]. AIChE Journal , 2017 , 63 (2 ): 843 - 854
DOI:10.1002/aic.15414
[本文引用: 1]
[5]
SPONFELDNER T, SOULOPOULOS N, BEYRAU F, et al The structure of turbulent flames in fractal and regular-grid generated turbulence
[J]. Combustion and Flame , 2015 , 162 (9 ): 3379 - 3393
DOI:10.1016/j.combustflame.2015.06.004
[本文引用: 1]
[6]
COMTE-BELLOT G, CORRSIN S The use of a contraction to improve the isotropy of grid-generated turbulence
[J]. Journal of Fluid Mechanics , 1966 , 25 (4 ): 657 - 682
DOI:10.1017/S0022112066000338
[本文引用: 1]
[7]
ANTONIA R A, ZHOU T, ZHU Y Three-component vorticity measurements in a turbulent grid flow
[J]. Journal of Fluid Mechanics , 1998 , 374 : 29 - 57
DOI:10.1017/S0022112098002547
[本文引用: 1]
[8]
SEOUD R E, VASSILICOS J C Dissipation and decay of fractal-generated turbulence
[J]. Physics of Fluids , 2007 , 19 (10 ): 105108
DOI:10.1063/1.2795211
[本文引用: 2]
[9]
MAZELLIER N, VASSILICOS J C Turbulence without Richardson-Kolmogorov cascade
[J]. Physics of Fluids , 2010 , 22 (7 ): 075101
DOI:10.1063/1.3453708
[本文引用: 2]
[10]
LAVOIE P, BURATTINI P, DJENIDI L, et al Effect of initial conditions on decaying grid turbulence at low R λ
[J]. Experiments in Fluids , 2005 , 39 (5 ): 865 - 874
DOI:10.1007/s00348-005-0022-8
[本文引用: 1]
[11]
LAVOIE P, DJENIDI L, ANTONIA R A Effects of initial conditions in decaying turbulence generated by passive grids
[J]. Journal of Fluid Mechanics , 2007 , 585 : 395 - 420
DOI:10.1017/S0022112007006763
[本文引用: 1]
[15]
LAIZET S, VASSILICOS J C Fractal space-scale unfolding mechanism for energy-efficient turbulent mixing
[J]. Physical Review E , 2012 , 86 (4 ): 046302
DOI:10.1103/PhysRevE.86.046302
[本文引用: 1]
[16]
LAIZET S, VASSILICOS J C Stirring and scalar transfer by grid-generated turbulence in the presence of a mean scalar gradient
[J]. Journal of Fluid Mechanics , 2015 , 764 : 52 - 75
DOI:10.1017/jfm.2014.695
[18]
LAIZET S, VASSILICOS J C. Direct numerical simulations of turbulent flows generated by regular and fractal grids using an immersed boundary method [C]// 6th International Symposium on Turbulence and Shear Flow Phenomena . Seoul : Begel House Inc, 2009.
[本文引用: 3]
[19]
NAGATA K, SUZUKI H, SAKAI Y, et al Direct numerical simulation of turbulent mixing in grid-generated turbulence
[J]. Physica Scripta , 2008 , (T132 ): 014054
[本文引用: 1]
[20]
SUZUKI H, NAGATA K, SAKAI Y, et al. DNS on a spatially developing grid turbulence [C]// Journal of Physics: Conference Series . [s. l. ]: IOP Publishing, 2011, 318(3): 032043.
[本文引用: 1]
[21]
DA SILVA C B, PEREIRA J C F Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets
[J]. Physics of Fluids , 2008 , 20 (5 ): 055101
DOI:10.1063/1.2912513
[本文引用: 1]
[22]
VAN REEUWIJK M, HOLZNER M The turbulence boundary of a temporal jet
[J]. Journal of Fluid Mechanics , 2014 , 739 : 254 - 275
DOI:10.1017/jfm.2013.613
[本文引用: 1]
[23]
DIAMESSIS P J, SPEDDING G R, DOMARADZKI J A Similarity scaling and vorticity structure in high Reynolds number stably stratified turbulent wakes
[J]. Journal of Fluid Mechanics , 2011 , 671 : 52 - 95
DOI:10.1017/S0022112010005549
[本文引用: 1]
[24]
GAMPERT M, BOSCHUNG J, HENNIG F, et al The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface
[J]. Journal of Fluid Mechanics , 2014 , 750 : 578 - 596
DOI:10.1017/jfm.2014.280
[本文引用: 1]
[25]
SMYTH W D, MOUM J N Length scales of turbulence in stably stratified mixing layers
[J]. Physics of Fluids , 2000 , 12 (6 ): 1327 - 1342
DOI:10.1063/1.870385
[本文引用: 1]
[26]
WATANABE T, ZHANG X, NAGATA K Turbulent/non-turbulent interfaces detected in DNS of incompressible turbulent boundary layers
[J]. Physics of Fluids , 2018 , 30 (3 ): 035102
DOI:10.1063/1.5022423
[本文引用: 1]
[27]
WATANABE T, NAGATA K Integral invariants and decay of temporally developing grid turbulence
[J]. Physics of Fluids , 2018 , 30 (10 ): 105111
DOI:10.1063/1.5045589
[本文引用: 2]
[29]
NAGATA K, SUZUKI H, SAKAI Y, et al. Direct numerical simulation of turbulence with scalar transfer around complex geometries using the immersed boundary method and fully conservative higher-order finite-difference schemes [M]// Numerical Simulations Examples and Applications in Computational Fluid Dynamics . [s. l. ] : IntechOpen, 2010, Chap. 3.
[本文引用: 1]
[31]
KEMPF A, KLEIN M, JANICKA J Efficient generation of initial-and inflow-conditions for transient turbulent flows in arbitrary geometries
[J]. Flow, Turbulence and Combustion , 2005 , 74 (1 ): 67 - 84
DOI:10.1007/s10494-005-3140-8
[本文引用: 1]
[32]
KITAMURA T, NAGATA K, SAKAI Y, et al On invariants in grid turbulence at moderate Reynolds numbers
[J]. Journal of Fluid Mechanics , 2014 , 738 : 378 - 406
DOI:10.1017/jfm.2013.595
[本文引用: 2]
[33]
LAIZET S, LAMBALLAIS E High-order compact schemes for incompressible flows: a simple and efficient method with quasi-spectral accuracy
[J]. Journal of Computational Physics , 2009 , 228 (16 ): 5989 - 6015
DOI:10.1016/j.jcp.2009.05.010
[本文引用: 1]
[34]
SENGUPTA T K, SHARMA N, SENGUPTA A Non-linear instability analysis of the two-dimensional Navier-Stokes equation: the Taylor-Green vortex problem
[J]. Physics of Fluids , 2018 , 30 (5 ): 054105
DOI:10.1063/1.5024765
[本文引用: 1]
[35]
LAIZET S, NEDIĆ J, VASSILICOS J C Influence of the spatial resolution on fine-scale features in DNS of turbulence generated by a single square grid
[J]. International Journal of Computational Fluid Dynamics , 2015 , 29 (3−5 ): 286 - 302
DOI:10.1080/10618562.2015.1058371
[本文引用: 1]
[37]
ZHOU Y, NAGATA K, SAKAI Y, et al Enstrophy production and dissipation in developing grid-generated turbulence
[J]. Physics of Fluids , 2016 , 28 (2 ): 025113
DOI:10.1063/1.4941855
[本文引用: 1]
[38]
LAIZET S, VASSILICOS J C. Direct numerical simulation of fractal-generated turbulence [M]// Direct and large Eddy simulation VII . [s. l. ] : Springer, Dordrecht, 2010: 17-23.
[本文引用: 1]
[40]
NAGATA K, SAIKI T, SAKAI Y, et al Effects of grid geometry on non-equilibrium dissipation in grid turbulence
[J]. Physics of Fluids , 2017 , 29 (1 ): 015102
DOI:10.1063/1.4973416
[本文引用: 1]
[41]
DICKEY T D, MELLOR G L Decaying turbulence in neutral and stratified fluids
[J]. Journal of Fluid Mechanics , 1980 , 99 (1 ): 13 - 31
DOI:10.1017/S002211208000047X
[本文引用: 1]
[43]
ZHOU Y, NAGATA K, SAKAI Y, et al Relevance of turbulence behind the single square grid to turbulence generated by regular-and multiscale-grids
[J]. Physics of Fluids , 2014 , 26 (7 ): 075105
DOI:10.1063/1.4890746
[本文引用: 1]
[44]
ZHOU Y, NAGATA K, SAKAI Y, et al Development of turbulence behind the single square grid
[J]. Physics of Fluids , 2014 , 26 (4 ): 045102
DOI:10.1063/1.4870167
[本文引用: 1]
[45]
HURST D, VASSILICOS J C Scalings and decay of fractal-generated turbulence
[J]. Physics of Fluids , 2007 , 19 (3 ): 035103
DOI:10.1063/1.2676448
[本文引用: 1]
[46]
ANTONIA R A, ORLANDI P Similarity of decaying isotropic turbulence with a passive scalar
[J]. Journal of Fluid Mechanics , 2004 , 505 : 123 - 151
DOI:10.1017/S0022112004008456
[本文引用: 1]
[47]
BURATTINI P, LAVOIE P, ANTONIA R A Velocity derivative skewness in isotropic turbulence and its measurement with hot wires
[J]. Experiments in Fluids , 2008 , 45 (3 ): 523 - 535
DOI:10.1007/s00348-008-0495-3
[本文引用: 1]
[48]
ZHOU Y, NAGATA K, SAKAI Y, et al Energy transfer in turbulent flows behind two side-by-side square cylinders
[J]. Journal of Fluid Mechanics , 2020 , 903 (A4 ): 1 - 31
[本文引用: 1]
[49]
TAYLOR G I Statistical theory of turbulence-II
[J]. Proceedings of the ROYAL SOCIETY of London. Series A, Mathematical and Physical Sciences , 1935 , 151 (873 ): 444 - 454
[本文引用: 1]
[51]
ALEXANDROVA O, CARBONE V, VELTRI P, et al Small-scale energy cascade of the solar wind turbulence
[J]. The Astrophysical Journal , 2008 , 674 (2 ): 1153
DOI:10.1086/524056
[本文引用: 1]
[53]
BATCHELOR G K, PROUDMAN I The large-scale structure of homogenous turbulence
[J]. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences , 1956 , 248 (949 ): 369 - 405
DOI:10.1098/rsta.1956.0002
[本文引用: 1]
[55]
北村拓也, 長田孝二, 酒井康彦, 等 格子乱流のエネルギー減衰域における不変量について
[J]. 日本機械学会論文集 B 編 , 2012 , 78 (795 ): 1928 - 1941
DOI:10.1299/kikaib.78.1928
[本文引用: 1]
KITAMURA T, NAGATA K, SAKAI Y, et al On invariants in energy decay region in grid turbulence
[J]. Transactions of the Japan Society of Mechanical Engineers. B , 2012 , 78 (795 ): 1928 - 1941
DOI:10.1299/kikaib.78.1928
[本文引用: 1]
仿生学的科学意义与前沿: 仿生学的意义与发展
1
2004
... 湍流现象出现在与流体力学相关的各种学科问题中,如大坝排水、大气流动、机翼尾流等. 湍流流动在工业设备中较为常见,如何有效实现湍流流动的控制,改善设备性能,一直以来备受相关领域的学者关注. 利用仿生学思想,设计工业元件来控制流动的方法已经成为趋势[1 ] . 在仿生学中Mandelbrot[2 ] 将分形定义为具有某种自相似性结构、功能和性质的集合. 因此分形流动(fractal-generated turbulent flow)泛指流体(液体或气体)绕/经过具有分形外形的物体时引发的紊乱、不规则流动. 流体流经分形结构或规则结构网格的现象被称为分形网格湍流(fractal grid turbulence, FGT)或规则网格湍流(regular grid turbulence, RGT). ...
仿生学的科学意义与前沿: 仿生学的意义与发展
1
2004
... 湍流现象出现在与流体力学相关的各种学科问题中,如大坝排水、大气流动、机翼尾流等. 湍流流动在工业设备中较为常见,如何有效实现湍流流动的控制,改善设备性能,一直以来备受相关领域的学者关注. 利用仿生学思想,设计工业元件来控制流动的方法已经成为趋势[1 ] . 在仿生学中Mandelbrot[2 ] 将分形定义为具有某种自相似性结构、功能和性质的集合. 因此分形流动(fractal-generated turbulent flow)泛指流体(液体或气体)绕/经过具有分形外形的物体时引发的紊乱、不规则流动. 流体流经分形结构或规则结构网格的现象被称为分形网格湍流(fractal grid turbulence, FGT)或规则网格湍流(regular grid turbulence, RGT). ...
1
... 湍流现象出现在与流体力学相关的各种学科问题中,如大坝排水、大气流动、机翼尾流等. 湍流流动在工业设备中较为常见,如何有效实现湍流流动的控制,改善设备性能,一直以来备受相关领域的学者关注. 利用仿生学思想,设计工业元件来控制流动的方法已经成为趋势[1 ] . 在仿生学中Mandelbrot[2 ] 将分形定义为具有某种自相似性结构、功能和性质的集合. 因此分形流动(fractal-generated turbulent flow)泛指流体(液体或气体)绕/经过具有分形外形的物体时引发的紊乱、不规则流动. 流体流经分形结构或规则结构网格的现象被称为分形网格湍流(fractal grid turbulence, FGT)或规则网格湍流(regular grid turbulence, RGT). ...
1
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
Power consumption and form drag of regular and fractal-shaped turbines in a stirred tank
1
2017
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
The structure of turbulent flames in fractal and regular-grid generated turbulence
1
2015
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
The use of a contraction to improve the isotropy of grid-generated turbulence
1
1966
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
Three-component vorticity measurements in a turbulent grid flow
1
1998
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
Dissipation and decay of fractal-generated turbulence
2
2007
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
... 由于时间模拟的网格湍流初始是层流状态,利用一定强度的初始脉动速度可以有效促进网格条产生的尾流从层流转变为湍流状态. 本研究采用Kempf等[31 ] 提出的扩散方法获得式(14)中的初始脉动场,其均方根(root-mean-square, RMS)速度约为 $ 0.5\text{%} {U_0} $ M . 该脉动速度产生的效果相当于风洞实验中网格尾流湍流,脉动速度强度与部分风洞实验[8 ,32 ] 报道的尾流湍流强度基本一样. ...
Turbulence without Richardson-Kolmogorov cascade
2
2010
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
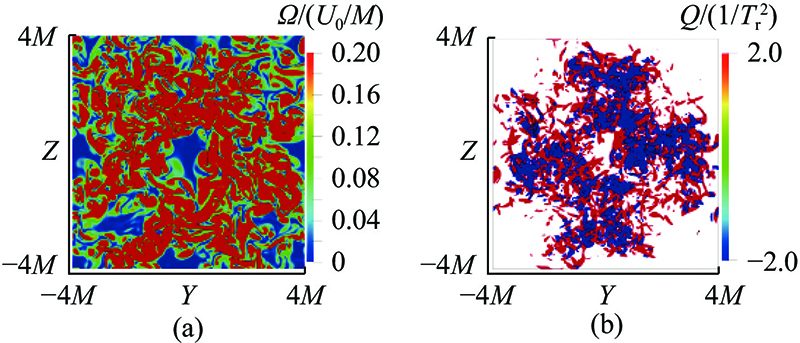
... 如图9 所示为FGT在 $ T = 25{T_{\text{r}}} $ $4M \leqslant Y,\;Z \leqslant 4M$ $ X = 4M $ ) 的瞬时涡量图,并给出了速度梯度张量第二不变量Q 图10 所示为RGT对应的可视化结果. 速度梯度的张量 ${{\boldsymbol{A}}_{ij}} = \partial {{\boldsymbol{u}}_i}/\partial {{\boldsymbol{x}}_j}$ ${{\boldsymbol{s}}_{ij}} = (\partial {{\boldsymbol{u}}_i}/\partial {{\boldsymbol{x}}_j}+ \partial {{\boldsymbol{u}}_j}/\partial {{\boldsymbol{x}}_i})/2$ ${{\boldsymbol{\omega}} _{ij}} = (\partial {{\boldsymbol{u}}_i}/\partial {{\boldsymbol{x}}_j} - \partial {{\boldsymbol{u}}_j}/\partial {{\boldsymbol{x}}_i})/2$ ${\boldsymbol{Q}} = {{\boldsymbol{Q}}_\omega }+{{\boldsymbol{Q}}_s}{\text{ = }}({{\boldsymbol{\omega}} _{ij}}{{\boldsymbol{\omega}} _{ij}}/2 - {{\boldsymbol{s}}_{ij}}{{\boldsymbol{s}}_{ij}}/2)$ . 正的Q Q 图9 、10 可以看出,在此计算域中充斥着类似于网格湍流空间演化的各种尺度结构. 须注意的是,尽管都处于相同的初始时刻( $ T{\text{ = }}25{T_{\text{r}}} $ ) ,FGT依然能识别出最大尺度湍流结构的形状,它起到了强化湍流的作用,导致FGT比RGT产生了更高的涡度值,而RGT此时明显已经进入衰减耗散阶段. 从本质上讲,这2种不同类型的网格湍流是以不同的方式产生的. 如图10 所示的规则网格湍流是相同大小的尾流在几个网格内相互作用,并在网格附近以均匀的方式混合在一起而形成的. 图9 分形网格的情况下,网格上最小的网格条产生最小的尾流,这些尾流在初始阶段相遇并混合在一起, 而较大的网格条产生较大的尾流,这些尾流将在随时间演化的过程中相遇并混合. 这一现象在最小到最大的湍流尺度上重复进行. Mazellier等[9 ] 与Laizet等[38 ] 在分形网格湍流空间演化研究中也得到了类似的结论. ...
Effect of initial conditions on decaying grid turbulence at low R λ
1
2005
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
Effects of initial conditions in decaying turbulence generated by passive grids
1
2007
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
格栅湍流场风参数沿风洞轴向变化规律
1
2015
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
格栅湍流场风参数沿风洞轴向变化规律
1
2015
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
被动格栅紊流场横向风速相关性实验研究
1
2013
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
被动格栅紊流场横向风速相关性实验研究
1
2013
... 国内外学者开展了一系列有关分形结构流场的实验和数值模拟研究. 在实验方面,Ferko等[3 ] 利用压电俘能器装置回收分形流场中的能量,研究表明与常规结构相比,利用分形结构可以使其能量转化的效率显著增加. Steiros等[4 ] 研究发现在搅拌器中利用分形刀刃,可以有效降低阻力系数. Sponfeldner等[5 ] 将分形结构应用在燃烧实验中,研究表明与规则湍流场相比,分形湍流场中的火焰燃烧更稳定以及燃烧速率更大. Comte-Bellot等[6 ] 利用风洞实验来探索改善网格湍流各向同性的方法. Antonia等[7 ] 对网格湍流场的涡量变化进行了深入研究. Seoud等[8 ] 和Mazellier等[9 ] 开展了分形流场机理研究,结果表明利用分形流场,将能量直接注入不同大小尺度的湍流结构中,可以改变流场中能量传递机制和湍动能耗散特性. Lavoie等[10 -11 ] 的实验表明FGT的统计特性受到初始条件的影响较大. 严磊等[12 ] 利用风洞实验发现风参数变化主要与测试点和格栅断面间距、格栅板条厚度和单元格栅边长有关. 周蓉[13 ] 在实验中发现风洞流向脉动风速在不同水平间距和湍流积分尺度下的相关性与两者比值相关,比值越大,相关性越弱. ...
Fractal-generated turbulence
1
2004
... 研究人员也利用直接数值模拟(direct numerical simulation, DNS)方法进行了有关方面的积极探索. Mazzi等[14 ] 研究了三维不可压缩湍流受幂律多尺度作用力影响的周期性和统计稳定的行为. Laizet等[15 -18 ] 采用DNS仿真开展了有关FGT和RGT的研究,结果表明分形湍流可以显著提高流体混合效率、增大标量的传递,并在此基础上提出了一种空间尺度展开(space-scale unfolding, SSU)机制. Nagata等[19 ] 对分形流场空间演化的DNS模拟结果,证实了在靠近网格的近场区域存在湍流产生区,远离网格的区域存在湍流衰减区. Suzuki等[20 ] 模拟并分析了规则网格湍流特性,发现即便是在流场远下游处( $ X/M \approx 100 $ X 为规则网格湍流空间演化时沿流向的距离,M 为规则网格的尺寸大小),大尺度脉动速度场也并非是完全各向同性的,各向异性约为17%. ...
Fractal space-scale unfolding mechanism for energy-efficient turbulent mixing
1
2012
... 研究人员也利用直接数值模拟(direct numerical simulation, DNS)方法进行了有关方面的积极探索. Mazzi等[14 ] 研究了三维不可压缩湍流受幂律多尺度作用力影响的周期性和统计稳定的行为. Laizet等[15 -18 ] 采用DNS仿真开展了有关FGT和RGT的研究,结果表明分形湍流可以显著提高流体混合效率、增大标量的传递,并在此基础上提出了一种空间尺度展开(space-scale unfolding, SSU)机制. Nagata等[19 ] 对分形流场空间演化的DNS模拟结果,证实了在靠近网格的近场区域存在湍流产生区,远离网格的区域存在湍流衰减区. Suzuki等[20 ] 模拟并分析了规则网格湍流特性,发现即便是在流场远下游处( $ X/M \approx 100 $ X 为规则网格湍流空间演化时沿流向的距离,M 为规则网格的尺寸大小),大尺度脉动速度场也并非是完全各向同性的,各向异性约为17%. ...
Stirring and scalar transfer by grid-generated turbulence in the presence of a mean scalar gradient
0
2015
DNS of fractal-generated turbulence
2
2011
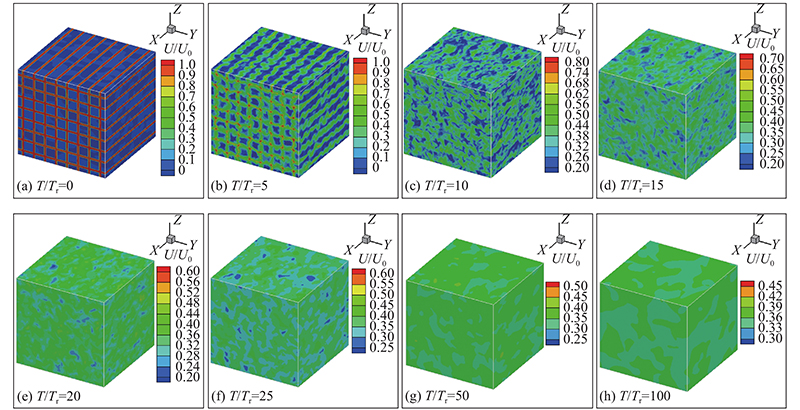
... 如图5 、6 所示分别展示了FGT和RGT不同时刻下流向(X 方向)瞬时速度三维可视化结果. 如图5 (a)、6(a)所示分别为2种网格湍流的初始状态( $ T = 0 $ ). 初始平均速度的影响在图5 (b)~(f)和图6 (b)~(e)中表现明显,平均速度产生的切应力导致网格条的尾流随时间从层流加速转变为湍流状态. 从图5 (g)开始,FGT中大尺度网格产生的尾流相互作用逐渐增强,流场湍流混合度增大. Laizet等[17 -18 ] 关于网格湍流空间演化研究表明随着分形网格横向厚度比 $ {D_{\text{r}}} $ $ X/M $ $ T/{T_{\text{r}}} $ $ {D_{\text{r}}}{\text{ = }}9.5 $ 图5 、6 对比也可以发现,FGT要演化更长的时间才能达到与RGT相同的湍流状态. 由图6 (f)开始,规则网格条的尾流相互作用逐渐合并形成网格湍流,并随时间逐渐发展为近似统计均匀状态. ...
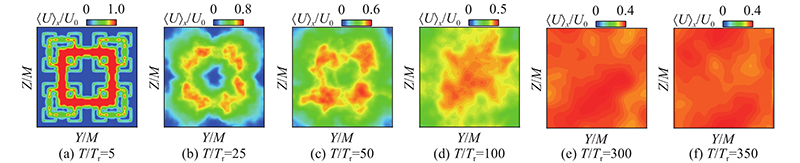
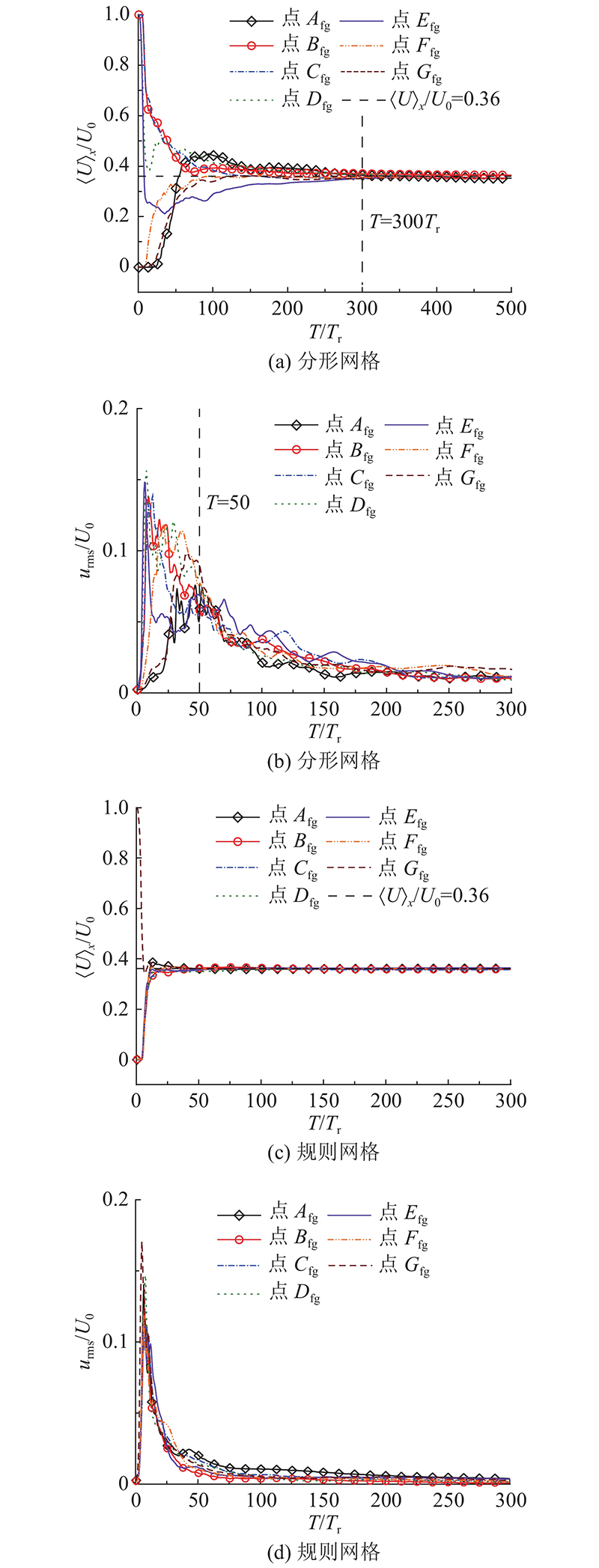
... 如图14 所示为FGT和RGT不同(Y , Z )位置上流向平均速度 $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}} $ Y , Z )点对应图13 . 在图14 (a)中,FGT各位置的流向平均速度在初始阶段表现出强烈的不均匀性,相比于图14 (c),初始条件对FGT的影响持续到 $ T \approx 300{T_{\text{r}}} $ $ {E_{{\text{fg}}}} $ $ {\langle U\rangle _x} $ $ {E_{{\text{fg}}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x} $ [43 ] 模拟的四阶FGT空间演化结果中,也提出了与上述类似的观点. 如图14 (b)、(d)所示为FGT与RGT的流向湍流强度. 可以看出,RGT所有位置的特性几乎呈现相同变化趋势,并在 $ T \approx {\text{6}}{T_{\text{r}}} $ $ {u_{{\text{rms}}}} $ A fg 点的中心线上峰值时刻最晚出现在 $ T \approx 50{T_{\text{r}}} $ [17 ] 关于FGT与RGT空间演化的对比研究结果中也存在该现象. ...
3
... 研究人员也利用直接数值模拟(direct numerical simulation, DNS)方法进行了有关方面的积极探索. Mazzi等[14 ] 研究了三维不可压缩湍流受幂律多尺度作用力影响的周期性和统计稳定的行为. Laizet等[15 -18 ] 采用DNS仿真开展了有关FGT和RGT的研究,结果表明分形湍流可以显著提高流体混合效率、增大标量的传递,并在此基础上提出了一种空间尺度展开(space-scale unfolding, SSU)机制. Nagata等[19 ] 对分形流场空间演化的DNS模拟结果,证实了在靠近网格的近场区域存在湍流产生区,远离网格的区域存在湍流衰减区. Suzuki等[20 ] 模拟并分析了规则网格湍流特性,发现即便是在流场远下游处( $ X/M \approx 100 $ X 为规则网格湍流空间演化时沿流向的距离,M 为规则网格的尺寸大小),大尺度脉动速度场也并非是完全各向同性的,各向异性约为17%. ...
... 如图5 、6 所示分别展示了FGT和RGT不同时刻下流向(X 方向)瞬时速度三维可视化结果. 如图5 (a)、6(a)所示分别为2种网格湍流的初始状态( $ T = 0 $ ). 初始平均速度的影响在图5 (b)~(f)和图6 (b)~(e)中表现明显,平均速度产生的切应力导致网格条的尾流随时间从层流加速转变为湍流状态. 从图5 (g)开始,FGT中大尺度网格产生的尾流相互作用逐渐增强,流场湍流混合度增大. Laizet等[17 -18 ] 关于网格湍流空间演化研究表明随着分形网格横向厚度比 $ {D_{\text{r}}} $ $ X/M $ $ T/{T_{\text{r}}} $ $ {D_{\text{r}}}{\text{ = }}9.5 $ 图5 、6 对比也可以发现,FGT要演化更长的时间才能达到与RGT相同的湍流状态. 由图6 (f)开始,规则网格条的尾流相互作用逐渐合并形成网格湍流,并随时间逐渐发展为近似统计均匀状态. ...
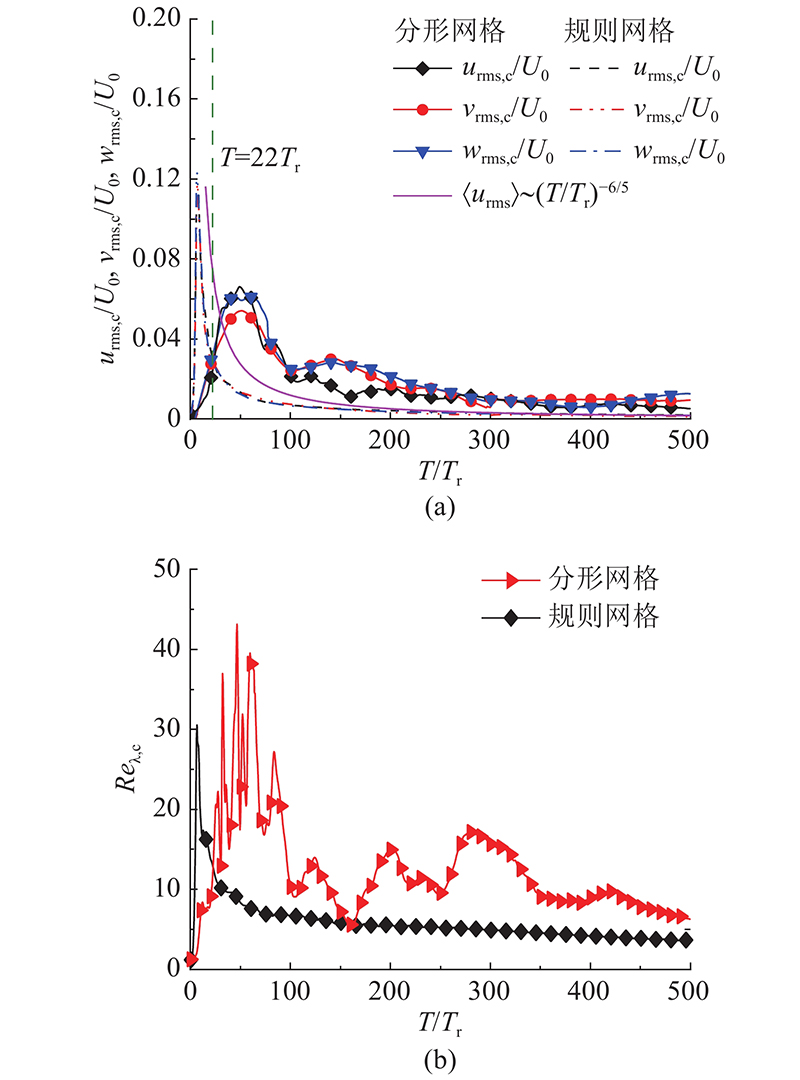
... 如图15 (a)、(b)所示分别为网格中心线上湍流强度 $ {u_{{\text{rms}},{\text{c }}}} $ $ {v_{{\text{rms}},{\text{c}}}} $ $ {w_{{\text{rms}},{\text{c}}}} $ $ R{e_{\lambda ,{\text{c}}}} = {u_{{\text{rms}},{\text{c}}}}{\lambda _{\text{c}}}/\nu $ $ {\lambda _{\text{c}}} = {u_{{\text{rms}},{\text{c}}}}/\langle {(\partial u'/\partial x)^2}\rangle _x^{1/2} $ 图15 (a)中,RGT中心线上 $ {u_{{\text{rms}},{\text{c }}}} $ $ {v_{{\text{rms,c}}}} $ $ {w_{{\text{rms}},{\text{c}}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ T \approx 50{T_{\text{r}}} $ ) 比RGT晚,这一点从图7 和图8 中时间在 $ T{\text{ = }}50{T_{\text{r}}} $ [44 ] 对RGT空间演化进行数值模拟研究,也验证了中心线上湍流强度峰值的位置 $ {X_{{\text{peak}}}} $ $ {N_{\text{f}}} = 3 $ ) 及网格横向厚度比 $ {D_{\text{r}}}{\text{ = }}9.5 $ [45 ] 的空间演化实验不同,但中心线上湍流强度大小刚好介于其实验中 $ {D_{\text{r}}}{\text{ = }}8.5 $ ${D_{\text{r}}}{\text{ = 13.0}}$ 图15 (a)与Laizet等[18 ] 的空间演化数值模拟结果相似的是,在本研究的时间演化初始阶段,RGT产生的尾流尺度要大于FGT产生的小尺度,导致其湍流强度大于FGT,但随着时间演化,FGT的大尺度运动加剧,此后( $ T > 22{T_{\text{r}}} $ ) 大部分衰减阶段FGT的湍流强度大小至少为RGT的2倍. 另外,在 $ T = 300{T_{\text{r}}} $ $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {(T/{T_{\text{r}}})^{ - 6/5}} $ $ {{\boldsymbol{u}}_{{\text{rms}}}} $ 图15 (b)中,RGT中心线上 $ R{e_{\lambda ,{\text{c}}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ R{e_{\lambda ,{\text{c}}}} $ $ T \approx 50{T_{\text{r}}} $ $ R{e_{\lambda ,{\text{c}}}} $
Direct numerical simulation of turbulent mixing in grid-generated turbulence
1
2008
... 研究人员也利用直接数值模拟(direct numerical simulation, DNS)方法进行了有关方面的积极探索. Mazzi等[14 ] 研究了三维不可压缩湍流受幂律多尺度作用力影响的周期性和统计稳定的行为. Laizet等[15 -18 ] 采用DNS仿真开展了有关FGT和RGT的研究,结果表明分形湍流可以显著提高流体混合效率、增大标量的传递,并在此基础上提出了一种空间尺度展开(space-scale unfolding, SSU)机制. Nagata等[19 ] 对分形流场空间演化的DNS模拟结果,证实了在靠近网格的近场区域存在湍流产生区,远离网格的区域存在湍流衰减区. Suzuki等[20 ] 模拟并分析了规则网格湍流特性,发现即便是在流场远下游处( $ X/M \approx 100 $ X 为规则网格湍流空间演化时沿流向的距离,M 为规则网格的尺寸大小),大尺度脉动速度场也并非是完全各向同性的,各向异性约为17%. ...
1
... 研究人员也利用直接数值模拟(direct numerical simulation, DNS)方法进行了有关方面的积极探索. Mazzi等[14 ] 研究了三维不可压缩湍流受幂律多尺度作用力影响的周期性和统计稳定的行为. Laizet等[15 -18 ] 采用DNS仿真开展了有关FGT和RGT的研究,结果表明分形湍流可以显著提高流体混合效率、增大标量的传递,并在此基础上提出了一种空间尺度展开(space-scale unfolding, SSU)机制. Nagata等[19 ] 对分形流场空间演化的DNS模拟结果,证实了在靠近网格的近场区域存在湍流产生区,远离网格的区域存在湍流衰减区. Suzuki等[20 ] 模拟并分析了规则网格湍流特性,发现即便是在流场远下游处( $ X/M \approx 100 $ X 为规则网格湍流空间演化时沿流向的距离,M 为规则网格的尺寸大小),大尺度脉动速度场也并非是完全各向同性的,各向异性约为17%. ...
Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets
1
2008
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
The turbulence boundary of a temporal jet
1
2014
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
Similarity scaling and vorticity structure in high Reynolds number stably stratified turbulent wakes
1
2011
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface
1
2014
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
Length scales of turbulence in stably stratified mixing layers
1
2000
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
Turbulent/non-turbulent interfaces detected in DNS of incompressible turbulent boundary layers
1
2018
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
Integral invariants and decay of temporally developing grid turbulence
2
2018
... 据文献统计,目前关于FGT的研究方法主要是实验与数值模拟,并且绝大部分都集中在空间演化流动(spatially evolving turbulent flow). 网格湍流空间演化的数值模拟在计算成本上存在较大的劣势,而时间演化湍流(temporally evolving turbulent flow)指的是,尽管流动在流向上是非均匀的,但仍然采用周期性边界条件,这样可以大幅缩小流向长度,节约计算成本. 近些年也有部分学者将此方法应用于湍流各领域的研究,如射流[21 -22 ] 、尾流[23 ] 、混合层[24 -25 ] 和边界层[26 ] 等流动. Watanabe等[27 ] 也对RGT开展过时间演化的DNS研究,但至今缺乏对分形网格湍流进行时间演化模拟研究. 因此本研究基于伪谱Fourier-Galerkin方法,布置三阶正方形分形网格流场,开展随时间演化的DNS仿真,探讨FGT相关统计特性随时间演化的特征. 并且开展了具有相同阻塞率的RGT的数值模拟,以进行对比分析. ...
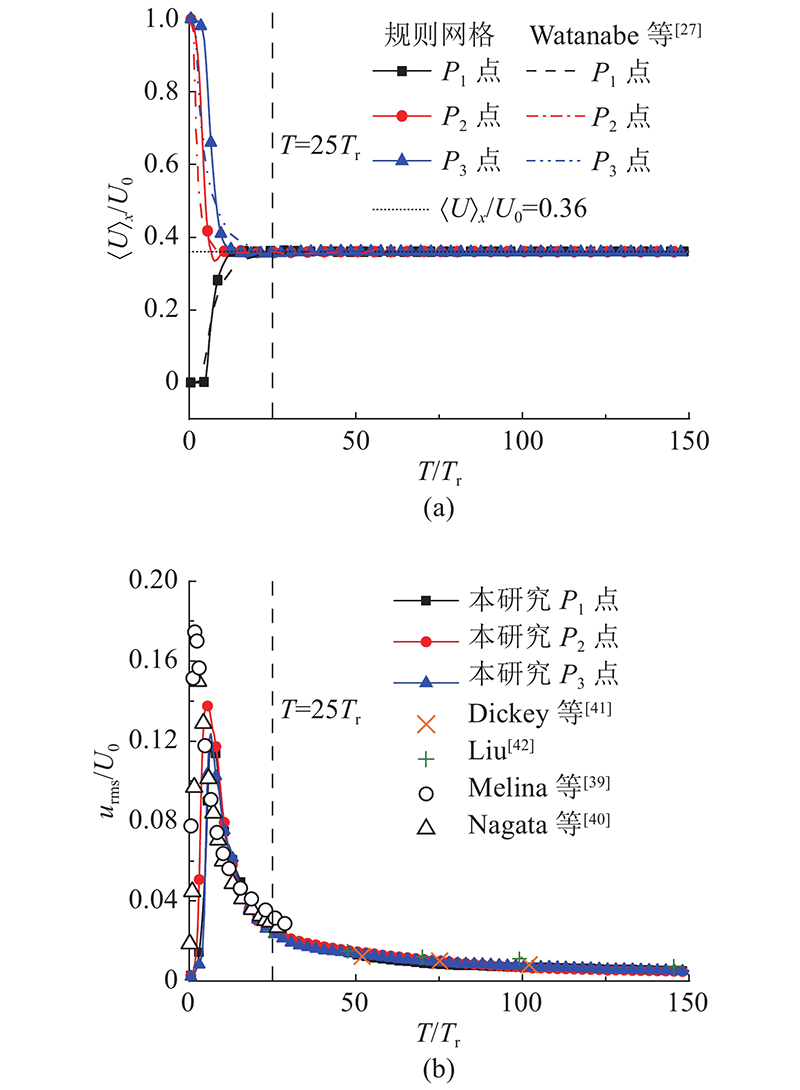
... 由于缺乏分形网格湍流时间演化的参考案例,选取前人[39 -42 ] 关于规则网格湍流的实验数据和数值模拟结果与本研究RGT工况进行对比,以此验证计算结果的准确性. 规则网格是由多个长度为M 的正方形格子重复组成,取其中的 $ {P_1} $ ( 虚拟中心Y /M =0,Z /M =0)、 $ {P_2} $ ( Y /M =0.5,Z /M =0)和 $ {P_3} $ ( Y /M =0.5,Z /M =0.5)点分析统计特性,平面位置如图1 所示. 如图11 所示为RGT中Y -Z 平面 $ {P_1} $ $ {P_2} $ $ {P_3} $ $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}}{\text{ = }}\langle u{'^2}\rangle _x^{1/2} $ 图11 (a)中,本研究设置的雷诺数 $ R{e_{\text{M}}} $ $ {\langle U\rangle _x} $ [27 ] 的数值模拟结果,但从 $ T \approx 25{T_{\text{r}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x}/{U_0} $ 图11 (b)所示为分别与Melina等[39 ] 、Nagata等[40 ] 在风洞实验近场区测的实验数据和Dickey等[41 ] 、Liu[42 ] 的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
Spectral methods in fluid dynamics
1
1987
... DNS仿真是基于伪谱-伽辽金方法[28 ] 进行空间离散实现的. 控制方程为连续性方程和不可压缩Navier-Stokes (NS)方程组,表达式如下: ...
1
... 考虑分形网格(fractal grid)流场和规则网格(regular grid)流场2组工况进行对比研究. 具体参数设置如表1 、2 所示. T end 为数值模拟结束的时间. 计算域3个方向的长度为 ${L_{X}} = {L_{Y}} = {L_{Z}} = 8M{\text{ = }} 8{M_2}$ $ {N_{\text{f}}} $ Y -Z 平面的几何维度(N f = $3 $ $ i = 0,1,2 $ ). 阻塞率的定义为 $ \sigma = {T_{{\text{bar}}}}/({L_{{Y}}}{L_{{Z}}}) $ $ {T_{{\text{bar}}}} $ $ {U_0} $ M , $ R{e_{\text{M}}} = {U_0}M/\nu $ . 由于须与规则格栅进行对比分析,同时为了研究小尺度结构的运动规律,须保证分形格栅具有比规则格栅更小的网格. 在相同阻塞率 $ \mathrm{\sigma }=0.36 $ ${{N}}_{\mathrm{f}}= 3$ ) 分形网格较为合适,而正方形网格也是目前研究最多,流动特性最为特殊的分形模式. 另外,Nagata等[29 ] 和Laizet等[30 ] 的研究表明,在法向/展向的最小网格条上最少须保证3个节点才能够精确模拟出合适的小尺度尾流迹象,本研究分形格栅的最小网格条上有5个节点 ${N}=5$ $ {M_i} = R_{\text{M}}^i{M_0} $ $ {M_0} $ $ {M_1} $ $ {M_2} $ ${M_0} = 0.5{L_{Y}}$ $ {R_{\text{M}}} = 0.5 $ . 网格条横向厚度 $ {d_i} = R_{\text{d}}^i{d_0} $ $ {d_0} $ $ {d_1} $ $ {d_2} $ $ {R_{\text{d}}} \approx 0.320 $ . 网格Y -Z 平面的具体效果可在图1 中观察. 分形网格的横向厚度比 $ {D_{\text{r}}} $ $ {D_{\text{r}}} = {d_0}/{d_2} $ . 计算域的网格节点数量为 ${N_{X}} {N_{Y}} {N_{Z}} = 800 \times 400 \times 400$ . ...
Multiscale generation of turbulence
1
2009
... 考虑分形网格(fractal grid)流场和规则网格(regular grid)流场2组工况进行对比研究. 具体参数设置如表1 、2 所示. T end 为数值模拟结束的时间. 计算域3个方向的长度为 ${L_{X}} = {L_{Y}} = {L_{Z}} = 8M{\text{ = }} 8{M_2}$ $ {N_{\text{f}}} $ Y -Z 平面的几何维度(N f = $3 $ $ i = 0,1,2 $ ). 阻塞率的定义为 $ \sigma = {T_{{\text{bar}}}}/({L_{{Y}}}{L_{{Z}}}) $ $ {T_{{\text{bar}}}} $ $ {U_0} $ M , $ R{e_{\text{M}}} = {U_0}M/\nu $ . 由于须与规则格栅进行对比分析,同时为了研究小尺度结构的运动规律,须保证分形格栅具有比规则格栅更小的网格. 在相同阻塞率 $ \mathrm{\sigma }=0.36 $ ${{N}}_{\mathrm{f}}= 3$ ) 分形网格较为合适,而正方形网格也是目前研究最多,流动特性最为特殊的分形模式. 另外,Nagata等[29 ] 和Laizet等[30 ] 的研究表明,在法向/展向的最小网格条上最少须保证3个节点才能够精确模拟出合适的小尺度尾流迹象,本研究分形格栅的最小网格条上有5个节点 ${N}=5$ $ {M_i} = R_{\text{M}}^i{M_0} $ $ {M_0} $ $ {M_1} $ $ {M_2} $ ${M_0} = 0.5{L_{Y}}$ $ {R_{\text{M}}} = 0.5 $ . 网格条横向厚度 $ {d_i} = R_{\text{d}}^i{d_0} $ $ {d_0} $ $ {d_1} $ $ {d_2} $ $ {R_{\text{d}}} \approx 0.320 $ . 网格Y -Z 平面的具体效果可在图1 中观察. 分形网格的横向厚度比 $ {D_{\text{r}}} $ $ {D_{\text{r}}} = {d_0}/{d_2} $ . 计算域的网格节点数量为 ${N_{X}} {N_{Y}} {N_{Z}} = 800 \times 400 \times 400$ . ...
Efficient generation of initial-and inflow-conditions for transient turbulent flows in arbitrary geometries
1
2005
... 由于时间模拟的网格湍流初始是层流状态,利用一定强度的初始脉动速度可以有效促进网格条产生的尾流从层流转变为湍流状态. 本研究采用Kempf等[31 ] 提出的扩散方法获得式(14)中的初始脉动场,其均方根(root-mean-square, RMS)速度约为 $ 0.5\text{%} {U_0} $ M . 该脉动速度产生的效果相当于风洞实验中网格尾流湍流,脉动速度强度与部分风洞实验[8 ,32 ] 报道的尾流湍流强度基本一样. ...
On invariants in grid turbulence at moderate Reynolds numbers
2
2014
... 由于时间模拟的网格湍流初始是层流状态,利用一定强度的初始脉动速度可以有效促进网格条产生的尾流从层流转变为湍流状态. 本研究采用Kempf等[31 ] 提出的扩散方法获得式(14)中的初始脉动场,其均方根(root-mean-square, RMS)速度约为 $ 0.5\text{%} {U_0} $ M . 该脉动速度产生的效果相当于风洞实验中网格尾流湍流,脉动速度强度与部分风洞实验[8 ,32 ] 报道的尾流湍流强度基本一样. ...
... 为了观察网格中心线上流向脉动速度偏导数的分布形态,利用其流向脉动速度偏导数的偏斜度 $ {S_{\partial u/\partial x}}{\text{ = }}{\langle {(\partial u'/\partial x)^3}\rangle _x}/\langle {(\partial u'/\partial x)^2}\rangle _x^{3/2} $ $ {F_{\partial u/\partial x}}{\text{ = }}{\langle {(\partial u'/\partial x)^4}\rangle _x}/\langle {(\partial u'/\partial x)^2}\rangle _x^2 $ 2 类统计量进行分析. 2类统计量随时间演化结果如图16 所示. 可以看出,分形网格的多尺度特性导致了FGT的 $ {S_{\partial u/\partial x}} $ $ {F_{\partial u/\partial x}} $ $ {S_{\partial u/\partial x}} $ $ {S_{\partial u/\partial x}} \approx - 0.5 $ . 并且Antonia等[46 ] 和Burattini等[47 ] 关于均匀各向同性湍流研究中也发现,当 $ R{e_\lambda } < 60 $ $ - {S_{\partial u/\partial x}} \sim 0.5 $ . 此外,尽管FGT的 $ {F_{\partial u/\partial x}} $ $ {F_{\partial u/\partial x}} $ [32 ] 之前在网格湍流空间演化实验中,发现当 $ R{e_\lambda } < 100 $ $ 2 \leqslant {F_{\partial u/\partial x}} \leqslant 5 $ $ {S_{\partial u/\partial x}} $
High-order compact schemes for incompressible flows: a simple and efficient method with quasi-spectral accuracy
1
2009
... 二维TGV数值模拟结果与解析解的均方根误差表达式[33 ] 为 ...
Non-linear instability analysis of the two-dimensional Navier-Stokes equation: the Taylor-Green vortex problem
1
2018
... 为了明确数值解与解析解之间的误差大小,两者的均方根误差如图3 (a)所示. 如图3 (b)所示为最大误差e max ,计算式参考Sengupta等[34 ] 的方法,即 ${\text{max}}\;(\left| {{{\boldsymbol{u}}_{\text{n}}} - {{\boldsymbol{u}}_{\text{a}}}} \right|)$ . 在无量纲时间 $ \tau \leqslant 150 $ −9 . 由此可见本研究的数值方法满足计算精度要求. ...
Influence of the spatial resolution on fine-scale features in DNS of turbulence generated by a single square grid
1
2015
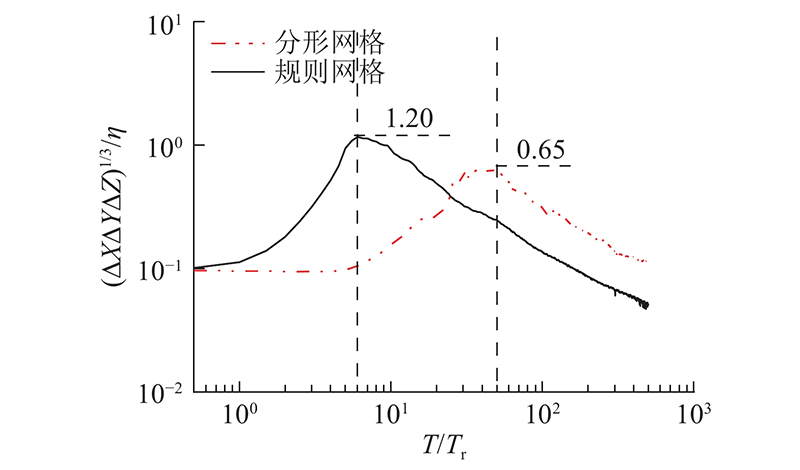
... 网格湍流的时间模拟须在高分辨率下才能更好地捕捉流场主要特征的变化. 通常主要集中观察网格中心线上统计信息的变化. 如图4 所示为分形网格和规则网格中心线上空间分辨率 $ {(\Delta X\Delta Y\Delta Z)^{1/3}}/\eta $ $ \eta {\text{ = }}{({\nu ^3}/\varepsilon )^{1/4}} $ Y , Z )=(0, 0), $ \varepsilon {\text{ = }}2\nu {\langle {s_{ij}}{s_{ij}}\rangle _x} $ $ {s_{ij}} = (\partial {u_j}/\partial {x_i}+ \partial {u_i}/\partial {x_j})/2 $ $ T \approx 50{T_{\text{r}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ {(\Delta X\Delta Y\Delta Z)^{1/3}} $ $ \eta $ . Laizet等[35 ] 的研究表明,当流场空间分辨率最差为7时,数值模拟结果与实验值相比误差仍能保证在约10%. Moin等[36 ] 也指出,当网格尺寸大小达到 $ 1.5\eta $
Direct numerical simulation: a tool in turbulence research
1
1998
... 网格湍流的时间模拟须在高分辨率下才能更好地捕捉流场主要特征的变化. 通常主要集中观察网格中心线上统计信息的变化. 如图4 所示为分形网格和规则网格中心线上空间分辨率 $ {(\Delta X\Delta Y\Delta Z)^{1/3}}/\eta $ $ \eta {\text{ = }}{({\nu ^3}/\varepsilon )^{1/4}} $ Y , Z )=(0, 0), $ \varepsilon {\text{ = }}2\nu {\langle {s_{ij}}{s_{ij}}\rangle _x} $ $ {s_{ij}} = (\partial {u_j}/\partial {x_i}+ \partial {u_i}/\partial {x_j})/2 $ $ T \approx 50{T_{\text{r}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ {(\Delta X\Delta Y\Delta Z)^{1/3}} $ $ \eta $ . Laizet等[35 ] 的研究表明,当流场空间分辨率最差为7时,数值模拟结果与实验值相比误差仍能保证在约10%. Moin等[36 ] 也指出,当网格尺寸大小达到 $ 1.5\eta $
Enstrophy production and dissipation in developing grid-generated turbulence
1
2016
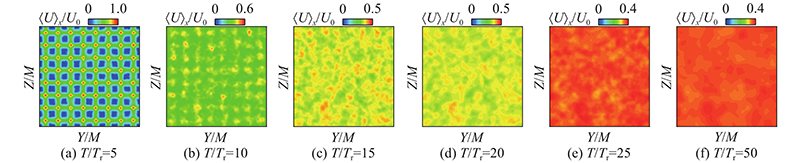
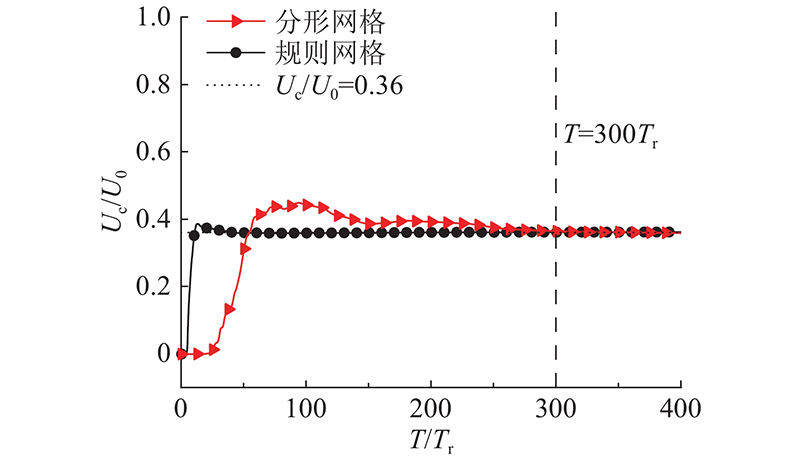
... 如图7 、8 所示分别为FGT和RGT的流向平均速度 $ {\langle U\rangle _x} $ ( 本研究网格中心线上 $ {\langle U\rangle _x} $ U c 表示,下标c表示中心线)随时间演化的可视化结果. 可以看出,由于初始平均速度剖面的不均匀性,统计量在初始阶段表现为高度不均匀状态. 与RGT相比,由于FGT受到初始条件影响更久,其流向平均速度分布与空间的相关性减弱的更慢,但随着时间演化,2类网格湍流终将会达到统计均匀状态. Zhou等[37 ] 的研究也表明,随着网格湍流空间演化的流向距离 $ X/M $ $ T/{T_{\text{r}}} $
1
... 如图9 所示为FGT在 $ T = 25{T_{\text{r}}} $ $4M \leqslant Y,\;Z \leqslant 4M$ $ X = 4M $ ) 的瞬时涡量图,并给出了速度梯度张量第二不变量Q 图10 所示为RGT对应的可视化结果. 速度梯度的张量 ${{\boldsymbol{A}}_{ij}} = \partial {{\boldsymbol{u}}_i}/\partial {{\boldsymbol{x}}_j}$ ${{\boldsymbol{s}}_{ij}} = (\partial {{\boldsymbol{u}}_i}/\partial {{\boldsymbol{x}}_j}+ \partial {{\boldsymbol{u}}_j}/\partial {{\boldsymbol{x}}_i})/2$ ${{\boldsymbol{\omega}} _{ij}} = (\partial {{\boldsymbol{u}}_i}/\partial {{\boldsymbol{x}}_j} - \partial {{\boldsymbol{u}}_j}/\partial {{\boldsymbol{x}}_i})/2$ ${\boldsymbol{Q}} = {{\boldsymbol{Q}}_\omega }+{{\boldsymbol{Q}}_s}{\text{ = }}({{\boldsymbol{\omega}} _{ij}}{{\boldsymbol{\omega}} _{ij}}/2 - {{\boldsymbol{s}}_{ij}}{{\boldsymbol{s}}_{ij}}/2)$ . 正的Q Q 图9 、10 可以看出,在此计算域中充斥着类似于网格湍流空间演化的各种尺度结构. 须注意的是,尽管都处于相同的初始时刻( $ T{\text{ = }}25{T_{\text{r}}} $ ) ,FGT依然能识别出最大尺度湍流结构的形状,它起到了强化湍流的作用,导致FGT比RGT产生了更高的涡度值,而RGT此时明显已经进入衰减耗散阶段. 从本质上讲,这2种不同类型的网格湍流是以不同的方式产生的. 如图10 所示的规则网格湍流是相同大小的尾流在几个网格内相互作用,并在网格附近以均匀的方式混合在一起而形成的. 图9 分形网格的情况下,网格上最小的网格条产生最小的尾流,这些尾流在初始阶段相遇并混合在一起, 而较大的网格条产生较大的尾流,这些尾流将在随时间演化的过程中相遇并混合. 这一现象在最小到最大的湍流尺度上重复进行. Mazellier等[9 ] 与Laizet等[38 ] 在分形网格湍流空间演化研究中也得到了类似的结论. ...
Vortex shedding effects in grid-generated turbulence
2
2016
... 由于缺乏分形网格湍流时间演化的参考案例,选取前人[39 -42 ] 关于规则网格湍流的实验数据和数值模拟结果与本研究RGT工况进行对比,以此验证计算结果的准确性. 规则网格是由多个长度为M 的正方形格子重复组成,取其中的 $ {P_1} $ ( 虚拟中心Y /M =0,Z /M =0)、 $ {P_2} $ ( Y /M =0.5,Z /M =0)和 $ {P_3} $ ( Y /M =0.5,Z /M =0.5)点分析统计特性,平面位置如图1 所示. 如图11 所示为RGT中Y -Z 平面 $ {P_1} $ $ {P_2} $ $ {P_3} $ $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}}{\text{ = }}\langle u{'^2}\rangle _x^{1/2} $ 图11 (a)中,本研究设置的雷诺数 $ R{e_{\text{M}}} $ $ {\langle U\rangle _x} $ [27 ] 的数值模拟结果,但从 $ T \approx 25{T_{\text{r}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x}/{U_0} $ 图11 (b)所示为分别与Melina等[39 ] 、Nagata等[40 ] 在风洞实验近场区测的实验数据和Dickey等[41 ] 、Liu[42 ] 的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
... [39 ]、Nagata等[40 ] 在风洞实验近场区测的实验数据和Dickey等[41 ] 、Liu[42 ] 的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
Effects of grid geometry on non-equilibrium dissipation in grid turbulence
1
2017
... 由于缺乏分形网格湍流时间演化的参考案例,选取前人[39 -42 ] 关于规则网格湍流的实验数据和数值模拟结果与本研究RGT工况进行对比,以此验证计算结果的准确性. 规则网格是由多个长度为M 的正方形格子重复组成,取其中的 $ {P_1} $ ( 虚拟中心Y /M =0,Z /M =0)、 $ {P_2} $ ( Y /M =0.5,Z /M =0)和 $ {P_3} $ ( Y /M =0.5,Z /M =0.5)点分析统计特性,平面位置如图1 所示. 如图11 所示为RGT中Y -Z 平面 $ {P_1} $ $ {P_2} $ $ {P_3} $ $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}}{\text{ = }}\langle u{'^2}\rangle _x^{1/2} $ 图11 (a)中,本研究设置的雷诺数 $ R{e_{\text{M}}} $ $ {\langle U\rangle _x} $ [27 ] 的数值模拟结果,但从 $ T \approx 25{T_{\text{r}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x}/{U_0} $ 图11 (b)所示为分别与Melina等[39 ] 、Nagata等[40 ] 在风洞实验近场区测的实验数据和Dickey等[41 ] 、Liu[42 ] 的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
Decaying turbulence in neutral and stratified fluids
1
1980
... 由于缺乏分形网格湍流时间演化的参考案例,选取前人[39 -42 ] 关于规则网格湍流的实验数据和数值模拟结果与本研究RGT工况进行对比,以此验证计算结果的准确性. 规则网格是由多个长度为M 的正方形格子重复组成,取其中的 $ {P_1} $ ( 虚拟中心Y /M =0,Z /M =0)、 $ {P_2} $ ( Y /M =0.5,Z /M =0)和 $ {P_3} $ ( Y /M =0.5,Z /M =0.5)点分析统计特性,平面位置如图1 所示. 如图11 所示为RGT中Y -Z 平面 $ {P_1} $ $ {P_2} $ $ {P_3} $ $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}}{\text{ = }}\langle u{'^2}\rangle _x^{1/2} $ 图11 (a)中,本研究设置的雷诺数 $ R{e_{\text{M}}} $ $ {\langle U\rangle _x} $ [27 ] 的数值模拟结果,但从 $ T \approx 25{T_{\text{r}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x}/{U_0} $ 图11 (b)所示为分别与Melina等[39 ] 、Nagata等[40 ] 在风洞实验近场区测的实验数据和Dickey等[41 ] 、Liu[42 ] 的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
Energetics of grid turbulence in a stably stratified fluid
2
1995
... 由于缺乏分形网格湍流时间演化的参考案例,选取前人[39 -42 ] 关于规则网格湍流的实验数据和数值模拟结果与本研究RGT工况进行对比,以此验证计算结果的准确性. 规则网格是由多个长度为M 的正方形格子重复组成,取其中的 $ {P_1} $ ( 虚拟中心Y /M =0,Z /M =0)、 $ {P_2} $ ( Y /M =0.5,Z /M =0)和 $ {P_3} $ ( Y /M =0.5,Z /M =0.5)点分析统计特性,平面位置如图1 所示. 如图11 所示为RGT中Y -Z 平面 $ {P_1} $ $ {P_2} $ $ {P_3} $ $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}}{\text{ = }}\langle u{'^2}\rangle _x^{1/2} $ 图11 (a)中,本研究设置的雷诺数 $ R{e_{\text{M}}} $ $ {\langle U\rangle _x} $ [27 ] 的数值模拟结果,但从 $ T \approx 25{T_{\text{r}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x}/{U_0} $ 图11 (b)所示为分别与Melina等[39 ] 、Nagata等[40 ] 在风洞实验近场区测的实验数据和Dickey等[41 ] 、Liu[42 ] 的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
... [42 ]的拖曳网格湍流实验数据进行对比. 其中利用 $ X/{U_\infty } $ $ {U_\infty } $ $ T \approx 25{T_{\text{r}}} $
Relevance of turbulence behind the single square grid to turbulence generated by regular-and multiscale-grids
1
2014
... 如图14 所示为FGT和RGT不同(Y , Z )位置上流向平均速度 $ {\langle U\rangle _x} $ $ {u_{{\text{rms}}}} $ Y , Z )点对应图13 . 在图14 (a)中,FGT各位置的流向平均速度在初始阶段表现出强烈的不均匀性,相比于图14 (c),初始条件对FGT的影响持续到 $ T \approx 300{T_{\text{r}}} $ $ {E_{{\text{fg}}}} $ $ {\langle U\rangle _x} $ $ {E_{{\text{fg}}}} $ $ {\langle U\rangle _x} $ $ {\langle U\rangle _x} $ [43 ] 模拟的四阶FGT空间演化结果中,也提出了与上述类似的观点. 如图14 (b)、(d)所示为FGT与RGT的流向湍流强度. 可以看出,RGT所有位置的特性几乎呈现相同变化趋势,并在 $ T \approx {\text{6}}{T_{\text{r}}} $ $ {u_{{\text{rms}}}} $ A fg 点的中心线上峰值时刻最晚出现在 $ T \approx 50{T_{\text{r}}} $ [17 ] 关于FGT与RGT空间演化的对比研究结果中也存在该现象. ...
Development of turbulence behind the single square grid
1
2014
... 如图15 (a)、(b)所示分别为网格中心线上湍流强度 $ {u_{{\text{rms}},{\text{c }}}} $ $ {v_{{\text{rms}},{\text{c}}}} $ $ {w_{{\text{rms}},{\text{c}}}} $ $ R{e_{\lambda ,{\text{c}}}} = {u_{{\text{rms}},{\text{c}}}}{\lambda _{\text{c}}}/\nu $ $ {\lambda _{\text{c}}} = {u_{{\text{rms}},{\text{c}}}}/\langle {(\partial u'/\partial x)^2}\rangle _x^{1/2} $ 图15 (a)中,RGT中心线上 $ {u_{{\text{rms}},{\text{c }}}} $ $ {v_{{\text{rms,c}}}} $ $ {w_{{\text{rms}},{\text{c}}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ T \approx 50{T_{\text{r}}} $ ) 比RGT晚,这一点从图7 和图8 中时间在 $ T{\text{ = }}50{T_{\text{r}}} $ [44 ] 对RGT空间演化进行数值模拟研究,也验证了中心线上湍流强度峰值的位置 $ {X_{{\text{peak}}}} $ $ {N_{\text{f}}} = 3 $ ) 及网格横向厚度比 $ {D_{\text{r}}}{\text{ = }}9.5 $ [45 ] 的空间演化实验不同,但中心线上湍流强度大小刚好介于其实验中 $ {D_{\text{r}}}{\text{ = }}8.5 $ ${D_{\text{r}}}{\text{ = 13.0}}$ 图15 (a)与Laizet等[18 ] 的空间演化数值模拟结果相似的是,在本研究的时间演化初始阶段,RGT产生的尾流尺度要大于FGT产生的小尺度,导致其湍流强度大于FGT,但随着时间演化,FGT的大尺度运动加剧,此后( $ T > 22{T_{\text{r}}} $ ) 大部分衰减阶段FGT的湍流强度大小至少为RGT的2倍. 另外,在 $ T = 300{T_{\text{r}}} $ $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {(T/{T_{\text{r}}})^{ - 6/5}} $ $ {{\boldsymbol{u}}_{{\text{rms}}}} $ 图15 (b)中,RGT中心线上 $ R{e_{\lambda ,{\text{c}}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ R{e_{\lambda ,{\text{c}}}} $ $ T \approx 50{T_{\text{r}}} $ $ R{e_{\lambda ,{\text{c}}}} $
Scalings and decay of fractal-generated turbulence
1
2007
... 如图15 (a)、(b)所示分别为网格中心线上湍流强度 $ {u_{{\text{rms}},{\text{c }}}} $ $ {v_{{\text{rms}},{\text{c}}}} $ $ {w_{{\text{rms}},{\text{c}}}} $ $ R{e_{\lambda ,{\text{c}}}} = {u_{{\text{rms}},{\text{c}}}}{\lambda _{\text{c}}}/\nu $ $ {\lambda _{\text{c}}} = {u_{{\text{rms}},{\text{c}}}}/\langle {(\partial u'/\partial x)^2}\rangle _x^{1/2} $ 图15 (a)中,RGT中心线上 $ {u_{{\text{rms}},{\text{c }}}} $ $ {v_{{\text{rms,c}}}} $ $ {w_{{\text{rms}},{\text{c}}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ T \approx 50{T_{\text{r}}} $ ) 比RGT晚,这一点从图7 和图8 中时间在 $ T{\text{ = }}50{T_{\text{r}}} $ [44 ] 对RGT空间演化进行数值模拟研究,也验证了中心线上湍流强度峰值的位置 $ {X_{{\text{peak}}}} $ $ {N_{\text{f}}} = 3 $ ) 及网格横向厚度比 $ {D_{\text{r}}}{\text{ = }}9.5 $ [45 ] 的空间演化实验不同,但中心线上湍流强度大小刚好介于其实验中 $ {D_{\text{r}}}{\text{ = }}8.5 $ ${D_{\text{r}}}{\text{ = 13.0}}$ 图15 (a)与Laizet等[18 ] 的空间演化数值模拟结果相似的是,在本研究的时间演化初始阶段,RGT产生的尾流尺度要大于FGT产生的小尺度,导致其湍流强度大于FGT,但随着时间演化,FGT的大尺度运动加剧,此后( $ T > 22{T_{\text{r}}} $ ) 大部分衰减阶段FGT的湍流强度大小至少为RGT的2倍. 另外,在 $ T = 300{T_{\text{r}}} $ $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {(T/{T_{\text{r}}})^{ - 6/5}} $ $ {{\boldsymbol{u}}_{{\text{rms}}}} $ 图15 (b)中,RGT中心线上 $ R{e_{\lambda ,{\text{c}}}} $ $ T \approx {\text{6}}{T_{\text{r}}} $ $ R{e_{\lambda ,{\text{c}}}} $ $ T \approx 50{T_{\text{r}}} $ $ R{e_{\lambda ,{\text{c}}}} $
Similarity of decaying isotropic turbulence with a passive scalar
1
2004
... 为了观察网格中心线上流向脉动速度偏导数的分布形态,利用其流向脉动速度偏导数的偏斜度 $ {S_{\partial u/\partial x}}{\text{ = }}{\langle {(\partial u'/\partial x)^3}\rangle _x}/\langle {(\partial u'/\partial x)^2}\rangle _x^{3/2} $ $ {F_{\partial u/\partial x}}{\text{ = }}{\langle {(\partial u'/\partial x)^4}\rangle _x}/\langle {(\partial u'/\partial x)^2}\rangle _x^2 $ 2 类统计量进行分析. 2类统计量随时间演化结果如图16 所示. 可以看出,分形网格的多尺度特性导致了FGT的 $ {S_{\partial u/\partial x}} $ $ {F_{\partial u/\partial x}} $ $ {S_{\partial u/\partial x}} $ $ {S_{\partial u/\partial x}} \approx - 0.5 $ . 并且Antonia等[46 ] 和Burattini等[47 ] 关于均匀各向同性湍流研究中也发现,当 $ R{e_\lambda } < 60 $ $ - {S_{\partial u/\partial x}} \sim 0.5 $ . 此外,尽管FGT的 $ {F_{\partial u/\partial x}} $ $ {F_{\partial u/\partial x}} $ [32 ] 之前在网格湍流空间演化实验中,发现当 $ R{e_\lambda } < 100 $ $ 2 \leqslant {F_{\partial u/\partial x}} \leqslant 5 $ $ {S_{\partial u/\partial x}} $
Velocity derivative skewness in isotropic turbulence and its measurement with hot wires
1
2008
... 为了观察网格中心线上流向脉动速度偏导数的分布形态,利用其流向脉动速度偏导数的偏斜度 $ {S_{\partial u/\partial x}}{\text{ = }}{\langle {(\partial u'/\partial x)^3}\rangle _x}/\langle {(\partial u'/\partial x)^2}\rangle _x^{3/2} $ $ {F_{\partial u/\partial x}}{\text{ = }}{\langle {(\partial u'/\partial x)^4}\rangle _x}/\langle {(\partial u'/\partial x)^2}\rangle _x^2 $ 2 类统计量进行分析. 2类统计量随时间演化结果如图16 所示. 可以看出,分形网格的多尺度特性导致了FGT的 $ {S_{\partial u/\partial x}} $ $ {F_{\partial u/\partial x}} $ $ {S_{\partial u/\partial x}} $ $ {S_{\partial u/\partial x}} \approx - 0.5 $ . 并且Antonia等[46 ] 和Burattini等[47 ] 关于均匀各向同性湍流研究中也发现,当 $ R{e_\lambda } < 60 $ $ - {S_{\partial u/\partial x}} \sim 0.5 $ . 此外,尽管FGT的 $ {F_{\partial u/\partial x}} $ $ {F_{\partial u/\partial x}} $ [32 ] 之前在网格湍流空间演化实验中,发现当 $ R{e_\lambda } < 100 $ $ 2 \leqslant {F_{\partial u/\partial x}} \leqslant 5 $ $ {S_{\partial u/\partial x}} $
Energy transfer in turbulent flows behind two side-by-side square cylinders
1
2020
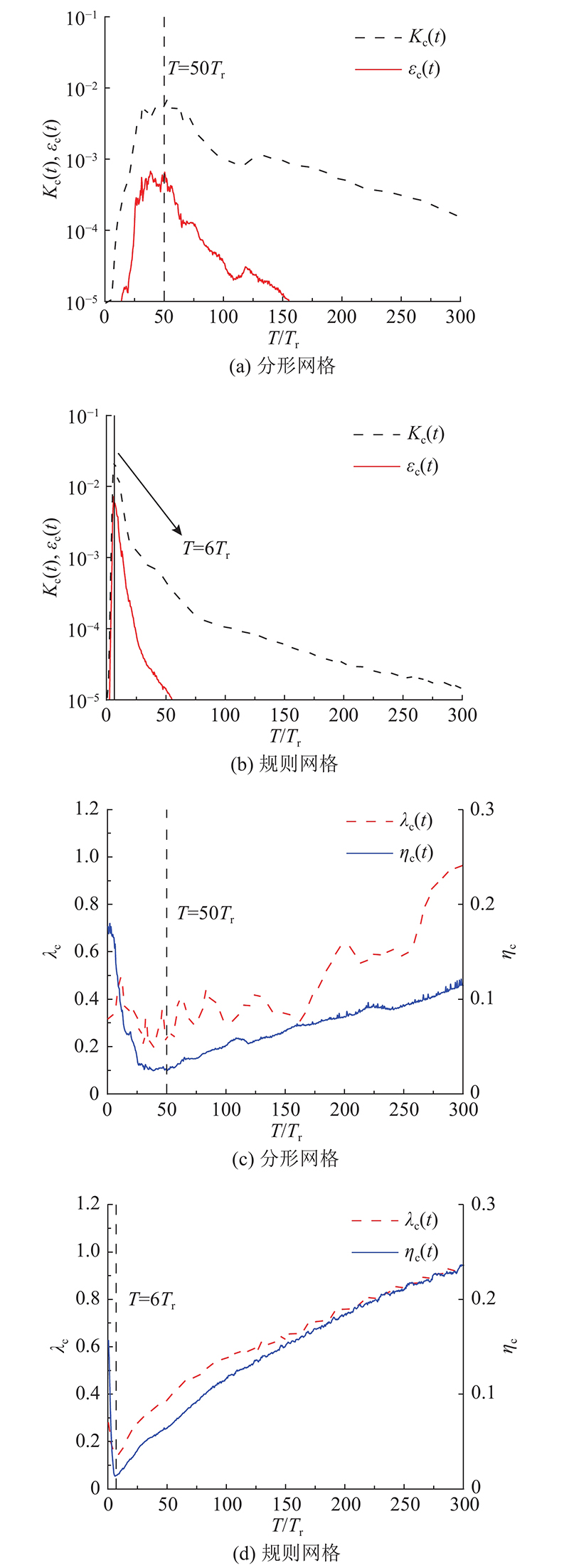
... 流场湍流动能(turbulent kinetic energy)的表达式为 $ K(t){\text{ = }}\langle u_{{\text{rms}}}^2+v_{{\text{rms}}}^2+w_{{\text{rms}}}^2\rangle /2 $ $ \langle \cdot \rangle $ X 、Y 和Z 这3个方向进行空间平均. 如图17 所示为网格中心线上 $ {K_{\text{c}}}(t) $ $ {\varepsilon _{\text{c}}}(t) $ $ {\lambda _{\text{c}}}(t) $ $ {\eta _{\text{c}}}(t) $ $ {\varepsilon _{\text{c}}}{\text{ = }}2\nu {\langle {S_{ij}}{S_{ij}}\rangle _x} $ $ {\eta _{\text{c}}} = {\varepsilon _{\text{c}}}^{ - 1/4}{\nu ^{3/4}} $ 图17 (a)、(b)中,FGT和RGT网格中心线上湍流动能始终大于能量耗散,2类网格湍流 $ {K_{\text{c}}}(t) $ $ {\varepsilon _{\text{c}}}(t) $ 图14 (b)、(d)湍流强度峰值时刻一致. 在图17 (c)、(d)中须注意的是,根据Kolmogorovs长度尺度的定义,在 $ T < 22{T_{\text{r}}} $ ( 见图15 (a))时,RGT中心线上湍流强度大于FGT的,尾流相互作用使得RGT的耗散率 $ {\varepsilon _{\text{c}}}(t) $ $ {\eta _{\text{c}}}(t) $ $ T > 22{T_{\text{r}}} $ 图17 (a)、(b)可知其耗散率 $ {\varepsilon _{\text{c}}}(t) $ $ {\eta _{\text{c}}}(t) $ 图17 (c)、(d)可以看出,2类湍流中心线上 $ {\lambda _{\text{c}}} $ $ {\lambda _{\text{c}}} $ [48 ] 在对双方柱绕流的能量逐尺度转移的研究中发现,在流场下游区域方柱产生的尾流近乎完全湍流,变得更加各向同性和均匀. 因此可以预知的是,本研究FGT和RGT经过较长的时间演化之后也会产生类似的效果. ...
Statistical theory of turbulence-II
1
1935
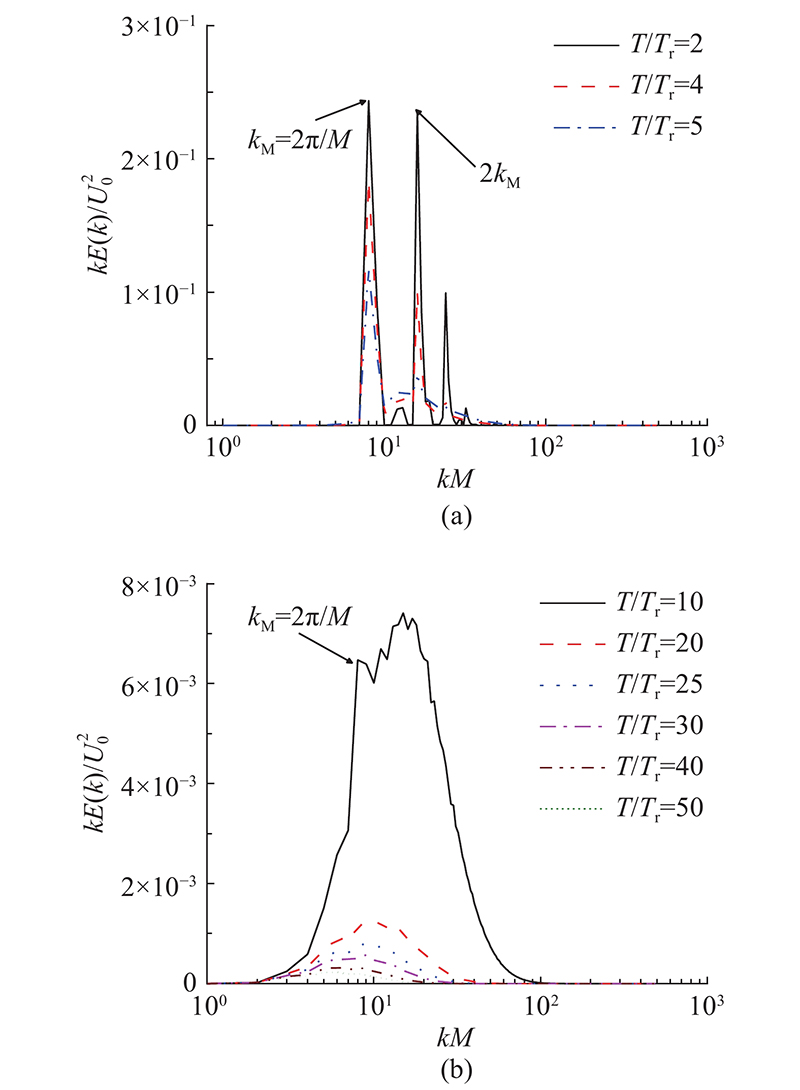
... 众所周知,泰勒耗散定律[49 ] $ \varepsilon (t) \propto {{\boldsymbol{u}}_{{\text{rms}}}}{{\text{(}}t{\text{)}}^3}/{L_{\text{u}}}(t) $ $ kM \approx L_{\text{u}}^{ - 1}( \approx {k_{\text{f}}}) $ $ {L_{\text{u}}} $ $ {k_{\text{f}}} = 1 $ [50 ] 进行了高雷诺数下外力强迫周期性盒子湍流的DNS仿真,结果表明该假说在 $ kM \geqslant 20{k_{\text{f}}} $ $ [k,\infty ] $ $ {K > }(k,t) $ $ {\varepsilon > }(k,t) $
Local equilibrium hypothesis and Taylor’s dissipation law
1
2016
... 众所周知,泰勒耗散定律[49 ] $ \varepsilon (t) \propto {{\boldsymbol{u}}_{{\text{rms}}}}{{\text{(}}t{\text{)}}^3}/{L_{\text{u}}}(t) $ $ kM \approx L_{\text{u}}^{ - 1}( \approx {k_{\text{f}}}) $ $ {L_{\text{u}}} $ $ {k_{\text{f}}} = 1 $ [50 ] 进行了高雷诺数下外力强迫周期性盒子湍流的DNS仿真,结果表明该假说在 $ kM \geqslant 20{k_{\text{f}}} $ $ [k,\infty ] $ $ {K > }(k,t) $ $ {\varepsilon > }(k,t) $
Small-scale energy cascade of the solar wind turbulence
1
2008
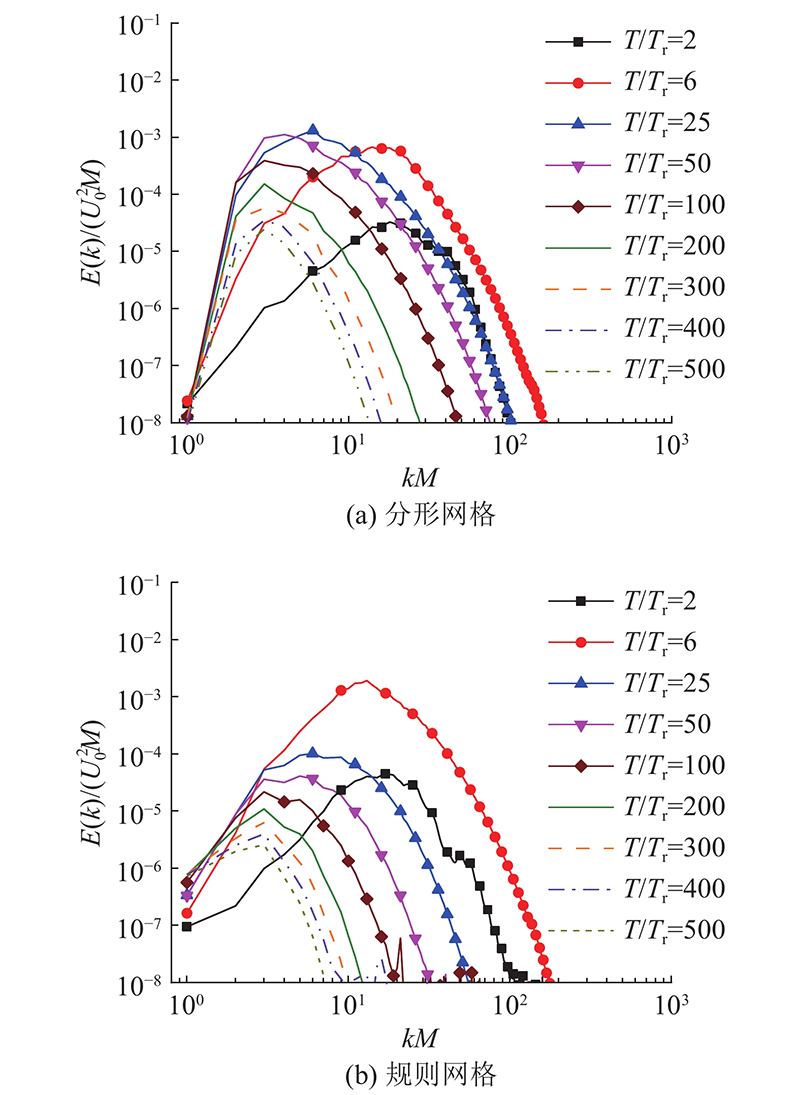
... 如图19 (a)、(b)所示分别为FGT和RGT在不同截断波数下的湍流动能和耗散率随时间演化的结果. 可以看出,2类网格湍流几乎都是当截断波数 $ kM \approx 20{k_{\text{f}}} $ [51 ] 过程中的能量传输与耗散相平衡的特点. 当波数 $ kM > 20{k_{\text{f}}} $ $ T \approx 6{T_{\text{r}}} $ 图14 (b)和(d)的湍流强度分析中. 结合图15 (a)和图18 ,在时间演化的初期,RGT在尾流运动产生的能量和耗散都大于FGT的,说明可以利用分形结构实现对流动的被动控制,进而有针对性的减缓能量的衰减. 在进入衰减期后,FGT产生的能量及耗散率比RGT更大,足以表明FGT大尺度运动逐渐加剧,起到了强化湍流的作用. ...
The large-scale structure of homogeneous turbulence
1
1967
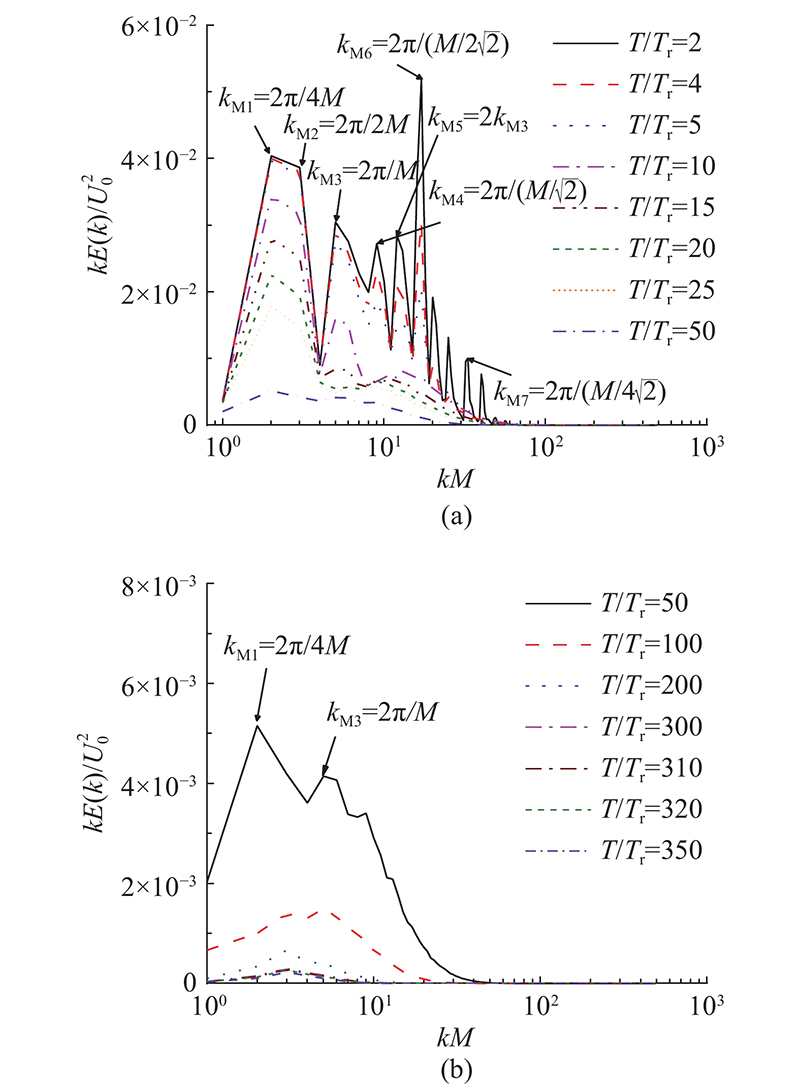
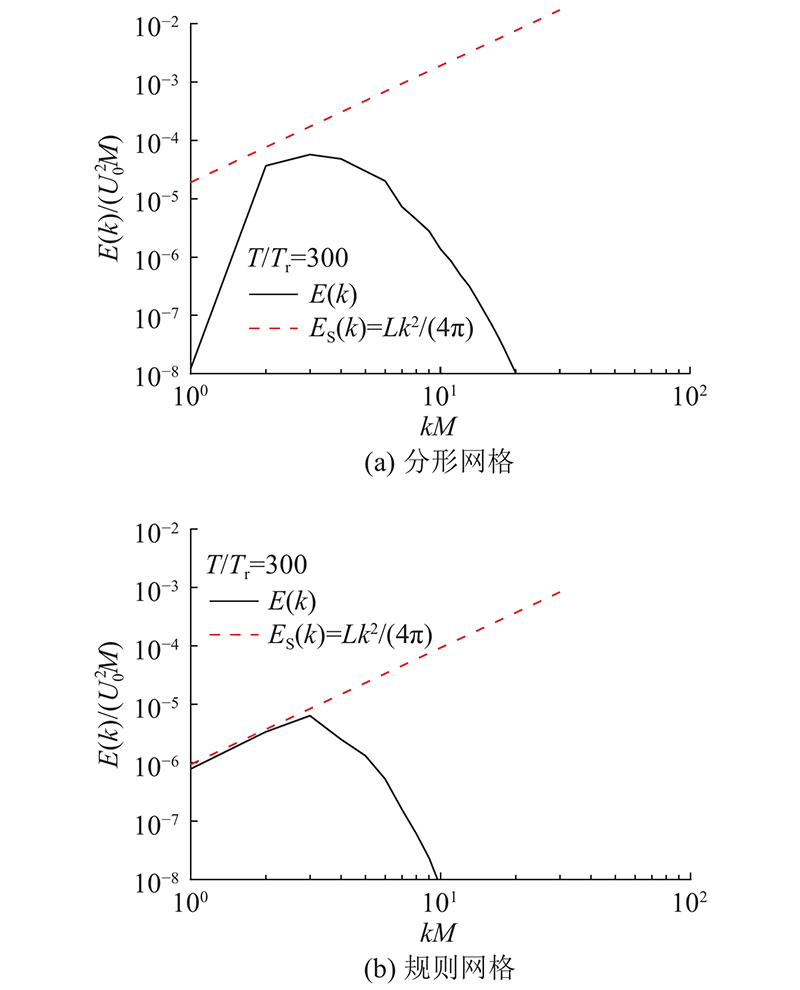
... 长期以来,学界对于网格湍流中的大尺度结构到底是属于Saffman类型还是Batchelor类型存在很大争议,尚未有明确的结论. 这2种湍流的衰减规律完全不同,其中Saffman湍流[52 ] 的湍动能衰减规律遵循 $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 6/5}} $ [53 ] 则遵循 $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 10/7}} $ . 结合图15 (a)的分析可知,在时间达到 $ T = 300{T_{\text{r}}} $ $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 6/5}} $ . 因此对比分析2类湍流场在低波数下的Saffman能谱[54 ] ${E_{\text{S}}}({{k}}){\text{ = }} L{k^2}/(4{{\text{π}} ^2})$ $ E(k) $
The large-scale structure of homogenous turbulence
1
1956
... 长期以来,学界对于网格湍流中的大尺度结构到底是属于Saffman类型还是Batchelor类型存在很大争议,尚未有明确的结论. 这2种湍流的衰减规律完全不同,其中Saffman湍流[52 ] 的湍动能衰减规律遵循 $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 6/5}} $ [53 ] 则遵循 $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 10/7}} $ . 结合图15 (a)的分析可知,在时间达到 $ T = 300{T_{\text{r}}} $ $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 6/5}} $ . 因此对比分析2类湍流场在低波数下的Saffman能谱[54 ] ${E_{\text{S}}}({{k}}){\text{ = }} L{k^2}/(4{{\text{π}} ^2})$ $ E(k) $
Is grid turbulence Saffman turbulence?
1
2010
... 长期以来,学界对于网格湍流中的大尺度结构到底是属于Saffman类型还是Batchelor类型存在很大争议,尚未有明确的结论. 这2种湍流的衰减规律完全不同,其中Saffman湍流[52 ] 的湍动能衰减规律遵循 $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 6/5}} $ [53 ] 则遵循 $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 10/7}} $ . 结合图15 (a)的分析可知,在时间达到 $ T = 300{T_{\text{r}}} $ $ \langle {\boldsymbol{u}}_{{\text{rms}}}^2\rangle \sim {t^{ - 6/5}} $ . 因此对比分析2类湍流场在低波数下的Saffman能谱[54 ] ${E_{\text{S}}}({{k}}){\text{ = }} L{k^2}/(4{{\text{π}} ^2})$ $ E(k) $
格子乱流のエネルギー減衰域における不変量について
1
2012
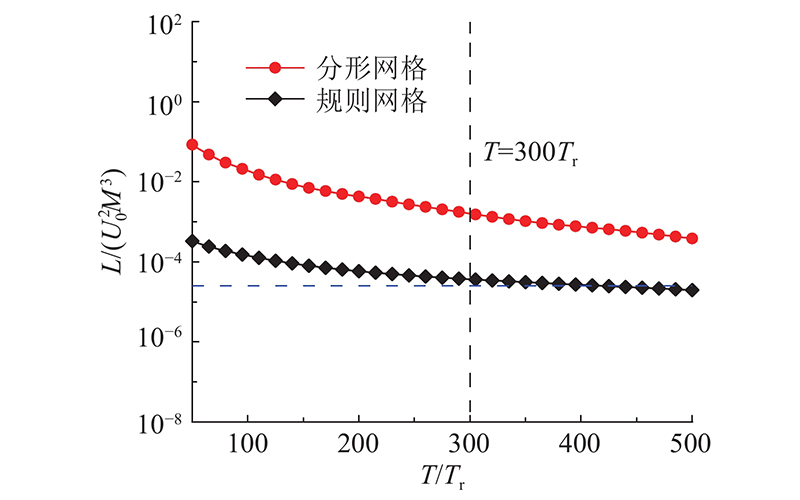
... 如图22 所示为Saffman积分L 的时间演化结果,积分范围为 $0 \leqslant \left| {\boldsymbol{r}} \right| \leqslant {r_0}$ $ {r_0} $ $\langle {\boldsymbol{u}}'({\boldsymbol{x}}){\boldsymbol{u}}'({\boldsymbol{x}}+ {r_0}{{\boldsymbol{e}}_x})\rangle = 0$ . 随着时间的推移,FGT和RGT的Saffman积分L 持续减小,尽管FGT减小的更加缓慢,但两者趋势基本相同. 北村拓也等[55 ] 的规则网格湍流空间演化实验证明了在远离网格的下游区域( $ X/M > 100 $ ) ,L 会保持不变. 在图22 中,RGT的L 在 $ T \approx 300{T_{\text{r}}} $ L 依然在大幅减小,说明RGT中的大尺度结构要比FGT更早显现出Saffman类型特征. ...
格子乱流のエネルギー減衰域における不変量について
1
2012
... 如图22 所示为Saffman积分L 的时间演化结果,积分范围为 $0 \leqslant \left| {\boldsymbol{r}} \right| \leqslant {r_0}$ $ {r_0} $ $\langle {\boldsymbol{u}}'({\boldsymbol{x}}){\boldsymbol{u}}'({\boldsymbol{x}}+ {r_0}{{\boldsymbol{e}}_x})\rangle = 0$ . 随着时间的推移,FGT和RGT的Saffman积分L 持续减小,尽管FGT减小的更加缓慢,但两者趋势基本相同. 北村拓也等[55 ] 的规则网格湍流空间演化实验证明了在远离网格的下游区域( $ X/M > 100 $ ) ,L 会保持不变. 在图22 中,RGT的L 在 $ T \approx 300{T_{\text{r}}} $ L 依然在大幅减小,说明RGT中的大尺度结构要比FGT更早显现出Saffman类型特征. ...