流体机械的内流仿真在现代透平机械设计中起着至关重要的作用,非均匀介质复杂流动现象(如相变和空化)为传统数值模拟方法带来挑战. 传统网格法(如有限体积法)在计算叶轮机械均质流动方面已较为成熟且有广泛工业应用,但前处理过程须分模块划分网格在计算时要引入混合平面法、旋转坐标系法或转子冻结法等假设或简化方法,捕捉多相界面须基于体积分数进行界面重构,上述设置易引入误差,丢失部分流动细节.
无网格粒子法在拉格朗日框架下,采用无固定拓扑关系的流体粒子代替网格和节点,适用于计算非定常大变形流动. 采用整体离散和整体求解,无须将流体域分块建模和拼接、无须额外处理动静交界,易于捕捉多相界面运动,有望为叶轮机械复杂内流模拟,尤其是针对非均质多相流动,提供一种新的解决方案.
已有许多学者将无网格法应用于流体机械内流数值模拟,Sun等[1]用移动粒子半隐式法(moving particle semi-implicit,MPS)模拟带有6个直叶片与6个导叶的三维搅拌器. 王锋等[2]利用MPS方法研究Y型微混合器内的流动混合机理. Rahim[3]采用改进的不可压缩光滑粒子流体动力学方法(incompressible smoothed particle hydrodynamic,ISPH)模拟微泵混合器内的流动和传质. Min等[4]建立了一个高压斜齿轮泵模型,采用MPS方法获得了较FVM更优的结果. Kakuda等[5]用MPS方法研究液环泵内水环的形成. 此外,由于在齿轮交界处难以建立高质量的动网格,无网格法也常用于模拟齿轮箱或减速器内的油液流动[6-8].
1. 数值方法
1.1. 控制方程
MPS方法用于模拟不可压缩流动,质量守恒方程与动量守恒方程如下:
式中:
1.2. 粒子间作用模型
MPS法将计算区域离散为带有物性、流动以及热力学参数的粒子,通过粒子间相互作用,离散控制方程中的各项微分算子,导出梯度算子和拉普拉斯算子的光滑近似式,计算各时间层粒子的流动参数,随时间推进动态获取整场流动信息.
式中:
式中:
1.3. 不可压缩模型
MPS法基于粒子数密度的偏移与修正来构造不可压缩模型,粒子数密度定义如下:
在拉格朗日框架下,将1个时间步分为显、隐2步来解耦合速度与压力. 显式计算黏性力以及体积力,得到粒子位移、速度的估算值,由此估算粒子数密度
采取散度自由条件法[19]构造压力泊松方程,引入伪可压系数
2. GSW-NSD壁面边界与验证
2.1. GSW-NSD原理
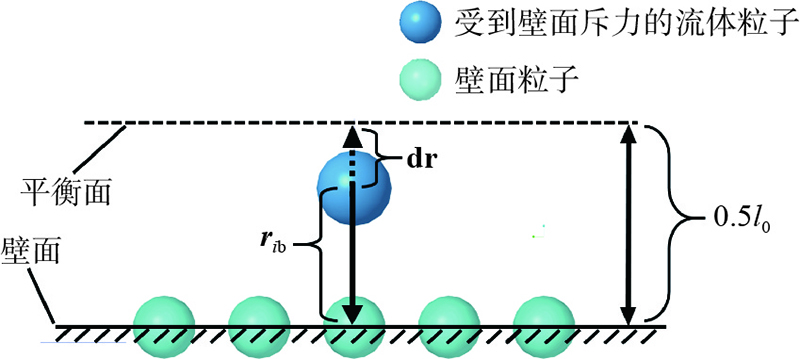
图 1
式中:
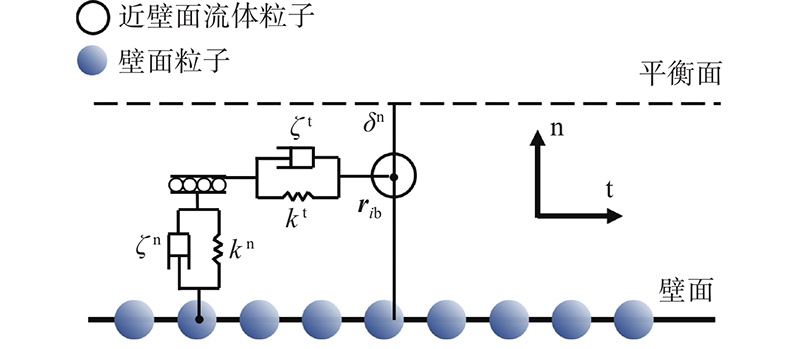
图 2
式中:
根据运动学定律,粒子向平衡面移动距离即
式中:m为粒子质量.
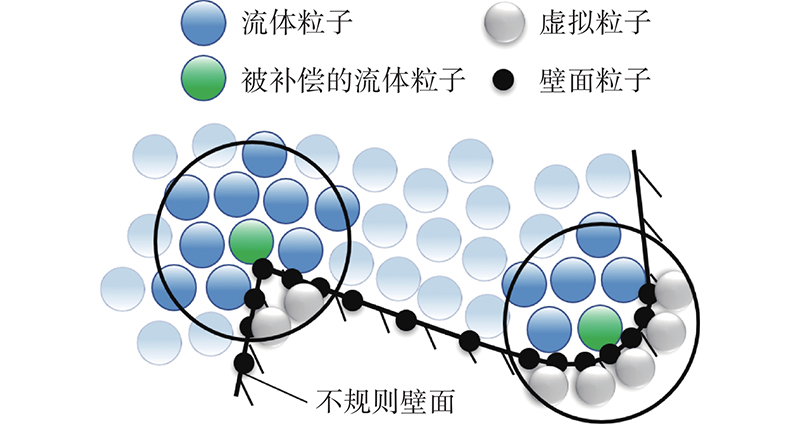
对于壁面附近液体粒子,其核近似域被壁面边界截断,粒子数密度偏小,导致各个算子计算不准. GSW基于经验公式构造壁面补偿函数,虽然在二维情况下补偿效果较好,但对于三维算例,较难得到合适的补偿函数. 本研究耦合无表面粒子判定技术(non-surface detection technique,NSD),引入虚拟粒子,补偿粒子数密度缺失的流体粒子,如图3所示.
图 3
图 3 复杂几何处的粒子数密度补偿方法
Fig.3 Approach to compensate particle-number-density loss around complex geometry
虚拟粒子从数值层面补足粒子数密度,补偿作用与流体粒子受到的核截断程度相关,即与壁面边界的形状相关,与壁面粒子的分布无关,在壁面加密后无须再引入虚拟粒子来解决边界缺失问题. 新的粒子数密度定义为
式中:
式中:M为i粒子搜索范围内的其余液体粒子数,
2.2. 壁面粒子模型建立
在采用GSW-NSD模型时,壁面粒子不参与压力计算,只通过法向量传递壁面信息,粒子尺度(疏密)与斥力大小无关,可以抽象看作节点. 据此特性提出适用于任意三维曲面的壁面粒子建模方法.
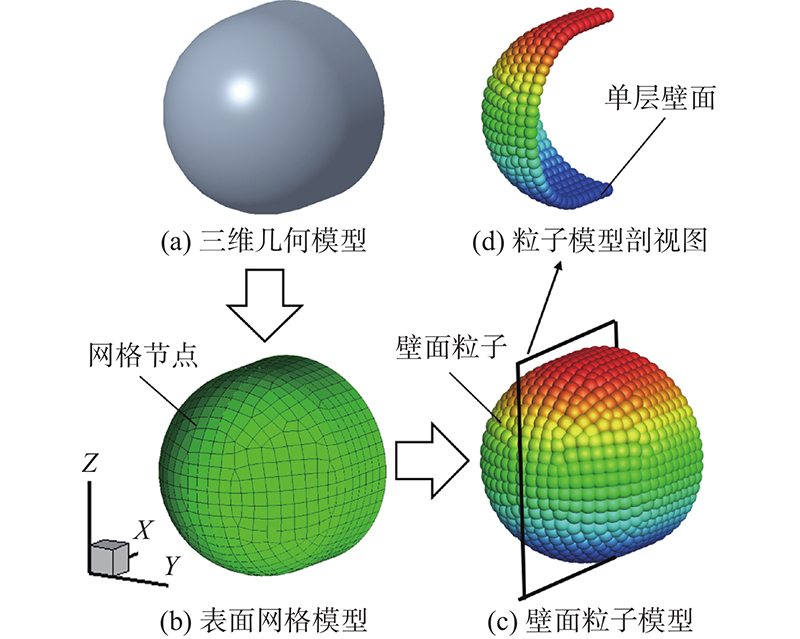
图 4
壁面粒子的生成不依赖网格的拓扑结构,即使是扭曲网格或负体积网格,只要节点分布足够密集,仍可利用本模型进行计算,网格质量对计算结果无影响. 本研究使用ICEM划分面网格,由于对网格质量要求不高,其他可在几何曲面上生成节点的常用软件或程序也可满足要求. 得到的壁面模型由单层粒子组成,叶片内部空心,且尖角以及大曲率表面都可以得到较好表达(见图4(c)).
2.3. 壁面粒子局部加密与嵌套加密技术
2.3.1. 局部加密
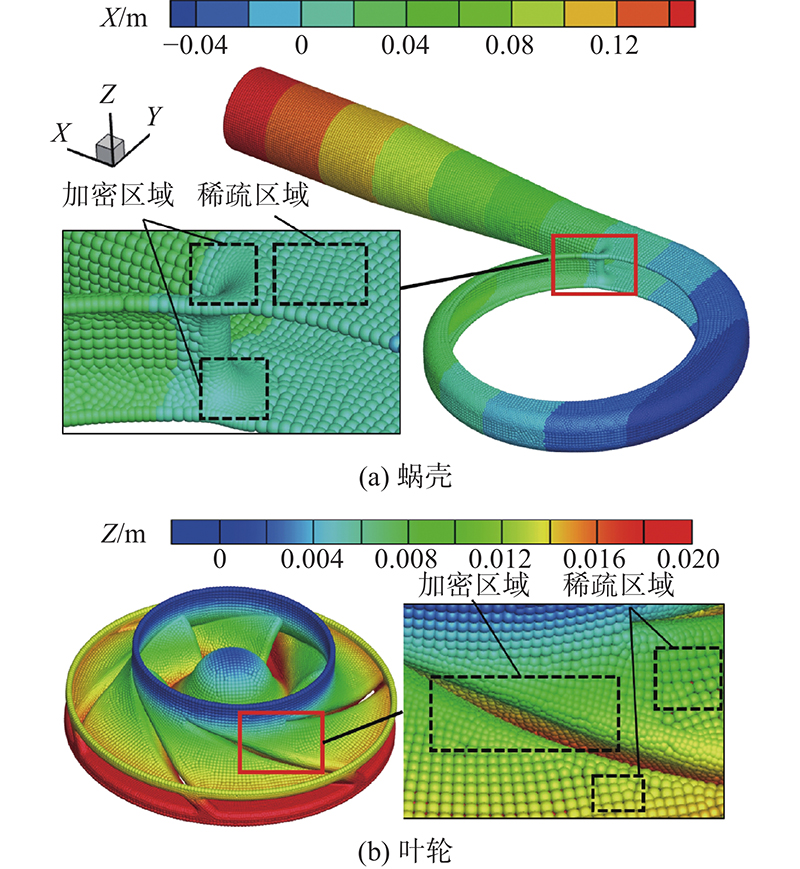
壁面粒子不参与压力计算,其间距对计算结果无影响,只体现壁面的离散程度. 3个壁面粒子即可精确表达1个平面,对于曲面离散,壁面粒子数量越多,离散精度越高. 本研究提出一种壁面粒子局部加密技术,即采用更多的壁面粒子来精确离散主曲率较大的曲面,如图5所示为离心泵蜗舌、倒圆角以及弯扭叶片的局部加密. 采用较少的粒子离散平面或主曲率较小的表面,从而在保证高离散精度的同时,减小计算量.
图 5
在本研究使用的光滑壁面(GSW)模型中,斥力的大小主要由流体粒子到壁面边界的距离决定,与壁面粒子的疏密无关;壁面粒子加密可以使流体粒子流经曲面时受到过渡更加光滑的斥力,从而减小非物理的压力振荡,提高计算稳定性并增强收敛性.
2.3.2. 异面粒子干涉与嵌套加密
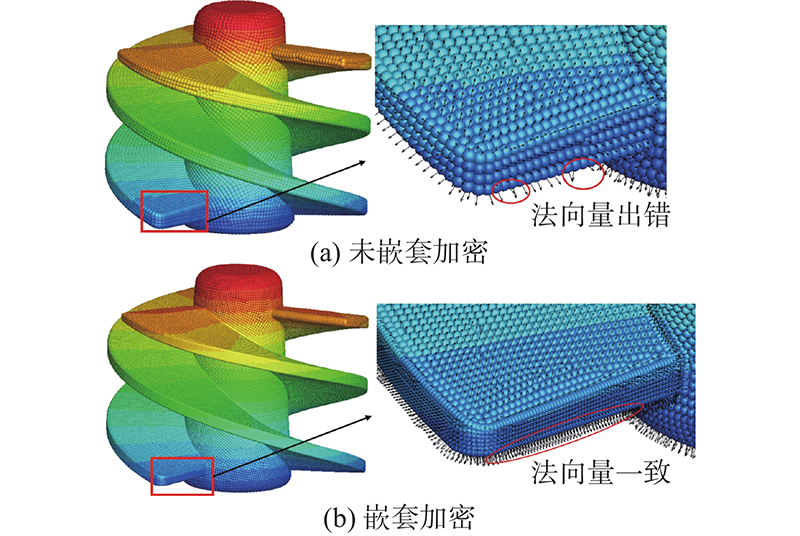
流体机械存在较多薄壁结构,如轮盘、轮盖和叶片等,在计算法向量时,薄壁结构端面粒子易受附近壁面(异面)粒子的干涉,导致法向量计算方向出错,如图6(a)所示.
图 6
常规基于网格法的加密技术由于拓扑结构的限制,较难实现相邻网格模块之间的网格(粒子)加密突跃. 本研究基于拉格朗日法无固定拓扑结构的特性,提出嵌套加密方法,可以将局部结构进行独立加密(见图6(b))并与其他结构直接组合,实现该薄壁结构的高精度离散与法向量的准确计算. 嵌套加密的层数与具体几何形状以及法向量计算精度相关,本研究建议端面离散一般需6层以上.
2.4. 模型离散精度评价指标
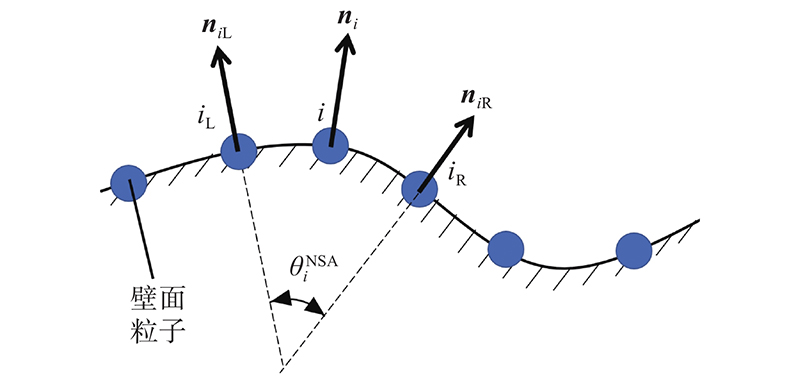
为了评价离散后粒子模型的几何精度,定义法向光滑角度(normal smooth angle)为评价指标. 如图7所示,以二维曲线为例,对于壁面粒子
图 7
各个壁面粒子的法向光滑角度取标准差即得到该壁面模型的离散精度评估参数
式中:
对于如图5所示的离心泵模型,采用本研究方法加密处理后的壁面粒子数为75377,离散精度为
3. 数值模拟与结果分析
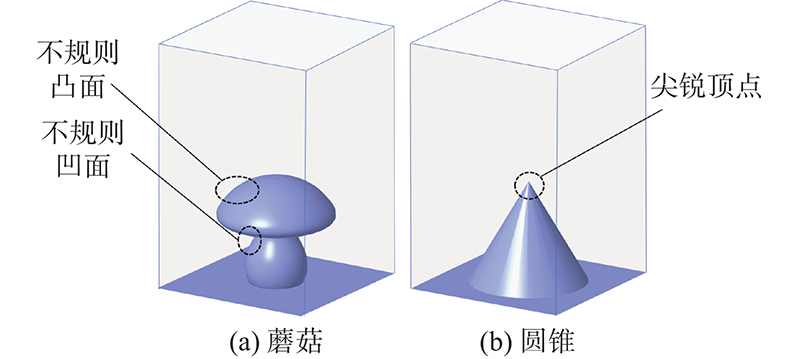
3.1. 带有典型结构的三维静水验证算例
图 8
蘑菇和圆锥表面采用加密布置,壁面粒子间距为1 mm,水箱壁面采用稀疏布置,粒子间距为2 mm. 蘑菇算例与圆锥算例的总壁面粒子数依次为31331、29504,模型离散精度
图 9
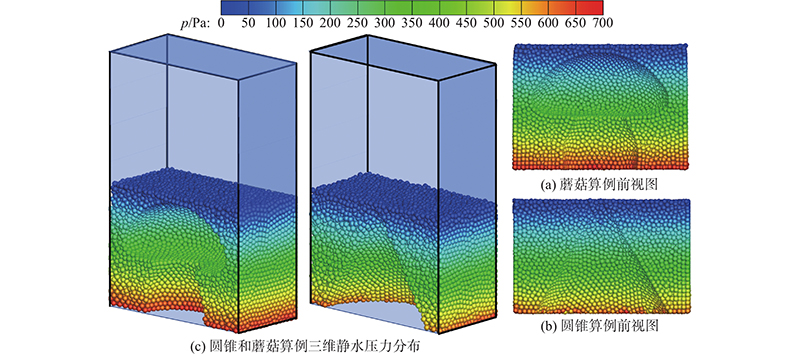
X方向半截面的压力分布如图10所示. 图中,p为压力. 静水压力分布连续且与理论值一致,蘑菇算例的不规则凹凸面被液体粒子均匀贴合. 圆锥算例尖角并未导致液体粒子非物理振荡,2个算例的自由面在长时间计算过程中均保持水平稳定. 蘑菇与圆锥算例的底部压力误差分别为0.6%、1.3%.
图 10
图 10 复杂静水算例半截面压力与自由面位置
Fig.10 Position of free surfaces and pressure distribution of complicated hydrodynamic cases
3.2. 溃坝撞击挡板算例
图 11
图 11 实验[21]液柱形态(t=0.4 s)与仿真结果(t=0.439 s)对比
Fig.11 Comparison of liquid’s shape between experiment result (t=0.4 s) and simulation result (t=0.439 s)
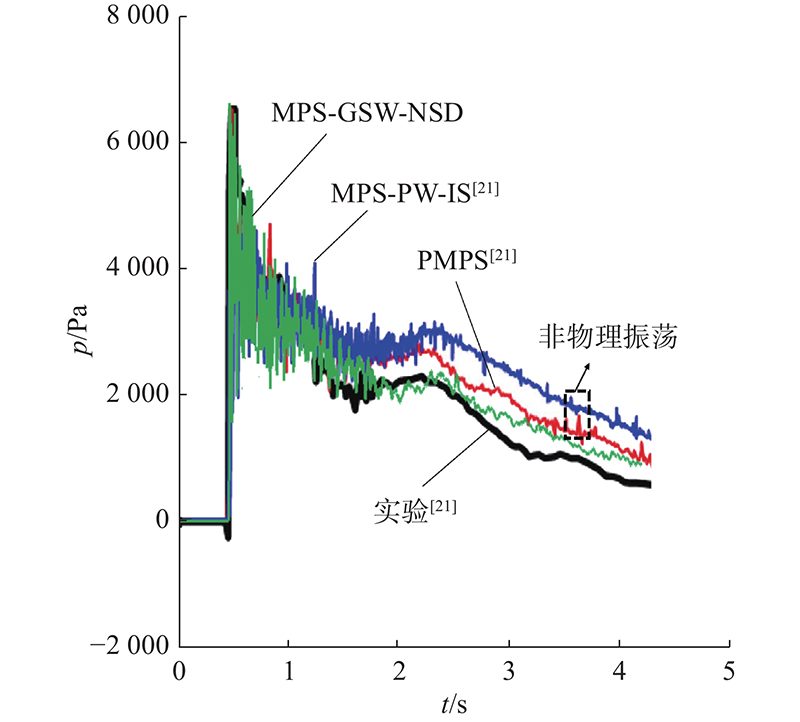
测点处压力随时间波动如图12所示,相较于其他高精度算法如MPS-PW-IS和PMPS,本研究结果更加接近实验结果,且在t=3 s后压力振荡尖峰较少,结果相对更稳定.
图 12
3.3. 诱导轮水中旋转算例
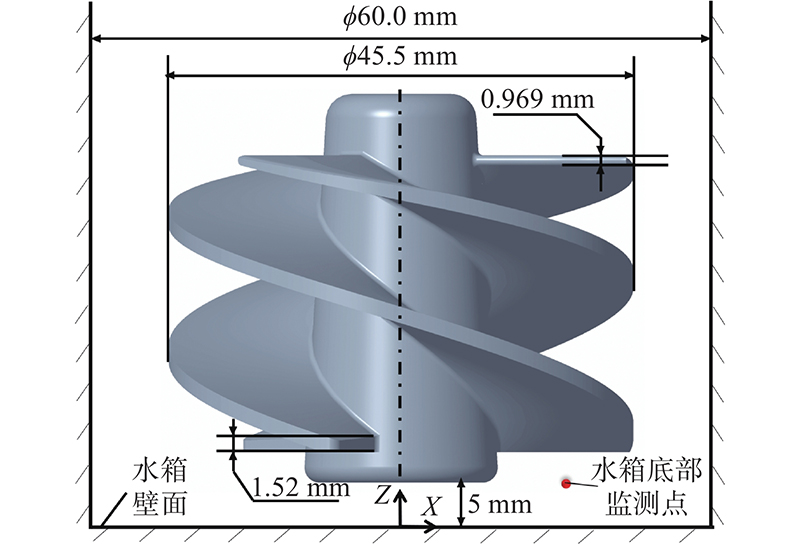
为了验证复杂流动情况下,经本方法离散出的壁面模型仍具有较好的力学性能,选取离心泵内的诱导轮结构进行计算,几何模型如图13所示. 叶片厚度较小,与诱导轮直径比约为1∶47,且该厚度沿轴向逐渐变化(最小厚度0.969 mm,最大厚度1.520 mm). 诱导轮叶片呈螺旋形,叶根、叶顶及叶片端面处的法向量计算易受轮毂及叶片工作面壁面粒子的干涉.
图 13
图 13 诱导轮算例几何模型与水箱底面监测点位置
Fig.13 Geometry of inducer and monitoring position at bottom of water tank
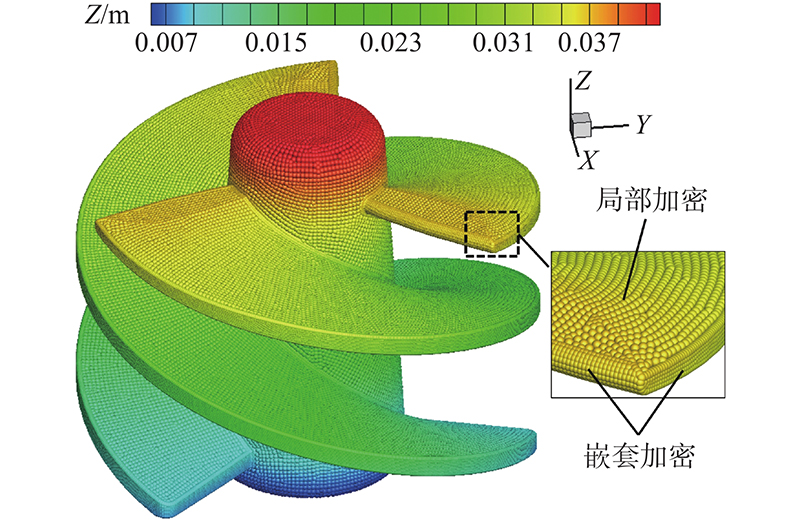
利用本研究方法对诱导轮不同部件进行局部加密,轮毂粒子和水箱壁面粒子间距均为0.8 mm,螺旋叶片粒子间距为0.6 mm. 对于尺寸较小的叶片侧壁,采用间距为0.2 mm的壁面粒子进行嵌套加密,加密结果如图14所示. 诱导轮模型壁面粒子数为80584,圆柱形水箱壁面粒子数为27417,整体模型离散精度为
图 14
螺旋叶片沿Z轴正方向转动,持续向水箱底面输运流体并造成压力冲击,转速为200 r/min. 底部流体经由叶片与水箱间隙流回自由面,尺寸较小的间隙使得叶片后沿易产生多个叶尖漩涡,加剧流动的复杂程度. 流体机械内部流动多为湍流,本研究主要关注前处理工作并验证离散方法和壁面模型有效性,暂未考虑湍流模型,相关研究内容将在后续工作中报道. 流体运动黏度为5.0×10−4 m2/s,密度为1000 kg/m3,
为了对比计算结果,采用有限体积法对同参数条件下该模型进行计算,通过网格无关性验证的网格数为752万. 2种方法针对流体域的离散过程如图15所示.
图 15
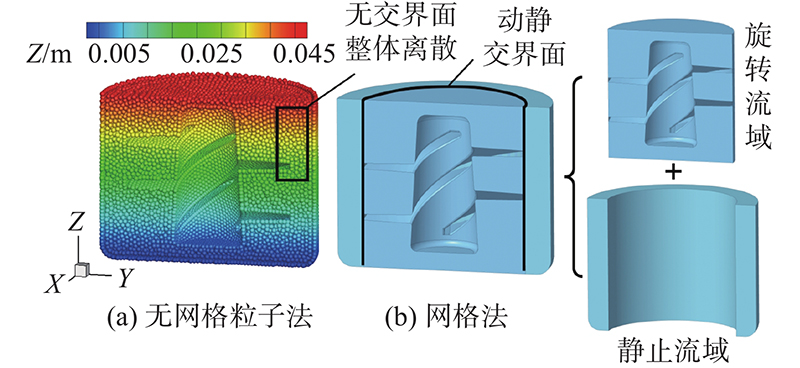
图 15 无网格法与网格法对流域的离散方式
Fig.15 Discretization of fluid domains by particle-based and mesh-based methods
传统网格方法往往须将流体域划分为旋转流域和静止流域,并建立动静交界面实现2个流域的信息传递,如图15(b)所示. 无网格粒子法利用带有物性的液体粒子整体离散流域,液体粒子依据NS方程流动到任意地方,再与当地周围的流体和固体粒子建立力学关系,无须将流体域分为动/静模块,也因此不涉及动静交界面.
初始流体域可以利用重力和粒子的自适应性对本方法建立的高精度壁面模型进行自动填充布置. 对于诱导轮算例,保持叶片静止,在叶轮上方布置足量的液体粒子并开始自由下落,液体粒子在重力作用下逐渐填充叶片间隙,当流体基本静止即平均粒子数密度稳定时,提取此时流体粒子坐标并作为初始分布.
图 16
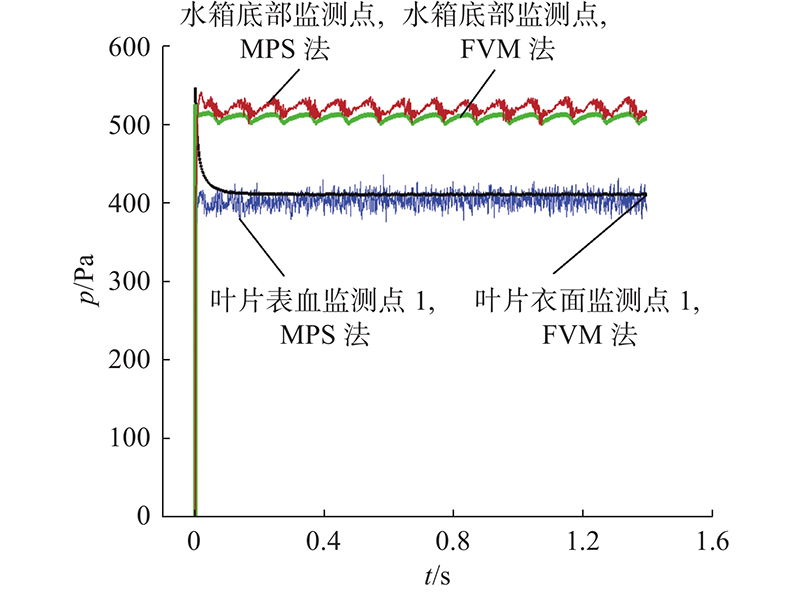
图 16 诱导轮旋转算例底部、表面压力对比
Fig.16 Comparison of pressure at bottom and surface of inducer rotating case
图 17
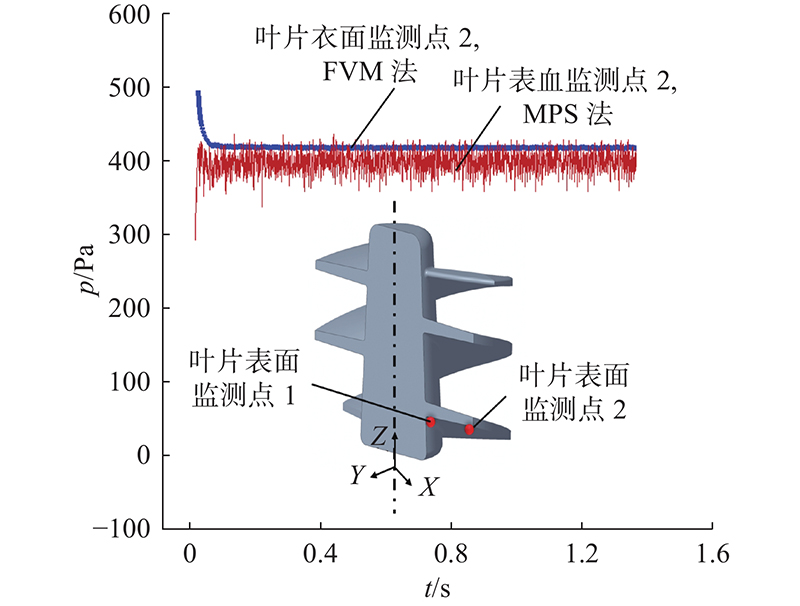
图 17 监测点位置与表面压力监测点处的压力对比
Fig.17 Position of monitoring points and comparison of pressure at surface monitoring points
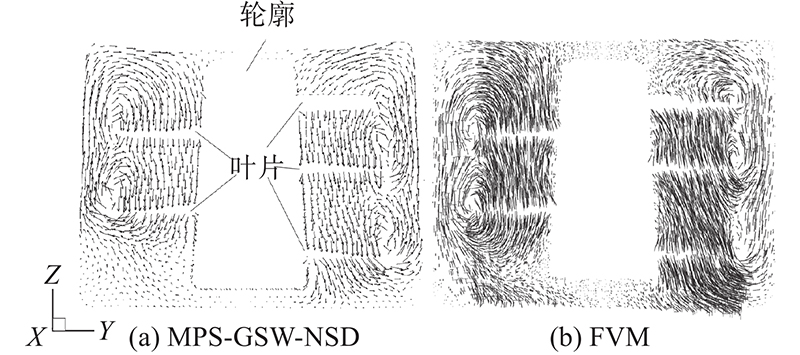
从定量比较看,2种方法在监测点的压力波动频率、幅值一致;压力值误差较小,水箱底部平均误差为2.31%,峰值误差为4.90%,叶片表面压力误差依次为4.1%和2.3%. 从流动细节看,2种方法计算出的流场分布较接近,图示时刻5个叶尖漩涡都得到了较好的体现. 在本方法计算过程中液体粒子紧贴壁面,较好地表达了壁面形状,说明在复杂流动情况下,经本方法离散后的壁面模型仍可保持较好的力学性能.
图 18
4. 结 论
本研究采用无网格MPS法,基于通用光滑壁面边界模型(GSW)与无表面粒子判定技术(NSD),针对目前无网格粒子法较难处理流体机械中常见复杂型面的问题,建立了一套任意三维曲面的高精度通用离散方法,结论如下:
(1)提出基于MPS-GSW-NSD的分级离散方法. 先整体离散复杂壁面,借助面网格建立高精度壁面粒子模型,再向壁面模型内填充布置流体粒子;整体离散复杂流域,无须分块处理动/静流体域.
(2)提出离散过程的嵌套加密技术. 区别对待不同尺寸及曲率复杂型面的壁面粒子分布密度,避免了异面粒子干涉,有效提升了壁面法向量计算的准确性. 针对流体机械中的特征几何形状如弯扭叶片和薄壁结构,建立了一套有效的离散方法.
(3)提出单一型面内局部加密技术. 基于GSW模型的壁面粒子尺度对计算无影响的特点,在单一几何型面内粒子离散分布密度任意可调,实现了计算精度与计算效率的可调节.
(4)建立粒子离散精度评价方法. 基于法向光滑角度建立离散精度的评价方法,为评估和优化粒子离散精度提供了分析工具和优化依据.
此外,本研究通过计算包含不规则凹凸面和尖点的三维静水算例,验证了本方法处理复杂三维几何的能力. 通过计算溃坝撞击挡板算例,验证了离散后的壁面模型的准确性;通过计算诱导轮水中旋转算例,证明了在复杂流动情况下,本模型仍能保证正确的壁面作用以及压力计算的稳定性. 本研究仅给出某型号离心泵的泵壳、闭式叶轮和诱导轮等主要通流结构的离散评估方法,后续可将本方法扩展至密封等间隙流动结构,实现更加细致和全面的数值模拟.
参考文献
Numerical simulation of the flow in straight blade agitator with the MPS method
[J].
Y型微混合器内流流场移动粒子半隐式法数值分析
[J].DOI:10.7652/xjtuxb202105018 [本文引用: 1]
Numerical analysis of flow field in the Y-type micromixer using MPS method
[J].DOI:10.7652/xjtuxb202105018 [本文引用: 1]
Incompressible SPH modeling of rotary micropump mixers
[J].
Study on fluid flow analysis of high-pressure positive displacement pump without clearance
[J].
Three-dimensional fluid flow simulations using GPU-based particle method
[J].
Lubrication mechanism in gearbox of high-speed railway trains
[J].
Numerical modeling of churning power loss of gear system based on moving particle method
[J].
Numerical simulations of oil flow inside a gearbox by Smoothed Particle Hydrodynamics (SPH) method
[J].
Moving-particle semi-implicit method for fragmentation of incompressible fluid
[J].DOI:10.13182/NSE96-A24205 [本文引用: 1]
无网格法中边界畸变的控制与计算效率的提高
[J].
Improvement of boundary aberration and computation efficiency in meshless method
[J].
Improved treatment of wall boundary conditions for a particle method with consistent spatial discretization
[J].
Improvement of pressure distribution to arbitrary geometry with boundary condition represented by polygons in particle method
[J].
Improvement of boundary conditions for non-planar boundaries represented by polygons with an initial particle arrangement technique
[J].DOI:10.1080/10618562.2016.1167194 [本文引用: 1]
A generic smoothed wall boundary in multi-resolution particle method for fluid-structure interaction problem
[J].
Improving stability of MPS method by a computational scheme based on conceptual particles
[J].
Multi-resolution MPS method
[J].
Improved MPS method with variable-size particles
[J].
An improved MPS method for numerical simulations of convective heat transfer problems
[J].
Stabilization and smoothing of pressure in MPS method by quasi-compressibility
[J].
A fully Lagrangian method for fluid-structure interaction problems with deformable floating structure
[J].
Enhancement of stabilization of MPS to arbitrary geometries with a generic wall boundary condition
[J].