受交通检测器自身故障、通讯异常及外部环境等一系列不确定因素的影响,采集的交通数据会出现不同程度的缺失问题. 交通数据质量决定后续数据分析与预测的准确性,影响交管部门对交通运行状况的合理诱导,因此有效的修复方法对交通数据的处理极其必要.
交通流数据缺失类型有完全随机缺失、随机缺失及非随机缺失[1]. 对于前2类缺失模式,主要有插补修复法和预测修复法. 前者常在限定时间范围内根据相邻点估计待插补点,该方法对插补点及相邻点间的关联关系考虑不足[1-4]. 后者以历史数据及其关联性为依据修复缺失值,主要方法有时间相关、空间相关和时空相关修复法. 时间相关修复法通过挖掘交通流时序规律,修复缺失数据[5-7]. 空间相关修复法依据不同位置检测器的数据,修复缺失值[8-10]. 单一的时间、空间修复法无法体现交通流完整的时空特性,目前该领域以时空相关修复法为研究热点. 陆百川等[11]建立神经网络模型,学习交通流时空关系,预测缺失值. 王薇等[12]依据3D形函数插值理论,利用交通流时空特性修复缺失值. 鉴于图卷积网络在空间特征提取方面的优势,Wang等[13]将路网结构嵌入图卷积层,捕获图节点间的空间关系. 张伟斌等[14]以路段为节点构建图序列,利用图卷积层提取相邻车道间的空间关系. 上述方法虽然较有效地修复了缺失数据,但对交通流潜在的时空关系刻画欠充分,如交通流时间自相关性、路网节点间的权连接关系.
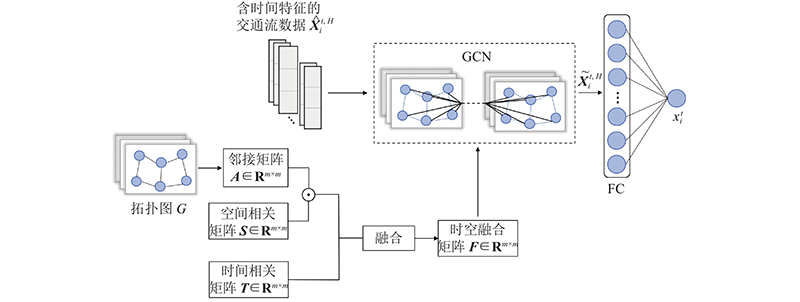
本文提出时空融合图卷积网络(spatio-temporal fusion graph convolutional network,STF_GCN),修复交通流缺失数据. STF_GCN分别采用自相关函数和关联函数,计算交通流时间自相关系数和空间关联度系数. 依据交通检测器的部署位置构建拓扑图,将拓扑图与关联系数构成的时间、空间矩阵进行融合,得到时空融合矩阵,用时空融合矩阵替代图卷积层的邻接矩阵,挖掘交通流细粒化的时空关系. 模型利用轻量级一维卷积学习原始多通道时序向量的时间特征,利用图卷积层,将时间特征和时空融合矩阵进行特征级融合,通过全连接得到缺失点的预测修复值.
1. 交通流时空特性分析
1.1. 交通流时间自相关性分析
交通流的时序特性主要表现为同一路段的交通流数据按照一定的趋势随时间变化[15]. 一方面,历史时刻的交通状态与当前时刻的交通状态具有自相关特性;另一方面,居民行程的规律性使得交通流变化趋势呈现一定程度的相似性和周期性. 对于检测器
式中:
式中:
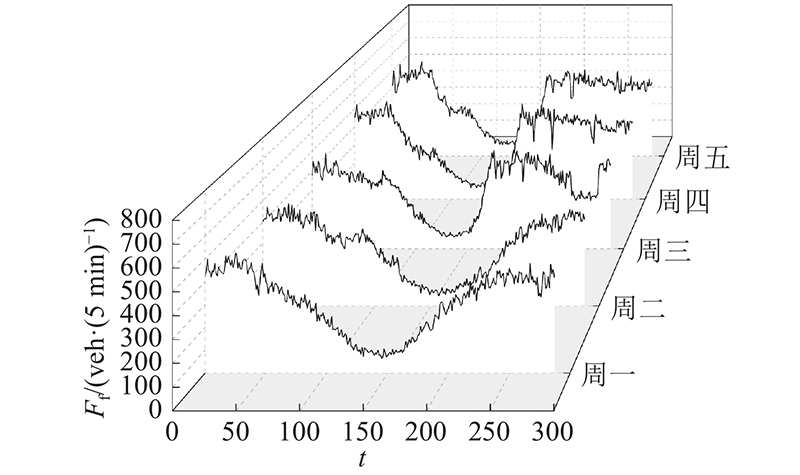
图 1
图 1 detect_0工作日交通流量的时间相关性分析
Fig.1 Time correlation analysis of traffic flow of detect_0 in working days
表 1 detect_0工作日交通流量的自相关性分析结果
Tab.1
| 检测器 | | 检测器 | | |
| detect_0 | 0.87 | detect_3 | 0.88 | |
| detect_1 | 0.88 | detect_4 | 0.86 | |
| detect_2 | 0.85 | — | — |
表 2 detect_0工作日交通流量的相关性分析结果
Tab.2
| 时间点 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 周一 | 1.00 | 0.90 | 0.66 | 0.75 | 0.77 |
| 周二 | 0.90 | 1.00 | 0.41 | 0.50 | 0.53 |
| 周三 | 0.66 | 0.41 | 1.00 | 0.90 | 0.89 |
| 周四 | 0.75 | 0.50 | 0.90 | 1.00 | 0.97 |
| 周五 | 0.77 | 0.53 | 0.89 | 0.97 | 1.00 |
1.2. 交通流空间权连接特性分析
交通流数据的空间关联性不仅表现为不同路段、相同路段上的不同检测器或上下游与研究路段间基本的空间位置关系,而且表现为路网节点的空间权连接关系. 现有研究大多通过表示节点间基本连接状态的邻接矩阵描述交通流的空间特性,较少考虑路网节点间的权连接关系[17],节点间的权连接是量化交通流空间内部特性的重要手段,因此以交通检测器的部署位置为节点,通过关联函数量化节点间的几何关联关系,挖掘交通流细粒化的空间特性.
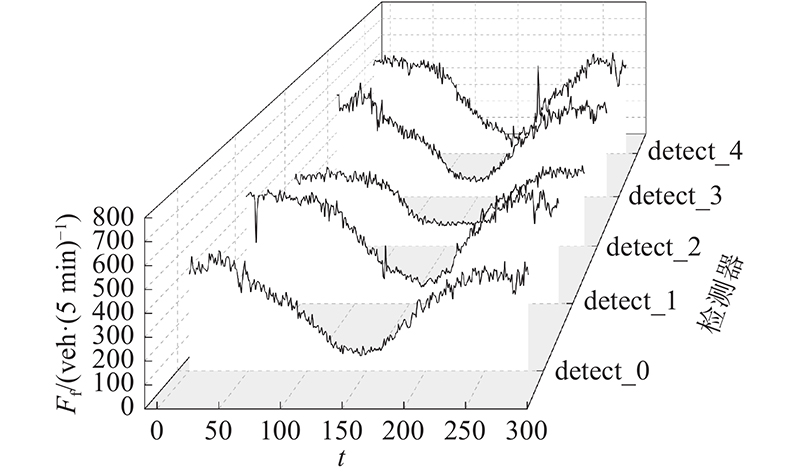
图 2
图 2 多检测器交通流量空间关联性分析
Fig.2 Spatial correlation analysis of traffic flow of multi-detector
依据式(2)计算检测器
表 3 多检测器交通流量的空间关联度系数
Tab.3
| 检测器 | detect_0 | detect_1 | detect_2 | detect_3 | detect_4 |
| detect_0 | 1.00 | 0.85 | 0.78 | 0.94 | 0.85 |
| detect_1 | 0.85 | 1.00 | 0.87 | 0.87 | 0.93 |
| detect_2 | 0.78 | 0.87 | 1.00 | 0.81 | 0.85 |
| detect_3 | 0.94 | 0.87 | 0.81 | 1.00 | 0.86 |
| detect_4 | 0.85 | 0.93 | 0.85 | 0.86 | 1.00 |
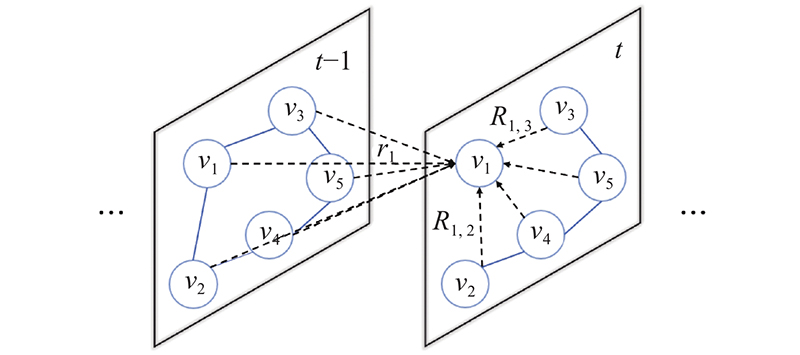
为了充分刻画交通流细粒化的时空关系,图3结合交通流时空特性及交通检测器的部署位置,构建时空融合权连接关系图. 图中,节点
图 3
2. 时空融合图卷积网络修复模型
区别于传统的图卷积网络,将多检测器节点的时空序列组织为图结构数据,构建可提取细粒化时空特性的时空融合图卷积网络修复模型STF_GCN. 考虑到图卷积网络(graph convolutional network, GCN)共享节点信息的特性会导致模型训练过程中易出现节点特征丢失的问题[18],图卷积中表示节点间连接状态的邻接矩阵仅能反映交通流最基本的空间位置关系,因此模型采用关联函数分别计算交通流时空维度的关联系数,构建时空融合矩阵,替代GCN的邻接矩阵,学习交通流细粒化的时空关系. 由于图卷积在处理多节点交通流序列时花费的时间代价较高,一维卷积网络(one-dimensional convolutional neural network,1D-CNN)被广泛应用于提取时序数据的关联信息,训练速度比循环神经网络更快[19].模型构建时在主要组件图卷积网络的前端加入一维卷积层,在数据降维的同时,保证了多节点交通流数据的细粒化时空特征提取,以满足实际场景中数据修复任务的精度和实时性要求.
2.1. 时空融合矩阵
为了描述交通流时间特性和空间特性所刻画的内在关联关系,依据图3时空融合权连接关系图的结构,通过线性融合规则构建时空融合矩阵
式中:
式中:
式中:
式中:矩阵
2.2. STF_GCN修复模型
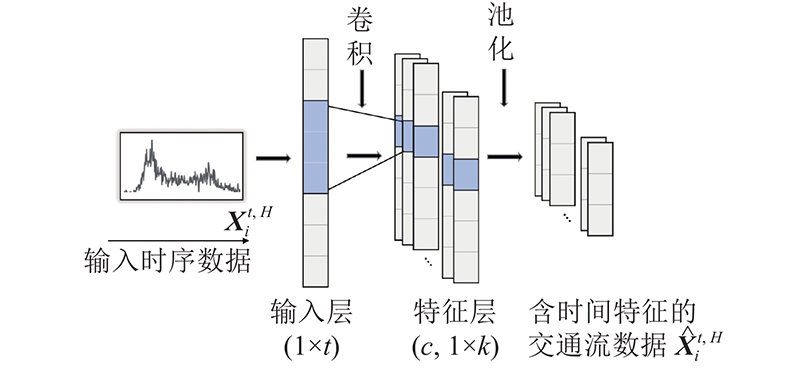
在时间层面上,交通流数据表现为随时间变化的一维向量. 提取时间特征传统的方法有循环神经网络(recurrent neural network, RNN)、长短时记忆神经网络(long-short term memory, LSTM)及变体,虽然RNN、LSTM及变体的时间特征提取模型在时序数据上表现良好,但模型训练所需要的时间复杂度较高,而一维卷积组件具有局部感知、权值共享、平移不变三方面的优势,可以大大缩减模型训练的参数量,使其在不改变输入数据结构的前提下,减少数据冗余,提取关键的时间变化特征,以降维的方式提高模型的训练效率. 1D-CNN网络结构如图4所示.
图 4
设
将
式中:·表示点积运算,
式中:
图 5
图5中,GCN的输入层包括2个部分:1D-CNN输出的含有时间特征信息的交通流数据
式中:
式中:
3. 实验验证
3.1. 数据集描述
以2016年7月至8月收集于San Bernaridino的PeMS08公共数据集为研究对象,PeMS08数据集共有170个检测器,采集的时间间隔为5 min,即1小时有12个时间片,可以将一天24小时划分为288个时间片,共计17 856个时间片,数据缺失比率为0.696%,属于连续时间序列中的部分随机缺失情况. 提出的STF_GCN模型可以修复连续时间序列上的任何缺失点数据,各个缺失点的修复相互独立. 实验以6∶2∶2的比例将数据集划分为训练集、验证集和测试集,其中验证集用来评价模型的泛化能力. 利用最大最小归一化,将交通流数据归一化为[0, 1.0]. 模型使用Adam优化器和均方损失函数,训练轮数ep为100,学习率lr和批次大小bt的设置如表4所示. 从表4可知,当lr = l0−3,bt = 64时,模型效果最优. 针对连续交通流数据中的随机缺失情况,将一小时12个时间片下的历史交通流作为输入时序向量,预测修复下一个时间片的交通流量,构建STF_GCN模型修复检测器
表 4 STF_GCN模型参数
Tab.4
| lr | bt | MAE | RMSE |
| 8×l0−4 | 32 | 31.517 | 35.689 |
| 8×l0−4 | 64 | 25.926 | 30.926 |
| 8×l0−4 | 128 | 25.935 | 32.121 |
| l0−3 | 32 | 30.438 | 34.633 |
| l0−3 | 64 | 24.981 | 29.952 |
| l0−3 | 128 | 26.505 | 32.489 |
| 1.2×l0−3 | 32 | 25.542 | 31.490 |
| 1.2×l0−3 | 64 | 25.520 | 30.561 |
| 1.2×l0−3 | 128 | 25.542 | 31.490 |
3.2. 结果分析
利用2.1节的时空融合矩阵构建方法,分别计算路网检测器的时间自相关系数和空间关联度系数. 依据检测器的部署位置构建拓扑图,得到邻接矩阵
表 5 时空融合矩阵的关联度分析结果
Tab.5
| 检测器 | detect_0 | detect_1 | detect_2 | ··· | detect_m-1 | detect_m |
| detect_0 | 0.8742 | 0 | 0 | ··· | 0 | 0 |
| detect_1 | 0 | 0.8827 | 0.8712 | ··· | 0 | 0 |
| detect_2 | 0 | 0 | 0.8523 | ··· | 0 | 0 |
| | | | | | | |
| detect_m-1 | 0 | 0 | 0 | ··· | 0.8677 | 0 |
| detect_m | 0 | 0 | 0 | ··· | 0 | 0.7901 |
选取图卷积网络(GCN)修复模型、基于拉普拉斯矩阵的图卷积网络(LGCN)修复模型、基于时空相关的1D-CNN_GCN修复模型、基于时空相关的LSTM_GCN修复模型,与本文所提的修复模型进行对比. LGCN将归一化的拉普拉斯矩阵作为GCN的输入. 1D-CNN_GCN修复模型将1D-CNN学习到的时间特征与拓扑图
为了验证本文模型的性能,选择平均绝对值误差(MAE)和均方根误差(RMSE)作为评价指标,验证模型的修复效果. MAE反映模型修复值与真实值间的绝对误差平均值,RMSE反映模型修复值与真实值间的偏离程度,即两者残差的标准偏差. 计算表达式如下:
式中:
图 6
图 6 不同方法在多个检测器上的修复结果
Fig.6 Repair results of different methods on multiple detectors
从图6可以看出,比较不同方法修复的交通流量值与真实值间的偏离程度可知,偏离程度最小的是STF_GCN修复模型. LSTM_GCN修复模型在高峰期的修复流量值和真实值间的偏离程度比其他模型大,高峰时段LGCN修复模型在多个检测器上的修复误差高于GCN,在低峰时段的修复误差低于GCN修复模型. 1D-CNN_GCN模型的修复效果在整体上优于GCN和LGCN修复模型.
图 7
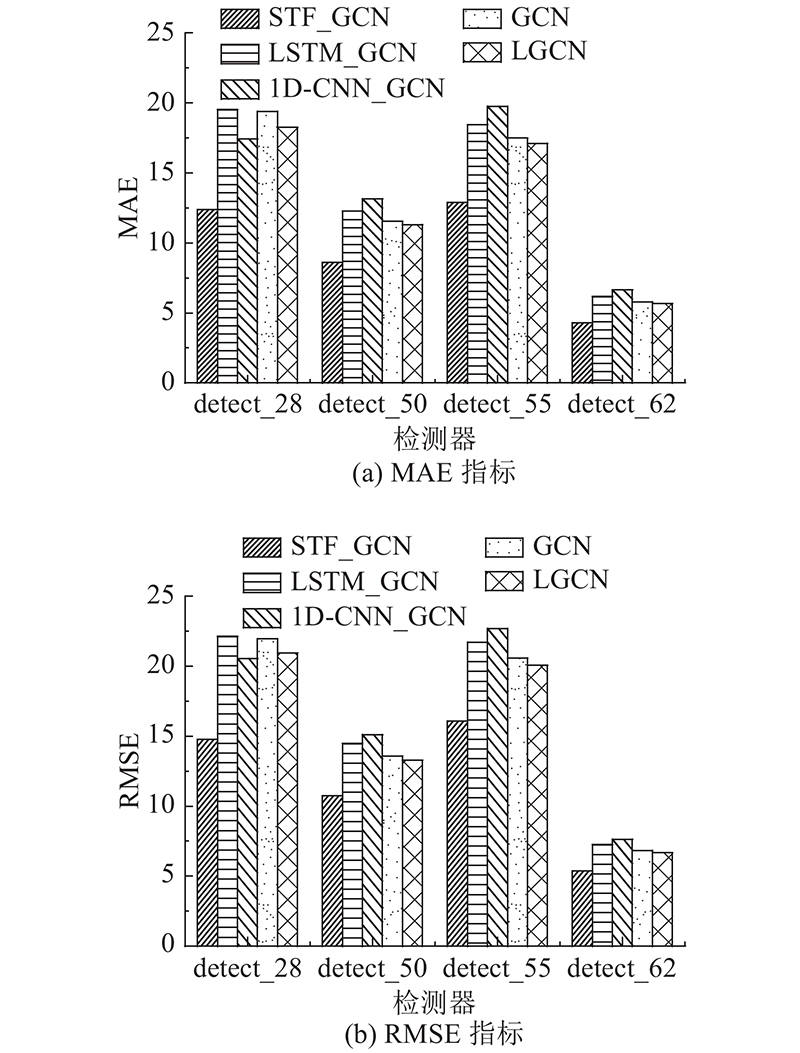
图 7 不同方法在多个检测器上的修复误差对比
Fig.7 Comparison of repair errors of different methods on multiple detectors
从图7可知,STF_GCN修复方法在多检测器场景中的修复精度和稳定性均优于其他方法. 从表6可知,经修复的detect_28、detect_50、detect_55、detect_62检测器的MAE分别为12.38、8.61、12.89、4.30,RMSE分别为14.77、10.74、16.08、5.36. STF_GCN修复模型在PeMS08数据集中的平均MAE和RMSE均低于其他修复模型, MAE和RMSE分别为24.98、29.95. 单一的空间相关修复模型GCN、LGCN虽然不是最优,但能够粗略地预测个别检测器的部分缺失流量. 交通流数据的本质是时间序列,单纯考虑空间相关的修复方法忽略了交通流数据的时序规律. 从整体上看,时空相关修复模型1D-CNN_GCN和LSTM_GCN的修复效果均优于GCN、LGCN,但MAE和RMSE值均高于STF_GCN. 1D-CNN_GCN和LSTM_GCN中表示节点间连接关系的邻接矩阵
STF_GCN通过线性融合规则建立的时空融合矩阵可以避免GCN训练过程中出现节点特征丢失的问题,捕获交通流更细粒化的时空特性. STF_GCN使用轻量级1D-CNN学习多通道时序向量的时间特征,使用GCN学习交通流数据的空间特征,可以保证在充分挖掘交通流时空特性的同时加快模型收敛速度. 如表7所示为不同修复模型收敛速度的测试结果. 表中,tc为模型计算时间. 可以看出,STF_GCN模型收敛最快. 1D-CNN_GCN模型的收敛速度与STF_GCN相当,但MAE和RMSE均高于STF_GCN. LSTM_GCN的时间复杂度最高,约为STF_GCN的3倍,与LSTM_GCN相比,所提的STF_GCN模型可以通过多通道时序向量降维的方式,加快模型的收敛速度.
表 6 不同方法的修复误差对比
Tab.6
| 检测器 | GCN | LGCN | 1D-CNN_GCN | LSTM_GCN | STF_GCN | |||||||||
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |||||
| detect_28 | 19.42 | 21.97 | 18.26 | 20.93 | 17.46 | 20.56 | 19.54 | 22.13 | 12.38 | 14.77 | ||||
| detect_50 | 11.54 | 13.59 | 11.31 | 13.27 | 13.16 | 15.11 | 12.29 | 14.47 | 8.61 | 10.74 | ||||
| detect_55 | 17.50 | 20.58 | 17.12 | 20.05 | 19.76 | 22.7 | 18.45 | 21.72 | 12.89 | 16.08 | ||||
| detect_62 | 5.80 | 6.84 | 5.69 | 6.66 | 6.65 | 7.63 | 6.17 | 7.26 | 4.30 | 5.36 | ||||
| | | | | | | | | | | | ||||
| PeMS08 | 26.77 | 31.69 | 28.38 | 33.40 | 28.72 | 33.85 | 25.65 | 30.52 | 24.98 | 29.95 | ||||
表 7 模型收敛速度的对比
Tab.7
| 模型 | tc | 模型 | tc | |
| GCN | 207.6 | LSTM_GCN | 589.1 | |
| LCGN | 191.3 | STF_GCN | 162.3 | |
| ID-GNN_GCN | 162.6 | — | — |
4. 结 语
为了解决时空修复法挖掘交通流时空信息粗粒化的问题,本文提出基于时空融合图卷积网络的交通流缺失数据修复模型STF_GCN. 该模型结合多检测器的部署位置建立空间拓扑图,通过线性融合规则构建时空融合矩阵,作为图卷积层的邻接矩阵. 在提取多节点交通流时间自相关性的同时挖掘图节点的空间权连接信息,利用轻量级一维卷积学习多通道时序向量的时间特征,减少后续输入GCN的参数量. 利用图卷积学习交通流数据的空间特征,在满足精度要求的前提下达到加快模型收敛速度的目的. 经实验例证分析可知,相较于其他修复法,STF_GCN在多检测器场景中的修复精度和模型收敛速度均优于其他方法,可以为交管部门后续的控制决策相关工作提供较可靠的数据保障. 限于计算量的原因,本文暂未考虑复杂路网和数据波动程度大的交通流缺失情况,未来将进一步探索多车道、多数据场景路网间的数据修复问题.
参考文献
A hybrid approach to integrate fuzzy C-means based imputation method with genetic algorithm for missing traffic volume data estimation
[J].DOI:10.1016/j.trc.2014.11.003 [本文引用: 2]
PPCA-based missing data imputation for traffic flow volume: a systematical approach
[J].
基于张量分解理论的车道级交通流数据修复算法
[J].
Lane-level traffic flow data restoration algorithm based on tensor decomposition theory
[J].
基于S-G滤波的交通流故障数据识别与修复算法
[J].
Traffic flow fault data identification and repair algorithm based on S-G filtering
[J].
基于交通流数据修复的GA-RF方法研究
[J].
Research on GA-RF method based on traffic flow data restoration
[J].
动态交通数据故障识别与修复方法
[J].DOI:10.3321/j.issn:1671-1637.2004.01.030 [本文引用: 1]
Fault identification and repair methods of dynamic traffic data
[J].DOI:10.3321/j.issn:1671-1637.2004.01.030 [本文引用: 1]
动态交通数据异常值的实时筛选与恢复方法
[J].
Real time screening and recovery method of outliers of dynamic traffic data
[J].
交通流缺失数据处理方法比较分析
[J].DOI:10.3963/j.issn.1674-4861.2018.02.009
Comparative analysis of missing data processing methods in traffic flow
[J].DOI:10.3963/j.issn.1674-4861.2018.02.009
基于灰色残差GM(1, N)模型的交通流数据恢复算法
[J].DOI:10.3969/j.issn.1009-6744.2012.01.008 [本文引用: 1]
Traffic flow data recovery algorithm based on grey residual GM(1, N) model
[J].DOI:10.3969/j.issn.1009-6744.2012.01.008 [本文引用: 1]
基于时空特性和灰色残差的交通故障数据诊断与修复
[J].
Traffic fault data diagnosis and repair based on temporal and spatial characteristics and grey residual
[J].
基于时空相关性的交通流故障数据修复方法
[J].
Traffic flow fault data repair method based on spatio-temporal correlation
[J].
基于自注意力机制与图自编码器的路网交通流数据修复模型
[J].
Road network traffic flow data restoration model based on self-attention mechanism and graph autoencoder
[J].
基于时空模型的交通流故障数据修正方法
[J].DOI:10.3969/j.issn.1671-1637.2015.06.012 [本文引用: 1]
Traffic flow fault data correction method based on spatio-temporal model
[J].DOI:10.3969/j.issn.1671-1637.2015.06.012 [本文引用: 1]
T-GCN: a temporal graph convolutional network for traffic prediction
[J].
Deep learning on graphs: a survey
[J].
基于改进贝叶斯神经网络的光伏出力概率预测
[J].
Forecast of photovoltaic output probability based on improved Bayesian neural network
[J].
基于图卷积网络的路网短时交通流预测研究
[J].
Research on short-term traffic flow prediction of road network based on graph convolution network
[J].
考虑时空影响下的图卷积网络短时交通流预测
[J].DOI:10.3778/j.issn.1002-8331.2006-0175 [本文引用: 1]
Short-term traffic flow prediction of graph convolutional network considering the influence of time and space
[J].DOI:10.3778/j.issn.1002-8331.2006-0175 [本文引用: 1]
基于图卷积神经网络的城市交通态势预测算法
[J].
Urban traffic situation prediction algorithm based on graph convolution neural network
[J].
Geometric deep learning: going beyond Euclidean data
[J].DOI:10.1109/MSP.2017.2693418 [本文引用: 1]